Allowing for never and episodic consumers when correcting for error in food record measurements of dietary intake

Abstract

Food records, including 24-hour recalls and diet diaries, are considered to provide generally superior measures of long-term dietary intake relative to questionnaire-based methods. Despite the expense of processing food records, they are increasingly used as the main dietary measurement in nutritional epidemiology, in particular in sub-studies nested within prospective cohorts. Food records are, however, subject to excess reports of zero intake. Measurement error is a serious problem in nutritional epidemiology because of the lack of gold standard measurements and results in biased estimated diet–disease associations. In this paper, a 3-part measurement error model, which we call the never and episodic consumers (NEC) model, is outlined for food records. It allows for both real zeros, due to never consumers, and excess zeros, due to episodic consumers (EC). Repeated measurements are required for some study participants to fit the model. Simulation studies are used to compare the results from using the proposed model to correct for measurement error with the results from 3 alternative approaches: a crude approach using the mean of repeated food record measurements as the exposure, a linear regression calibration (RC) approach, and an EC model which does not allow real zeros. The crude approach results in badly attenuated odds ratio estimates, except in the unlikely situation in which a large number of repeat measurements is available for all participants. Where repeat measurements are available for all participants, the 3 correction methods perform equally well. However, when only a subset of the study population has repeat measurements, the NEC model appears to provide the best method for correcting for measurement error, with the 2 alternative correction methods, in particular the linear RC approach, resulting in greater bias and loss of coverage. The NEC model is extended to include adjustment for measurements from food frequency questionnaires, enabling better estimation of the proportion of never consumers when the number of repeat measurements is small. The methods are applied to 7-day diary measurements of alcohol intake in the EPIC-Norfolk study.

1. INTRODUCTION

1.1. Measuring dietary intake

In nutritional epidemiology, the exposure of interest is typically the long-term average daily intake of a nutrient, food, or food group (Willett, 1998). The main method of assessing dietary intake in large prospective studies is the food frequency questionnaire (FFQ), on which participants report their habitual frequency of intake of a predefined list of food items, usually over the past year. FFQs are a relatively inexpensive measurement instrument but are subject to errors due to the difficulty of translating frequencies into absolute measures, omission of foods from the questionnaire, difficulty of recall, and person-specific errors (Willett, 1998), (Kristal and others, 2005). Some large cohort studies have asked participants, often a subset of the study population, to provide more detailed information about dietary intake using food records (Bingham and others, 2001), (Riboli, 2001), (Dahm and others, 2010), (Thompson and others, 2008). Food records include 24-hour recalls, in which individuals recall intake on the previous day, and diet diaries, in which participants record intake over a few days (Willett, 1998). Food records contain detailed portion size information and do not rely on long-term recall or restrict participants to a prespecified list of items.

Error in measures of dietary intake results in biased estimates of diet–disease associations (Willett, 1998), (Carroll and others, 2006). The lack of any gold standard measurement for most nutrients and all foods means that it is difficult to assess the nature of error in dietary measurements. However, for the few nutrients for which a biomarker exists, food record measurements have been found to be more highly correlated with the objective biological measures than FFQ measurements (Kipnis and others, 2001), (Kipnis and others, 2002), (Kipnis and others, 2003), (Schatzkin and others, 2003), (Day and others, 2001). Food records are expensive to process and are not yet, to our knowledge, fully available in any large prospective cohort study. However, they are used as the main dietary measurement in case–control studies nested within cohorts, and some studies have observed statistically significant diet–disease associations using diet diaries but not FFQs (Bingham and others, 2003), (Dahm and others, 2010), (Freedman and others, 2006).

The short-term nature of food records can result in excess reports of zero intake for foods which are not consumed on a daily or even weekly basis. These “episodically consumed” foods include alcohol, fish, and certain vegetables. However, there are also some foods which some people never consume or spend periods of many years without consuming. A measurement error modeling and correction procedure allowing for both never consumers and excess zeros has not been previously outlined in detail or compared with alternative approaches and these are the contributions of this paper.

1.2. Correcting for measurement error

Let T_i and R_ij denote true food intake and the food record measurement, respectively, for individual i on the jth measurement occasion. The diet–disease association is assumed linear on the appropriate scale for the outcome type, and β denotes the true association, for example, the log odds ratio (OR). Regression calibration (RC) estimates β by replacing T_i with E(T_i|R_ij) in the diet–disease model (Carroll and others, 2006). The expectation E(T_i|R_ij) is typically found by assuming a linear relationship between true and observed intake (Rosner and others, 1989): T_i = λ₀ + λ₁R_ij + e_i. This model can be fitted provided an additional food record measurement is available for at least a subset of individuals, under the crucial assumption that food record measurements are subject only to random within-person variability, that is, R_ij = T_i + ϵ_ij, where ϵ_ij is a random term with mean 0.

When food record measurements are subject to excess reports of zero intake, the linear association between T_i and R_ij no longer holds. Tooze and others (2006) developed a 2-part model for error in 24-hour recall measurements, with the aim of estimating the distribution of usual intake of episodically consumed foods in dietary surveillance studies. We refer to this as the episodic consumers (EC) model. A review of methods for estimating usual intake of episodically consumed foods is given by Dodd and others (2006). Kipnis and others (2009) extended the EC model for use in RC to correct for the effects of measurement error in 24-hour recalls on diet–disease associations.

1.3. Outline

The EC model of Tooze and others (2006) and Kipnis and others (2009) makes the assumption that all individuals in the surveillance population or the epidemiologic cohort are consumers, to some degree, of the food in question. The first aim is to extend the EC model to accommodate never consumers. The resulting 3-part model is called the never and episodic consumers (NEC) model and is outlined in Section 2. Kipnis and others (2009) suggested the extension of their model in this way in their discussion. In Section 3, the NEC model is fitted to 7-day diet diary measurements of alcohol intake in the EPIC-Norfolk study. We use simulation studies in Section 4 to assess how well the NEC model can be fitted using different numbers of repeat measurements, how successful it is in allowing correction for measurement error in diet–disease association studies, and what advantages, if any, it offers over alternative approaches. In Section 5, we outline an extension of the NEC model to incorporate FFQ measurements. We conclude with a discussion in Section 6.

2. THE NEC MODEL

It is assumed that never consumers will never report nonzero intake, that is, Pr(R_ij = 0|T_i = 0) = 1. We let H(γ₀) be the probability of being a consumer, where H(x) = exp(x)/(1 + exp(x)) and define a binary effect u_0i which indicates whether or not individual i is a consumer, such that

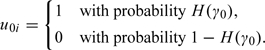(2.1)

Conditionally on consumer status, the probability of reporting nonzero intake at time j is modeled as

(2.2)

Conditionally on reporting nonzero intake, the error in R_ij is modeled as

(2.3)

where u_i = {u_0i,u_1i,u_2i} and (u_1i,u_2i) are random effects independent of u_0i with a bivariate normal distribution (Olsen and Schafer, 2001) with means 0, variances σ_u1² and σ_u2², respectively, and correlation ρ. The errors ϵ_ij are assumed to be independently normally distributed with mean 0 and variance σ_ϵ² and independent of u_i. The set of model parameters is θ = {γ₀,γ₁,γ₂,σ_u1²,σ_u2²,ρ,σ_ϵ²}. The random effects u_i represent information about true intake T_i, and we assume that the observed measurements R_ij are unbiased estimates of T_i, so

(2.4)

The NEC model defined by (2.1–2.3) can be fitted by maximum likelihood provided at least a subset of the population has repeat measurements. Suppose that the ith individual in the study population has J_i observed measurements and denote the set of measurements for individual i by R_i = {R_i1,…,R_iJi}. For consumers, the joint conditional distribution of R_i given u_i is

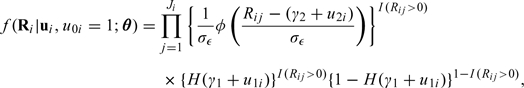(2.5)

where φ(·) denotes the probability density function for the standard normal distribution and I(R_ij > 0) is an indicator taking value 1 if R_ij > 0 and value 0 otherwise. It follows that the joint distribution of R_i given u_i is

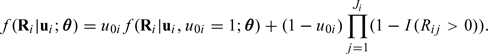(2.6)

The joint distribution of R_i is therefore

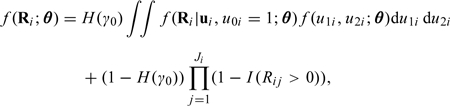(2.7)

where f(u_1i,u_2i;θ) denotes the probability density function of the bivariate normal distribution for (u_1i,u_2i). The full likelihood is L(θ) = ∏_if(R_i;θ).

2.1. Fitted values for use in RC

To correct for measurement error using RC, we need to find the fitted values from the NEC model, 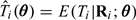. Using (2.4), we have

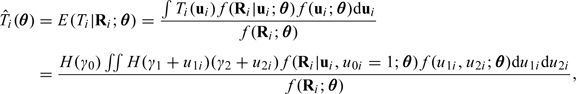(2.8)

where f(u_i;θ) is the joint distribution of u_i. The fitted values are estimated by first obtaining the maximum likelihood estimates for the model parameters, 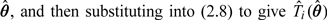(Kipnis and others, 2009). Kipnis and others (2009) also allowed for a transformation g(T_i) to be used in the diet–disease model instead of T_i and (2.8) can be extended to calculate E(g(T_i)|R_i;θ). The NEC model can be easily extended to include covariates in all 3 parts, giving conditional fitted values. For use in RC any covariates in the diet–disease model should be included.

2.2. Using transformed R_ij in the NEC model

Here, we extend the NEC model to allow the nonzero R_ij to be normally distributed on a transformed scale. This extension has been previously suggested by Tooze and others (2006) and Kipnis and others (2009) in their descriptions of the EC model. Suppose that there exists a Box–Cox transformation (Box and Cox, 1964) g(x,λ) = (x^λ − 1)/λ, where λ = 0 indicates the log transformation, such that transformed measurements R_ij^* = g(R_ij,λ) are normally distributed for R_ij > 0. The NEC model is now applied to the transformed measurements by replacing the first R_ij term in (2.3) by R_ij^*. For consumers, the joint conditional distribution of R_i^* = {R_i1^*,…,R_iJ^*} given u_i, f(R_i^*|u_i,u_0i = 1;θ), is as in (2.5), but with R_ij^* in place of R_ij in the function φ(·) only. The unconditional joint distribution f(R_i^*;θ) follows as before.

To calculate the fitted values, we maintain the assumption that the R_ij are unbiased for T_i on the untransformed scale, giving

(2.9)

Using a second-order Taylor expansion, the expectation E(g ^{− 1}(R_ij^*)|u_i,R_ij > 0;θ,λ) can be approximated by

(2.10)

The fitted values are

(2.11)

The nonzero R_ij^* in fact have a truncated normal distribution with R_ij^* ≥ − 1/λ because R_ij ≥ 0. Allowing R_ij^* < − 1/λ implies that γ₂ + u_2i can be negative, presenting difficulties in the approximation in (2.10). In (2.11), therefore, it is appropriate to integrate over only the values of u_2i satisfying u_2i > − γ₂ − 1/λ. Integrals in the likelihood and in calculation of fitted values have to be found numerically; we used Gauss–Hermite quadrature.

3. APPLICATION: 7-DAY DIARY MEASUREMENTS OF ALCOHOL INTAKE

EPIC-Norfolk is a cohort of 25 639 individuals recruited during 1993–1997 from the population of individuals aged 45–75 years in Norfolk, UK (Day and others, 1999). During follow-up, study participants attended health checks at which dietary intake was assessed using 7-day diet diaries and FFQs (Bingham and others, 2001). Many 7-day diaries from 2 health checks have now been processed, from which measures of average daily alcohol intake (grams/day) are available. 17 971 individuals have at least one measurement and 2562 (15%) have 2. Of those with 2 measurements, 531 (21%) reported zero alcohol intake on both occasions, while 510 (21%) reported zero alcohol intake on one occasion only. Nonzero measurements of alcohol intake are approximately normally distributed after a Box–Cox transformation with λ = 0.25. The NEC model was fitted to the transformed 7-day diary measurements of alcohol intake using all the data. Parameter estimates are shown in Table 1, and it is estimated that 12% of individuals are never consumers of alcohol.

Table 1.

Parameter estimates (standard error [SE]) from fitting the NEC model using maximum likelihood to one or two 7-day diary measurements of alcohol intake in EPIC-Norfolk

Parameter	Estimate (SE)
γ1	2.13 (0.09)
γ2	2.67 (0.06)
σu12	4.13 (0.77)
σu22	4.45 (0.15)
ρ	0.91 (0.01)
σϵ2	1.17 (0.04)
H(γ0)	0.88 (0.02)

4. SIMULATION STUDY

We use a simulation study to investigate how well we can estimate the parameters of the NEC model using J repeat measurements for each individual, for values J = 2,4,10, and whether estimation of fitted values using the NEC model enables us to make successful corrections for measurement error in diet–disease association models. We use logistic models with true ORs of 1.2, 1.5, and 2. We also compare the corrected ORs found using the NEC model with those found using 3 alternative approaches: a crude analysis in which T_i is replaced by the mean of the observed measurements in the diet–disease model; replacing T_i with the fitted values from a linear RC model; and replacing T_i with the fitted values from the EC model. The EC model (Tooze and others, 2006), (, Kipnis:2009) is equivalent to parts (2.2) and (2.3) of the NEC model, under the assumption that u_0i = 1 for all i. Implementation of the crude and linear RC methods is outlined in Appendix A of the supplementary material available at Biostatistics online.

We base our simulation study on the results from fitting the NEC model to the EPIC-Norfolk 7-day diary data on alcohol intake (Table 1). The proportion of never consumers is also increased to 25%. In practice, not all individuals in the study population will have repeat measurements, so we also investigate the case where 15% of the study population has J repeat measurements and the rest only have one.

Additional simulations were performed to further investigate the performance of the NEC model. The sample size for each simulated data set was increased from 1000 to 5000; we changed σ_u1² to be larger and smaller than that in Table 1 (σ_u1² = 2,8); and we increased σ_ϵ² to 4. The effects on results of falsely assuming that the u_1i are normally distributed were investigated by repeating the simulations using heavy tailed and skew distributions for u_1i. Finally, we investigated the effect on results of misspecifying the Box–Cox transformation parameter λ. Full details of the simulation study are in Appendix B of the supplementary material available at Biostatistics online.

4.1. Parameter estimation

Table 2 shows the mean estimate of each NEC model parameter across 500 simulated data sets when H(γ₀) = 0.88 or 0.75 and when all or only a subset of individuals have J = 2,4,10 repeat measurements. Some parameter estimates are biased when the NEC model is fitted using 2 repeat measurements (J = 2), with H(γ₀) and σ_u1² both biased upward. When J = 4, there is little bias in the parameter estimates, except for σ_u1², whose bias is substantially less than when J = 2. The empirical standard deviation of the estimates is lowered by increasing the number of repeats to J = 10, though there is little to be gained in terms of reducing bias, except in the estimation of σ_u1². When there is a higher proportion of never consumers, the bias in parameter estimates when J = 2 becomes more severe. When only 15% of individuals have a complete set of repeat measurements, a similar pattern of results is seen, with increased empirical standard deviations for parameter estimates.

Table 2.

Mean (empirical standard deviation) of maximum likelihood estimates of parameters from the NEC model across 500 simulated data sets using J = 2, 4, 10 repeat measurements, where 100% or 15% of individuals have a complete set of J measurements

Parameter	True value	Complete repeats			Incomplete repeats
		J = 2	J = 4	J = 10	J = 2	J = 4	J = 10
12% never consumers
γ1	2.13	2.01 (0.21)	2.14 (0.11)	2.13 (0.08)	2.07 (0.37)	2.16 (0.23)	2.15 (0.16)
γ2	2.67	2.51 (0.17)	2.67 (0.09)	2.67 (0.07)	2.54 (0.22)	2.67 (0.15)	2.69 (0.11)
σu12	4.13	7.41 (3.11)	4.39 (0.75)	4.16 (0.38)	8.16 (4.88)	4.89 (2.27)	4.18 (0.93)
σu22	4.45	4.72 (0.43)	4.45 (0.29)	4.44 (0.24)	4.65 (0.55)	4.43 (0.43)	4.39 (0.33)
ρ	0.91	0.87 (0.03)	0.90 (0.02)	0.90 (0.01)	0.85 (0.03)	0.88 (0.05)	0.89 (0.03)
σϵ2	1.17	1.17 (0.07)	1.17 (0.04)	1.16 (0.02)	1.16 (0.17)	1.16 (0.10)	1.17 (0.05)
H(γ0)	0.88	0.94 (0.05)	0.88 (0.02)	0.88 (0.01)	0.93 (0.07)	0.88 (0.04)	0.87 (0.02)
25% never consumers
γ1	2.13	1.85 (0.43)	2.13 (0.12)	2.13 (0.09)	1.81 (0.60)	2.14 (0.29)	2.15 (0.18)
γ2	2.67	2.43 (0.28)	2.66 (0.10)	2.67 (0.08)	2.42 (0.35)	2.66 (0.19)	2.68 (0.12)
σu12	4.13	9.24 (6.12)	4.40 (0.84)	4.16 (0.41)	11.56 (9.69)	5.17 (3.27)	4.20 (1.03)
σu22	4.45	4.85 (0.59)	4.46 (0.32)	4.45 (0.27)	4.85 (0.75)	4.46 (0.50)	4.40 (0.38)
ρ	0.91	0.87 (0.03)	0.90 (0.02)	0.90 (0.01)	0.85 (0.05)	0.88 (0.04)	0.89 (0.02)
σϵ2	1.17	1.17 (0.08)	1.17 (0.04)	1.17 (0.02)	1.16 (0.19)	1.17 (0.11)	1.17 (0.06)
H(γ0)	0.75	0.83 (0.09)	0.75 (0.02)	0.75 (0.01)	0.85 (0.11)	0.76 (0.05)	0.75 (0.03)

Tables 1–3 in the supplementary material available at Biostatistics online show parameter estimates from the NEC model under the additional simulations. As σ_u1² increases there is greater variability in the estimates, though the results are not strongly affected. When σ_ϵ² increases there is also a small increase in the empirical standard deviations. A false assumption of normality of the random effects u_1i results in some bias in NEC parameter estimates, especially in σ_u1² which is underestimated as J increases when the u_1i have a heavy tailed or skew distribution. The estimated proportion of consumers, H(γ₀), is slightly underestimated as J increases when the u_1i have a heavy tailed distribution but practically unaffected when the u_1i have a skew distribution. When λ is misspecified, the estimated proportion of consumers is more severely biased upward when there are a small number of repeats than when λ is correctly specified. All maximum likelihood estimations converged, with the exception of 3 simulations when the value of Box–Cox parameter λ was misspecified in the analysis using 2 repeats in the incomplete data situation.

Table 3.

Mean (empirical standard deviation [SD]) of log OR estimates and coverage of 95% confidence intervals across 500 simulated data sets using different correction methods when there are J = 2, 4, 10 repeat measurements per person (for 100% or 15% of individuals) and 25% of individuals are {never consumers}

True β		Method
		Using Ti	NEC model	Crude	Linear RC	EC model
Complete repeats
J = 2
0.182	Mean (SD)	0.181 (0.070)	0.183 (0.076)	0.155 (0.065)	0.179 (0.075)	0.181 (0.076)
	Coverage	0.95	0.96	0.95	0.96	0.96
0.405	Mean (SD)	0.409 (0.065)	0.411 (0.071)	0.349 (0.060)	0.404 (0.071)	0.406 (0.070)
	Coverage	0.93	0.93	0.78	0.92	0.93
0.693	Mean (SD)	0.695 (0.065)	0.677 (0.069)	0.585 (0.060)	0.677 (0.070)	0.671 (0.068)
	Coverage	0.97	0.94	0.53	0.94	0.93
J = 4
0.182	Mean (SD)	0.181 (0.070)	0.182 (0.073)	0.167 (0.067)	0.180 (0.072)	0.179 (0.072)
	Coverage	0.95	0.95	0.96	0.95	0.95
0.405	Mean (SD)	0.409 (0.065)	0.411 (0.066)	0.376 (0.061)	0.406 (0.066)	0.403 (0.065)
	Coverage	0.93	0.94	0.90	0.94	0.94
0.693	Mean (SD)	0.695 (0.065)	0.687 (0.067)	0.635 (0.062)	0.685 (0.067)	0.675 (0.065)
	Coverage	0.97	0.96	0.85	0.95	0.94
J = 10
0.182	Mean (SD)	0.181 (0.070)	0.181 (0.070)	0.175 (0.068)	0.181 (0.070)	0.179 (0.069)
	Coverage	0.95	0.95	0.96	0.95	0.95
0.405	Mean (SD)	0.409 (0.065)	0.409 (0.066)	0.395 (0.063)	0.407 (0.066)	0.403 (0.065)
	Coverage	0.93	0.93	0.92	0.93	0.93
0.693	Mean (SD)	0.695 (0.065)	0.691 (0.066)	0.670 (0.064)	0.691 (0.066)	0.683 (0.065)
	Coverage	0.97	0.97	0.92	0.96	0.95
Incomplete repeats
J = 2
0.182	Mean (SD)	0.181 (0.070)	0.185 (0.083)	0.138 (0.061)	0.195 (0.104)	0.184 (0.082)
	Coverage	0.95	0.96	0.94	0.91	0.96
0.405	Mean (SD)	0.409 (0.065)	0.413 (0.076)	0.310 (0.055)	0.438 (0.144)	0.410 (0.075)
	Coverage	0.93	0.91	0.52	0.70	0.91
0.693	Mean (SD)	0.695 (0.065)	0.669 (0.079)	0.517 (0.058)	0.728 (0.221)	0.666 (0.079)
	Coverage	0.97	0.89	0.16	0.52	0.88
J = 4
0.182	Mean (SD)	0.181 (0.070)	0.186 (0.083)	0.139 (0.062)	0.193 (0.100)	0.180 (0.080)
	Coverage	0.95	0.95	0.94	0.90	0.95
0.405	Mean (SD)	0.409 (0.065)	0.415 (0.073)	0.312 (0.055)	0.433 (0.134)	0.402 (0.071)
	Coverage	0.93	0.93	0.55	0.72	0.92
0.693	Mean (SD)	0.695 (0.065)	0.673 (0.074)	0.522 (0.058)	0.721 (0.203)	0.656 (0.072)
	Coverage	0.97	0.92	0.17	0.57	0.88
J = 10
0.182	Mean (SD)	0.181 (0.070)	0.186 (0.081)	0.140 (0.062)	0.191 (0.096)	0.177 (0.077)
	Coverage	0.95	0.96	0.94	0.90	0.96
0.405	Mean (SD)	0.409 (0.065)	0.416 (0.073)	0.314 (0.056)	0.430 (0.130)	0.396 (0.069)
	Coverage	0.93	0.92	0.55	0.72	0.93
0.693	Mean (SD)	0.695 (0.065)	0.675 (0.071)	0.525 (0.059)	0.714 (0.190)	0.647 (0.069)
	Coverage	0.97	0.93	0.17	0.60	0.87

4.2. Correcting for measurement error

Table 3 shows the mean, empirical standard deviation, and coverage of log OR estimates associated with a 10 grams/day increase in T_i found using fitted values from the NEC model, and under the 3 alternative approaches when H(γ₀) = 0.75. The corresponding results when H(γ₀) = 0.88 are shown in Table 4 of the supplementary material available at Biostatistics online. Log OR estimates found using the NEC model are subject to minor attenuation as the true log OR increases, which is alleviated as J increases. The attenuation is greater when only a subset of individuals have a complete set of repeat measurements. There is a corresponding slight loss of coverage in estimates. The crude approach results in attenuated log OR estimates, with the attenuation more severe as the true log OR increases and when fewer repeat measurements are used. There is a considerable loss of coverage when J = 2. This method performs particularly badly when only 15% of the study population has repeat measurements because the data are dominated by those with only one measurement.

Table 4.

Mean (empirical standard deviation) of maximum likelihood estimates of parameters from the NEC model across 500 simulated data sets using J = 2,4,10 repeat measurements when the true proportion of never consumers is 87%: With and without FFQ adjustment

Parameter	Without FFQ adjustment			With FFQ adjustment
	J = 2	J = 4	J = 10	J = 2	J = 4	J = 10
γ1	1.87 (0.19)	2.03 (0.10)	2.06 (0.08)	0.14 (0.09)	0.13 (0.06)	0.13 (0.04)
γ2	2.58 (0.14)	2.78 (0.08)	2.84 (0.07)	0.92 (0.08)	0.92 (0.06)	0.92 (0.05)
σu12	7.19 (2.26)	3.67 (0.59)	3.17 (0.27)	0.14 (0.16)	0.07(0.06)	0.04 (0.02)
σu22	4.17 (0.35)	3.79 (0.24)	3.66 (0.18)	0.61 (0.07)	0.61 (0.05)	0.61 (0.04)
ρ	0.88 (0.03)	0.91 (0.01)	0.92 (0.01)	0.41 (0.50)	0.61 (0.32)	0.72 (0.19)
σϵ2	1.28 (0.07)	1.28 (0.04)	1.28 (0.02)	1.28 (0.07)	1.28 (0.04)	1.28 (0.02)
ξ1	-	-	-	0.91 (0.06)	0.90 (0.04)	0.90 (0.02)
ξ2	-	-	-	0.88 (0.02)	0.88 (0.02)	0.88 (0.02)
H(γ0)	0.96 (0.04)	0.88 (0.01)	0.88 (0.01)	0.38 (0.04)	0.37 (0.04)	0.37 (0.03)
Proportion of consumers	0.96 (0.04)	0.88 (0.01)	0.88 (0.01)	0.87 (0.01)	0.87 (0.01)	0.87 (0.01)

Surprisingly, the linear RC correction for measurement error works well when all individuals in the study population have a complete set of repeat measurements. An explanation for this is outlined in Appendix C of the supplementary material available at Biostatistics online. However, in the more realistic situation in which only a subset of the study population has a complete set of repeat measurements, linear RC results in log OR estimates which are biased away from zero, resulting in a loss of coverage as the true log OR increases. The bias is only slightly moderated as the number of repeat measurements per person in the subset of the data with complete measurements increases. However, the bias is reduced when the sample size increases from 1000 to 5000 (Table 5, supplementary material available at Biostatistics online), though there is in fact a small decrease in coverage. Alongside the bias, standard errors for parameter estimates are underestimated under this method.

Table 5.

Mean (empirical standard deviation [SD]) of log OR estimates and coverage of 95% confidence intervals across 500 simulated data sets using the unadjusted and FFQ-adjusted NEC model when there are J = 2,4,10 repeat measurements per person

True β		Method
		Using Ti	Without FFQ adjustment	With FFQ adjustment
Complete repeats
J = 2
0.182	Mean (SD)	0.177 (0.076)	0.180 (0.084)	0.180 (0.081)
	Coverage	0.96	0.96	0.96
0.405	Mean (SD)	0.410 (0.064)	0.410 (0.071)	0.413 (0.069)
	Coverage	0.95	0.94	0.94
0.693	Mean (SD)	0.693 (0.067)	0.671 (0.072)	0.684 (0.070)
	Coverage	0.95	0.91	0.94
J = 4
0.182	Mean (SD)	0.177 (0.076)	0.180 (0.078)	0.180 (0.081)
	Coverage	0.96	0.97	0.96
0.405	Mean (SD)	0.410 (0.064)	0.412 (0.068)	0.413 (0.069)
	Coverage	0.95	0.94	0.94
0.693	Mean (SD)	0.693 (0.067)	0.684 (0.069)	0.684 (0.069)
	Coverage	0.95	0.95	0.95
J = 10
0.182	Mean (SD)	0.177 (0.076)	0.179 (0.077)	0.178 (0.077)
	Coverage	0.96	0.96	0.97
0.405	Mean (SD)	0.410 (0.064)	0.413 (0.065)	0.412 (0.066)
	Coverage	0.95	0.95	0.94
0.693	Mean (SD)	0.693 (0.067)	0.690 (0.068)	0.690 (0.068)
	Coverage	0.95	0.95	0.94

The EC model also gives estimates which are very close to those found under the NEC model when all individuals in the study population have repeat measurements. However, when only a subset of the study population has a complete set of repeat measurements, the EC model results in log OR estimates which have more conservative bias and there is greater loss of coverage as the true log OR increases.

Our additional analyses (Tables 6–8, supplementary materials available at Biostatistics online) show that σ_u1² does not have a strong effect on the success of the measurement error correction. When σ_ϵ² is large the bias in estimates is greater, there is greater loss of coverage under the NEC and EC models, and the crude method performs very badly. The comparisons between the methods are not materially altered by changes in these parameters. Results are also robust to departures from normality in the distribution of the u_1i and to misspecification of the Box–Cox parameter λ (Tables 9–11, supplementary material available at Biostatistics online).

5. USING ADDITIONAL DIETARY MEASUREMENTS

Kipnis and others (2009) used FFQ measurements as a covariate in the EC model to improve the precision of parameter estimates. Here, we extend this to the NEC model. The lowest frequency of intake which can be reported on an FFQ is typically “never or less than once a month,” to which a measurement of zero is usually attributed. A comparison of FFQs from 2 time points in EPIC-Norfolk (11 824 individuals) found that 14% reported zero alcohol intake on both FFQs, while 10% reported zero intake on one but not the other. Of those 17 356 who completed both FFQ and 7-day diary at the first health check, 17% reported zero intake on both, 14% reported zero intake on the diary but not the FFQ, and 4% reported zero intake on the FFQ but not the diary. In light of these observations, we consider it inappropriate to use FFQ measurements of zero as implying zero intake, but we do assume that a positive FFQ measurement implies a consumer.

Let 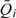denote the mean of the available FFQ measurements for individual i and 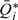denote the mean after an appropriate transformation, which takes value zero when all the FFQ measurements are zero. For generality, we let X_i denote a vector of other covariates. The FFQ- and covariate-adjusted NEC model is

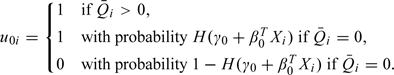(5.1)

(5.2)

(5.3)

FFQ measurements are assumed uncorrelated with ϵ_ij, and the random effects (u_1i,u_2i) are independent of u_0i and have a bivariate normal distribution conditional on 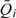and X_i. Estimation of model parameters is via the conditional joint distribution 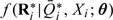, obtained as in Section (2.2).

To investigate the potential advantages of adjustment for FFQ measurements, we performed a simulation study in which data is generated according to the FFQ-adjusted model and then fitted with and without FFQ-adjustment. Full details are given in Appendix D of the supplementary material available at Biostatistics online. We compare the model parameter estimates and corrected ORs obtained using the unadjusted and FFQ-adjusted NEC model. The results are shown in Tables 4 and 5. When using J = 2 repeat measurements per individual, 8 out of 500 simulations failed to converge, and 2 out of 500 failed to converge when J = 4; these are omitted from the results below. There was also uncertainty as to whether 69 out of 492 of the remaining simulations fully converged when J = 2 and 29 out of 498 when J = 4 and 5 out of 500 when J = 10; in these cases it appears that all parameters were correctly estimated except for σ_u1² for which the estimate was close to zero. In Table 4, we are primarily interested in the ability of the model to estimate the proportion of never consumers. With FFQ-adjustment the proportion of consumers is not overestimated when using only 2 repeat measurements per individual, as it is in the unadjusted model. The estimated ORs from the unadjusted and FFQ-adjusted models are similar (Table 5).

6. DISCUSSION

Until recently (Tooze and others, 2006), (, Kipnis:2009), there has been a gap in the statistical methodology for applying RC when there are zeros in the observed dietary measurements. This paper extends the earlier work to allow for a distinction between “real” zeros, due to never consumers, and excess zeros, which occur as a limitation of the dietary assessment instrument. We focused on use of the NEC model in nutritional epidemiological studies, where it is desirable to make corrections for measurement error. The model is relevant for the case–control studies nested within prospective cohorts which are beginning to use food records instead of FFQs as the main dietary measurement. In the future, some prospective studies will be able to perform full cohort analyses using food record measurements.

Our simulation studies showed that use of the NEC model, the EC model, or, unexpectedly, the standard linear RC model to make corrections for measurement error in diet–disease associations gives very similar results when all individuals in the study population have more than one food record measurement. Using only 2 repeat measurements results in underestimation of the proportion of never consumers in the NEC model. The greater the number of repeat measurements, the greater the ability of the model to distinguish never consumers from episodic consumers. The shorter the food record assessment period, the greater the problem of excess zeros will be.

Repeat measurements are usually available for only a small subset of the study population. In practice, therefore, the simulation study results relating to this situation are of most interest. In this case, the NEC model performed better than the alternative methods in terms of both bias and coverage of corrected estimated diet–disease associations. There is some conservative bias and modest loss of coverage in the estimates from the NEC model when the number of repeat measurements in the subset is small (e.g. 2) and as the size of the association gets large. The EC model has marginally greater conservative bias and greater loss of coverage, though the differences between the 2 approaches are fairly small. In this situation, using a linear RC model can result in biased estimated diet–disease associations in finite samples and large loss of coverage.

Additional information about dietary intake from FFQ measurements can be used to improve estimation of the proportion of consumers in an adjusted NEC model when the number of repeat measurements J is small because measurements of zero from the FFQ are very informative about whether an individual is a never consumer. The trade-off is that FFQ-adjusted models may be more likely to fail to converge when J is small. Additional simulations (not shown) using covariate-adjustment in all parts of the model suggest the same problem may occur and that estimates for parameters associated with being a never consumer may be unstable when J is small.

There is evidence that food record measurements can be subject to systematic error. We show in Appendix E of the supplementary material available at Biostatistics online, how this can be accommodated by the NEC model, though systematic errors would have to be investigated using sensitivity analyses. It is not clear that adjustment for FFQ in the NEC model allows for excess zeros in the FFQ measurements. Areas for further work include NEC models for both FFQs and food records with correlated random effects, and incorporation of biomarker measurements. An important extension will be to diet–disease models containing several dietary variables measured with error, one or more of which may be subject to excess zeros.

In summary, it is recommended that the NEC model be used to perform corrections for the effects of error in food record measurements where it is suspected that a substantial proportion of the study population may be never consumers, and when only a subset of the study population has repeat dietary measurements, using FFQ adjustment where possible. The EC model performs almost as well in many situations, and in some situations the standard linear RC method also performs well.

SUPPLEMENTARY MATERIALS

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

Medical Research Council (U.1052.00.006) to Ian White.