Integrative analysis and variable selection with multiple high-dimensional data sets

Abstract

In high-throughput -omics studies, markers identified from analysis of single data sets often suffer from a lack of reproducibility because of sample limitation. A cost-effective remedy is to pool data from multiple comparable studies and conduct integrative analysis. Integrative analysis of multiple -omics data sets is challenging because of the high dimensionality of data and heterogeneity among studies. In this article, for marker selection in integrative analysis of data from multiple heterogeneous studies, we propose a 2-norm group bridge penalization approach. This approach can effectively identify markers with consistent effects across multiple studies and accommodate the heterogeneity among studies. We propose an efficient computational algorithm and establish the asymptotic consistency property. Simulations and applications in cancer profiling studies show satisfactory performance of the proposed approach.

1. INTRODUCTION

The development of -omics technologies makes it possible to survey the whole genome and identify markers associated with the development and progression of common diseases. In this article, we focus on microarray gene expression profiling studies and note that the proposed approach is also applicable to other high-throughput profiling studies. In gene profiling studies, markers identified from analysis of single data sets often suffer from a lack of reproducibility (Choi and others, 2007, Shen and others, 2004, Ma and Huang, 2009). Among the many possible causes, the most important one is perhaps the relatively small sample sizes and hence lack of power of individual studies. A typical cancer microarray study measures the expressions of 10^{3 − 4} genes on 10^{1 − 3} samples. An ideal solution is to conduct large-scale studies, which are extremely expensive and time-consuming. For many biomedical problems, there are multiple independent and comparable studies (Knudsen, 2005). A cost-effective remedy to the small sample size problem is to pool and analyze data from multiple studies.

Available multi-data sets approaches include meta-analysis and integrative analysis approaches. Meta-analysis is conducted by pooling and analyzing “summary statistics” from multiple studies (Guerra and Goldstein, 2009). In contrast, integrative analysis approaches pool and analyze “raw data” from multiple studies. Published studies have shown that integrative analysis can be more effective than meta-analysis. A family of integrative analysis approaches developed for microarray data, called “intensity approaches,” search for transformations that make gene expressions comparable across different data sets/platforms (Shabalin and others, 2008). After transformation, multiple data sets are combined and analyzed using single data set methods. Such approaches need to be conducted on a case-by-case basis. In addition, there is no guarantee that the desired transformations always exist. There are also approaches that do not require the direct comparability of measurements from different studies (Shen and others, 2004, Choi and others, 2007, Ma and Huang, 2009).

The goal of this study is to propose a method that can efficiently extract useful information through the analysis of multiple heterogeneous high-dimensional data sets. Multiple data sets inevitably bring along additional complications, including selection of comparable independent data sets, interpretation of analysis results, and utilization of obtained models for prediction. We acknowledge the importance of those issues. However, since they are not the focus of this study, we refer to publications such as Guerra and Goldstein (2009) for established guidelines.

In this article, we investigate integrative analysis of multiple heterogeneous data sets and propose a penalization approach for marker selection. This study has been motivated by the effectiveness of integrative analysis and ineffectiveness of marker selection techniques used in existing studies. It takes advantage of recent development in single data set penalization methods but advances from them by adopting a new penalty function and analyzing multiple heterogeneous data sets. It advances from existing integrative analysis studies by using a more effective marker selection approach with the desired consistency property.

The rest of the article is organized as follows. In Section 2, we describe the data and model setup. In Section 3, we describe marker selection using the 2-norm group bridge approach, propose an efficient computational algorithm and establish the consistency property. In Section 4, we conduct numerical studies, including simulation and analysis of liver and pancreatic cancer microarray studies, to investigate finite-sample performance. The article concludes with discussion in Section 5.

2. INTEGRATIVE ANALYSIS OF MULTIPLE DATA SETS

In this article, we focus on the scenario where multiple studies share the same biological ground, particularly the same set of susceptibility genes. As discussed in Grutzmann and others (2005) and others, it is feasible to carefully evaluate and select studies sharing comparable designs using the MIAME criteria and personal expertize. In addition, for data deposited at NCBI, GEO data sets have been assembled by GEO staff using a collection of biologically and statistically comparable samples. With those selected studies, it is reasonable to expect that they share the same susceptibility genes.

Of note, it is also possible that different studies have different sets of susceptibility genes. We conduct simulation study of such scenario and present results in the Supplementary File of the supplementary material available at Biostatistics online. With multiple studies having different susceptibility genes, pooling and analyzing multiple studies may be inappropriate, as “borrowing strength across studies” for marker identification is no longer possible.

Although we assume that the data sets available for integrative analysis share the same biological features, it is not appropriate to directly pool them for analysis because of certain heterogeneous aspects among them. For example, measurements using different profiling platforms are not directly comparable. Thus, one unit increase in complementary DNA (cDNA) measurement is not directly comparable to one unit increase in Affymetrix measurement. There is no guarantee that cross-platform (study) normalization or transformation always exists. In addition, other risk factors may alter the relationship between markers and outcome variables. For example, for both smokers and nonsmokers, gene NET1 is a marker for lung cancer. However, the strengths of associations (magnitudes of regression coefficients) are different between the 2 groups.

Let M( > 1) be the number of independent studies. For simplicity of notation, assume that the same set of d covariates (gene expressions) are measured in all studies. Let Y¹,…,Y^M be the response variables and x¹,…,x^M be the covariates. For m = 1,…,M, assume that Y^m is associated with x^m via the model Y^m∼φ(β^m′x^m), where β^m is the regression coefficient, β^m′ is the transpose of β^m, and φ is the link function. Although the proposed methods can accommodate different link functions in different studies, we assume the same link function for better interpretability.

To illustrate the basic features of the model setup here, consider 2 independent studies with d( > 2) gene expression measurements. Assume that only the first 2 genes are associated with disease outcomes. Then the regression coefficients may look like β¹ = (0.1,0.2,0,…,0)^′ and β² = (0.05,0.3,0,…,0)^′. The regression coefficients and corresponding models have the following features. First, only the first 2 disease-associated genes have nonzero regression coefficients (i.e. the models are sparse). Thus, marker identification amounts to discriminate genes with nonzero coefficients from those with zero coefficients. This strategy has been commonly adopted in regularized marker selection. Second, as the 2 studies share the same susceptibility genes, the 2 models have the same sparsity structure. Third, to accommodate heterogeneity, the nonzero coefficients of markers are allowed to differ across studies. This strategy shares the same spirit with the fixed-effect model method in Stevens and Doerge (2005).

To be specific, we describe the proposed approach for studies with binary outcomes under logistic regression models. We note that the proposed approach is also applicable to other types of outcomes. In study m( = 1,…,M), Y^m = 1 and 0 denote the presence and absence of disease. We assume the logistic regression model, where 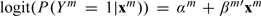Here, α^m is the intercept and β^m is the length d vector of regression coefficient. Assume n_m i.i.d. observations. The log-likelihood is 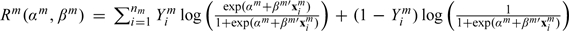Since α^m will not be subject to penalization, for simplicity of notation, we denote 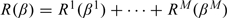as R^m(β^m). Denote R(β) = R¹(β¹) + ⋯ + R^M(β^M), where β = (β¹,…,β^M) is the d×M regression coefficient matrix.

3. PENALIZED ESTIMATION AND MARKER SELECTION

3.1. Two-norm group bridge

Denote β_j^m as the coefficient of covariate j in study m. β_j = (β_j¹,…,β_j^M) is the jth row of β and represents the coefficients of covariate j across M studies. Consider

(3.1)

where λ_n is a data-dependent tuning parameter and J is the penalty function. We propose the 2-norm group bridge penalty

(3.2)

where 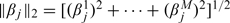and 0 < γ < 1 is the fixed bridge index.

The proposed penalty has been motivated by the following considerations. For a given covariate, we treat its regression coefficients in multiple studies as a “group,” so that we can evaluate its effects in multiple studies. With penalty on the L_γ group norm of the regression coefficients, a group is either selected, which leads to nonzero estimated coefficients in all studies, or not. For a fixed j, the proposed penalty does not force β_j^m to be equal across m, which allows for different strengths of associations in different studies.

When γ = 1, the proposed penalty becomes the group Lasso (GLasso) penalty (Meier and others, 2008). Section 3.4 establishes that the 2-norm group bridge is selection consistent, whereas the GLasso tends to overselect. The proposed penalty is also related to the one in Huang and others (2009). However, the goal of Huang and others (2009) is to conduct both group and within-group selections. In contrast, we aim at identifying a common set of covariates across multiple studies. The within-group selection is undesired. The most significant differences between this study and published ones come from the data structure. Multiple data sets are analyzed in this study, whereas other studies focus on single data sets. In addition, in other studies, the grouping structure comes from dummy variables for single covariates or clusters of covariates. In this study, one group represents the effects of one covariate in multiple studies, and the grouping structure is natural.

3.2. Computational algorithm

To facilitate the proposed computational algorithm, we first establish the following result.

LEMMA 1. Denote η = (1 − γ)/γ. Define where β(λ_n) maximizes the objective function defined in (3.1) if and only if β(λ_n) = argmax_βS(β;λ_n) subject to θ_j ≥ 0(j = 1,…,d).

Lemma 1 can be proved using Proposition 1 of Huang and others (2009). Based on Lemma 1, we propose the following algorithm. For a fixed λ_n,

1. Initialize β(λ_n) as the GLasso estimate;

2. Compute θ_j = (η/τ)^{1/(1 + η)}‖β_j‖₂^{1/(1 + η)} for j = 1,…,d;

3. Compute ;

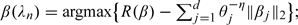4. Repeat Steps 2 and 3 until convergence.

In Theorem 1, we show that with the GLasso estimate as the initial estimate, important covariates are not missed. In Step 3, we transform the bridge-type maximization to a weighted GLasso–type maximization. The iteration continues until the set of nonzero regression coefficients stablize and the L₂-norm of the difference of estimates from 2 consecutive iterations is less than 10 ^{− 3}. In our numerical studies, convergence is achieved within 20 iterations.

We use the coordinate descent algorithm described in Meier and others (2008) to compute the GLasso estimates. An interesting observation is that, for a fixed j and any k≠l, ∂²R(β)/∂β_j^k∂β_j^l = 0. Thus, the Hessian for the coefficients in a single group is a diagonal matrix. With this special form, the maximization does not need to be limited to the “special direction” assumed in Meier and others (2008). The unique form of the objective function makes the coordinate descent algorithm computationally less expensive.

3.3. Tuning parameter selection

The tuning parameter λ_n balances sparsity and goodness of fit. We adopt V-fold cross validation (Zou and Hastie 2005) for tuning parameter selection.

In Section 3.4, we establish the asymptotic rate of λ_n that leads to consistency. As a limitation of this study, we are not able to establish the asymptotic optimality of V-fold cross validation. We have carefully examined published penalization studies and found that this problem has not been satisfactorily solved under comparable settings. We have experimented with several other tuning parameter selection techniques, including Bayesian information criterion (BIC), Akaike information criterion (AIC), and leave-one-out (LOO) cross validation (results omitted). We find that performance of other tuning parameter selection techniques is comparable to or worse than that of V-fold cross validation. We choose V-fold cross validation because of its computational simplicity. Since there is a lack of theoretical justifications, we do not further pursue this issue.

3.4. Asymptotic properties

In the computational algorithm described in Section 3.2, the GLasso estimate is used as the starting value. Covariates not selected by the GLasso will not be selected by the proposed approach. Thus, we first consider properties of the GLasso estimate. We then establish the properties of the estimator computed using the algorithm described in Section 3.2 with the GLasso as the initial estimator.

The GLasso estimate.

The GLasso estimate is defined as

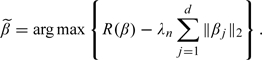With 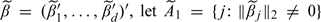be the set of GLasso selected covariates. Define n = ∑_mn_m. For m = 1,…,M and j = 1,…,d, let x_·j^m = (x_1j^m,…,x_nmj^m)^′ be the n_m×1 vector of the jth covariate. For any A⊆{1,…,d}, denote X_A^m = (x_·j^m:j∈A),1 ≤ m ≤ M,andX_A = (X_A^1′,…,X_A^M′)^′. When A = {1,…,d}, we simply write X^m for X_A^m and X for X_A. Define 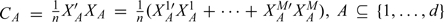Denote the cardinality of A by |A|. Define 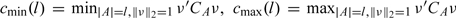where ν∈ℝ^q. Matrix X satisfies the sparse Riesz condition (Zhang and Huang, 2008), or SRC, with rank q and spectrum bounds 0 < c_* < c^* < ∞ if

(3.3)

Since ‖X_Aν‖²/n = ν^′C_Aν, all the eigenvalues of C_A are inside the interval [c_*,c^*] under (3.3) when the size of A is not greater than q. The SRC ensures that the models with dimension lower than q are identifiable. Let ρ_n be the maximum of eigenvalues of matrices X^mX^m′,1 ≤ m ≤ M. Let β₀ be the true value of β. Denote the set of nonzero regression coefficients by A^o = {j:‖β_0j‖₂≠0,1 ≤ j ≤ d}. Let k_n = |A^o| and m_n = d − k_n. Let b_n2 = max{‖β_0j‖₂:j∈A^o} be the largest L₂ norm of the nonzero β_0js. We assume

• (A1) (a) There exists 0 < b₂ < ∞ such that b_n2 < b₂; (b) There exists 0 < C₁ < ∞ such that

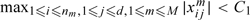
• (A2) There exists 0 < C₂ < ∞ such that with q_n = C₂n²/λ_n², the covariate matrix X satisfies the SRC with rank q_n and spectrum bounds {c_*,c^*} and that k_n ≤ q_n.

Under (A1a), the regression coefficients do not diverge to infinity. This ensures that the models stay stable as n→∞. (A1b) requires bounded covariates. This condition is usually satisfied in practice. Condition (A2) requires that the eigenvalues of all q_n×q_n submatrices of X are bounded away from zero and infinity. This is to ensure that the underlying model is identifiable. Under (A1), there exists 0 < ε₀ < 1/2 such that 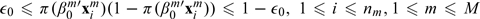where π(u) = exp(u)/(1 + exp(u)).

THEOREM 1 Suppose that (A1) and (A2) hold. Suppose that there exists a constant ρ > 0 such that ρ_n ≤ ρ for all n sufficiently large. (i) Let . Then, with probability one, (ii) If h_n(q_nlogn)^1/2→0, then where h_n = n ^{− 1}q_nlogd + n ^{− 2}λ_n²(k_n + 1). (iii) Let b_n1 = min{‖β_0j‖₂:j∈A^o}. Suppose that . Then all covariates with nonzero coefficients are selected by the GLasso with probability converging to one.

Part (i) provides an upper bound for the dimension of the GLasso model. In particular, the number of nonzero estimates is inversely proportional to λ_n². Part (ii) shows that the rate of convergence is h_n^1/2. The first term in h_n represents the variance of the estimate, and the second term represents the bias introduced by the penalty. When q_nlogd/n→0 and λ_n²|A_o|/n²→0, h_n→0. We note that when d and q_n are fixed and λ_n = 0, the rate of convergence becomes the standard n ^{− 1/2}. Part (iii) implies that all covariates with nonzero coefficients are selected with a high probability. This justifies using the GLasso as the initial estimate in the proposed computational algorithm.

The iterative estimate.

Consider 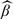, the 1-step estimate after one iteration in the algorithm described in Section 3.2. For simplicity of notation, set γ = 1/2.

Simple algebra shows that θ_j computed in Step 2 of the proposed algorithm is 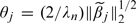. Thus, the 1-step estimator is

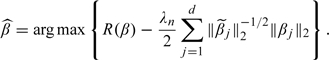With the convention 0×∞ = 0, 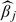will be set as 0 if .

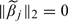In addition to (A1) and (A2), we further assume

• (A3) Denote .

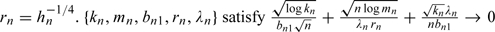This condition restricts the number of covariates with zero and nonzero coefficients, the penalty parameter, and the smallest norm of nonzero coefficients. Since only the logarithm of m_n enters the equation, the results are applicable to models with dimension much larger than n. There are 2 special cases where (A3) is especially simple. The first is in a conventional model with fixed d. Then b_n1 is bounded away from zero. In this case, (A3) is satisfied if λ_n/n→0 and λ_nr_n/n^1/2→∞. The second case is when the number of nonzero coefficients k_n is fixed, but d is larger than n. This is a reasonable assumption for microarray studies where the total number of genes is larger than n, but the number of genes associated with the responses is small. In this case, b_n1 is bounded away from zero. (A3) is satisfied if λ_n/n→0 and logd = o(1)(λ_nr_n/n^1/2)². Therefore, depending on r_n and λ_n, the total number of covariates can be as large as exp(n^a) for some 0 < a < 1.

For 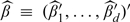and β₀≡(β₀₁^′,…,β_0d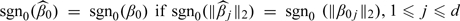^′)^′, , where sgn₀(u) = 1 if |u| > 0, and = 0 if u = 0.

THEOREM 2 Suppose that (A1)–(A3) hold and the matrix C_A^o is positive definite. Then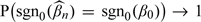

Theorem 2 establishes that the estimate from 1-step iteration can consistently distinguish covariates with zero and nonzero regression coefficients. Following similar arguments, we can prove that the iterative estimate is selection consistent. Of note, although the 1-step estimate is selection consistent, iterating until convergence may improve finite-sample performance. A sensible setting that satisfies the conditions postulated above is finite k_n. With the selection consistency and finite k_n, estimation consistency can be easily obtained.

4. NUMERICAL STUDIES

4.1. Practical considerations

In data analysis, normalization of gene expressions needs to be conducted for each data set separately. For Affymetrix measurements, a floor and a ceiling may be added, and then the measurements are log2 transformed. We fill in missing expressions with means across samples. We then standardize each gene expression to have zero mean and unit variance. The proposed approach does not require the direct comparability of measurements from different studies. Additional transformations, which are necessary for intensity approaches, are not needed.

For simplicity of notation, we have assumed matched gene sets across multiple studies. When different sets of genes are measured in different studies, we use the following rescaling approach. Assume that gene 1 is measured only in the first K( < M) studies. We set β₁^{K + 1} = ⋯ = β₁^M = 0 and J(β₁) = [(β₁¹)² + ⋯ + (β₁^K)²]^γ/2×(M/K)^γ. The proposed approach and computational algorithm are then applicable with minor modifications.

4.2. Simulation

We simulate data for 4 independent studies, each with 50 or 100 subjects. We simulate 50 or 250 gene clusters, with 20 genes in each cluster. Gene expressions have marginally normal distributions. Genes in different clusters have independent expressions. For genes within the same clusters, their expressions have the following correlation structures: (i) auto-regressive correlation, where expressions of genes j and k have correlation coefficient ρ^{|j − k|}; (ii) banded correlation, where expressions of genes j and k have correlation coefficient max(0,1 − |j − k|×ρ); and (iii) compound symmetry, where expressions of genes j and k have correlation coefficient ρ when j≠k. Under each correlation scenario, we consider 2 different ρ values. Within each of the first 3 clusters, there are 10 genes associated with the responses. There are a total of 30 important genes, and the rest are noises. For important genes, we generate their regression coefficients from Unif[0,2]. Thus, some genes have large effects, and others have small to moderate effects. Six important genes are only measured in 2 studies. In addition, 10% noisy genes are only measured in 2 studies. We generate the binary response variables from the logistic regression models and Bernoulli distributions. The simulation settings closely mimic pharmacogenomic studies, where genes have the pathway structures. Genes within the same pathways tend to have correlated expressions, whereas genes within different pathways tend to have weakly correlated or independent expressions. Among a large number pathways, only a few are associated with the responses. Within those important pathways, there are some important genes and others are noises.

To better gauge performance of the proposed approach, we also consider the following alternative approaches: (a) meta-analysis. We analyze each data set separately using the Lasso or the bridge approaches. Genes that are identified in at least one study are identified in meta-analysis. An alternative is to consider genes identified in all studies. However, we have examined all simulation settings and found that there are very few such genes; (b) an intensity approach. Since all 4 data sets are generated under similar settings, we adopt the intensity approach in Shabalin and others (2008), make transformations of covariates, combine 4 data sets, and analyze as if they were from a single study. Both the Lasso and the bridge are used for analysis; (c) integrative analysis using the GLasso. For all approaches, we select the tuning parameters using 3-fold cross validation.

We evaluate the number of genes identified and the number of true positives. In addition, in -omics studies, we may also be interested in the prediction performance of identified markers. For each set of 4 data sets (training), we simulate 4 additional data sets (testing). We generate estimates using the training data, make prediction for subjects in the testing data and compute prediction errors.

Simulation suggests that the proposed approach is computationally affordable, with analysis of one replicate taking less than 2 min on a desktop PC. Summary statistics based on 500 replicates are shown in Table 1. We can see that the proposed approach is capable of identifying a majority of the true positives with a reasonable number of false positives. It outperforms alternatives under almost all scenarios, with a smaller number of genes identified, more true positives, and smaller error rates. We have examined a few other simulation scenarios and reached similar conclusions.

Table 1.

Simulation study: summary statistics based on 500 replicates

			Meta-analysis		Intensity		Integrative analysis
n	# clus	ρ	Lasso	Bridge	Lasso	Bridge	GLasso	Proposed
Correlation structure: Auto-regressive
50	50	0.30	179/16/44	135/15/42	43/16/33	28/14/28	38/20/31	22/19/30
50	50	0.70	130/23/34	105/21/31	53/20/21	34/18/16	26/23/19	23/21/14
100	50	0.30	162/29/36	150/26/34	36/23/25	31/21/21	76/24/22	46/24/17
100	50	0.70	145/26/24	93/26/21	52/25/16	36/22/12	48/24/13	44/24/8
50	250	0.30	94/7/48	59/5/46	58/13/37	41/11/34	54/18/30	40/18/31
50	250	0.70	152/15/40	124/13/38	38/16/21	33/15/18	39/20/21	36/19/16
100	250	0.30	160/17/42	71/13/40	53/21/26	44/20/23	32/23/24	30/22/23
100	250	0.70	147/27/27	90/20/25	29/21/16	28/21/13	30/24/14	29/22/9
Correlation structure: Banded
50	50	0.20	189/22/34	102/15/32	52/19/19	33/16/16	25/22/18	25/22/13
50	50	0.33	162/16/38	92/12/36	32/17/24	26/15/20	31/19/24	29/18/22
100	50	0.20	139/29/24	89/26/21	50/22/15	36/21/12	44/22/12	40/22/7
100	50	0.33	149/28/29	95/25/26	26/21/20	25/21/15	59/23/16	45/23/11
50	250	0.20	129/20/40	125/18/38	39/15/20	32/13/17	38/21/19	36/20/16
50	250	0.33	100/18/44	95/16/44	47/14/27	36/13/23	46/17/26	44/17/24
100	250	0.20	134/22/26	86/21/23	27/20/15	26/19/13	27/23/14	25/22/9
100	250	0.33	72/18/34	59/16/32	36/20/21	29/19/17	32/24/19	30/24/14
Correlation structure: Compound symmetric
50	50	0.30	175/21/34	87/19/32	34/18/22	26/16/18	31/19/21	30/18/16
50	50	0.70	119/21/22	79/20/20	45/16/14	29/13/12	41/16/13	38/16/8
100	50	0.30	106/26/26	72/23/22	32/23/18	29/22/14	57/25/14	45/25/9
100	50	0.70	150/25/17	99/23/15	27/21/12	32/19/9	68/24/9	52/24/4
50	250	0.30	71/12/40	62/11/40	44/17/23	36/15/20	80/20/22	48/19/21
50	250	0.70	107/15/28	66/12/24	28/14/15	26/13/11	88/18/15	55/17/11
100	250	0.30	112/25/31	116/22/28	36/23/18	35/23/15	27/25/17	27/25/12
100	250	0.70	149/26/19	105/22/15	61/21/12	34/18/10	50/24/10	46/23/5

n: sample size of each data set. # clus: number of gene clusters. ρ: correlation coefficient parameter. In cells with “a/b/c”: a is the number of genes identified, b is the number of true positives, and c is the number of prediction errors per 100 subjects.

4.3. Pancreatic cancer studies

Pancreatic ductal adenocarcinoma (PDAC) is a major cause of malignancy-related death. Apart from surgery, there is still no effective therapy and even resected patients usually die within 1 year postoperatively. We collect and analyze 4 data sets (Table 2), which have been described in Iacobuzio-Donahue and others (2003), Logsdon and others (2003), Crnogorac-Jurcevic and others (2003), and Friess and others (2003). Two studies used cDNA arrays and the other 2 used oligonucleotide arrays. The 2 sample groups analyzed are the PDAC and normal pancreatic tissues. We remove genes with more than 30% missingness. Although it is possible to use all genes, missingness may make the analysis less reliable. 1204 genes are included in analysis. For each data set, we conduct preprocessing as described in Section 4.1.

Table 2.

Pancreatic cancer studies

Data set	D1	D2	D3	D4
Author	Logsdon	Friess	Iacobuzio-Donahue	Crnogorac-Jurcevic
PDAC	10	8	9	8
Normal	5	3	8	5
Array	Affy. HuGeneFL	Affy. HuGeneFL	cDNA Stanford	cDNA Sanger
UG	5521	5521	29 6215794

PDAC: number of PDAC samples. Normal: number of normal samples. Array: type of array used. UG: number of unique UniGene clusters.

We employ the proposed approach. Five genes are identified (Table 3). We can see that the estimates are nonzero in all 4 studies. For a specific gene, the magnitudes of estimates are not equal across studies. These observations are in line with discussion in Section 2. With real data, it is not possible to evaluate the gene identification accuracy. We evaluate the prediction performance using the LOO approach. We first remove one subject. With the reduced data, we carry out V-fold cross validation and penalized estimation. We then use the estimate to make prediction for the one removed subject. With the logistic model, the predicted probability can be computed. We use 0.5 as the cut off and predict the class label. We repeat this procedure over all subjects. Prediction error can then be computed. With the LOO approach, 2 subjects cannot be correctly classified, leading to an error rate of 0.036.

Table 3.

Pancreatic cancer studies: nonzero estimates

Gene	D1	D2	D3	D4
Symplekin (SYMPK)	−0.155	−0.178	−0.107	−0.149
ELAV-like 1 (Hu antigen R) (ELAVL1)	−0.728	−0.812	−0.552	−0.705
Jumonji domain containing 2A (JMJD2A)	0.871	0.948	0.898	0.645
Solute carrier family 18, member 2 (SLC18A2)	−0.233	−0.237	−0.274	−0.129
SWI/SNF related, matrix associated, actin-dependent regulator of chromatin, subfamily a(SMARCA2)	0.249	0.144	0.282	0.222

We also analyze using the following alternative approaches. (a) Meta-analysis. We analyze each data set using the Lasso approach. In data sets D1–D4, 9, 9, 10, and 5 genes are identified. A total of 29 genes are identified in at least one data set, with no gene identified in all 4 data sets. For each data set, we use the LOO approach to evaluate the prediction performance. A total of 8 subjects (2, 1, 2, and 3 in D1–D4, respectively) cannot be properly classified. We also analyze each data set using the bridge approach. In data sets D1–D4, 5, 9, 6, and 4 genes are identified, respectively. A total of 20 genes are identified in at least one data set, with no gene identified in all 4 data sets. With the LOO evaluation, a total of 4 subjects (1 in each data set) cannot be properly classified; (b) Intensity approach. We transform gene expressions, combine the 4 data sets, and analyze using the Lasso. Eight genes are identified. We use the LOO approach for prediction evaluation and 3 subjects are not properly classified. We also analyze the combined data using the bridge approach. Seven genes are identified, and 3 subjects are not properly classified in the LOO evaluation; (c) Integrative analysis using the GLasso. Eleven genes are identified. With the LOO evaluation, 4 subjects cannot be correctly classified.

4.4. Liver cancer studies

Gene profiling studies have been conducted on hepatocellular carcinoma, which is among the leading causes of cancer death in the world. Four microarray studies are described in Choi and others (2004) and in Table 4. Data sets D1–D4 were generated in 3 different hospitals in South Korea. Although the studies were conducted in a controlled setting, the researchers “failed to directly merge the data even after normalization of each data set” (Choi and others, 2004). 9984 genes were measured in all 4 studies. 3122 genes have less than 30% missingness and are analyzed. We also remove 8 subjects that have more than 30% gene expression measurements missing. The effective sample size is 125 (Table 4). For each data set, we conduct preprocessing as described in Section 4.1.

Table 4.

Liver cancer studies

Data set	D1	D2	D3	D4
Experimenter	Hospital A	Hospital B	Hospital C	Hospital C
Tumor	16 (14)	23	29	12 (10)
Normal	16 (14)	23	5	9(7)
Chip type	cDNA(Version 1)	cDNA(Version 1)	cDNA(Version 1)	cDNA(Version 2)
(Cy5:Cy3)	Sample:normal liver	Sample:placenta	Sample:placenta	Sample:sample

Tumor: number of tumor samples. Normal: number of normal samples. Numbers in the “()” are the number of subjects used in analysis. Version 2 chips have different spot locations from Version 1 chips.

With the proposed approach, 23 genes are identified (Table 5). We observe similar behaviors as with the pancreatic cancer studies. We evaluate the prediction performance using the LOO approach. A total of 18 subjects cannot be properly classified, leading to an error rate of 0.144.

Table 5.

Liver cancer studies: nonzero estimates

Gene	D1	D2	D3	D4
11.3.F.6/noseq/	−0.019	−0.048	−0.020	−0.015
11.4.G.9/alcohol dehydrogenase 1C (class I), gamma polypeptide, mRNA	−0.099	−0.255	−0.024	−0.105
12.2.D.6/noseq/	−0.080	0.126	0.013	−0.056
15.2.D.10/EST387826 cDNA /	−0.097	−0.070	−0.009	−0.043
15.4.G.9/podocalyxin-like (PODXL), mRNA /	−0.123	−0.084	−0.013	−0.038
17.2.B.11/ATPase, H+ transporting, lysosomal 9kD (ATP6H), mRNA	0.057	0.116	0.036	0.004
20.3.E.12/nomatch/	−0.008	−0.007	−0.008	−0.006
20.4.B.3/nomatch/	0.125	0.034	0.005	0.033
22.2.F.6/noseq/	0.009	0.049	0.004	0.011
3.2.E.10/Human G protein-coupled receptor V28 mRNA, complete cds	−0.008	−0.007	−0.004	−0.005
3.3.B.11/stromal cell-derived factor 1 (SDF1), mRNA	−0.294	−0.175	−0.165	−0.199
3.3.B.6/noseq/	−0.039	−0.004	0.016	0.006
4.1.F.6/noseq/	0.067	0.043	0.006	0.014
4.2.H.5/solute carrier family 22, member 1 (SLC22A1), mRNA	−0.018	−0.067	−0.082	−0.047
4.3.C.1/noseq/	−0.230	−0.087	−0.042	−0.027
4.4.B.9/noseq/	−0.112	−0.214	−0.113	−0.139
5.1.A.9/noseq/	−0.049	−0.277	−0.080	−0.037
6.3.B.3/noseq/	0.169	0.189	0.043	0.033
7.3.A.5/nomatch/	−0.054	−0.085	−0.050	−0.044
7.4.A.5/betaine-homocysteine methyltransferase (BHMT), mRNA	−0.109	−0.007	−0.045	−0.068
8.2.D.8/RNA helicase-related protein (RNAHP), mRNA	−0.446	−0.899	−0.628	−0.803
9.3.H.1/chromosome 8 open reading frame 4 (C8orf4), mRNA	−0.013	−0.004	−0.021	−0.005

We also analyze the data using the following alternative approaches. (a) Meta-analysis. When the Lasso is used to analyze each data set, 19, 25, 25, and 10 genes are identified, respectively. A total of 76 genes are identified in at least one data set, with no gene identified in all 4 data sets. The LOO evaluation misclassifies 4, 9, 4, and 5 subjects in D1–D4, respectively, leading to an overall error rate of 0.176. When the bridge is used to analyze each data set, 12, 16, 8, and 7 genes are identified, respectively. A total of 38 genes are identified in at least one data set, with no gene identified in all 4 data sets. The LOO evaluation misclassifies 4, 10, 5, and 9 subjects in D1–D4, respectively, leading to an overall error rate of 0.224; (b) Intensity approach. When the Lasso is used to analyze the combined data set, 34 genes are identified, and 35 subjects are not properly classified in the LOO evaluation. When the bridge is used to analyze the combined data set, 20 genes are identified and 40 subjects are not properly classified in the LOO evaluation; (c) Integrative analysis using the GLasso. 28 genes are identified. With the LOO evaluation, 21 subjects cannot be properly classified, leading to an error rate of 0.168.

5. DISCUSSION

In high-throughput biomedical studies, integrative analysis provides an effective way of improving the reproducibility of identified markers by pooling and analyzing multiple data sets. In this study, we develop a penalized marker selection method for integrative analysis. We rigorously establish the consistency properties. Numerical studies show that the proposed approach has satisfactory finite-sample properties.

In penalized marker selection, it is usually assumed that a small number of covariates have nonzero effects, while the majority of covariates have “exactly” zero effects. With a fixed data set, the number of markers that penalization methods can identify is limited by the sample size. Dimension reduction methods (e.g. principal component analysis) may not have this limitation, at the price of poor interpretability. The 2-norm group bridge penalty is partly motivated by the bridge penalty. In analysis of single data sets, several penalties, including the bridge, smoothly clipped absolute deviation (SCAD), and minimax concave penalty (MCP), have been shown to have the “oracle properties” for certain models. There is no study showing that one of those penalties is dominatingly better than others. We conjecture that it is possible to develop the integrative analysis counterparts of SCAD and MCP penalties. In the proposed penalty, we require 0 < γ < 1. In our numerical study, we fix γ = 1/2. It is possible to choose γ using, for example, cross validation. However, as long as 0 < γ < 1, varying γ will increase computational cost without improving the asymptotic properties. With single data sets and data/model settings significantly different from the present one, Tian and others (2009) selects γ in the bridge penalty. Numerical studies in Tian and others (2009) shows that γ as small as 0.1 may be selected. Loosely speaking, smaller γs make the objective function “less smooth” (γ = 0 corresponds to an AIC, BIC-type penalty). To reduce computational cost, we fix the value of γ. In this study, we have assumed the same link function in multiple studies. Different link functions across studies can be accommodated but difficult to interpret. With a fixed number of covariates, there exist a few approaches that can be used to determine the link functions. However, to the best of our knowledge, their validity has not been established with high-dimensional data. The proposed approach has no built-in robustness. It is expected that specifying the wrong link functions may lead to unsatisfactory marker identification.

In simulation study, there are a few weak signals that are extremely hard to detect. That explains the small number of false negatives and false positives we observe. We use V-fold cross validation for tuning parameter selection. At this moment, it is not clear whether other tuning parameter selection methods may have better asymptotic properties. Our limited simulation (results omitted) suggests that V-fold cross validation has the best empirical performance among the a few tuning parameter selection methods we consider. The primary goal of this study is to identify disease markers. In simulation, we also evaluate the prediction performance, which is also of interest in pharamacogenomic studies and show the satisfactory properties of the proposed approach. In Section 4.2, we have focused on the scenario where multiple studies have the same susceptibility genes. A related but different scenario is where multiple studies have overlapping but different susceptibility genes. In the supplementary material available at Biostatistics online, we present a simulation study on such a scenario. We show that the proposed approach can still identify a reasonable number of true positives. However, the number of false positives can be significantly higher. In data analysis, as it is difficult to objectively evaluate the identification accuracy, we focus on the prediction evaluation, which may provide an indirect evaluation of the identification accuracy.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

National Institutes of Health (CA120988; CA142774; and LM009828 to S.M. and J.H.).