Passive Hand Movements Disrupt Adults’ Counting Strategies

Abstract

In the present study, we experimentally tested the role of hand motor circuits in simple-arithmetic strategies. Educated adults solved simple additions (e.g., 8 + 3) or simple subtractions (e.g., 11 − 3) while they were required to retrieve the answer from long-term memory (e.g., knowing that 8 + 3 = 11), to transform the problem by making an intermediate step (e.g., 8 + 3 = 8 + 2 + 1 = 10 + 1 = 11) or to count one-by-one (e.g., 8 + 3 = 8…9…10…11). During the process of solving the arithmetic problems, the experimenter did or did not move the participants’ hand on a four-point matrix. The results show that passive hand movements disrupted the counting strategy while leaving the other strategies unaffected. This pattern of results is in agreement with a procedural account, showing that the involvement of hand motor circuits in adults’ mathematical abilities is reminiscent of finger counting during childhood.

Introduction

During development, children all go through a stage in which they count on their fingers to solve simple-arithmetic problems like 8 + 5 and 7 − 4. They use their fingers to represent numerosities before they acquire symbolic representations of numbers (such as number words and Arabic digits). It is thus no surprise that finger gnosia or “finger sense” (i.e., the ability to mentally represent one's fingers) plays an important role in the development of numerical abilities. Indeed, Noël (2005) showed that finger gnosia tested at the beginning of grade 1 predicted numerical abilities (tested by tasks such as digit comparison and subitizing) and mathematical abilities (tested by an addition task) in grade 2; whereas it did not predict reading abilities (see also Fayol et al., 1998). Similarly, Penner-Wilger et al. (2007) showed that children able to use their fingers as representational tools performed better in mathematics. Training children's finger differentiation even increases finger gnosia and improves numerical performance (Gracia-Bafalluy and Noël, 2008, but see Fischer, 2010).

Generally, adults no longer use their fingers to solve arithmetic tasks, and the correlation between finger use and math accuracy decreases across development (Jordan et al., 2008). One may therefore suppose that the link between finger gnosia and numerical or mathematical abilities is absent in adults. However, there is evidence that indicates that this might not be true.

In a seminal electromyographic (EMG) experiment, Andres et al. (2004) showed that adults’ grip closure was initiated faster in response to small digits, while grip opening was initiated faster in response to large digits (see also Andres et al., 2008). In a similar vein, it has been shown that adults’ precision grip was initiated faster in response to small numbers, while power grip was initiated faster in response to large numbers (Lindemann et al., 2007; Moretto and di Pellegrino, 2008). Finally, using transcranial magnetic stimulation (TMS), Sato et al. (2007) observed increased corticospinal excitability of adults’ hand muscles during a parity judgment task. Taken together, all these studies show that adults still exhibit a neural link between fingers and numbers.

The neuro-cognitive relationship between fingers and adults’ mathematical abilities remains debated, though. Rusconi et al. (2005) showed that repetitive TMS on adults’ left angular gyrus interfered with finger gnosia and explicit magnitude processing but did not affect the network of stored arithmetic facts. Andres et al. (2007), in contrast, showed that TMS affected the corticospinal excitability of adults’ hand muscles during a dot counting task. It thus seems that the relationship between hands and mathematical abilities is functionally differentiated, with a connection between hands and counting dots but not between hands and retrieving arithmetic facts.

With the present study, we wanted to pursue the role of hand motor circuits in adults’ mathematical abilities. More specifically, we wanted to test if the functional relationship between hand movements and mathematical abilities depends on the arithmetical strategy used. In the domain of simple arithmetic, three main strategies can be distinguished (Campbell and Timm, 2000): (a) direct memory retrieval, for example knowing that 8 + 3 = 11, (b) transformation or using intermediate steps, for example first retrieving 8 + 2 = 10 and then 10 + 1 = 11, and (c) one-by-one counting, for example 8 + 3 = 8…9…10…11. The question now is: to what extent do hand movements play a role in these different strategies? According to the representational account, the configuration of our fingers is used to mentally represent and process numbers (Di Luca et al., 2006; Fischer, 2008). Because we need to access numerical information irrespective of the applied strategy, this theory predicts a functional relationship between hand movements and all three strategies. According to the procedural account, in contrast, the involvement of hand motor circuits in adults’ mathematical abilities is reminiscent of finger counting during childhood, a universal behavior observed in several different cultures (Butterworth, 1999). Hence, this theory predicts that adults will mainly use their fingers to support one-by-one counting strategies and will not use their fingers to retrieve answers from long-term memory.

In order to distinguish between both theories, we conducted an experiment in which adults solved simple-arithmetic problems applying one of the three strategies described above. While solving these problems, the experimenter did or did not move the participants’ hand on a four-point matrix. We chose for this passive hand movement task so as not to load attentional or executive resources, which have been shown to play a role in simple-arithmetic problem solving (Hecht, 2002; Seyler et al., 2003; Imbo and Vandierendonck, 2007a,b,c)¹. The representational account predicts that the passive hand movements will affect all strategies whereas the procedural account predicts that mainly the counting strategy will be affected.

Materials and Methods

Participants

Twenty participants took part in the present experiment, 10 solving subtraction problems and 10 solving addition problems. They were all first year psychology students at Ghent University and participated for course requirements and credits. The two participant groups did not differ from each other in age, calculator use (rated on a scale from 1 “never” to 5 “always”), math experience (i.e., the number of mathematics lessons per week during the last year of secondary school), or arithmetic skill (tested with the French Kit; French et al., 1963; see Table 1).

Table 1.

Participant information for the addition group (N = 10) and the subtraction group (N = 10).

	Addition	Subtraction	Difference
Females:males	8:2	8:2
Age (in years)	18.4	18.8	t(18) = 1.1
Calculator use questionnaire	3.3	3.3	t(18) < 1
Arithmetic skill (French Kit score)	34.3	35.9	t(18) < 1
Math experience (number of arithmetic lessons)	4.5	4.7	t(18) < 1

Procedure

Each participant was tested individually in a quiet room for approximately 1 h. The choice/no-choice method, designed by Siegler and Lemaire (1997), was used to independently assess strategy selection and strategy efficiency. This entails that the participants solved the simple-arithmetic problems under four conditions: first the choice condition, in which they were allowed to choose strategies, and then three no-choice conditions, in which they had to solve all problems with the same specified strategy. The order of the no-choice conditions was randomized across participants. Data obtained in no-choice conditions are unbiased because they are not susceptible to selection effects (e.g., if a certain strategy is only used on easier problems, this strategy may look more efficient than it actually is). In the choice condition, 5 practice problems and 32 experimental problems were presented. The no-choice conditions comprised the 32 experimental problems. Each condition was further divided into two blocks: one without passive hand movements and one with passive hand movements. For half of the participants, each condition started with hand movements whereas for the other half of the participants each condition started without hand movements.

Simple-arithmetic task

The addition problems consisted of two one-digit numbers. Problems involving 0 or 1 as an operand or answer (e.g., 5 + 0) and tie problems (e.g., 3 + 3) were excluded. All problems crossed 10 (e.g., 3 + 8). Since commuted pairs (e.g., 9 + 4 and 4 + 9) were considered as two different problems, this resulted in 32 addition problems (ranging from 2 + 9 to 9 + 8). The 32 subtraction problems were the reverse of the addition problems. A trial started with the presentation of a fixation point for 500 ms. Then the arithmetic problem was presented horizontally in the center of the screen, with the operation sign at the fixation point. The problem remained on the screen until the participant responded. Timing began when the stimulus appeared and ended when the response triggered the sound-activated relay. To enable this sound-activated relay, participants wore a microphone that was activated when they spoke their answer. This microphone was connected to a software clock accurate to 1 ms. On each trial, feedback was presented to the participants: a green “Correct” when their answer was correct and a red “Incorrect” when it was not. Immediately after solving each problem, participants in the choice condition were presented four strategies on the screen: retrieval, counting, transformation, and other. These four choices had been extensively explained by the experimenter:

1. Retrieval: you solve the problem by remembering or knowing the answer directly from memory. For example, you know that 8 + 3 = 11 because 11 “pops into your head.”

2. Counting: you solve the problem by counting one-by-one to get the answer. For example, 8 + 3 = 8…9…10…11.

3. Transformation: you solve the problem by making an intermediate step to 10. For example, 8 + 3 = 8 + 2 + 1 = 10 + 1 = 11.

4. Other: you solve the problem by a strategy unlisted here, or you do not know what strategy you used to solve the problem. For example, guessing.

After each problem, participants were asked to verbally report which of these strategies they had used. In the no-choice conditions, participants were asked to use one particular strategy to solve all problems. In no-choice/retrieval, they were asked to retrieve the answer. More specifically, they had to say the answer that first popped into their head. In no-choice/transformation, they were asked to transform the problem by making an intermediate step to 10. In no-choice/counting, finally, they had to count one-by-one (subvocally) until they reached the correct total. After having solved the problem, participants also had to answer yes or no to indicate whether they had succeeded in using the required strategy. The answer of the participant, the strategy information, and the validity of the trial were recorded on-line by the experimenter. All invalid trials (e.g., failures of the voice-activated relay) were discarded and returned at the end of the block, which minimized data loss due to unwanted failures.

Passive hand movements

In the block with passive hand movements, participants were told to stretch their index finger while keeping their wrist and arm muscles relaxed so that the experimenter could move hand and arm. The experimenter moved the non-dominant hand and arm of the participant on a four-point matrix in such a way that the participant's index finger sequentially tapped the numbers 1, 7, 9, and 3 (i.e., clockwise) on a numerical keyboard. There was about one tap per second.

Results

Failures of the sound-activated relay spoiled 6.7% of the trials. Since all these invalid trials returned at the end of the block, most of them were recovered from data loss, which reduced the trials lost due to failures of the sound-activated relay to 1.1%. All incorrect trials (2.7%), all choice trials on which participants reported having used another strategy (0.4%), and all no-choice trials on which participants failed to use the required strategy (10.5%) were deleted. All data were analyzed on the basis of the multivariate general linear model, and all reported results were considered to be significant if p < 0.05, unless stated otherwise.

Strategy efficiency

Only the RTs uncontaminated by strategy choices (i.e., no-choice RTs) will be considered, since only these RTs provide clear data concerning strategy efficiency. A 2 × 2 × 3 ANOVA was conducted on correct RTs with Operation (addition or subtraction) as between-subjects factor and Movement (with or without passive hand movements) and Strategy (retrieval, transformation, counting) as within-subjects factors (see Table 2). The main effects of Operation and Movement were significant. Participants were faster on addition (1.8 s) than on subtraction (2.7 s), F(1,18) = 13.20, MSe = 1925240, ${\eta }_p^2=0.42$ and faster without than with passive hand movements (2.1 vs. 2.4 s), F(1,18) = 12.60, MSe = 130460, ${\eta }_p^2=\mathrm{0.41.}$ The main effect of Strategy was significant as well, F(2,17) = 69.89, MSe = 838067, ${\eta }_p^2=\mathrm{0.80.}$ Retrieval (1.0 s) was faster than transformation (1.6 s), F(1,18) = 35.55 and transformation was faster than counting (4.1 s), F(1,18) = 147.25.

Table 2.

Reaction times (in seconds) as a function of Operation, Movement, and Strategy.

	No hand movement	Passive hand movement
ADDITION
Retrieval	0.8 (0.1)	0.9 (0.1)
Transformation	1.2 (0.2)	1.3 (0.2)
Counting	3.1 (0.3)	3.4 (0.5)
SUBTRACTION
Retrieval	1.1 (0.1)	1.1 (0.1)
Transformation	1.9 (0.2)	1.9 (0.2)
Counting	4.7 (0.3)	5.5 (0.5)

Standard errors are shown in parentheses.

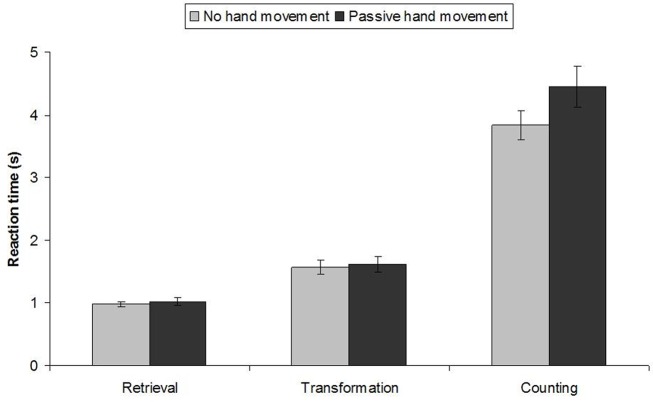
Strategy interacted with Operation, F(2,17) = 4.44, MSe = 838067, ${\eta }_p^2=\mathrm{0.21.}$ The difference between addition and subtraction was larger when counting (1.9 s) than when transforming (0.6 s), F(2,17) = 8.73, and slightly larger when transforming than when retrieving (0.2 s), F(1,18) = 3.99 (p = 0.06). As predicted, Strategy also interacted with Movement, F(2,17) = 7.00, MSe = 115034, ${\eta }_p^2=\mathrm{0.29.}$ As can be seen in Figure 1, participants slowed down when their hands were passively moved in the counting condition, F(1,18) = 12.08, but not in the retrieval or transformation conditions (each F < 1). The Operation × Movement and Operation × Movement × Strategy interactions were not significant (both ps > 0.20).

Figure 1.

Reaction times (in seconds) as a function of Strategy and Movement. Error bars denote standard errors.

Strategy selection

In order to test whether passive hand movements affected people's strategy choices, a 2 × 2 ANOVA was conducted on percentages use of each strategy (in the choice condition), with Operation (addition or subtraction) as between-subjects factor and Movement (with or without passive hand movements) as within-subjects factor (see Table 3). The main effects of Operation and Movement did not reach significance for any of the strategies (highest F = 1.1, each p > 0.30). The Operation × Movement interaction was significant for neither strategy (highest F = 1.5, each p > 0.23). The absence of dual-task effects on adults’ strategy choices is in agreement with earlier studies showing that choosing among simple-arithmetic strategies does not load on working-memory resources (Hecht, 2002; Imbo and Vandierendonck, 2007a,b).

Table 3.

Strategy choices (%) as a function of Operation, Movement, and Strategy.

	No hand movement	Passive hand movement
ADDITION
Retrieval	62.5 (8.4)	64.1 (6.8)
Transformation	36.2 (8.4)	33.8 (6.6)
Counting	1.3 (1.0)	2.0 (0.7)
SUBTRACTION
Retrieval	57.5 (8.4)	65.2 (8.4)
Transformation	40.9 (8.4)	34.4 (6.6)
Counting	1.7 (1.0)	0.3 (0.7)

Standard errors are shown in parentheses.

Discussion

Adults solved simple-arithmetic problems applying three different strategies: retrieval, transformation, and counting. While they solved these problems, the experimenter did or did not move their hand. The question was to which extent these passive hand movements would affect the different strategies. According to the representational account, all strategies would be affected, whereas according to the procedural account, mainly the counting strategy would be affected. The results clearly supported the latter account, since adults counted slower during passive hand movement, while their retrieval and transformation efficiencies stayed unaffected.

Alternative explanations

Can the selective effect of hand movements on counting be explained by characteristics of the counting strategy, such as (a) its slowness, (b) its difficulty, or (c) its subvocalization? In following, we disprove these three alternative explanations.

First, we tested whether the movement effects on the counting strategy could be due to the fact that counting takes much more time than retrieval and transformation. The same 2 × 2 × 3 ANOVA with Operation (addition or subtraction) as between-subjects factor and Movement (with or without passive hand movements) and Strategy (retrieval, transformation, counting) as within-subjects factors was conducted on the on z-scores of the correct RTs. That is, we subtracted each participant's mean RT (averaged over conditions) from his/her observed RT and divided this by each participant's SD. These z-scores correct for the latency differences between strategies and between operations, as proven by the insignificant main effect of Strategy (F = 1.1), the insignificant main effect of Operation (F < 1), and the insignificant interaction between Strategy and Operation (F < 1). The main effect of Movement and the Movement × Strategy interaction were still significant though, F(1,18) = 9.70 and F(2,17) = 3.62. Planned comparisons showed significant effects of movement on counting, F(1,18) = 16.21, but not on retrieval or transformation (each p > 0.25). Hence, the observed effect cannot be due to the fact that counting takes more time than retrieval and transformation.

Second, we tested whether the movement effects on the counting strategy could be due to the fact that counting is more difficult than retrieval and transformation. Problems get more difficult when problem size increases (Ashcraft, 1992; Zbrodoff, 1995). Hence, if the passive hand movements simply interfered with problem difficulty, we would expect a Size × Load interaction. This was tested by means of a 2 × 2 × 2 × 3 ANOVA on correct RTs with Operation (addition or subtraction) as between-subjects factor and Size (small or large), Movement (with or without passive hand movements) and Strategy (retrieval, transformation, counting) as within-subjects factors. Problems were coded as small when the sum (for additions) or the subtrahend (for subtractions) was smaller or equal to 13 (= the median) and coded as large otherwise. The Load × Size and Load × Size × Strategy were not significant (each F < 1), indicating that load effects were equally large for small problems (237 ms) as for large problems (214 ms). Hence, the observed load effects cannot be attributed to cognitive interference caused by problem difficulty.

Finally, one could argue that load effects were found for counting only because counting relies on subvocalization. Indeed, subvocalization requires the movement of speech muscles, which in their turn evolved from manual gestures (Gentilucci and Corballis, 2006; Gentilucci and Volta, 2008). However, previous studies also showed that subvocalization is not only applied in counting strategies but also in transformation strategies (Imbo and Vandierendonck, 2007a,b). Hence, if the load effects would be driven by mouth movements rather than by hand movements, we should have found load effects in the transformation strategy. However, the effect of passive hand movements on transformation was not significant, indicating that the load effects cannot be attributed to subvocalization processes.

Theoretical interpretation

Hand motor circuits are thus involved in one-by-one counting but not in other simple-arithmetic strategies. This result extends the – previously observed – neural link between hands and numbers (Sato et al., 2007) by giving it a functional interpretation. In the domain of mathematical abilities, the link between hands and numbers seems to depend on the procedure that is applied: hand movements are irrelevant for retrieval and retrieval-like strategies (such as transformation) but relevant for counting. This observation also solves the discrepancy between two earlier TMS studies, one observing a link between hands and counting dots (Andres et al., 2007) and another one observing no link between hands and retrieving arithmetic facts (Rusconi et al., 2005).

The fact that hand motor circuits are involved in counting is in agreement with the premotor theory of counting (Andres et al., 2007). According to this theory, counting in adults consists in building a motor plan for moving fingers sequentially without actually executing these movements. Adults’ finger and number sense are thus still related because of the functional role fingers play in numeracy development (Butterworth, 1999). Indeed, children use their fingers to point to objects when counting, to represent cardinality (e.g., raising fingers to show how old they are), and to keep track of the counting steps when solving arithmetic problems. When learning arithmetic facts, at the other hand, children do not use their fingers.

Finger gnosia and computational abilities are also supported by neighboring brain regions in the posterior parietal lobe (Dehaene et al., 2003). Retrieval and transformation strategies, in contrast, would not rely on motor plans but on a verbal number code. This verbal number code is located in the angular gyrus of the left hemisphere (Dehaene and Cohen, 1995), distant from the brain areas supporting the representation of fingers and magnitudes. Our results suggest that adults’ counting strategies do not only (re-)use the same neural substrates that serve finger counting, they also inherit the functional properties of these basic motor processes. Indeed, according to embodied cognition theories (Barsalou, 2008; Domahs et al., 2010), mathematical knowledge is represented together with the sensory and motor activity that was present during its acquisition. The motor function of counting thus extends to adulthood.

In conclusion, our data show that developmental processes that were thought to be transient (e.g., finger calculation) still affect adults’ mathematical performance. Finger and hand movements are thus not just an arbitrary and transient stage of cognitive development, they still exert their effects in educated adults. It would be interesting to test the effect of passive hand movements in groups that show a more frequent use of counting strategies, such as children and mathematically disabled persons. We predict that the disturbing effect of passive hand movements will even be greater in these groups. It would also be interesting to test the effect of active rather than passive hand movements. Indeed, passive hand movements mostly affect proprioception, which is just one component of the hand motor circuit. We predict that the disturbing effect of active hand movements will even be greater than the effect of passive hand movements.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.