Abstract
Recently, a strong functional relationship between finger counting and number processing has been suggested. It has been argued that bodily experiences such as finger counting may influence the structure of the basic mental representations of numbers even in adults. However, to date it remains unclear whether the structure of finger counting systems also influences educated adults’ performance in mental arithmetic. In the present study, we pursued this question by examining finger-based sub-base-five effects in an addition production task. With the standard effect of a carry operation (i.e., base-10 crossing) being replicated, we observed an additional sub-base-five effect such that crossing a sub-base-five boundary led to a relative response time increase. For the case of mental arithmetic sub-base-five effects have previously been reported only in children. However, it remains unclear whether finger-based numerical effects in mental arithmetic reflect an important but transitory step in the development of arithmetical skills. The current findings suggest that even in adults embodied representations such as finger counting patterns modulate arithmetic performance. Thus, they support the general idea that even seemingly abstract cognition in adults may at least partly be rooted in our bodily experiences.
Keywords: mental arithmetic, finger counting, embodied cognition, sub-base-five
Introduction
In recent years, accumulating evidence suggests a functional relationship between the mental representation of number magnitude and bodily representations of finger movements (e.g., Fayol et al., 1998; Noël, 2005; Fischer, 2008). In particular, it was found that finger counting habits exhibit a reliable influence on the mental processing of number magnitude (e.g., Domahs et al., 2010, this issue;Imbo et al., 2011; Lindemann et al., 2011; DiLuca and Pesenti, this issue; but see also Andres et al., 2004; Badets et al., 2007; Song and Nakayama, 2008 for reciprocal influences of number magnitude on finger movements). Based on such data, it is argued that finger counting habits may influence the structure of the basic mental representations of numbers even in adults.
This is in line with recent findings in neuroscience (e.g., Andres et al., 2008 for a review) stating that the motor system not just controls and/or monitors actions, but also contributes to cognitive representations. As a possible explanation for these findings, several theories of embodied cognition have been proposed (see Wilson, 2002, for an overview). The most basic interpretation is that human cognition is originally rooted in sensorimotor processes and, thus, determined by bodily experiences. Such an interaction between the cognitive and physical world has been theoretically elaborated by Hommel et al. (2001) in the Theory of Event Coding. This theory provides an interpretative framework for many of the respective findings. While Hommel and colleagues did not examine the connection of numerical magnitude and motor activity explicitly, the idea of an embodied representation of numerosity has been considered by other researchers (e.g., Fischer, 2008). For instance, Fischer was able to show that finger counting habits are strongly related to spatial numerical processing. Moreover, Badets et al. (2010) found first evidence for a general effect of finger counting when pictures of finger gestures were explicitly presented in simple addition in adults. However, as the authors reported a main effect of presentation format (finger gestures vs. rods) the case of finger-based representations in arithmetic involving symbolic digital input remains to be evaluated.
So far, the influence of finger-based representations has only been investigated for more basic numerical task. For instance, in a magnitude comparison task with Arabic numbers performed by adult participants, Domahs et al. (2010) observed that whenever one of the to-be-compared number was larger than five (i.e., exceeding the magnitude which can be represented by one hand in the German finger counting system, e.g., 4_6) RT increased more strongly (compared to e.g., 2_4) than could be expected from the higher problem size of the former example. Importantly, this effect was observed in a number comparison task on symbolically presented numbers assumed to preclude any explicit reference to finger-based representations containing a sub-base-five system. Moreover, the authors were able to provide further evidence suggesting the origin of this effect to be rooted in influences of finger-based representations. When comparing this so-called 5 break effect between German and Chinese participants they found the 5 break effect to be present in the former but absent in the latter. Taking into account that the Chinese finger counting system allows for representing numbers from 1 to 9 on only one hand, whereas in the German finger counting system the numbers 6–10 are represented using both hands, this finding further corroborates the notion that even in adult numerical cognition finger counting is still influential for number processing. Interestingly, these behavioral findings converge with results from neuro-imaging data (e.g., Simon et al., 2002; Rusconi et al., 2005; Kaufmann et al., 2008) which pointed to shared or neighboring neuronal substrates of finger and number representations. These findings support the idea that the establishment of seemingly abstract representations is at least partially rooted in our bodily experiences.
Against this background evaluating the influence of bodily representations like finger patterns on number processing in children seems particularly promising, because almost all children recruit their fingers to aid counting and/or first arithmetic at some point of their numerical development (e.g., Butterworth, 1999). Accordingly, influences of finger gnosia on numerical development were observed (Fayol, et al., 1998; Noël, 2005) and it was also shown that training bodily experiences of numerical information is capable of improving numerical development (Gracia-Bafalluy and Noël, 2008; Fischer et al., 2011). Importantly, for children there is first evidence indicating that influences of bodily representations such as finger counting habits generalize to mental arithmetic (Domahs et al., 2008). In a longitudinal study, the authors examined the development of simple and complex addition and subtraction in grades 1 and 2. In line with the notion of finger-based influences, they observed that so-called split-five errors in simple calculation (i.e., errors with a difference of five from the correct result, i.e., erroneous results differing from the correct result by “a full hand”) were reliably more frequent than expected at the beginning of grade 2. Domahs et al. (2008) interpreted these split-five errors as a failure to retrieve and/or keep track of the number of fives (i.e., full hands) involved while children calculated the result, possibly recruiting their fingers and hands. Nevertheless, most children use their hands in initial arithmetic (e.g., Butterworth, 1999). Moreover, Domahs et al. (2008) observed that the proportion of split-five errors decreased back to normal at the end of grade 2. Thus, it might be claimed that such sub-base-five effects may only be a transient stage during numerical development. Therefore, Domahs et al. (2008) concluded that mental number representations may at least temporarily inherit features of early external finger representations. This conclusion is further corroborated by the description of an addition strategy reported by Thompson (1999): solving the problem 6 + 7, Scott, a young boy, explained: “13... I took 5 out of the 6 and 5 out of the 7 and I was left with 3....” Although Scott is not reported to rely on overt finger counting anymore, this description indicates a specific role for the sub-base-five in his calculation procedure. Therefore, it seems plausible to assume that he used a mental representation that inherited characteristics of finger-based representations. In fact, in finger calculation it makes no considerable difference to refer to one or two full hands.
In sum, there is evidence for a functional relationship between finger and number representations in mental arithmetic at least during numerical development.
However, it remains unclear whether there are similar influences of finger-based representations on mental arithmetic performance of educated adults. In the present study we pursue this issue in a simple addition task requiring participants to verbally produce the result of the addition problems. We hypothesize that finger-based representations may not only influence mental arithmetic at a specific developmental stage, but that this influence generalizes to adult mental arithmetic. Consequently, if the influence of finger-based representations on mental arithmetic were only a transient stage during numerical development, no influences of finger-based sub-base-five effects should be found in adult mental arithmetic. On the other hand, we argue that when influences of finger-based representations persist into adulthood, we should observe sub-base-five effects in the current addition task. In particular, we expect addition problems, in which the sum of the unit digits exceeds 5 (e.g., 4 + 3 = 7) and thus crosses the sub-base-five boundary, reflecting the numerosity coded by one hand in German finger counting, to be significantly more difficult than problems in which adding the units does not cross the sub-base-five boundary (e.g., 5 + 2 = 7). As outlined above, comparable sub-base-five effects were recently observed for adults in a simple magnitude comparison task (Domahs et al., 2010). Yet, the present study is the first aiming at evaluating sub-base-five influences in mental arithmetic in educated adults. Such an effect of embodied numerosity would indicate that mental finger-based representations of numerosity are not restricted to a transient stage during numerical development. Instead, it would imply finger-based embodied representations of number to be used even by numerate adults in seemingly abstract operations. In turn, this would corroborate the notion that not only language and its comprehension (e.g., Glenberg and Kaschak, 2002; Hauk et al., 2004; Tettamanti et al., 2005; Zwaan and Taylor, 2006) but also mental arithmetic may be grounded in embodied experiences.
Materials and Methods
Participants
Twenty-two students from the Medical Faculty of the RWTH Aachen University (mean age: 24.6 years; SD = 3.5 years), participated in this study. It should be noted that none of the participants of the present study did show any signs of mathematics difficulties. This is important because people with math difficulties may use immature strategies such as finger counting to solve simple math problems even in adulthood (e.g., Butterworth, 1999; Kaufmann et al., this issue), which in turn would have biased the current results. All of them were native speakers of German and had normal or corrected to normal vision. They gave their informed consent and were paid for participation.
Stimuli
In an addition production paradigm, 54 simple addition problems as well as 31 filler items were presented. The 54 critical addition problems consisted of three conditions. In the first condition (comprising 18 items) a sub-base-five boundary was crossed in the addition problem (e.g., in 12 + 4 the sum of 2 + 4 is larger than 5). In the second condition (comprising 18 items), the sub-base-10 boundary had to be crossed as these items involved a carry operation (e.g., 7 + 4). Generally, a carry operation is necessary whenever the sum of the unit digits (here: 7 + 4) is equal to or larger than 10. In the third condition (also comparison 18 items), neither a sub-base-5 nor a sub-base-10 boundary had to be crossed (e.g., 7 + 2). Finally, of the 31 filler items 21 included a sub-base-5 break, while none of the fillers required a base-10 break. Moreover, filler items included the digit 0 or 5 in unit position of either the first operand or the sum. For an overview of the whole stimulus set the reader is referred to the Appendix.
While the first summand in all critical items ranged from 4 to 37, the second summand was always 2, 3, or 4; thus, the position of the smaller addend within the problem was always on the right side. To ensure the validity of the collected data, absolute as well as logarithmic sum, mean magnitude of the unit and decade digit of the sum, and the parity of the correct result were matched between the three stimulus categories and the filler items where appropriate. No multiples of 10 or problems with a 5 in unit position were included in the critical addition problems as either addends or sum of the equation. Finally, no addition problem was part of a multiplication table.
Procedure
Participants were seated approximately 50 cm from the screen of a laptop computer in a dimly lit room. All stimuli were presented in white NRC-7-BIT 172 size (approximately 2.0 cm height and up to 1.4 cm width per digit) against a black background using ERTS software version 3.18 (BeriSoft Cooperation, Frankfurt, Germany; Beringer, 1996). In each trial, an addition problem was presented in central position. Addition problems were presented in Arabic notation, while responses were given orally. Response time data was measured using a voice-key. Each response had to be initiated with the same word: “macht” (“equals”) before the actual result was named, ensuring that all responses started with the same phoneme. Importantly, participants were instructed to respond in a fluent manner, so there were no pauses between the words “macht” and the actual result. Trials on which this was not the case were excluded from analyses (see Korvorst et al., 2006, for a similar procedure).
Instructions focused on both speed and accuracy. To familiarize participants with display layout and task requirements, 10 additional practice problems had to be solved before starting the experiment. None of these practice problems was repeated during the experiment. All addition problems were presented pseudo-randomized in blocks of 21 items. Between the blocks a short pause was incorporated to ensure that participants could have a short resting period. Each problem was presented until a response was given or the time limit of 5 s was reached.
Analysis
Response times measured by voice-key were evaluated in an item-based approach. Only RTs for correct responses were entered into the analyses. Moreover, problems, where participants made an irrelevant noise or a self-correction, were disregarded in the RT analyses. Furthermore, response latencies shorter than 300 ms were not considered and in a second step responses outside the interval of ±3 SD around the individual mean were excluded. Considering erroneous responses and trimming this resulted in a total loss of 4.4% of the data. As error rates were very low (M = 3.8%; SD = 3.6%) the following analyses will focus on response latencies.
First, we ran an item-based univariate ANCOVA (i.e., no break vs. 5 break vs. 10 break) incorporating unit sum (reflecting the sum of the unit digits of the summands) as the covariate to compensate for any systematic disadvantages in solving the addition problems due to increasing unit sum (see Klein et al., 2010a,b for a more detailed evaluation of possible influences of unit sum). Please note that this covariate was necessary as only the conditions 5 break and no break were matched for absolute and logarithmic mean of the individual summands, overall sum, and unit sum. On the other hand, it is mathematically impossible to match the carry condition with the conditions 5 break and no break with regard to the factor unit sum because unit sum needs to be larger than 10 in the carry and smaller than 10 in the other conditions per definition.
Second, results were analyzed using a stepwise multiple linear regression analysis on mean item RT. The stepwise regression analysis was stopped when the inclusion of another predictor would not lead to an additional significant increase of R2 (at p < 0.05). Predictors included presence or absence of 5 break (e.g., 23 + 4 crossing 25) or carry operation (e.g., 28 + 4 crossing 30) as well as more general structural variables such as problem size (measured as the sum of the addends), and unit sum (Deschuyteneer et al., 2005; Klein et al., 2010a,b) as well as the interaction terms of problem size and unit sum and problem size and presence of a 5 break. The predictors for 5 break and carry operation were coded categorically: +1 in the case the addition problem required a carry of sub-base-5 or base-10 and −1 for problems not requiring a carry, while the predictor unit sum simply reflects the sum of the digits at the unit position of the two addends, respectively (Klein et al., 2010a,b). For instance, the unit sum ranged from 3 (as in 31 + 2) to 9 (as in 26 + 3). Further predictors were included into the regression analysis which were directly or indirectly motivated from models and/or previous findings reported in the literature (see Table 1).
Table 1.
Critical predictors (necessary for testing our hypotheses) and controlled predictors (motivated by the literature on mental addition and included to substantiate the results) included in the stepwise multiple regression analysis.
| Critical predictors | |
|---|---|
| Break 5 | |
| Carry | |
| Problem size | |
| Unit sum | |
| Break 5 × carry | |
| Problem size × carry | |
| Problem size × break 5 × carry | |
| Controlled predictors | Citation |
| Size of the second (smaller) summand | Groen and Parkman (1972) |
| Logarithmic sum | Butterworth et al. (2001) |
| Logarithmic unit sum | Dehaene (2007), Deschuyteneer et al. (2005) |
| Square of the sum | Ashcraft and Battaglia (1978) |
| Product of the summands | Widaman et al. (1989) |
| Sum of the square of the addends (SSA) | Widaman et al. (1989) |
| Parity of the two summands | Campbell et al. (2004) |
| Lemaire and Siegler (1995) | |
| Vandorpe et al. (2005) |
For the latter, the respective citation (referencing one or more studies indicating the impact of this predictor) is provided.
Results
ANCOVA
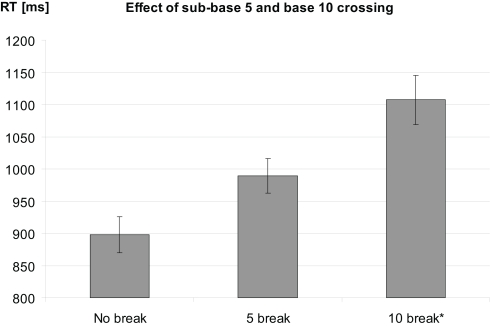
To control for any systematic disadvantages in solving the addition problems due to increasing unit sum, we additionally ran an ANCOVA incorporating this variable as a covariate. The ANCOVA revealed a main effect of item group [F(50, 3) = 12.06, p < 0.001]. Moreover, Bonferroni–Holm corrected pairwise comparisons (Holm, 1979) revealed that all possible group differences were significant (see Figure 1) with no break problems being responded to fastest followed by 5 break and 10 break problems (Δno break vs. 5 break = 91 ms, Δno break vs. 10 break = 209 ms, Δ5 break vs. 10 break = 118 ms, all p < 0.05). Additionally, there was no reliable influence of the covariate unit sum [F(1, 33) < 1].
Figure 1.
Response latencies for addition problems with and without 5 break as well as for problems with 10 break (carry). Error bars depict 1 standard error of the mean (SEM). *Please note that problems with a 10 break could not be fully matched regarding the units of the result with the two other groups (problems with and without 5 break).
Regression analysis
The final model comprised only the predictors carry and 5 break [R2 = 0.418, adjusted R2 = 0.395, F(2, 51) = 18.3, p < 0.001], while the predictors problem size and unit sum failed to explain significant amounts of additional variance. Inspection of the individual beta weights indicated a significant influence of both the fact whether a base-10 [b = 0.75, t(20) = 6.0, p < 0.001] or a sub-base-five was crossed [b = 0.34, t(20) = 2.28, p < 0.001]. This means that the addition of two numbers became relatively slower when a 5 break as well as when a 10 break had to be crossed (for detailed results for all variables entered in the stepwise multiple regression analysis see Table 2).
Table 2.
Results for all variables entered in the stepwise multiple regression analysis.
| Variables included in the model | Standardized beta | t | Sign. |
|---|---|---|---|
| Break 10 (carry) | 0.746 | 6.044 | <0.001 |
| Break 5 | 0.341 | 2.765 | >0.01 |
| Variables excluded from the model | Standardized beta | t | sign. |
| Problem size | −0.004 | −0.037 | 0.970 |
| Unit sum | −0.053 | −0.263 | 0.794 |
| Logarithmic sum | 0.017 | 0.159 | 0.874 |
| Logarithmic unit sum | −0.024 | −0.144 | 0.886 |
| Squared problem size | −0.007 | −0.064 | 0.949 |
| Product of summands | 0.026 | 0.234 | 0.816 |
| SSA | −0.012 | −0.111 | 0.912 |
| Parity of summand 1 | 0.028 | 0.245 | 0.807 |
| Parity of summand 2 | 0.097 | 0.906 | 0.369 |
| Break 10 × problem size | −0.027 | −0.098 | 0.923 |
| Break 5 × break 10 × problem size | −0.12 | −0.433 | 0.667 |
Discussion
There is growing evidence suggesting that bodily experiences such as finger-based representations may exert reliable influences on number processing even in educated adults (e.g., Domahs et al., 2010). For the case of mental arithmetic so far such a finger-based effect was only reported for children (Domahs et al., 2008). Therefore, it was argued that such finger-based effects on mental arithmetic may be limited to an important but transitory step in numerical development during which children recruit their fingers for counting/arithmetical processes. The present study aimed at evaluating the influence of finger-based representations in numerate adults solving an addition production task. Crucially, reliable influences of finger-based representations in adults were indicated by a detrimental 5 break effect in mental addition. This means that addition problems in which the sum of the unit digits exceeds 5 (e.g., 3 + 4 = 7) were more difficult to solve than problems without such a break (e.g., 5 + 2 = 7), even when controlling for overall unit sum (i.e., 7 in the present examples).
In line with our hypothesis we indeed observed consistent sub-base-five effects: when summing up the unit digits crossed the sub-base-five boundary, this was associated with a significant increase of response times. First, the comparison of addition problems involving a 5 break with no break problems revealed reliably prolonged reaction times for the former. Importantly, these two problem categories were matched for variables such as size of the global sum or unit sum, etc. indicating that it was indeed the 5 break which delayed responses. Second, this finding was replicated in a regression analysis. Here, we observed that apart from the well known carry effect, the presence of a 5 break was the only reliable predictor of item RT. The current findings thus suggest that even in numerate adults finger-based representations of numerosity moderate arithmetic performance. Importantly, the response modality used in our paradigm further corroborates this interpretation. As participants were required to produce the result to the addition problems verbally, the recruitment of any kind of finger-based representations should not have been triggered by finger and/or hand movements related to the answer modality. Additionally, there were no obvious signs of actual finger movements while participants completed the addition task. However, it has to be noted that corticospinal excitability of fibers enervating hand muscles has been associated with the processing of numerical information even in the absence of finger movements (e.g., Andres et al., 2007). But based on the methodology of our study we cannot evaluate whether the finger-based influence of the sub-base-five effect is driven by entirely abstract mental representations of embodied origin or generalizes to neural activity/excitability associated with finger movements. This question is open to future studies using neuro-cognitive methods such as fMRI or TMS.
Moreover, we consistently observed a carry effect (i.e., an RT-increase due to the crossing of a 10 break, e.g., 28 + 6 vs. 31 + 3) in both the ANCOVA and the regression analysis. This is a standard finding in mental addition (Deschuyteneer et al., 2005; Kong et al., 2005; Imbo et al., 2007; Klein et al., 2010a,b). Therefore, we are confident that the current task assessed the processing of addition problems in an appropriate way. However, while base-10 effects may be caused by the structure of both the stimuli or the internal representations related to different notations (e.g., Arabic digits, finger counting patterns), this is not true for sub-base-five effects. The latter cannot be related to the Arabic notation as the number 5 is not of particular importance as regards the organization principle of the base-10 Arabic number system. However, sub-base-five effects may index traces of finger-based representations influencing mental numerical representations.
Nevertheless, the fact that we did not observe a problem size effect was unexpected and deserves further discussion. Generally, most previous studies indicated that addition performance – like performance in all kinds of mental arithmetic – is largely determined by overall problem size, i.e., response performance declines as the size of the numbers involved increases (e.g., 8 + 4 is less difficult than 38 + 4, see Ashcraft, 1995; Zbrodoff and Logan, 2005 for reviews). However, it must be considered that the largest addend was always presented first (e.g., 34 + 2) and did not change substantially in size due to the addition operation itself as only 2, 3, or 4 had to be added. This means that overall problem size was reflected almost entirely by the first summand and did not change substantially by adding the second summand. However, we observed a substantial correlation between the predictor “unit of the second summand” (which was either 2, 3, or 4) and overall RT (r = 0.44, p < 0.001). This continuous increase of reaction time with the increase of the second addend is in line with the literature (Groen and Parkman, 1972) and indicates negative influences of increasing digit magnitude on task performance. From a broader perspective this indicates that adults may have indeed relied on counting or even finger-counting related strategies to solve the current addition task, because such a correlation is hard to reconcile with participants relying on arithmetic fact retrieval (see Domahs et al., 2006, for a disappearing problem size effect in multiplication when controlling for structural variables). Furthermore, this correlation of the unit of the second summand with overall RT can be interpreted as a problem size effect for the unit of the second summand. This interpretation of digit specific influences of increasing magnitude are corroborated by the fact that the raw correlation of unit sum with overall RT (which is one possible measure of problem size in addition) was highly significant (r = 0.48, p < 0.001). As the predictors carry (which was considered in the final model) and unit sum are highly intercorrelated (r = 0.81) unit sum may not have been incorporated in the final regression model. Nevertheless, it is well conceivable that parts of the variance associated with unit sum as a measure of problem size are accounted for by the categorical carry predictor in the final model. This suggests that the carry effect observed may partially reflect influences of (unit) problem size as well (cf. Klein et al., 2010a). This indicates that, although we did not observe an effect of problem size overall, we nevertheless observed specific results reflecting an negative influence of increasing magnitude on performance as expected by the problem size effect. Finally, it has been argued that overall problem size seems to affect primarily carry addition problems (Deschuyteneer et al., 2005). As the majority of the current stimuli were non-carry problems, this property in combination with the above mentioned argument, might have further reduced the influence of overall problem size1.
Taken together, we are well aware that we used a specific stimulus set (i.e., adding a single-digit to a two-digit number); thus, the lack of a standard problem size effect may be driven by our stimulus selection. In particular, the use of very small symbolic numbers as addends (2, 3, 4) makes it very likely that even in educated numerate adults processes related to (finger) counting may have been recruited. However, using exclusively symbolic digital stimulus material should not have triggered explicitly the access to finger-based representations such as the presentation of finger gestures (cf. Badets et al., 2010). From this we suggest that in adult numerical cognition finger-based representations affect mental arithmetic because the presence or absence of a 5 break exerted a reliable influence on response latencies. In summary, this strongly suggests that finger-based representations exhibit a reliable influence on mental arithmetic not only during a transitory developmental phase in children's arithmetic performance but even in educated numerate adults.
To conclude, the present study provides first evidence that the influence of finger-based (sub-base-five) representations on number processing in adults generalizes to the case of mental arithmetic. This was observed for arithmetical problems presented in purely digital-symbolic notation with verbal responses given. Importantly, the structure of both, input and output (Arabic numbers and spoken number words, respectively) do not reference sub-base-five representations in any way. Thus, the present findings support the general idea of embodied numerosity: even seemingly abstract numerical representations and operations involved in adult mental arithmetic may at least partially be rooted in bodily sensorimotor experiences.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix
Overview of the whole stimulus set used.
| No break | 5 Break | 10 Break | Filler items | |
|---|---|---|---|---|
| 1 | 6 + 3 | 4 + 2 | 7 + 4 | 3 + 2 |
| 2 | 7 + 2 | 4 + 3 | 8 + 3 | 11 + 4 |
| 3 | 11 + 2 | 12 + 4 | 8 + 4 | 12 + 3 |
| 4 | 11 + 3 | 13 + 3 | 9 + 2 | 13 + 2 |
| 5 | 12 + 2 | 13 + 4 | 9 + 3 | 21 + 4 |
| 6 | 16 + 2 | 14 + 2 | 9 + 4 | 22 + 3 |
| 7 | 16 + 3 | 14 + 3 | 17 + 4 | 23 + 2 |
| 8 | 17 + 2 | 14 + 4 | 18 + 3 | 31 + 4 |
| 9 | 21 + 2 | 22 + 4 | 18 + 4 | 32 + 3 |
| 10 | 21 + 3 | 23 + 3 | 19 + 2 | 33 + 2 |
| 11 | 22 + 2 | 23 + 4 | 19 + 3 | 10 + 2 |
| 12 | 26 + 2 | 24 + 2 | 19 + 4 | 10 + 3 |
| 13 | 26 + 3 | 24 + 3 | 27 + 4 | 10 + 4 |
| 14 | 31 + 2 | 32 + 4 | 28 + 3 | 20 + 2 |
| 15 | 31 + 3 | 33 + 3 | 28 + 4 | 20 + 3 |
| 16 | 32 + 2 | 33 + 4 | 29 + 2 | 20 + 4 |
| 17 | 36 + 3 | 34 + 2 | 29 + 3 | 30 + 2 |
| 18 | 37 + 2 | 34 + 3 | 29 + 4 | 30 + 3 |
| 19 | 30 + 4 | |||
| 20 | 5 + 2 | |||
| 21 | 5 + 3 | |||
| 22 | 5 + 4 | |||
| 23 | 15 + 2 | |||
| 24 | 15 + 3 | |||
| 25 | 15 + 4 | |||
| 26 | 25 + 2 | |||
| 27 | 25 + 3 | |||
| 28 | 25 + 4 | |||
| 29 | 35 + 2 | |||
| 30 | 35 + 3 | |||
| 31 | 35 + 4 |
Footnotes
1Additionally, it should be noted that in the domain of mental arithmetic a distinction between simple (single-digit) and complex (multi-digit) addition has been suggested. However, the results of additional analyses exploring possible differential processing of exclusively single-digit problems and those involving two-digit summands did not differ from the overall regression analysis with respect to the influence of problem size. This means that problem size was a reliable predictor neither for simple nor for complex problems in our study while “carry,” representing a measure of the problem size of the units, was.
References
- Andres M., Davare M., Pesenti M., Olivier E., Seron X. (2004). Number magnitude and grip aperture interaction. Neuroreport 15, 2773–2777 [PubMed] [Google Scholar]
- Andres M., Olivier E., Badets A. (2008). Actions, words, and numbers. A motor contribution to semantic processing? Curr. Direct. Psychol. Sci. 17, 313–317 10.1111/j.1467-8721.2008.00597.x [DOI] [Google Scholar]
- Andres M., Seron X., Olivier E. (2007). Contribution of hand motor circuits to counting. J. Cogn. Neurosci. 19, 563–576 10.1162/jocn.2007.19.4.563 [DOI] [PubMed] [Google Scholar]
- Ashcraft M. H. (1995). “Cognitive psychology and simple arithmetic: a review and summary of new directions,” in Mathematical Cognition, ed. Butterworth B. (London: Psychology Press Ltd.), 3–34 [Google Scholar]
- Ashcraft M. H., Battaglia J. (1978). Cognitive arithmetic: evidence for retrieval and decision processes in mental addition. J. Exp. Psychol. Hum. Learn. Mem. 4, 527–538 10.1037/0278-7393.4.5.527 [DOI] [Google Scholar]
- Badets A., Andres M., Di Luca S., Pesenti M. (2007). Number magnitude potentiates action judgments. Exp. Brain Res. 180, 525–534 10.1007/s00221-007-0870-y [DOI] [PubMed] [Google Scholar]
- Badets A., Pesenti M., Olivier E. (2010). Response–effect compatibility of finger–numeral configurations in arithmetical context. Q. J. Exp. Psychol. 63, 16–22 10.1080/17470210903134385 [DOI] [PubMed] [Google Scholar]
- Beringer J. (1996). Handbook for ERTS: Experimental Run Time System. Frankfurt a.M.: BeriSoft Corporation [Google Scholar]
- Butterworth B. (1999). The Mathematical Brain. London: Macmillan [Google Scholar]
- Butterworth B., Zorzi M., Girelli L., Jonckheere A. R. (2001). Storage and retrieval of addition facts: the role of number comparison. Q. J. Exp. Psychol. A 54, 1005–1029 10.1080/02724980143000064 [DOI] [PubMed] [Google Scholar]
- Campbell J. I. D., Parker H. R., Doetzel N. L. (2004). Interactive effects of numerical surface form and operand parity in cognitive arithmetic. J. Exp. Psychol. Learn. Mem. Cogn. 30, 51–64 10.1037/0278-7393.30.1.51 [DOI] [PubMed] [Google Scholar]
- Dehaene S. (2007). “Symbols and quantities in parietal cortex: elements of a mathematical theory of number representation and manipulation,” in Attention and Performance XXII. Sensori-motor Foundations of Higher Cognition, Eds Haggard P., Rossetti Y. (Cambridge, MA: Harvard University Press; ), 527–574 [Google Scholar]
- Deschuyteneer M., De Rammelaere S., Fias W. (2005). The addition of two-digit numbers: exploring carry vs. no-carry problems. Psychol. Sci. 47, 74–83 [Google Scholar]
- Domahs F., Delazer M., Nuerk H.-C. (2006). What makes multiplication facts difficult – problem size or neighborhood consistency? Exp. Psychol. 53, 275–282 [DOI] [PubMed] [Google Scholar]
- Domahs F., Domahs U., Schlesewsky M., Ratinckx E., Verguts T., Willmes K., Nuerk H.-C. (2007). Neighborhood consistency in mental arithmetic: behavioral and ERP evidence. Behavioral and Brain Funct. 3, 66. 10.1186/1744-9081-3-66 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domahs F., Krinzinger H., Willmes K. (2008). Mind the gap between both hands: evidence for internal finger-based number representations in children's mental calculation. Cortex 44, 359–367 10.1016/j.cortex.2007.08.001 [DOI] [PubMed] [Google Scholar]
- Domahs F., Moeller K., Huber S., Willmes K., Nuerk H.-C. (2010). Embodied numerosity: implicit hand-based representations influence symbolic number processing across cultures. Cognition 116, 251–266 10.1016/j.cognition.2010.05.007 [DOI] [PubMed] [Google Scholar]
- Fayol M., Barrouillet P., Marinthe C. (1998). Predicting arithmetical achievement from neuro-psychological performance: a longitudinal study. Cognition 68, B63–B70 10.1016/S0010-0277(98)00046-8 [DOI] [PubMed] [Google Scholar]
- Fischer M. H. (2008). Finger counting habits modulate spatial-numerical associations. Cortex 44, 386–392 10.1016/j.cortex.2007.08.004 [DOI] [PubMed] [Google Scholar]
- Fischer U., Moeller K., Bientzle M., Cress U., Nuerk H.-C. (2011). Embodied spatial numerical training of number magnitude representation – an intervention study. Psychon. Bull. Rev. 18, 177–183 10.3758/s13423-010-0031-3 [DOI] [PubMed] [Google Scholar]
- Glenberg A. M., Kaschak M. P. (2002). Grounding language in action. Psychon. Bull. Rev. 9, 558–565 10.3758/BF03196313 [DOI] [PubMed] [Google Scholar]
- Gracia-Bafalluy M., Noël M. P. (2008). Does finger training increase young children's numerical performance? Cortex 44, 368–375 10.1016/j.cortex.2007.08.020 [DOI] [PubMed] [Google Scholar]
- Groen G. J., Parkman J. M. (1972). A chronometric analysis of simple addition. Psychol. Rev. 79, 329–343 10.1037/h0032950 [DOI] [Google Scholar]
- Hauk O., Johnsrude I., Pulvermüller F. (2004). Somatotopic representation of action words in human motor and premotor cortex. Neuron 41, 301–307 10.1016/S0896-6273(03)00838-9 [DOI] [PubMed] [Google Scholar]
- Holm S. (1979). A simple sequentially rejective multiple test procedure. Scand. J. Stat. 6, 65–70 [Google Scholar]
- Hommel B., Müsseler J., Aschersleben G., Prinz W. (2001). The theory of event coding (TEC): a framework for perception and action planning. Behav. Brain Sci. 24, 849–937 10.1017/S0140525X01000103 [DOI] [PubMed] [Google Scholar]
- Imbo I., Vandierendonck A., De Rammelaere S. (2007). The role of working memory in the carry operation of mental arithmetic: number and value of the carry. Q. J. Exp. Psychol. 60, 708–731 10.1080/17470210600762447 [DOI] [PubMed] [Google Scholar]
- Imbo I., Vandierendonck A., Fias W. (2011). Passive hand movements disrupt adults’ counting strategies. Front. Psychology 2:201. 10.3389/fpsyg.2011.00201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufmann L., Vogel S. E., Wood G., Kremser C., Schocke M., Zimmerhackl L. B., Koten J. W. (2008). A developmental fMRI study of nonsymbolic numerical and spatial processing. Cortex 44, 376–385 10.1016/j.cortex.2007.11.009 [DOI] [PubMed] [Google Scholar]
- Klein E., Moeller K., Dressel K., Domahs F., Wood G., Willmes K., Nuerk H.-C. (2010a). To carry or not to carry – is this the question? Disentangling the carry effect in multi-digit addition. Acta Psychol. (Amst) 135, 67–76 10.1016/j.actpsy.2010.06.002 [DOI] [PubMed] [Google Scholar]
- Klein E., Willmes K., Dressel K., Domahs F., Wood G., Nuerk H.-C., Moeller K. (2010b). Categorical and continuous – disentangling the neural correlates of the carry effect in multi-digit addition. Behav. Brain Funct. 6, 70. 10.1186/1744-9081-6-70 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong J., Wang C., Kwong K., Vangel M., Chuac E., Gollub R. (2005). The neural substrate of arithmetic operations and procedure complexity. Cogn. Brain Res. 22, 397–405 10.1016/j.cogbrainres.2004.09.011 [DOI] [PubMed] [Google Scholar]
- Korvorst M., Roelofs A., Levelt W. J. M. (2006). Incrementality in naming and reading complex numerals: evidence from eye tracking. Q. J. Exp. Psychol. 59, 296–311 10.1080/17470210500151691 [DOI] [PubMed] [Google Scholar]
- Lemaire P., Siegler R. S. (1995). Four aspects of strategic change: contributions to children's learning of multiplication. J. Exp. Psychol. Gen. 124, 83–97 10.1037/0096-3445.124.1.83 [DOI] [PubMed] [Google Scholar]
- Lindemann O., Alipour A., Fischer M. (2011). Finger counting habits in middle eastern and western individuals: an online survey. J. Cross Cult. Psychol. 42, 10.1177/0022022111406254 [DOI] [Google Scholar]
- Noël M. P. (2005). Finger gnosia: a predictor of numerical abilities in children? Child Neuropsychol. 11, 413–430 10.1080/09297040590951550 [DOI] [PubMed] [Google Scholar]
- Rusconi E., Walsh V., Butterworth B. (2005). Dexterity with numbers: rTMS over left angular gyrus disrupts finger gnosis and number processing. Neuropsychologia 43, 1609–1624 10.1016/j.neuropsychologia.2005.01.009 [DOI] [PubMed] [Google Scholar]
- Simon O., Mangin J.-F., Cohen L., Le Bihan D., Dehaene S. (2002). Topographical layout of hand, eye, calculation and language-related areas in the human parietal lobe. Neuron 33, 475–487 10.1016/S0896-6273(02)00575-5 [DOI] [PubMed] [Google Scholar]
- Song J.-H., Nakayama K. (2008). Numerical comparison in a visually guided manual reaching task. Cognition 106, 994–1003 10.1016/j.cognition.2007.03.014 [DOI] [PubMed] [Google Scholar]
- Tettamanti M., Buccino G., Saccuman M. C., Gallese V., Danna M., Scifo P., Fazio F., Rizzolatti G., Cappa S. F., Perani D. (2005). Listening to action-related sentences activates frontoparietal motor circuits. J. Cogn. Neurosci. 17, 273–281 10.1162/0898929053124965 [DOI] [PubMed] [Google Scholar]
- Thompson I. (1999). Mental calculation strategies for addition and subtraction. Math. Sch. 28, 1–4 [Google Scholar]
- Vandorpe S., De Rammelaere S., Vandierendonck A. (2005). The odd-even effect in addition: an analysis per problem type. Exp. Psychol. 52, 47–54 [DOI] [PubMed] [Google Scholar]
- Widaman K. F., Geary D. C., Cormier P., Little T. D. (1989). A componential model for mental addition. J. Exp. Psychol. Learn. Mem. Cogn 15, 898–919 10.1037/0278-7393.15.5.898 [DOI] [PubMed] [Google Scholar]
- Wilson M. (2002). Six views of embodied cognition. Psychon. Bull. Rev. 9, 625–636 10.3758/BF03196314 [DOI] [PubMed] [Google Scholar]
- Zbrodoff N. J., Logan G. D. (2005). “What everyone finds: The problem-size effect,” in Handbook of Mathematical Cognition Ed. Campbell J. I. D. (New York, NY: Psychology Press; ). [Google Scholar]
- Zwaan R. A., Taylor L. J. (2006). Seeing, acting, understanding: motor response in language comprehension. J. Exp. Psychol. Gen. 135, 1–11 10.1037/0096-3445.135.1.1 [DOI] [PubMed] [Google Scholar]