Chromosomal Haplotypes by Genetic Phasing of Human Families

Abstract

Assignment of alleles to haplotypes for nearly all the variants on all chromosomes can be performed by genetic analysis of a nuclear family with three or more children. Whole-genome sequence data enable deterministic phasing of nearly all sequenced alleles by permitting assignment of recombinations to precise chromosomal positions and specific meioses. We demonstrate this process of genetic phasing on two families each with four children. We generate haplotypes for all of the children and their parents; these haplotypes span all genotyped positions, including rare variants. Misassignments of phase between variants (switch errors) are nearly absent. Our algorithm can also produce multimegabase haplotypes for nuclear families with just two children and can handle families with missing individuals. We implement our algorithm in a suite of software scripts (Haploscribe). Haplotypes and family genome sequences will become increasingly important for personalized medicine and for fundamental biology.

Introduction

Combinations of genetic variants occurring on the same DNA molecule are known as haplotypes. Each gene in the diploid genome has two sequences, one on each haplotype. Because of genetic variation, each of the two sequences of a gene could determine distinct biological functions for its gene products.^1,2 Consequences can include recessive disease due to compound heterozygosity and alterations in expression level or allelic exclusion of gene products due to phasing of promoter or enhancer variants with respect to coding variants. The combination of two or more variants on a haplotype could alter the splicing, stability, transport, and translation of mRNA or could code for sets of amino acids that together alter protein properties such as stability, enzymatic activity, and binding constants. The importance of haplotypes extends beyond protein-coding sequences. For example, they could affect sites of epigenetic modification. In turn, epigenetic phenomena such as lyonization³ could exacerbate perturbations due to phase by causing one haplotype to be preferentially expressed.

Most documented examples of the importance of haplotypes are for local haplotypes that span no more than a single gene, but the very important MHC haplotypes are a notable exception.⁴ However, blocks of genes on the same chromosome that work together in functional networks could alter the function of those networks based on the phasing of the transcripts for each gene in the network. Information encoded in each chromosome molecule controls its folding, interaction with the nuclear proteins, and recombination with its homolog.⁵ The sequences encoding this information are poorly understood, in part because full haplotypes spanning entire chromosomes would be critical to a full understanding. Such chromosome-spanning haplotypes have never before been available. Many different haplotypes occur in the human population. Because of recombination and mutation, the haplotype of each chromosome of every individual is different from all others, with the exception of some chromosomes shared by identical twins. Therefore, haplotypes that include rare alleles and span entire chromosomes, or large portions of them, will play an increasingly important role in understanding biology, health, and disease.

There are three general strategies for deriving haplotypes: (1) population inference, (2) molecular haplotyping, and (3) genetic analysis.⁶ Population inference assigns, where possible, haplotypes from a database to an individual's genome and then might infer haplotypes on the homologous chromosomes by exclusion. Generation of the database and assignment of haplotypes might be done simultaneously and iteratively on a number of haplotypes. Molecular haplotyping begins by isolating single molecules or populations of identical molecules of DNA by cloning, molecular biology, or physical manipulation. Each molecule is then partially or completely sequenced, and all resulting variants are determined to be in a cis relationship. Genetic analysis infers haplotypes by applying principles of genetic inheritance to genotype data in the context of a pedigree. If overlapping haplotypes derived from any of these three strategies are sufficiently characteristic, longer haplotypes can be generated by tiling, or haplotype assembly.⁷ For example, in the early stages of the Human Genome Project, molecular haplotyping was performed by sequencing isolated clones followed by haplotype assembly to produce haplotypes spanning many hundred kilobases.⁸

Molecular haplotyping is currently limited because most techniques can only provide a sequence from short molecules, whereas other techniques that can be applied to long molecules cannot provide a sequence for all variants. Some new techniques show promise for large-scale phasing. Kitzman et al.⁹ achieved haplotype blocks of approximately 350 kb by employing a strategy of pooling fosmid libraries. Fan et al.¹⁰ dispersed intact chromosomes from a single cell and phased almost 90% of a panel of ∼970,000 SNPs. Fan et al.¹⁰ also haplotyped rare SNVs on a portion of chromosome 6. These techniques could be improved, particularly if their development can be driven with reference to fully determined chromosomal haplotypes.

Current whole-genome sequences do not directly produce full-chromosome haplotype information because they are based on short molecular reads. Even in the context of the pairwise end-sequencing strategy, many read pairs do not span more than a single variant, and the remaining reads provide only meager grist for haplotype assembly. However, despite this apparent inadequacy, we demonstrate here that whole-genome sequences in the context of pedigrees can generate complete chromosomal haplotypes.

Whole-genome sequencing is required to generate these complete chromosomal haplotypes because it is the only approach that assays all alleles, including rare alleles such as those arising by de novo mutation in recent generations. We present here an algorithm for phasing by genetic analysis and apply it to two nuclear-family pedigrees. Our derived haplotypes span entire chromosomes, are nearly 100% accurate, and will be suitable for use in medical diagnostics. Our method can serve as a gold standard for other approaches to phasing. The comprehensiveness is limited mostly by the completeness of sequencing data. Therefore, as whole-genome sequencing methods become increasingly comprehensive, so will the haplotypes determined with our algorithm. For families with at least two children, all genomes in the pedigree can be phased, including parental genomes. Families with more than two children provide sufficient information to allow assignment of nearly all recombinations to specific meioses, as recently hypothesized.¹¹ The implementation of our algorithm, Haploscribe, brings a powerful approach to chromosomal haplotype specification that will open up new possibilities for exploring the functional implications of the phasing of various types of chromosomal variants across short to large chromosomal spans.

Subjects and Methods

Overview of Workflow

If the parental origin of both alleles of the variants of a chromosome were known, then the phase of those variants would also be known, as all the variants from one parent reside on one haplotype, and all the variants from the other parent reside on the other haplotype. Knowing the result of every meiosis in every individual in a pedigree would provide this parental origin information. Every allele in each founder can be traced forward through the pedigree through every descendant as if it were an informational packet flowing through a series of binary switches following Mendel's Law of Segregation. The status of each of these switches at a given position of the pedigree is encoded in algorithms as meiosis-indicator vectors.¹² Under this analogy, the packets of allele information also flow through splitters to allow the same allele to be distributed to more than one child of a parent. Each bit in these binary meiosis-indicator vectors corresponds to the parental origin (either maternal or paternal) of each allele in every gamete. Each nonfounder (i.e., child) is the product of two gametes, so each meiosis-indicator vector has two positions for every nonfounder. For example, the pedigrees in Figure 1 each have four nonfounders, so the meiosis-indicator vectors for these pedigrees are eight-bit vectors. Our algorithm determines meiosis-indicator vectors at every position of the reference genome. Where this is not possible, such as in short blocks encompassed by the confidence intervals for assignment of recombination positions, the algorithm determines as many bits of the meiosis-indicator vector as possible and leaves the remaining bits ambiguous.

Figure 1.

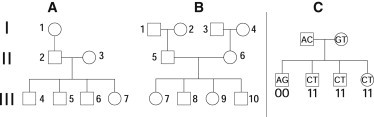
Sextet Pedigrees and Representation of Inheritance States

(A) Pedigree A and (B) pedigree B (CEPH 1463). Genomes for only the individuals in generations II and III were used for genetic phasing (nuclear-family sextets). The displayed grandparents in generation I of pedigrees A and B have been sequenced, but the data were not used for haplotyping. Grandparental data were used to confirm the phasing of haplotyping for the nuclear families composed by generations II and III.

(C) Inheritance states are represented by binary vectors indicating the result of Mendel's first law of segregation at a given aligned position of all the genomes in a pedigree. For example, at this hypothetical tetra-allelic position, the first child has received the first allele from the first parent and the first allele from the second parent; these are indicated as “00.” The other children receive the other alleles, indicated as “11.” Combined, the binary inheritance-state vector for this pedigree at this position is “00111111.” Because the labeling of the parental genotypes is arbitrary, the first two bits in a two-generation nuclear-family inheritance-state vector can always be set to 0. Most variant positions in the genome are biallelic, and so inheritance state must be deduced from sets of adjacent variants.

Following an arbitrary convention, we use the label 0 to indicate paternal origin in meiosis-indicator vectors, and 1 to indicate maternal origin. With the exception of sex chromosomes in males, the parental origin of the haplotypes of the founders cannot be known from genetic data alone. Therefore, for autosomes assignment of the labels 0 and 1 is arbitrary in founders, and any packet of allele information that flows through the pedigree from a particular founder can have all of its bits flipped without changing the information contained in the meiosis-indicator vectors, as long as all the bits are also flipped for the other allele of that founder. If the number of nonfounders is n, and the number of founders is f, then from an informational standpoint the number of distinct meiosis-indicator vectors is 2²ⁿ/2f. Each informationally distinct meiosis-indicator vector is an inheritance state.¹³ For a nuclear family of four, there are four inheritance states.¹⁴ For a nuclear sextet, there are sixty-four inheritance states.

Genetic analysis is effective for determining the inheritance state for nearly all segments of a reference genome.¹⁴ Because of genetic linkage, the inheritance states of adjacent positions in a pedigree are nearly certain to be identical. For example, in a family quartet, the inheritance state will change between two positions only if there has been a recombination between those positions in one of the four meioses of the pedigree. If a recombination occurs once every hundred megabases per meiosis (approximately a Morgan), then an inheritance-state block will average 25 Mb. Variants in whole-genome sequencing of quartets occur about one per kilobase, so blocks contain an average of about 25,000 variants. Pattern recognition in the aggregate of all the variants in a block nearly always uniquely determines the inheritance state of that block. Boundaries between blocks can be precisely established to within the boundaries set by a few variants (and thus to within a few kilobases) because of the characteristic patterns of these variants.

The assignment of indicator labels to founder alleles is arbitrary but must be consistent across the entire length of each chromosome. Therefore, the inheritance states of all blocks on a chromosome for the pedigree can be converted to meiosis-indicator vectors by setting the assignment of allele labels in those blocks consistently with the arbitrary labeling of the first block. This assignment is performed under the parsimonious assumption that only one (or very few) recombinations occur between blocks. The resulting meiosis-indicator vectors can be used to phase nearly every position for which data are available. The more children per generation, the more likely the parsimony assumption holds, and therefore the more likely it is that adjacent blocks will be properly phased with respect to each other.

Phasing a position requires assigning an observed allele (e.g., A, G, C, T, or Δ) to each of the indicators (0 or 1) in a founder and then using the meiosis-indicator vectors to trace the allele through the pedigree. As long as at least one individual in the pedigree is homozygous at a position, then allele assignment in that individual is trivial, and assignment in all other individuals in the pedigree follows by iterative exclusion of previously assigned alleles. Therefore, the only positions that cannot be phased are positions at which every individual in the pedigree is heterozygous for the same two alleles (e.g., all six individuals in a sextet have the T/G genotype). Such positions are rare in large pedigrees and furthermore could often not be “true” heterozygous positions but rather reflect mapping of variant copies of repetitive DNA to one locus. The larger a pedigree, the less likely it is that all individuals will be truly heterozygous at any reference position, and the resulting haplotypes will be more complete.

In the implementation of our algorithm presented here, we first compute recombinations and blocks in all family quartets, including overlapping quartets, and assign one of the four quartet inheritance states to each block. We then build inheritance states for the entire nuclear family from the intersections of all quartet blocks, reconciling any conflicts and preserving any ambiguities. In nuclear families with more than two children, such as the sextet examples presented here, this process also permits phasing of adjacent blocks with respect to each other. Meiosis-indicator vectors are then determined by choosing parsimonious labelings of founder haplotypes, and haplotypes are determined by matching alleles to meiosis indicators.

Pedigrees

We present data from two sextets (pedigrees A and B) to provide example applications of our algorithm (Figures 1A and 1B). Pedigree A is part of a clinical study; data are not available because of preclusions in human subjects protocols. This study was performed under the Western Institutional Review Board's protocol number 20100003. Procedures followed were in accordance with institutional and national ethical standards of human experimentation. Proper informed consent was obtained. Pedigree B is Centre d'Etude du Polymorphisme Humain (CEPH) pedigree number 1463 and is described by Coriell (Web Resources) with whole-genome sequence data available from Complete Genomics Incorporated (CGI) (Web Resources). CEPH labels for the individuals in pedigree B are, in order: 12889, 12890, 12891, 12892, 12887, 12878, 12885, 12886, 12887, and 12893 (Figure 1B).

Genotype Sequence Generation

Generation of genotypes is also known as diploid genome sequencing or whole-genome resequencing, and more succinctly if less accurately as “whole-genome sequencing.” For pedigree A, we contracted with CGI to sequence the genomes of these seven individuals. These data had 21,891 Mendelian inheritance errors (MIEs) across the sextet pedigree among 3,143,886 SNV positions variant in at least one individual along the 2,684,578,480 autosomal bases of the Genome Reference Consortium's reference genome GRCh37 also known as hg19. Of all sporadic errors, four out of six will occur in one of the four children, so the per-genome sporadic genotype error ratio is 2.0 × 10⁻⁶. The fraction of the reference genome that was fully called for the individuals of pedigree A ranged from 93.6 to 96.9%. Data for pedigree B were obtained from the CGI website.

Our algorithm is able to phase all variants that are mapped to particular positions on a linear reference chromosome. Such variants include SNVs, insertions, deletions, and microsatellites. However, assignment of identical-by-descent (IBD) status between pairs of individuals at sites of complex indels requires specialized algorithms. Errors in phasing indels and microsatellites are more likely to arise from uncertainty in mapping these variants to the reference than they are from a failure of the haplotyping algorithm. For this reason, SNVs are superior to indels for the purpose of benchmarking haplotyping algorithms.

Compressions

Many loci in raw genome data that are heterozygous in all family members and thus appear to be unphaseable are not truly heterozygous—they reside in repetitive DNA, such as copy-number variations or compression blocks. Compression blocks are regions of the human reference sequence that represent more than one portion of the actual human genome. For example, a duplication present in all humans but represented only once in the reference is a compression. Compressions were identified as regions of excess heterozygosity in multiple pedigrees with unrelated founders. Positions within compression blocks were filtered prior to further analysis. We excluded positions from 57 compression blocks encompassing 2946 kb of the reference genome.

De Novo Mutations and Genotyping Errors

De novo mutations and genotyping errors were identified, insomuch as data allowed, and filtered prior to further analysis. MIEs (including de novo mutations) and inheritance-state consistency errors were identified as described previously.¹⁴ Multiple independent coverages of a haplotype from sequencing several siblings enables error correction. For example, in blocks where all four children are genetically identical, a single allele error in one child could be corrected to the value observed in the other three children. However, to maximally protect our algorithms from noise that might result from incorrect error correction, we did not apply such corrections to our workflow—we simply filtered all detected mutations and errors by excluding data from these positions from all individuals in the pedigree.

Quartet Inheritance States

Inheritance states were determined for all pairs of children with respect to the two parents as described previously.¹⁴ A hidden Markov model (HMM) algorithm predicted one of four states: identical, haploidentical maternal, haploidentical paternal, or nonidentical. To reduce noise, we prefiltered positions that are heterozygous in all individuals. Such positions are likely to arise from mapping errors associated with repeats, copy number variations, or unrecognized compressions. Partially called positions were also prefiltered. Such positions are more likely to contain errors than fully called positions. Aggressive filtering of variants reduces false-state transitions that might otherwise result from application of the HMM. Postprocessing of inheritance states further suppresses false blocks reported by the HMM. Postprocessing eliminates short states with atypical emission distributions such as could arise from hemizygous inheritance patterns.

The binary representations of the four inheritance states are: “0000,” “0001,” “0010,” and “0011.” The first position in each binary-state representation specifies the origin of the paternal allele of the first child. The second position specifies the origin of the maternal allele of the first child. The third position specifies the origin of the paternal allele of the second child. The fourth position specifies the origin of the maternal allele of the second child. For example, “0010” indicates that the first child received one allele from the first chromosome of their father and the other allele from the first chromosome of their mother and that the second child received one allele from the second chromosome of their father and one from the first chromosome of their mother. In the absence of grandparental data, which are excluded by definition from quartet analysis, labeling of the parental chromosomes as “first” or “second” is arbitrary. Therefore, the inheritance state that might be represented as “1001” could just as well be written as “0011” by switching the labels of the paternal chromosomes. We canonically record binary representations of inheritance states as the lowest binary number that can be achieved by switching labels of one or both of the two sets of parental chromosomes. Therefore, the first two digits in a binary representation of an inheritance state are always 0.

Partial Quartet Inheritance States

Each position is assigned the state traversed by the most probable Viterbi path through the HMM at that position. Thus, positions that separate two high-confidence inheritance-state blocks and that are consistent with both blocks will be assigned to one or the other block. If these potential misassignments were not detected, inheritance-state errors could occur because of inaccurate block boundaries. In a postprocessing step, these uncertain positions are removed from the edges of adjoining states, chewing back the edges of states until an informative position is reached. As a result, not all positions in the genome are assigned to a high-confidence, fully determined quartet state. For example, in the first family presented here, only 98.2% of the reference genome is assigned to a high-confidence fully determined quartet state. Much but not all of the remaining 1.8% of the reference genome lies in reference gap positions.

For a given pair of children, portions of the genome between two fully called inheritance states typically have ambiguity in either but not both of the maternal- or paternal-state indicators. For example, the short state between the confident states “0010” and “0011” most parsimoniously will harbor no recombinations from the paternal meiosis and one from the maternal meiosis. Therefore, the short, partially ambiguous state can be represented with a ⋅ as an ambiguity variant: “0⋅1⋅”. Intervals in which two recombinations occur between informative variants might be fully ambiguous; their inheritance states are represented as ⋅⋅⋅⋅. For record-keeping purposes, intervals at the beginning and end of chromosomes preceding or following the first informative variant are represented as xxxx. The x represents the absence of information; the ⋅ character represents ambiguous information. Most probably, no recombination occurs in an interval represented with an x. Barring multiple recombinations in other meioses in a short interval, a recombination most probably does occur in an interval marked with a ⋅. A more general probabilistic framework could more precisely capture probabilities of recombination in short intervals, but given the data density of whole-genome sequencing, the use of such a framework would be unlikely to alter results, except to indicate uncertainty across long regions with no variants—but such uncertainty is known before analysis is begun, so there is no gain. The process of intercalating partially determined inheritance states is illustrated in Table 1.

Table 1.

Partial Inheritance State

Before Intercalation	After Intercalation
0010	0010
0000	00⋅0
0001	0000
0011	000⋅
0010	0001
0011	00⋅1
	0011
	001⋅
	0010
	001⋅
	0011

Column 1 is a list of quartet inheritance states as determined by an HMM algorithm with postprocessing to eliminate the uncertain edges of blocks. Between each inheritance state is an interval in which a recombination occurred. In this interval, the inheritance state is partially unknown. The indicator for this ambiguity is a dot. The first two indicators for inheritance-state vectors are always zero when they are represented in canonical form.

Sextet Inheritance States

Six overlapping quartets can be formed from a family with four children. The inheritance state for the entire family at any position can be constructed from the six quartet states at that position. Each of the eight binary-state indicators (Figure 1C) for a sextet inheritance state is represented in three of the 24 indicators of the quartet states (four indicators for each of six states). Therefore, considering all 64 possible labelings of parental chromosomes for the six quartets (2⁶ = 64 possible labelings, but because of symmetry only 2³ = 8 need be considered), one chooses the set of labelings that maximizes the concordance of the three indicators for each of the eight meioses. For almost all positions, there will exist a labeling for which all indicators are concordant. The x and • indicators are considered concordant with all other indicators. However, positions in intervals that contain two recombinations between informative variants will have overconfident inheritance-state indicators called in at least one quartet. Therefore, if the number of ambiguity (•) indicators exceeds the most frequent 0 or 1 indicator, a position is called ambiguous. The process of building higher-order inheritance states from quartet inheritance states is illustrated in Figure 2.

Figure 2.

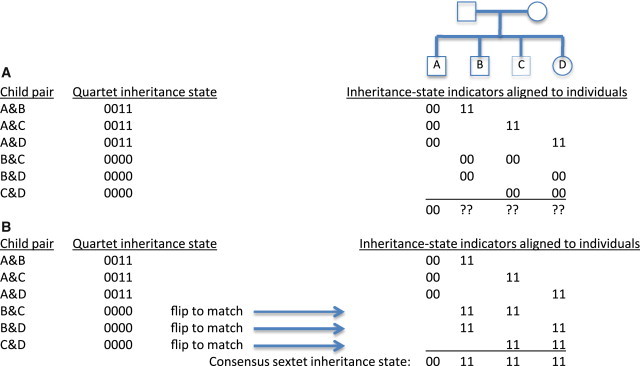
Constructing a Higher-Dimensional Inheritance State from Tiled Quartet States

(A) Initially, the inheritance states of each quartet pair are independently labeled. Considering the pedigree shown, at some particular position of the reference genome individuals B, C, and D have all received identical alleles from the two parents, and so are genetically identical. Individual A received distinct alleles from both parents and so is nonidentical with respect to each of the other three. The binary representations of each quartet state are inconsistent when placed in register with respect to each other.

(B) After enumerating all arbitrary reassignments of the first two indicators, the best consistent matching of all six indicators produces a consensus binary representation of the sextet inheritance state. At this position, the first two indicators of each of the B and C, B and D, and C and D quartets are flipped, requiring that the second two indicators in each quartet also be flipped in order to maintain the consistency of the inheritance state.

Alternative Approaches for Inferring n-tet Inheritance States

A family with n − 2 children is an n-tet, or a “nuclear family of n.” Such a family can be tiled as a set overlapping quartets for all possible pairs of children, or C(n−2,2) quartets. For example, a family with four children provides six ways of pairing two of the children into quartets. Once determined, these C(n−2,2) quartet inheritance states can be overlaid to arrive at a single n-tet inheritance state. Considering S inheritance-states and a genome of length G, the computational complexity of an HMM-based state inference is O(GS²). Therefore, the computational complexity of deriving inheritance states for an n-tet by tiling quartets is O(C(n−2,2)G4²), or more simply O(GC(n−2,2)). Alternatively, for larger families, not all quartets need be determined. However, ignoring one or more quartets could lead to haplotyping ambiguity or errors, so computational speed increases would be offset by degradation of the quality of the results.

As another alternative, all the data can be analyzed in a single pass to directly arrive at an n-tet inheritance state without the use of tiled quartet states. The number of inheritance states in an n-tet is 2²ⁿ⁻⁶, so the complexity of an HMM approach would be O(G2⁴ⁿ⁻¹²). Despite this much greater complexity compared to tiling algorithms, the direct approach is feasible. Even without optimization, an HMM can resolve all sextet states for a human genome in a few hours on a modest processor. Certain speedups substantially reduce the complexity of HMM algorithms. For example, one approach is to only consider transitions between states requiring exactly one recombination. Furthermore, non-HMM algorithms for partitioning work fairly well and run with complexity O(GS) or less. However, despite computational feasibility, it is harder to parameterize and train algorithms that operate directly on large pedigrees, both because fewer datasets are available and because they have a larger number of parameters. Furthermore, the shorter the average length of a state, the more easily noise can falsely invoke a state transition. Average state length drops proportionally to the number of possible states, and therefore noise becomes harder to suppress in larger families unless the assumption of first-order Markov dependence is abandoned. Noise can arise from real data aspects such as those resulting from ancient selective sweeps, data generation errors, mismapping of reads to the reference sequences, or imperfect reference sequences. The complexity of postprocessing to identify ambiguous state indictors also rises with the number of states. Therefore, we focused our development on a robust workflow based on initial determination of quartet inheritance states and then application of tiling algorithms to build a single encompassing inheritance state for larger pedigrees.

Sextet Meiosis Indicators

The freedom in labeling parental chromosomes permits labelings to vary between adjacent inheritance states. Therefore, if inheritance states are used to directly infer haplotypes, the phase of haplotypes could be incorrect across inheritance-state boundaries, and switch errors could be introduced. A switch error is an incorrect assignment of phase between two variants.¹⁵ To avoid switch errors, inheritance-state vectors must be converted into meiosis-indicator vectors before phasing. Meiosis-indicator vectors assume a prior specific labeling of parental chromosomes. For each chromosome in a nuclear family (assuming no grandparental information is available) there is one degree of freedom for labeling each parent. This degree of freedom is used to fix the labeling of the parental chromosomes relative to a single inheritance-state block of that chromosome. For clerical convenience we use the first block for this purpose. Therefore, the first two bits of the first nonambiguous full meiosis-indicator vector for each chromosome will always be 0. If grandparental information is later (or concurrently) added to supplement the genetic analysis of a two-generation nuclear family, the labels could be switched to match grandparental haplotypes. Each meiosis-indicator vector (representing a block of the chromosome) is obtained by parsimony from the preceding vector by choosing a labeling of parental chromosomes that minimizes the number of bit flips (Hamming distance) between the vectors. The resulting minimal distance between fully determined vectors is the number of recombinations between the vectors. In nearly all cases, this distance is exactly one. When the distance is greater than one, multiple recombinations have occurred, and there are two equally parsimonious assignments of meiosis indicators. Subsequent use of such meiosis indicators could result in a switch error (see Results). In practice, all fully called vectors are separated from the next fully called vector by a vector with an ambiguous bit corresponding to the recombinant meiosis (or meioses) unless a recombination has occurred precisely between informative variants that are at adjacent positions of the reference genome (not seen in our data). The process of determining meiosis indicators is illustrated in Figure 3.

Figure 3.

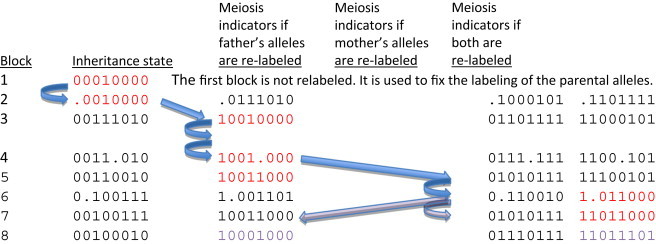
Phasing Inheritance-State Blocks by Parsimony

An inheritance-state vector for four children of a sextet consists of 8 bits. The first, third, fifth, and seventh bits relate the paternal alleles of each of the four children, and the second, fourth, sixth, and last bit relate the maternal alleles. If two bits are identical (i.e., 0 and 0 or 1 and 1), the alleles are IBD. If the bits are not identical (e.g., 1 and 0), the alleles are not IBD. If one of the bits is the ambiguity character (•) then IBD is not determined between that pair of individuals. By convention, the first two bits of an inheritance-state vector are always set to 0. Inheritance-state vectors can be converted to meiosis-indicator vectors by relabeling the bits for each block so that they consistently correspond to the meiotic origin of each allele, rather than simply relating IBD status between individuals. There are four possible meiosis-indicator vectors for each inheritance-state vector. Adjacent blocks of the genome are separated by short distances between informative variants that localize recombinations and so the parsimonious choice of the four labelings is the one that minimizes the number of recombinations between adjacent states. If there has been a single recombination, there is exactly one choice of labeling that represents a single recombination from the previous block (blue arrows). If there are two or more recombinations, then there could be more than one parsimonious choice and ambiguity results (purple arrows). The set of meiosis-indicator vectors in red corresponds to the parsimonious labelings that reflect one recombination each between blocks 1 and 3, 3 and 5, and 5 and 7. Blocks 2, 4, and 6 are intervals in which recombinations have occurred and so contain an ambiguity character.

Meiosis-Indicator Hypercube

A hypercube provides a convenient visualization of the process of converting inheritance-state vectors to meiosis-indicator vectors. Any bit vector of length l can be represented as an l-dimensional hypercube. A recombination flips a single bit of a meiosis-indicator vector and so can be represented as a single edge of the hypercube connecting two adjacent vertices.¹⁶ A surjective mapping of the meiosis-indicator vertices to inheritance states maps four vertices each to a single state. This surjective mapping corresponds to the four informationally equivalent labelings of the alleles of the two parents. Initially, our algorithm assigns blocks of the reference genome to one of the inheritance states, but does not immediately assign one of the four possible meiosis-indicator vectors that might give rise to that state. A seed block (e.g., the leftmost) is assigned to a position in the meiosis-indicator hypercube. An adjacent block then has four possible vertices to which it might be assigned. The chosen vertex for the adjacent block is the closest, usually adjacent, of these four vertices to the seed vertex. The assignment process continues sequentially until all blocks are assigned. Ambiguity might arise if two vertices of the four possible vertices of the next block are equally distant to the vertex of the current block.

We use the initial block of each chromosome as the seed block. The choice of seed block is irrelevant unless the assigned inheritance state is so grossly incorrect that parsimony cannot phase it with respect to both flanking high-confidence blocks such that those two blocks are properly phased with each other. Because the first block is not flanked on both sides, it cannot be an improper seed choice. Seed choice would not have altered any results for either of the two pedigree analyses we present here. Seed choice might be more important if there were long blocks of odd inheritance states, as might occur if some DNAs analyzed were sufficiently aneuploid. In this case, an improvement to the algorithm might result if it checked for the possibility that the most parsimonious explanation of the data is to ignore one or more blocks.

To avoid some potential for ambiguity, the process can be simplified. Paternal and maternal meioses can be treated distinctly and separately, resolving first one set and then the other. For each set, each inheritance state could map to one of two (rather than four) vertices of an (l−1)-dimensional hypercube. If n is the number of children in a nuclear family, and r is the number of recombinations between variants in different meioses of the same parent, ambiguity arises if r = n/2. Ambiguity never arises with an odd number of children—but errors can occur. An error because of failure of the parsimony assumption can occur in any sized pedigree if r > n/2. Therefore, in nuclear families with four children, two recombinations in the same parent occurring independently in different meioses in the same interval will be recognizable but unresolvable in the sense that the recombinations cannot be unambiguously assigned to meioses. Three recombinations will be recognized as one recombination and be falsely assigned to the child with no recombination. Ambiguous or incorrect phasing because of multiple recombinations can only occur in the genomes of parents (founders). Errors and ambiguity in children (nonfounders) cannot occur because phase is fixed by reference to parental genotypes.

Once the process is complete for the paternal hypercube, it is repeated for the maternal hypercube. By separating analyses for the two parental hypercubes, the calculation of potential ambiguity and errors is simplified. For example, in a pedigree with five children, even if there are four recombinations between two variants in four separate meioses, they will all be assignable to specific meioses if two are paternal and two are maternal.

Autosomes and Sex Chromosomes

Our method is described in detail for autosomes. Extensions to the sex chromosomes are trivial and are derived from simplifications of the algorithms for the autosomes. The pseudoautosomal region is treated as an autosome with the constraint that the meiosis indicators of the pseudoautosomal region match those of the X and Y chromosomes where they abut. The meiosis indicator of the Y chromosome is always 0—indicating paternal origin.

Haplotypes

All possible orderings of the genotypes for all individuals in the pedigree at a coordinate can be considered in the context of the meiosis indicators for that position. For the special case of all biallelic variants, if x individuals are heterozygous or partially called, the number of such orderings is 2^x. Orderings incompatible with the meiosis indicators are rejected. The remaining orderings provide a list of all possible alleles for each of the two haplotypes for each individual. For each of these lists, if at least one allele is called and all called alleles are identical, that allele is recorded. Otherwise, ambiguity is recorded at that position. As long as at least one individual in the pedigree has a homozygous genotype, there will be a single consistent ordering, and so there will be no ambiguity in haplotyping. If all individuals' genotypes are heterozygous (or cannot be distinguished from heterozygosity due to partial or absent base-calling), then all orderings are consistent with the meiosis indicators, and so the haplotypes will be ambiguous at that position. If a vector has a homozygous genotype in one individual and partial or absent base-calling in one or more other individuals, then the genotype vector can usually be unambiguously phased with the partial calls assigned to particular haplotypes. The placement of these partial calls can result in ambiguous haplotypes at these positions even though all the called alleles are phased. Haplotyping within a block is illustrated in Figure 4.

Figure 4.

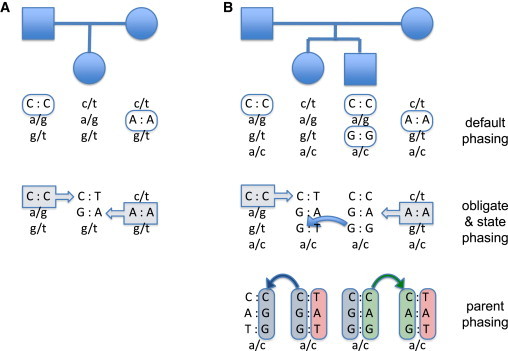
Example of Haplotype Inference

Upper-case alleles are phased genotypes; lower-case alleles are unphased. Haplotyping can be performed as a series of steps. The first step, default or trivial phasing, assigns phase to all homozygous positions. The second steps phases alleles in children or siblings that are identical by descent to alleles phased in the first step. For nuclear families with more than one child, a third step phases parental alleles. (A) Trios permit phasing in the child, but not at positions heterozygous in all three individuals. (B) Quartets permit phasing in the children, as well as within inheritance-state blocks in the parents, but not at positions heterozygous in all four individuals. Phasing in blocks of the parental chromosomes is possible because it is known that no meiotic recombinations occur within a block. Haploscribe performs all of these phasing steps simultaneously by matching all possible phased genotypes to meiosis-indicator vectors. Phasing between inheritance-state blocks requires data from additional children, as described in the text.

An incidental result of the haplotyping algorithm is that missing data are inferred to the fullest extent allowed by the called data. Briefly, any uncalled allele that can be assigned identity by descent to any called allele can be matched to the called allele by tracing the allele flow through the pedigree via meiosis indicators.

Results

Genetic Haplotyping

We haplotyped two nuclear-family pedigrees (Figure 1). For each, we phased all the autosomes of a nuclear family with four children. The density of SNVs permitted near deterministic identification of all recombinations (Figure 5). For pedigree A, genetic analysis phased 98.8% of the 3,082,065 fully called variants. For pedigree B, genetic analysis phased 98.4% of the 3,262,115 fully called variants. Variants that are heterozygous in all six family members of a pedigree cannot be phased.

Figure 5.

The High Density of Variants Determined by Whole-Genome Sequence Data Permits Full-Genome Haplotyping

(A) Haplotypes of all the autosomes for the four children of pedigree A. Blue and orange shades represent the two paternal and maternal chromosomes, respectively; dark and light shades represent segments inherited from the corresponding grandfather or grandmother, respectively.

(B) Expanded view of chromosome 1 showing the density of variants supporting the meiotic origins of each haplotype. Red, blue, magenta, and green represent regions inherited from the paternal grandfather, paternal grandmother, maternal grandfather, and maternal grandmother, respectively. The height of the gray bracket to the right of each graph corresponds to 1000 variants/Mb.

Recombination Intervals

Pedigree A harbored 283 recombinations, and pedigree B harbored 224 recombinations. The median resolution of recombination location was 6.4 kb (mean: 15.1 kb). Many of the longer intervals span centromeres or gap intervals in the reference genome. In pedigree A, there were two instances of recombinations occurring at the same locus in two separate meioses within the same parent, each at known hotspot.

Coverage of HapMap Markers

The markers chosen by the HapMap project are a useful independent reference for the completeness of generated haplotypes.¹⁷ There are 3,724,356 HapMap-verified SNP positions (excluding compressions) in dbSNP131. In pedigree A, 3,061,628 (82.2%) of these SNPs were fully called in all six individuals and 3,612,554 (97.0%) were at least partially called in at least one individual. In addition, the alleles at some partially or uncalled positions could be inferred from inheritance patterns. Most HapMap SNPs were homozygous in all individuals, but 1,149,248 were variable across the sextet genotypes. We phased 96.6% of HapMap SNPs in at least one member of the pedigree and 84.4% in all six members of the pedigree.

Use of a Grandparent for Verification of Phasing

Errors in raw data, a flawed reference sequence, or imperfections in implementing an algorithm could result in errors in predicting recombinations. To estimate error, we obtained sequences for one of the grandparents from pedigree A (I-1 in Figure 1A) and all four grandparents for pedigree B (I-1, I-2, I-3, and I-4 in Figure 1B). These grandparental sequences were not used in our phasing algorithm. For each grandparent, the set of all homozygous positions defines a haplotype that must have been transmitted to their child, a parent in one of the pedigrees. By comparing this transmitted haplotype to our computed haplotype, we determine an upper bound for error resulting from our algorithm, because differences observed between the two haplotypes are due to a combination of sequencing errors, de novo germline mutations, somatic variation, and haplotyping errors.

Of the homozygous positions in the genome of individual I-1 from pedigree A, 889,227 were heterozygous in her son (II-2). At each of these positions, this homozygous allele should be transmitted from grandmother to father, and all of these alleles will reside on the same haplotype of individual II-2. We compared these transmitted grandparental alleles to the alleles of the haplotypes determined for individual II-2 by our method as applied to the nuclear sextet of pedigree A. This comparison bounded our switch-error ratio to be less than 0.045% (Table 2). In two instances our inheritance-state analysis of this sextet had demonstrated two recombinations at the same location in different meioses of the same parent—one instance each for the mother and father. Genetic haplotyping in a nuclear sextet pedigree cannot parsimoniously phase across such an interval (Figure 3), resulting in phase ambiguity. Our software arbitrarily assigns phase across such ambiguities and so led to one long-range phase error in this haplotype. Switch-error ratios for pedigree B were comparable to those for pedigree A (Table 3). Our bioinformatics workflow will treat blocks of adjacent variants as a set of SNVs rather than as an indel. Therefore, for statistics reported here, SNVs with identical genotype vectors that are within 10 bp of each other are considered to be a single genetic variant for purposes of tabulating switch errors.

Table 2.

Switch-Error Ratios for the Father in Pedigree A

Smoothing	All Variants	Fully Called Variants Only	Ambiguous Transitions	Switch-Error Ratio for Fully Called Variants (%)
0	2154	366	2	0.0455%
1	182	22	2	0.0030%
2	44	2	2	0.0005%
3	14	2	2	0.0005%
4	6	0	2	0.0002%
5	4
6	4
7	4
8	0

All phase errors involve blocks of less than eight variants. The smoothing value is the number of consecutive discordant variants for which a breakpoint is not counted. In addition to outright errors, there are two ambiguous transitions due to recombinations in a short interval in separate meioses of the same parent. These two counts have been added to the switch-error count for tabulation of the last column (switch-error ratio), thus producing a slight overestimate of the error ratio. These ratios are low compared to previously reported switch-error ratios, which are typically 0.5%–15%.¹⁵ Local errors produce two switch errors, unless they are at the end of a chromosome; values in the table therefore tend to be even.

Table 3.

Switch-Error Counts for the Pedigree B (CEPH 1463) Considering Fully Called Positions Only

Smoothing	Paternal Grandpaternal	Paternal Grandmaternal	Maternal Grandpaternal	Maternal Grandmaternal
0	521	114	100	168
1	102	16	12	20
2	57	10	4	0
3	32	8	2
4	24	8	2
5	16	8	2
6	14	4	2
7	12	4	2
8-9	6	4	2
10-11	4	2	2
12-15	2	2	2
16-39	0	2	2
40-48		2	0
49		0

There are no ambiguous phasings in this pedigree. The two intervals with two recombinations partition the recombinations one to each parent, so phase is resolvable.

Reciprocal Switch Errors

If our algorithm incorrectly predicts the positions of recombinations that form the boundaries of inheritance states, then any errors in assigning haplotypes to a set of parental genotypes should be reciprocal. That is, if one allele of a genotype is improperly assigned to one haplotype, the other allele will be assigned to the other haplotype, producing switch errors on both haplotypes. All true switch errors should be reciprocal with the exception of those positions in a genome for which Mendel's first law of segregation is violated. These positions are most typically due to de novo mutations. If an apparent error based on comparison to grandparental sequences were due to an isolated sequencing error of an allele in one of the grandparents, then we would observe a discrepancy in one of the parental haplotypes but not the other.

Our ability to detect reciprocal switch errors at single positions in a genome is limited because we assay switch errors only at SNVs for which the parental genome is heterozygous and one or both of the grandparental genomes are homozygous. Almost all such positions derive from a single homozygous grandparent, a single heterozygous grandparent, and the heterozygous parent. To directly detect a single-position switch error would require two grandparents who were homozygous but for different alleles. Such positions are very rare. Switch errors are also very rare. Not surprisingly, we do not see a concordance of these two events and do not have data to report single-position switch errors. However, if switch errors span more than one variant, we could see evidence of reciprocity if at least one of these variants is represented by a homozygous position in each of the two grandparents.

Because we had sequences for all four grandparents in pedigree B (I-1, I-2, I-3, and I-4), we were able to check for reciprocity of switch errors. For this pedigree, there was one observed reciprocal switch error in the father's genome (II-5) and one in the mother's genome (II-6). The first reciprocal error spanned two adjacent SNVs in MUC3A/MUC3B (MIM 158371 and 605633). These paralogs reside in a compression block, and so their positions are prone to mismapping between paralogs. The second error spanned three adjacent SNVs in an ancient LINE element at positions prone to mismapping to other LINEs. The dearth of reciprocity of errors indicates that the vast majority of errors detected in our haplotypes arise from a subset of the rare errors in whole-genome sequencing data or in the reference genome and do not arise from errors in assignments of meiosis indicators within our algorithm. Therefore, the quality of genetic phasing can be expected to improve even beyond its current accuracy as the quality of genome sequence data and the reference improve.

Comparison with Molecular Data

We compared the pedigree A haplotypes with short molecular haplotypes derived from short-read data. Of 89,381 short molecular haplotypes linking heterozygous variants, only 15 were discordant with the genetic haplotyping. Of the 39,827 loci that were heterozygous in all individuals and therefore not genetically phaseable, 7,522 were resolved by molecular phasing.

Quartet Phasing

Haplotyping on a quartet works very well with the algorithm presented here. However, inferred haplotypes for a parent will not span any position for which a recombination occurs in one of that parent's gametes. Inheritance-state changes can be used to infer whether a recombination is maternal or paternal but are not sufficiently informative in a quartet to infer which paternal or maternal meiosis accommodated the recombination. Furthermore, if two recombinations occur in separate meioses of the same parent in the same interval (i.e., between two informative variants), a switch error will result. For many purposes, such as evaluation of compound heterozygosity within genes, a phase ambiguity or error will only be important if it occurs within the bounds of a particular gene. This likelihood depends on the length (in Morgans) of the gene, which is best empirically measured because of the uneven distribution and intensity of recombination hotspots. Considering each of the six quartets of pedigree B independently, on average the confidence intervals of the positions of 42 recombinations (37% of 112) intersected known genes, impacting 47 of 20,545 genes with National Center for Biotechnology Information GeneIDs, or 0.023%. Therefore, when quartets are employed for whole-genome genetic analysis, the haplotypes of much less than 1% of genes will be ambiguously phased in the parents. Phasing in the children of quartets will be unambiguous, as it is for all nuclear-family pedigrees.

Trio Phasing

A trivially degenerate application of our algorithm will phase a family trio—a nuclear family with one child. There is exactly one inheritance state that can be inferred for a trio, so the inheritance-state portion of the workflow is simply skipped. Equivalent algorithms for phasing a trio have been previously described (e.g., by Marchini¹⁸). For a trio, only the child's chromosomes can be genetically haplotyped and only at positions for which at least one of the three individuals is homozygous. To compare our results to those one would obtain by only sequencing a trio, we considered all four trio subsets of our analyzed family sextet for pedigree A. There were 6,671,910 instances of positions in which the genotype of a child was heterozygous. In 1,147,344 instances, the two parents were also heterozygous, so the child's genotype could not be phased from trio data. Of these instances, 988,040 were resolvable in the sextet because at least one sibling was homozygous. Therefore, for full chromosomes, the extent of heterozygous variant phasing in children rises from 83% in a trio to 98% in a sextet, and the extent of heterozygous variant phasing in the parents rises from near 0% to 98%.

In a trio, short sequence elements in the parents can be phased by employing the exceptionally parsimonious assumption that there are no recombinations in any meiosis and that each parent transmits unaltered chromosomes. Therefore, each chromosome of each parent has one haplotype identical to that transmitted to the child. In this case the number and position of switch errors in parental chromosomes is unknown, and the number of errors will average one per Morgan. This approach is capable of phasing genes with some confidence but cannot phase chromosomes. Therefore, we do not include this approach in our algorithm.

Density of Variants

Three parameters are directly relevant for designing a genetic haplotyping project for a nuclear family: raw data quality, the number of children sequenced, and the density of variants genotyped. Choice of reference sequence is a fourth parameter that tends not be easily adjustable; ideally, the reference sequence is collinear with the genomes of the pedigree. Raw data quality is primarily responsible for local switch-errors, as reported above. Long-range switch errors can only occur in parents, as discussed above. These can be largely eliminated in families with at least three children. In such families, long-range switch errors could occur when recombinations occur at the same position in different meioses of the same parent. Increasing the number of children analyzed will decrease such switch errors, as the number of recombinations within an interval that can be uniquely assigned to meioses rises. Such errors will increase with decreasing variant density as longer intervals between variants are more likely to harbor multiple recombinations. In pedigree B there is one interval with two recombinations. These two recombinations occur in separate parents, so no haplotyping ambiguity results. If the set of variants were to be restricted to a SNP panel containing 425,220 fully called variant positions in the pedigree (the set from the Affymetrix Genome-Wide Human SNP Array 5.0), then two such intervals occur, again resolvable because the recombinations are in different parents. If the set of variants is further restricted (GeneChip Human Mapping 500K Array), then three such intervals occur, all again resolvable because the recombinations are in different parents. However, if the variant density were to be restricted to 56,232 positions (GeneChip Human Mapping 100K Array Set), then eight such intervals occur, one of which would contain three recombinations. We conclude that haplotyping parental genomes of nuclear families works best with whole-genome data but that it will have a fairly low long-range switch-error ratio even if the variant density is as low as a few hundred thousand well-chosen SNPs per genome. However, the number of local haplotyping errors rises as variant density decreases. For the panel of 425,220 SNPs, 0.11% of heterozygous genotypes were discordantly phased with respect to the whole-genome analysis. For the panel of 56,232 SNPs, 1.2% of heterozygous genotypes were discordantly phased. These local errors increase primarily because of increasing uncertainty in the bounds of inheritance-state intervals.

Use of Partially Called Positions to Improve Resolution

To err on the conservative side, all inheritance-state blocks were based on variant positions fully called in all individuals in the pedigree. Inclusion of partially called positions improves resolution of some recombination intervals. For example, for pedigree B, the mean length of intervals drops from 14.1 kb to 12.2 kb. Of the 224 intervals, 29 were further constrained, resulting in the reduction of the number of reference bases assigned to ambiguous sextet inheritance states by 417,911 bp. The average reduction of each of these 29 intervals was 14.4 kb. The longer an interval (with length in this case excluding reference gaps), the more likely an informative partially called variant will exist within. Therefore, the intervals with increased resolution tended to be longer than average, with a mean of 29.4 kb when determined with fully called variants. In a few cases there was a large percent reduction in interval length (e.g., 74,134 to 2,209 bp = 97%) or reduction to very short length (e.g., 1021 to 368 bp). Partially called variants tend to have slightly higher sporadic error than fully called variants. Use of partially called variants would result in a small increase in the number of phased genotypes in one or more individuals, but the phase of these positions would be more uncertain than the phase of fully called positions.

For some purposes, such as identifying target sequences associated with recombination hotspots, there could be increased value in further precision in localizing positions of recombinations, ultimately to an interval between adjacent base pairs. It is not clear how one could achieve such precision in the absence of variants denser than those found in human populations. Our attainment of a mean precision (including reference gaps and centromeres) of about 6 kb probably approaches the maximum achievable precision without sacrificing accuracy. We could, for example, assign every recombination to a single base interval at the center of our confidence intervals or inform our localization with population-level data on hotspots. However, for haplotyping there is no value in assigning a recombination more precisely than to an interval between variants. Therefore, for purposes of the work described in this paper, we have achieved a precision and accuracy in defining recombination locations near the theoretical maximum, as defined by utility for haplotyping.

Discussion

Many algorithms exist for haplotyping, although none to our knowledge have been incorporated into workflows capable of handling whole-genome data. Algorithms implemented in Merlin and Genehunter recognize and use inheritance states (summarized in Roach et al.¹⁴). These software implementations were designed to work with variants of relatively low density in comparison to whole-genome sequence data. They employed probabilistic approaches because the exact localization of recombinations was imprecise. Now, whole-genome sequence data permit the assignment of 99.9% of the genome to exact inheritance states. This high confidence in state determination enhances noise suppression because otherwise each position must be considered as possibly being one of several states. Consequently, the haplotyping output from our algorithms has an extremely low switch-error ratio (Tables 2 and 3).

Completeness and Accuracy

Phasing algorithms (including Haploscribe) can be tuned to increase the number of variants phased (increased completeness) but at an increased switch-error ratio (decreased accuracy). Therefore, comparisons and contrasts between different algorithms must include these two parameters. For example, a comparison might explore the switch-error ratio of an algorithm as a function of the number of variants covered. Furthermore, not all variants are equivalently easy to phase. For example, very common SNPs are more likely to be heterozygous in all family members than very rare SNPs, and such fully heterozygous positions are not possible to phase genetically. Also, some panels of SNPs are more informative than others for the purpose of recombination inference.

Our algorithm by default leaves unphased all variants for which phase cannot be determined with near certainty. These unphased variants either have uncalled or partially called genotypes (about 5%–10% of all variants in current CGI data) or reside in the small percentage of the genome for which the inheritance state is too ambiguous for phasing (affecting less than 0.1% of all variants). Because the algorithm only reports results that are nearly certain, it sacrifices some completeness for accuracy. This sacrifice is appropriate if haplotypes are intended for diagnostic purposes. The algorithm could be tuned to report more complete results but with more switch errors. Currently the single best approach to improving our results would be to increase completeness and accuracy of genotype data. Improvements in completeness and accuracy of whole-genome data are rapidly being made by the research community, so the specific results we report here should be considered as reflecting a snapshot with the expectation that these metrics will improve over time.

Molecular Phasing

Molecular phasing is a straightforward complement for genetic phasing. In many cases, whole-genome sequencing data include some information about local phase relationships. For example, variants on the same sequenced DNA fragment can be phased with respect to each other. Molecular phase data can be used to phase positions that are heterozygous in all individuals in a pedigree or to phase across inheritance-state boundaries for which the phase is ambiguous. The generation of sequence reads that are of 10,000 bases or more and that span at least several variants should facilitate molecular phasing, as will application of strategies such as pairwise end sequencing that provide the sequences of nonadjacent alleles on the same molecule. Haplotypes derived from genetic and molecular phasing can be combined through the jigsaw-puzzle-like process of haplotype assembly.^19,20

Population-Based Phasing

Algorithms for population-based haplotyping, such as Clark's algorithm or that of PHASE,⁶ rely on the inference of haplotypes by application of strong parsimony assumptions, such as requiring that alleles be assigned to common haplotypes if at all possible. Therefore, such algorithms overpredict common haplotypes. Also, if haplotypes are sufficiently long, there are no common haplotypes because even in isolated populations the most frequent haplotypes are diluted among rare or unique combinations of the many thousands of variants on these haplotypes. At most, these haplotypes can span a fraction of a Morgan because otherwise they would probably be broken by recombination at least once in any pedigree. Furthermore, population-based algorithms are incapable of accurately phasing rare variants, such as those that never occur in population reference data. Rare variants are important for personalized medicine because they are often responsible for detrimental functions. Even in the absence of rare variation, these methods could incorrectly phase rare combinations of common variants, and these combinations could be detrimental through their interactions. Therefore, we do not recommend combining population-based haplotypes with molecular and genetic haplotypes for use in personalized medical applications.

Missing Individuals

Actual data for either or both parents are not strictly necessary to enable our algorithms or workflow. A substantial fraction of such missing data can be inferred from child genotypes. However, missing data decrease signal and increase noise, and so many of the advantages of our approach would be attenuated. However, some phase information could be obtained by sequencing two siblings and not their parents. An exploration of the degradation of the inheritance-state signal is provided in Figure 2 of Roach et al.¹⁴ If only two siblings are available, uncertainty in recombination location increases by several thousand bases, but otherwise quartets can be assigned to identical, nonidentical, and haploidentical states. In identical and nonidentical states only homozygous alleles can be phased (trivially), but in a haploidentical state if one of the siblings is homozygous, heterozygous alleles of the other sibling can be phased.

Multigenerational Pedigrees

We present algorithms and implementations for two-generation nuclear families. These algorithms are extensible to larger pedigrees. The most straightforward extensions are by using tiling algorithms similar to those described elsewhere (e.g., by Wijsman²¹ as well as Qian and Beckmann²²) and similar to those we use here to build inheritance states for large families from tiled quartets. We can phase multigenerational pedigrees with existing algorithms by using approaches such as tiling information from trio analysis.²¹ However, to take full advantage of multigenerational pedigrees with embedded quartets, our algorithm can be extended by extending the scope of inheritance states as implemented in our HMMs to arbitrarily structured pedigrees. Labelings of parental haplotypes are matched where tiles overlap by matching the alleles of haplotypes. Such extensions have been successfully applied to earlier generations of similar algorithms such as those of Merlin and Genehunter.

Cell Lines

DNA for pedigree B was extracted from cell lines. Thus, we had a greater expectation of somatic structural variations than if we sequenced DNA from blood. Structural variations can produce errors in quartet inheritance states. If they occur in one of the children, these errors will manifest in all quartets involving that child but not in other quartets. Therefore, the utility of multiple children facilitates increased accuracy when data are derived from cell lines because structural variations can be detected as discrepancies between subsets of quartet inheritance states. However, for the cell lines in our studied pedigree B, this increased power to identify errors did not result in any detected errors. We conclude that these cell lines were sufficiently euploid to enable full and accurate haplotyping. However, many cell lines will harbor aneuploidy. Our methodology should be useful for haplotyping such cell lines in the context of large pedigrees.

Existing Methods

Existing methods for haplotyping have shortcomings limiting their broadest applicability. Rule-based haplotyping (e.g., the algorithm of Wijsman²¹) has focused on the power of trios and multigenerational families to haplotype single variants. In these methods, recombinants are identified by trio-based phasing on families with at least three generations of data. Addition of inheritance-state-based inference permits increased resolution of recombination localization. The information present in genotypes of variants can then be maximally utilized. This increased use of data permits phasing of parents and a larger number of successfully phased variants throughout the pedigree. Many algorithms apply a very stringent parsimony criterion—that the total recombinations be minimized across a pedigree. We relax this criterion considerably. Our parsimony criterion is that the number of recombinations in a given interval between informative variants is no more than half the number of children. We can therefore observe biological phenomena involving frequent or closely spaced recombinations. Without a parsimony criterion, multiple solutions would exist for the assignment of recombinations to meioses.

Errors

Despite the near 100% accuracy of genetic phasing, a handful of errors can remain. Genetic haplotyping can result in ambiguities or errors in parents if multiple recombinations occur in the same interval but in different meioses of the same parent. This source of ambiguity, however, does not impair phasing in children, because their phase is fixed by reference to homozygous positions in the parents. In this study, genetic haplotyping resulted in two ambiguities in pedigree A and none in pedigree B. In pedigree A, there were two distinct short intervals in the genome at which two recombinations occurred in separate meioses in the same parent. For a family with fewer than five children, genetic phasing in parents across such an interval cannot be performed, and ambiguity results (Figure 3). Our specific algorithmic implementation chooses phase arbitrarily in such instances. In one case of two paternal meioses, it chose the incorrect phase resulting in a switch error. In the other case, because no grandparental information was available, we could not determine if a switch error resulted. Barring unknown mechanisms, the chance of more than two recombinations in separate meioses of the same parent between informative variants is likely to be near zero, and so families with five children should be impeccably phaseable with genetic methods. Only two generations are needed by our algorithm. Grandparental genomes, if available, provide an extra check on sequence accuracy and will resolve any ambiguities that could rarely arise in families with smaller numbers of children.

In addition to the global ambiguities, there were isolated variants that were ambiguously or incorrectly phased. Ambiguous phasing will occur at any position for which all individuals in a pedigree are heterozygous. Ambiguous phasing could rarely occur for some individuals at positions in short segments for which the inheritance state is incompletely known (less than 0.1% of the genome). However, even in these short segments, most phasing is clear. These segments occur at the ends of chromosomes and in recombination intervals between informative variants. Isolated incorrect phasing of a variant could result if there is a sequencing error or an error in assigning inheritance states and meiosis indicators. For pedigree A, considering fully called positions that are homozygous in the paternal grandmother, there are 197 inconsistencies between the reported allele in the grandmaternal genome and the paternal allele derived from that genome. Several dozen of these will be due to de novo mutations in the paternal germline arising from the grandmaternal gamete,¹⁴ a few will be from undetected errors in the paternal genome sequence, and most will be from sequencing errors in the grandmaternal genome (Table 2). Increasing the size of pedigrees to include three or more generations rather than two should reduce such errors. Our implementations of our algorithms do not handle pedigrees more complex than a two-generation nuclear family, but could be extended, because the concept of inheritance states and meiosis indicators can be applied to any pedigree. Additionally, improvements to data quality could be accomplished by combining molecular and genetic techniques. For example, molecular techniques that locally resolve intervals with fully heterozygous positions or with multiple recombinations would complement the two rare weaknesses of genetic phasing. Population data can also be used to leverage these other phasing techniques. However, for medical purposes, results that include population inference are likely to have an unacceptably high error ratio.

Utility

Accurate haplotypes have many uses. Most importantly, the information they sequentially encode determines biological function and underlies human disease. They can be used to improve power in disease association studies by reducing multiple test correction. They can be used in studies of population genetics, including the study of human migrations and evolutionary selection. They provide data that permit insight into mechanisms and control of basic biological phenomena such as recombination, nuclear organization, and allelic exclusion. Together with increased understanding of population genetics and recombination mechanics, they might explain observations of linkage disequilibrium that abound in the genome, such as throughout the MHC locus. Finally, haplotyping algorithms aid the detection and correction of errors and inference of missing data in pedigrees.

Our prediction is that as the cost of human genome sequencing declines, individual genome data will increasingly become a part of a personal medical record. We suggest that this should be done in the context of sequencing family genomes. The advantages include decreased sequencing error due to the application of genetic analysis, the ability to distinguish rare variants from sporadic error, and the ability to determine chromosomal haplotypes. With the addition of phenotypic data, family sequences might enable identification of Mendelian disease genes and possibly modifier genes. Comprehensive personalized medicine will increasingly require both identification of rare alleles in patients and their assignment to haplotypes.

The medical utility of genetic methods for haplotyping is limited to individuals who have access to the genome sequences of their parents and siblings. Approximately 65% of women in the USA have or will have two or more children. Approximately 80% of the remaining 35% have or will have at least one sibling. Assuming similar statistics for males, 81% of the American population could directly benefit from genetic haplotyping, if genetic information from at least one sibling and/or at least two children was obtained.²³ To gain confidence levels appropriate for clinical utility for quartets that are missing one or both parents, genotyping data would have to be supplemented by molecular haplotyping data and employed in a hybrid algorithm. There are two ways in which genetic haplotyping can also benefit individuals not part of a quartet or larger nuclear family. First, accumulated data from many thousands of individuals will provide exact genetic global haplotype references including rare alleles, much as the HapMap currently provides approximate population-based local haplotypes for common alleles. Second, molecular or population-based inference methods for haplotyping can be developed and constantly improved through virtuous cycles of technology refinement by reference to gold standard haplotypes derived from genetic analysis.

Appendix A: Ambiguity and Error as a Function of Number of Children

Proof Outline

Only the paternal inheritance hypercube need be considered. Results on the maternal hypercube follow by symmetry. The number of vertices of the hypercube is 2^2(n−2)−1, where n is the family size, and n − 2 is the number of children. Because labeling of the first indicator is arbitrary, the minimum recombination distance D_r between binary complement vectors is zero (e.g., D_r(1111,0000) = 0 and D_r(1010,0101) = 0). Let HD be the Hamming distance. Then Dr(v₁,v₂) = min[(HD(v₁,v₂)),(HD(v₁,complement(v₂)))]. Let v_n and v_n+1 be adjacent inheritance-state vectors. Ambiguity in the meiosis-indicator vector phasing will arise if HD(v_n,v_n+1) = HD(v_n,complement(v_n+1)). An error will arise if the true number of recombinations is greater than the minimum recombination distance. Because of symmetry of the hypercube, one only need consider a single recombination path between the zero vector and the vector of all ones. So for example, for a four-child pedigree, one such path is 0000↔0001↔0011↔0111↔1111. If the inheritance state 0011 were to precede the v_n+1 inheritance state 1111, it would not be clear whether the best parsimonious choice for v_n+1 would be 0000 or 1111. Therefore, phasing would be ambiguous across that junction. Generalizing, two results follow. First, if n is the number of children in a nuclear family, and r is the number of recombinations between variants in different meioses of the same parent, ambiguity arises if r = n/2. Ambiguity never arises with an odd number of children, but errors can occur. Second, an error because of failure of the parsimony assumption can occur in any sized pedigree if r > n/2. Setting degenerate parameterization of n produces results that are consistent with intuition. For example, if n = 1 (a family trio), then all parental phasing is “wrong” in the sense that the likelihood of a phase error cannot be estimated from the data. If n = 2 (a family quartet), then all single recombinations can be detected but phasing is always ambiguous.

Appendix B: Description of Haploscribe

Four PERL scripts currently constitute the Haploscribe workflow:

• 1.The script “intercalate_partial_binary_blocks.pl” is applied to the quartet states of each individual. The output from this script is a list of blocks that encompass every position on all chromosomes. Ambiguity indicators are placed for positions without clearly determined inheritance-state indicators. The input file is “smoothed_blocks.txt.” The output file is “smoothed_blocks_with_intercalated_partial_blocks.txt.”
• 2.The script “increase_dimensionality_of_inheritance_state_hypercube.pl” takes all tiled quartets of the sextet and builds a single list of sextet inheritance states. The input files are the six “smoothed_blocks_with_intercalated_partial_blocks.txt” files. The output file is “increased_dimensionality_blocks.txt.”
• 3.The script “decanonicalize_binary_inheritance_vectors.pl” converts sextet inheritance-state indicator vectors into meiosis-indicator vectors. The haplotype assignment of the first block of each chromosome is arbitrarily set, and all other blocks are phased relative to the preceding block. The output file is “decanonicalized_blocks.txt.”
• 4.The script “haplotype_sextet.pl” takes as input the list of meiosis-indicator vectors for each block together with a list of genotype vectors and their positions. The output is the set of haplotypes for the genome. The output file is “phased_genotype_vector.txt.”

Web Resources

The URLs for data presented herein are as follows:

• CEPH Resources, http://ccr.coriell.org/Sections/Collections/NIGMS/CEPHResources.aspx?PgId=525&coll=GM

• Institute for Systems Biology, http://www.systemsbiology.org/Public_Resources/Downloadable_Software

• Online Mendelian Inheritance in Man (OMIM), http://omim.org

• Whole-genome sequence data for pedigree A from Complete Genomics, www.completegenomics.com/sequence-data/download-data/