A General Framework for Detecting Disease Associations with Rare Variants in Sequencing Studies

Abstract

Biological and empirical evidence suggests that rare variants account for a large proportion of the genetic contributions to complex human diseases. Recent technological advances in high-throughput sequencing platforms have made it possible for researchers to generate comprehensive information on rare variants in large samples. We provide a general framework for association testing with rare variants by combining mutation information across multiple variant sites within a gene and relating the enriched genetic information to disease phenotypes through appropriate regression models. Our framework covers all major study designs (i.e., case-control, cross-sectional, cohort and family studies) and all common phenotypes (e.g., binary, quantitative, and age at onset), and it allows arbitrary covariates (e.g., environmental factors and ancestry variables). We derive theoretically optimal procedures for combining rare mutations and construct suitable test statistics for various biological scenarios. The allele-frequency threshold can be fixed or variable. The effects of the combined rare mutations on the phenotype can be in the same direction or different directions. The proposed methods are statistically more powerful and computationally more efficient than existing ones. An application to a deep-resequencing study of drug targets led to a discovery of rare variants associated with total cholesterol. The relevant software is freely available.

Introduction

Genome-wide association studies (GWAS) with tagSNPs have successfully identified common SNPs with small to modest effects for virtually every complex human disease. Technological advances in high-throughput sequencing platforms have made it possible for researchers to extend association studies to rare variants in targeted exons and soon in the entire genome. Rare variants tend to be functional alleles and have stronger effects on complex diseases than common variants.^1,2 Indeed, deep-resequencing studies of candidate genes have already demonstrated the influence of rare variants on several complex traits.^3–5

Association testing with a single rare variant has limited power because only a small percentage of study subjects carry a rare mutation and there are a large number of tests to be adjusted for. Collapsing or grouping methods, which combine information across multiple variant sites within a gene, can enrich association signals and reduce the penalty of multiple testing. The simplest collapsing method is the burden test, which is based on the number of rare mutations each subject carries in a gene.^6,7 A second approach is the weighted sum statistic of Madsen and Browning,⁸ which weights each mutation according to its frequency in the unaffected subjects and permutes the disease status to assess the significance of a Wilcoxon-type test statistic. A third approach is the variable-threshold (VT) idea of Price et al.,⁹ which uses the maximum of the test statistics over all allele-frequency thresholds and assesses statistical significance by permutation. The forgoing methods assume that the effects of the combined rare mutations on the phenotype are in the same direction. To detect opposite effects, Han and Pan¹⁰ incorporated the signs of the observed effects into the burden test, whereas Neale et al.¹¹ and Wu et al.¹² tested the variance of the effects.

In this article, we provide a general framework for association testing with rare variants that reflects the spirits of the existing methods but is statistically more powerful and computationally more efficient. Our framework covers all major study designs (i.e., case-control, cross-sectional, cohort and family studies) and all common phenotypes (e.g., binary and quantitative traits, and potentially censored ages at onset of disease) and allows any covariates (e.g., environmental factors and ancestry variables). The ability to accommodate covariates is critically important because population stratification is expected to be a more severe issue with rare variants than with common variants but could be corrected by including suitable ancestry variables (e.g., the percentage of African ancestry or principal components for ancestry) in the association analysis. We combine information across multiple variant sites within a gene by taking a weighted sum of the mutation counts for each study subject and relate the combined information and covariates to disease phenotypes through appropriate regression models. We derive theoretically optimal weights that would produce the most powerful tests among all valid tests and develop the corresponding testing procedures. We employ score-type statistics, which are numerically stable even in the case of extremely rare variants and computationally fast even in the presence of covariates. We provide asymptotic normal approximation for both fixed-threshold and VT methods and develop permutation and other resampling tests that can accommodate covariates. We investigate theoretically and numerically when normal approximation is appropriate and when resampling is required. We modify the popular methods of Madsen and Browning⁸ and Price et al.⁹ to enhance statistical power, avoid permutation, and accommodate covariates. We construct data-adaptive test statistics that are powerful even when the combined rare mutations have opposite effects on the phenotype. The advantages of the proposed methods over the existing ones are demonstrated both analytically and empirically. The software implementing the proposed methods is available at our website.

Material and Methods

Suppose that a total of n subjects are genotyped on a total of m SNPs in a gene and that there are d covariates. Here, the word “gene” refers to the group of variants that will be collectively analyzed and might pertain to a subset of SNPs within a gene or to a region or pathway involving multiple genes; covariates might include nongenetic variables, such as age and smoking status, as well as ancestry variables, such as the percentage of African ancestry and principal components for ancestry. For $i=1,\text{…},n$, let Y_i be the phenotype value of the ith subject; for $i=1,\text{…},n$ and $j=1,\text{…},m$, let X_ji denote the number of the rare mutation the ith subject carries at the jth SNP; for $i=1,\text{…},n$ and $j=1,\text{…},d$, let Z_ji denote the value of the jth covariate on the ith subject. We can define

$$X_i=\left[\begin{array}{c}{X}_{1i}\\ ⋮\\ X_{mi}\end{array}\right],Z_i=\left[\begin{array}{c}1\\ Z_{1i}\\ ⋮\\ Z_{di}\end{array}\right].$$

We focus on binary phenotypes in the main text but consider all common phenotypes in Appendix A. It is natural to relate Y_i to X_i and Z_i through the logistic regression model:

$$\mathrm{Pr}\left(Y_i=1\right)=\frac{e^{{\beta }^{\text{T}}{X}_i+{\gamma }^{\text{T}}{Z}_i}}{1+e^{{\beta }^{\text{T}}{X}_i+{\gamma }^{\text{T}}{Z}_i}},$$ (Equation 1)

where β and γ are m × 1 and (d + 1)×1 vectors of unknown regression coefficients. Because the first component of Z_i is 1, the first component of γ corresponds to the intercept. We can write $\beta =\tau \xi$, where τ is a scalar constant, and $\xi =\beta /\tau$. Then Equation (1) becomes

$$\mathrm{Pr}\left(Y_i=1\right)=\frac{e^{\tau S_i+{\gamma }^{\text{T}}{Z}_i}}{1+e^{\tau S_i+{\gamma }^{\text{T}}{Z}_i}},$$ (Equation 2)

where $S_i={\xi }^{\text{T}}{X}_i$. Note that $\xi ={\left({\xi }_1,\text{…},{\xi }_m\right)}^{\text{T}}$ is a m × 1 vector of weights and that S_i is a weighted linear combination of $X_{1i},\text{…},X_{mi}$ with X_ji receiving the weight ξ_j. We will refer to ξ as the weight function.

The score statistic for testing the null hypothesis $H_0:\tau =0$ takes the form

$$U=\sum _{i=1}^n\left(Y_i-\frac{e^{{\hat{\gamma }}^{\text{T}}{Z}_i}}{1+e^{{\hat{\gamma }}^{\text{T}}{Z}_i}}\right)S_i,$$

where $\hat{\gamma }$ is the restricted maximum likelihood estimator of γ and solves the equation

$$\sum _{i=1}^n\left(Y_i-\frac{e^{{\gamma }^{\text{T}}{Z}_i}}{1+e^{{\gamma }^{\text{T}}{Z}_i}}\right)Z_i=0.$$

The variance of U is estimated by

$$V=\sum _{i=1}^n{v}_i{S}_i^2-{\left(\sum _{i=1}^n{v}_i{S}_i{Z}_i\right)}^{\text{T}}{\left(\sum _{i=1}^n{v}_i{Z}_i{Z}_i^{\text{T}}\right)}^{-1}\left(\sum _{i=1}^n{v}_i{S}_i{Z}_i\right),$$

where

$$v_i=\frac{e^{{\hat{\gamma }}^{\text{T}}{Z}_i}}{{\left(1+e^{{\hat{\gamma }}^{\text{T}}{Z}_i}\right)}^2}.$$

Under H₀, the test statistic $T={U/V}^{1/2}$ is asymptotically standard normal. In the absence of covariates,

$$U=\sum _{i=1}^n\left(Y_i-\overline{Y}\right)S_i,$$

and

$$V=\overline{Y}\left(1-\overline{Y}\right)\left\{\sum _{i=1}^n{S}_i^2-n^{-1}{\left(\sum _{i=1}^n{S}_i\right)}^2\right\},$$

where $\overline{Y}=n^{-1}{\sum }_{i=1}^n{Y}_i$.

The true value of the weight function $\xi ={\left({\xi }_1,\text{…},{\xi }_m\right)}^{\text{T}}$ is unknown and must be determined biologically or empirically. If we set ${\xi }_j=1$$\left(j=1,\text{…},m\right)$, then T is a burden test, which counts the total number of rare mutations each subject carries over the m SNPs. If we believe that common variants are not associated with the phenotype, then we set ${\xi }_j=0$ if $p_j>c$, where p_j is the minor allele frequency (MAF) of the jth SNP, and c is a given threshold. If we set ${\xi }_j={\left\{p_j\left(1-p_j\right)\right\}}^{-1/2}$$\left(j=1,\text{…},m\right)$, then the weight function is in the same vein as that of Madsen and Browning.⁸

If the choice of the weight function ξ is not proportional to β or ξ is estimated from the data, then U is no longer the score statistic. However, we show in Appendix A that the test statistic T is asymptotically standard normal under H₀ regardless of how ξ is determined. The only condition is that if ξ is estimated from the data, then the estimate converges to a constant vector as the sample size n increases. This condition is satisfied by all sensible estimates, including those based on estimated allele frequencies. If the choice of ξ or the limit of the estimate of ξ is proportional to β, then the corresponding test statistic T is the most powerful among all valid tests.

The weight function ξ is similar to that of Price et al.⁹ The latter authors showed that, for case-control studies with known allele frequencies in the control population, the choice of ${\xi }_j={\left\{p_j\left(1-p_j\right)\right\}}^{-1/2}$$\left(j=1,\text{…},m\right)$ corresponds to the implicit assumption that $\log \left(O{R}_j\right)\propto {\left\{p_j\left(1-p_j\right)\right\}}^{-1/2}$$\left(j=1,\text{…},m\right)$, where OR_j is the odds ratio in the 2 × 2 table for the jth SNP. Our theory is much more general in that it assumes unknown allele frequencies and accommodates covariates. Indeed, the proposed test statistic is optimal if ξ is proportional to the set of regression coefficients (in the limit); this result holds for all phenotypes, including binary and continuous traits, as well as potentially censored ages at onset of disease.

Madsen and Browning⁸ suggested to set ${\xi }_j={\left\{{\hat{p}}_j\left(1-{\hat{p}}_j\right)\right\}}^{-1/2}$ $\left(j=1,\text{…},m\right)$, where ${\hat{p}}_j$ is the estimate of the MAF of the jth SNP in the unaffected subjects. Because the weights depend on the phenotype values, the authors suggested a permutation-based test. Our testing framework allows such data-dependent weights because the frequency estimates converge to the true values as n increases. To improve the accuracy of asymptotic approximation, we suggest estimating the frequencies from all study subjects rather than the unaffected subjects. Because the variants can be very rare, we recommend adding pseudocounts when estimating the frequencies, as was done by Madsen and Browning.⁸ The weight functions based on the frequency estimates in the pooled sample and the unaffected subjects will be denoted by F_p and F_u, respectively; the constant weight function will be denoted by C. The corresponding tests will be referred to as the F_p test, the F_u test and the C test.

Although F_u is the weight function used by Madsen and Browning,⁸ our F_u test is fundamentally different from the Madsen and Browning (MB) test. The latter is based on the sum of the ranks of the S_i's with weight function F_u over the affected subjects. Madsen and Browning⁸ proposed to assess the statistical significance of their rank-sum statistic by permutation. They also suggested an asymptotic normal approximation by standardizing the rank-sum statistic by its mean and standard derivation. Because the mean and standard derivation are estimated by permutation, the asymptotic version of the MB test is many orders of magnitudes slower than our asymptotic tests. The rank-sum statistic is confined to case-control analysis without covariates.

Price et al.⁹ developed a VT method by taking the maximum of the test statistics (i.e., Z scores) over all allele-frequency thresholds and assessing statistical significance by permutation. We describe below a more general approach that allows not only multiple allele-frequency thresholds but also different types of weight function; it also accommodates covariates and does not require permutation.

We consider K choices of ξ, which could correspond to different thresholds or different types of weight function, or both. (It is assumed that K is small relative to n.) For the kth choice of ξ, the corresponding S_i is denoted by S_ki. Then the score statistic is

$$U_k=\sum _{i=1}^n\left(Y_i-\frac{e^{{\hat{\gamma }}^{\text{T}}{Z}_i}}{1+e^{{\hat{\gamma }}^{\text{T}}{Z}_i}}\right)S_{ki},$$

and the test statistic is $T_k=U_k/V_k^{1/2}$, where

$$V_k=\sum _{i=1}^n{v}_i{S}_{ki}^2-{\left(\sum _{i=1}^n{v}_i{S}_{ki}{Z}_i\right)}^{\text{T}}{\left(\sum _{i=1}^n{v}_i{Z}_i{Z}_i^{\text{T}}\right)}^{-1}\left(\sum _{i=1}^n{v}_i{S}_{ki}{Z}_i\right).$$

It is shown in Appendix A that, under H₀, the random vector ${\left(U_1,\text{…},U_K\right)}^{\text{T}}$ is approximately K-variate normal with mean 0 and covariance matrix $\left\{V_{kl};k,l=1,\text{…},K\right\}$, where

$$V_{kl}=\sum _{i=1}^n{U}_{ki}{U}_{li},$$

and

$$U_{ki}=\left(Y_i-\frac{e^{{\hat{\gamma }}^{\text{T}}{Z}_i}}{1+e^{{\hat{\gamma }}^{\text{T}}{Z}_i}}\right)\left\{S_{ki}-{\left(\sum _{i=1}^n{v}_i{S}_{ki}{Z}_i\right)}^{\text{T}}{\left(\sum _{i=1}^n{v}_i{Z}_i{Z}_i^{\text{T}}\right)}^{-1}{Z}_i\right\}.$$

For the two-sided test, we consider the maximum of the absolute test statistics

$$T_{\max }=\underset{k=1,\text{…},K}{\max }\left|T_k\right|.$$

Let $t_{\max }$ be the observed value of $T_{\max }$. The p value is given by

$$\mathrm{Pr}\left(T_{\max }\ge t_{\max }\right)=1-\mathrm{Pr}\left(\left|T_1\right|<t_{\max },\text{…},\left|T_K\right|<t_{\max }\right),$$

which is evaluated by treating ${\left(T_1,\text{…},T_K\right)}^{\text{T}}$ as a K-variate normal random vector with a mean of 0 and a covariance matrix of $\left\{r_{kl};k,l=1,\text{…},K\right\}$, where $r_{kl}=V_{kl}/{\left(V_{kk}{V}_{ll}\right)}^{1/2}$. (The one-sided p value can be calculated in a similar manner.) We reject H₀ if the p value is smaller than the nominal significance level α.

The tests based on positive weight functions, such as C, F_u, and F_p, will have low power if the mutations being combined have opposite effects on the phenotype. The optimal choice of ξ_j is β_j, which is unknown. We can estimate β_j from the data. It would be tempting to set ξ_j to ${\hat{\beta }}_j$, where ${\hat{\beta }}_j$ is an appropriate estimate of β_j. There are two major problems with this strategy. First, the test statistic T will not be asymptotically normal. Second, the ${\hat{\beta }}_j$'s are highly variable (because the individual variants are very rare) and can be quite different from the true values of the β_j's. As a compromise, we set ${\xi }_j={\hat{\beta }}_j+\delta$, where δ is a given constant. We refer to this weight function as EREC, an abbreviation of estimated regression coefficients. The corresponding test statistic T will be asymptotically standard normal as long as δ is nonzero. Indeed, the EREC test is asymptotically optimal in that ξ_j will converge to β_j if we let δ decrease to 0 as the sample size n increases to ∞. The asymptotic normality and optimality require very large samples. For small samples, we recommend to use a relatively large value of δ so that the weights are not unduly driven by the highly variable ${\hat{\beta }}_j$'s. For n < 2000, we set $\delta =1$ for binary traits and $\delta =2$ for standardized quantitative traits.

The sequence kernel association test (SKAT) of Wu et al.¹² assumes that β_j follows an arbitrary distribution with a mean of 0 and a variance of ${\xi }_j\nu$, and tests the null hypothesis that $\nu =0$ by using a variance-component score statistic. The SKAT statistic can be written as $Q={\sum }_{j=1}^m{\xi }_j{U}_j^2$, where U_j is the jth component of the score statistic for testing the null hypothesis that $\beta =0$ under Equation 1. The C-alpha statistic of Neale et al.¹¹ is a special case of Q with ${\xi }_j=1$ for binary traits without covariates. Our score statistic U can be written as ${\sum }_{j=1}^m{\xi }_j{U}_j$. The Han and Pan¹⁰ (HP) statistic is a special case of U (for binary traits without covariates) in which ${\xi }_j=-1$ if ${\hat{\beta }}_j<0$ and the corresponding p value <0.1 and in which ${\xi }_j=1$ otherwise.

Because the asymptotic approximation might not be accurate in small samples, especially when the weight function ξ involves the phenotype values Y_i's, we also provide permutation-type tests. In the absence of covariates, we simply permute the phenotype values Y_i's and calculate the test statistic T for each permutation. Note that it is necessary to recalculate the S_i's after permuting the Y_i's if the weight function ξ depends on the Y_i's.

Our permutation differs from that of Price et al.⁹ in that we permute T, whereas they permuted ${\sum }_{i=1}^n{Y}_i{S}_i$. The former is a pivotal statistic, whereas the latter is not. (It is desirable to permute a pivotal statistic.¹³) If the test is one-sided and the weight function does not depend on the phenotype values, then our permutation is equivalent to Price et al.'s⁹; otherwise, the two are different. For VT methods, the numerators in the Z scores of Price et al.⁹ are the same as ours, but the denominators are not the same as or proportional to ours. Thus, the permutation p values are generally different between the two methods. The permutation version of the MB test requires ranking the S_i's for each permutation and is thus substantially slower than our permutation tests.

In the presence of covariates, permuting the Y_i's it is not appropriate because Y_i is generally correlated with Z_i. Instead, we generate $Y_i^{\ast }$ from the fitted null model:

$$\mathrm{Pr}\left(Y_i^{\ast }=1\right)=\frac{e^{{\hat{\gamma }}^{\text{T}}{Z}_i}}{1+e^{{\hat{\gamma }}^{\text{T}}{Z}_i}},$$

replace the Y_i's with the $Y_i^{\ast }$'s, and recalculate the test statistic. (The recalculation of the test statistic starts with re-estimating γ and recalculating the S_i's.) This process is repeated and is called (parametric) bootstrap.¹³ Both permutation and bootstrap are resampling methods. In the absence of covariates, $\mathrm{Pr}\left(Y_i^{\ast }=1\right)$ is the sample proportion of cases.

Obtaining an accurate estimate of a small p value requires a large number of resamples (i.e., permutations or bootstrap samples). However, most p values are relatively large and can be estimated accurately with a small number of resamples. Thus, we employ a multistage procedure which filters out large p values with small numbers of resamples and uses large numbers of resamples only for the most extreme p values.

Results

Simulation Studies

We conducted extensive simulation studies to investigate the performance of the proposed and existing methods. We simulated case-control data with an equal number of cases and controls from Equation 1 in which the first component of γ was set to –2. We considered mainly the following six combinations of MAFs: (1) $p_j=0.001j$ $\left(j=1,\text{…},10\right)$ with a total frequency of 5.5%; (2) $p_j=0.0005j$ $\left(j=1,\text{…},10\right)$ with a total frequency of 2.75%; (3) $p_j=0.00025j$$\left(j=1,\text{…},20\right)$ with a total frequency of 5.25%; (4) $p_j=0.005$ $\left(j=1,\text{…},10\right)$ with a total frequency of 5%; (5) $p_j=0.0025$ $\left(j=1,\text{…},10\right)$ with a total frequency of 2.5%; and (6) $p_j=0.0025$$\left(j=1,\text{…},20\right)$ with a total frequency of 5%. The genotype values were simulated under Hardy-Weinberg equilibrium and linkage equilibrium. We did not use sophisticated population genetics models because we wished to control the number of variants and their frequencies, which allowed us to see clearly how the proposed and existing methods perform under various scenarios. We evaluated both asymptotic and resampling methods. When the simulation studies involved asymptotic methods only, we used 10 millions replicates (i.e., simulated data sets) to evaluate type I error and 100,000 replicates to evaluate power at $\alpha ={10}^{-2},{10}^{-3}$, and ${10}^{-4}$. When the simulation studies involved resampling methods, we used 1 million replicates to evaluate type I error and 10,000 replicates to evaluate power at $\alpha ={10}^{-2}$ and ${10}^{-3}$. The resampling p values were obtained from a three-stage procedure with a maximum of 1 million resamples. The null hypothesis corresponded to $H_0:{\beta }_j=0$$\left(j=1,\text{…},m\right)$. We considered alternative hypotheses such as $H_1:{\beta }_j=x$$\left(j=1,\text{…},m\right)$ and $H_1:{\beta }_j=x/{\left\{p_j\left(1-p_j\right)\right\}}^{1/2}$$\left(j=1,\text{…},m\right)$, where x was chosen such that the power (of the most powerful method) was reasonably high at $\alpha ={10}^{-2}$. We report below results from six series of simulation studies, the first four without covariates and the last two with covariates. The tests were two-sided except for the third series.

We designed our first series of simulation studies to evaluate the proposed asymptotic methods with different weight functions. We considered the aforementioned six combinations of MAFs and generated data under the null hypothesis $H_0:{\beta }_j=0$$\left(j=1,\text{…},m\right)$, as well as two alternative hypotheses $H_1:{\beta }_j=x$$\left(j=1,\text{…},m\right)$ and $H_1:{\beta }_j=x/{\left\{p_j\left(1-p_j\right)\right\}}^{1/2}$$\left(j=1,\text{…},m\right)$. We considered three (positive) weight functions: C, F_p, and F_u. We also considered the maximum of the test statistics based on weight functions C and F_p, which will be referred to as $T_{\max }$. The results for the first combination of MAFs are displayed in Table 1, whereas those of the remaining five combinations are provided in Tables S1–S5, available online. The performance of the tests is affected more by the total allele frequency than the number of variants or individual MAFs. The C test, F_p test, and $T_{\max }$ are conservative but less so as n, α, or total allele frequency increases. As expected, the C test is more powerful than the F_p test under the first alternative hypothesis and less powerful under the second alternative hypothesis; $T_{\max }$ is nearly as powerful as the C test under the first alternative and nearly as powerful as the F_p test under the second alternative. The F_u test is unacceptably liberal; therefore, we will not consider this asymptotic test any further.

Table 1.

Type I Error^a and Power of Asymptotic Methods with Different Weight Functions

n	α	H0 : βj = 0				H1 : βj = x				βj = x/{pj(1 − pj)}1/2
		C	Fp	Tmax	Fu	C	Fp	Tmax	Fu	C	Fp	Tmax	Fu
500	10−2	0.95	0.95	0.93	2.12	0.76	0.73	0.75	0.86	0.75	0.77	0.77	0.89
	10−3	0.82	0.79	0.78	2.51	0.49	0.44	0.47	0.64	0.47	0.49	0.48	0.68
	10−4	0.68	0.63	0.60	2.52	0.25	0.21	0.23	0.39	0.23	0.25	0.24	0.42
1000	10−2	0.98	0.97	0.97	1.96	0.81	0.77	0.80	0.88	0.89	0.91	0.90	0.96
	10−3	0.92	0.89	0.89	2.53	0.55	0.50	0.54	0.67	0.68	0.73	0.71	0.84
	10−4	0.88	0.74	0.78	3.05	0.31	0.27	0.30	0.43	0.44	0.49	0.47	0.65
2000	10−2	0.98	0.98	0.98	1.64	0.92	0.90	0.92	0.95	0.95	0.97	0.96	0.98
	10−3	0.96	0.95	0.95	2.04	0.76	0.71	0.75	0.81	0.82	0.86	0.85	0.92
	10−4	0.91	0.88	0.88	2.44	0.54	0.47	0.52	0.61	0.62	0.68	0.67	0.79
4000	10−2	1.00	0.99	0.99	1.37	0.97	0.96	0.97	0.98	0.97	0.98	0.97	0.99
	10−3	0.98	0.98	0.97	1.61	0.88	0.84	0.87	0.90	0.86	0.90	0.89	0.94
	10−4	0.98	0.96	0.94	1.85	0.72	0.65	0.70	0.74	0.69	0.75	0.73	0.82

^aDivided by α.

Our second series of studies was devoted to comparisons of asymptotic and permutation methods. In addition to the proposed methods, we evaluated the asymptotic and permutation versions of the MB test, as well as the permutation method of Price et al.⁹ with weight function F_u. We simulated data in the same manner as the first series of studies. We performed one-sided tests because the MB and Price et al. tests were designed as one-sided. The results for the first combination of MAFs are displayed in Table 2. Because of the discreteness of the test statistic, the permutation version of the C test is more conservative than its asymptotic counterpart and consequently less powerful. The permutation F_p and F_u tests do not appear to be conservative; the former appears to be slightly more powerful than the latter. The MB test was designed for the second alternative hypothesis, for which the proposed asymptotic test based on weight function F_p is more powerful than the asymptotic version of the MB test whereas the proposed permutation tests based on weight functions F_p and F_u are more powerful than the permutation version of the MB test. For weight function F_u, our permutation test is more powerful than that of Price et al.⁹

Table 2.

Type I Error^a and Power of Asymptotic and Permutation Methods

n	α	Asymptotic			Permutation
		C	Fp	MB	C	Fp	Fu	Priceb	MB
H0 : βj = 0
500	10−2	0.99	0.98	0.98	0.71	1.02	1.02	1.01	1.00
	10−3	0.89	0.87	0.89	0.62	0.99	1.01	0.99	1.01
1000	10−2	1.00	1.00	1.00	0.79	1.01	1.03	1.01	1.01
	10−3	0.96	0.96	0.93	0.72	1.01	1.02	1.01	1.02
H1 : βj = x
500	10−2	0.84	0.81	0.82	0.81	0.81	0.81	0.79	0.82
	10−3	0.57	0.54	0.54	0.54	0.55	0.54	0.49	0.56
1000	10−2	0.86	0.84	0.85	0.85	0.84	0.84	0.82	0.85
	10−3	0.63	0.58	0.60	0.60	0.59	0.58	0.53	0.60
H1 : βj = x/{pj(1 − pj)}1/2
500	10−2	0.83	0.85	0.82	0.80	0.85	0.84	0.81	0.82
	10−3	0.56	0.59	0.54	0.52	0.59	0.57	0.51	0.55
1000	10−2	0.93	0.95	0.92	0.92	0.95	0.94	0.93	0.92
	10−3	0.75	0.80	0.73	0.73	0.80	0.77	0.74	0.74

^aDivided by α.

^bWith weight function F_u.

In the third series of studies, we compared fixed-threshold and VT methods. We simulated 11 SNPs with MAFs $p_j=0.001j$$\left(j=1,\text{…},10\right)$ and $p_{11}=0.03$. We considered the null hypothesis $H_0:{\beta }_1={\beta }_2=\text{…}={\beta }_{11}=0$, as well as two alternative hypotheses $H_1:{\beta }_1={\beta }_2=\text{…}={\beta }_{10}=x$, ${\beta }_{11}=0$ and $H_1:{\beta }_1={\beta }_2=\text{…}={\beta }_{11}=x$. For fixed-threshold methods, we considered the thresholds of 0.01 and 0.05; the corresponding tests are referred to as the T1 and T5 tests. For VT methods, we excluded the thresholds for which the total numbers of rare mutations were fewer than 10. As shown in Table 3, all the tests appear to be conservative, especially when n and α are small. The permutation T1 and T5 tests are more conservative than their asymptotic counterparts. In theory, T1 and T5 are the most powerful under the first and second alternatives, respectively. Because the frequency estimates for rare variants are highly variable, T1 turns out to be the least powerful among all the tests under the first alternative. The VT tests have good power under both alternatives, and the asymptotic and permutation versions have similar power. The permutation version of our VT test is slightly more powerful than that of Price et al.⁹

Table 3.

Type I Error^a and Power of Fixed-Threshold and VT Methods

n	α	Asymptotic			Permutation
		T1	T5	VT	T1	T5	VT	Priceb
H0 : βj = 0
500	10−2	0.91	0.96	0.84	0.62	0.72	0.90	0.88
	10−3	0.79	0.85	0.57	0.54	0.61	0.83	0.83
1000	10−2	0.96	0.99	0.86	0.73	0.81	0.93	0.93
	10−3	0.88	0.90	0.66	0.68	0.70	0.89	0.88
H1 : β1 = … = β10 = x, β11 = 0
500	10−2	0.39	0.59	0.66	0.34	0.55	0.67	0.67
	10−3	0.15	0.29	0.36	0.13	0.27	0.40	0.39
1000	10−2	0.50	0.61	0.68	0.46	0.58	0.69	0.69
	10−3	0.23	0.33	0.40	0.21	0.30	0.43	0.43
H1 : β1 = … = β11 = x
500	10−2	0.29	0.82	0.71	0.25	0.80	0.72	0.71
	10−3	0.10	0.57	0.42	0.09	0.54	0.46	0.45
1000	10−2	0.35	0.82	0.68	0.32	0.81	0.69	0.68
	10−3	0.13	0.57	0.41	0.12	0.54	0.44	0.42

^aDivided by α.

^bVT method of Price et al.⁹

In the fourth set of studies, we compared the C test, F_p test, and EREC test, as well as the HP, C-alpha, and SKAT tests. Note that the last four tests were designed to detect variants with opposite effects. The EREC, HP, and C-alpha tests were based on permutation, whereas the SKAT was based on the Davies method.¹² For the EREC test, ${\hat{\beta }}_j$ was the estimate of the log odds ratio β_j (after adding a pseudocount of 1 to each of the four cells in the 2×2 table). For the SKAT test, we used the default weighted linear kernel function. We set $p_j=0.001j$$\left(j=1,\text{…},10\right)$ and considered the null hypothesis $H_0:{\beta }_j=0$$\left(j=1,\text{…},10\right)$ and six alternative hypotheses representing different numbers of causal variants and different patterns of positive and negative effects. As shown in Table 4, the SKAT is highly conservative, especially when n and α are small. The EREC test is slightly less powerful than the C test and F_p test when the SNP effects are all positive but is much more powerful than the latter when there are opposite effects. The EREC test is more powerful than the HP test. It is also more powerful than the C-alpha and SKAT, especially when the mean of the regression coefficients is not 0.

Table 4.

Type I Error^a and Power of Asymptotic and Permutation Tests for Detecting Potentially Opposite Effects

n	α	Asymptotic			Permutation
		C	Fp	SKAT	C	Fp	EREC	HP	C-alpha
H0 : βj = 0
500	10−2	0.95	0.95	0.53	0.68	1.00	1.01	0.89	0.91
	10−3	0.83	0.77	0.26	0.60	0.94	0.97	0.91	0.87
1000	10−2	0.99	0.98	0.75	0.77	1.02	1.02	0.97	0.96
	10−3	0.97	0.95	0.57	0.73	1.02	1.04	1.01	0.97
H0 : βj = x
500	10−2	0.77	0.74	0.33	0.73	0.74	0.72	0.71	0.36
	10−3	0.49	0.45	0.09	0.46	0.47	0.44	0.41	0.14
1000	10−2	0.81	0.77	0.41	0.78	0.77	0.78	0.73	0.42
	10−3	0.56	0.50	0.16	0.53	0.51	0.51	0.42	0.17
H1 : βj = x/{pj(1 − pj)}1/2
500	10−2	0.76	0.78	0.26	0.73	0.79	0.71	0.70	0.27
	10−3	0.47	0.50	0.06	0.44	0.51	0.41	0.39	0.08
1000	10−2	0.66	0.70	0.22	0.63	0.70	0.65	0.57	0.21
	10−3	0.37	0.41	0.06	0.35	0.42	0.35	0.26	0.06
H1 : β1 = … = β8 = x, β9 = −x, β10 = − 2x
500	10−2	0.29	0.23	0.58	0.25	0.23	0.76	0.63	0.61
	10−3	0.09	0.06	0.25	0.08	0.06	0.49	0.38	0.32
1000	10−2	0.31	0.27	0.81	0.28	0.27	0.88	0.86	0.81
	10−3	0.10	0.08	0.54	0.09	0.09	0.66	0.65	0.56
H1 : β1 = … = β9 = x, β10 = −x / 2
500	10−2	0.77	0.74	0.50	0.74	0.75	0.82	0.76	0.54
	10−3	0.49	0.45	0.21	0.46	0.47	0.57	0.47	0.26
1000	10−2	0.86	0.85	0.69	0.84	0.85	0.92	0.86	0.70
	10−3	0.64	0.61	0.40	0.61	0.62	0.73	0.60	0.42
H1 : β2 = β4 = β6 = β8 = x, β10 = −x, βj = 0 (j = 1, 3, 5, 7, 9 )
500	10−2	0.19	0.13	0.41	0.16	0.14	0.56	0.34	0.47
	10−3	0.05	0.03	0.14	0.05	0.03	0.26	0.13	0.21
1000	10−2	0.24	0.17	0.65	0.21	0.17	0.71	0.54	0.67
	10−3	0.07	0.04	0.35	0.06	0.05	0.42	0.27	0.39
H1 : β3 = 2x, β4 = −2x, β5 = x, β6 = −x, β j = 0 (j = 1, 2, 7 ∼ 10)
500	10−2	0.10	0.02	0.61	0.08	0.02	0.69	0.18	0.65
	10−3	0.01	0.00	0.27	0.01	0.00	0.36	0.06	0.36
1000	10−2	0.12	0.03	0.88	0.11	0.03	0.90	0.43	0.86
	10−3	0.03	0.00	0.63	0.02	0.00	0.66	0.21	0.62

^aDivided by α.

The above four sets of studies contained no covariates. We also conducted extensive studies with covariates. We generated data in the same manner as before except that we added a normally distributed covariate whose mean is equal to the total number of rare mutations and whose variance is equal to 1 and we set its regression coefficient to 0.3. Some key results are presented in Tables 5 and 6. The T1, T5, F_p, and VT tests are less conservative than in the case of no covariates, and their asymptotic and bootstrap versions have similar power. The EREC test has similar power to the C and F_p tests when all SNP effects are positive and is much more powerful than the latter when there are opposite effects. The EREC test tends to be more powerful than the SKAT, especially when the mean of the regression coefficients is not 0.

Table 5.

Type I Error^a and Power of Fixed-Threshold and VT Methods with Covariates

n	α	Asymptotic				Bootstrap
		T1	T5	Fp	VT	T1	T5	Fp	VT
H0 : βj = 0
500	10−2	0.97	1.00	0.98	0.90	1.01	1.02	1.01	1.01
	10−3	0.82	0.99	0.92	0.75	0.94	1.00	0.98	0.97
1000	10−2	0.97	0.99	0.99	0.88	0.99	1.00	1.00	0.98
	10−3	0.90	0.98	0.94	0.79	0.94	0.98	0.96	0.94
H1 : β1 = … = β10 = x, β11 = 0
500	10−2	0.23	0.46	0.56	0.53	0.23	0.46	0.57	0.55
	10−3	0.06	0.19	0.27	0.25	0.07	0.19	0.27	0.27
1000	10−2	0.31	0.50	0.62	0.58	0.31	0.50	0.62	0.59
	10−3	0.11	0.23	0.33	0.30	0.11	0.23	0.33	0.32
H1 : β1 = … = β11 = x
500	10−2	0.19	0.79	0.77	0.72	0.19	0.79	0.77	0.73
	10−3	0.04	0.54	0.48	0.44	0.05	0.54	0.49	0.45
1000	10−2	0.26	0.89	0.82	0.77	0.27	0.89	0.82	0.78
	10−3	0.08	0.68	0.56	0.51	0.08	0.68	0.56	0.53

^aDivided by α.

Table 6.

Type I Error^a and Power of Asymptotic and Bootstrap Tests for Detecting Potentially Opposite Effects in the Presence of Covariates

n	α	Asymptotic			Bootstrap
		C	Fp	SKAT	C	Fp	EREC
H0 : βj = 0
500	10−2	0.97	0.97	0.63	1.00	1.00	0.97
	10−3	0.85	0.80	0.37	0.94	0.92	0.93
1000	10−2	0.98	0.97	0.81	0.99	0.99	0.98
	10−3	1.01	0.96	0.56	1.05	1.01	0.99
H1 : βj = x
500	10−2	0.67	0.63	0.14	0.67	0.63	0.67
	10−3	0.37	0.33	0.02	0.37	0.33	0.37
1000	10−2	0.74	0.69	0.23	0.74	0.70	0.75
	10−3	0.45	0.40	0.06	0.46	0.41	0.47
H1 : βj = x/{pj(1 − pj)}1/2
500	10−2	0.65	0.68	0.32	0.65	0.68	0.65
	10−3	0.35	0.37	0.08	0.36	0.38	0.35
1000	10−2	0.58	0.63	0.47	0.59	0.63	0.62
	10−3	0.30	0.33	0.18	0.30	0.33	0.32
H1 : β1 = … = β8 = x, β9 = −x, β10 = − 2x
500	10−2	0.20	0.14	0.55	0.20	0.14	0.73
	10−3	0.05	0.03	0.23	0.06	0.03	0.44
1000	10−2	0.22	0.18	0.81	0.22	0.18	0.84
	10−3	0.06	0.04	0.55	0.07	0.04	0.61
H1 : β1 = … = β9 = x, β10 = −x / 2
500	10−2	0.67	0.63	0.31	0.67	0.63	0.78
	10−3	0.36	0.32	0.09	0.37	0.33	0.50
1000	10−2	0.79	0.76	0.53	0.79	0.77	0.89
	10−3	0.51	0.48	0.23	0.52	0.49	0.67
H1 : β2 = β4 = β6 = β8 = x, β10 = −x, βj = 0 (j = 1, 3, 5, 7, 9 )
500	10−2	0.13	0.08	0.34	0.13	0.08	0.48
	10−3	0.03	0.01	0.11	0.03	0.01	0.21
1000	10−2	0.17	0.12	0.61	0.17	0.12	0.64
	10−3	0.05	0.03	0.31	0.05	0.03	0.35
H1 : β3 = 2x, β4 = −2x, β5 = x, β6 = −x, β j = 0 (j = 1, 2, 7 ∼ 10)
500	10−2	0.04	0.02	0.47	0.04	0.02	0.53
	10−3	0.01	0.00	0.14	0.01	0.00	0.23
1000	10−2	0.07	0.01	0.82	0.07	0.01	0.81
	10−3	0.01	0.00	0.52	0.01	0.00	0.52

^aDivided by α.

Real Data

We considered high-depth sequence data from the exons of 202 genes encoding known or potential drug targets¹⁴ for 1957 subjects randomly drawn from the CoLaus population-based collection.¹⁵ We analyzed total cholesterol (available in 1899 subjects) as a quantitative trait and included eight covariates in the analysis: gender, age, age², and the top five principal components for ancestry constructed from the GWAS SNP data. One subject without the gender and age information was removed. We employed the methods for quantitative traits described in Appendix A.

We restricted our analysis to polymorphic variants that are nonsense, missense, or splice site mutations. We removed variants with observed MAFs>5% or missingness>10%. We excluded any gene whose total number of rare mutations is less than five and ended up with a total of 172 genes. There were a total of 2304 variants in these 172 genes, and the number of variants per gene varied from 1 to 70, with a median of 11. We applied both the asymptotic and permutation versions of our T1, T5, F_p, and VT tests, as well as the permutation EREC test. We calculated the two-sided p values. With 172 genes, the Bonferroni threshold at the 0.05 significance level corresponds to a p value of 0.0003 or –log₁₀(p value) of 3.5.

The results based on the asymptotic and permutation methods are shown in Figures 1 and 2, respectively. One gene was identified as the most significant by all the tests: the asymptotic p values for T1, T5, F_p, and VT are 0.00011, 0.00011, 0.00021, and 0.00057, respectively; the corresponding permutation p values are 0.00013, 0.00013, 0.00025, and 0.0012, respectively; the p value of the EREC test is 0.00012. (The name of the gene is not disclosed here because the main study has not been published yet.) All the p values, except the VT's, pass the Bonferroni criterion. Similar evidence of association has been observed in other samples of the sequencing project.¹⁴ There were 13 variants in the top gene. Their observed MAFs ranged from 0.00026 to 0.0024, the total frequency being 1.13%. Because the observed MAFs are all less than 1% in this case, T1 and T5 are the same test. For the VT test, the maximum occurs at the highest MAF. It is interesting to point out that common SNPs in the top gene were previously identified to be associated with total cholesterol.¹⁶

Figure 1.

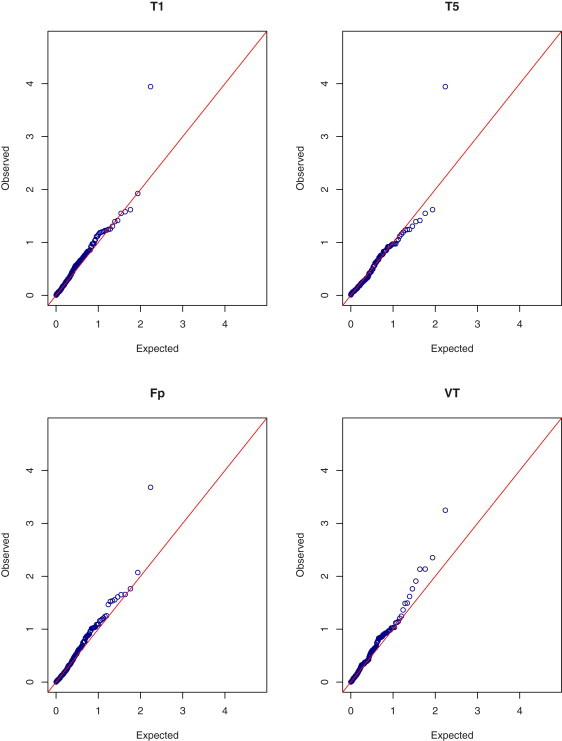
Quantile-Quantile Plots of p Values on the –log₁₀ Scale for the Asymptotic T1, T5, F_p, and VT Tests in the Quantitative Trait Analysis of Total Cholesterol

Figure 2.

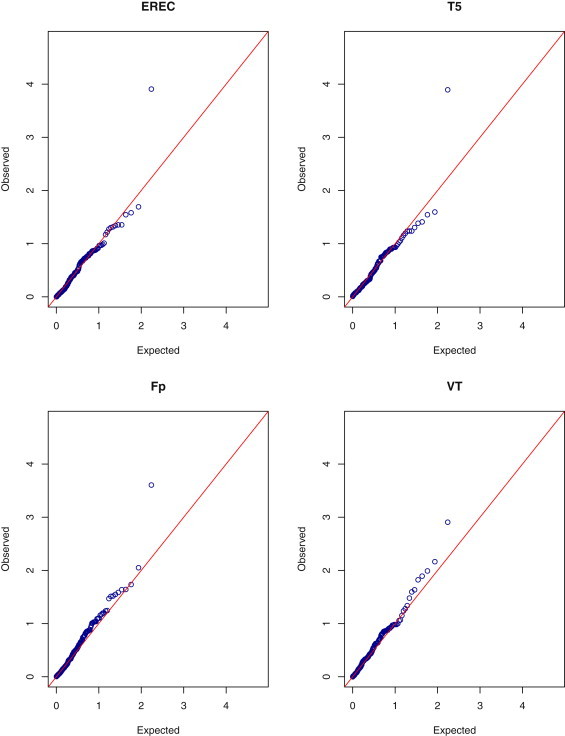
Quantile-Quantile Plots of p Values on the –log₁₀ Scale for the Permutation EREC, T5, F_p, and VT Tests in the Quantitative Trait Analysis of Total Cholesterol

We also performed a binary trait analysis by comparing high (i.e., >6.2 mmol/l) and desirable (i.e., <5.2mmol/l) total cholesterol values. There were 451 subjects with high total cholesterol and 683 subjects with desirable total cholesterol. The results of the analysis are shown in Figures 3 and 4. All the tests identified the same top gene as was identified in the quantitative trait analysis: the asymptotic p values for T1, T5, F_p, and VT are 0.00022, 0.00022, 0.00057, and 0.00088, respectively; the corresponding bootstrap p values are 0.00019, 0.00019, 0.00039, and 0.00033, respectively. Again, T1 and T5 are the same test. The maximum of the VT test occurs at the highest MAF, at which threshold 18 out of the 451 subjects with high cholesterol values carry the rare mutations as opposed to 7 out of 683 subjects with desirable cholesterol values. The p value of the bootstrap EREC test is 0.000021, which is the most extreme among all the tests and is even more extreme than all the p values of the quantitative trait analysis. For eight out of the 10 variants in the top gene, there were more mutations in the high group than in the desirable group (17 versus two); for the remaining two variants, there were fewer mutations in the high group than in the desirable group (one versus five). Thus, allowing opposite effects yielded stronger evidence of association than assuming effects of the same direction.

Figure 3.

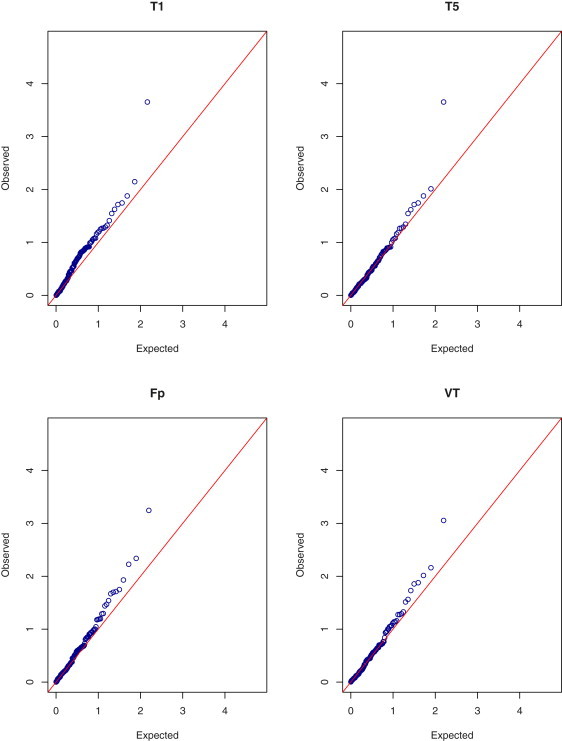
Quantile-Quantile Plots of p Values on the –log₁₀ Scale for the Asymptotic T1, T5, F_p, and VT Tests in the Binary Trait Analysis of Total Cholesterol

Figure 4.

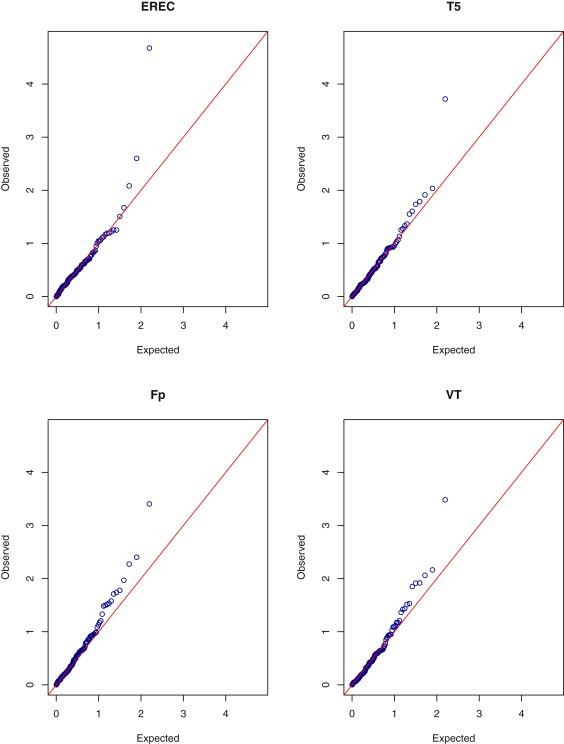
Quantile-Quantile Plots of p Values on the –log₁₀ Scale for the Bootstrap EREC, T5, F_p, and VT Tests in the Binary Trait Analysis of Total Cholesterol

Finally, we compared the proposed methods to the existing ones. The results for the SKAT are shown in Figure S1 (top panel). For the top gene, the SKAT yielded the p values of 0.0014 and 0.00024 in the quantitative and binary trait analyses, respectively, which are 10 times larger than the p values of our EREC test. Because the other existing methods do not allow covariates and some of them require binary traits, we also performed the binary trait analysis without the covariates for all the methods. The results are shown in the bottom panel of Figure S1 and in Figures S2–S4. Although the top gene remains the same, the results without covariate adjustment (for the top gene) are considerably less significant than those with covariate adjustment. For the top gene, the EREC test yielded a much more significant result (p value =0.00013) than all the other tests.

Discussion

We developed a very general framework for the association analysis of rare variants. This framework enabled us to evaluate existing methods and develop other methods. Our theoretical analysis and simulation studies yielded insights into the behavior of the existing methods. The normal approximation works very well for the proposed methods, and resampling is required only when the weight function depends on the phenotype values. The proposed methods are numerically stable and easy to implement. The asymptotic tests are extremely fast. A computer program implementing the proposed methods is posted at our website. For a typical exome-sequencing study, it takes only a few hours to run all the proposed asymptotic and resampling tests.

We have adopted score-type statistics, which are computationally faster and more stable than Wald and likelihood ratio (LR) statistics because the null model does not involve rare variants and needs to be fit only once. Our simulation studies revealed that Wald tests tend to be overly conservative (resulting in substantial loss of power) whereas likelihood ratio tests tend to be too liberal (resulting in excessive false-positive findings), especially for small n and low MAFs; see Tables S6–S8.

Our work improves upon the pioneer work of Madsen and Browning⁸ by using more powerful test statistics, accommodating covariates and avoiding permutation. For case-control studies, Madsen and Browning⁸ estimated the allele frequencies in the unaffected subjects only so that a true signal from an excess of mutations in the affected subjects would not be deflated by using the total number of mutations in both affected and unaffected subjects. According to our theory, the allele frequencies in the unaffected subjects will be optimal if $\log \left(O{R}_j\right)\propto {\left\{p_j\left(1-p_j\right)\right\}}^{-1/2}$$\left(j=1,\text{…},m\right)$ and p_j is the frequency of the jth variant in the unaffected subjects. Even if that is the truth, the frequency estimates are highly variable and can be very different from the true values. The frequency estimates in the pooled sample of affected and unaffected subjects are more stable and the corresponding F_p test can be implemented through normal approximation (rather than resampling).

The optimal choice of the frequency threshold depends on the nature of association, which is generally unknown. In addition, the frequency estimates for rare variants are highly variable, especially for small samples with substantial missing data. Thus, VT methods might be preferable to fixed-threshold methods. Our VT approach improves upon that of Price et al.⁹ in three aspects: (1) it uses more powerful test statistics, (2) it can accommodate covariates, (3) it can be implemented by normal approximation instead of permutation.

The EREC test is capable of detecting rare mutations with opposite effects. Simulation studies (Tables 4 and 6) showed that the EREC test has similar power to the tests assuming the same direction of effects when that assumption holds and is much more powerful than the latter when that assumption fails. In addition, the EREC test outperforms the HP, C-alpha and SKAT tests. In the real data example, the EREC test produced the most convincing evidence of association for the top gene among all the tests. Thus, we recommend the EREC test for general use.

The SKAT is computationally faster than the EREC, HP, and C-alpha tests because it calculates p values analytically. Simulation studies revealed that the SKAT is overly conservative, especially when n and α are small. The resampling methods developed in this article can be used to obtain accurate p values for the SKAT, and indeed any other tests, with or without covariates.

Statistical analysis of rare variants is a very active research area. Several other methods have been published during the preparation of this article.^17–19 We have not compared our methods to all existing methods for several reasons: (1) we wished to focus on the most commonly used current methods, (2) some of the newly published methods are based on different philosophies and thus would be difficult to compare directly, (3) a comprehensive comparison of all existing methods is beyond the scope of this article.

It is possible to incorporate biological and computational information about the functional effects of rare variants, such as SIFT²⁰ and PolyPhen²¹ scores, into the association analysis. Indeed, our theory allows incorporation of any prior knowledge into the weight function. Efficient use of functional or bioinformatics information requires further investigation. It would be worthwhile to explore Bayesian methods.

Grouping methods for rare variants are in the same vein as the SNP-set methods for GWAS studies^22–24 in that multiple SNPs within a group are analyzed collectively to enhance statistical power. Because the data are extremely sparse for individual rare variants, the SNP-set methods for common variants might not be applicable to rare variants. On the other hand, the methods for rare variants can potentially be used to combine low-frequency SNPs in GWAS studies.

We have considered one group of variants at a time. It might be desirable to analyze several groups of variants simultaneously. Our approach can be readily extended to multiple groups of variants. Specifically, we divide variants into, say, K groups according to certain criteria (e.g., MAFs) and combine the information within each group. We can express the score statistic for each group of variants as a sum of n efficient score functions (see Appendix A) so that the asymptotic joint distribution of the K score statistics follows from the multivariate central limit theorem. We can then use the asymptotic joint distribution to form a multivariate test statistic. If we choose the maximum of the K test statistics, then the formulas for K weight functions presented in Material and Methods can be directly applied. If we choose the chi-square statistic with K degrees of freedom, then our method would be a generalization of the combined multivariate and collapsing (CMC) method of Li and Leal.⁷

We used the Bonferroni correction in the analysis of the real data. This criterion is conservative if there is strong linkage disequilibrium (LD) among the genes. More accurate correction for multiple testing can be achieved by accounting for the correlations of the test statistics. There are two possible ways to do so: one is to use permutation and the other is to use Monte Carlo.²⁵ The latter is based on efficient score functions, which are provided in Appendix A.

This work and indeed all existing literature assume that the quantitative trait data are obtained from a random sample. In many sequencing studies, including several in the National Heart, Lung, and Blood Institute (NHLBI) Exome Sequencing Project that we are involved with, only the subjects with the extreme values of a quantitative trait are selected for sequencing. The case-control testing is a valid option but might be inefficient if there is a quantitative association. In addition, it might be desirable to analyze quantitative traits that are not the one used to select the subjects for sequencing. We are currently developing valid and efficient methods for the association analysis of quantitative traits under such trait-dependent sampling.

Appendix A

We relate Y_i to X_i and Z_i through a generalized linear model with the linear predictor ${\beta }^{\text{T}}{X}_i+{\gamma }^{\text{T}}{Z}_i$, where $\beta =\tau \xi$. Let η consist of γ and other nuisance parameters. Let $l\left(\tau ,\eta ;\xi \right)$ denote the log-likelihood function for τ and η with a fixed value of ξ. The corresponding score function and observed Fisher information matrix are

$$\left[\begin{array}{c}{U}_{\tau }\left(\tau ,\eta ;\xi \right)\\ U_{\eta }\left(\tau ,\eta ;\xi \right)\end{array}\right],$$

and

$$\left[\begin{array}{cc}{I}_{\tau \tau }\left(\tau ,\eta ;\xi \right)& I_{\tau \eta }\left(\tau ,\eta ;\xi \right)\\ I_{\eta \tau }\left(\tau ,\eta ;\xi \right)& I_{\eta \eta }\left(\tau ,\eta ;\xi \right)\end{array}\right],$$

where $U_{\tau }\left(\tau ,\eta ;\xi \right)=\partial l\left(\tau ,\eta ;\xi \right)/\partial \tau$,$U_{\eta }\left(\tau ,\eta ;\xi \right)=\partial l\left(\tau ,\eta ;\xi \right)/\partial \eta$, $I_{\tau \tau }\left(\tau ,\eta ;\xi \right)=-{\partial }^{2}l\left(\tau ,\eta ;\xi \right)/\partial {\tau }^2$, $I_{\tau \eta }\left(\tau ,\eta ;\xi \right)=-{\partial }^{2}l\left(\tau ,\eta ;\xi \right)/\partial \tau \partial {\eta }^{\text{T}}$, $I_{\eta \tau }\left(\tau ,\eta ;\xi \right)=I_{\tau \eta }^{\text{T}}\left(\tau ,\eta ;\xi \right)$, and $I_{\eta \eta }\left(\tau ,\eta ;\xi \right)=-{\partial }^{2}l\left(\tau ,\eta ;\xi \right)/\partial \eta \partial {\eta }^{\text{T}}$. The score statistic for testing the null hypothesis $H_0:\tau =0$ is $U_{\tau }\left(0,\hat{\eta };\xi \right)$, where $\hat{\eta }$ is the solution to the equation $U_{\eta }\left(0,\eta ;\xi \right)=0$. Under H₀, the random variable $n^{-1/2}{U}_{\tau }\left(0,\hat{\eta };\xi \right)$ is asymptotically zero-mean normal with a variance that can be consistently estimated by²⁶

$$n^{-1}\left\{I_{\tau \tau }\left(0,\hat{\eta };\xi \right)-I_{\tau \eta }\left(0,\hat{\eta };\xi \right)I_{\eta \eta }^{-1}\left(0,\hat{\eta };\xi \right)I_{\eta \tau }\left(0,\hat{\eta };\xi \right)\right\}.$$

Suppose that ξ is estimated from the data by $\hat{\xi }$. Then we replace ξ in $U_{\tau }\left(0,\hat{\eta };\xi \right)$ by $\hat{\xi }$. It can be shown that $U_{\tau }\left(0,\eta ;\xi \right)={\xi }^{\text{T}}{U}_{\beta }\left(0,\eta \right)$, where $U_{\beta }\left(\beta ,\eta \right)$ is the score function of β under Equation 1. Because $n^{-1/2}{U}_{\beta }\left(0,\hat{\eta }\right)$ is asymptotically zero-mean normal, ${\hat{\xi }}^{\text{T}}{n}^{-1/2}{U}_{\beta }\left(0,\hat{\eta }\right)$ has the same asymptotic distribution as ${\xi }^{\ast \text{T}}{n}^{-1/2}{U}_{\beta }\left(0,\hat{\eta }\right)$, where ${\xi }^{\ast }$ is the limit of $\hat{\xi }$. As a result, $n^{-1/2}{U}_{\tau }\left(0,\hat{\eta };\hat{\xi }\right)$ has the same asymptotic distribution as $n^{-1/2}{U}_{\tau }\left(0,\hat{\eta };{\xi }^{\ast }\right)$. Thus, the test statistic

$$\frac{U_{\tau }\left(0,\hat{\eta };\hat{\xi }\right)}{{\left\{I_{\tau \tau }\left(0,\hat{\eta };\hat{\xi }\right)-I_{\tau \eta }\left(0,\hat{\eta };\hat{\xi }\right)I_{\eta \eta }^{-1}\left(0,\hat{\eta };\hat{\xi }\right)I_{\eta \tau }\left(0,\hat{\eta };\hat{\xi }\right)\right\}}^{1/2}}$$

is asymptotically standard normal as long as $\hat{\xi }$ converges to a nonzero constant as $n\to \mathrm{\infty }$.

Let $U_{\tau ,i}\left(\tau ,\eta ;\xi \right)$ and $U_{\eta ,i}\left(\tau ,\eta ;\xi \right)$ be the ith subject's contributions to $U_{\tau }\left(\tau ,\eta ;\xi \right)$ and $U_{\eta }\left(\tau ,\eta ;\xi \right)$, respectively, and let ${\text{Σ}}_{\tau \eta }$ and ${\text{Σ}}_{\eta \eta }$ be the limits of $n^{-1}{I}_{\tau \eta }\left(0,\eta ;\xi \right)$ and $n^{-1}{I}_{\eta \eta }\left(0,\eta ;\xi \right)$, respectively. It is easy to show that $n^{-1/2}{U}_{\tau }\left(0,\hat{\eta };\xi \right)$ is asymptotically equivalent to $n^{-1/2}{\sum }_{i=1}^n{u}_i$, where

$$u_i=U_{\tau ,i}\left(0,\eta ;\xi \right)-{\text{Σ}}_{\tau \eta }{\Sigma }_{\eta \eta }^{-1}{U}_{\eta ,i}\left(0,\eta ;\xi \right).$$

We refer to u_i as the ith subject's efficient score function.²⁷ To derive the joint distribution of the test statistics with K weight functions, we use the fact that $n^{-1/2}{U}_k$ is asymptotically equivalent to $n^{-1/2}{\sum }_{i=1}^n{u}_{ki}$, where u_ki is the ith subject's efficient score function associated with the kth weight function. Note that $\left(u_{1i},\text{…},u_{Ki}\right)$$\left(i=1,\text{…},n\right)$ are n independent random vectors. By the multivariate central limit theorem and law of large numbers, the null distribution of $n^{-1/2}\left(U_1,\text{…},U_K\right)$ is asymptotically zero-mean normal, and the covariance between $n^{-1/2}{U}_k$ and $n^{-1/2}{U}_l$ is consistently estimated by $n^{-1}{\sum }_{i=1}^n{U}_{ki}{U}_{li}$, where the U_ki's are obtained from the u_ki's by replacing all unknown parameters by their sample estimators.

For quantitative traits, we replace Equation 2 with the linear regression model:

$$Y_i=\tau S_i+{\gamma }^{\text{T}}{Z}_i+{\mathit{ϵ}}_i,$$

where ε_i is normal with mean 0 and variance σ². Then the score statistic and its variance are

$$U=\sum _{i=1}^n\left(Y_i-{\hat{\gamma }}^{\text{T}}{Z}_i\right)S_i,$$

and

$$V={\hat{\sigma }}^2\left\{\sum _{i=1}^n{S}_i^2-{\left(\sum _{i=1}^n{S}_i{Z}_i\right)}^{\text{T}}{\left(\sum _{i=1}^n{Z}_i{Z}_i^{\text{T}}\right)}^{-1}\left(\sum _{i=1}^n{S}_i{Z}_i\right)\right\},$$

where

$$\hat{\gamma }={\left(\sum _{i=1}^n{Z}_i{Z}_i^{\text{T}}\right)}^{-1}\sum _{i=1}^n{Y}_i{Z}_i,$$

and

$${\hat{\sigma }}^2=n^{-1}\sum _{i=1}^n{\left(Y_i-{\hat{\gamma }}^{\text{T}}{Z}_i\right)}^2.$$

For multiple weight functions,

$$U_k=\sum _{i=1}^n\left(Y_i-{\hat{\gamma }}^{\text{T}}{Z}_i\right)S_{ki},$$

and

$$U_{ki}=\left(Y_i-{\hat{\gamma }}^{\text{T}}{Z}_i\right)\left\{S_{ki}-{\left(\sum _{i=1}^n{S}_{ki}{Z}_i\right)}^{\text{T}}{\left(\sum _{i=1}^n{Z}_i{Z}_i^{\text{T}}\right)}^{-1}{Z}_i\right\}.$$

To perform permutation tests without covariates, we simply permute the Y_i's. In the presence of covariates, we adopt the following procedure: (1) calculate the residuals $R_i=Y_i-{\hat{\gamma }}^{\text{T}}{Z}_i$$\left(i=1,\text{…},n\right)$, (2) permute the R_i's to yield the $R_i^{\ast }$'s, (3) create new trait values $Y_i^{\ast }={\hat{\gamma }}^{\text{T}}{Z}_i+R_i^{\ast }$$\left(i=1,\text{…},n\right)$, (4) replace the Y_i's by the $Y_i^{\ast }$'s, (5) recalculate the test statistic, and (6) repeat steps 2–5 a large number of times.

We have implicitly assumed that the trait is univariate and the subjects are unrelated. For repeated measures or family studies, we use generalized linear mixed models²⁸ to capture the dependence of trait values. Suppose that the study contains n families with n_i members in the ith family. For $i=1,\text{…},n$ and $l=1,\text{…},n_i$, let Y_il, S_il and Z_il denote the values of Y, S, and Z for the lth member of the ith family. The random effects b_i $\left(i=1,\text{…},n\right)$ are independent zero-mean random vectors with density function $f\left(b;\theta \right)$ indexed by a set of parameters θ. Conditional on b_i, the trait values $Y_{i1},\text{…},Y_{i,n_i}$ are independent and follow a generalized linear model with density $f\left(y|S_{il},Z_{il};b_i\right)$. The log-likelihood function is

$$l\left(\tau ,\eta ;\xi \right)=\sum _{i=1}^n\log \underset{b}{\int }\prod _{l=1}^{n_i}f\left(Y_{il}|S_{il},Z_{il};b\right)f\left(b;\theta \right)db,$$

where τ is the fixed effect of S_il, and η includes the fixed effects of Z_il and parameters θ. For repeated measures, the log-likelihood takes the same form with Y_il and Z_il being the trait and covariate values at the lth measurement time for the ith subject and with S_il replaced by S_i. We can then use the arguments of the first three paragraphs to derive the test statistics.

For potentially censored age-at-onset traits, we specify that the hazard function for the age at onset conditional on S_i and Z_i satisfies the proportional hazards model²⁹

$$\lambda \left(t|S_i,Z_i\right)={\lambda }_0\left(t\right)e^{\tau S_i+{\gamma }^{\text{T}}{Z}_i},$$

where λ₀ is an arbitrary baseline hazard function and Z_i is redefined to exclude the unit component. Let T_i denote the duration of follow-up for the ith subject, and let Δ_i indicate, by the values 1 versus 0, whether T_i is the actual age at onset or the censoring time. Then the score statistic and its variance are

$$U=\sum _{i=1}^n{\text{Δ}}_i\left(S_i-\frac{\sum _{j\in {\mathcal{R}}_i}{e}^{{\hat{\gamma }}^{\text{T}}{Z}_j}{S}_j}{\sum _{j\in {\mathcal{R}}_i}{e}^{{\hat{\gamma }}^{\text{T}}{Z}_j}}\right),$$

and $V=I_{\tau \tau }-I_{\tau \gamma }{I}_{\gamma \gamma }^{-1}{I}_{\gamma \tau }$, where ${\mathcal{R}}_i$ denotes the set of subjects whose durations of follow-up are no shorter than T_i, $\hat{\gamma }$ is the solution to the equation

$$\sum _{\text{i}=1}^n{\text{Δ}}_i\left(Z_i-\frac{\sum _{j\in {\mathcal{R}}_i}{e}^{{\gamma }^{\text{T}}{Z}_j}{Z}_j}{\sum _{j\in {\mathcal{R}}_i}{e}^{{\gamma }^{\text{T}}{Z}_j}}\right)=0,$$

$$\left[\begin{array}{cc}{I}_{\tau \tau }& I_{\tau \gamma }\\ I_{\gamma \tau }& I_{\gamma \gamma }\end{array}\right]=\sum _{i=1}^n\frac{{\text{Δ}}_i}{\sum _{j\in {\mathcal{R}}_i}{e}^{{\hat{\gamma }}^{\text{T}}{Z}_j}}\left\{\sum _{j\in {\mathcal{R}}_i}{e}^{{\hat{\gamma }}^{\text{T}}{Z}_j}{\left[\begin{array}{c}{S}_j\\ Z_j\end{array}\right]}^{\otimes 2}-{\left(\sum _{j\in {\mathcal{R}}_i}{e}^{{\hat{\gamma }}^{\text{T}}{Z}_j}\right)}^{-1}{\left(\sum _{j\in {\mathcal{R}}_i}{e}^{{\hat{\gamma }}^{\text{T}}{Z}_j}\left[\begin{array}{c}{S}_j\\ Z_j\end{array}\right]\right)}^{\otimes 2}\right\},$$

and $a^{\otimes 2}=a{a}^{\text{T}}$. For multiple weight functions, we obtain the efficient score functions by approximating the partial likelihood score function with a sum of n independent terms.³⁰

Web Resources

The URL for data presented herein is as follows:

• SCORE-Seq: Score-Type Tests for Detecting Disease Associations With Rare Variants in Sequencing Studies, http://www.bios.unc.edu/∼lin/software/SCORE-Seq/