The Reduction in Fatigue Crack Growth Resistance of Dentin with Depth

Abstract

The fatigue crack growth resistance of dentin was characterized as a function of depth from the dentino-enamel junction. Compact tension (CT) specimens were prepared from the crowns of third molars in the deep, middle, and peripheral dentin. The microstructure was quantified in terms of the average tubule dimensions and density. Fatigue cracks were grown in-plane with the tubules and characterized in terms of the initiation and growth responses. Deep dentin exhibited the lowest resistance to the initiation of fatigue crack growth, as indicated by the stress intensity threshold (ΔK_th ≈ 0.8 MPa•m^0.5) and the highest incremental fatigue crack growth rate (over 1000 times that in peripheral dentin). Cracks in deep dentin underwent incremental extension under cyclic stresses that were 40% lower than those required in peripheral dentin. The average fatigue crack growth rates increased significantly with tubule density, indicating the importance of microstructure on the potential for tooth fracture. Molars with deep restorations are more likely to suffer from the cracked-tooth syndrome, because of the lower fatigue crack growth resistance of deep dentin.

Introduction

Excavation of enamel and dentin is a routine component of restorative dentistry. The methods utilized in removing demineralized tissue in today’s practices have been developed to balance the concerns of conservation and prevention, as well as to minimize the time required for a preparation. Understandably, patient comfort and the rate of material removal are both relevant. The rate of material removal is also important in the machining of engineering materials. However, the introduction of damage to the substrate and/or strength-limiting flaws is an equal concern. For example, surface defects introduced during machining/grinding of brittle materials are extremely detrimental, and often lead to a reduction in strength (Marshall et al., 1983; Xu et al., 1995; Quinn et al., 2005).

Sehy and Drummond (2004) introduced Class I or Class II MOD preparations in molars using either a high-speed handpiece with coarse diamond bur or Er:YAG laser. The preparation was followed by placement of a resin composite, bulk curing to maximize interfacial stresses, and evaluation of the tooth-composite interface by scanning electron microscopy. Neither method of preparation resulted in consistent or significant evidence of microcracking in dentin. But two more recent studies reported that flaws introduced within dentin during material removal processes served as the origin of fracture (Yan et al., 2009) and caused reductions in dentin strength (Staninec et al., 2009). In fact, cracks exceeding 100 µm in length have been observed in dentin following some conditions of laser treatment (Staninec et al., 2009). Flaws introduced to the tooth during restorative processes are generally considered too small to cause tooth fractures during oral function. But dentin is susceptible to fatigue (Nalla et al., 2003; Arola and Reprogel, 2005, 2006; Arola et al., 2010), and small (i.e., non-critical) flaws may undergo extension via fatigue crack growth. That process can facilitate tooth fracture when the flaw reaches a critical length (Arola et al., 1999; Nalla et al., 2003). Evidence of fatigue crack growth has been identified on the fracture surfaces of cracks in restored teeth (Bajaj et al., 2008). The fate of flaws introduced during a cavity preparation may be a function of the spatial variations in the local microstructure of dentin. Yet, no study has examined the importance of natural gradients in the microstructure of dentin on the propensity for fatigue crack growth and tooth fracture.

The primary objective of this study was to evaluate the fatigue crack growth behavior of coronal dentin at different depths below the dentino-enamel junction (DEJ). The investigation was designed to assess the importance of microstructure on fatigue crack growth and the relative growth rate under driving forces indicative of those incurred during mastication.

Materials & Methods

Non-carious third molars were obtained from dental practices in Maryland according to an approved protocol issued by the Institutional Review Board of the University of Maryland (Approval Y04DA23151). The teeth were stored in Hanks’ Balanced Salt Solution (HBSS) with record of age and gender. Within 1 month of extraction they were sectioned by means of a numerically controlled slicer/grinder under water-based coolant with diamond abrasive slicing wheels. Serial sections were made perpendicular to the tooth’s axis, and then secondary sections were introduced to obtain compact tension (CT) specimens (Fig. 1). The dentin tubules were oriented in-plane with the fatigue crack surface, and perpendicular to the length of crack extension. The specimens were divided into 3 groups, i.e., peripheral (n = 9), middle (n = 12), and inner (n = 10) dentin (N = 31), which corresponded to the distance from the DEJ (i.e., depth). Specimens of peripheral, middle, and inner dentin were located approximately 0.5 mm, 2 mm, and 3.5 mm, respectively, below the DEJ. Fatigue crack growth properties were determined as a function of the depth and also as a function of tubule density.

Figure 1.

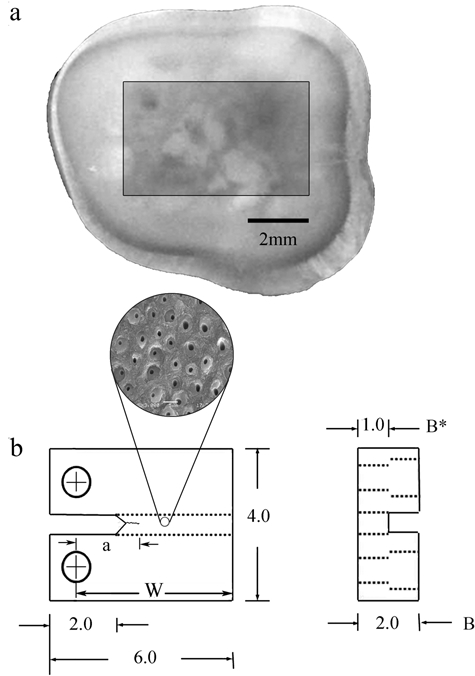
Preparation of a compact tension (CT) specimen machined from a human third molar. (a) View of a sectioned tooth and potential specimen; (b) final geometry and dimensions of the CT specimen. Note that the tubules are oriented perpendicular to the direction of crack extension, but in-plane with the fracture surface produced by the crack. All dimensions in mm.

Fatigue loading of the CT specimens was performed with a BOSE ElectroForce 3200 universal testing system (ElectroForce 3200 BOSE, Eden Prairie, MI, USA) by routine methods described elsewhere (Bajaj et al., 2006; Arola, 2007). Briefly, the specimens were subjected to cyclic loading at 5 Hz under load control, and testing was conducted within an HBSS bath at room temperature (22°C). The loads were applied in opening mode (Mode I). Crack initiation was achieved to obtain a sharp crack tip using a ratio of the minimum and maximum stress (R) of 0.5, whereas cyclic crack growth was conducted with R = 0.1. We computed the incremental crack growth rates (da/dN) by dividing the measured incremental crack extension (Δa) by the increment of loading cycles (ΔN). Crack length measurements were achieved by digital microscopy (Navitar IEEE 1394, Rochester, NY, USA) at a magnification of 60X. The number of cycles between measurements (ΔN) was chosen according to the observed crack growth rate and typically ranged between 5 and 20 kcycles; the average increment of extension was between 60 and 120 µm.

The incremental fatigue crack growth rate (da/dN) within the region of steady-state (Region II) response was quantified according to the Paris Law (Paris et al., 1961),

$$\frac{\text{da}}{\text{dN}}=\text{C}{\left(\Delta \text{K}\right)}^{\text{m}}$$ (1)

where ΔK is the stress intensity range, and the quantities C and m are the fatigue crack growth coefficient and exponent, respectively. The stress intensity range (ΔK) is determined from the difference in stress intensity at the minimum and maximum loads according to Bajaj et al. (2006). Using the incremental crack length measurements and the corresponding stress intensity, we plotted the fatigue crack growth rate (da/dN) in terms of ΔK to estimate the quantities m and C for each specimen. In addition, the apparent stress intensity threshold (ΔK_th) was estimated for a fatigue crack growth rate of 1E-07 mm/cycle, which defines a critical stress intensity below which fatigue crack growth either does not occur, or occurs at a negligible rate. A comparison of the fatigue crack growth parameters for specimens obtained from the 3 depths was conducted by one-way Analysis of Variance, with significant differences identified by p < 0.05.

The dentin specimens were dehydrated in air for 24 hrs, then sputtered with gold palladium, and the fracture surfaces were evaluated with a scanning electron microscope in secondary electron imaging mode (JEOL Model JSM-5600, Mitaka, Tokyo, Japan). Micrographs were also obtained from the viewing surface monitored during fatigue crack growth at 2000X magnification to estimate the tubule density. Commercial image analysis software (Image J 1.42i, National Institutes of Health, Bethesda, MD, USA) was used for counting the number of lumens per unit area, and for quantifying the average lumen dimensions in each of the 3 regions of evaluation. Correlations between the ΔK_th and lumen density, as well as between the parameters C, m, and lumen density, were tested by Pearson’s r, with significance identified by p < 0.05.

Results

A fatigue crack growth history with the important quantities characterizing cyclic extension highlighted is shown in Fig. 2(a). The cumulative fatigue crack growth responses for all specimens are shown as a function of the stress intensity range in Fig. 2(b). The large range in responses suggests that microstructure is important to the relative fatigue crack growth resistance of dentin.

Figure 2.

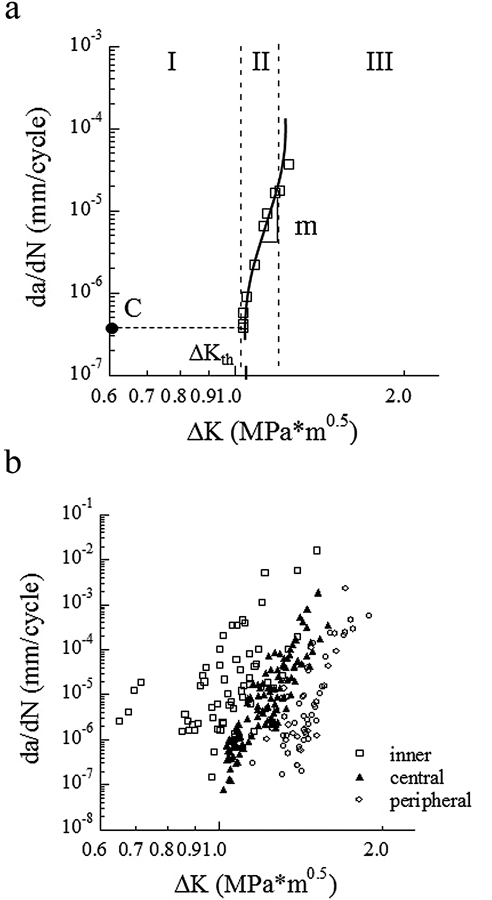
Fatigue crack growth (FCG) resistance of coronal dentin. (a) A typical fatigue crack growth response distinguishing all 3 regions of cyclic extension; (b) a comparison of the FCG resistance of young coronal dentin from the inner, central, and peripheral regions.

Average values for the fatigue crack growth rate parameters were determined from the responses of specimens in each of the 3 groups. Initiation of cyclic extension in the deep dentin occurred at a significantly lower (p < 0.0001) stress intensity range (ΔK_th ≈ 0.8 ± 0.12 MPa•m^0.5) than in the middle (ΔK_th ≈ 1.0 ± 0.06 MPa•m^0.5) and peripheral dentin (ΔK_th ≈ 1.2 ± 0.08 MPa•m^0.5). Stable cyclic crack growth within the Region II response [Fig. 2(a)] was characterized according to the Paris Law parameters. For deep dentin, the fatigue crack growth exponent (m) and coefficient (C) were 27.5 ± 7 and 1.64 E-05 ± 0.02 E-05 (mm/cycle) (MPa•m^0.5)^-m, respectively. These measures for the middle and peripheral dentin were found to be 25.5 ± 2.9 and 4.41 E-08 ± 0.21 E-08 (mm/cycle) (MPa•m^0.5)^-m, and 26.7 ± 2.8 and 5.61 E-10 ± 0.12 E-10 (mm/cycle) (MPa•m^0.5)^-m, respectively. Though there was not a significant difference in the fatigue crack growth exponents, the differences in crack growth coefficients were significant (p < 0.0001).

The microstructural analysis revealed that the dentin specimens exhibited a tubule density ranging from approximately 10,000 tubules/mm² to 60,000 tubules/mm². The apparent ΔK_th is plotted in terms of the density measurements in Fig. 3(a). There was a significant reduction in the ΔK_th (r = −0.774; p < 0.0001) with increasing tubule density, indicating that there is a decrease in the resistance to the initiation of cyclic crack growth. Similarly, the fatigue crack growth coefficients are presented in terms of the density measurements in Fig. 3(b). There was a significant increase in C with increase in lumen density (r = -0.754; p < 0.0001). There was no correlation between m and tubule density (p > 0.05).

Figure 3.

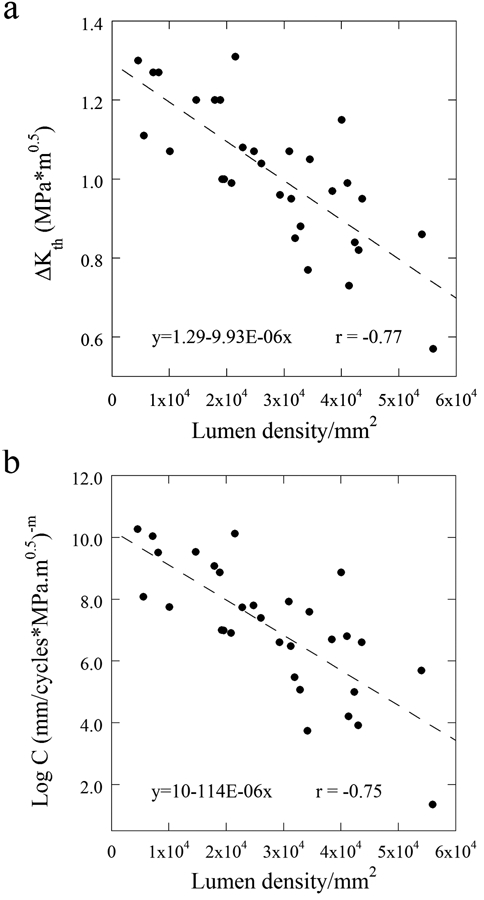
Structure/property relationships that contribute to the fatigue behavior of dentin. (a) Stress intensity range average as a function of lumen density, and (b) FCG coefficient.

Digital images of the crack tip and its propagation were captured for selected specimens. A representative crack growth path over approximately 1 mm of extension in a selected CT specimen of middle dentin is shown in Fig. 4(a). A small degree of crack curvature is evident in this figure with respect to the direction of loading (vertical plane). Note that an unbroken portion of tissue (i.e., a “ligament”) has developed, which resulted from the crack undergoing a change in the path of extension. Unbroken ligaments and crack curving were frequently observed and represent an important mechanism of crack growth toughening in dentin (Kruzic et al., 2003; Kruzic and Ritchie, 2008). A more highly magnified view of the highlighted region [Fig. 4(a)] is shown after a period of approximately 12 kcycles in Fig. 4(b). Note that the crack preferred to extend through a region of high lumen density adjacent to that with lower tubule count. The fracture surfaces examined by SEM also revealed that ligaments developed during cyclic crack extension.

Figure 4.

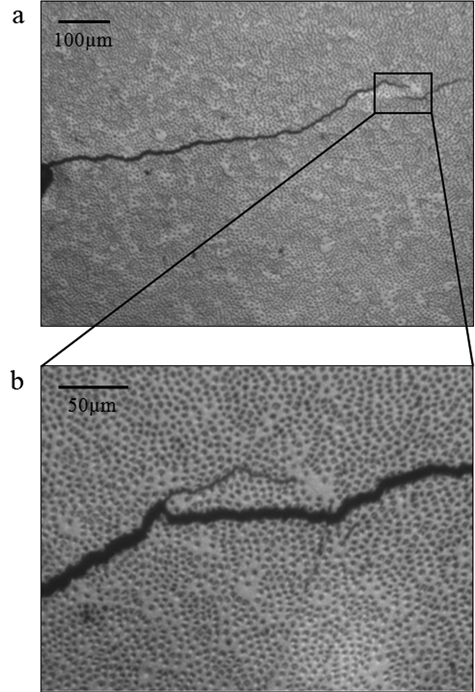
Crack extension from the notch in a sample of central dentin from a 32-year-old male. (a) Low-magnification view; (b) a higher magnification view after a period of 12,500 cycles of a crack that has reached a location of low lumen density. The crack has become partially arrested, and a secondary crack has developed in the closest region with highest lumen density. This view is consistent with the imaging plane examined during crack growth measurements.

Discussion

According to previous investigations, the mechanical properties of dentin should be assessed by a damage mechanics approach that accounts for intrinsic flaws (Staninec et al., 2002; Kinney et al., 2003). The potential for flaws to contribute to the failure of teeth is dependent on the presence and population of defects, the stress level, as well as the apparent “flaw sensitivity” of dentin. These characteristics are often assessed from the statistical distribution of failures and/or the differences in strength related to the contributions of existing flaws. Here the flaw sensitivity of dentin was characterized in terms of the tissue’s resistance to the propagation of a known defect (i.e., a crack) under cyclic loading. The experimental routine is a model for fatigue crack growth in a restored tooth where the driving forces for cyclic extension occur through mastication. The flaws responsible can be intrinsic, i.e., a region of very high lumen density, or a defect resulting from the restorative process.

Previous studies have reported a reduction in hardness (Pashley et al., 1985; Kinney et al., 1996; Fuentes et al., 2003), ultimate tensile strength (Carvalho et al., 2001; Staninec et al., 2002; Inoue et al., 2003; Giannini et al., 2004), and shear strength (Watanabe et al., 1996; Konishi et al., 2002) of dentin with increasing distance from the DEJ. Results from this investigation showed that deep dentin exhibits significantly lower ΔK_th and significantly greater C, both signifying a lower resistance to the growth of fatigue cracks. But how do these quantities reflect on the cracked-tooth syndrome? Based on fatigue crack markings in restored teeth, the average stress intensity (ΔK) contributing to cyclic extension is approximately 0.7 MPa•m^0.5 (Bajaj et al., 2008). Results obtained for the ΔK_th imply that, at this driving force, fatigue crack growth would most likely develop in the deep dentin only. Overall, the results reveal that tooth fracture is most common in teeth with deep restorations, due to the reduced thickness of remaining dentin compounded by the lower fatigue crack growth resistance of deep dentin.

Differences in the properties of dentin with depth have been primarily attributed to tubule density and dimensions. For instance, the reduction in hardness was reasoned to arise from the increase in tubule diameter and a reduction in the intertubular dentin with depth. Furthermore, the reduction in strength of deep coronal dentin is due to the greater tubule density and reduction in the effective area of a material-bearing load (Carvalho et al., 2001; Inoue et al., 2003). The tubule diameter and the cross-sectional area occupied by the tubules increase by approximately 20% from peripheral dentin to the pulp (Pashley, 1984); that would equate to an approximately 20% reduction in strength. However, according to the definition of Mode I stress intensity range in terms of cyclic stress, cracks in deep dentin begin to undergo cyclic extension at stresses approximately 40% lower than those required in peripheral dentin. Thus, the gradients in fatigue crack growth resistance of dentin with depth are far greater than those noted in the hardness and strength of this tissue.

The average Paris Law exponent for crack extension in-plane with the tubules (0° orientation; m = 25.4 ± 4.3) examined herein is nearly twice that reported earlier for cracks extending perpendicular to the tubules (90° orientation; m = 13.3 ± 1.1) (Bajaj et al., 2006). Furthermore, the range in ΔK_th reported in that study for the 90° orientation (0.65 to 0.90 MPa•m^0.5) is most consistent with that of deep dentin. This difference highlights that the fatigue crack growth resistance of dentin exhibits substantial anisotropy. It also emphasizes the preference for cracks to undergo cyclic extension perpendicular to the tubules rather than in directions that are in-plane with the tubules. Based on the range in responses for the 0° orientation, dentin exhibits the greatest degree of anisotropy near the DEJ, and it decreases with depth from peripheral to inner dentin.

The primary mechanisms active in resisting cyclic extension were crack deflection, crack bridging by unbroken ligaments of tissue, crack branching, and microcracking. These mechanisms were previously documented during in situ experiments by Koester et al. (2008). Here, the contributions of these mechanisms were inversely proportional to the tubule density. In regions with low density, the crack would undergo retardation and proceed by a deflection along a path of higher tubule density, or initiate a secondary peripheral crack with a peritubular cuff that underwent microcracking. This process resulted in the formation of unbroken ligaments that promoted extrinsic toughening. Cracks in deep dentin extended uniformly along the path of highest stress intensity through adjacent tubules. Crack branching and unbroken ligaments were seldom observed in deep dentin, which are regarded as the most potent mechanisms of crack growth resistance (Koester et al., 2008). Though the majority of these mechanisms are also active during fatigue crack growth in the 90° orientation (Bajaj et al., 2006), they appear to be less potent than the concert of extrinsic toughening mechanisms active in the 0° orientation.

There is one factor that was not considered in the evaluation. An increase in patient age is associated with a reduction in both fatigue strength and fatigue crack growth resistance (Arola and Reprogel, 2005; Kinney et al., 2005; Bajaj et al., 2006). This change in behavior occurs as a result of the lumens filling with mineral and corresponding suppression of the mechanisms of toughening. Filling of the lumens begins in the root and continues to the coronal region. In addition, the process initiates at the terminal points of the tubules (Arola, 2007). Thus, the spatial gradient in fatigue crack growth resistance of coronal dentin may change with patient age and will be addressed in our future studies.

In summary, an investigation concerning fatigue crack growth in the deep, middle, and peripheral regions of coronal dentin was conducted. Contributions from the microstructure within these 3 regions to the initiation and growth of fatigue cracks were assessed. Deep dentin exhibited significantly (p < 0.0001) lower resistance to the initiation of fatigue crack growth and a significantly (p < 0.0001) greater average rate of incremental crack extension than both middle and peripheral dentin. The changes in fatigue crack growth behavior with depth correlated with the increasing density of tubules and resulted from a reduction in potency of the mechanisms of toughening.