Identification of significant genes in genomics using Bayesian variable selection methods

Abstract

In the studies of genomics, it is essential to select a small number of genes that are more significant than the others for research ranging from candidate gene studies to genome-wide association studies. In this study, we proposed a Bayesian method for identifying the promising candidate genes that are significantly more influential than the others. We employed the framework of variable selection and a Gibbs sampling based technique to identify significant genes. The proposed approach was applied to a genomics study for persons with chronic fatigue syndrome. Our studies show that the proposed Bayesian methodology is effective for deriving models for genomic studies and for providing information on significant genes.

Introduction

In the studies of genomics, the problem of identifying significant genes remains a challenge for researchers. Single nucleotide polymorphisms (SNPs) can be used in clinical association studies to determine the contribution of genes to disease susceptibility or drug efficacy. By using candidate gene approaches or genome-wide association studies, the key goal is to find responsible genes and SNPs for certain events (for example, certain diseases or certain drug efficacy). It is vital to select a small number of SNPs that are more significant than the others and ignoring the SNPs of lesser significance, thereby allowing researchers to focus on the most promising candidate genes and SNPs for diagnostics and therapeutics (Lee et al 2003; Lin et al 2007a). As we have 2^p models with p SNPs, exhaustive computation over this model space is not feasible when the model space is very large (Lee et al 2003).

A variety of Bayesian variable selection methods based on Markov chain Monte Carlo (MCMC) approaches have been proposed for variable selection including the stochastic search variable selection (SSVS) of George and McCulloch (1993), the unconditional priors (UP) approach of Kuo and Mallick (1998), and the Gibbs variable selection (GVS) by Dellaportas and colleagues (2000, 2002). These three Bayesian variable selection methods utilize one particular MCMC method, the Gibbs sampler. The SSVS method has been applied to the identification of quantitative trait loci (QTL) and treats mapping QTL as a problem of model determination and variable selection (Yi et al 2003). Lee and colleagues (2003) applied the SSVS method to the problem of gene selection with microarray data for discovering significant disease genes on breast tumors. Similarly, Oh and colleagues (2003) utilized the SSVS method to identify the markers that are associated with the disease genes related to a high rate of increase in cholesterol. Furthermore, the SSVS approach was extended to the multivariate regression model in the multivariate Bayesian variable selection method (Brown et al 1998). Sha and colleagues (2004) used the multivariate Bayesian variable selection method to classify disease stages in microarray data. In addition, Swartz and colleagues (2006, 2007a) utilized the SSVS method with a conditional logistic regression likelihood to identify genetic loci relevant to a disease using case-parent triads. Oh (2007) also coupled the SSVS method with the new Haseman-Elston method to perform linkage analysis in rheumatoid arthritis. Similarly, Kwon and colleagues (2007) applied an iterative SSVS method to find SNPs that are associated with rheumatoid arthritis.

The rest of the paper is organized as follows. First, we propose a Bayesian-based methodology to identify the promising candidate genes that are significantly more influential than the others. Secondly, we evaluate and compare the proposed methods using a real dataset in a candidate gene study. Finally, we present the discussion and provide the conclusion.

Methods

Population

The study population was original to the previous study by the CDC Chronic Fatigue Syndrome Research Group. More information is available on the website (http://www.camda.duke.edu/camda06/datasets/index.html). In the present study, we only focused on the 42 SNPs as described in Table 1. There were 109 subjects, including 55 subjects having had experienced chronic fatigue syndrome (CFS) and 54 nonfatigued controls. In this analysis, we employed the 71 subjects, including 35 CFS subjects and 36 nonfatigue subjects, without any missing SNP values.

Table 1.

A panel of 42 SNPs by the CDC Chronic Fatigue Syndrome Research Group.

Gene	SNPs
POMC	rs12473543
TH	rs4074905, rs2070762
MAOA	rs1801291, rs979606, rs979605
MAOB	rs3027452, rs2283729, rs1799836
TPH2	rs2171363, rs4760816, rs4760750, rs1386486, rs1487280, rs1872824, rs10784941
COMT	rs4646312, rs740603, rs6269, rs4633, rs165722, rs933271, rs5993882
NR3C1	rs2918419, rs1866388, rs860458, rs852977, rs6196, rs6188, rs258750
SLC6A4	rs2066713, hCV7911132, rs140701
CRHR1	rs110402, rs1396862, rs242940, rs173365, rs242924, rs7209436
CRHR2	rs2267710, rs2267714, rs2284217

Gibbs variable selection

Assume that we observe p SNPs along the genome. Among the p SNPs, some may be tightly linked with large effects, and others may have only weak effects. Our aim is to identify a small number of SNPs that have the greatest discriminating power.

We consider binary responses as Y_i = 1 indicates that the subject has a certain disease and Y_i = 0 indicates that the subject is a control, for i = 1, ..., n. The observed phenotypic value Y_j can be described by the linear model as follows (Dellaportas et al 2000; Oh et al 2003):

$$Y_i={\beta }_0+\sum _{j=1}^p{\gamma }_j{\mathbf{X}}_j{\beta }_j+\varepsilon ,$$ (1)

where X_j is the design matrix, β_j the parameter vector related to the j th term, and ɛ ~ N(0,σ²). In GVS, a set of binary indicator variables γ_j (j = 1, …, p), where γ_j = 1 or 0 represents the presence or absence of covariate j in the model, respectively.

The prior for (γ, β ) is specified as f (γ, β ) = f (γ ) f ( β |γ ). Furthermore, β can be partitioned into two vectors β_γ and β _\γ corresponding to those components of β that are included (γ_j = 1) or not included (γ_j = 0) in the model. Then, the prior f (β |γ ) may be partitioned into model prior f (β_γ |γ ) and pseudoprior f (β _\γ |β_γ,γ ).

The sampling procedure is summarized by the following three steps (Dellaportas et al 2000):

1. We sample the parameters included in the model by the posterior

   $$f({\beta }_{\gamma }\mid {\beta }_{\backslash \gamma },\gamma ,\mathbf{y})\propto f(\mathbf{y}\mid \beta ,\gamma )f({\beta }_{\gamma }\mid \gamma )f({\beta }_{\backslash \gamma }\mid {\beta }_{\gamma },\gamma ),$$ (2)

   where y denotes the observed data.

2. We sample the parameters excluded from the model from the pseudoprior

   $$f({\beta }_{\backslash \gamma }\mid {\beta }_{\gamma },\gamma ,\mathbf{y})\propto f({\beta }_{\backslash \gamma }\mid {\beta }_{\gamma },\gamma ).$$ (3)

3. We sample each variable indicator j from a Bernoulli distribution with success probability O_j /(1 + O_j); where O_j is given by

   $$O_j=\frac{f(\mathbf{y}\mid \beta ,{\gamma }_j=1,{\gamma }_{\backslash j})f(\beta \mid {\gamma }_j=1,{\gamma }_{\backslash j})f(\gamma =1,{\gamma }_{\backslash j})}{f(\mathbf{y}\mid \beta ,{\gamma }_j=0,{\gamma }_{\backslash j})f(\beta \mid {\gamma }_j=0,{\gamma }_{\backslash j})f(\gamma =0,{\gamma }_{\backslash j})},$$ (4)

   where γ _{\ j} denotes all terms of γ except γ _j.

For the simplest approach, it is assumed that the prior β_j depends only on γ_j and is given by

$$f({\beta }_j\mid {\gamma }_j)=(1-{\gamma }_j)f({\beta }_j\mid {\gamma }_j=0)+{\gamma }_{j}f({\beta }_j\mid {\gamma }_j=1).$$ (5)

The simplified prior (5) results in the following full conditional posterior distribution

$$f({\beta }_j\mid \gamma ,{\beta }_{\backslash j},\mathbf{y})\propto \{\begin{array}{ll}f(\mathbf{y}\mid \gamma ,\beta )f({\beta }_j\mid {\gamma }_j=1)\hfill & {\gamma }_j=1\hfill \\ f({\beta }_j\mid {\gamma }_j=0)\hfill & {\gamma }_j=0\hfill \end{array}.$$ (6)

A mixture of Normal distribution is used for model parameters as follows:

$$\begin{array}{l}f({\beta }_j\mid {\gamma }_j=1)\equiv N(0,{\mathrm{\Sigma }}_j)\hspace{0.17em}\text{and\hspace{0.17em}}f({\beta }_j\mid {\gamma }_j=0)\\ \equiv N({\overline{\mu }}_j,S_j),\end{array}$$ (7)

where μ̄_j, S_j are the mean and variance respectively in the corresponding pseudoprior distributions and ∑_j is the prior variance, when the j term is included in the model.

Stochastic search variable selection and unconditional priors

In summary, we present the similarities and differences between the three Bayesian variable selection methods including GVS, SSVS, and UP as follows. In the SSVS strategy, unlike GVS and UP, variables corresponding to γ_j = 0 are included in the model as follows (George and McCulloch 1993; Oh et al 2003):

$$Y_i={\beta }_0+\sum _{j=1}^p{\mathbf{X}}_j{\beta }_j+\varepsilon .$$ (8)

And in the SSVS strategy, β_j parameters are constrained to be close to zero when γ_j = 0 (George and McCulloch 1993). In this situation, f (y| β,γ ) is independent of γ. Thus, the first term on the right hand side of (4) can be omitted as follows:

$$O_j=\frac{f(\beta \mid {\gamma }_j=1,{\gamma }_{\backslash j})f(\gamma =1,{\gamma }_{\backslash j})}{f(\beta \mid {\gamma }_j=0,{\gamma }_{\backslash j})f(\gamma =0,{\gamma }_{\backslash j})}.$$ (9)

In the UP approach, a prior distribution for (γ,β ) is specified with β independent of γ (Kuo and Mallick 1998). Then, the second term on the right hand side of (4) is absent as follows:

$$O_j=\frac{f(\mathbf{y}\mid \beta ,{\gamma }_j=1,{\gamma }_{\backslash j})f(\gamma =1,{\gamma }_{\backslash j})}{f(\mathbf{y}\mid \beta ,{\gamma }_j=0,{\gamma }_{\backslash j})f(\gamma =0,{\gamma }_{\backslash j})}.$$ (10)

Two-stage Bayesian variable selection methodology

In this study, we propose a two-stage selection methodology based on GVS. In Stage I, we conduct GVS on all potential variables (that is, genetic markers) and calculate the estimated posterior probabilities for all potential variables. After ranking the variables according to the posterior probabilities, we then select a subset of N variables with top main effects based on the estimated posterior probabilities. That is, we identify the top N candidate genetic markers in Stage I.

In Stage II, we perform GVS again only on the N variables selected in Stage I and rank the selected N variables according to the estimated posterior probabilities. Next, we choose a small subset of M variables with top main effects based on the sorted posterior probabilities. That is, we identify the top M candidate genetic markers as a panel of significant genetic markers in Stage II.

Similarly, we can utilize SSVS or UP with the above two-stage selection methodology.

OpenBUGS software

The proposed Bayesian methodology can be implemented using the OpenBUGS software (Thomas et al 2006). The implementation involves the definition with a likelihood of the model f (y| β,γ ) and the specification of the prior distributions f ( β,γ )and f (γ )using OpenBUGS (Ntzoufras 2002). The posterior probabilities are calculated using OpenBUGS and can be monitored using the command “summaryStats” in the OpenBUGS environment (Ntzoufras 2002).

When no restrictions on the model space are imposed, a common prior for the indicator variables γ_j is f (γ_j) = Bernoulli(1/2) (Ntzoufras 2002). According to George and McCulloch (1993, 1997), the Gibbs sampler should begin with all γ_j = 1, which corresponds to starting with the full model. A selection of μ̄_j = 0 and S_j = ∑_j /k² with k =10 has been proven to be an adequate choice (Ntzoufras 2002). The pseudoprior parameters μ̄_j, S_j, and k are only relevant to the behavior of the MCMC chain and do not affect the posterior distribution (Ntzoufras 2002). Dellaportas and colleagues (2000) suggested that the Gibbs sampler is run for 100,000 iterations for GVS, 500,000 iterations for SSVS, and 500,000 iterations for UP, respectively, after discarding the first 10,000 iterations for the burn-in period.

Results

We applied the proposed Bayesian strategy to the published dataset in CFS as described previously for discovering significant genes.

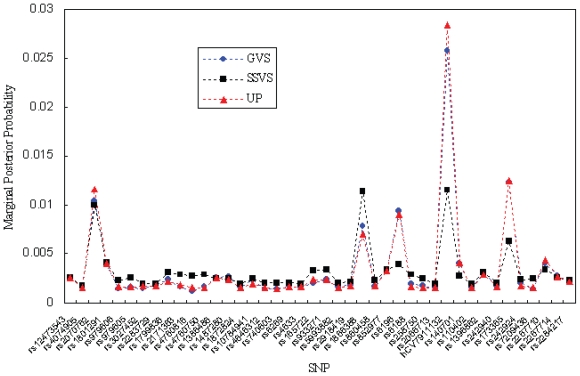
First, we calculated the estimated marginal posterior probabilities based on GVS, SSVS, and UP for all the potential SNPs by using OpenBUGS. Figure 1 shows the results of the estimated marginal posterior probabilities in Stage I. Then, we ranked the SNPs according to the estimated marginal posterior probabilities and selected ten SNPs with top main effects. Table 2 summarizes the top ten SNPs based on the calculated marginal posterior probabilities in Stage I. The results in Figure 1 were based on 100,000 iterations for GVS, 500,000 iterations for SSVS, and 500,000 iterations for UP, respectively. For all methods, we discarded 10,000 iterations as a burn-in period. All three methods provided similar marginal posterior probabilities in Stage I. As shown in Table 2, the top ten SNPs in GVS were the same as the ones in UP, although the ranking in GVS was slightly different from the one in UP. And there were two different SNPs between GVS and SSVS among the top ten SNPs.

Figure 1.

Table 2.

In Stage I, the top ten SNPs based on their marginal posterior probabilities using the OpenBUGS software for three Bayesian variable selection methods including the Gibbs variable selection (GVS), the Stochastic Search Variable Selection (SSVS), the unconditional priors (UP) approach.

Posterior Ranking	GVS	SSVS	UP
1	hCV7911132	hCV7911132	hCV7911132
2	rs173365	rs1866388	rs173365
3	rs2070762	rs2070762	rs2070762
4	rs6196	rs173365	rs6196
5	rs1866388	rs1801291	rs1866388
6	rs140701	rs6196	rs2267710
7	rs2267710	rs2267710	rs140701
8	rs1801291	rs852977	rs1801291
9	rs852977	rs933271	rs852977
10	rs1396862	rs165722	rs1396862

Secondly, we calculated the estimated marginal posterior probabilities based on GVS, SSVS, and UP again for the selected ten SNPs on the first run. Then, we ranked the SNPs according to the estimated marginal posterior probabilities and selected five SNPs with top main effects as a panel of significant SNPs. Table 3 shows the top five SNPs based on the calculated marginal posterior probabilities in Stage II. The results in Table 3 were based on 100,000 iterations for GVS, 500,000 iterations for SSVS, and 500,000 iterations for UP, respectively. For all methods, we discarded 10,000 iterations as a burn-in period. All three methods provided similar marginal posterior probabilities in Stage II. Furthermore, all three methods selected the same top five SNPs, although the ranking in GVS was different from the one in SSVS and was the same as the one in UP.

Table 3.

In Stage II, the top five SNPs based on their marginal posterior probabilities using the OpenBUGS software for three Bayesian variable selection methods including the Gibbs variable selection (GVS), the Stochastic Search Variable Selection (SSVS), the unconditional priors (UP) approach.

Posterior Ranking	GVS	SSVS	UP
1	hCV7911132	hCV7911132	hCV7911132
2	rs173365	rs2070762	rs173365
3	rs2070762	rs1866388	rs2070762
4	rs6196	rs173365	rs6196
5	rs1866388	rs6196	rs1866388

For all three methods, the OpenBUGS programs were run on a 2.4 GHz processor. The CPU execution time in Stage I was approximately 139 minutes for GVS, 45 minutes for SSVS, and 703 minutes for UP, respectively. Furthermore, the CPU execution time in Stage II was approximately 9.8 minutes for GVS, 4 minutes for SSVS, and 60 minutes for UP, respectively. Based on the above CPU execution time, SSVS seemed to be most efficient among these three methods.

Discussion

We have developed a Bayesian-based methodology to address the problem of identifying genetic markers such as SNPs and genes that are more significant than the others. This problem occurs frequently in genomic and epidemiologic studies ranging from candidate gene studies to high-density genome scans. Our method treats the mapping of genetic markers as a problem of model determination and variable selection. Variable selection approaches for gene mapping include Bayesian methods and frequentist methods (Swartz et al 2007b). Several reports compared Bayesian methods to frequentist methods and found that the Bayesian methods may provide fewer false positives (Swartz et al 2007b). Because the dimensionality is kept constant across all possible models, the Bayesian-based methodology can be easily implemented via the Gibbs sampler (Dellaportas et al 2000). The Bayesian procedure can even be implemented using the publicly available software OpenBUGS (Thomas et al 2006) and thus can be widely used in genomic studies.

As shown in the MCMC results, we compared three Bayesian variable selection strategies including GVS, SSVS, and UP. The proposed SSVS method was shown to be more efficient than two other methods for discovering significant genes under typical situations of a genomics study. These three methods are all based on the Gibbs sampler. Compared with the reversible-jump MCMC, the Gibbs sampling approach has advantages on simplicity of computation and diagnosis of convergence (George and McCulloch 1997). Another major advantage is that these methods can be easily applied with the Gibbs sampling software such as OpenBUGS (Dellaportas et al 2000). The UP approach is extremely easy to implement, but may be insufficiently flexible for many practical problems (Dellaportas et al 2000). In the cases of hundreds of genetic markers, a second iteration of SSVS might be considered with a subset of variables based on the first run (George and McCulloch 1993). Accuracy of estimating the main effects and the posterior probabilities may be improved by using this two-stage strategy (Yi et al 2003). Similarly, our proposed two-stage Bayesian method may have better accuracy by conducting a second run with a reduced set of genetic markers based on the first run. Moreover, Beattie and colleagues (2002) proposed a two-stage Bayesian variable selection strategy that incorporates the SSVS method with the intrinsic Bayes factor (IBF). In the first stage, the SSVS procedure is employed on all factors. Then, in the second stage, the factors identified in the first stage are used as the input for the IBF analysis. The difference between our proposed two-stage Bayesian method and theirs was that only Bayesian variable selection strategies such as GVS, SSVS, and UP were used for both stages in our study.

To the best of our knowledge, this is the first study that proposes to use the Bayesian-based approach to provide a way to find a panel of genetic markers that is more significant than the others in CFS. It has been reported that subjects with CFS were distinguished by genetic markers that were involved in either hypothalanmic-pituitary-adrenal (HPA) axis function or neurotransmitter systems, including monoamine oxidase A (MAOA), monoamine oxidase B (MAOB), nuclear receptor subfamily 3; group C, member 1 glucocorticoid receptor (NR3C1), proopiomelanocortin (POMC) and tryptophan hydroxylase 2 (TPH2) genes (Smith et al 2006). Moreover, it has been shown that genetic markers, including catechol-O-methyltransferase (COMT), NR3C1 and TPH2 genes, could predict whether a person has CFS (Geortzel et al 2006). In this study, we identified significant SNPs in solute carrier family 6 member 4 (SLC6A4), corticotropin releasing hormone receptor 1 (CRHR1), tyrosine hydroxylase (TH), and NR3C1 genes. An interesting finding was that an association of NR3C1 with CFS compared with nonfatigued controls appeared to be consistent across several studies. Thus, this significant association strongly suggests that NR3C1 may be involved in biological mechanisms with CFS. However, these two previous studies (Smith et al 2006; Geortzel et al 2006) identified the TPH2 gene among the reported associations, which was not included in this study. The potential reason for the discrepancies between the results of this study and those of other studies may be the sample sizes. The studies conducted on small populations may have biased a particular result. Future research with independent replication in large sample sizes is needed to confirm the role of the candidate genes identified in this study.

In this study, we focused the context of this paper being a candidate gene approach. In future research, we will investigate the identifiability (Gelfand and Sahu 1999) of the proposed method and explore the possibility of extension to larger scale problems such as genome-wide association studies, where thousands of SNPs for a chromosome scan are examined. Moreover, the proposed Bayesian-based methodology was employed for modeling genetic markers associated with diseases and may be suitable for association studies in pharmacogenomics. In the studies of pharmacogenomics, genetic markers such as SNPs can be used to understand the relationship between genetic inheritance and the body’s response to drugs (Lin et al 2006a, 2006b). In future work, we aim to investigate the Bayesian-based methodology for application in pharmacogenomics.

Furthermore, we focused on the issue of selecting the significant genes without considering epistatic models in this study. Epistasis analysis for gene-gene and gene-environment interactions have been advocated for deciphering these complex mechanisms, particularly when each involved genetic marker only demonstrates a minor marginal effect (Lin et al 2007a, 2007b). It is important to address gene–gene and gene–environment interactions for describing a trait involving complex disease-related, pharmacokinetic and pharmacodynamic mechanisms. In future work, we will investigate gene–gene and gene–environment interactions based on the Bayesian variable selection strategies.

Conclusion

In this study, we propose an alternative Bayesian method for assessing significant genes in genomic studies. Our method is based on the Bayesian variable selection methods. Our findings suggest that our approach may provide a plausible way to identify a panel of genetic markers that is more significant than the others. Over the next few years, the results of our studies could be utilized to develop molecular diagnostic/prognostic tools. However, application of genomics in routine clinical practice will become a reality after a prospective clinical trial has been conducted to validate genetic markers.