Elucidating Protein Binding Mechanisms by Variable-c ITC

Isothermal Titration Calorimetry (ITC) is a powerful method for characterizing the energetics of biological interactions.¹ The approach yields the thermodynamic signature of binding (ΔH, ΔS and K_D) through an analysis of the heat released or absorbed as a ligand is incrementally titrated into a solution of its binding partner. ITC is commonly applied to simple binary complexes, but can also provide important insights into more complicated systems in which ligands bind at multiple sites that are allosterically coupled.² Allostery and cooperativity are central to biological regulation, and it is of great interest to elucidate the underlying molecular mechanisms.³ Studying these systems by ITC remains a significant challenge.² For example, a number of different binding models can sometimes provide essentially identical fits to the same data, as is shown to be the case in this study. If the binding mechanism is not known a priori, it can be very difficult to determine which model is correct. Here we report a simple approach for discriminating between different binding mechanisms, based on a global analysis of ITC data obtained over a range of sample concentrations.

In the case of a single binding site, it is convenient to express the protein analyte concentration, [P]_T, in terms of the parameter c = [P]_T/K_D. ITC experiments performed with [P]_T≫K_D and thus high c values (>50) produce isotherms with sharp transitions occurring at [X]_T=[P]_T, where [X]_T is the total concentration of injected ligand. Data obtained with low [P]_T and c values (<10) produce isotherms with shallow slopes that extend to higher [X]_T:[P]_T ratios.⁴ This trend is also followed in more complicated systems with multiple binding sites. In these cases we find that the dependence of ITC isotherms on [P]_T and c provides an effective criterion for selecting an appropriate binding model.

We have applied this approach to the interaction between the enzyme aminoglycoside N-(6′)-acetyltransferase-Ii (AAC(6′)-Ii) and one of its substrates, acetyl Coenzyme A (AcCoA). AAC(6′)-Ii is a homodimeric enzyme which transfers an acetyl group from AcCoA to the 6′-N position of aminoglycosides and confers bacterial resistance to these antibiotics.⁵ ITC traces, shown in Figure 1, exhibit minima at [X]_T:[P]_T molar ratios of about 1:1. The simplest binding model, which consists of a single set of identical independent binding sites, predicts that ITC traces increase or decrease monotonically, and is therefore inconsistent with these data. Instead, the following more complicated models are the most likely candidates; 1) Multiple Independent Sites: This model comprises two different classes of binding site that interact with AcCoA independently. Each enzyme dimer contains n₁ type 1 sites with affinity K_D1 and binding enthalpy ΔH₁, and n₂ type 2 sites with affinity K_D2 and binding enthalpy ΔH₂. This model has been used previously to account for binding of aminoglycosides to AAC(6′)-Ii.⁶ 2) Cooperative Sites: This model is based on a second-order (two-site) binding polynomial⁷ in which we have interpreted the phenomenological parameters in terms of two identical sites where binding at one site influences the thermodynamics of binding at the other site. The first molecule of AcCoA binds to either site of the apo-enzyme with an affinity K_D1 and enthalpy ΔH₁. The second AcCoA molecule binds any singly-bound enzyme with an affinity K_D2 and enthalpy ΔH₂. Although superficially similar, these two models represent very different binding mechanisms. The independent model predicts that the enzyme contains multiple structurally distinct and non-interacting binding surfaces for AcCoA, while the cooperative model predicts that the enzyme contains two identical binding sites that are energetically coupled.

Figure 1.

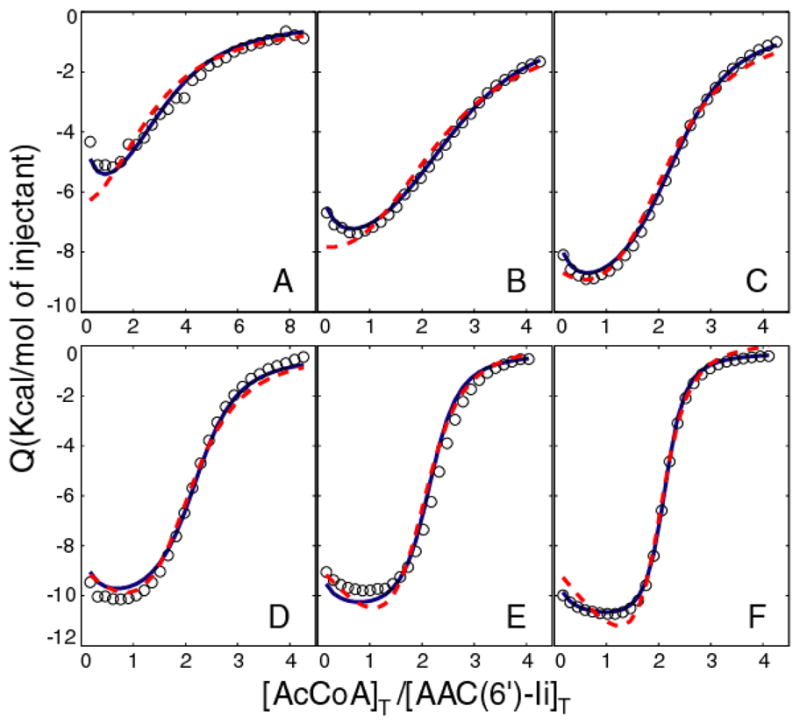
ITC binding isotherms (circles) of AAC(6′)-Ii at A) 6 B) 12 C) 24 D) 48 E) 96 F) 192 μM titrated with AcCoA at 20°C. Dashed red and solid blue lines correspond to global fits using the independent and cooperative models, respectively, as described in the text. Values of c range from 0.4 to 11 and 2 to 64 for the first and second binding events.

ITC experiments were performed on 6 different samples with AAC(6′)-Ii concentrations ranging 6 to 192 μM. We first fit the independent and cooperative models on an individual basis, with different binding parameters extracted for each sample. Both models provided excellent agreement with the experimental data in the individual fits, with slightly lower residual-sum-of-squared deviations (RSS) obtained for the independent sites model, compared to the cooperative model, 8.6×10⁵ versus 9.8×10⁵, respectively (See Supplemental Material). This reflects the fact that the independent sites model contains additional stoichiometric parameters (n₁ and n₂) not present in the cooperative model and consequently has fewer degrees of freedom. The independent sites model suffers from correlation between the fitted parameters, leading to large uncertainties in some of the extracted values. Nevertheless it provides a physically realistic description of binding and gave superior agreement with experimental data in these calculations. In contrast, when the fits were performed globally with a single set of binding parameters for all samples, the cooperative model clearly outperformed the independent sites model, despite having fewer adjustable parameters, with RSS values of 9.7×10⁶ versus 2.4×10⁷ (Figure 1). This is particularly evident in Figure 1A,B, where the cooperative but not the independent model accounts for the initial negative slopes of the ITC data. Thus analyses of ITC data obtained with any single [P]_T value do not effectively discriminate between the two binding models, while a global analysis of the variable-c dataset conclusively shows that the cooperative model is the more appropriate description of AcCoA binding.

This result is consistent with the structure of AAC(6′)-Ii. The two cooperative binding sites likely correspond to the two symmetrical active sites in the homodimeric protein. Enzyme kinetic analyses show that there are cooperative interactions between the catalytic subunits.⁶ The model parameters extracted here indicate that AcCoA binding is positively cooperative, with K_D1=17±1 μM and K_D2=3.0±0.2 μM. This roughly 6-fold increase in affinity is due to differences in binding enthalpy, (ΔH₂-ΔH₁)=−3.1 kcal/mol, and entropy, (ΔS₂-ΔS₁)=−6.8 cal/mol/K, that imply an additional exothermic, disorder-to-order transition of the protein and/or solvent accompanies binding of the second molecule of AcCoA.

Previous studies have employed global fitting of ITC datasets to characterize complicated binding mechanisms. In the case of heterologous cooperativity in multi-component complexes, ITC titrations involving one ligand may be repeated in the presence of various fixed concentrations of the other ligands.^8,9 However, this approach cannot be applied to systems exhibiting homologous cooperativity involving a single type of ligand. Alternatively, titration and reverse-titration datasets, with either the ligand or the protein as the injectant, may be fitted simultaneously.⁹ However, this approach becomes problematic if a protein self-associates at the high concentrations required in the injection syringe.⁹ In contrast, the variable-c method presented here can be applied to homologous cooperative systems and demands that only one, not both binding components be injected at high concentrations from the ITC syringe. To our knowledge, this approach has not been previously used to differentiate among binding models.

A key requirement for this approach is that the ITC isotherms vary as a function of the protein concentration. In order to investigate the general applicability of the method, we have examined theoretical variable-c datasets for an array of cooperative scenarios (Figure 2). Each panel shows a set of overlaid ITC traces calculated with a range of [P]_T values and otherwise identical binding parameters. Panels A,D correspond to positively-cooperative and C,F correspond to negatively-cooperative variable-c datasets. Panels B,E correspond to systems where both ligands bind with equal affinities, but with different enthalpies. In panels A–C, binding of the second ligand releases more heat than binding of the first. In panels D–F, binding of first ligand releases more heat than binding of the second. In all cases, ITC traces depend strongly on [P]_T and thus lend themselves to global fitting. Notably, the largest variations in the shapes of the isotherms occur at low [P]_T with c-values less than 1 for the weaker binding event. This range is significantly below the c-values employed in typical studies, yet appears to be optimal for investigating complex binding mechanisms.

Figure 2.

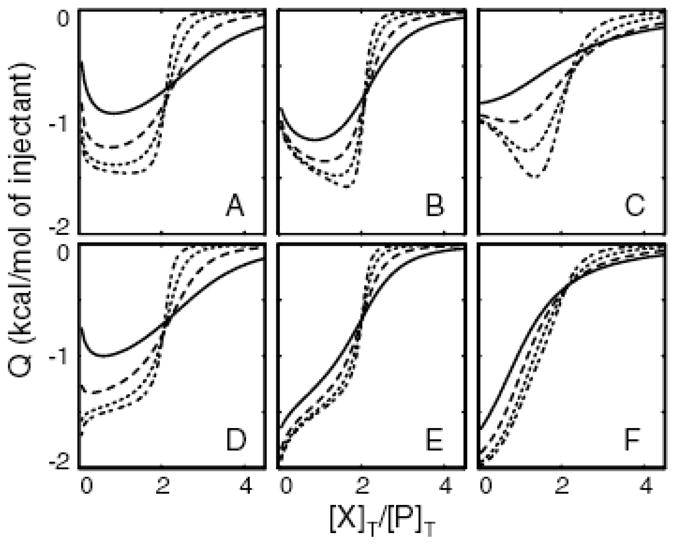
Theoretical ITC isotherms generated according to a 2-site cooperative model, with [P]_T = 0.5, 1.5, 4.5, 13.5 μM for the solid, dashed, dotted, and dash-dotted lines respectively. Values of K_D1(μM), K_D2(μM), ΔH₁(kcal/mol), ΔH₂(kcal/mol) employed are: A) 10,1,−1, −2 B) 10,10, −1, −2 C)1,10, −1, −2 D)10,1, −2, −1 E)10,10, −2, −1 F)1,10, −2, −1.

ITC studies of macromolecular interactions usually involve series of replicate measurements made under nearly identical conditions. We propose that it would be advantageous to repeat measurements at different [P]_T values and globally fit the results. Our findings show that this offers a stringent test of the binding model used to interpret the data.