Energy design for protein-protein interactions

Abstract

Proteins bind to other proteins efficiently and specifically to carry on many cell functions such as signaling, activation, transport, enzymatic reactions, and more. To determine the geometry and strength of binding of a protein pair, an energy function is required. An algorithm to design an optimal energy function, based on empirical data of protein complexes, is proposed and applied. Emphasis is made on negative design in which incorrect geometries are presented to the algorithm that learns to avoid them. For the docking problem the search for plausible geometries can be performed exhaustively. The possible geometries of the complex are generated on a grid with the help of a fast Fourier transform algorithm. A novel formulation of negative design makes it possible to investigate iteratively hundreds of millions of negative examples while monotonically improving the quality of the potential. Experimental structures for 640 protein complexes are used to generate positive and negative examples for learning parameters. The algorithm designed in this work finds the correct binding structure as the lowest energy minimum in 318 cases of the 640 examples. Further benchmarks on independent sets confirm the significant capacity of the scoring function to recognize correct modes of interactions.

INTRODUCTION

Protein-protein interactions and their associated structures are of fundamental importance in cellular biology. These interactions are used for signaling, creating biochemically active complexes, inhibit enzymes, and more.^{1, 2} In many cases they are also constantly dynamic. They form, dissociate and rebind as required by cell functions. Modeling complex formation is therefore particularly challenging, and requires in many cases accurate prediction of weak physical forces and marginal binding.

In the present paper we focus on the prediction of the correct geometry of a protein pair that is known to bind. For the task at hand, the prediction of the absolute binding energy is less critical and we focus instead on ranking. We determine the complex geometry that will have the lowest (free) energy compared to all other docking alternatives. This geometry should be in agreement with experiment. The mesoscopic size of proteins and their complexes, and their rough energy landscape make the prediction of the geometry of the complexes challenging.

We differentiate between two cases: (i) bound and (ii) unbound docking. In bound docking we consider a complex of two protein chains with a known structure. We separate the complex to two chains and attempt to re-assemble them. Since the two chains are taken directly from the complex there exists at least a single docked complex in which the fitted geometry is excellent. The second case of (ii) unbound docking is more complicated. We are given the structures of the two isolated chains and are told that these proteins form a complex. However, the structures at hand are approximate. The atomic positions, taken from the experimental structures of the separated chains (or homologous structures), are not necessarily the same as in the complex. Side chain geometries and tertiary conformations adjust during complex formation and can cause significant deviation from the initial structure. Therefore bound docking (case (i)) for which rigid modeling of the individual chains is exact is considered easier than unbound docking (case (ii)).

In actual applications we do not have the structure of the complex (if we had it, we did not have to predict it) and only unbound docking is relevant. Bound docking is used to assess new algorithms and learn energy parameters by presenting to a program cases that carry unusually strong signals. For an algorithm to be successful it must (as a minimum) solve these easy cases. Despite the significant differences in difficulty, docking of type (ii) is handled in a similar way to case (i). We dock rigid models of the proteins, allowing for larger errors during the process for unbound docking, with the hope that the differences between the bound and the unbound structures are not so large as to diminish the signal completely. Adjustments of complexes of type (ii) to more relaxed and chemically sound structures are done for a small number of candidates identified earlier.

Both bound and unbound docking require two separate computational tasks: (a) search for plausible docked conformations and (b) assessment of alternative complexes and ranking. It is useful to compare these two tasks to another problem in structural biology, the problem of protein structure prediction. Docking (determination of protein complexes) is simpler since the number of the degrees of freedom is much smaller. It can be as small as six for three rotations and three translations if the structures of the individual protein chains are assumed rigid. In our searches, which are exhaustive, we examine a million translations and 54 000 rotations. The total number of complexes we examine is therefore on the order of 10¹⁰. This not-so-small set is a uniform sampling of docking space. Exhaustive sampling is unlikely in the general protein-folding problem. In protein folding, the number of conformations is exponentially large in the protein length L –z^L where z is a number of order 10 and L ∼ 100. As a result exhaustive search is not feasible for folding and conformational sampling is made stochastically and heuristically which reflects on the design of appropriate energy functions. In contrast, the option of a comprehensive search of docked conformations makes it possible to solve optimally potential parameters for the learnt set in docking that minimizes the error in docking calculations. Even if the problem is infeasible and there is no set of parameters that recognizes all the correctly docked conformations, it is possible to find a parameter set that minimizes the extent of mispredictions.

In contrast to protein folding, rigid docking has only six dimensions (the relative translations and rotations of one rigid protein with respect to the second protein). The smaller dimensionality makes exact enumeration of discrete space possible. In Appendix A we analyze the errors of a discrete space representation and illustrate that they are bounded, and provide practical grid spacing. Based on the analysis presented in Appendix A, and for a pair of proteins with radii of about 40 Å we estimate a translational grid spacing of 1.6 Å and 68 760 rotations. This estimate provides ∼10¹⁰ alternative docked conformations.

In the present paper we do not introduce a new sampling algorithm for docking and use instead approaches that were employed successfully in the past. These techniques are based on fast Fourier transforms (FFT) (Refs. ^{3, 11, 27, 28, 29, 30, 35}) of translational space and grid based searches of rotational space. The contribution of the present paper is in the calculation of the energy. This brings us to the second step of determining a scoring function.

Besides exhaustive search of conformations, we also need to score (or compute the energies of) the structures of the complexes or folds. Obviously an exact energy surface for solvated proteins should work for both folding and docking. Physically, however, while protein folding emphasizes hydrophobicity, docking may include more subtle polar interactions. The use of different potentials for each case allows emphasizing physical interactions that better fit the problem we study. Hence, it makes sense to design an energy function specifically tailored to docking, as is done in the present paper.

While the sampling of conformational space is significantly easier in docking compared to folding, the design of energy functions for docking and folding is comparable in complexity. There are a number of reasons for the additional complexity of energy design for protein-protein interactions: First, the energies of complex formation are small and are sometimes as low as a few kT – the thermal energy. The demands from ab initio or physics-based energies are therefore very high. Physics-based energies are usually not accurate enough in separating wrong and correct structures in protein folding calculations. Reproducing smaller energy difference in docking is even more difficult. Note that free energy differences, including changes in solvent reorganization, are required for this estimate. Hence, not only the accuracy is insufficient but also the significant computational cost forbids large scale examination of docked alternatives. Due to computational costs most estimates of solvation effects are implicit and approximate (such as the GBSA model of solvation⁴).

Second, not only the overall binding energy but also the number of individual pair interactions in protein complexes is small compared to the number of interactions of folded proteins. The stability of complexes, supported by only a few contacts, is marginal and leaves little room for errors (a contact is set between two residues or atoms if the distance between the two objects is smaller than a critical value).

Third, the statistics of empirical complexes is rather poor. This observation has important consequences for machine learning approaches to potential design. Determining parameters of energies learned directly from the structures of the complexes, the so-called knowledge-based potentials, depends on the availability of ample empirical data. In protein folding a large number of correct folds is available (about ∼72 000 in the Protein Data Bank (PDB) (Ref. ⁵)). Each of these folds contributes (in principle) residue-residue contacts to the statistics. In our fold database⁶ we have about ∼18 K independent structures. The statistics for protein complexes is significantly smaller. There are less than 1000 structures of independent protein-protein complexes in the PDB and each of these complexes has fewer contacts at the interface compared to a typical number of contacts in folded proteins. Smaller statistics of correct complexes make estimate of parameters for knowledge-based potential more difficult.

One of the more popular models of deriving knowledge-based potentials for protein folding is the log-odd ratio or a statistical potential.^{7, 8} In this design the structures of the proteins are examined and probability densities for contacts are computed. The energy of interaction is given by a sum of pair interactions U = ∑_{i > j}W_{α(i), β(j)}(r_ij). The indices i, j denote positions of the amino acids (or other particles) along the chain, and α, β are the indices of particle types. If the geometric center of an amino acid side chain type α is r_g, the potential of mean force between a pair of amino acids is estimated as

$$W_{\alpha \beta }\left(r_{\alpha \beta }\right)=-\log \left[\frac{P_{\alpha \beta }\left(r_{\alpha \beta }\right)}{P_{\alpha \beta ,ref}\left(r_{\alpha \beta }\right)}\right]r_{\alpha \beta }=\left|r_{\alpha g}-r_{\beta g}\right|,$$

where P(r_αβ) is the probability of observing a distance, r_αβ, between the two amino acid types α and β, anywhere in the learned set. P_{αβ, ref}(r_αβ) is a reference distribution of a model expected by chance. For example, it can be a product of probabilities: The probability for a distance between any two amino acids times the probabilities of observing amino acid α and β, i.e., P_{αβ, ref}(r_αβ) ≈ P_αP_βP(r).

This simple model and method, learning from known structures of proteins, was proven very effective in studying protein structures and is at the core of many successful protein-folding programs.^{9, 10} However, direct applications of statistical potentials “as are” to docking is limited due to the small statistics available as we also illustrate in the present paper. Some programs for docking are using a combination of physical interactions (e.g., electrostatic, exposed surface area) and statistical potentials.¹¹ Here we re-emphasize the learning from negative examples. Negative examples are not used in learning statistical potentials and are particularly promising in docking, in which exhaustive enumeration of all false complexes is made.

General consideration for design of docking potential with mathematical programming

For the purpose of separating correct from incorrect structures we consider the approach of linear and quadratic programming. In linear programming one learns from both positive and negative examples by requiring that the following inequalities are satisfied:

$$U\left(X_d;P\right)-U\left(X_n;P\right)>0\forall n,d,$$ (1)

where U is the potential energy, X_n and X_d are the coordinate vector of the correct (native) and decoy structures, respectively, and P is a vector of potential parameters. The energy depends linearly on the parameters P, which are the unknowns we wish to determine. Equation 1 is therefore re-written as

$$\sum _{\alpha }{p}_{\alpha }\left[f_{\alpha }\left(X_d\right)-f_{\alpha }\left(X_n\right)\right]>0.$$ (2)

The α summation is over the parameters, and the functions f_α(X) depend only on geometrical variables, for example, the distance between two amino acids. The linear dependence is not a theoretical limitation since any potential can be expanded in a basis set with linear coefficients to be determined. However, in practice the choice of the expansion can impact the flexibility and reliability of the results, and is discussed further in the paper.

Docking one pair of proteins generates about 10¹⁰ candidates. Therefore consideration of the complexes available in the PDB (∼600) requires the solution of ∼10¹³ inequalities. This fantastically large number suggests that the available statistics for learning a potential in this case is significant. There are, however, a number of technical problems that we need to address. We provide below a verbal description of the challenges. This is to help follow the more detailed mathematical formulation of the following sections.

The first challenge in solving the linear programming problem we just formulated is the problem of infeasibility. The number of potential parameters that we determined for the set is in the hundreds and is obviously much smaller than the number of inequalities. While it is not impossible that a set of parameters exists that satisfies exactly the 10¹³ inequalities, it is not likely. The set of functions, f_α(X), that we use for the potential is not exact and the optimization of parameters is limited by the flexibility of the functional form. Vendruscolo and Domany¹² have shown that there are no parameters of a contact potential that ranks correctly decoy and native structures of a selected protein. Tobi et al.^{13, 14} pushed this argument further to demonstrate that a general parameterization of a pair potential as a function of distance is also insufficient. Their sets were much smaller than the set of 10¹³ inequalities we consider here, while the Tobi's potential¹⁴ was more flexible than the current choice.

We therefore expect (as is indeed the case) that a straightforward application of a linear programming approach to the problem at hand will detect infeasibilities, i.e., we find that there is no set of parameters that satisfies all the inequalities at hand. How should we deal with such an imperfect potential? One solution is to come up with a more flexible functional form for which a desired set of parameters could be found. This is, however, not always possible. We must keep in mind that the structures we usually employ are approximate. It may be the case that an energy function that scores the nearest to native approximations as the best models, simply does not exist. Hence, the current learning of a potential is of learning with noise. If we try too hard to learn an energy function by adding a large number of parameters we may end up learning the noise and not the molecular data. How can we determine if the potential is the best for the current (approximate) functional form?

In machine learning it is a common practice to test models learned from data with noise on independent test sets to check the transferability and generality of the designed score. Hence while learning data with noise we are willing to accept some inaccuracies to retain simple-to-use functional form that is generalizable to other sets. The adjusted goal of optimizing with noise is reflected in a new set of inequalities and an optimization of a target function together with the solution of the inequalities,

$$\begin{array}{ccc}& & U\left(X_d;P\right)-U\left(X_n;P\right)>1-\frac{{\eta }_{nd}}{{\Delta }_{nd}}{\eta }_{n,d},{\Delta }_{n,d}\ge 0\forall n,d\hfill \\ & & \left(P,\eta \right)=\mathrm{argmin}\left({\left|P\right|}^2+C\sum {\eta }_{n,d}\right)\hfill \end{array}$$ (3)

The slack variables η_{n, d} measure the degree of inequality violations and their sum is minimized in formulation 3. Note that formulation 3 is not exactly what we had in mind. The prime goal is to optimize the ranking, making the correct structure lower in energy than any other decoy structure. The above formulation minimizes the differences in energy, or the energy gap, not the ranking. It is possible that a solution in which many wrong structures are only slightly lower in energy than a correct structure will be preferred to a solution in which only one structure scores better than the native by a wide margin. It turns out that optimizing the ranking directly is harder. We therefore stay with optimization of the sum of the slack variables. The scaling of the slack variables with a distance measure discussed below helps remove high-scoring decoys with significant distance from the correct assembly (penalty is higher for larger mistakes).

The distance measure, Δ_n.d, is introduced to bias the energy landscape towards a funnel.¹⁵ We penalize violations less if the structures are reasonably similar. The penalty increases for structures far from the native that have energy lower than the correct structure. In docking, a common distance measure between the model and the correct structure of the complex is the interface root mean square difference (“i-RMSD”) after optimal overlaps of the residues at the interface). We will use the i-RMSD for Δ_n.d in the present paper; however, this choice is clearly not unique. Finally the “1” in the above formulation set a scale for the potential parameters that are scale-free in Eq. 1. The coefficient C determines the penalty for violation.

Equation 3 addresses the infeasibility problem. We note that Eq. 3 is known in the field of quadratic programming and is used widely in machine learning. It is most popular nowadays in the form of support vector machine (SVM),¹⁶ which is used for classification and more recently in ranking. Support vector machine was introduced as a method for binary classification—to learn a linear separator to differentiate between two classes. The framework argues that maximizing the margin between the plane and its closest points leads to good generalization. In the present paper we built on recent results in structural SVM (Refs. ¹⁷ and ¹⁸) but our learning algorithm has useful additional twists appropriate for the docking problem.

The second challenge of our plan to solve 10¹³ inequalities is computational. Solving all the inequalities directly is not possible today even with the most advanced computing technologies. We have spent considerable time to extend interior point code¹⁹ to our purposes. Indeed parallelization and exploitation of the special structure of the problem (relatively small number of parameters and huge number of inequalities)²⁰ increase the number of constraints that we can address in one run by more than two orders of magnitude. In the present paper we exploit clustering to make the calculations more efficient and accurate. The asymmetry of the number of inequalities, N, versus the number of parameters, L, is particularly worth exploiting within the primal-dual representation of linear and quadratic programming problems (see Appendix C and Ref. 20). The linear system solved during the process of determining an optimizing step can be made as small as LxL (rather than NxN), which is clearly advantageous for our problem. The formation of the matrix involved though is expensive but can be done in a data parallel fashion even when constraints are grouped based on clusters.

However, even with these enhancements we are not able to solve more than ∼10⁸ inequalities, which is still a smaller number than 10¹³. It means that a solution of the complete convex programming problem must be made with a selected part of the inequalities. In the past we sampled heuristically subsets of inequalities by considering the first few millions of constraints.^{13, 14, 22, 23} This was also the approach taken in our first design of a docking potential reported in Ref. 22. While it is an appealing choice, it is not obvious that the sampled constraints are the needed set. For example, it is possible that we over sample constraints of one parameter while leaving other parameters ill determined. Rather than picking inequalities heuristically and risking missing important constraints on parameter values it is desirable to have a rigorous approach that allows for a systematic selection of a subset of inequalities. The selection is expected to provide error estimates and provides systematic means of improving the selection of a subset of inequalities.

Structural SVM (Ref. ¹⁷) was proposed as a method for learning sequence alignments^{18, 24} in which inequalities are iteratively and systematically selected and added to the set of inequalities to be solved (Eq. 3). The authors used quadratic programming as the optimization method and showed that the procedure converged in linear number of steps in the number of examples. However, structural SVM is based on using one slack variable for all decoys associated with the same native data point (correct alignment). As argued in section “Learning with clustering,” this choice is not ideal for the docking problem since some violated pairs are over penalized. In the present paper we suggest another way of selecting slack variables and inequalities. The new selection addresses this issue while preserving the attractive and formal features of structural SVM. Even in this case, we obtain an iterative procedure of determining the inequalities to solve. The iterations are guaranteed to improve the quality of the solution of Eq. 3.

The new approach for the selection of inequalities, exploits the low dimensionality of the problem (only six dimensions). The large number of decoy structures that we generate includes complexes that are quite similar to each other. Similar decoys yield inequalities that are not significantly different and contain little new information. Furthermore, particular violations are oversampled. Since we do not use all inequalities, oversampling of some constraints may cause other important constraints to be missed. Hence clustering allows more uniform sampling. We assign a single slack variable to a cluster of decoys.

The paper is organized as follows. We consider first the functional form of the energy that we choose to optimize. Second, we describe the grid that we employ to represent the space of docking configurations. Third, we discuss the algorithm to determine the potential parameters. Finally, we consider examples and benchmarks.

FUNCTIONAL FORM FOR DOCKING ENERGY

The energy function depends on the translation and rotation (or transformation) of one protein chain (L ligand) with respect to the other chain (R receptor). We denote a transformation by τ (τ = (t, u) where t and u are the translation and rotation of the ligand, respectively), and τ(r_j) are the transformed coordinates of particle j,

$$\begin{array}{ccc}\hfill U\left(\tau \right)& =& U_{attr}\left(\tau \right)+p_{repul}·U_{repul}\left(\tau \right)\hfill \\ & & +\sum _{i,j(i\le j)}{p}_{\alpha \left(i,j\right)}{n}_{ij}\left(r_{ij}\right)r_{ij}=\left|r_i-\tau \left(r_j\right)\right|,\hfill \end{array}$$ (4)

where U(τ) is the total energy of the complex, as created with the transformation τ. U_attr(τ) and U_repul(τ) are attractive and repulsive components of the energy. The last term is a summation over interactions of pairs of amino acids. n_ij(r_ij) is a function of the distance between particles placed at different protein chains. Following Tobi and Bahar,²⁵ we use 20 side chain centers of mass (cntd),the backbone carbonyl oxygen, and amide groups (bkbn) as different particle types. The parameter p_repul determines the strength of the overall repulsion. The coefficient p_{α(i, j)} determines the strength of the interaction type α of particles (i, j). We provide below the explicit functional form of these sub-energies.

Residue and backbone contact potential

Most knowledge-based potentials in the protein folding field employ contact potentials^{11, 26} (residue or otherwise) which are $U_{contact}\left(\tau \right)={\sum }_{i,j=1}^{N_R,N_L}{p}_{\alpha \left(i,j\right)}{n}_{ij}\left(r_{ij}\right)$ where p_{α(i, j)} is the score for contact type α and $n_{ij}\left(r_{ij}\right)=\left\{\begin{array}{cc}\hfill 1& \hfill r_{ij}\le R_c\\ \hfill 0& \hfill r_{ij}>R_c\end{array}\right\}$ (a step function) defines a contact. The total number of particles of the first protein (receptor) is N_R and the second (ligand) is N_L. The total energy is therefore a sum of weighted step functions. For a continuous description of the contact as a function of distance, we use a linear interpolation function h(r) in place of n(r) where

$$\begin{array}{c}h\left(r\right)=\left\{\begin{array}{cc}\hfill 1& \hfill r\le R_{\min }\\ \hfill \frac{R_{\max }-r}{R_{\max }-R_{\min }}& \hfill R_{\min }<r\le R_{\max }\\ \hfill 0& \hfill r>R_{\max }\end{array}\right\}.\hfill \end{array}$$ (5)

This function interpolates continuously from zero to one, using two distances R_min and R_max with a range determined as

$$R_{\min }=\left\{\begin{array}{c}6\AA \mathit{cntd},\mathit{cntd}\\ 5\AA \mathit{cntd},\mathit{bkbn}\\ 4\AA \mathit{bkbn},\mathit{bkbn}\end{array}\right.R_{\max }=\left\{\begin{array}{c}8\AA \mathit{cntd},\mathit{cntd}\\ 7\AA \mathit{cntd},\mathit{bkbn}\\ 5\AA \mathit{bkbn},\mathit{bkbn}\end{array}\right..$$ (6)

For efficient calculations of the energy it is convenient to define a receptor grid. If a grid is available the calculation of the energy is proportional to the number of particles.

Receptor grid

The function representing the potential experienced by a particle type q due to the particles of the receptor is defined as

$$R_{q\left(j\right)}(l,m,n)=\sum _{i=1}^{N_R}{p}_{q\left(i\right)q\left(j\right)}h\left(r_{i,(l,m,n)}\right),$$ (7)

where r_{i, (l, m, n)} is the distance from particle i and the corner of the cell (l, m, n) with smallest coordinates (least l, m, n). The receptor grid R_j provides a discretization of potential experienced by a particle j of type q(j). For the calculation of the grid it is convenient to consider a single particle type (q(j)) instead of a contact type α(i, j) as in Eq. 4. The receptor is placed in a rectangular box that is partitioned into cubic cells of side length g. Consider a point r contained in cell (l, m, n); the value of potential experienced by particle of type j can be approximated by the value at the center of the cell (l, m, n). More accurate, however, would be an interpolation of the potential within the cell, and we use a trilinear interpolation. Consider a point r in cell (l, m, n). The integers (l, m, n) are defined as the largest integers that are less or equal the Cartesian component of r, that is (l = ⌊r_x/g⌋, m = ⌊r_y/g⌋ and n = ⌊r_z/g⌋). The displacement of the point with respect to the lattice (grid) point (l, m, n) is given by

$$x=\frac{r_x}{g}-l,y=\frac{r_y}{g}-m,z=\frac{r_z}{g}-n.$$

Let χ_αβγ(r) = (xδ_{α, 0} + (1 − x)δ_{α, 1})(yδ_{β, 0} + (1 − y)δ_{β, 1})(zδ_{γ, 0} + (1 − z)δ_{γ, 1}) (δ is the Kronecker delta). The potential for a particle of type q at r is approximated as a linear combination of the potential on the eight corners of the grid cube containing r. The function χ_αβγ is the weight for the contribution of the potential R at the corner αβγ of the cube,

$${\Phi }_q\left(r\right)=\sum _{\alpha ,\beta ,\gamma \in \{0,1\}}{\chi }_{\alpha \beta \gamma }\left(r\right)R_q(l+\alpha ,m+\beta ,n+\gamma ),$$ (8)

which is essentially a linear interpolation between corners and edges of the box. The ligand grid L_q provides occupancies of particles of type q. It is defined as L_q(l, m, n) = ∑_{α, β, γ ∈ {0, 1}}∑_{j ∈ (l − α, m − β, n − γ)}χ_αβγ(r^(j)) where j is a particle of type q with position r^(j) in cell (l − α, m − β, n − γ).

Vdw attraction and repulsion

Shape complementarity is an important determinant of protein-protein docking. FFT-based docking algorithms^{11, 27, 28, 29, 30} define shells of various sizes around the surface of each protein and discretize them on a grid. For a translation and rotation the overlap between the translated and rotated shells of the ligand and the shells of the receptor are computed and the shape complementarity is quantified as a linear combination of these overlaps.

The total interface vdw energy of a complex when the proteins are docked according to transformation τ is $E_{vdw}^{exact}\left(\tau \right)={\sum }_{i=1,j=1}^{N_R,N_L}{V}_{ij}\left(r_{ij}\right)$ where r_ij = |r_i − τ(r_j)| and $V_{ij}\left(r_{ij}\right)=4D_{ij}({\sigma }_{ij}^{12}∕r_{ij}^{12}-{\sigma }_{ij}^6∕r_{ij}^6)$. The indices i, j are running over the particles of the receptor and the ligand, respectively, and N_R, N_L are the number of particles of the two proteins in the complex. We use the OPLS force field—Optimized Potentials for Liquid Simulations is a standard force field for modeling proteins derived by optimizing fitness for gas phase and liquid phase properties of water, capped amino-acids and small peptides.³¹ The energy and the contact distance factorize to single particle properties as: $D_{ij}=\sqrt{D_{ii}{D}_{jj}}\equiv \sqrt{D_i{D}_j}$ and ${\sigma }_{ij}=\sqrt{{\sigma }_{ii}{\sigma }_{jj}}\equiv \sqrt{{\sigma }_i{\sigma }_j}$. We use an approximation

$$\begin{array}{c}{E}_{vdw}\left(\tau \right)=-4\sum _{j=1}^{N_L}\sqrt{D_j}\frac{{\sigma }_j^3}{3.2^3}\left(\sum _{i=1}^{N_R}\sqrt{D_i}\phi \left(\frac{r_{ij}}{\sqrt{3.2{\sigma }_i}}\right)\right)\mathrm{where}\hfill \\ \phi \left(x\right)=\left\{\begin{array}{cc}\hfill p_{repul}\times (0.8-x),& \hfill x\le 0.8\\ \hfill 0.5\times (x-0.8),& \hfill 0.8<x\le 1.1\\ \hfill 0.15,& \hfill 1.1<x\le 1.32\\ \hfill 0.15\times (1.8-x)∕0.48,& \hfill 1.32<x\le 1.8\\ \hfill 0,& \hfill x>1.8\end{array}\right.\hfill \end{array}$$ (9)

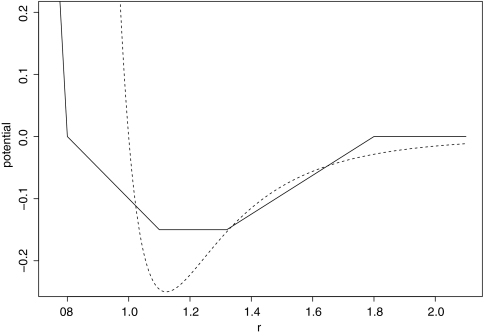
We adopt this approximation because it is convenient to handle using FFTs and it resembles 6–12 intermolecular potentials (comparison provided in Fig. 1).

Figure 1.

The relation of vdw approximation function to the Lennard-Jones 6/12 potential (dotted line), w_vdw̱repul was set to −9.

The receptor and ligand grids are defined as

$$\begin{array}{c}\hfill R_{vdw}(l,m,n)=\sum _{p_i\in (l,m,n)}\sqrt{D_i}f\left(\frac{r_{i,(l,m,n)}}{\sqrt{3.2{\sigma }_i}}\right)\\ \hfill \mathrm{where}f\left(x\right)=\left\{\begin{array}{cc}\hfill \sqrt{-1}{p}_{repul}\times (0.8-x)& \hfill x\le 0.8\\ \hfill 0.5\times (x-0.8)& \hfill 0.8<x\le 1.1\\ \hfill 0.15& \hfill 1.1<x\le 1.32\\ \hfill 0.15\times (1.8-x)∕0.48& \hfill 1.32<x\le 1.8\\ \hfill 0& \hfill x>1.8\end{array}\right.,\end{array}$$ (10)

$$L_{vdw}(l,m,n)=4\sum _{\alpha ,\beta ,\gamma \in \{0,1\}}\sum _{k\in (l-\alpha ,m-\beta ,n-\gamma )}\sqrt{D_j}\frac{{\sigma }_j^3}{3.2^3}{\chi }_{\alpha \beta \gamma }\left(r^{\left(k\right)}\right).$$

Note that the grid R_vdw(l, m, n) has complex values. The imaginary component of the calculation stores the repulsion due to overlap. Note the change in sign, in our formulation higher scores are better.

With the energy terms in place we discuss the algorithm to generate alternate docked conformations. The inputs for the algorithm are the coordinates of the receptor and the ligand. In the sketched algorithm below we allow for (only) rigid body transformations to be performed, but even with this restriction the number of conformations is ∼10¹⁰. Rather than saving all transformations, we calculate the energies of the complexes on-the-fly and store only top Λ candidates.

In the present paper we do not consider the process of final selection and refinement. Refinement is the adjustment of the unbound conformations to remove sterically unacceptable shapes of complexes and bring the final structures closer to the true bound form. We comment that the algorithm as described is not new and was used in docking experiments elsewhere.^{11, 26, 27, 28, 29, 30, 35} We provide it for completeness since the search is strongly coupled to the learning process and to our concrete choice of energy functions. For the algorithm to function efficiently, every energy term must be presented as a product or a convolution.

The use of grid representation for molecular positions and interaction energies is common to the field. In some cases energies are defined directly on the grid and are discontinuous. It is not obvious if discontinuous energy functions are mapped correctly from the grid to the continuous space, as the grid size is made smaller. Such mapping is important since by the end of the day we wish to determine docked conformations in continuous space and score these conformations with energies appropriate for that space. In Appendix A we analyze the errors of our implementation of the different energy terms and demonstrate that in our case the functions go to the correct limit.

ALGORITHM TO DETERMINE OPTIMAL POTENTIAL PARAMETERS

We are not the first group to propose a docking energy function. Below we review some of the leading potentials and algorithms and discuss them in the context of the present study. An important docking program is ZDOCK.¹¹ ZDOCK uses an atomic contact energy (ACE)—a statistical potential^35a derived with a random crystal structure as the reference state (atom pairs were randomly exchanged in the crystal structure to obtain the reference state) that explained protein solvation energies very well. While the ability of transferring potential parameters between fields is impressive and important, one may expect that a potential designed specifically for the protein-docking problem will be better at that specific task.

Another statistical potential (atomic) derived from decoys obtained from docking algorithm as the reference state is employed in PIPER.^{36, 37} Perhaps the most challenging problem in the design of statistical potentials is the definition of the reference state. The reference state represents hits by chance or predictions that are false. PIPER uses decoys as reference state but assumes that the distribution of pairwise contacts are independent of each other. Distribution of contacts is highly dependent during hydrophobic collapse. The convex programming approach, which we advocate here, implicitly generates a reference state by considering explicitly pairs of false and positive predictions. No independence assumptions are made in the generation of the reference state. The disadvantage of the convex programming approach is that typically the statistics of false positive is expensive to generate and in many cases it is too poor to get an accurate grasp on the overall shape of the false positive distribution. On the other hand, sampling directly from the false positive distribution has the advantage that no ad hoc assumptions are made while proposing a reference state. The difficult task of choosing a functional form for the reference distribution is avoided.

Self-consistent iterative procedures that circumvent the choice of a reference state in deriving statistical contact potentials were proposed³⁸ and applied to the design of scoring functions for protein-protein docking.³⁹ The method is restricted to the class of contact potentials and is based on separating the near-native from the average incorrect structure. Again, the statistics of the average incorrect structure is not too difficult to obtain. However, the direct comparison of pairs of false and true predictions provides richer information.

Algorithm for docking

1: Input: receptor, ligand, tolerated error in energy (ε), and minimum number of transformations to retain (Λ). The tolerated error in energy is how far the best solution found by the discrete space search deviate from the optimal solution in continuous space. In the training and testing we used Λ = 219 = 524 388.

2: Find radius of each protein and determine the density of rotational sampling and grid spacing to be used such that the error can be bounded by ε (see Appendix A).

3: Compute grids Rvdw and ∀j ∈ {1, …, 22}Rj on the receptor protein and their inverse Fourier transforms: IFT(Rvdw) and IFT(Rj)∀j ∈ {1, …, 22}

4: Initiate the set of conformations selected (Γ) to empty set.

5: Let uα be a rotation matrix in discrete grid on the space of all rotations SU3. Begin loop on uα

5.1 compute grids Lvdw and ∀j ∈ {1, …, 22}Lj on the ligand-protein rotated according to uα and their Fourier transforms

5.2 compute scores for all translations (Γα) involving current rotation α using the convolution theorem (all functions below carry the index α to denote the current rotation), $E_{\alpha }^{vdw}=\frac{1}{N_x{N}_y{N}_z}IFT\left\{FFT\left\{L_{vdw}\right\}IFT\left\{R_{vdw}\right\}\right\}$, (Nx, Ny, Nz are the dimensions of the grid used) $E_{\alpha }^{particle̱pair}=\frac{1}{N_x{N}_y{N}_z}IFT\left\{{\sum }_{j=1}^{22}FFT\left\{L_j\right\}IFT\left\{R_j\right\}\right\}$ and $E_{\alpha }=\mathrm{Re}\left\{E_{\alpha }^{vdw}\right\}+\mathrm{Im}\left\{E_{\alpha }^{vdw}\right\}+\mathrm{Re}\left\{E_{\alpha }^{particle̱pair}\right\}$.

5.3 Consider the set of conformations and their energies just discovered (Γα, Eα) and the set of the other conformations (other rotations) that were already explored (Γ, E). In this step we merge the two sets. We sort both sets in decreasing order of score and retain transformations that are within top Λ (their energies are the lowest) or have a score within ε from the best solution. (Γ, E) is updated.

6: End loop

7: Output: (Γ, E)

We designed parameters for scoring docked conformations in our earlier work.²² In that work an extensive set of 2-chain complexes (462 bound-bound, 123 bound-unbound, and 55 unbound-unbound cases) was derived from the PDB.⁵ In that work we did not perform exhaustive sampling of all docked conformations, but instead use Patchdock to sample nativelike and incorrect transformations for each case. We then derive parameters p_α by minimizing the slack variables ∑_{ij, ik}η_{ij, ik} similar to Eqs. 2, 3 such that

$$\begin{array}{c}\hfill \sum _{\alpha }{p}_{\alpha }\left[f_{\alpha ,ij}-f_{\alpha ,jk}\right]>1-{\eta }_{ij,ik}\mathrm{and}{\eta }_{ij,ik}>0\forall ij,ik,\end{array}$$ (11)

where f_α, ij is a vector of interface properties of the jth correctly docked structure for complex i and f_{α, ik} is the interface property vector of the kth mis-docked structure for complex i. The results of the parameter optimization, using structures sampled by Patchdock, may have been program dependent and not appropriate for other sampling techniques. No exhaustive enumeration of all possible translations and rotations was performed. The potential derived there compared favorably against other docking energies²² using Patchdock and Zdock generated structural sets. It is only when we tried to use that potential for exhaustive sampling that we found out that our original potential also generates significant number of false positives.

In this work we derive parameters that ensure selection of nativelike structures from all possible transformations. If one follows the linear programming formulation, one is faced with enormous number of constraints – the number of possible transformations for a pair of proteins when transformations are sampled on a cubic grid discretized into 100 intervals in each dimension and when around 54 000 rotations are used (the number of rotations required to sample SU₃ at 6°) is 54 × 10⁹; the total number of constraints would be 36 trillion, the resultant linear program cannot be solved in practice. The number of inequalities is simply too large to load directly to linear programming solvers.²⁰

A solution is possible by sampling a subset of the inequalities. In principle many inequalities do not provide new information (e.g., of the inequalities a > 5 and a > 3 it is sufficient to keep only the first inequality a > 5). While the problem at hand is usually more complex it is still expected that a smaller number of inequalities of the total possible will be sufficient to obtain a satisfactory solution. In the past we have sampled heuristically Λ inequalities (Λ is much smaller than the total number of inequalities possible) and still we were able to find high quality solutions.^{13, 14, 22} The inequalities chosen were the ones least satisfied.

This choice is intuitively appealing, however, it is not precise. A potential problem might be that many of the selected inequalities do not provide additional information. Sampling more of (almost) the same inequalities does not add significant new information. For a fixed total number of inequalities that we can consider this procedure may miss important constraints and some parameters may be left ill determined. It is therefore desired to have a more systematic way of choosing inequalities, perhaps using iterations if they are guaranteed to improve the solution.

Joachims et al.¹⁸ and Tsochantaridis et al.¹⁷ provide a quadratic programming formulation for these classes of learning problems and demonstrate an iterative scheme that solve these quadratic programs efficiently. The algorithm is based on iteratively adding selected violated constraints that ensure that the optimal parameters are found in number of iterations that is linear in the number of complexes. The optimization problem to be solved in their framework (quadratic programming: structural SVM) for learning docking potentials is

$$\begin{array}{ccc}& & QP(\mathit{STR}̱\mathit{SVM})\hfill \\ & & \left(P^{*},{\eta }^{*}\right)=\arg \min {\left[\frac{1}{2}{P}^{t}P+\frac{C}{n}\sum _i{\eta }_i\right]}_{P,\eta }\mathrm{such}\mathrm{that}\hfill \\ & & {\displaystyle \sum _{\alpha }{p}_{\alpha }\left[f_{\alpha }\left(\tau \right)-f_{\alpha }\left({\tau }_i\right)\right]\ge 1-\frac{{\eta }_i}{\Delta \left({\tau }_i,\tau \right)}}\hfill \\ & & {\eta }_i\ge 0\forall i,\tau ,{\tau }_i{\tau }_i\ne \tau \hfill \end{array}$$ (12)

n is the number of complexes in the training set, τ is a rigid body transformation,τ_i is the transformation for correctly docked structure of complex i, and f_α(τ) is the α element of a vector of interface properties of transformation τ. The elements of the parameter vector P are the p_α. The function Δ(τ_i, τ) is the i-RMSD between structures generated by the transformations τ and τ_i. The i-RMSD (or other dissimilarity measures of the interfaces that we could have chosen) helps shape the potential like a funnel. As the complex is getting closer to the correctly docked conformation the penalty for mis-ranking becomes smaller. It imposes larger penalty if the interfaces in the complexes (decoy and native) are less similar to each other, creating an energy landscape with a funnel structure. (^x**)= argmin [f(x)] is a notation to indicate x* minimizes the value of the function f(x).

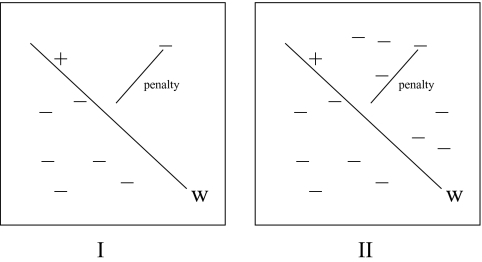
The formulation with a single slack variable per complex belongs to the algorithm category $SV{M}_1^{\Delta s}$ (Sec. 2.2.3 of Tsochantaridis et al.¹⁷). The algorithm proposed there can be directly used to solve the problem and it provably converges. The efficiency of algorithms in the structural SVM framework¹⁷ comes from the intelligent formulation involving only a single slack variable per instance of observed sequence-structure pair (there is only one slack variable η_i per complex). This formulation has a serious limitation in our case –η_i reflects the maximum difference between the score of the optimal mapping (τ*) according to current set of parameters (p_α) and the observed output (τ_i); that is, ${\sum }_{\alpha }{p}_{\alpha }{f}_{\alpha }\left({\tau }^{*}\right)\ge {\sum }_{\alpha }{p}_{\alpha }{f}_{\alpha }\left({\tau }_i\right)+1-\frac{{\eta }_i}{{\Delta }_{\min }}$. This means that the score of the native transformation is within $\frac{{\eta }_i}{{\Delta }_{\min }}$ from the optimal solution. This measure is not an indicator of how many mispredictions would result from a docking algorithm based on the parameter set P (see illustration in Fig. 2). The reason is that all violations for a particular complex are going to be penalized according to the worst-case scenario while no information is provided on the extent of violations of the rest of the inequalities. There can be many violations that are close to the native and therefore over-penalized. For example, we find in our learning of parameters that many inequalities do not satisfy the gap criterion (their difference is smaller than one) but have scores worse that the score of the correct complex. Hence, the recognition is actually better than one may expect from the number of violations.

Figure 2.

The problem of learning to dock is approached as learning a linear separator w(represented by the line here) that scores the native transformation (+) above all possible transformations (−). In formulation QP_strucṯsvm same penalty is paid in both cases while case 2 has many false positives.

It would be nice to minimize the false positive rate (the number of misclassified complexes) rather than empirical risk which is the sum of the slack variables, or extent of violation, but minimizing false positive rate is NP-hard (the computational cost grows exponentially with the number of complexes) even when all constraints are explicitly listed (this is a simple corollary of the construction employed by Hoffgen et al.⁴⁰ to show that finding a separating plane with minimum misprediction rate is NP-hard).

Building on results in linear programming approach²⁰ for learning protein threading potentials, we propose a quadratic programming approach for sum-slack minimization. In place of counting number of false positives, we penalize a false positive by the extent to which it scores above the native,

$$\begin{array}{ccc}& & QP(\mathit{extent}̱\mathit{misprediction})\hfill \\ & & \left(P^{*},{\eta }^{*}\right)=\underset{P,\eta }{\arg \min }\left[{\displaystyle \frac{1}{2}{P}^{t}P+\frac{C}{n}\sum _{i,j}{\eta }_{ij}}\right]\mathrm{such}\mathrm{that}\hfill \\ & & {\displaystyle \sum _{\alpha }{p}_{\alpha }\left[f_{\alpha }\left({\tau }_{ij}\right)-f_{\alpha }\left({\tau }_i\right)\right]\ge 1-\frac{{\eta }_{ij}}{\Delta \left({\tau }_i,{\tau }_{ij}\right)}{\eta }_{ij}\ge 0}\hfill \\ & & \forall i,j,{\tau }_{ij},{\tau }_i{\tau }_i\ne {\tau }_{ij}\hfill \end{array}$$ (13)

The above representation is more flexible than the method of structural SVM, better measures the extent of violations for a particular complex, and is therefore likely to produce better potential parameters. The main assumption is that the noise level is low, since if it is high the sum of the slack variables will be higher (there are now a lot more slack variables) and the noise will bias the minimization.

Furthermore, if some generated decoy structures are highly similar (and so are the inequalities) we would end up over penalizing for the same mistake (by adding similar inequalities we repeatedly add similar slack variables to the function to be optimized). To address both of these concerns we introduced the idea of clustering to assist in selection and weighting of inequalities. Clustering of solutions is implicit in structure prediction tasks, so similar false positives should not be penalized multiple times. A natural way of clustering is to choose ε-balls in a metric Θ on the output space (the space of all translations and rotations – SE3). Complexes that fall within a single ε-ball are collected to one cluster. One would like to have a penalty per mispredicted cluster. The goal is to derive parameters P such that an exhaustive search algorithm based on P that uses clustering of predicted outputs, results in the minimum extent of misprediction. An optimization problem that captures these properties is

$$\begin{array}{ccc}& & QP(\mathit{extent}̱\mathit{misprediction}̱\mathit{with}̱\mathit{clustering})\hfill \\ & & \left(P^{*},{\eta }^{*},{\Pi }^{*}\right)=\underset{\Pi ,P,\eta \left(\Pi \right)}{\arg \min }\hfill \\ & & \times \left[{\displaystyle \frac{1}{2}{P}^{t}P+\frac{C}{n}\sum _{i,j}{\eta }_{{\Pi }_{ij}}}\right]\mathrm{such}\mathrm{that}\hfill \\ & & {\displaystyle \sum _{\alpha }{p}_{\alpha }\left[f_{\alpha }\left({\tau }_{ij}\right)-f_{\alpha }\left({\tau }_i\right)\right]\ge 1-\frac{{\eta }_{{\Pi }_{ij}}}{\Delta \left({\tau }_i,{\tau }_{ij}\right)}{\eta }_{{\Pi }_{ij}}\ge 0}\hfill \\ & & \forall i,j,{\tau }_{ij},{\tau }_i{\tau }_i\ne {\tau }_{ij}\hfill \end{array}$$ (14)

where Π_ik is the cluster covering transformation τ_ik, and _ηΠik are the slack cost associated with cluster k of the complex i. A direct solution for QP(extenṯmisprediction) or QP(extenṯmispredictioṉwitẖclustering) would require listing all negative transformations which is impractical. For a natural metric on SE3, we provide an iterative algorithm that finds P⁺ which is comparable in quality to the solution P* of QP(extenṯmispredictioṉwitẖclustering).

Algorithm description

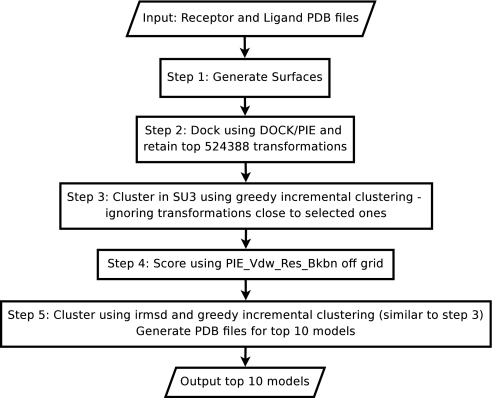
The idea of the algorithm in short is – iteratively – dock all pairs of proteins using the current estimate for P, as new violations are discovered, (a violation is when the score of a decoy complex is better (higher) that the score of the correctly docked protein pair). If current set of clusters does not cover the points causing the violations, add new clusters (that is create new slack variables), else use existing clusters. Over-sampling a neighborhood of a cluster does not lead to extra penalty as the penalty assignment is per cluster and not per inequality. Add new constraints requiring the slacks to be large enough to cover the violations; and retrain the potential. Continue this process until no new violations are discovered, the number of iterations is bounded by the minimum extent of misprediction attainable on the explicit enumeration of all constraints. The comprehensive screening of all transformations to find the most violated constraints for a given choice of parameters is needed for the correctness of the algorithm. Our code DOCK/PIE and a fast rmsd algorithm accomplish the exhaustive enumeration. The rmsd between a pair of docked structures arising in rigid body docking is computed in constant time (independent of the protein sizes) with the addition of a simple pre-processing step (Appendix B).

We provide a constant-time algorithm to calculate rms between a pair of docked structures arising in rigid body docking (Appendix B). Together with DOCK/PIE this completes the description of the procedure for efficient generation of the top Λ violated constraints in step 8 of the learning algorithm.

Below, we discuss the proof that the algorithm converges within known error bars from the exact solution. Readers that are more interested in the practical aspects of the algorithm are encouraged to skip sections: Algorithm convergence, Duality theory and a summary of previous work, and Learning with clustering.

Algorithm convergence

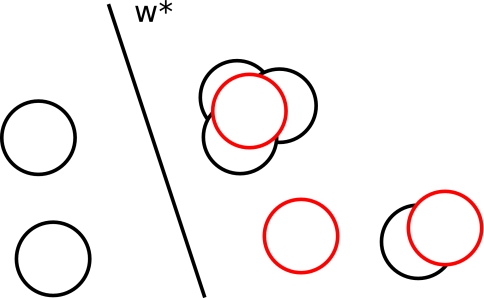
The proof of convergence of the learning algorithm depends on properties of the clustering algorithm. The optimal clustering should be connected to the iterative clustering procedure used in the algorithm (problem is portrayed in Fig. 3). We show that the number of clusters that the iterative procedure ends up adding for every cluster in the optimal clustering is bounded. When comparing two clustering schemes, the covering number is defined as the largest number of clusters in one scheme that intersect a cluster in another scheme. In the following text we show that the covering number is small for the docking problem and so the iterative clustering scheme is relatable to the optimal clustering.

Figure 3.

Elements of the optimal cover Π* are in red and elements of the current cover Π^e are in black. When the set of parameters w* is used, slack cost is paid only for points in a red cluster.

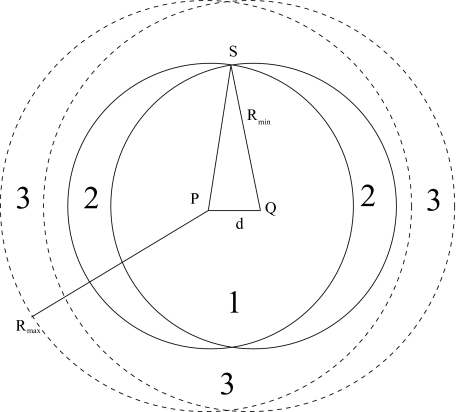
Definition. A metric Θ on space X is said to satisfy small-cover property if there is a constant K such that for all ε > 0,x ∈ X, B_ε(x) = {x′ ∈ XΘ(x, x′) < ε} (ε-ball around x) and covers P(ɛ)=⋃_i{B_ɛ(x_i)} of X that satisfy the condition ∀_ijΘ(x_i, x_j) > ε; at-most K elements of P(ε) are sufficient to cover B_ε(x). K is said to be the covering number of X, Θ.

Theorem. For the metric $\Theta ((t_1,u_1),(t_2,u_2))=\sqrt{\parallel t_1-t_2{\parallel }^2+L^2\times {\parallel u_1{u}_2^{-1}-I\parallel }_{Frobenius}}$ on the space of rigid body transformations SE3, and for covers P(ε) with $\varepsilon \le L\sqrt{8}$, the covering number K ⩽ 4⁶.

Proof. Frobenius-distance is a metric on the space of matrices. For an orthogonal matrix $O=\left\{\begin{array}{ccc}{o}_{11}& o_{12}& o_{13}\\ o_{21}& o_{22}& o_{23}\\ o_{31}& o_{32}& o_{33}\end{array}\right\}$, ${\parallel O-I\parallel }_F=\sqrt{2Trace(I-O)}$

$$\begin{array}{ccc}\hfill {\left({∥O-I∥}_F\right)}^2& =& {(1-o_{11})}^2+o_{12}^2+o_{13}^2+o_{21}^2+{(1-o_{22})}^2\hfill \\ & & +o_{23}^2+o_{31}^2+o_{32}^2+{(1-o_{33})}^2\hfill \\ & =& 3-2(o_{11}+o_{22}+o_{33})+(\left(o_{11}^{2^2}+o_{12}^2+o_{13}^2\right)\hfill \\ & =& +\left(o_{21}^2+o_{22}^{2^2}+o_{23}^2\right)+\left(o_{31}^2+o_{32}^2+o_{33}^2\right))\hfill \\ & =& 2Trace(I-O).\hfill \end{array}$$

Frobenius norm is invariant under rigid body rotation (Theorem 3.1 in Trefethen and Bau⁴²). So, we have $\parallel u_1{u}_2^{-1}{-I\parallel }_F=\parallel u_1{u}_2^T-I{\parallel }_F=\parallel (u_1-u_2)\times u_2^T{\parallel }_F={\parallel u_1-u_2\parallel }_F$. Hence Θ is a metric.

Algorithm for learning to dock

1: Input: Set of correctly docked conformation Xij (i is the complex index and j is the index of the protein chain, total of n complexes and 2n chains), their sequences, and their transformations τi ((X11, X12), τ1), …, ((Xn1, Xn2), τn), C – the weight of the slack variable penalty, tolerated approximation error υ, size of region in output space ε.

2: Start the search by calculating an initial set of potential parameters. For all n complexes with known empirical structures generate set of incorrect transformations ${\Gamma }_i^{\left(0\right)}$ ∀i = 1, …, n (i is index of the complex). Any set of decoys can be used to boot strap the algorithm. In the present study we used Patchdock.41

3: Calculate the set of constraints Si ∀i and a set of clusters of transformations Gk ∀k (k is the index of the cluster) $S_i\leftarrow \{\forall G_k\in {\Gamma }_i^{\left(0\right)}\forall {\tau }_i^{\left(j\right)}\in G_k:{\sum }_{\alpha }{p}_{\alpha }(f_{\alpha }\left({\tau }_i\right)-f_{\alpha }\left({\tau }_i^{\left(j\right)}\right))\ge 1-\frac{{\eta }_{ik}}{\Delta ({\tau }_i,{\tau }_i^{\left(j\right)})}\}$ where $\Delta ({\tau }_i,{\tau }_i^{\left(j\right)})=irmsd({(X_{i1},X_{i2})}^{\left({\tau }_i\right)},{(X_{i1},X_{i2})}^{\left({\tau }_i^{\left(j\right)}\right)})$, ${\tau }_i^{\left(j\right)}$ is an element in the cluster of transformations Gk.

4: Solve the quadratic programming problem $(P,\eta )={\mathrm{argmin}}_{w,\xi }\frac{1}{2}{P}^{t}P+\frac{C}{n}{\sum }_{i,k}{\eta }_{ik}$ subject to the constraints ${\bigcup }_{i=1}^n{S}_i$ and ∀i, kηik ⩾ 0

5: Start the main iteration cycle and set the number of iterations:ς = 0

6: Repeat: ς = ς + 1

7: fori = 1, …, ndo /* Loop over all complexes*/

8.1: Find most violated transformations, ${\mathrm{T}}_i^{\left(\varsigma \right)}$, the energies of the violating decoys, E, and their similarity to the native, Δ. The input is the coordinates of the two chains Xi1 and Xi2 of complex i, the set of transformations, τi to model complex i, the set of parameters P, tolerated energy error υ, the geometrical size of a ball ε that determines the boundary of a cluster, and the number of complex structures to retain,Λ. We also provide the set of clusters added in previous iterations cycles ${\bigcup }_{\beta =0}^{\varsigma -1}{\cup }_k{\Gamma }_{ik}^{\left(\beta \right)}$ so that clusters are added only if not already present.

find_top_violations:

• Input: receptor XR, ligand XL, native transformation τnat, scoring function parameters w, tolerated error υ, existing clusters T, cluster size ε and minimum number of solutions to retain Λ

• find radius of each protein and determine the density of rotational sampling and grid spacing to be used such that the error can be bounded by υ

• compute score of native transformation Enat

• compute grids Rvdw and ∀j ∈ {1, …, 22}Rj on the receptor protein and their inverse Fourier transforms

• (Γ, E, Δ) ← Ø /* set of high scoring transformations, their energies and distances from native */

•Vsorted = [0, 0, …, 0] (sorted array of extents of top Λ violations)

• foruα ∈ U(the space of rotations) do

○ compute scores $E_{\alpha }^{Grid}$ for all transformations (Γα) involving current rotation

○ for τ ∈ Γαwith$E_{{\tau }_{nat}}-E_{\tau }^{Grid}\le 1+\upsilon$do

▪ compute Δ(τ,τnat)=irmsd((XR,XL)(τ),(XR,XL)(τnat))

▪ if$(1-(E_{{\tau }_{nat}}-E_{\tau }^{Grid}))>\frac{V_{sorted}\left[\Lambda \right]}{\Delta (\tau ,{\tau }_{nat})}-\upsilon$, then

▪ compute exact score Eτ

▪ if$(1-(E_{{\tau }_{nat}}-E_{\tau }))>\frac{V_{sorted}\left[\Lambda \right]}{\Delta (\tau ,{\tau }_{nat})}$ and Eτnat−Eτ≤1, then

○ compute Vτ=Δ(τ,τnat)(1−(Eτnat−Eτ)), update Vsorted

• fi

▪ fi

• end for

○ end for

• incremental cluster retained transformations and add/update clusters, let Tout be the final set of clusters

• Output: (Tout, E, Δ)

More compactly: $({\mathrm{T}}_i^{\left(\varsigma \right)},E,\Delta )=\mathrm{find}̱\mathrm{top}̱\mathrm{violations}(X_{i1},X_{i2},{\tau }_i,P,\upsilon ,\varepsilon ,\Lambda ,{\bigcup }_{\beta =0}^{\varsigma -1}{\cup }_k{\Gamma }_{ik}^{\left(\beta \right)})$

8.2: Create new clusters if regions of top scoring transformations have not been seen so far according to current set of parameters.

/* add violated constraints to the working set */

for$G_k\in {\mathrm{T}}_i^{\left(\alpha \right)}$do

for${\tau }_i^{\left(j\right)}\in G_k$do

if $\Delta ({\tau }_i^{\left(j\right)},{\tau }_i)(1-{\sum }_{\alpha }{p}_{\alpha }\left[f_{\alpha }\left({\tau }_i\right)-f_{\alpha }\left({\tau }_i^{\left(j\right)}\right)\right])>0$ /* have a violation */

if cluster ik exists from previous iteration or added in this loop (say it was ${\Gamma }_{il}^{\left(\iota \right)}$) and $\Delta ({\tau }_i^{\left(j\right)},{\tau }_i)(1-{\sum }_{\alpha }{p}_{\alpha }\left[f_{\alpha }\left({\tau }_i\right)-f_{\alpha }\left({\tau }_i^{\left(j\right)}\right)\right])>{\eta }_{il}+\upsilon$, ${\Gamma }_{il}^{\left(\iota \right)}={\Gamma }_{il}^{\left(\iota \right)}\cup \left\{{\tau }_i^{\left(j\right)}\right\}$ fi

if new cluster ik, ${\Gamma }_{ik}^{\left(\varsigma \right)}=\left\{{\tau }_i^{\left(j\right)}\right\}$ fi

fi

end for

end for

9: Set constraints

$S_i\leftarrow {\bigcup }_{\beta =0}^{\varsigma }\{\forall G_k\in {\Gamma }_i^{\left(\beta \right)}\forall {\tau }_i^{\left(j\right)}\in G_k:{\sum }_{\alpha }{p}_{\alpha }\left[f_{\alpha }\left({\tau }_i\right)-f_{\alpha }\left({\tau }_i^{\left(j\right)}\right)\right]\ge 1-\frac{{\eta }_{ik}}{\Delta ({\tau }_i,{\tau }_i^{\left(j\right)})}\}$ and solve the quadratic programming problem: $(P,\eta )={\mathrm{argmin}}_{P,\eta }\frac{1}{2}{P}^{t}P+\frac{C}{n}{\sum }_{i,k}{\eta }_{ik}$ subject to the constraints ${\bigcup }_{i=1}^n{S}_i$ and ∀i, kηik ⩾ 0

10: end for

11: until no new constraints found during iteration (${\bigcup }_{i,k}{\Gamma }_{ik}^{\left(\varsigma \right)}=Ø$)

12: Output:P

Distances max out at $\sqrt{8}$ (under the Frobenius norm) in the rotation space while they could get arbitrarily large in the translation space. We introduce a scaling factor L to combine distances in both spaces in the metric Θ. For $\varepsilon \le L\sqrt{8}$, consider covers P(ε) of SE3 that are collections of ε-balls (It is sufficient to show the covering property for small ε, the proof can be extended to all values of ε by taking into account the maxing out of distances in SO3.), such that the centers of any pair of balls are at least ε apart. The number of elements in P(ε) is infinite, but we are interested in covering arbitrary ε-balls in SE3 using elements in P(ε). Let B be the given ε-ball that needs to be covered, let R(B) be its center. Consider all balls {B₁, B₂, …, B_n} in P(ε) that intersect B and let R(B₁), R(B₂), …, R(B_n) be their centers. Then d(R(B), R(B_i)) < 2ε; since d(R(B_i), R(B_j)) > ε, every ball B_i has a sphere of radius $\frac{\varepsilon }{2}$ around R(B_i) that does not intersect any other element of P(ε). So K times volume of radius $\frac{\varepsilon }{2}$< = volume of radius of 2ε.

Lemma. For $\varepsilon \le L\sqrt{8}$, the volume of an ε-ball is proportional to ε⁶.

Proof of lemma. Consider the quaternion representation of SO3, let $O\cong a+b\vec{i}+c\vec{j}+d\vec{k}$. We have a² + b² + c² + d² = 1

$$\begin{array}{c}{\left({∥O-I∥}_F\right)}^2=2Trace(I-O)\hfill \\ =2\times (3-(a^2+b^2-c^2-d^2)+(a^2-b^2\hfill \\ +c^2-d^2)+(a^2-b^2-c^2+d^2)\hfill \\ =2\times (3-3a^2+b^2+c^2+d^2)\hfill \\ =8\times (b^2+c^2+d^2),\hfill \end{array}$$

i.e., for ν ⩽ 1, the volume of a ν-ball in SO3 is $\frac{4}{3}\pi {\left(\frac{v}{\sqrt{8}}\right)}^{3^3}$. The volume of an ε-ball in SE3 is given by $volume={\int }_{t_x^2+t_y^2+t_z^2+L^2\times 8(a^2+b^2+c^2)\le {\varepsilon }^2}d{t}_{x}d{t}_{y}d{t}_{z}dadbdc=\frac{{\pi }^3}{6\times {\left(L\sqrt{8}\right)}^3}{\varepsilon }^6$.

$$\begin{array}{c}{\displaystyle \mathit{volume}={\int }_{t_x^2+t_y^2+t_z^2+L^2\times 8(a^2+b^2+c^2)\le {\varepsilon }^2}d{t}_{x}d{t}_{y}d{t}_{z}dadbdc}\hfill \\ {\displaystyle =\frac{1}{{\left(L\sqrt{8}\right)}^3}{\int }_{t_x^2+t_y^2+t_z^2+x_a^2+x_b^2+x_c^2\le {\varepsilon }^2}d{t}_{x}d{t}_{y}d{t}_{z}d{x}_{a}d{x}_{b}d{x}_c}\hfill \\ {\displaystyle =\frac{{\pi }^3}{6\times {\left(L\sqrt{8}\right)}^3}{\varepsilon }^6}\hfill \end{array}$$

Hence K ⩽ 4⁶.

With the metric Θ we perform greedy incremental clustering. We add new clusters if the distance (using Θ) to the existing cluster centers exceeds 10 Å. The clustering is performed as follows. We start with the most violated constraint as the center of the first cluster. If there are more violations that are farther than 10 Å from existing clusters we take the most violated constraint and add it as a new cluster. This process is repeated until all the violations are counted for. In practice, in a single iteration we allow the addition of 10⁵ clusters per complex.

Duality theory and a summary of previous work

We state results from duality theory that are used later in proving that the algorithm converges. Given a clustering Π of transformations, denoting η(Π)_ik by η_ik, the quadratic optimization problem with all constraints included is

$$\begin{array}{ccc}\hfill Z(P,\eta )& =& \frac{1}{2}{P}^{t}P+\frac{C}{n}\sum _{i,k}{\eta }_{ik}\mathrm{such}\mathrm{that}\forall i,\forall \tau \in SE3\setminus {\tau }_i:\hfill \\ & & {\displaystyle \times \sum _{\alpha }{p}_{\alpha }\left[f_{\alpha }\left({\tau }_i\right)-f_{\alpha }\left({\tau }_i^{\left(j\right)}\right)\right]\ge 1-\frac{{\eta }_{ik}}{\Delta ({\tau }_i,{\tau }_i^{\left(j\right)})}}\hfill \\ & & \mathrm{and}{\eta }_{ik}\ge 0(P^{*},{\eta }^{*})=\underset{P,\eta }{\mathrm{argmin}}Z(P,\eta )\hfill \end{array}$$ (15)

Define M as the matrix of inequalities $M(ij,\alpha )=f_{\alpha }\left({\tau }_i\right)-f_{\alpha }\left({\tau }_i^{\left(j\right)}\right)$, ${\mathrm{N}}_{j,k}=\{\begin{array}{ccc}\frac{1}{\Delta ({\tau }_i,{\tau }_i^{\left(j\right)})}& if& k=j\left(i\right)\\ 0& else& \end{array}$(transformation ${\tau }_i^{\left(j\right)}$ belongs to cluster k). Let e be a column vector with each element equal to 1. The constraints can be written in matrix form as MP + Nη ⩾ e.

Let $L(P,\eta ,\alpha ,t,s)=\frac{1}{2}{P}^{T}P+\frac{C}{n}{e}^T\eta -{\alpha }^T(MP+\mathrm{N}\eta -s-e)-t^T\eta$ such that η ⩾ 0, α ⩾ 0, s ⩾ 0, t ⩾ 0 and $D\left(\alpha \right)=-\frac{1}{2}{\alpha }^{T}M{M}^T\alpha +e^T\alpha$ such that ${\mathrm{N}}^T\alpha \le \frac{C}{n}e$. The problem (P*, η*) = argmin_{P, η} Z(P, η) is said to be primal problem and ^α**= argmax _αD(α) is said to be the dual problem. A point is said to be feasible point of a problem if it satisfies the constraints associated with the problem.

The following properties hold:

1. For every feasible point (P, η, α, t, s) of L if (P, η) is a feasible point of the primal, L(P, η, α, t, s) ⩽ Z(P, η).

2. For every feasible point (P, η) of the primal there exist α, s, t such that (P, η, α, t, s) is a feasible point of L.

3. For every feasible point (α) of the dual there exist P, η, s, t such that (P, η, α, t, s) is a feasible point of L.

4. For every feasible point (P, η, α, t, s) of L if (α) is a feasible point of the dual, D(α) ⩽ L(P, η, α, t, s).

5. If (P*, η*) = argmin_{P, η}Z(P, η) and α^**= argmax _αD(α), there exist s, t such that D(α*) = L(P*, η*, α*, t, s) = Z(P*, η*). Further (P*, η*, α*, t, s) satisfy $P^{*}-{\left({\alpha }^{*}\right)}^{T}M=0\left(\frac{\partial L}{\partial P}=0\right)$, $\frac{C}{n}e-t-{\left({\alpha }^{*}\right)}^T\mathrm{N}=0\left(\frac{\partial L}{\partial \eta }=0\right)$, $MP+\mathrm{N}\eta -s-e=0\left(\frac{\partial L}{\partial \alpha }=0\right)$.

6. As a result of 1–5; if (P, η) is a feasible point of the primal and α a feasible point of the dual, Z(P, η) ⩾ D(α).

We summarize the framework of Tsochantaridis et al.¹⁷ here for the benefit of the reader. Our proof extends their ideas to incorporate clustering. Let Δ_i = max _τ{Δ(τ_i, τ)}, $\overline{\Delta }={\max }_i\left\{{\Delta }_i\right\}$, R_i = max _τ{∑_α∥f_α(τ) − f_α(τ_i)∥},$\overline{R}={\max }_i\left\{R_i\right\}$. For docking, $\overline{\Delta }$ would be the maximum i-RMSD and $\overline{R}$ is the maximum feature difference (in absolute terms) encountered in the problem.

The authors show that one does not have to list all constraints to solve the primal problem. They show that it is sufficient to add violations that incur the largest penalty at each iteration. Although a quadratic optimization is solved to update parameters at each iteration, the analysis is in terms of progress made in solving the dual D. They show that the dual improves by at least a constant amount in each iteration. Since P = 0 and $\eta =\overline{\Delta }e$ is a feasible solution of primal, $D\left({\alpha }^{*}\right)=Z(P^{*},{\eta }^{*})\le Z(0,\overline{\Delta }e)$ and so the procedure converges.

Learning with clustering

Proposition. (Extension to Proposition 16 of Tsochantaridis et al.¹⁷): The improvement in dual objective function δ is lower bounded by $\delta \ge \min \{\frac{C\upsilon }{2n},\frac{{\upsilon }^2}{8{\overline{\Delta }}^2{\overline{R}}^2}\}$.

While the dual problem stays the same during the solution to SVM^struct, the dual changes as new clusters are added during the course of our algorithm, i.e., new columns and new rows are added to the MM^T matrix. The old solution with additions of zeroes in the new dimensions is feasible for the new problem (since we get a trivial solution for the new component). This solution can now be improved following Proposition 16, i.e., given a new D(α) the solution can now be optimized.

Our task here is complicated by the fact that we do not know the best clustering scheme and we use instead clustering on-the-fly as more inequalities are added. The impact of less than optimal clustering on the learning needs to be evaluated. The covering property discussed previously allows us to estimate the cost of clustering in the worst case scenario that still provide coverage of the conformation space leading to violations.

Theorem.Let$(P^{*},{\eta }^{*},{\Pi }^{*})={\mathrm{argmin}}_{\Pi ,w,\eta \left(\Pi \right)}\frac{1}{2}{P}^{t}P+\frac{C}{n}{\sum }_{i,k}\eta {\left(\Pi \right)}_{ik}$such that$\forall i,\forall \tau \in SE3\setminus {\tau }_i:{\sum }_{\alpha }{p}_{\alpha }\left[f_{\alpha }\left({\tau }_i\right)-f_{\alpha }\left({\tau }_i^{\left(j\right)}\right)\right]\ge 1-\frac{{\eta }_{{\Pi }_{ik}}}{\Delta ({\tau }_i,{\tau }_i^{\left(j\right)})}$ (the least expensive solution over all possible clustering schemes). Let${\sigma }^{*}=\frac{1}{2}{P}^{*t}{P}^{*}+\frac{C}{n}{\sum }_{i,k}{\eta }_{ik}^{*}$. For a given υ > 0, the learning algorithm terminates after$K\times \max \left\{\frac{2n{\sigma }^{*}}{C\upsilon },\frac{8{\overline{\Delta }}^2{\overline{R}}^2{\sigma }^{*}}{{\upsilon }^2}\right\}$iterations.

Proof. At each step the dual objective function increases by at least $\delta =\min \{\frac{\upsilon }{2n},\frac{\upsilon }{8{\overline{\Delta }}^2{\overline{R}}^2}\}$. Suppose the algorithm does not converge in said number of iterations; let (P^e, η^e, Π^e) be the solution at this stage and let σ_Z, σ_D be the values of the primal and dual objective functions (with partial covering Π^e of transformation space – clustering of a space induces a cover on it) and ${\sigma }_Z^{+}$ be the cost of the optimal parameters P* when the current clustering Π^e is used.

• σ_D ⩽ σ_Z(primal is a minimization problem)

• ${\sigma }_Z\le {\sigma }_Z^{+}$ (P^e minimizes the primal objective function when clustering Π^e is used)

• Claim. ${\sigma }_Z^{+}\le K{\sigma }^{*}$

Proof of claim. Consider the following mapping from Π^e to Π*∪{O}: for each cluster in $G_{ik}^e\in {\Pi }^e$, if it does not intersect any element in Π*, map it to O, if it does intersect, map it to the intersecting element with the largest slack cost. By the covering property, the number of elements that get mapped to any element of Π* is at most K and P* does not incur any penalty on elements mapped to O. So ${\sigma }_Z^{+}\le K{\sigma }^{*}$.

Since the algorithm makes progress of at least δ in each iteration we have σ_D ⩾ Kσ*, leading to a contradiction. Hence the theorem.

It follows from the proof that the solution returned satisfies σ_Z ⩽ Kσ*.

We emphasize that we retain all inequalities in the iterations and clustering procedure. Clustering is only used to determine the slack variables.

RESULTS

Derivation of parameters

We used the set of 640 protein-protein dimer complexes prepared in our earlier work.²² The scoring function is based on a linear combination of vdw attraction, vdw repulsion, and contacts between 22 different particle types (a particle type was chosen for the backbone carbonyl group, backbone amide group, and each residue type was represented by a different particle type). We used a piecewise linear interpolation to represent the functional form for the contact function (see section “Residue and backbone contact potential”).

The initial parameter set was computed with straightforward linear programming using decoys generated by Patchdock (as outlined in our earlier work²²). This study does not include exhaustive set of transformations and it relies instead on another docking program (Patchdock⁴¹) to provide a set of structures appropriate for learning.

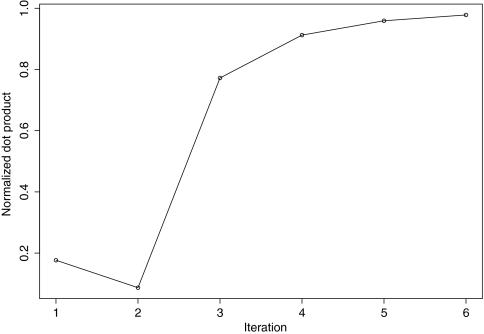
The parameters determined from optimization with the Patchdock-based set of structures were used in exhaustive ranking of all docking candidates on a grid at the first iteration, as described in the text. At each iteration, we docked protein partners using the current parameter set. To reduce the noise in the learning we added a new constraint requiring that the native (bound) transformation score above any false transformation. If the false positive led to a new cluster, we added a new slack variable. For each complex, up to 100 000 top violated constraints were added in each iteration. All constraints from the 640 complexes were pooled with the constraints discovered so far and the resultant quadratic program was solved for the new set of parameters. The dimension of the feature space was 252. The largest quadratic optimization problem solved as part of the learning involved 258 127 822 constraints with 27 564 303 slack variables. We follow the framework outlined in OOQP,⁴³ use the parallel routines reported in an earlier work,²⁰ and develop a primal-dual interior point algorithm for solving the QP arising in the learning algorithm. The final quadratic program was solved in 32 h on 618 cores on Ranger, a super computer maintained by Texas Advanced Computing Center. The potential converges with successive iterations (illustrated in Fig. 4 and Table 1).

Figure 4.

The scoring function converges as iterative learning proceeds, for each iteration we plot the dot product between the parameters (normalized to have L2 norm 1) at this iteration and the previous iteration. The blip at iteration 2 arises due to switching from linear programming to quadratic programming for parameter estimation.

Table 1.

A complex is said to be explained if a high quality hit – ((irmsd≤3Å)∨(C_αrmsd≤3)∧(frac̱native̱contacts≥0.5)) is ranked within top N.

				No. of complexes explained
Iteration	Method	No. of constraints	No. of clusters	Top 1	Top 10	Top 100	Top 1000
Zdock3.0				333	375	441	489
Patchdock				201	302	431	513
0	LP	25 719 027	…	179	237	337	437
1	QP	66 893 447	8 293 956	171	212	278	387
2	QP	101 088 699	12 090 751	234	303	401	497
3	QP	134 079 719	15 109 006	270	353	446	535
4	QP	168 055 994	18 911 122	291	364	454	526
5	QP	204 805 256	22 225 252	315	389	471	546
6	QP	258 127 822	27 564 303	318	398	484	557

We obtained the initial guess (iteration 0) from linear programming framework following the procedure explained in our earlier work,²² this switch from linear programming to quadratic programming probably caused the blip at iteration 2. The normalized dot product between the normalized parameter vectors estimated at iteration 5 and 6 is 0.978. Our results reaffirm the observation of Lu et al.³² that subtle differences in the potential grossly affect its performance in structure prediction tasks; the dot product between the parameters estimated at iterations 0 and 6 is 0.7 while the performance on protein-protein docking improves from iteration 0 to iteration 6 by a factor of 2. The final potential is provided in Table 2.

Table 2.

Vdw residue backbone scoring function (PIE_Vdw_Res_Bkbn).

	ILE	VAL	LEU	PHE	CYS	MET	ALA	GLY	THR	SER	TRP	TYR	PRO	HIS	ASN	GLN	ASP	GLU	LYS	ARG	NH	CO
ILE	0.132	0.072	0.09	0.086	0.066	0.1	0.055	0.077	0.058	0.03	0.016	0.063	0.001	0.024	0.018	0.034	0.016	−0.007	−0.025	0.009	−0.041	0.006
VAL	0.072	0.16	0.104	0.059	−0.006	0.058	0.038	0.015	0.026	0.017	−0.005	0.066	0.043	0.025	0.025	−0.007	0.006	0.04	−0.007	0.041	−0.029	−0.001
LEU	0.09	0.104	0.1	0.1	0.049	0.05	0.072	0.044	0.027	0.029	0.059	0.092	0.043	0.019	0.004	0.021	−0.001	0.001	−0.008	0.023	−0.052	0.007
PHE	0.086	0.059	0.1	0.071	0.067	0.094	0.036	0.041	0.065	0.032	0.021	0.089	0.074	0.049	0.051	0.049	0.034	0.02	−0.023	0.029	−0.037	0.005
CYS	0.066	−0.006	0.049	0.067	0.118	0.124	0.007	0.034	0.005	0.02	−0.049	0.068	0.03	0.09	−0.049	−0.04	−0.016	−0.048	0.018	0.047	0.021	−0.021
MET	0.1	0.058	0.05	0.094	0.124	0.059	0.058	0.057	0.056	0.048	0.054	0.099	0.006	0.044	0.047	0.025	0.012	−0.01	−0.015	0.003	−0.049	0.009
ALA	0.055	0.038	0.072	0.036	0.007	0.058	0.052	0.026	0.027	0.032	0.07	0.046	−0.024	0.01	−0.002	0.027	−0.023	0.011	0.007	−0.002	−0.009	−0.025
GLY	0.077	0.015	0.044	0.041	0.034	0.057	0.026	0.061	0.028	0.036	0.028	0.051	0.032	0.005	0.034	0.005	0.011	−0.006	−0.006	0.043	−0.033	−0.008
THR	0.058	0.026	0.027	0.065	0.005	0.056	0.027	0.028	0.012	0.034	0.006	0.042	0.019	0.044	0.025	0.052	0.039	0.029	−0.035	0.022	−0.03	−0.007
SER	0.03	0.017	0.029	0.032	0.02	0.048	0.032	0.036	0.034	0.034	0.019	0.007	0.038	0.047	0.007	0.013	0.01	0.034	0.01	−0.007	−0.015	−0.022
TRP	0.016	−0.005	0.059	0.021	−0.049	0.054	0.07	0.028	0.006	0.019	0.186	0.003	0.074	0.107	0.053	0.069	−0.063	−0.039	0.034	0.057	−0.004	0.027
TYR	0.063	0.066	0.092	0.089	0.068	0.099	0.046	0.051	0.042	0.007	0.003	0.103	0.078	0.022	0.057	0.013	0.014	0.004	−0.002	0.046	−0.033	0.013
PRO	0.001	0.043	0.043	0.074	0.03	0.006	−0.024	0.032	0.019	0.038	0.074	0.078	0.01	0.014	0.021	0.024	0.01	0	−0.052	−0.013	−0.045	0.004
HIS	0.024	0.025	0.019	0.049	0.09	0.044	0.01	0.005	0.044	0.047	0.107	0.022	0.014	0.026	0.026	−0.025	0.035	0.018	0.016	−0.041	−0.041	0.018
ASN	0.018	0.025	0.004	0.051	−0.049	0.047	−0.002	0.034	0.025	0.007	0.053	0.057	0.021	0.026	0.054	0.015	−0.002	−0.008	−0.018	−0.002	−0.028	−0.001
GLN	0.034	−0.007	0.021	0.049	−0.04	0.025	0.027	0.005	0.052	0.013	0.069	0.013	0.024	−0.025	0.015	0.003	0.008	−0.031	0.023	0.005	−0.025	0.008
ASP	0.016	0.006	−0.001	0.034	−0.016	0.012	−0.023	0.011	0.039	0.01	−0.063	0.014	0.01	0.035	−0.002	0.008	−0.009	−0.034	0.039	0.085	0.006	−0.041
GLU	−0.007	0.04	0.001	0.02	−0.048	−0.01	0.011	−0.006	0.029	0.034	−0.039	0.004	0	0.018	−0.008	−0.031	−0.034	−0.038	0.059	0.062	0.018	−0.042
LYS	−0.025	−0.007	−0.008	−0.023	0.018	−0.015	0.007	−0.006	−0.035	0.01	0.034	−0.002	−0.052	0.016	−0.018	0.023	0.039	0.059	−0.04	−0.065	−0.022	0.018
ARG	0.009	0.041	0.023	0.029	0.047	0.003	−0.002	0.043	0.022	−0.007	0.057	0.046	−0.013	−0.041	−0.002	0.005	0.085	0.062	−0.065	−0.016	−0.042	0.027
NH	−0.041	−0.029	−0.052	−0.037	0.021	−0.049	−0.009	−0.033	−0.03	−0.015	−0.004	−0.033	−0.045	−0.041	−0.028	−0.025	0.006	0.018	−0.022	−0.042	0.03	0.011
CO	0.006	−0.001	0.007	0.005	−0.021	0.009	−0.025	−0.008	−0.007	−0.022	0.027	0.013	0.004	0.018	−0.001	0.008	−0.041	−0.042	0.018	0.027	0.011	0.001
VDW	0.009

Test on newly deposited complexes

There were 157 heterodimeric protein-protein complexes deposited in the PDB since 2008 that were not similar to any complex in the training set. Of these 55 complexes had no ligand molecules or ions close to the interface, no disulphide bonds and did not involve extensive conformational change upon docking (terminal unfolding/insertion, domain rearrangement). Twelve of these complexes had unbound configurations (homolog with tm-score⁴⁵ below 0.95) for at least one chain; these constitute the test set. When using homologs we always model the structure of the native sequence based on the homolog and dock models. The input pdbs are available at http:∕/users.ices.utexas.edu∕~ravid∕pie∕test_set∕.

Our protocol (flowchart illustrated in Fig. 5) is to dock using the learnt potential, sort the solutions, cluster them based on i-RMSD, and return high scoring representatives from these clusters. The same algorithm was used for CAPRI targets 46, 48, 49, and 50 (parameters from iteration 3 were used for target 46). This protocol identifies a near native solution within top 10 (100) on 5 of 12 cases (8 of 12) cases compared to 3 of 12 (6 of 12) by Zdock3.0 + Zrank; 5 of 12 (7 of 12) by Cluspro³⁴ and 2 of 12 (5 of 12) by Gramm-X.³⁵ The comparison on each case is provided in Table 3. Note that the algorithm presented in the text is coarse grained, using residue-based potential, and rigid protein shapes. The other algorithms we compared to are using more sophisticated description, including atomic models and refinement of the initial structures. We find it encouraging that the simplified model is doing consistently better than other approaches.

Figure 5.

Outline of algorithm used in CAPRI to predict mode of binding in a protein-protein interaction, testing and available as web service. We only retain 2¹⁹ = 524 388 conformations due to computational limitations.

Table 3.

Performance of Dock/PIE is comparable to Zdock (Ref. ¹¹) with Zrank (Ref. ³³), Cluspro (Ref. ³⁴), and Gramm-X (Ref. ³⁵). A model is said to be a hit if (irmsd ⩽ 4 Å) from native. The entries of Besthit indicate the lowest ranked model that is a hit. ZD3.0ZR is the result of rescoring transformations generated by Zdock3.0 using Zrank. We use the greedy i-RMSD based clustering developed as part of our algorithm on structures generated by Zdock3.0 with Zrank and report the results under the columns labeled ZDZR + cluster. In summary, Dock/PIE predicted correctly 0/5/8 complexes in the top 1/top 10/top 100 hits, Zdock3.0 1/3/6, ZD3.0ZR 1/1/4, ZDZR + cluster 1/1/6, Cluspro 0/5/7, and Grammx 0/2/5. Dock∕PIE according to this test is at par with these leading technologies.

	Dock∕PIE and cluster			Zdock3.0	ZD3.0ZR		ZDZR + cluster		Cluspro		Gramm-X
Case	Besthit	No. of hits	No. of clusters	Besthit	Besthit	No. of Hits	Besthit	No. of hits	Besthit	No. of hits	Besthit	No. of hits
2wfx_from_3ho4B_-_2ibgH_-	1078	4	9604	6825	3012	4	0	0	0	0	190	1
3d65_from_3d65_E_3btmI_-	5	75	2228	77	108	1547	45	52	3	10	2	17
3di3_from_3di3_B_3di2C_-	49	8	2744	27	166	384	35	7	0	0	0	0
3fpn_from_3fpn_A_2nmvA_-	10	7	1001	1	24	462	17	4	10	1	270	1
3g9a_from_3ed8D_-_3g9a_B	10	33	3762	106	431	675	174	19	10	1	198	1
3hct_from_1fxtA_-_3hct_A	0	0	1038	20 084	662	1	0	0	0	0	137	1
3jrq_from_2iq1A_-_3jrq_B	4	3	1619	4	26	405	12	1	9	1	34	3
3l1z_from_3fshB_-_3l1z_B	75	10	3154	4985	3897	98	720	4	13	1	4	4
3l9j_from_2tnfB_-_3l9j_C	175	9	1409	108	1	624	1	11	0	0	50	1
3m18_from_3m18_A_1i56A_-	88	16	4258	5	1284	234	1128	6	0	0	134	3
3m62_from_3m62_A_1nddB_-	2	60	2357	40	26	743	17	35	4	8	16	2
3nbp_from_1mu2A_-_3nbp_B	262	1	5365	0	0	0	0	0	24	1	0	0

Tests on Zlab benchmark

The Zlab benchmark is the de facto standard in the field. We therefore decided to test our potential on this set as well. We removed constraints corresponding to cases similar to Zlab Benchmark 2 (Ref. ⁴⁶) from the learning set and retrained the potential. This potential was used for evaluating the learning procedure on the benchmark. We docked every pair listed in the Zlab benchmark using our docking procedure and ranked solutions according to the potential designed here. We did not use the potential reported in Ref. 22 since it does not work well for exhaustive sampling. When asked to pick the best transformation from all possibilities in the rigid transformation space, the scoring potential almost always picks up an incorrect solution. This issue is addressed here. Benchmark 2 comprises 84 complexes for unbound protein-protein docking. Our algorithm selects a near native solution on the top/top 10/top 100 in 12/28/52 cases compared to 10/21/41 by Zdock3.0 + Zrank (Table 4).

Table 4.

Comparing Dock/PIE and ZDOCK + ZRANK on Zlab benchmark. Dock/PIE ranks a near native solution at the top 1/top10/top 100 in 12/28/52 cases compared to 10/21/41 by Zdock3.0.

	DOCK∕PIE			ZDOCK + ZRANK
Case	Besthit	Nos. returned	No. of hits	Besthit	No. of hits
1A2K	2	5784	23	1038	570
1ACB	1	813	4	780	581
1AHW	64	3299	5	27	347
1AK4	50	1720	17	1315	253
1AKJ	1064	3341	3	175	236
1ATN	670	14 708	11	1076	15
1AVX	5	7291	45	11	744
1AY7	24	817	4	74	407
1B6C	3	1353	5	1	509
1BGX	0	4776	0	0	0
1BJ1	3	1553	12	19	1637
1BUH	5	1396	5	353	514
1BVK	321	6793	52	116	425
1BVN	2	2252	34	10	946
1CGI	13	1818	20	22	1167
1D6R	39	13 847	107	2347	32
1DE4	4	47 977	117	426	133
1DFJ	1	2100	4	2	334
1DQJ	401	2236	11	753	374
1E6E	14	7823	84	3	448
1E6J	7	660	10	1	1244
1E96	2	3023	16	24	196
1EAW	2	787	6	1	597
1EER	97	12 028	5	330	11
1EWY	27	985	5	21	586
1EZU	1	1763	4	2247	340
1F34	19	3664	6	62	172
1F51	40	3973	7	3	304
1FAK	0	10 006	0	0	0
1FC2	96	903	15	154	92
1FQ1	189	8187	4	15 260	9
1FQJ	1301	9687	5	491	24
1FSK	1	2045	25	1	851
1GCQ	407	1602	4	922	146
1GHQ	0	6887	0	2982	2
1GRN	321	1025	1	558	166
1HE1	7	1666	4	36	253
1HE8	323	10 776	17	75	8
1HIA	1	824	6	618	145
1I2M	11	1366	1	473	98
1I4D	19	2407	4	1349	351
1I9R	112	4585	16	31	370
1IB1	26	7290	18	33 099	2
1IBR	0	2346	0	0	0
1IJK	107	3773	16	444	116
1IQD	1	4171	23	1	802
1JPS	135	2143	5	1	385
1K4C	3663	34 627	78	162	1323
1K5D	798	1514	1	84	143
1KAC	725	7541	35	11	160
1KKL	115	2815	12	70	173
1KLU	907	11 041	24	13 333	18
1KTZ	1003	3369	12	397	90
1KXP	1	5639	7	12	283
1KXQ	4	1848	3	14	200
1M10	3705	4175	1	10 647	4
1MAH	16	11 048	170	3	1177
1ML0	1	5999	167	1	548
1MLC	129	2715	17	5	616
1N2C	4	12 875	47	3203	129
1NCA	317	10 089	37	14	126
1NSN	375	28 750	121	468	174
1PPE	1	370	28	1	3616
1QA9	0	3170	0	1850	29
1QFW	1737	3265	7	192	107
1RLB	9	9268	70	1	1767
1SBB	2334	3298	1	3639	26
1TMQ	2	8857	59	71	353
1UDI	1	2855	23	2	359
1VFB	92	1571	5	437	341
1WEJ	65	1059	9	2	907
1WQ1	41	2082	2	296	142
2BTF	51	11 102	26	151	295
2HMI	67	13 332	21	272	331
2JEL	1	2696	20	42	1285
2MTA	68	940	9	57	627
2PCC	13	1549	8	218	389
2QFW	16	3978	15	6	510
2SIC	14	1010	4	1	768
2SNI	1	608	6	114	554
2VIS	6084	25 047	4	8	703
7CEI	2	1488	10	3	965

Comparison to other residue contact potentials

The algorithm to generate decoys influences the learning of a potential. It is therefore not trivial to compare score functions on decoy structures that were generated by the same approach that is used for the learning. In the previous sections we compared the algorithms (not the energy functions) letting every protocol generate its own candidates for correct docking. Nevertheless, there are docking potentials learnt with different techniques (statistical potentials, or linear programming) without clearly defined docking algorithm that we wish to evaluate and compare to our approach. To conduct the comparison it is necessary to generate decoy structures that are independent of our own (and others) procedures. We therefore use Zdock3.0 to computed 54 000 decoys for the 640 complexes that were included in the training set. The results of scoring these structures with different energy functions are provided in Table 5. Statistical potential derived for template identification⁴⁷ is better than random (has p-value below 0.5), potentials derived on protein-protein interfaces³² perform better, discriminative learning improves them further. Accounting for exhaustive enumeration of conformation space improves the result even further. Ignoring the OPLS factor in our potential (set P_vdw to 0 and use the remaining terms as is from Table 2), which results in a function closer to a contact potential, still explains a significant fraction of complexes in the training set.

Table 5.

Top 54 000 structures generated by Zdock3.0 are re-ranked under various schemes, for each case the rank for which the probability that a random scoring function will do better with probability 0.5 is computed, the row labeled reference summarizes this evaluation (Zdock3.0 generated a lot of near native structures, scoring at random would pick up a hit in top 100 models in 162 cases). Statistical potentials capture signal in protein-protein interfaces in the PDB, our iterative learning procedure does a better job of mining this information. Round6 potential does a better job when used for sampling and scoring rather than rescoring alone.

	No. of complexes explained
Method	Top 1	Top 10	Top 100	Top 1000
Reference	0	1	162	501
MJ3	50	104	224	386
LLS	94	179	282	417
TB	148	229	350	460
Round6 potential	290	361	434	502
Round6 potential no	244	334	417	489
shape complementarity

DISCUSSIONS

Mathematical programming was used extensively in the field of protein folding,^{12, 13, 14, 48, 49} protein docking,^{22, 25} and protein design.^{51, 52} These algorithms are invariably based on heuristic sampling of constraints. As carefully as the selections were made, there was no proof that the algorithms converge or even improve with the addition of new constraints. The extension provided in the present work provides an algorithm that shows systematic and monotonic improvement in the energy function as the number of constraints that are added to the set increases.

The learning algorithm presented in this work connects iterative learning procedures used for potential design in protein folding and protein docking community with research in support vector machines. Learning a contact potential (residue, atomic, even after inclusion of distance dependence) that always scores native above all possible conformations is infeasible¹² and it is critical to develop approaches to select the best model under these circumstances. Other simpler methods that optimize Z-scores⁹ or work with limited conformational sampling^{13, 38, 47, 48, 49} have worked well in practice and the quality of the potential generally improved with the extent of the conformational space explored. However, in these approaches there are no theoretical guarantees on the quality of solution, and it is difficult to further improve the solution upon the discovery of new examples. As more data become available, it is important for algorithms to continue systematically and consistently to improve their capacity. This is the promise of convex programming.

Recent research in structured output prediction has provided significant breakthroughs on this front.¹⁷ When the global optimum can be found, learning procedures can be designed with provable guarantees. Efficient procedures exist for finding the global optimum in certain models for protein docking, which makes the above advances particularly relevant to docking. We extend the structural SVM framework to include notions of clustering, traditionally used in protein structure prediction, and illustrate the learning procedure on protein docking.

The learning algorithm presented in this work connects iterative learning procedures used in protein docking community to the rich body of research on support vector machines. For the first time, we provide a learning procedure that provably and systematically improved the quality of the parameter set by a large-scale minimization of misprediction extent. The procedure has a simple-minded explanation – “progress in learning is achieved by looking at the largest mistakes, the more the better.”

Interestingly, a single residue-based potential is doing well for both filtering and ranking. It is of course possible to re-rank the final results with more fine tuned energy functions and protocols and perhaps improve the results. However, the current potential is putting together the ranking and filtering quite successfully, and on coarse level.

The framework is applicable for parameter optimization in a wide range of tasks in structural bioinformatics – wherever the problems of finding the global minimum and finding the largest violation with a given choice of parameters are tractable and one can look at the output space as a low dimensional space. For instance, potentials can be designed for protein structure refinement by iteratively adjusting the model using the current potential, accumulating mistakes made, and constraining the potential to avoid (pay for) these mistakes. Nonlinear functional forms using Gaussian kernel functions in quadratic programming have shown promise in designing scoring functions for protein design.⁵³ These approaches could be explored through extensions to the QP solver.

APPENDIX A: ERROR ANALYSIS

Theorem.Let τ* = (t*, u*) be the optimal solution for docking based on the scoring function parameterized by w, let D(g, U) be the discretization used. There is a solution τ = (t, u) ∈ D such that ε = |E(τ*) − E_Grid(τ)| approaches 0 along with ∥t* − t∥ and ∥u* − u∥ as g, err(U) approach 0.

Proof. Let u= argmin _uj∈U(∥u^*−u_j∥)(the rotation in the discrete set closest to the correct rotation) and t=[ argmin _(l,m,n)(∥(l,m,n)×s−t^*∥)]×g(the translation in the discrete set closest to the correct translation), let τ = (t, u).

$$\begin{array}{c}E\left({\tau }^{*}\right)-E_{Grid}\left(\tau \right)=(E\left({\tau }^{*}\right)-E\left(\tau \right))+(E\left(\tau \right)-E_{Grid}\left(\tau \right))\hfill \\ =\underset{1}{\underbrace{(E^{vdw}\left({\tau }^{*}\right)-E^{vdw}\left(\tau \right))}}\hfill \\ +\underset{2}{\underbrace{(E^{particle̱pair}\left({\tau }^{*}\right)-E^{particle̱pair}\left(\tau \right))}}\hfill \\ +\underset{3}{\underbrace{(E^{vdw}\left(\tau \right)-E_{Grid}^{vdw}\left(\tau \right))}}\hfill \\ +\underset{4}{\underbrace{(E^{particle̱pair}\left(\tau \right)-E_{Grid}^{particle̱pair}\left(\tau \right))}}.\hfill \\ Term2.E^{particle̱pair}\left({\tau }^{*}\right)-E^{particle̱pair}\left(\tau \right)\hfill \\ {\displaystyle =\sum _{j=1}^{22}{E}^{particle̱pai{r}_j}\left({\tau }^{*}\right)-E^{particle̱pai{r}_j}\left(\tau \right).}\hfill \end{array}$$

Claim. $|E^{particle̱pai{r}_j}\left({\tau }^{*}\right)-E^{particle̱pai{r}_j}\left(\tau \right)|\le N_L^{\left(j\right)}\times \max error\left({\phi }_j\left(r\right)\right)$where$N_L^{\left(j\right)}$is the number of particles of typejin the ligand.

Proof. Consider a particle p of type j of the ligand, let P be its position upon application of transformation τ* and Q be the position upon application of transformation τ. Consider spheres of radii R_min and R_max around P and Q; let Ω₁ be the region common to the smaller spheres, Ω₂ be the region not common to the smaller spheres and Ω₃ be the region enclosed by the larger spheres not in Ω₁ and Ω₂. These regions are illustrated in Fig. 6.

$$\begin{array}{ccc}\hfill d_p& =& |\stackrel{\rightharpoonup }{PQ}|=|{\tau }^{*}\left({\stackrel{\rightharpoonup }{r}}_p\right)-\tau \left({\stackrel{\rightharpoonup }{r}}_p\right)|=|(t^{*}-t)+(u^{*}-u)\left({\stackrel{\rightharpoonup }{r}}_p\right)|\hfill \\ & \le & |(t^{*}-t)|+|(u^{*}-u)\left({\stackrel{\rightharpoonup }{r}}_p\right)|\le \frac{\sqrt{3}}{2}gs+d_{L}err\left(U\right)\mathrm{also},\hfill \\ \hfill d& =& {\displaystyle \underset{1\le p\le N_L}{\max }\left\{d_p\right\}\le \frac{\sqrt{3}}{2}g+d_{L}err\left(U\right).}\hfill \end{array}$$

Figure 6.

In proof of the theorem for error analysis of DOCK/PIE, P is the position of the particle upon application of transformation τ* and Q is the position upon application of transformation τ. Consider spheres of radii R_min and R_max around P and Q. The difference between contact potential at P and Q is only dependent on particles in the regions 2 and 3.

The error in the potential $\Delta {\Phi }_j^{\left(p\right)}={\Phi }_j\left(P\right)-{\Phi }_j\left(Q\right)\le \frac{d_p}{R_{\max }-R_{\min }}\times {\max }_{i\in \{1,...,22\}}\left\{\right|w_{ij}\left|\right\}\times \eta$ where η is the number of particles of the receptor with centers in the region Ω₂∪Ω₃.

η ⩽ N_R, (actually one can derive a tighter upper bound on η if one uses a proposition that the particles of the receptor are packed such that they have impenetrable cores) so $\mathrm{maxerror}\left({\Phi }_j\left(r\right)\right)\le \frac{d}{R_{\max }-R_{\min }}\times {\max }_{i\in \{1,...,22\}}\left\{\right|w_{ij}\left|\right\}\times N_R$

$$\begin{array}{ccc}& & \mathrm{so},|E^{particle̱pai{r}_j}\left({\tau }^{*}\right)-E^{particle̱pai{r}_j}\left(\tau \right)|\le N_L^{\left(j\right)}\hfill \\ & & {\displaystyle \times \frac{d}{R_{\max }-R_{\min }}\times \underset{i\in \{1,...,22\}}{\max }\left\{\right|w_{ij}\left|\right\}\times N_R}\hfill \end{array}$$

$$\begin{array}{ccc}& & \mathrm{Hence}|E^{particle̱pair}\left({\tau }^{*}\right)-E^{particle̱pair}\left(\tau \right)|\le \frac{d}{R_{\max }-R_{\min }}\hfill \\ & & {\displaystyle \times N_L\times \underset{i\in \{1,...,22\}}{\max }\left\{\right|w_{ij}\left|\right\}\times N_R}\hfill \end{array}$$

$$\begin{array}{ccc}& & Term4.E^{particle̱pair}\left(\tau \right)-E_{Grid}^{particle̱pair}\left(\tau \right)\hfill \\ & & =\sum _{j=1}^{22}{E}^{particle̱pai{r}_j}\left(\tau \right)-E_{Grid}^{particle̱pai{r}_j}\left(\tau \right)\hfill \end{array}$$

$$\begin{array}{ccc}& & Claim.|E^{particle̱pai{r}_j}\left(\tau \right)-E_{Grid}^{particle̱pai{r}_j}\left(\tau \right)|\le N_L^{\left(j\right)}\hfill \\ & & \times \max ̱\mathrm{approx}̱\mathrm{error}\left({\Phi }_j\left(r\right)\right).\hfill \end{array}$$

Proof. The error in the potential is given by

$$\begin{array}{ccc}& & \Delta {\Phi }_j^{\left(p\right)}={\Phi }_j\left(P\right)-{\Phi }_j^{Grid}\left(P\right)\hfill \\ & & \le \sum _{1\le q\le N_R}{w}_{type\left(q\right)j}(h\left(r_{pq}\right)-h_{\mathrm{interpolate}}\left(r_{pq}\right))\hfill \\ & & {\displaystyle \le \underset{k\in \{1,...,22\}}{\max }\left\{\right|w_{kj}\left|\right\}\times \sum _{p_i}(h\left(r_{pq}\right)-h_{\mathrm{interpolate}}\left(r_{pq}\right))}\hfill \\ & & h\left(r_{pq}\right)-h_{\mathrm{interpolate}}\left(r_{pq}\right)=\sum _{\alpha ,\beta ,\gamma \in \{0,1\}}{w}_{\alpha \beta \gamma }\left(h\left(r_{pq}\right)-h\left(r_{pq}^{\alpha \beta \gamma }\right)\right),\hfill \end{array}$$

where $r_{pq}^{\alpha \beta \gamma }$ is the distance between center of particle q and corner αβγ of the cell containing the point P.

$$\begin{array}{ccc}& & h\left(r_{pq}\right)-h\left(r_{pq}^{\alpha \beta \gamma }\right)\le \frac{|r_{pq}-r_{pq}^{\alpha \beta \gamma }|}{R_{\max }-R_{\min }}\le \frac{\sqrt{3}g}{R_{\max }-R_{\min }},\mathrm{so},\hfill \\ & & \times h\left(r_{pq}\right)-h_{\mathrm{interpolate}}\left(r_{pq}\right)\le \frac{\sqrt{3}g}{R_{\max }-R_{\min }}.\hfill \end{array}$$

Therefore $\Delta {\Phi }_j^{\left(p\right)}\le {\max }_{k\in \{1,...,22\}}\left\{\right|w_{kj}\left|\right\}\times {\eta }_2\times \frac{\sqrt{3}g}{R_{\max }-R_{\min }}$ where η₂ is the maximum number of particles of the receptor with centers in the region spawned by the union of spheres of radii R_max centered at corners of a grid cell.

$${\displaystyle {\eta }_2\le N_R,\mathrm{so},\Delta {\Phi }_j^p\le \underset{k\in \{1,...,22\}}{\max }\left\{\right|w_{kj}\left|\right\}\times N_R\times \frac{\sqrt{3}g}{R_{\max }-R_{\min }};}$$

therefore

$$\begin{array}{ccc}& & |E^{particle̱pai{r}_j}\left(\tau \right)-E_{Grid}^{particle̱pai{r}_j}\left(\tau \right)|\le N_L^{\left(j\right)}\hfill \\ & & {\displaystyle \times \underset{k\in \{1,...,22\}}{\max }\left\{\right|w_{kj}\left|\right\}\times N_R\times \frac{\sqrt{3}g}{R_{\max }-R_{\min }}}\hfill \end{array}$$

and

$$\begin{array}{ccc}& & |E^{particle̱pair}\left(\tau \right)-E_{Grid}^{particle̱pair}\left(\tau \right)|\le \frac{\sqrt{3}g}{R_{\max }-R_{\min }}\hfill \\ & & {\displaystyle \times N_L\times \underset{k\in \{1,...,22\}}{\max }\left\{\right|w_{kj}\left|\right\}\times N_R}\hfill \end{array}$$

$$\begin{array}{ccc}& & Term1.|E^{vdw}\left({\tau }^{*}\right)-E^{vdw}\left(\tau \right)|\le \max \{0.5,|w_{vdw̱repul}\left|\right\}\hfill \\ & & {\displaystyle \times \underset{i,j}{\max }\left[\frac{4\sqrt{{\varepsilon }_i{\varepsilon }_j}{\sigma }_j^{2.5}}{3.2^{3.5}}\right]\times N_L^{atom}\times N_R^{atom}\times d}\hfill \end{array}$$

$$\begin{array}{ccc}& & Term3.\left|E^{vdw}\left(\tau \right)-E_{Grid}^{vdw}\left(\tau \right)\right|\le \max \{0.5,|w_{vdw̱repul}\left|\right\}\hfill \\ & & {\displaystyle \times \underset{i,j}{\max }\left[\frac{4\sqrt{{\varepsilon }_i{\varepsilon }_j}{\sigma }_j^{2.5}}{3.2^{3.5}}\right]\times N_L^{atom}\times N_R^{atom}\times \sqrt{3}g}\hfill \end{array}$$

Hence the theorem.

APPENDIX B: FAST COMPUTATION OF RMSD IN RIGID BODY DOCKING

We provide a constant-time algorithm to calculate rms between a pair of docked structures arising in rigid body docking. Together with DOCK/PIE this completes the description of the procedure for efficient generation of the top Λ violated constraints in step 8 of the learning algorithm.

Preprocess

1: Input: Sets of points $X_R=\{{\vec{r}}_1,{\vec{r}}_2,...,{\vec{r}}_m\},X_L=\{{\vec{l}}_1,{\vec{l}}_2,...,{\vec{l}}_n\}$ representing the receptor and ligand in the native structure.

2: Center the point sets,

$$〈r〉=\frac{{\sum }_{i=1}^n{\vec{r}}_i}{m},〈l〉=\frac{{\sum }_{i=1}^m\vec{l}}{n},c=\frac{m〈r〉+n〈l〉}{m+n}{\vec{r}}_i={\vec{r}}_i-c$$

and ${\vec{l}}_i={\vec{l}}_i-c$, recalculate $〈r〉=\frac{{\sum }_{i=1}^n{\vec{r}}_i}{m}$ and $〈l〉=\frac{{\sum }_{i=1}^m\vec{l}}{n}$

3: Compute

$$A=\left\{\begin{array}{ccc}\hfill a_{xx}& \hfill a_{xy}& \hfill a_{xz}\\ \hfill a_{yx}& \hfill a_{yy}& \hfill a_{yz}\\ \hfill a_{zx}& \hfill a_{zy}& \hfill a_{zz}\end{array}\right\}$$

where

$$a_{\alpha \beta }=\sum _{i=1}^n{r}_{i\alpha }\times r_{i\beta }$$

and

$$B=\left\{\begin{array}{ccc}\hfill b_{xx}& \hfill b_{xy}& \hfill b_{xz}\\ \hfill b_{yx}& \hfill b_{yy}& \hfill b_{yz}\\ \hfill b_{zx}& \hfill b_{zy}& \hfill b_{zz}\end{array}\right\}$$

where

$$b_{\alpha \beta }=\sum _{i=1}^m{l}_{i\alpha }\times l_{i\beta }$$

RMSD calculation

1: Input: Rigid body transformation τ = (t, u), to compute RMSD((X_R, X_L), (X_R, τ(X_L)))

2: Compute

$$\Re =\left\{\begin{array}{ccc}\hfill {\rho }_{xx}& \hfill {\rho }_{xy}& \hfill {\rho }_{xz}\\ \hfill {\rho }_{yx}& \hfill {\rho }_{yy}& \hfill {\rho }_{yz}\\ \hfill {\rho }_{zx}& \hfill {\rho }_{zy}& \hfill {\rho }_{zz}\end{array}\right\}$$

where

$$\begin{array}{ccc}\hfill {\rho }_{\alpha \beta }& =& \frac{a_{\alpha \beta }+{\sum }_{i=1}^n{\left(\tau \left(l_i\right)\right)}_{\alpha }\times l_{i\beta }}{m+n}\hfill \\ & =& \frac{a_{\alpha \beta }+{\sum }_{i=1}^n(u_{\alpha x}{l}_{ix}+u_{\alpha y}{l}_{iy}+u_{\alpha z}{l}_{iz}+t_{\alpha })\times l_{i\beta }}{m+n}\hfill \\ & =& \frac{a_{\alpha \beta }+u_{\alpha x}{b}_{x\beta }+u_{\alpha y}{b}_{y\beta }+u_{\alpha z}{b}_{z\beta }+t_{\alpha }\times {〈l〉}_{\beta }}{m+n}\hfill \end{array}$$

3: Calculate rmsd from eigen-values of ℜ^Tℜ

Claim. LetN_R, N_Lbe the number of points in the receptor and ligand. The algorithm RMSD_RIGID_DOCK takesO(N_R + N_L + M) time to processMtransformations.

The straight forward approach of computing RMSD between the model and the native by explicitly listing the points of the model would involve Θ((m + n)M) operations. This procedure is also applicable to cluster solutions according the I-RMSD, all pairwise distances between M transformations are calculated in O((m + n)M + M²) (the straight forward procedure would involve Θ((m + n)M²) operations).

APPENDIX C: QP SOLVER

OOQP (Ref. ⁴³) provides open source framework with tools for solving general quadratic programs and quadratic programs arising from binary classification problems. We follow the framework outlined in OOQP, use the parallel routines reported in an earlier work (Wagner et al.²⁰), and develop a primal-dual interior point algorithm for solving the QP arising in the learning algorithm. Predictor-corrector based interior point algorithms iteratively approach the optimal solution by alternatively reducing the duality gap and maintaining centrality.

We develop two algorithms for quadratic programming. The first one follows the infeasible starting point algorithm introduced by Potra.⁵⁴ The solution traverses a path guided by the Karush-Kuhn-Tucker (KKT) conditions. KKT conditions are a generalization of the method of Lagrange multipliers for solution of systems with inequality constraints. After each update, the new point is closer to satisfying feasibility and the KKT conditions compared to the starting point. The second algorithm follows Gondzio's approach.⁵⁵

Primal.

$(w,\xi )={\mathrm{argmin}}_{w,\xi }\frac{1}{2}{\left|\right|w\left|\right|}^2+\frac{C}{n}{\sum }_{i,k}{\xi }_{ik}$ subject to ξ_ik ⩾ 0 and ${\bigcup }_{\beta =0}^{\alpha }\left\{\forall {\tau }_i^{\left(j\right)}\in S_i:w^T\left(P_{{\tau }_i}-P_{{\tau }_i^{\left(j\right)}}\right)\ge \left(1-\frac{{\xi }_{ik}}{\Delta ({\tau }_i,{\tau }_i^{\left(j\right)})}\right)\right\}$, rewritten as Mw + Nξ ⩾ e where ${\mathrm{N}}_{j,k}=\{\begin{array}{ccc}\frac{1}{\Delta ({\tau }_i,{\tau }_i^{\left(j\right)})}& if& k=j\left(i\right)\\ 0& else& \end{array}$ (transformation ${\tau }_i^{\left(j\right)}$ belongs to cluster k)

Primal-dual.

$\frac{1}{2}{\left|\right|w\left|\right|}^2+\frac{C}{n}{e}^T\xi -{\upsilon }^T(Mw+\mathrm{N}\xi -s-e)-t^T\xi$ subject to ξ ⩾ 0, υ ⩾ 0, s ⩾ 0, t ⩾ 0

KKT conditions.

w − M^Tυ = 0,Mw + Nξ − s − e = 0,$\frac{C}{n}e-\mathrm{N}\upsilon -t=0$,VSe = 0 and TΞe = 0. Where, V is a diagonal matrix with V[i, i] = v_i; S, T, Ξ are similar diagonal matrices defined by s, t, ξ.

The system of equations to be solved for the update at each iteration is

$$\left[\begin{array}{ccccc}\hfill I& \hfill -M^T& \hfill 0& 0& 0\\ \hfill M& \hfill 0& \hfill \mathrm{N}& -I& 0\\ \hfill 0& \hfill -N& \hfill 0& 0& -I\\ \hfill 0& \hfill S& \hfill 0& V& 0\\ \hfill 0& \hfill 0& \hfill T& 0& \Xi \end{array}\right]\left[\begin{array}{c}\Delta w\\ \Delta \upsilon \\ \Delta \xi \\ \Delta s\\ \Delta t\end{array}\right]=\left[\begin{array}{c}-r_w\\ -r_M\\ -r_C\\ -r_{SV}\\ -r_{T\Xi }\end{array}\right]$$

Which reduces after block eliminations to,

$$\begin{array}{ccc}\hfill (I+M^{T}DM)\Delta w& =& -r_w+M^{T}D(-r_M-V^{-1}{r}_{SV}\hfill \\ & & +\mathrm{N}{T}^{-1}{r}_{T\Xi }+\mathrm{N}{T}^{-1}\Xi r_C)\hfill \end{array}$$

where

$$D={(V^{-1}S+\mathrm{N}{T}^{-1}\Xi {\mathrm{N}}^T)}^{-1}.$$

The computationally intensive task is to form and compute the Cholesky factorization of I + M^TDM quickly so that the linear system arising in each iteration of the interior point algorithm can be solved efficiently. We reuse the procedure described in an earlier work²⁰ (after minor extensions to handle clustering) for the calculation of I + M^TDM in a completely data parallel fashion. We modified the SVM module in OOQP to parallelized combined weighted slack 1-class SVM to handle our formulation.