Mechanism-Based Pharmacokinetic–Pharmacodynamic Modeling of the Dopamine D₂ Receptor Occupancy of Olanzapine in Rats

Abstract

Purpose

A mechanism-based PK-PD model was developed to predict the time course of dopamine D₂ receptor occupancy (D₂RO) in rat striatum following administration of olanzapine, an atypical antipsychotic drug.

Methods

A population approach was utilized to quantify both the pharmacokinetics and pharmacodynamics of olanzapine in rats using the exposure (plasma and brain concentration) and D₂RO profile obtained experimentally at various doses (0.01–40 mg/kg) administered by different routes. A two-compartment pharmacokinetic model was used to describe the plasma pharmacokinetic profile. A hybrid physiology- and mechanism-based model was developed to characterize the D₂ receptor binding in the striatum and was fitted sequentially to the data. The parameters were estimated using nonlinear mixed-effects modeling .

Results

Plasma, brain concentration profiles and time course of D₂RO were well described by the model; validity of the proposed model is supported by good agreement between estimated association and dissociation rate constants and in vitro values from literature.

Conclusion

This model includes both receptor binding kinetics and pharmacokinetics as the basis for the prediction of the D₂RO in rats. Moreover, this modeling framework can be applied to scale the in vitro and preclinical information to clinical receptor occupancy.

INTRODUCTION

Schizophrenia is a life-long and often devastating psychiatric disorder which often begins in late adolescence or early adulthood (1). Although the fundamental pathology of schizophrenia remain ambiguous, it has been hypothesized that an excessive level of striatal dopamine, which can be caused by several factors, is responsible for development of psychotic symptoms (2). This is also supported by the elevation of dopamine release in naïve patients following an acute amphetamine challenge (3). Preclinical and clinical studies suggest that blockade of dopamine-2 receptors (D₂ receptors) is the key pharmacological component to the antipsychotic efficacy of both the typical and the newer atypical antipsychotics (4,5). However, the degree of D₂ receptor antagonism required for an antipsychotic efficacy is still unclear. Some antipsychotics, for example clozapine, show antipsychotic activity at a lower receptor blockade (20―67%) than other antipsychotics (6). Aripiprazole, an atypical antipsychotic, has been shown to be a partial agonist on the D₂ receptors (7). Kapur et al. (8) reported that the rate of dissociation of antipsychotics from the D₂ receptors drives their efficacy and safety. These studies show that little is known about the degree of target occupancy and the role of the dynamic interactions between the drugs and the receptor in schizophrenia treatment. Moreover, the importance and influence of the distribution to the target site on the receptor binding is not yet elucidated, and it is known that some antipsychotics, e.g. risperidone and its active metabolite paliperidone, are P-gp substrates and that therefore their transport into brain involves a complex process of active and passive transport (9). In addition, one of the other challenges in schizophrenia drug discovery and development is scaling and extrapolating the dopamine-2 receptor occupancy (D₂RO) obtained in preclinical studies to the clinical situation in a quantitative manner.

Hence, there is a need for a tool in the drug discovery process to characterize both penetration of the candidate compound into the brain (target site distribution) and the degree of D₂RO, which could also support the scaling of D₂RO from rat to human. It is essential to have sufficient information about the cascade of processes (distribution to and in the brain, receptor occupancy as a net result of association and dissociation) to generate such a tool. In schizophrenia drug discovery research, the information available to study the drug distribution into brain and the time course of D₂RO is rather sparse. Brain concentration and D₂RO are usually measured at the terminal time point, unless a labor-intensive microdialysis technique is used. Standard radioligand binding study protocols provide limited data with respect to brain exposure and receptor binding obtained at only one time point from one animal.

Pharmacokinetic and pharmacodynamic (PK-PD) modeling tools are extensively used to characterize the process between drug administration and its effect. In the last two decades, population-based approaches have become utilized to integrate the available sparse information from different resources to study the underlying PK-PD processes. These approaches provide population mean parameter estimates and allow partition into inter-individual and intra-individual variability. Mechanism-based pharmacokinetic–pharmacodynamic models integrated with population approaches were used to characterize and predict the time course of pharmacodynamic responses in rats and human (10,11). These models parameterize biophase equilibration kinetics and receptor association-dissociation kinetics to describe the drug binding to receptors. The important feature of these mechanistic models is their ability to distinguish the system- and drug-specific parameters, which has been proven to be useful in the extrapolation of treatment effects from rat to human. Moreover, these PK-PD models, when combined with physiological parameters, have the ability to predict human PK-PD properties using prior information from in vitro and preclinical studies (12).

In the present analysis, PK-PD tools were utilized to describe the brain distribution and D₂RO of olanzapine, an atypical antipsychotic drug which is a dopamine D₂ receptor antagonist which has been proven to have antipsychotic effects in the treatment of patients with schizophrenia (13).

Hence, a mechanism-based population PK-PD model was developed to describe the time course of D₂RO of olanzapine, with emphasis on the modelling of receptor association/dissociation kinetics. This model can be utilized in the future to translate the in vitro and preclinical information to D₂RO in humans.

METHODS

Data Management

This work was performed within the framework of the Dutch Top Institute Pharma project: mechanism-based population PK-PD modeling (http://www.tipharma.com). This mechanism-based population PK-PD modeling platform involves leading pharmaceutical companies worldwide and academic institutes from The Netherlands. The data used for this analysis were contributed by the pharmaceutical companies who are the members of this mechanism-based population PK-PD platform. The data was anonimized, except the modeler was aware that the data were sourced from three industrial partners: Janssen Research and Development, Belgium, Merck Sharp and Dohme Limited—The Netherlands, and Pfizer Global Research and Development—USA. The dataset included plasma and brain exposure data of olanzapine and its D₂RO measured at different time intervals from 12 different studies, which consisted of 283 rats of either the Wistar or Sprague-Dawley strain. The experimental procedures for the plasma sample collection, brain dissection, tissue homogenization, and D₂RO measurements were similar across the different study sites, and these procedures were published elsewhere (4,14). Exposure and occupancy information was obtained following the administration of olanzapine by either intraperitoneal, subcutaneous or intravenous route in a wide range of single doses (0.01 to 40 mg/kg body weight). More details about the studies and data are depicted in Table I.

Table I.

Brief Description of the Studies That Were Used in This Analysis

Study number	Dose in mg/kg (min–max)	Number of animals	Type of observations	Route of administration	Observation time points (h)	Mode of D2RO measurement
1	0.03	18	PC	IP	0.25, 0.5,1,1.5,2,4	NA
2	0.3–30	15	PC, BC, RO	IP	1	In vivo binding
3	0.01–10	28	PC	IP	1	NA
4	0.01–30	32	PC	IP	1	NA
5	3	20	PC, BC, RO	IP	0.25, 0.5, 1,1.5,2	In vivo binding
6a	0.01–30	26	PC, BC, RO	IP	1	In vivo binding
6b	0.01–30	22	PC, RO	IP	1	In vivo binding
7	3	20	PC, BC, RO	SC	0.5,1,2,4,6	In vivo binding
8	0.32 & 20	30	PC, BC, RO	SC	0.5,1,2,4,8	Ex vivo binding
9	0.04–40	18	RO	SC	1	In vivo binding
10	2.5	15	RO	SC	0.25,0.5,2,4, 6	In vivo binding
11	0.01–40	33	RO	SC	2	Ex vivo binding
12	2.5	3	PC	IV	0.12,0.33,1,2,4,8, 24	NA

PC plasma concentration; BC total brain concentration; RO dopamine D2 receptor occupancy; IP intraperitoneal; SC subcutaneous; IV intravenous; NA not applicable; min minimum dose used in the study; max maximum dose used in the study; In vivo binding and ex vivo binding studies were performed using [³H]raclopride and [¹²⁵I]sulpiride as the radioligand, respectively

Modeling Tools

A population-based approach was employed to utilize all the relevant information in order to obtain population parameter estimates along with both the inter-animal and residual variability. All the parameter estimations were performed with the nonlinear mixed effects modeling software NONMEM (version VI level 2.0) (15). Log-transformed plasma and brain olanzapine concentrations were used for the data analysis, and concentrations below the limit of quantification were excluded from this analysis.

The inter-animal variability on the parameters was modeled according to

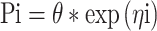in which Pi is the estimate of parameter P for the ith animal, θ the population estimate for parameter P, and exp(ηi) the inter-animal random deviation of Pi from P. The values of ηi are assumed to be normally distributed with mean zero and variance 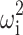. Inter-animal variability is expressed as percent coefficient of variation which is the square root of .

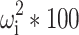The adequacy of the PK model was assessed on the basis of goodness-of-fit plots, parameter correlations, and precision in parameter estimates. An additional structural parameter or inter-animal variability (IAV) was included in the model if the resulting change in objective function value (OFV) was >6.64 (p < 0.01). Different types of residual error models (proportional, additive, combined proportional, and additive) were tested. Based on the visual inspection of the diagnostic plots, a proportional error model was proposed to describe residual error in the plasma and brain drug concentration, as ln(Yobs_ij) = ln(Ypred_ij) + ε _ij in which Yobs_ij is the jth observed concentration in the ith animal, Ypred_ij is the predicted concentration. An additive term was used to account for the unexplained variability in D₂RO as Yobs_ij = Ypred_ij + ε _ij, in which Yobs_ij is the jth observed D₂RO in the ith animal, Ypred_ij is the predicted D₂RO. The residual random variable (ε _ij) was assumed to be normally distributed with mean zero and variance σ ². The residual error describes the error terms which remain unexplained and refers to, for example, dosing inaccuracies, assay and experimental error (e.g., error in recording sampling times) and structural model misspecifications.

During the analysis, Census (16) integrated with Xpose (R package) (17) was used for NONMEM run management and also for making different types of diagnostic plots, which were used in the model selection process.

Population Pharmacokinetic Analysis

To determine the basic structural pharmacokinetic model for olanzapine, one- and two-compartment models were tested. Population pharmacokinetic values of olanzapine were estimated using the first-order conditional estimation method (FOCE). This model was implemented by user-defined differential equations using the ADVAN 9 subroutine in NONMEM. Using this routine, the parameter’s systemic clearance (CL in l/h/kg), volume of the central compartment (V₁ in l/kg), volume of the peripheral compartment (V₂ in l/kg), intercompartmental clearance (Q in l/h/kg), and bioavailability for intraperitoneal (F_IP) and subcutaneous (F_SC) routes of administration were estimated.

Hybrid Physiology-Based PK-PD Model

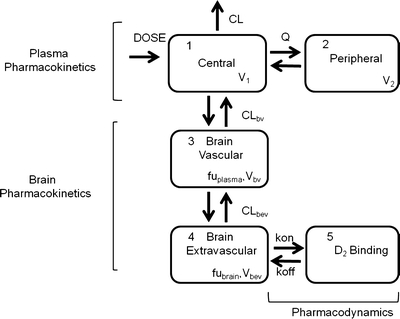
A mechanism- and physiology-based PK-PD model was developed and evaluated for its usefulness in describing the time course of brain concentration and D₂RO. A four-compartment hybrid physiology-based pharmacokinetic and pharmacodynamic (PBPKPD) model was sequentially linked to the plasma population pharmacokinetic model to describe the concentration-time profile of olanzapine in brain and the binding to D₂-receptors in striatum, which consists of brain-vascular, brain-extravascular, striatum-free, and striatum-bound compartments (Fig. 1). Following administration, olanzapine is transported from the plasma compartment to the brain-vascular compartment; this process is assumed to be influenced only by the cerebral blood flow. Only the unbound olanzapine in this intravascular compartment crosses the blood–brain barrier (BBB) and is transported into the brain-extravascular compartment, which is governed by the brain-extravascular clearance (CL_bev). Furthermore, olanzapine is transported from the brain-extravascular compartment to the striatum compartment, where it can reversibly bind to the dopamine receptor complex (Fig. 1). The receptor association and dissociation processes were described using kon as the receptor association rate constant (nM⁻¹h⁻¹), koff as the receptor dissociation rate constant (h⁻¹), and the Dopamine D₂ receptor density (B_max) in rat striatum. The volumes of brain-vascular (V_bv) and brain-extravascular (V_bev) compartments were assumed to be equal to the physiological values in the rat: 0.00024 l/kg and 0.00656 l/kg, respectively (18). The clearance from the brain-vascular compartment (CL_bv) was assumed to be equal to the cerebral blood flow in rats, which is 0.312 l/h/kg (18). The brain-extravascular and striatum-free compartments were assumed to be equilibrated rapidly. This was achieved by fixing the clearance between brain-extravascular and striatum-free compartments (CL_st) to a high value. The unbound fraction of olanzapine in plasma (fu_plasma) and brain (fu_brain) was fixed to the values obtained from literature: 0.23 and 0.034, respectively (19). The brain-extravascular clearance (CL_bev), the binding parameters (kd and koff), and the B_max were estimated by fitting the PBPKPD model to the experimentally obtained brain concentrations and dopamine receptor occupancy data. Kd (an equilibrium constant) and koff were estimated from the model, and kon was derived as kon = koff/Kd. During this analysis, the plasma pharmacokinetic parameters were fixed to the parameter estimates obtained from the population pharmacokinetic analysis. This model was implemented through user-defined differential equations in the ADVAN 9 subroutine in NONMEM, and differential equations related to this processes are provided in Appendix 1.

Fig. 1.

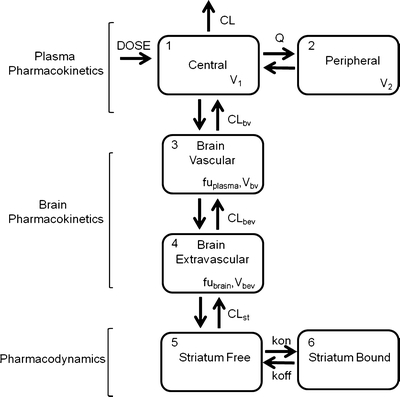
A schematic representation of the PBPKPD model. The model incorporates different processes to explain the time course of D₂RO. The plasma pharmacokinetics describe the disposition of the drug in the plasma, the brain pharmacokinetics describe the processes involved in the transport of drug from plasma to brain, and the striatum compartment explains the drug binding to receptors through the binding constants.

This model was based on the following assumptions: (1) Cerebrospinal fluid flow does not significantly influence the brain disposition, and (2) plasma pharmacokinetics are not affected by brain disposition. The latter assumption allows the plasma concentration-time profile to be described by a conventional two-compartment model, independent of the brain distribution. In addition, it allows a separate analysis of the plasma concentration data to the population pharmacokinetic model.

During model development, it was observed that the model was not able to estimate B_max, so this parameter was assumed to be 48 nM, calculated as the maximum concentration of olanzapine bound to this receptor (20).

Due to the scarcity of data, no inter-animal variability was assumed in the PBPKPD model. In vivo and ex vivo binding studies were performed to measure the D₂RO in rats, so it was also attempted to estimate separate binding constants for each in vivo and ex vivo studies. Moreover, an active efflux parameter was added in the model to check for the influence of active drug transport across the BBB.

Sensitivity Analysis

The objective of this analysis was to develop a stable mechanism- and physiology-based PK-PD model that could be supported by the data used in the analysis and with a minimum number of parameters to be estimated. Hence, it was decided to perform a sensitivity analysis so that the model could be reduced by removing parameters, which have little or no influence on the model outputs. Hence, the pharmacodynamic parameters Kd (derived as koff/kon), koff, kon, and B_max were perturbed to determine their influence on the D₂RO. A series of simulations were conducted with differing parameter values, which were varied 5- and 10-fold on the lower and higher side of the base value (model parameter estimate). Each simulation was conducted by altering one parameter at a time and fixing all remaining parameter values. The outputs considered for the parameter sensitivity analysis were the simulated D₂RO-time profiles with respect to the altered pharmacodynamic parameter. All simulations were performed using R (version 2.10). Primarily, 3 mg/kg dose was selected for this analysis, as this is the intermediate dose in the available dataset. Subsequently, lower and higher dose levels to 3 mg/kg dose were also included in this analysis. D₂RO profiles were generated over a 24-hour time interval.

Model Evaluation

The bootstrap resampling technique and stochastic simulation and estimation (SSE) were used as model evaluation tools to check the stability and adequacy of the model, respectively. In the bootstrap resampling technique, bootstrap replicates were generated by sampling randomly from the original data set with replacement. One thousand replicate data sets were obtained using the bootstrap option in the software package Perl Speaks NONMEM (PsN, version 3.2.4) (21). This resampling was stratified based on the three dose levels (low, medium, and high). Low, medium, and high dose levels included the doses ranges from 0.01 to 0.63 mg/kg, 1 to 3 mg/kg, and 10 to 40 mg/kg, respectively. Parameter estimates for each of the re-sampled data sets were obtained by fitting the final model using NONMEM. Finally, median and 90% confidence intervals of all model parameters were calculated, and the medians of the bootstrap estimates were compared with parameter values obtained from the original dataset. Furthermore, a simulation-based evaluation was performed using the SSE option as implemented in PsN. Briefly, the final PBPKPD model was used to both stimulate 1,000 datasets and subsequently estimate PK-PD parameters from these simulated datasets. The accuracy in parameter estimation was assessed from the bias as calculated below.

For instance, bias is calculated for koff as

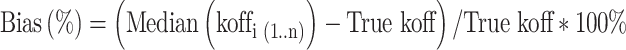where koff_i is the population mean koff for the ith simulated dataset, n is the number of simulations, True koff is the value which was used for the simulation.

Predictive Check for D₂RO

A predictive check was performed to determine whether the final PBPKPD model provides an adequate description of D₂RO. One thousand datasets were simulated from the final PBPKPD parameter estimates to compare the distribution of simulated D₂RO with the observed D₂RO. The median, lower (5%), and upper (95%) quantiles of the simulated D₂RO were calculated for a time period between 0 and 360 min after olanzapine administration.

Application of the Rat PBPKPD Model

Rat PBPKPD model structure was integrated with available population pharmacokinetic parameters from human plasma concentration-time data, in vitro binding constants, fraction unbound in human plasma (22), and human brain physiological information (23) to predict the human D₂RO of olanzapine. All the parameters which were used for the simulations are tabulated in Table II. Distribution of olanzapine across the BBB surrogated with permeability surface area product (PS) was calculated as a product of in vitro apparent membrane permeability (Papp, which is 15.7 *10⁻⁶ cm/s) (19) value and human brain endothelial surface area (20 m²) (24). One thousand human D₂RO-time curves were simulated for 10 mg/day and 20 mg/day dose levels, administered orally. Inter-individual variability (IIV) in the plasma population pharmacokinetic parameters was accounted in these simulations. The observed human D₂RO was taken from the published literature domain (25,26). These observed values were measured at steady-state conditions after varying treatment duration across different studies. Hence, the simulations were made at steady-state conditions, which were achieved within 2 weeks of drug treatment. Berkeley Madonna (version 8.3.18, Berkeley Madonna Inc, University of California, USA) was used in this simulation study. The predictive power of this translational approach was determined by comparing the simulations with observed human D₂RO.

Table II.

Population Pharmacokinetic Parameters, Passive Membrane Permeability, Physiological Parameters and In Vitro Binding Values Used for the Simulations

Parameter	Values used in human D2RO Simulations	Source
CL/F (l/h)	19.5 (58)a	(25)
V/F (l)	1,150 (75)a	(25)
Ka (h−1)	0.600 (32)a	(25)
koff (h−1)	2.34	(37)
Kd (nM)	5.10b	(38)
fraction unbound in plasma	0.0700	(22)
fraction unbound in brain	0.034	(19)
Human cerebral blood flow (l/h)	36.0	(24)
Human brain extravascular volume (l)	1.4	(23)
Human brain vascular volume (l)	0.150	(23)
CLbev (l/h)	11.3	–c

CL/F clearance; Ka absorption rate constant; V/F central volume of distribution

^aPopulation mean (inter-individual variability as %CV)

^b In vitro Ki value assumed as Kd

^cCalculated as Papp* human brain endothelial surface area

RESULTS

Population Plasma Pharmacokinetics

A two-compartment model best described the plasma pharmacokinetics of olanzapine. The appropriateness of the two-compartment over the one-compartment model was based on the visual comparison of goodness-of-fit (GOF) plots and the lower objective function. Population pharmacokinetic parameter estimates are given in Table III. The observed and population-predicted concentration of olanzapine is depicted in Fig. 2. All structural pharmacokinetic parameters were estimated precisely with acceptable relative standard error (RSE) which varied between 9% and 30%. The absorption rate constant was not estimable due to lack of information on early time points for both the intraperitoneal and the subcutaneous routes of administration, and hence it was assumed that olanzapine was administered directly into the central compartment. A relative bioavailability was estimated for the intraperitoneal route of administration. The bioavailability for the subcutaneous route of administration was estimated to be close to 1. Indeed, fixing this parameter improved the model convergence with a successful covariance step, so the bioavailability for the subcutaneous route of administration was assumed to be complete for further modeling. Estimation of inter-animal variability was possible only for CL and F_IP and was estimated as 56% and 87%, respectively. No trend or pattern was observed in the conditional weighted residual diagnostics versus time and in the population predictions versus time, which demonstrates that this model adequately describes the time course of olanzapine plasma concentration (Figs. 2 and 3).

Table III.

Population Pharmacokinetic Parameter Estimates from the Original Data Set and Resulting from 1,000 Bootstrap Replicates for V1, CL, V2, Q with 90% Confidence Interval (CI)

Parameter	Original dataset (%RSE)	Median of 1,000 bootstrap replicates	90% CI from Non-parametric bootstrap
V1(l/kg)	4.22 (9)	4.17	3.61–4.93
CL (l/h/kg)	3.21 (9)	3.12	2.74–3.65
V2 (l/kg)	2.23 (14)	2.23	1.87–2.87
Q (l/h/kg)	1.70 (30)	1.67	1.19–2.92
FIP	0.636 (12)	0.633	0.538–0.771
Inter-animal variability
IAV-CL (%CV)	56 (19)	55	47–66
IAV-F1 (%CV)	87 (18)	87	73–98
Residual variability
Proportional error	0.141 (7)	0.130	0.073–0.159

%RSE = Relative standard error as obtained from the COVARIANCE option of NONMEM

IAV = Inter-animal variability calculated as 100×√ω ², where ω ² is the variance term

Fig. 2.

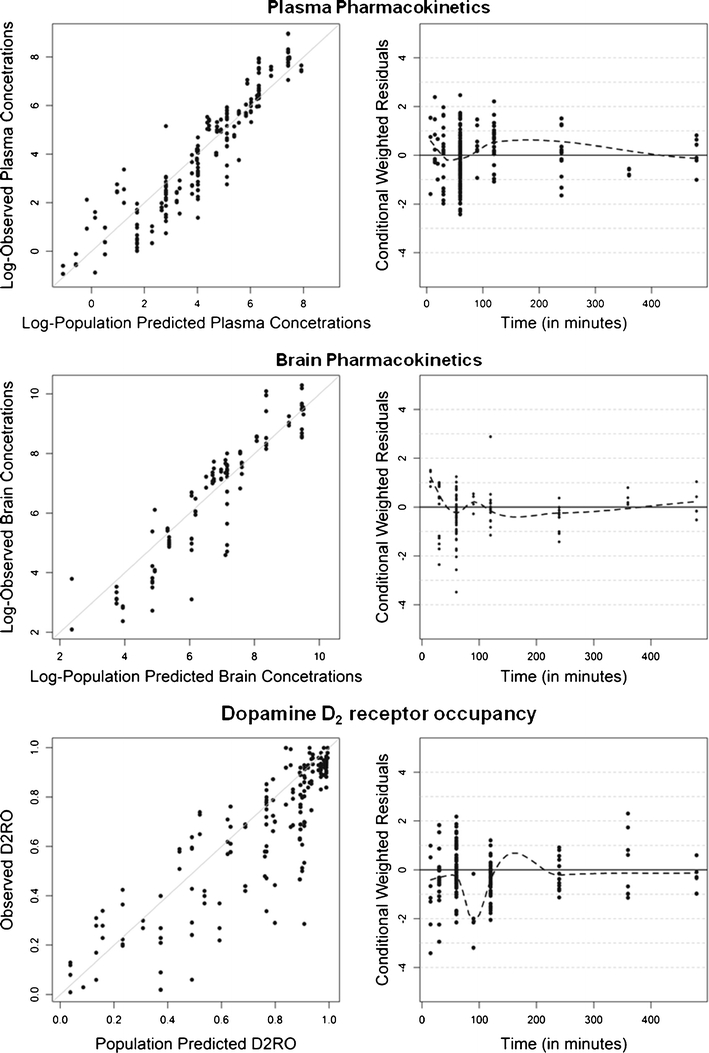
Goodness-of-fit plots for the final PBPKPD model. Depicted are scatter plots of the observed olanzapine concentrations or D₂RO vs. population predictions and scatter plots of the population conditional weighted residuals vs. time.

Fig. 3.

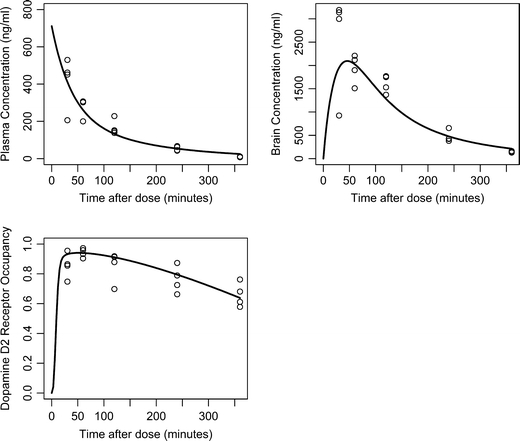
Observed and predicted olanzapine concentrations and D₂RO vs. time. Open circles represent the observed olanzapine concentrations or D₂RO; the solid line represent the population predictions for 3 mg/kg dose of olanzapine administered subcutaneously.

Hybrid Physiology-Based PK-PD Model

Initially, a PBPKPD model was developed, which included the effect of binding to the receptor on the free drug concentrations at the receptor binding sites (Fig. 1). Parameter estimates that were obtained using this model are tabulated (Table IV). Later, a sensitivity analysis was performed to identify whether the model could be reduced by removing any parameters that were not influencing the model output(s). The simulated D₂RO profiles (model outcome) following variations in Kd, kon, koff, and B_max for a dose of 3 mg/kg are shown in Fig. 4. This sensitivity analysis clearly showed that B_max did not influence the model output when perturbed to different values, whereas perturbations of the values Kd, kon, and koff all affected the D₂RO to some extent. This sensitivity analysis was also performed using lower and higher dose levels, which resulted in similar observations to those at the 3 mg/kg dose level. As little or no influence of the parameter B_max was shown at any of the doses, a reduced model with an alternative assumption was proposed as described in Fig. 5. Briefly, this model assumes that binding to dopamine receptors does not affect the brain concentration significantly and thereby allows for dropping the striatum-free compartment from the full model. In other words, it is assumed that a relatively low fraction of the drug in the brain extra-vascular compartment binds to the dopamine receptor. Further, this reduced model was subjected to model evaluation. The parameter estimates obtained from this model were close to the earlier model with B_max (Table IV), indicating that the reduced model is equivalent to the full model. There were no significant parameter correlations (R > 0.95) reported in the NONMEM output between any of the PK-PD model parameters, indicating the uniqueness of the parameter estimates obtained from the reduced model. Information about the brain concentration levels was limited to one observation per animal, which leaves no opportunity to estimate both inter- and intra-individual variability for brain clearance. No trend or pattern was observed in the conditional weighted residual diagnostics versus time and in the population predictions versus time, which demonstrates that this model adequately describes the time course of olanzapine brain concentration and D₂RO (Figs. 2 and 3). Different sources of the data and data scarcity explain the high residual variability of the brain concentrations.

Table IV.

Population Brain Pharmacokinetic and Pharmacodynamic Parameter Estimates from Full and Reduced PBPKPD Model

Parameter	Full model (FM)	Reduced model (RM)	% difference
	Population mean (%RSE)	Population mean (%RSE)
CLbev(l/h/kg)	0.433 (16)	0.394 (15)	−10
Kd (nM)	14.6 (7)	14.7 (8)	<1
koff (h−1)	3.04 (24)	2.62 (24)	−16
kon (nM−1 h−1)a	0.208	0.178	−17
Proportional error (BC)	0.479 (6)	0.479 (6)	<1
Additive error (D2RO)	0.136 (5)	0.136 (5)	<1

%RSE = Relative standard error as obtained from the COVARIANCE option in NONMEM

% difference calculated as 100-(Parameter estimate-RM*100/Parameter estimate-FM)

BC brain concentration; D ₂ RO dopamine D₂ receptor occupancy

^akon derived as koff/Kd

Fig. 4.

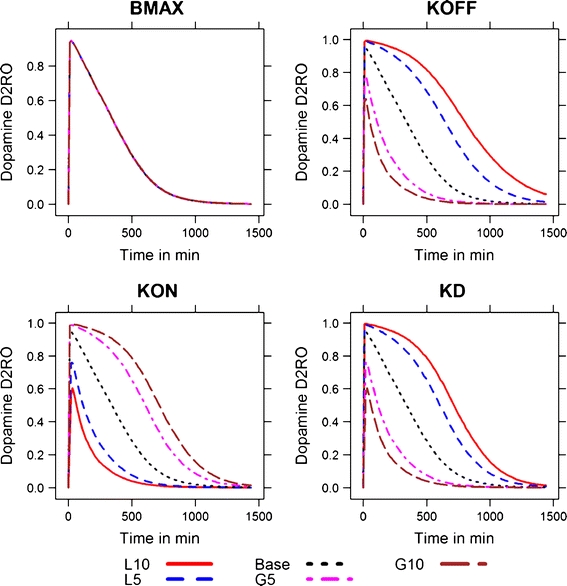
Simulated drug concentration-time profiles for perturbations in different pharmacodynamic parameters at the 3 mg/kg dose level. The values were perturbed 5- and 10-fold at the higher and lower end of the base value. The fold variations are denoted by numerals corresponding to the extent of variation. The perturbations at the lower end of the base parameter values are denoted by the letter L and at the higher end by the letter G. For example, L10 indicates a value 10-fold lower than the base value of the parameter. This nomenclature is adapted from reference 27.

Fig. 5.

Simulated drug concentration-time profiles for perturbations in different pharmacodynamic parameters at the 3 mg/kg dose level. The values were perturbed 5- and 10-fold at the higher and lower end of the base value. The fold variations are denoted by numerals corresponding to the extent of variation. The perturbations at the lower end of the base parameter values are denoted by the letter L and at the higher end by the letter G. For example, L10 indicates a value 10-fold lower than the base value of the parameter. This nomenclature is adapted from reference 43.

Model Evaluation

Population Plasma Pharmacokinetic Model

In the bootstrap analysis of the population plasma pharmacokinetic model, all the replicates were minimized successfully. The population estimates as well as the residual error of this model are in close agreement with the median values as depicted in Table III. Difference in the estimated parameters from the final model between the original observed plasma data and the combined bootstrap replicates was <3% for all the parameter estimates.

Hybrid Physiology-Based PK-PD Model

In the bootstrap analysis, 960 out of 1,000 bootstrap replicates minimized successfully. The population estimates as well as the residual error terms of the final model are in close agreement with the median values of the 960 successful bootstrap replicates. The median bootstrap estimates and 90% non-parametric bootstrap confidence intervals are depicted in Table V. In Fig. 6, the distribution of the PK-PD parameter estimates from the 1,000 simulated datasets is displayed as a histogram. Nine hundred fifty-five out of 1,000 simulated datasets minimized successfully. The bias for CL_bev, Kd, koff was 2.2, 0.7, and 0.5%, respectively. The bias for the residual variability on brain concentration and D₂RO was −0.2 and −0.7%, respectively.

Table V.

Population Pharmacokinetic Parameters, Passive Membrane Permeability, Physiological Parameters and In Vitro Binding Values Used for the Simulations

Parameter	Values used in human D2RO Simulations	Source
CL/F (l/h)	19.5 (58)a	(25)
V/F (l)	1,150 (75)a	(25)
Ka (h−1)	0.600 (33)a	(25)
koff (h−1)	2.34	(37)
Kd (nM)	5.10b	(38)
fraction unbound in plasma	0.0700	(22)
fraction unbound in brain	0.034	(19)
Human cerebral blood flow (l/h)	36.0	(24)
Human brain extravascular volume (l)	1.4	(23)
Human brain vascular volume (l)	0.150	(23)
CLbev (l/h)	11.3	–c

CL/F clearance; Ka absorption rate constant; V/F central volume of distribution

^aPopulation mean (Inter-Individual variability as %CV)

^b In vitro Ki value assumed as Kd

^cCalculated as Papp* human brain endothelial surface area

Fig. 6.

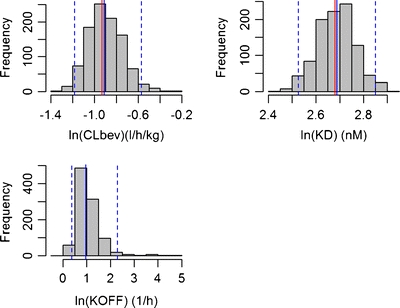
Histograms of CL_bev, Kd, and koff (in logarithmic scale) based on the 1,000 stochastic simulations and estimations. Median values are plotted with blue solid lines and overlaid with the true parameter estimates (red solid lines). The blue dotted lines represent the 25th and 975th values of 1,000 parameter estimates.

Predictive Check for D₂RO

The result of the predictive check for D₂RO is depicted in Fig. 7. More than 80% of the observed olanzapine D₂RO are within the range of the simulated upper (95%) and lower (5%) quantiles of the simulated D₂RO.

Fig. 7.

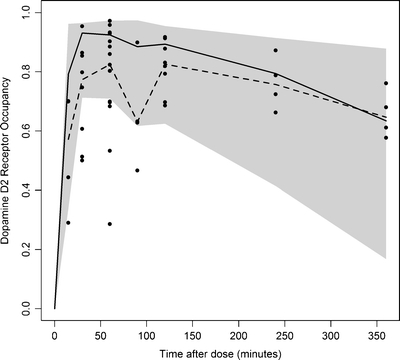
Predictive check of the PBPKPD model for D₂RO after olanzapine administration, at 3 mg/kg dose. A number of 1,000 data sets were simulated from the final PBPKPD parameter estimates. Depicted are the observed D₂RO (dots) and the shaded area represents the upper (95%) and lower (5%) quantile of the simulated D₂RO. Median of the simulated D₂RO are represented as solid line; median of the observed D₂RO are represented as dashed line.

Application of the Rat PBPKPD Model

This hybrid PBPKPD model structure, using available human pharmacokinetic model parameters, in vitro permeability, and binding data, predicted the human D₂RO for olanzapine at both 10 mg/day and 20 mg/day dose levels well. The result of these simulations is depicted in Fig. 8.

Fig. 8.

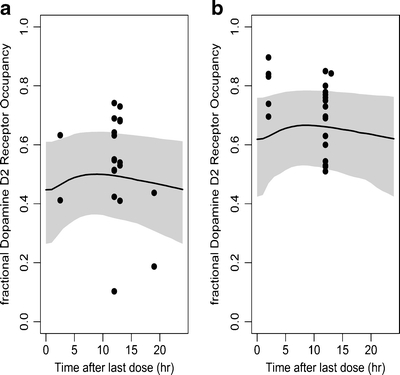
Observed and predicted steady-state D₂ receptor occupancy in humans after oral administration of 10 mg/day (a) or 20 mg/day (b) of olanzapine. Simulations were performed using the rat PBPKPD model structure integrated with in vitro apparent permeability and in vitro binding information (Table II). Depicted are the observed D₂RO (dots); shaded area represents the 95% prediction limits of the simulated D₂RO. The medians of the simulated D₂RO are represented as a solid line.

DISCUSSION

This work aimed at developing a mechanism- and physiology-based PK-PD model for olanzapine, which takes into account the barriers in drug transport to the brain and describes the association and dissociation kinetics of the drug to the D₂-receptor. The mechanistic nature and population basis of this model could provide a reliable tool for translating D₂RO between species that may support future drug discovery efforts, both specifically in the development of antipsychotics and more generally in the development of drug targeting other receptors in the brain.

A population approach is utilized here to integrate sparse data from a range of experimental sources to estimate the PK-PD parameters. Plasma pharmacokinetics were fitted well using a two-compartment classical pharmacokinetic model. There were only 3 rats with a full plasma concentration-time profile after intravenous olanzapine administration, and during the modeling exercise, it was observed that bioavailability of olanzapine administered through the subcutaneous route was close to one with low inter-animal variability. Hence, to stabilize and increase the F_IP parameter precision, it was assumed that olanzapine administered by the subcutaneous route had a bioavailability of 100%. However, high variability in F_IP was estimated, which may reflect dosing inaccuracies or a variable first-pass effect. There are some deviations in the observed and population-predicted olanzapine concentrations, which could potentially be explained by covariates. Nevertheless, a covariate analysis was not performed due to lack of information on the individual characteristics of the animals. Possible sources of this variability were differences in the analytical methodologies which were used to measure the plasma concentration. In addition, the study sites where studies were performed (three different pharmaceutical companies) could also be a source of variation. However, no covariate relations were graphically observed between different study sites and pharmacokinetic parameters. Finally, population PK model evaluation demonstrated the accuracy and precision of the developed population PK model. This population pharmacokinetic model was utilized as a driving force for the brain PBPKPD model.

Target-site distribution might be complex for drugs acting on targets in organs protected by specific barriers (e.g. the brain), so a detailed characterization of these barriers is required to be included in the brain PBPKPD for meaningful concentration and effect relationships. Drug distribution across the BBB was previously described by several pharmacokinetic models, which utilized the drug levels from extracellular fluid of brain to model the drug transport across the BBB (28–30). These models explained both the passive and active drug transport across the BBB in a quantitative manner. The objective of this study was to make a PK-PD model structure to explain the drug transport of antipsychotics across the BBB and the time course of D₂RO which later can be utilized for translating PK-PD information from rat to human. It is expected that these PK-PD models, when combined with physiological basis, have the ability to predict human PK-PD properties using prior information from in vitro and preclinical studies, so this PBPKPD model was developed on a physiology basis, including brain-vascular and brain-extravascular compartments to describe the brain pharmacokinetics and striatum compartments to explain the binding to dopamine D₂ receptors. This physiology basis is expected to enable this model structure to utilize the in vitro permeability and any efflux-related information as a surrogate to explain drug transport across the brain in humans. Additionally, the observed brain drug concentrations were obtained from the whole brain homogenates, which represent the drug in both vascular and extravascular compartments of the brain. The brain-vascular and brain-extravascular compartment structure enable this PBPKPD model to adapt this type of brain drug concentration data without any correction. This PBPKPD model adequately described both the brain concentration and D₂RO. The brain pharmacokinetic parameter CL_bev describes the passive transport of olanzapine across the blood-brain barrier. It has been reported that olanzapine is a substrate for the BBB drug transporter P-glycoprotein (P-gp) in mice (31). Therefore, an active efflux parameter was added in the model to account for the active transport of olanzapine across the BBB. However, this additional parameter did not improve the model fit, and, consequently, this additional parameter was not retained in the final model. Moreover, there are ambiguous reports about the active transport of olanzapine across the BBB in different species from both in vivo and in vitro studies (32–34). A significant influence of lag-time between drug exposure and D₂RO is expected for antipsychotic compounds and seen in the data. This model identifies both brain distribution (transfer across BBB) and binding kinetics (kon and koff) as determinants of this time delay on effect. A simulation-based analysis also showed that both these components are essential to explain this time delay process (not shown).

The limited information on the brain concentrations (one observation per animal) did not allow separating the inter-animal and residual variability. Hence, no inter-animal variability for brain pharmacokinetics were estimated, and this resulted in a high residual variability (48%) for the brain concentrations. In addition to the possible sources that were discussed earlier, different surgical procedures, brain dissections and extraction procedures could also cause high residual variability.

The pharmacodynamic parameters were estimated by incorporating a binding model to the brain pharmacokinetic model. This modeling exercise was started with the assumption that the binding to the dopamine receptor did affect the free drug concentration in the receptor vicinity, which included the parameter for maximum binding capacity (as B_max) in the model. Later, sensitivity analysis showed that the value of the parameter B_max hardly affected the model output. This observation could be either due to the model structure or to the limited information about this parameter. Hence, in the final model it was assumed that binding to D₂ receptors did not affect the free drug concentration in the receptor vicinity. Nevertheless, this model still holds its mechanistic nature by characterizing the time course of D₂RO on the basis of receptor association and dissociation kinetics. It has been demonstrated that antipsychotics differ in their koff (dissociation) rate, which may determine the efficacy and safety of the antipsychotics (35). Hence, the current population PK-PD model for olanzapine is proposed, which allows the separate characterization of the kinetics of target site distribution and the receptor association and dissociation kinetics as determinants of the time course of the dopamine D₂RO. This model, as implemented in NONMEM, was able to estimate Kd and koff with acceptable RSE of 8 and 24%, respectively. Kd and koff were estimated using the D₂RO data from both in vivo and ex vivo binding studies. However, when it was attempted to estimate separate values of Kd and koff for in vivo and ex vivo binding studies, this resulted in imprecise koff estimates. Zasadny et al. (36) found a significant correlation in the D₂RO measured using ex vivo binding and in vivo imaging techniques in rats. Hence, it is agreeable to estimate single values of Kd and koff using the D₂RO from both ex vivo and in vivo studies. The validity of the proposed model is supported by the good agreement between the estimated pharmacodynamic parameters and the in vitro koff (2.34 h ⁻¹) and Ki (17 nM) values in rats (35,37).

The model evaluation tools indicated that some parameters (CL_bev and koff) had wide bootstrap confidence intervals. These wide bootstrap confidence intervals could be due to scattered and unbalanced information available from our dataset, which consists of D₂RO information from a wide range of doses (Table I), so the bootstrap procedure could resample unrealistic datasets with very limited information to estimate the PK-PD parameters, resulting in wide confidence intervals. However, the median bootstrap parameter estimates are close to the model parameter estimates, which indicates that this model could still be accepted with confidence. Moreover, the results of the predictive check for D₂RO showed that most of the observed D₂RO at 3 mg/kg dose levels were within the 5th and 95th percentiles of the simulated values, so this model described the observed D₂RO reasonably well. However, the median of the simulated values was not in close agreement with the median of the observed data (Fig. 6). This could be due to the limited and unbalanced amount of D₂RO observations available at each time points.

This proposed PBPKPD model is intended to be utilized in a translational framework to scale pharmacokinetic and pharmacodynamic information from rats to human, so this general translational framework was based on a mechanism-based approach which accounts for the different processes involved in the transport of drug to brain. Moreover, this mechanism- and physiology-based PK-PD model separates the drug-specific properties, which describe the interaction between the drug and the biological system (target affinity, occupancy), and system-specific properties, which describe the functioning of the biological system. Further, the utility of this proposed PBPKPD model was tested for its ability to predict the human dopamine D₂ receptor occupancy. These simulations were based on in vitro koff values obtained from rat studies (35), in vitro human D₂ receptor binding values (38), and calculated surrogate (for example, PS) for the drug transport across BBB. Danhof et al. (39) proposed that the values of drug-specific parameters such as target affinity are likely to be identical between species and individuals. This would imply that the binding rate constants estimated in rats can be used in human as well to extrapolate the pharmacodynamics from rat to human. However, several other studies showed differences in receptor affinity and protein binding between species (40). Notwithstanding divergent reports on the species independence of drug-specific parameters, an integration of allometric principles (41–43), in vitro information, and a physiological basis to PK-PD modeling would increase the prospective of translating effects from rat to human. The human D₂RO predictions at both dose levels are acceptable as 24 out of 39 observed values are within the 95% prediction limits. The predictions might improve further by considering the inclusion of allometric principles and in vitro in vivo correlations. Some antipsychotics, e.g. risperidone and its active metabolite paliperidone, have been extensively studied as P-gp substrates, and, therefore, their transport into and from brain involves a complex process of active and passive transport (9). This model structure, with few modifications, will also allow for extending this approach for other drugs with active transport across the BBB.

Hence, this proposed PBPKPD model, which accounts for the barriers in drug transport and describes the association and dissociation kinetics, may be a useful tool to extrapolate the D₂RO of antipsychotics from rat to human.

ABBREVIATIONS

BBB

blood–brain barrier

B_max

dopamine D₂ receptor density

CB

concentration of olanzapine bound to receptor

CEV

concentration in extravascular brain compartment

CL

systemic clearance

CL_bev

brain-extravascular clearance

CL_bv

brain-vascular clearance

D₂RO

dopamine-2 receptor occupancy

F_IP

bioavailability for intraperitoneal route of administration

FOCE

first order conditional estimation method

F_SC

bioavailability for subcutaneous route of administration

fu_brain

unbound fraction in brain

fu_plasma

unbound fraction in plasma

GOF

goodness-of-fit plots

IAV

inter-animal variability

koff

receptor dissociation rate constant

kon

receptor association rate constant

MW

molecular weight

nM

nanomoles/litre

OFV

objective function value

PBPKPD

physiology-based pharmacokinetic and pharmacodynamic

PK-PD

pharmacokinetic and pharmacodynamic

Q

intercompartmental clearance

RSE

relative standard error

SSE

stochastic simulation and estimation

V₁

volume of the central compartment

V₂

volume of the peripheral compartment

V_bev

volume of brain-extravascular compartment

V_bv

volume of brain-vascular compartment

APPENDIX 1

Full Model:

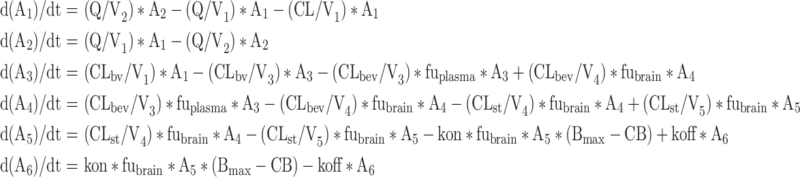where subscripts 1–6 represent volumes (V) and amount (A) of olanzapine at central, peripheral, brain-vascular, brain-extravascular, striatum-free and striatum-bound compartments, respectively; CL, Q, CL_bv, CL_bev, CL_st represent clearance of olanzapine in the central, peripheral, brain-vascular, brain-extravascular, striatum-free compartments, respectively; CB is concentration bound to receptor as (A₆/V₆)/(MW/1,000) in nM; MW is molecular weight of olanzapine; and D₂RO is calculated as CB/B_max.

Note that the transport from the central compartment to the brain-vascular compartment is not included in the equation d(A₁)/dt. This allows the plasma concentration-time profile to be described by a conventional two-compartment model, independent of the brain distribution.

Reduced Model:

Equations for d(A₁)/dt, d(A₂)/dt, and d(A₃)/dt are identical to the full model:

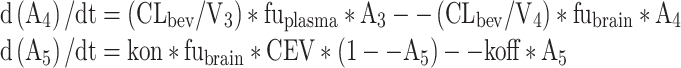where subscripts 1–4 represent volumes (V) and amount (A) of olanzapine at central, peripheral, brain-vascular, brain-extravascular compartments, respectively; A₅ is the fractional D2 receptor occupancy; CL, Q, CL_bv, CL_bev represent clearance of olanzapine in the central, peripheral, brain-vascular, brain-extravascular compartments, respectively; and CEV is the concentration in extravascular brain compartment as (A₄/V₄)/(MW/1,000) in nM.