Maximally reliable Markov chains under energy constraints

Abstract

Signal to noise ratios in physical systems can be significantly degraded if the output of a system is highly variable. Biological processes for which highly stereotyped signal generation is a necessary feature appear to have reduced their signal variabilities by employing multiple processing steps. To better understand why this multi-step cascade structure might be desirable, we prove that the reliability of a signal generated by a multi-state system with no memory (i.e. a Markov chain) is maximal if and only if the system topology is such that the process steps irreversibly through each state, with transition rates chosen such that an equal fraction of the total signal is generated in each state. Furthermore, our result indicates that by increasing the number of states, it is possible to arbitrarily increase the reliability of the system. In a physical system, however, there is an energy cost associated with maintaining irreversible transitions, and this cost increases with the number of such transitions (i.e. the number of states). Thus an infinite length chain, which would be perfectly reliable, is infeasible. To model the effects of energy demands on the maximally reliable solution, we numerically optimize the topology under two distinct energy functions that penalize either irreversible transitions or incommunicability between states respectively. In both cases, the solutions are essentially irreversible linear chains, but with upper bounds on the number of states set by the amount of available energy. We therefore conclude that a physical system for which signal reliability is important should employ a linear architecture with the number of states (and thus the reliability) determined by the intrinsic energy constraints of the system.

1 Introduction

In many physical systems, a high degree of signal stereotypy is desirable. In the retina, for example, the total number of G proteins turned on during the lifetime of activated rhodopsin following a photon absorption event needs to have a low variability to ensure that the resulting neural signal is more or less the same from trial to trial [Rieke and Baylor, 1998]. If this were not the case, accurate vision in low light conditions would not be possible. Biology offers us a myriad of other examples where signal reproducibility or temporal reliability are necessary for proper function: muscle fiber contraction [Edmonds et al., 1995b], action potential generation and propagation [Kandel et al., 2000], neural computations underlying motor control [Olivier et al., 2007] or time estimation [Buhusi and Meck, 2005], ion channel and pump dynamics [Edmonds et al., 1995a], circadian rhythm generation [Reppert and Weaver, 2002], cell-signalling cascades [Locasale and Chakraborty, 2008], etc. In some cases it may be possible to reduce signal variability by making a system exceedingly fast, but in many cases a nonzero mean processing time is necessary. The mechanism involved in the inactivation of rhodopsin, for example, needs to have some latency in order for enough G proteins to accumulate to effect the neural signal. In this paper we address the question of how to design a physical system that has a low signal variability while maintaining some desired nonzero mean total signal (and thus a nonzero mean processing time).

A previous numerical study of the variability of the signal generated during the lifetime of activated rhodopsin found that a multistep inactivation procedure (with the individual steps proposed to be sequential phosphorylations) was required to account for the low variability observed experimentally [Hamer et al., 2003]. This theoretical prediction was borne out when knockouts of phosphorylation sites in the rhodopsin gene were seen to result in an increased variability [Doan et al., 2006]. These results led us to consider more generally whether a multi-step system is optimal in terms of the reliability of an accumulated signal. Specifically, we limit ourselves to consider memoryless systems where the future evolution of the system dynamics depends on the current configuration of the system but not simultaneously on the history of past configurations. If such a memoryless system has a finite or countable number of distinct configurations (states) with near instantaneous transition times between them, it can be modeled as a continuous time Markov chain. This class of models, though somewhat restricted, is sufficiently rich to adequately approximate a wide variety of physical systems, including the phosphorylation cascade employed in the inactivation of rhodopsin. By restricting ourselves to systems which can be modeled by Markov chains, our goal of identifying the system design that minimizes the variance of the total generated signal while maintaining some nonzero mean may be restated as the goal of determining the Markov chain network topology that meets these requirements given a set of state-specific signal accumulation rates.¹ This is the primary focus of the present work.

The paper is organized as follows: in Sec. 2, we review basic continuous time Markov chain theory, introduce our notation, and review the necessary theory of the “hitting time”, or first passage time, between two states in a Markov network. We then define a random variable to represent the total signal generated during the path between the first and last states in the network and show that this is a simple generalization of the hitting time itself. The squared coefficient of variation of this variable (the CV², or ratio of the variance to the square of the mean) will be our measure of the variability of the system modeled by the Markov chain. In Sec. 3, we present our main theoretical result regarding the maximally reliable network topology. Simply stated, we prove that a linear Markov chain with transition rates between pairs of adjacent states that are proportional to the state-specific signal accumulation rates is optimal in that it minimizes the CV² of the total generated signal. In the special case that the state-specific signal accumulation rates are all equal to one, the total generated signal is the hitting time, and the optimally reliable solution is a linear chain with the same transition rate between all adjacent states (see Fig. 1b). As an intermediate step, we also prove a general bound regarding the signal reliability of an arbitrary Markov chain (Eq. 10) which we show to be saturated only for the optimal topology. In Sec. 4, we numerically study the deviations from the optimal solution when additional constraints are applied to the network topology. Specifically, we develop cost functions that are meant to represent the energy demands that a physical system might be expected to meet. As the available “energy” is reduced, the maximally reliable structure deviates further and further from the optimal (i.e. infinite energy) solution. If the cost function penalizes a quantity analogous to the Gibbs free energy difference between states, then the resulting solution is composed of two regimes: a directed component, which is essentially an irreversible linear subchain, followed by a diffusive component where the forward and backward transition rates between pairs of states along the chain become identical (Sec. 4.2). In the zero energy limit, the maximally reliable solution is purely diffusive, which is a topology that is amenable to analytic interpretation (Sec. 4.2.1). If, instead, the cost function penalizes all near-zero transition rates, then states are seen to merge until, at the minimum energy limit, the topology reduces to a simple 2-state system (Sec. 4.3). In Secs. 4.4 and 4.5, we present a brief analytic comparison of the solutions given by the two energy functions to show that, while they superficially seem quite different, they are in fact analogous. In both cases, the amount of available energy sets a maximum or effective maximum number of allowable states, and, within this state space, the maximally reliable Markov chain architecture is a linear chain with transition rates between each pair of adjacent states that are proportional to the state-specific signal accumulation rates. Finally, in Sec. 4.6, we argue that structure is necessary for reliability, and that randomly connected Markov chains do not confer improved reliability with increased numbers of states. From this we conclude that investing the energy resources needed to construct a linear Markov chain would be advantageous to a physical system.

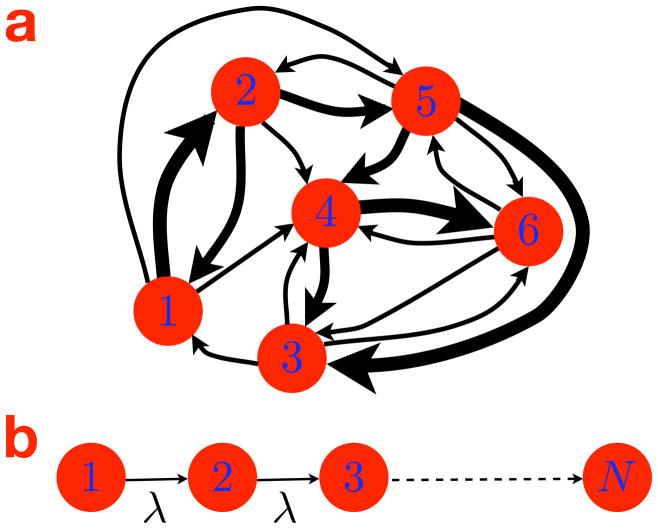
Figure 1.

a. A schematic of a 6-state Markov chain. The circles and arrows represent the states and the transitions between states respectively. The thicknesses of the arrows correspond to the values of the transition rates or, equivalently, the relative probabilities of transition. Nonexistent arrows (e.g. between states 2 and 3) reflect transition rates of zero. b. A linear Markov chain with the same transition rate λ between all pairs of adjacent states in the chain (i.e. λ_i+1,i = λ). This topology uniquely saturates the bound on the CV² of the hitting time t_1N (Eq. 10).

2 Continuous time Markov chains

A Markov chain is a simple model of a stochastic dynamical system that is assumed to transition between a finite or countable number of states (see Fig. 1a). Furthermore, it is memoryless—the future is independent of the past given the present. This feature of the model is called the Markov property.

In this paper, we will consider homogeneous continuous time Markov chains. These are fully characterized by a static set of transition rates {λ_ij : ∀i, ∀j ≠ i} that describe the dynamics of the network, where λ_ij is the rate of transition from state j to state i. The dwell time in each state prior to a transition to a new state is given by an exponentially distributed random variable, which appropriately captures the Markovian nature of the system. Specifically, the dwell time in state j is given by an exponential distribution with time constant τ_j, where

$${\tau }_j\equiv \frac{1}{{\sum }_{k\ne j}{\lambda }_{kj}},$$ (1)

the inverse of the sum of all of the transition rates away from state j. Once a transition away from state j occurs, the probability p_j→i that the transition is to state i is given by the relative value of λ_ij compared to the other rates of transitions leaving state j. Specifically,

$$\begin{array}{l}{p}_{j\to i}=\frac{{\lambda }_{ij}}{{\sum }_{k\ne j}{\lambda }_{kj}}\\ ={\lambda }_{ij}{\tau }_j.\end{array}$$ (2)

It is convenient to construct an N × N transition rate matrix to describe a homogeneous continuous time Markov chain as follows:

$$\mathbf{A}\equiv \left(\begin{array}{cccc}{q}_1& {\lambda }_{12}& \cdots & {\lambda }_{1N}\\ {\lambda }_{21}& q_2& \cdots & {\lambda }_{2N}\\ ⋮& ⋮& \ddots & ⋮\\ {\lambda }_{N1}& {\lambda }_{N2}& \cdots & q_N\end{array}\right),$$ (3)

where q_j = −1/τ_j. Note that each column of A sums to zero and that all off-diagonal elements (the transition rates) are non-negative. The set of N × N matrices of this form corresponds to the full set of N-state Markov chains. For an introduction to the general theory of Markov chains, see, for example, [Norris, 2004].

2.1 Hitting times and total generated signals

In this paper we consider the reliability of the total signal generated during the time required for a Markovian system to arrive at state N given that it starts in state 1.² This time is often referred to as the hitting time, which can be represented by the random variable t_1N. The total generated signal, F_1N, can subsequently be defined in terms of the hitting time and the state-specific signal accumulation rates. If the rate of signal accumulation in state i is given by the coefficient f_i, and the current state at time t is denoted q(t), then we can define the total signal as

$$F_{1N}={\int }_0^{t_{1N}}{f}_{q(t)}dt.$$ (4)

Note that in the case that f_i = 1, ∀i, the total generated signal equals the hitting time. The statistics of these random variables are governed by the topology of the network, namely, the transition matrix A. Our goal is to identify the network topology that minimizes the variance of the total signal, and thus maximizes the reliability of the system, while holding the mean total signal constant.

Recall that the standard expression for the probability that a Markovian system that starts in state 1 is in state N at time t is given as

$$p(q(t)=N)={\mathbf{e}}_N^T{e}^{\mathbf{A}t}{\mathbf{e}}_1,$$ (5)

where e₁ ≡ (1, 0, …, 0)^T and e_N ≡ (0, …, 0, 1)^T (i.e. the first and N^th standard basis vectors respectively) [Norris, 2004]. If the N^th column of A is a zero vector so that transitions away from state N are disallowed making N a so-called collecting state of the system, then p(q(t) = N) is equivalent to the probability that the hitting time t_1N is less than t. Assuming that this is true,³ then the time derivative of Eq. 5 is the probability density of the hitting time itself:

$$p(t_{1N})={\mathbf{e}}_N^T{\mathbf{A}e}^{{\mathbf{A}t}_{1N}}{\mathbf{e}}_1.$$ (6)

Note that state N must be collecting in order for this distribution to integrate to 1. Additionally, p(t_1N ) is only well-defined if state N both is accessible from state 1 and is the only collecting state or collecting set of states accessible from state 1. We only consider topologies for which these three properties hold.

We can show that studying the statistics of the hitting time t_1N is equivalent to studying the statistics of the the total generated signal F_1N since the two random variables are simple transforms of each other. To determine the probability distribution of F_1N, we can consider the signal accumulation rates to simply rescale time. The transition rate λ_ij can be stated as the number of transitions to state i per unit of accumulated time when the system is in state j, and so the ratio λ_ij/f_j can similarly be stated as the number of transitions to state i per unit of accumulated signal when the system is in state j. Thus by dividing each column of A by the corresponding signal accumulation rate, we can define the matrix à with elements φ_ij ≡ λ_ij/f_j. Then, the probability distribution of F_1N is given, by analogy with the hitting time distribution (Eq. 6), as

$$p(F_{1N})={\mathbf{e}}_N^T\stackrel{\sim }{\mathbf{A}}{e}^{\stackrel{\sim }{\mathbf{A}}{F}_{1N}}{\mathbf{e}}_1.$$ (7)

Thus, for the remainder of the paper we focus solely on the reliability of a Markovian system as measured by the statistics of the hitting time rather than of the total generated signal (i.e. we consider f_i = 1, ∀i). This can be done without loss of generality since the results we present regarding the reliability of the hitting time can be translated to an equivalent set of results regarding the reliability of the total generated signal by a simple column-wise rescaling of the transition rate matrices.

2.2 The CV² as a measure of reliability

It is clear that given a Markov chain with a set of fixed relative transition rates, the reliability of the system should be independent of the absolute values of the rates (i.e. the scale) since a scaling of the rates would merely rescale time (e.g. change the units from seconds to minutes). Furthermore, the variance and the square of the mean of the hitting time t_1N would be expected to vary in proportion to each other given a scaling of the transition rates, since again this is just a rescaling of time. This can be demonstrated by noting, from Eq. 3, that scaling the rates of a Markov chain by the same factor is equivalent to scaling A, since A is linear in the rates λ_ij, and, from Eq. 6, that scaling A is equivalent to rescaling t_1N and thus the statistics of t_1N. Therefore, we use the squared coefficient of variation (CV², or the dimensionless ratio of the variance to the square of the mean) to measure the reliability of a Markov chain, and seek to determine the network topology (i.e. with fixed relative rates, but not fixed absolute rates) which minimizes the CV² and thus is maximally reliable.

3 Optimal reliability

Intuitively, it seems reasonable that an irreversible linear chain with the same transition rate between all pairs of adjacent states (i.e. λ_i+1,i = λ for all i and for some constant rate λ, and λ_ij = 0 for j ≠ = i − 1; see Fig. 1b) may be optimal. For such a chain, the hitting time t_1N equals the sum from 1 to M (where we define M ≡ N −1 for convenience) of the dwell times in each state of the chain t_i,i+1. This gives the CV² as

$$\begin{array}{l}{\text{CV}}^2\equiv \frac{var(t_{1N})}{{\langle t_{1N}\rangle }^2}\\ =\frac{var\left({\sum }_{i=1}^M{t}_{i,i+1}\right)}{{\langle {\sum }_{i=1}^M{t}_{i,i+1}\rangle }^2}\\ =\frac{{\sum }_{i=1}^{M}var(t_{i,i+1})}{{\left({\sum }_{i=1}^M\langle t_{i,i+1}\rangle \right)}^2},\end{array}$$ (8)

where we use the fact that the dwell times are independent random variables and so their means and variances simply add. Since the t_i,i+1 are drawn from an exponential distribution with mean 1/λ and variance 1/λ², the CV² reduces further as

$$\begin{array}{l}{\text{CV}}^2=\frac{{\sum }_{i=1}^M\frac{1}{{\lambda }^2}}{{\left({\sum }_{i=1}^M\frac{1}{\lambda }\right)}^2}\\ =\frac{\frac{M}{{\lambda }^2}}{{\left(\frac{M}{\lambda }\right)}^2}\\ =\frac{1}{M}.\end{array}$$ (9)

It is trivial to show via simple quadratic minimization that the constant-rate linear chain is optimal over all possible irreversible linear chains since its variance is minimal for a given mean, but the proof that no other branching, loopy, or reversible topologies exist that may have equal or lower variabilities as measured by the CV² appears to be less obvious. The main mathematical result of this paper is that, in fact, no other topologies reach a CV² of 1/M. Our proof, detailed in Sec. A.1, proceeds in two steps. First, we prove that the following bound holds for all N-state Markov chains:

$${\text{CV}}^2\ge \frac{1}{M}.$$ (10)

Second, we show that our proposed constant-rate linear chain is the unique solution which saturates this bound.

Confirming the relevance of this theoretical result to natural systems, the best fit of a detailed kinetic model for rhodopsin inactivation to experimental data has exactly the constant-rate linear chain architecture although for the total generated signal rather than for the lifetime of the system (i.e. in each phosphorylation state, the rate of subsequent phosphorylation is proportional to the state-specific G protein activation rate, and so the mean fraction of the total signal accumulated in each state is constant) [Gibson et al., 2000, Hamer et al., 2003]. We postulate that studies of other biological systems for which temporal or total signal reliabilities are necessary features will uncover similar constant-rate linear topologies. Although not experimentally validated, previous theoretical work [Miller and Wang, 2006] has shown that a constant-rate linear chain could be implemented by the brain as a potential mechanism for measuring an interval of time. Specifically, if a set of strongly intra-connected populations of bistable integrate-and-fire neurons are weakly inter-connected in a series, then the total network works like a stochastic clock (i.e. in the presence of noise). By activating the first population through some external input, each subsequent population is activated in turn after some delay given by the strength of the connectivity between the populations. The time from the activation of the first population until the last is equivalent to the hitting time in a linear Markov chain with each population representing a state. Interestingly, in [Miller and Wang, 2006], the authors use this timing mechanism as a way to explain the well-known adherence to Weber’s Law seen in the behavioral data for interval timing [Gibbon, 1977, Buhusi and Meck, 2005], while our result indicates that this timing architecture is optimal without reference to the data.⁴

4 Numerical studies of energy constraints

Given the inverse relationship between the CV² of the hitting time (or the total generated signal) and the number of states for a system with a linear, unidirectional topology, (Eq. 9) it would seem that such a system may be made arbitrarily reliable by increasing the number of states. Why, then, do physical systems not employ a massively large number of states to essentially eliminate trial to trial variability in signal generation? The inactivation of activated rhodopsin, for example, appears to be an eight [Doan et al., 2006] or nine [Hamer et al., 2003] state system. Why did nature not increase this number to hundreds of thousands of states? In the case of rhodopsin, one might speculate that the reduction in variability achieved with only eight or nine states is sufficient to render negligible the contribution that the variability in the number of G proteins generated by rhodopsin adds to the total noise in the visual system (i.e. it is small compared to other noise components such as photon shot-noise and intrinsic noise in the retinothalamocortical neural circuitry); more generally, for an arbitrary system, it is reasonable to hypothesize that a huge number of states is infeasible due to the cost incurred in maintaining such a large state-space. We will attempt to understand this cost by defining a measure of “energy” over the topology of the system.

The optimal solution given in the previous section consists entirely of irreversible transitions. We can analyze the energetics of such a topology by borrowing from Arrhenius kinetic theory and considering transitions between states in the Markov chain to be analogous to individual reactions in a chemical process. An irreversible reaction is associated with an infinite energy drop and thus our optimal topology is an energetic impossibility. Even if one deviates slightly from the optimal solution and sets the transitions to be nearly, but not perfectly, irreversible, then each step is associated with a large though finite energy drop. Thus, the total energy required to reset the system following its progression from the first to the final state would equal the sum of all of the energy drops between each pair of states. In this context it is apparent why a physical system could not maintain the optimal solution with a large number of states N since each additional state would add to the total energy drop across the length of the chain. At some point, the cost of adding an additional state would outweigh the benefit in terms of reduced variability, and thus the final topology would have a number of states that balances the counteracting goals of variability reduction and conservation of energy resources.

Specifically, in Arrhenius theory, energy differences are proportional to the negative logarithms of the reaction rates (i.e. ΔE ∝ −ln λ). In Secs. 4.2 and 4.3 below, we define two different energy functions, both of which are consistent with this proportionality concept, but apply it differently and have different interpretations. We then numerically optimize the transition rates of an N-state Markov chain to minimize the CV² of the hitting time while holding the total energy E_tot constant. This process is repeated for many values of E_tot to understand the role that the energy constraints defined by the two different energy functions play in determining the minimally variable solution. As expected and shown in the results below, the CV² of the optimal solution increases with decreasing E_tot.

4.1 Numerical methods

Constrained optimization was performed using the optimization toolbox in MATLAB. Rather than minimize the CV² of the hitting time directly, the variance was minimized while the mean was constrained to be 1, thus making the variance equal to the CV². Expressions for the mean and the variance of the hitting time for arbitrary transition rate matrices are given using the known formula for the moments of the hitting time distribution ([Norris, 2004]; see Sec. A.2 for a derivation). In order to implicitly enforce the constraint that the rates must be positive, the rates λ_ij were reparameterized in terms of θ_ij, where θ_ij ≡ − ln λ_ij. The variance was then minimized over the new parameters rather than the rates themselves. The gradients of these functions with respect to θ were also utilized to speed the convergence of the optimization routine. The gradients of the mean, variance, and energy functions are given in Sec. A.3.

For each value of E_tot, parameter optimization was repeated with multiple initial conditions to both discard locally optimal solutions and avoid numerically unstable parameter regimes. For the second energy function (Sec. 4.3), local optima were encountered, while none were observed in the parameter space of the first (Sec. 4.2).

4.2 Energy cost function I: constrain irreversibility of transitions

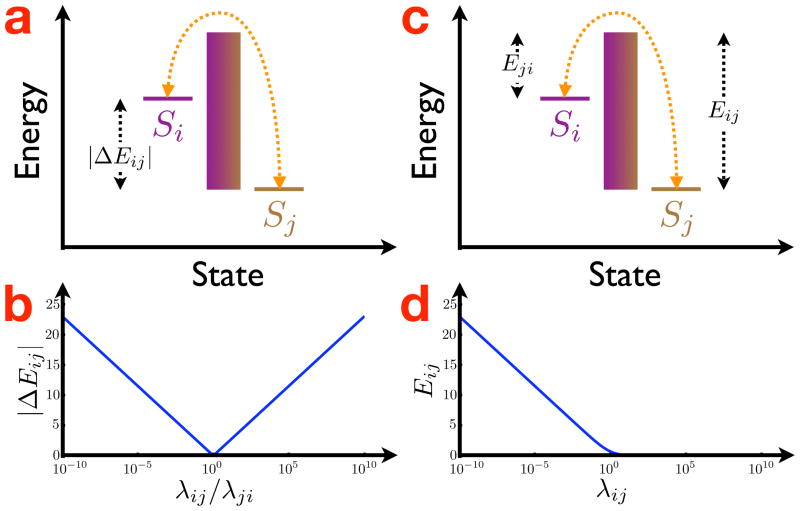
Our first approach at developing a reasonable energy cost function is predicated on the idea that if the values of the reciprocal rates between a single pair of states (e.g. λ_ij and λ_ji for states i and j) are unequal, then this asymmetry should be penalized, but that the penalty should not depend on the absolute values of the rates themselves. Thus if two states have equal rates between them (including zero rates), no penalty is incurred, but if the rates differ significantly, then large penalties are applied. In other words, perfectly reversible transitions are not penalized, while perfectly irreversible transitions are infinitely costly. From an energy standpoint, different rates between a pair of states can be thought of as resulting from a quantity analogous to the Gibbs free energy difference between the states. In chemical reactions, reactants and products have intrinsic energy values which are defined by their specific chemical makeups. The difference between the product and the reactant energies is the Gibbs free energy drop of a reaction. If this value is negative then the forward reaction rate exceeds the backward rate, and vice versa if the value is positive. By analogy then, we can consider each state in a Markov chain to be associated with an energy, and thus that the relative difference between the transition rates in a reciprocal rate pair is due to the energy drop between their corresponding states.⁵ For nonzero energy differences, one of the rates is fast because it is associated with a drop in energy, while the other is slow since energy must be invested to achieve the transition. On the other hand, if the energy difference is zero, then both rates are identical. This idea is schematized in Fig. 2a where the energy drop ΔE_ij between states i and j results in a faster rate λ_ji than λ_ij.

Figure 2.

a. A schematization of the energy associated with the transitions between states i and j for the energy cost function given in Eq. 13. The energies of each state are not equal, and so the transition rates differ (i.e. λ_ji from state i to j is faster than λ_ji from j to i). For this cost function, the height of the energy barrier in the schematic, which can be thought to represent the absolute values of λ_ji and λ_ji, does not contribute to E_tot, which is only affected by the difference between the energies associated with each state |ΔE_ij|. b. The contribution to the total energy E_tot for the pair of transition rates λ_ji and λ_ji under the first energy function (Eq. 13). For rates that are nearly identical (i.e. when the ratio λ_ji/λ_ji is close to one), |ΔE_ji| is near zero, but it increases logarithmically with the relative difference between the rates. c. Similar to a, but for the energy cost function given in Eq. 25. In this case, the transition rate λ_ji from state i to j is faster, and thus associated with a lower energy barrier, than the rate λ_ji from j to i. d. The contribution to the total energy E_tot for the transition rate λ_ji under the second energy function (Eq. 25). For large transition rates, E_ij is near zero, but it increases logarithmically for near-zero rates. Note that the abscissae in b and d are plotted on a log scale.

Thus, the total energy of the system E_tot can then be given as the sum of the energy drops between every pair of states:

$$E_{\text{tot}}\equiv \sum _{i,j}\mid \mathrm{\Delta }{E}_{ij}\mid ,$$ (11)

where we exclude pairs that contain state N (i.e. since the outgoing rates for transitions away from state N do not affect the hitting time t_1N and thus can always be set to equal the reciprocal incoming rates to state N, making those energy drops zero) and only count each rate pair once (because |ΔE_ij| = |ΔE_ji|). From Arrhenius kinetic theory, the Gibbs free energy difference is proportional to the logarithm of the ratio of the forward and backward reaction rates, and so we use the following definition for the energy drop (plotted in Fig. 2b for a single pair of reciprocal rates):

$$\mathrm{\Delta }{E}_{ij}=ln\frac{{\lambda }_{ij}}{{\lambda }_{ji}}.$$ (12)

Therefore, the complete energy cost function is

$$E_{\text{tot}}=\sum _{i,j}\left|ln\frac{{\lambda }_{ij}}{{\lambda }_{ji}}\right|.$$ (13)

Note that the individual magnitudes of the rates do not enter into the energy function, only the relative magnitudes between pairs of reciprocal rates.

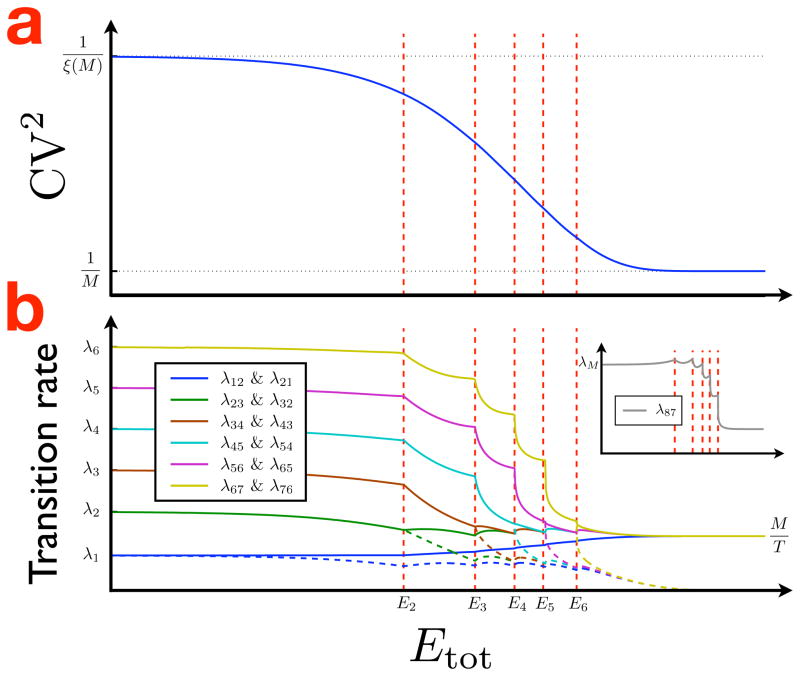
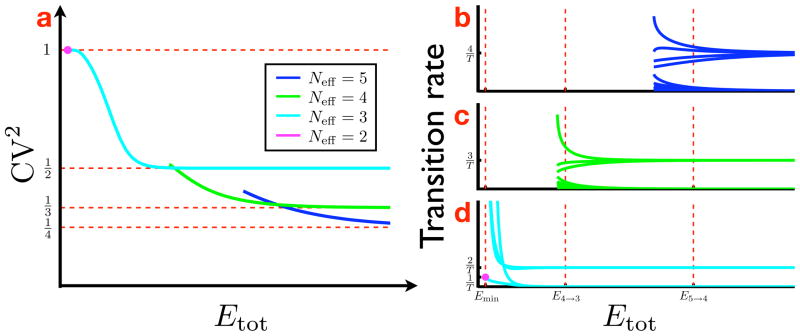
The results of numerical optimization of the rates λ_ij to minimize the CV² of the hitting time t_1N under the energy function defined in Eq. 13 are given in Fig. 3a. At large values of E_tot, the optimized solution approaches the asymptotic CV² limit of $\frac{1}{M}$ (i.e. the CV² of the unconstrained or infinite energy, ideal linear chain; see Eq. 9). As the available energy is decreased, the CV² consequently increases until, at E_tot = 0, the CV² reaches a maximal level of $\frac{1}{\xi (M)}$ (the function ξ(M ) will be defined in Sec. 4.2.1 below).

Figure 3.

a. The minimum CV² achieved by the numerical optimization procedure as a function of E_tot for an 8-state Markov chain using the energy function defined in Eq. 13. At large energy values, the CV² approaches the asymptotic infinite energy limit ( $\frac{1}{M}$), while at E_tot = 0, the CV² reaches its maximum value of $\frac{1}{\xi (M)}$ (the function ξ(M) is given by Eq. 17). b. The transition rate values for the six nonzero pairs of rates between adjacent states along the linear chain (e.g. λ₁₂ & λ₂₁, λ₂₃ & λ₃₂, etc.). At large values of E_tot the forward rates (solid lines) and the backward rates (dashed lines) approach the infinite energy limits of $\frac{M}{T}$ (for T ≡ 〈t_1N〉) and zero respectively. As the energy is decreased, the rates smoothly deviate from these ideals until, at energy value E₆, the rates λ₆₇ & λ₇₆ (in yellow) merge and remain merged for all lower energy values. Between E₆ and E₅, the rates again change smoothly until the rates λ₅₆ & λ₆₅ (in purple) merge. This pattern repeats itself until ultimately the first rate pair in the chain— λ₁₂ & λ₂₁ (in blue)—merges at E_tot = 0. The zero energy solutions λ₁,…, λ₆ are given by Eq. 15. Inset. The final, unpaired rate in the chain (λ₈₇) versus E_tot. Its zero energy solution λ_M is also given by Eq. 15. As discussed in Sec. 4.2.1, this rate is proportional to M, whereas the zero energy solutions of the paired rates are proportional to i², and so λ_M is considerably slower then, for example, λ_M−1. Note that the abscissae are plotted on a log scale and that the ordinate in b is plotted on a square-root scale for visual clarity.

Upon inspection, for large values of the total energy, the optimized transition rate matrix is seen, as presumed, to be essentially identical to the ideal, infinite energy solution. Specifically, the forward transition rates along the linear chain (i.e. the elements of the lower subdiagonal of transition rate matrix; see Eq. 3) are all essentially equal to each other, while the remaining rates are all essentially zero. Since the energy function does not penalize symmetric reciprocal rate pairs, the reciprocal rates between nonadjacent states in a linear chain (which are both zero and thus symmetric) would not contribute to the energy. Thus it would be expected that the optimal solutions found using this energy function would be linear chains, and indeed the minimization procedure does drive rates between nonadjacent states to exactly zero, or, more precisely, the numerical limit of the machine. The only deviations away from the ideal, infinite energy solution occur in the rates along the lower and upper sub-diagonals of the transition rate matrix (i.e. the forward and backward rates between adjacent states in the linear chain). As the available energy is decreased, these deviations become more pronounced until the lower and upper subdiagonals become equal to each other at E_tot = 0. An analytical treatment of the structure of this zero energy solution is given in the subsection 4.2.1.

An inspection of the transition rate matrix at intermediate values of E_tot reveals that as the minimum CV² solution deviates between the infinite energy and the zero energy optima, the pairs of forward and backward transition rates between adjacent states become equal, and thus give no contribution to E_tot, in sequence, starting from the last pair in the chain (λ_M−1,M & λ_M,M−1) at some relatively high energy value and ending with the first pair (λ₁₂ & λ₂₁) at E_tot = 0. This sequential merging of rate pairs, from final pair to first pair, with a decrease in the available energy was a robust result over all network sizes tested. In Fig. 3b, for example, the results are shown for the optimization of an 8-state Markov chain. It is clear from the figure that the transition rates deviate smoothly from the infinite energy ideal as E_tot is decreased until the final rate pair (in yellow) merges together at the energy level E₆. At all lower energy values, these two rates remain identical and thus, given the definition of the energy function (Eq. 13), are noncontributory to E_tot. After this first merging, the rates again deviate smoothly with decreasing E_tot until the next rate pair (in purple) merges. This pattern repeats itself until, at E_tot = 0, all rate pairs have merged. The value of the unpaired rate at the end of the chain (i.e. λ₈₇ in this case) as a function of the available energy is shown in the figure inset. At intermediate values of E_tot, the as-of-yet unmerged rate pairs (except for the first rate pair λ₁₂ & λ₂₁) are all identical to each other. That is, all of the forward rates in these unmerged rate pairs are equal as are all of the backward rates. For example, above E₆ in Fig. 3b, the forward rates λ₃₂, …, λ₆₅ are equal as are the backward rates λ₂₃, …, λ₅₆. In other words, the green, brown, cyan, and purple traces lie exactly on top of each other. Only the yellow traces, corresponding to the rate pair which is actively merging in this energy range, and the blue traces, corresponding to the first rate pair, deviate from the other forward and backward rates. Between E₅ and E₆, the same unmerged rates continue to be equal except for λ₅₆ & λ₆₅ (in purple) which have begun to merge.⁶ Essentially, this means that the behavior of the system at intermediate values of E_tot is insensitive to the current position along the chain anywhere within this set of states with unmerged rate pairs (i.e. the forward and backward rates are the same for all states in this set).

We can understand why rate pairs should merge by considering the energy function to be analogous to a prior distribution over a set of parameters in a machine-learning style parameter optimization (e.g. a maximum a posteriori fitting procedure). In this case, the parameters are the logarithms of the ratios of the pairs of rates and the prior distribution is the Laplace, which, in log-space, gives the L₁-norm of the parameters (i.e. exactly the definition of the individual terms of E_tot; see Eq. 13). As is well known from the machine-learning literature, a Laplace prior or, equivalently, an L₁-norm regularizer, gives rise to a sparse representation where parameters on which the data are least dependent are driven to zero and thus ignored while those that capture important structural features of the data are spared and remain nonzero [Tibshirani, 1996]. In this analogy, E_tot is similar to the standard deviation of the prior distribution (or the inverse of the Lagrange multiplier of the regularizer), in that, as it is decreased towards zero, it allows fewer and fewer nonzero log-rate ratios to persist. Ultimately, at E_tot = 0, the prior distribution overwhelms optimization of the CV², and all the pairs of rates are driven to be equal, thus making the log-rate ratios zero. This analogy might lead one to consider energy functions which correspond to other prior distributions (e.g. the Gaussian), but, unlike Eq. 13, functions based on other priors (e.g. a quadratic which would correspond to a Gaussian prior) do not result in a clear interpretation of what the energy means and thus they were not pursued in this work.

One interpretation of the solutions of the optimization procedure at different energy values shown in Fig. 3b is as follows. Before a rate pair merges, the corresponding transition can thought of as “directed” with the probability of a forward transition exceeding that of a backward transition. On the other hand, after a merger has taken place, the probabilities of going forward and backward become equal, and we term this behavior as “diffusive”. At high values of E_tot, the solution is entirely directed, with the system marching from the first state to the final state in sequence. At E_tot = 0, the solution is purely diffusive, with the system performing a random walk along the Markov chain. At intermediate energy values, both directed and diffusive regimes coexist. Interestingly, the directed regime always precedes the diffusive regime (i.e. the rate pairs towards the end of the chain merge at higher energy values than those towards the beginning of the chain). Recalling our analogy from the previous paragraph, the first parameters to be driven to zero using a Laplace prior are those which have the least impact in accurately capturing the data. Therefore, in our case, we expect that the first log-rate ratios driven to zero are those that have the least impact on minimizing the CV² of the hitting time t_1N. Thus, our numerical results indicate that at energy levels where a completely directed solution is not possible, it is better, in terms of variability reduction, to first take directed steps and then diffuse rather than diffuse and then take directed steps or mix the two regimes arbitrarily. We will present a brief interpretation as to why this structure is favored in Sec. 4.2.2 below. A schematic of an intermediate energy solution is shown in Fig. 4.

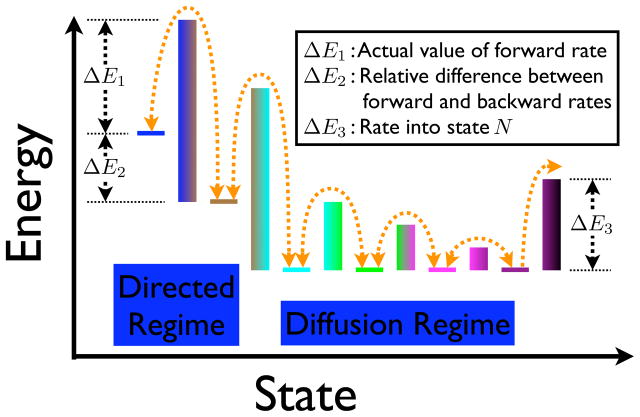
Figure 4.

A schematic of a nonzero, finite energy solution for a 7-state Markov chain optimized under the energy function given in Eq. 13. In this case, the first two transitions can be called directed since their forward rates exceed their backward rates. The forward rate λ₂₁, for example, is determined by the height of the energy barrier between states 1 and 2 (i.e. it is proportional to e^{−Δ E₁}. This rate will be a larger value than the backward rate λ₁₂ (proportional to e^{−ΔE₁ − ΔE₂}). On the other hand, the rates between states towards the end of the chain are equal as represented by states that are at the same energy level. The decreasing energy barriers towards the end of the chain represent the empirical result that the rates increase down the length of the chain (see Fig. 3). The larger energy barrier for the final transition to state N represents the result that this rate is much slower than the other rates at the end of the chain. As shown in Sec. 4.2.1 for the E_tot = 0 solution, the final rate is a linear function of M while the other rates grow quadratically (Eq. 15). Note that the energy level of state N is not represented since there is no reverse transition N → M to consider.

4.2.1 Zero energy or pure diffusion solution

If E_tot is zero under the energy function given by Eq. 13, then all the pairs of rates λ_ij and λ_ji are forced to be equal. The rates corresponding to transitions between non-adjacent states in the linear chain (i.e. for |i − j| ≠ = 1), are driven to zero by the optimization of the CV², while the adjacent state transition rates remain positive. It is possible to analytically solve for the rates in such a zero energy chain as well as find a semi-closed form expression for the CV² of the hitting time t_1N (see Sec. A.4 for details).

To simplify notation a bit, since transitions between adjacent states are equal and, between non-adjacent states, zero, we can consider only the rates λ_i for i ∈ {1,…, M} where λ_i = λ_i,i+1 = λ_i+1,i. Then the CV² can be shown to be

$${\text{CV}}^2=\frac{{\mathbf{x}}^T\mathbf{Zx}}{T^2},$$ (14)

where we have defined the vector x as $x_i\equiv \frac{1}{{\lambda }_i}$, the matrix Z as Z_ij ≡ min (i,j)², and, for notational convenience, T as 〈t_1N〉. The λ_i that minimize this CV² are

$${\lambda }_i=\{\begin{array}{l}\frac{\xi (M)}{2T}(4i^2-1),i\ne M\hfill \\ \frac{\xi (M)}{T}(2M-1),i=M\hfill \end{array},$$ (15)

which, substituted back into Eq. 14, give the minimum CV² as

$${\text{CV}}^2=\frac{1}{\xi (M)},$$ (16)

where ξ(M) is calculated as

$$\xi (M)=\frac{1}{2}(\mathrm{\Psi }(M+\frac{1}{2})+\gamma )+ln2,$$ (17)

where Ψ(x) is the digamma function defined as the derivative of the logarithm of the gamma function (i.e. $\mathrm{\Psi }(x)\equiv \frac{d}{dx}ln\mathrm{\Gamma }(x)$) and γ is the Euler–Mascheroni constant. Although Ψ (x) has no simple closed-form expression, efficient algorithms exist for determining its values. For M = 1, ξ (1) = 1, and, as can be shown by asymptotic expansion of Ψ (x), ξ(M) grows logarithmically with M.

Compared to the CV² versus number-of-states relationship at infinite energy (Eq. 9), in the zero energy setting, the CV² scales inversely with log N (Eq. 16) rather than with N, and thus adding states gives logarithmically less advantage in terms of variability reduction. Furthermore, even to achieve this modest improvement with increasing N, the rates must scale with i² (i.e. λ_i ∝ 4i² − 1; see Eq. 15), and thus the rates towards the end of the chain need to be O(N² ln N) while those near the start are only O(ln N). To summarize then, the zero energy setting has two disadvantages over the infinite energy case. First, for the optimal solution, the CV² is inversely proportional to the logarithm of N rather than to N itself, and second, even to achieve this modest variability reduction, a dynamic range of transition rates proportional to N² must be maintained.

4.2.2 The diffusive regime follows the directed regime

We can understand the numerical result that, at intermediate energy values, the diffusive regime always follows the directed regime by careful consideration of the structure of this solution. First, let us assume that for some value of E_tot the directed regime consists of M_i directed transitions and that the remainder of the system consists of a purely diffusive tail with M_r transitions (where N = M_i + M_r + 1). Recalling that transitions to state N are unpaired, then there are actually M_i + 1 directed transitions for this intermediate energy solution: M_i in the directed regime and one at the end of the diffusive tail. However, the energy resources of the system are being devoted solely to maintain the M_i transitions composing the directed regime, since the energy function (Eq. 13) does not penalize perfectly reversible transitions or transitions leading to state N, such as the one at the end of the diffusive tail.

Now consider if the diffusive regime preceded the directed regime. Then, though there would still be M_i+1 directed transitions (one at the end of the diffusive regime leading into the directed regime and M_i in the directed regime), the energy resources would be apportioned in a new manner. The final transition of the directed regime, since it leads to state N, would not incur any penalty, while the final transition of the diffusive regime would incur a penalty since it now leads to the first state of the directed regime rather than to state N. In other words, the final transition of the diffusive regime is penalized as are the first M_i − 1 transitions of the directed regime. It is now possible to understand why our numerical optimizations always yield solutions with directed-first, diffusive-second architectures. If the transition rate at the end of the diffusive regime λ_Mr (to use the notation introduced in Sec. 4.2.1 above) is greater than the transition rate at the end of the directed regime λ, then more energy would be required for the diffusive-first architecture, which would penalize λ_Mr, than for the directed-first architecture, which does not. Numerically, λ_Mr is always seen to be greater than λ, and the following simple analysis also supports this idea.

If we approximate the directed regime as consisting of M_i perfectly irreversible transitions with backward rates of exactly zero, then the directed and diffusive subchains can be considered independently and thus their variances can be added as

$$\begin{array}{l}var(t_{1N})=var(t_i)+var(t_r)\\ =\frac{T_i^2}{M_i}+\frac{T_r^2}{\xi (M_r)},\end{array}$$ (18)

where we have multiplied the expressions for the CV² of an ideal linear chain (Eq. 9) and a zero energy, purely diffusive chain (Eq. 16) by the squares of the mean processing times for each subchain (T_i and T_r) to get the variances. In order to find the relative rates between the directed and diffusive portions of the chain, we minimize Eq. 18 with respect to the subchain means subject to the constraint that the mean total time is T. This gives

$$T_i=\frac{M_i}{M_i+\xi (M_r)}T$$ (19)

and

$$T_r=\frac{\xi (M_r)}{M_i+\xi (M_r)}T.$$ (20)

The forward rate along the directed portion of the chain is thus

$$\begin{array}{l}\lambda =\frac{M_i}{T_i}\\ =\frac{M_i+\xi (M_r)}{T},\end{array}$$ (21)

and the final rate along the diffusive portion (Eq. 15) is thus

$$\begin{array}{l}{\lambda }_{M_r}=\frac{\xi (M_r)}{T_r}(2M_r-1)\\ =\frac{M_i+\xi (M_r)}{T}(2M_r-1)\\ =\lambda (2M_r-1).\end{array}$$ (22)

Therefore, for the case of a perfectly irreversible directed regime, the final transition rate of the diffusive regime is always larger than the rate of the directed regime as long as M_r > 1. Although this result does not necessarily hold for real intermediate energy solutions (where the directed regime is not perfectly irreversible), this analysis seems to explain the numerical result that the directed-first architecture is optimal.

4.3 Energy cost function II: constrain incommunicability between states

Although the results from the previous section are revealing and provide insight into why a physical system might be limited in the number of directed steps it can maintain (as discussed in Sec. 4.4 below, the diffusive tail found at intermediate values of E_tot in the previous section is essentially negligible in terms of variability reduction), it is unclear whether the energy cost function given in Eq. 13 is generally applicable to an arbitrary multi-state physical process. Therefore, as a test of the robustness of our results, we defined an additional cost function to determine the behavior of the optimal solution under a different set of constraints. As shown in Secs. 4.4 and 4.5 below, the results given by our second cost function, while superficially appearing to be quite different, are in fact analogous to the those given in the preceding section.

Our second energy cost function is predicated on the idea that there should be a large penalty for all near-zero rates, or, equivalently, that the maintenance of incommunicability between states should be costly. Although not as neatly tied to a physical energy as the first energy function (which is exactly analogous to the Gibbs free energy; see Sec. 4.2), a small rate of transition between two states can be thought of as resulting from a high “energy” barrier that is preventing the transition from occurring. Inversely, a large rate corresponds to a low energy barrier, and in the limit, one can think of two states with infinite transition rates between them as in fact the same state. This idea is schematized in Fig. 2c for the transitions between a pair of states i and j. The energy E_ji can be thought of as the energy needed to permit the transition from i to j, and similarly for E_ij. Given our intuition regarding the relationship between energies and rates, from the diagram one expects that the rate λ_ji is faster than the rate λ_ij, since E_ji is less than E_ij. The total energy in the system E_tot can simply be defined as the sum of energies associated with each transition in the system:

$$E_{\text{tot}}\equiv \sum _{i,j}{E}_{ij}.$$ (23)

The energies of the transitions originating in state N are excluded from the preceding sum since their associated transition rates do not effect the hitting time t_1N (i.e. transitions away from state N are irrelevant).

To determine a reasonable expression for the individual transition energies, we choose a function such that, for near-zero transition rates, E_ij → ∞, and, for large transition rates, E_ij → 0, which corresponds to our intuition from the previous paragraph. The following definition for the transition energy, plotted in Fig. 2d, meets these two conditions:

$$E_{ij}\equiv -ln{\lambda }_{ij}+ln({\lambda }_{ij}+1).$$ (24)

Therefore, the sceond energy cost function is

$$E_{\text{tot}}=\sum _{i,j}-ln{\lambda }_{ij}+ln({\lambda }_{ij}+1).$$ (25)

Our results are insensitive to the exact definition of the function as long as the asymptotic behaviors at transition rates of zero and infinity are retained.

The results of numerical optimization of the rates λ_ij to minimize the CV₂ for a 5-state Markov chain are given in Fig. 5a. For large values of E_tot, the optimal solution is represented in blue. This solution asymptotes to $\frac{1}{4}$, which is the theoretical minimum for N = 5 (see Eq. 9). Thus the optimized transition rate matrix looks essentially identical to the ideal, infinite energy solution:

$$\mathbf{A}=\left(\begin{array}{ccccc}-\frac{4}{T}& 0& 0& 0& 0\\ \frac{4}{T}& -\frac{4}{T}& 0& 0& 0\\ 0& \frac{4}{T}& -\frac{4}{T}& 0& 0\\ 0& 0& \frac{4}{T}& -\frac{4}{T}& 0\\ 0& 0& 0& \frac{4}{T}& 0\end{array}\right),$$ (26)

where T ≡ 〈t_1N 〉. Since E_tot is finite, transition rates of exactly zero are not possible, but, for large enough values of E_tot, the rates given as zero in Eq. 26 are in fact optimized to near-zero values. Note that this is a different behavior than that seen in the previous section where reciprocal rates between nonadjacent states in the linear chain were optimized to exactly zero (or, at least, the machine limit) and only the forward and backward rates along the linear chain were affected by the amount of available energy. In this case, all of the rates in the matrix are affected by E_tot and the degree which the rates given as zero in Eq. 26 deviate from true zero depends on the energy. Thus, while in the previous section the linear architecture is maintained at all value of E_tot, optimization under the second energy function would be expected to corrupt the linear structure, and, indeed, as E_tot is decreased, all of the near-zero rates, including those between nonadjacent states in the linear chain, deviate farther from zero. Concomitantly, the minimum CV², as shown in Fig. 5a, is seen to rise as expected.

Figure 5.

a. The minimum achievable CV² resulting from numerical optimization of the rates of a 5-state Markov chain as a function of E_tot (given by Eq. 25). The blue trace corresponds to a solution close to the 5-state linear chain given by Eq. 26, which is the theoretical optimum. As E_tot decreases, this solution deviates from the optimal linear chain and the CV² increases from the theoretical limit ( $\frac{1}{4}$) until, at the intersection of the blue and green traces, the solution corresponding to a linear chain with four effective states (i.e. two of the five available states have merged; see Eq. 27) becomes optimal. This 4-state chain also deviates from its theoretical minimum with decreasing E_tot until the linear chain with three effective states (Eq. 28), shown in cyan, becomes optimal. The minimum energy limit corresponds to a chain with two effective states (Eq. 29), and this solution is represented with the magenta dot. See the text for a fuller interpretation of these results, b–d. The optimal transition rates as they vary with E_tot for Markov chains with five (b), four (c), and three (d) states. At large energy values, the rates along the lower subdiagonal of the transition rate matrix (i.e. the rates which compose the linear chain) are equal to $\frac{M}{T}$, while all other rates are essentially zero (thus the upper and lower sets of curves in b–d). These are the optimal solutions. As E_tot decreases, the rates deviate from their ideal values and the CV² grows as in a. The dashed vertical red lines mark the energy values where the CV² is equal for numerically optimized chains of different lengths. At E_5→4, for example, the minimum achievable CV² is the same for both the 5 and 4-state Markov chains. This is where the blue and green traces cross in a. It is clear from these crossing points that the linear structure of the shorter chain is essentially fully intact while that of the longer chain has started to degrade significantly. In d, the 3-state Markov chain is seen to converge to the 2-state solution (shown with the magenta dot) at E_min. One of the rates becomes $\frac{1}{T}$ while the others diverge to infinities (i.e. two of the three states merge).

The green trace in Fig. 5a corresponds to another stable solution of the optimization procedure, which, for large values of E_tot, is not globally optimal. Inspection of the solution reveals the following transition rate matrix:

$$\mathbf{A}=\left(\begin{array}{ccccc}-\frac{3}{T}& 0& \infty & 0& 0\\ \frac{3}{T}& -\frac{3}{T}& \infty & 0& 0\\ 0& \frac{3}{2T}& -{\infty }^2& \infty & 0\\ 0& \frac{3}{2T}& {\infty }^2& -\infty & 0\\ 0& 0& \infty & \frac{3}{T}& 0\end{array}\right),$$ (27)

where, in the third column, ∞² is an infinity of a different order than the other infinities in the column (e.g. 10¹⁰⁰ versus 10⁵⁰). This hierarchy of infinities is an artifact of the numerical optimization procedure, but the solution is nonetheless revealing. Essentially, states 3 and 4 are merged into a single state in this solution. Whenever the system is in state 3, it immediately transitions to state 4 because the infinity of the higher order (i.e. ∞²) dominates. From state 4, the system immediately transitions back to state 3, and thus states 3 and 4 are equivalent. There is a single outflow available from this combined state to state 5 with rate $\frac{3}{T}$. Furthermore, there are two sources of input into states 3 and 4 both from state 2, but, since the states are combined, this is the same as a single source with a total rate also of $\frac{3}{T}$. Finally, there is an irreversible transition from state 1 to 2 with rate $\frac{3}{T}$. This then is exactly the optimal solution for 4-state Markov chain: for large values of E_tot every forward rate is equal to $\frac{3}{T}$, all other rates are near zero, and the CV² asymptotes to the theoretical minimum of $\frac{1}{3}$.

The solution to which the cyan trace corresponds can be interpreted similarly to that of the green trace, except that in this case states 2, 3 and 4 have all merged and thus the effective number of states is three, not four. For large E_tot, the transition matrix approaches

$$\mathbf{A}=\left(\begin{array}{ccccc}-\frac{2}{T}& \infty & \infty & 0& 0\\ \frac{2}{3T}& -{\infty }^2& \infty & \infty & 0\\ \frac{2}{3T}& \infty & -{\infty }^2& \infty & 0\\ \frac{2}{3T}& {\infty }^2& {\infty }^2& -\infty & 0\\ 0& \infty & \infty & \frac{2}{T}& 0\end{array}\right),$$ (28)

which is the optimal solution for a 3-state Markov chain (i.e. the forward rates are $\frac{2}{T}$, the others rates are zero, and the asymptotic CV² is $\frac{1}{2}$).

The magenta dot represents the 2-state system where the first four states have all merged:

$$A=\left(\begin{array}{ccccc}-{\infty }^2& \infty & \infty & \infty & 0\\ \infty & -{\infty }^2& \infty & \infty & 0\\ \infty & \infty & -{\infty }^2& \infty & 0\\ {\infty }^2& {\infty }^2& {\infty }^2& -\infty & 0\\ \infty & \infty & \infty & \frac{1}{T}& 0\end{array}\right).$$ (29)

In this case, the constraints on the desired mean and on E_tot cannot both be met for arbitrary values of the two variables. There is only one rate available to the optimization procedure in a 2-state system, and thus, for mean T, the transition rate must be $\frac{1}{T}$. Therefore, E_tot is not a free variable and is locked to ln (T + 1) by Eq. 25. This is another point of difference from the results in the preceding section where the constraint on the mean could still be satisfied when the energy was zero (i.e. when all reciprocal pairs of rates of were equal).

Analysis of the behavior of the solutions with greater than two states as the total energy is decreased is revealing. In all cases, as expected, the minimum values of the CV² deviate from the infinite energy asymptotes, but, more interestingly, the curves cross. At the point when the blue and green traces cross in Fig. 5a, for example, the 4-state system becomes the globally optimal solution despite the fact that its theoretical minimum at infinite energies is higher than that of the 5-state system (i.e. $\frac{1}{3}>\frac{1}{4}$). This can be understood by considering how the available energy that constitutes a given value of E_tot is divided up amongst the rates of the system. The largest penalties are being paid for the near-zero rates, and thus most of the available energy is apportioned to maintain them. As E_tot is decreased, maintaining the near-zero rates becomes impossible, and so the network topology begins to deviate significantly from the infinite energy optimum with the CV² growing accordingly. This deviation occurs at higher values of E_tot for a 5-state system than for a 4-state system because there are more near-zero rates to maintain for a larger value of N.

Thus we can understand the tradeoff imposed on the system by the energy function given in Eq. 25. The inability to maintain a long irreversible linear chain at decreasing energy values drives the system to discard states and focus on maintaining a linear chain of a shorter length, rather than a branching or loopy chain with more states. Figs. 5b–d shows the degree to which the transition rates deviate from their optimal values for Markov chains of five, four, and three states. The energy thresholds below which a 4-state chain outperforms a 5-state chain and a 3-state chain outperforms a 4-state chain are indicated in the figures. It is clear that at these crossing points the linear structure of the shorter chain is essentially totally intact while that of the longer chain has been significantly degraded.

4.4 Comparison of energy functions I and II at finite nonminimal energies

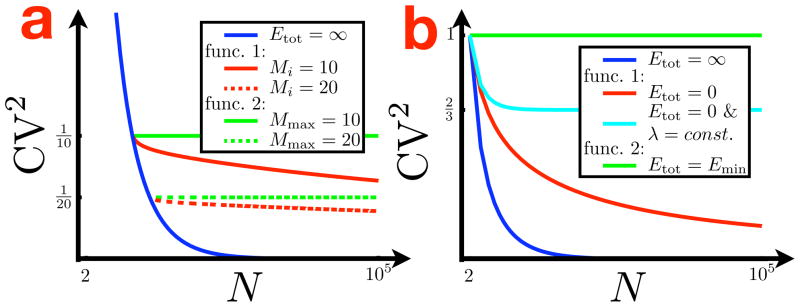
The results of the optimizations under the two energy functions in the preceding sections are illuminating. From the theoretical development of the optimal linear Markov chain topology (see Sec. 3), we saw that the CV² of the hitting time was equal to $\frac{1}{M}$ (Eq. 9), which suggests that a physical system can arbitrarily improve its temporal reliability by increasing the number of states. If, however, as in the second energy function (Eq. 25), a cost is incurred by a system for maintaining zero transition rates (which, functionally, results in incommunicability between states), then, given a finite amount of available energy, we see from Sec. 4.3 that there is some maximum number of states N_max achievable by the system regardless of the total allowable size of the state space N. The CV² is thus at best equal to $\frac{1}{M_{max}}$ where M_max ≡ N_max − 1 (i.e. assuming that the linear chain architecture with N_max states is essentially fully intact; see Fig. 5).

Alternatively, as in the first energy function (Eq. 13), by employing a cost incurred for the inclusion of asymmetries between reciprocal pairs of transition rates in the system topology (i.e. irreversible transitions), then, as shown in Sec. 4.2, only a subset of the total number of transitions can be close to irreversible, while the rest must be fully reversible with equal forward and backward transition rates (see Fig. 3). Although in this case a larger N will always result in a lower CV², a simple analysis reveals that an effective maximum number of states N_eff can be defined which is much less than N itself. If, as in the analysis in Sec. 4.2.2, one assumes that the first M_i transitions form a perfect, irreversible linear chain and that the remainder of the system consists of M_r fully reversible transitions (where N = M_i + M_r + 1), then, by combining Eqs. 18, 19, and 20, the CV² is given as

$${\text{CV}}^2=\frac{1}{M_i+\xi (M_r)}.$$ (30)

By comparing Eq. 30 with the CV² equation for the ideal chain (Eq. 9), we can equate the denominators and thus define an effective number of states as

$$N_{\text{eff}}\equiv M_i+\xi (M_r)+1.$$ (31)

Since ξ(M) grows logarithmically, N_eff ≈ M_i unless the magnitude of N is on the order of e^M_i or greater. Furthermore, since the available energy dictates what fraction of the N-state chain can be irreversible and thus the value of M_i, then, in the absence of a massive state space, the energy is the primary determining factor in setting the temporal variability while the value of N itself secondary.

From this it appears that the maximally reliable solutions at finite nonminimal energies under either energy constraint are in fact quite similar. If irreversibility is penalized, then, as long as N is limited enough such that ξ (M_r) ≪ M_i, the available energy sets the number of states to N_eff (≈ M_i). If, rather, incommunicability is penalized, then, regardless of how large N is permitted to be, the available energy mandates that the number of states be limited to N_max. Furthermore, in both cases, the solutions are essentially irreversible linear chains. The only difference between the two solutions—the diffusive tail at the end of the chain optimized under the first energy function—has minimal impact on the behavior of the system.⁷

Fig. 6a shows the relationship between the total allowable number of states N and the minimum achievable CV² under the two energy cost functions where the available energies have been tuned such that M_max and M_i are equal, finite, and nonzero. As is clear from the figure, although the variability does continue to decrease as N is increased past M_i for the solutions determined under the first energy function (in red), the difference compared to the variability resulting from the second energy function (in green) is minimal. The values of the CV² as functions of N are shown for two different settings of M_max and M_i, and although the domain of N stretches over several orders of magnitude in the figure, the primary determinants of the CV² are the values of M_max and M_i, not N, for both settings.

Figure 6.

a. The decrease in the CV² as a function of the total allowable size of the state space N for maximally reliable solutions determined under the first (in red) and second (in green) energy functions where the energies have been tuned such that M_i = M_max = 10 (solid lines) and M_i = M_max = 20 (dashed lines). Over a large range of N, the solutions determined under the first energy function are seen to deviate little from those determined under the second despite their long diffusive tails. The CV² in the infinite energy case ( $\frac{1}{M}$) is shown in blue as a reference. b. The CV² as a function of N for the minimal energy solutions resulting from the first energy function ( $\frac{1}{\xi (M)}$; in red) and the second energy function (1; in green). Unlike in a for nonminimal energies, these solutions differ quite significantly with N. However, if the range of transition rates is restricted, then the CV² of the solution determined under the first energy function does not decrease to zero with increasing N but rather reaches a constant as in the cyan trace for a maximally restricted range where all the transition rates are equal (then ${\text{CV}}^2=\frac{2}{3}$; see text for more details). The infinite energy solution is again shown for comparison. Note that the abscissae are plotted on a log scale.

4.5 Comparison of energy functions I and II at minimal energies

Although optimization at finite nonminimal energy values under the two cost functions results in similar solutions, at minimal energies, the solutions seem quite different. Recall from Sec. 4.2.1, that at E_tot = 0 (the minimal energy value under the first energy function), the CV² of the minimally variable solution is equal to $\frac{1}{\xi (M)}$ and thus decreases towards zero with increasing N. Under the second energy function, however, the CV² is always equal to 1 for all N at the minimal energy value (recall from Sec. 4.3 that, with mean hitting time T, the minimal energy value is ln(T + 1) at which point all of the states have merged leaving N_max equal to 2). These different behaviors as functions of N are shown in Fig. 6b in red and green respectively. Although $\frac{1}{\xi (M)}$ approaches zero much more slowly than the CV² of the infinite energy solution ( $\frac{1}{M}$), it is still significant compared to the CV² of the minimal energy solution under the second cost function (i.e. 1). However, as discussed in Sec. 4.2.1, to achieve a CV² of $\frac{1}{\xi (M)}$, the transition rates near the end of the linear chain must be on the order of N² times larger than the values of the rates near the beginning of the chain.

Maintaining such a large dynamic range of rates may be infeasible in the context of a specific system, and so it is reasonable to consider what the advantage is in terms of variability reduction of having such a large range of rates versus having a single nonzero rate (i.e. a constant rate λ for all reciprocal pairs of rates between adjacent states in the linear chain). By substituting a constant rate into Eq. 14 and simplifying, the following can be shown:

$${\text{CV}}^2=\frac{2}{3}\left(1+\frac{1}{N^2-N}\right).$$ (32)

This rapidly gives a CV² of $\frac{2}{3}$ with increasing N (as shown in cyan in Fig. 6b), and thus it is clear that only with an unrestricted range of rates can the variability be driven arbitrarily close to zero by adding states. If an unrestricted range is not feasible, then even at minimal energy values, the solutions given by the two energy cost functions are not qualitatively different. That is, both result in constant values of the CV² that are independent of N (compare the green and cyan traces in Fig. 6b).

4.6 Reliability of random transition rate matrices

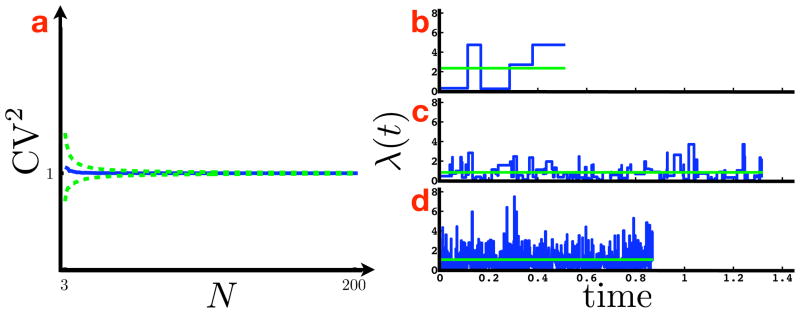
In all cases, under either energy function at any amount of available energy from the minimal possible value to infinity, the goal of the system is to reduce the temporal variability within the given energy constraints, and, as has been shown throughout this paper, this is achieved by choosing the maximally reliable network structure amongst the set of structures which meet the constraints. Thus, it is reasonable to consider the value of choosing an explicit structure rather than an arbitrary random connectivity between a set of states. In Fig. 7a we show the distribution of the CV² as a function of N, calculated empirically from 2000 random transition matrices at each value of N, with transition rates λ_ij drawn as independent identically distributed samples from an exponential distribution. As N increases, the distribution of the CV² quickly converges to a delta function centered at one. This is the CV² of a minimally reliable 2-state system. Numerical studies using other random rate distributions with support on the positive real line (e.g. the uniform, gamma, log-normal, etc.) produced similar results.

Figure 7.

a. The mean (in blue) and the ±1σ deviations (in green) of the CV² as a function of N, determined empirically from 2000 random transition rate matrices at each value of N, with rates drawn as i.i.d. samples from an exponential distribution. For large N, the distribution of the CV² is a delta function at 1. This indicates that random. N-state chains are performing identically to 2-state chains. b–d. The instantaneous (in blue) and mean (in green) transition rates to state N as the system transitions between the first N − 1 states of random (b) 10, (c) 100, and (d) 1000-state chains with transition rates drawn i.i.d. from an exponential distribution with mean 1. The correlation time of the instantaneous transition rate scales as 1/N, and so, for large N, the mean rate, which is also the mean of the distribution from which the transition rates are drawn, dominates.

While initially surprising, the convergence observed in Fig. 7a can be easily understood as a consequence of the averaging phenomenon illustrated in Figs. 7b–d. These figures show λ (t), the instantaneous transition rate to state N, for sample evolutions of random matrices with 10, 100, and 1000 states. If the state of the system at time t is given by q(t), then λ (t) equals λ_Nq(t), the rate of transition from state q(t) to state N. As is clear from the figures, the correlation time of λ (t) goes to zero with increasing N (it can be shown to scale as 1/N), and so a law of large numbers averaging argument can be applied to replace λ (t) with its mean (i.e. λ̄, the mean of the distribution from which the transition rates are drawn). In particular, the time-rescaling theorem [Brown et al., 2002] establishes that the random variable u, defined as

$$u={\int }_0^{t_{1N}}\lambda (t)dt,$$ (33)

is drawn from an exponential distribution with mean one. By the averaging argument, u reduces as follows:

$$\underset{N\to \infty }{lim}u=\overline{\lambda }{t}_{1N}.$$ (34)

Finally, since u is distributed exponentially with mean one, then t_1N is distributed exponentially with mean 1/λ̄, and thus must have a CV² of one (confirming the numerical results).

These results make clear the advantage of specific network structure over arbitrary connectivity. A CV² of 1 is the same as the reliability of a 2-state, one-step process. That is, a random network structure, regardless of the size of N, is minimally reliable.

5 Summary

Many physical systems require reliability in signal generation or temporal processing. We have shown that, for systems which may be modeled reasonably well as Markov chains, an irreversible linear chain architecture with the same transition rate between all pairs of adjacent states (Fig. 1b) is uniquely optimal over the entire set of possible network structures in terms of minimizing the variability of the hitting time t_1N (equivalently, the architecture that optimally minimizes the variability of the total generated signal F_1N is a linear chain with transition rates between pairs of adjacent states that are proportional to the state-specific signal accumulation rates). This result suggests that a physical system could become perfectly reliable by increasing the length of the chain, and so we have attempted to understand why perfect reliability is not observed in natural systems by employing energy cost functions which, depending on the amount of available energy, reduce the possible set of network structures by some degree. Although the two functions are quite different, the optimal network structures resulting from maximizing the system reliability under the constraints of either function are in fact quite similar. In short, they are irreversible linear chains with a fixed maximum length.

We would predict to see that natural systems for which temporal or total signal reliabilities are necessary features would be composed of linear chains of finite length with the length determined by the specific constraint encountered by the system. This prediction has applications across many disciplines of biology. For example, it suggests both that the sequence of openings and closings in the assemblage of ion channels responsible for active membranes processes (i.e. action potentials), and the progression of a dynamical neural network through a set of intermediate attractor states during the cognitive task of estimating an interval of time, should be irreversible linear processes. Our analysis is also useful in the event that some system for which signal reliability is important is found to have a branching or loops structure. By setting the linear structure as the theoretical limit, deviations from this limit may offer insight into what other counteracting goals physical systems are attempting to meet.

Appendix

A.1 Proof of the optimality of the linear, constant-rate architecture

The primary theoretical result of this paper is that a linear Markov chain with the same transition rate between all pairs of adjacent states is optimally reliable in terms of having the lowest CV² of the hitting time from state 1 to state N of any N-state Markov chain (see Fig. 1b). To establish this result, we prove the following two theorems.

Theorem 1 (General bound)

The following inequality holds for all Markov chains of size N and all pairs of states i and j:

$${\text{CV}}_{ij}^2\ge \frac{1}{N-1},$$ (35)

where the ${\text{CV}}_{ij}^2$ is the squared coefficient of variation of t_ij, the hitting time from state i to j.

Theorem 2 (Existence and uniqueness)

The equality ${\text{CV}}_{ij}^2=\frac{1}{N-1}$ holds if and only if states i and j are the first and last states of an irreversible, N-state linear chain with the same forward transition rate between all pairs of adjacent states and with state j as a collecting state.

We employ an inductive argument to prove these theorems (i.e. by assuming that they hold for networks of size N − 1 and proving that they hold for networks of size N). It is trivial to establish the base case of N = 2. Since the random variables t₁₂ and t₂₁ are both exponentially distributed (i.e. with means 1/λ₂₁ and 1/λ₁₂ respectively), and since the CV² for exponential distributions is known to be unity, Thm. 1 holds. Furthermore, both t₁₂ and t₂₁ satisfy the conditions for Thm. 2 (i.e. they are hitting times between the first and last states of linear chains with the same transition rates between all pairs of adjacent states), and both saturate the bound. As they are the only hitting times in a 2-state network, then Thm. 2 also holds for N = 2. This establishes a base case and allows us to employ an inductive argument to prove the general result (i.e. by assuming that Thms. 1 and 2 hold for networks of size N − 1 and proving that they hold for networks of size N).

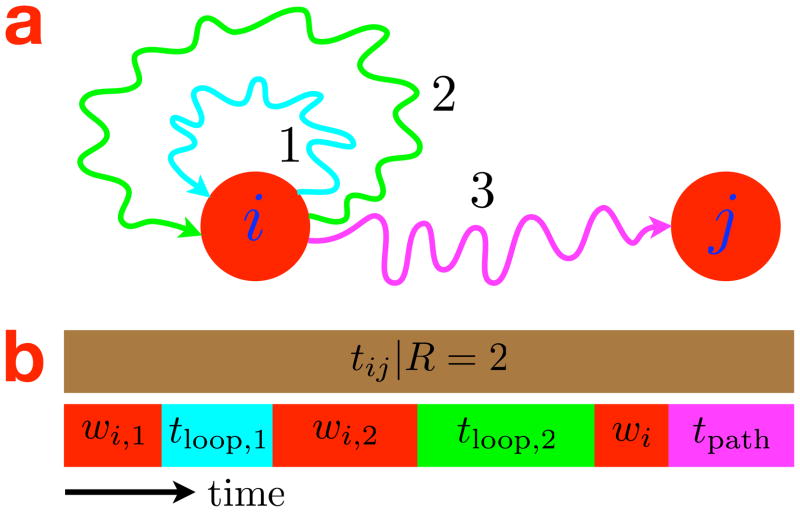
The logic of the proof is illustrated in Fig. 8. We break up the hitting time t_ij into a sum of simpler, independent random variables whose means and variances can be easily determined and to which some variance inequalities and the induction principle can be applied. Specifically, t_ij can be decomposed into the following sum:

$$t_{ij}=t_{i+1}+t_{\text{path}},$$ (36)

where t_i+l is the total time the system spends in the start state i and during any loops back to state i, while t_path is the time required for the transit along the path through the network to state j after leaving state i for the final time. The important part of this decomposition is that t_path is a random variable over a reduced network of size N −1 (excluding state i), which will allow us to apply the inductive principle. Since t_i+l and t_path are independent variables due to the Markov property, their means and variances simply add, and so we can write down the following expression for the ${\text{CV}}_{ij}^2$ of the hitting time t_ij:

$$\begin{array}{l}{\text{CV}}_{ij}^2\equiv \frac{var(t_{ij})}{{\langle t_{ij}\rangle }^2}\\ =\frac{var(t_{i+l})+var(t_{\text{path}})}{{(\langle t_{i+l}\rangle +\langle t_{\text{path}}\rangle )}^2}.\end{array}$$ (37)

Figure 8.

a. A sample path through an N-state Markov chain conditioned on the assumption that the system loops back to return to the start state i twice (R = 2). By conditioning the hitting time t_ij on such a path, proof-by-induction is possible since the time required for the final transit to state j refers, by definition, to a network of size N − 1 excluding state i. The wavy lines indicate unspecified paths requiring unspecified numbers of transitions, b. A schematic of how the hitting time t_ij conditioned on two loops (R = 2) is decomposed into a set of conditionally independent random variables according to Eqs. 36 and 38. The brown box represents the conditional hitting time t_ij|R, while the smaller boxes represent the proportion of the total time due to, in sequential order from left to right: w_i,1, the dwell time in state i prior to loop 1; t_loop,1, the subsequent time required to loop back to i; w_it2, the dwell time in i prior to loop 2; tl_oop,2, the subsequent time required to loop back to i; w_i, the dwell time in i prior to the final transit to j; and t_path, the time required for the final transit to j. Note that the blocks representing the loop times and the final transit time correspond in color to the analogous wavy lines in a.

To establish Thm. 1, this quantity must not be less than $\frac{1}{N-1}$ for any topology, and, to establish Thm. 2, it must equal $\frac{1}{N-1}$ only for a hitting time t_ij where i is the first state and j the final state of a constant-rate, irreversible linear chain of length N. To analyze Eq. 37 and thus establish these theorems, we need expressions for the means and variances of the total pre-final transit time t_i+l and of the final transit time t_path.

A.1.1 The mean and variance of the pre-final transit time t_i+l

The statistics of t_i+l can be determined by first considering the conditional case where the number of return loops back to state i prior to hitting state j is assumed to be R. Then t_i+l (the sum of the total dwell time in start state i plus the total loop time) conditioned on R can be further decomposed as follows:

$$t_{i+l}\mid R=\left(\sum _{r=1}^R{w}_{i,r}+t_{\text{loop},r}\right)+w_i,$$ (38)

where w_i,r is the dwell time in state i at the beginning of the r^th loop, t_loop,r is the time required to return to state i for the r^th loop, and w_i is the dwell time in state i prior to the final transit to state j.⁸ The total hitting time t_ij conditioned on R loops is given as the sum of the right-hand side of Eq. 38 and t_path (see Fig. 8 for a schematic when R = 2).

The conditional pre-final transit time t_i+l|R is simple to analyze since, due to the Markov principle, the random variables on the right-hand side of Eq. 38 are all conditionally independent given R. Thus, we can calculate the conditional mean and variance as

$$\begin{array}{l}{\langle t_{i+l}\rangle }_{p(t_{i+l}\mid R)}=\left(\sum _{r=1}^R\langle w_{i,r}\rangle +\langle t_{\text{loop},r}\rangle \right)+\langle w_i\rangle \\ =(R+1)\langle w_i\rangle +R\langle t_{\text{loop}}\rangle \end{array}$$ (39)

and

$$\begin{array}{l}var{(t_{i+l})}_{p(t_{i+l}\mid R)}=(R+1)var(w_i)+Rvar(t_{\text{loop}})\\ =(R+1){\langle w_i\rangle }^2+Rvar(t_{\text{loop}}),\end{array}$$ (40)

where we have used the notation that 〈f(x)〉_p(x) and var(f (x))_p(x) are defined, respectively, as the mean and variance of f(x) over the distribution p(x). In Eqs. 39 and 40, we are able to drop the r indices since we assume time homogeneity and thus that (1) the distribution over the dwell time in state i prior to loop r (w_i,r) is the same for every loop r and the same as the distribution over the dwell time in i prior to the final transit to j (w_i), and that (2) the distribution over the time required to loop back to i for the r^th loop (t_loop,r) has the same distribution for each loop. Furthermore, in Eq. 40, since the dwell time w_i is an exponentially distributed random variable and thus has a variance equal to the square of its mean, we have substituted var(w_i) with 〈w_i〉².

To construct expressions for the marginal mean and variance of the pre-final transit time (〈t_i+l〉_p(ti+l) and var(t_i+l)_p(ti+l)) from the conditional mean and variance (Eqs. 39 and 40), the following identities are useful:

$${\langle x\rangle }_{p(x)}={\langle {\langle x\rangle }_{p(x\mid y)}\rangle }_{p(y)}$$ (41)

and

$$var{(x)}_{p(x)}=var{\left({\langle x\rangle }_{p(x\mid y)}\right)}_{p(y)}+{\langle var{(x)}_{p(x\mid y)}\rangle }_{p(y)}.$$ (42)

Thus, for the marginal mean, we have

$$\begin{array}{l}{\langle t_{i+l}\rangle }_{p(t_{i+l})}={\langle {\langle t_{i+l}\rangle }_{p(t_{i+l}\mid R)}\rangle }_{p(R)}\\ ={\langle (R+1)\langle w_i\rangle +R\langle t_{\text{loop}}\rangle \rangle }_{p(R)}\\ =(\langle R\rangle +1)\langle w_i\rangle +\langle R\rangle \langle t_{\text{loop}}\rangle .\end{array}$$ (43)

Similarly, for the marginal variance, we have

$$\begin{array}{l}var{(t_{i+l})}_{p(t_{i+l})}=var{\left({\langle t_{i+l}\rangle }_{p(t_{i+l}\mid R)}\right)}_{p(R)}+{\langle var{(t_{i+l})}_{p(t_{i+l}\mid R)}\rangle }_{p(R)}\\ =var{\left((R+1)\langle w_i\rangle +R\langle t_{\text{loop}}\rangle \right)}_{p(R)}+{\langle (R+1){\langle w_i\rangle }^2+Rvar(t_{\text{loop}})\rangle }_{p(R)}\\ =var{\left(R\langle w_i\rangle +R\langle t_{\text{loop}}\rangle \right)}_{p(R)}+(\langle R\rangle +1){\langle w_i\rangle }^2+\langle R\rangle var(t_{\text{loop}})\\ =var(R){(\langle w_i\rangle +\langle t_{\text{loop}}\rangle )}^2+(\langle R\rangle +1){\langle w_i\rangle }^2+\langle R\rangle var(t_{\text{loop}})\\ =\langle R\rangle (\langle R\rangle +1){(\langle w_i\rangle +\langle t_{\text{loop}}\rangle )}^2+(\langle R\rangle +1){\langle w_i\rangle }^2+\langle R\rangle var(t_{\text{loop}}),\end{array}$$ (44)

where we have used the fact that the mean dwell time 〈w_i〉 and the mean loop time 〈t_loop〉 are both independent of R, and, in the final step, the fact that the number of loops R is given by a shifted geometric distribution, and thus has a variance equal to 〈R〉(〈R〉 + 1).

By expanding the first term in Eq. 44, and then refactorizing and substituting in the expression for the mean (Eq. 43), we can rewrite the variance of t_i+l as

$$\begin{array}{l}var(t_{i+l})=\langle R\rangle \left(var(t_{\text{loop}})+{\langle t_{\text{loop}}\rangle }^2\right)+{\left((\langle R\rangle +1)\langle w_i\rangle +\langle R\rangle \langle t_{\text{loop}}\rangle \right)}^2\\ =\langle R\rangle \left(var(t_{\text{loop}})+{\langle t_{\text{loop}}\rangle }^2\right)+{\langle t_{i+l}\rangle }^2.\end{array}$$ (45)

A.1.2 The variance of the final transit time t_path in terms of hitting times

In order to get an expression for the variance of the time for the final transit t_path in terms of hitting times over reduced networks of size N − 1 (so that we can use induction), we apply the identity given in Eq. 42 to decompose the variance of t_path as

$$\begin{array}{l}var(t_{\text{path}})\equiv var{(t_{\text{path}})}_{p(t_{\text{path}})}\\ =var{\left({\langle t_{\text{path}}\rangle }_{p(t_{\text{path}}\mid k)}\right)}_{\widehat{p}(k)}+{\langle var{(t_{\text{path}})}_{p(t_{\text{path}}\mid k)}\rangle }_{\widehat{p}(k)},\end{array}$$ (46)

where state k is the first state visited by the system after state i at the beginning of the final transit from i to j. The random variable t_path was originally defined as the time required for the final transit to state j, and so, given a specific start state, t_path|k is thus the time required for the path from state k to state j, which is exactly the definition of the hitting time t_kj. Substituting this equivalence into Eq. 46, we get the following:

$$\begin{array}{l}var(t_{\text{path}})=var{(\langle t_{kj}\rangle )}_{\widehat{p}(k)}+{\langle var(t_{kj})\rangle }_{\widehat{p}(k)}\\ =var{(\langle t_{kj}\rangle )}_{\widehat{p}(k)}+{\langle {\text{CV}}_{kj}^2{\langle t_{kj}\rangle }^2\rangle }_{\widehat{p}(k)},\end{array}$$ (47)

where we have replaced the variance of the hitting time t_kj with the product of the squares of the CV and the mean, an equivalent formulation.

A.1.3 Establishing Theorem 1

Returning to the ${\text{CV}}_{ij}^2$ of the hitting time t_ij (Eq. 37), we can replace var(t_i+l) with the second term of Eq. 45 and var(t_path) with the second term of Eq. 47 (the first terms of Eqs. 45 and 47 are nonnegative) to state the following bound:

$${\text{CV}}_{ij}^2\ge \frac{{\langle t_{i+l}\rangle }^2+{\langle {\text{CV}}_{kj}^2{\langle t_{kj}\rangle }^2\rangle }_{\widehat{p}(k)}}{{(\langle t_{i+l}\rangle +\langle t_{\text{path}}\rangle )}^2}.$$ (48)

Next, we can employ the inductive step of the proof and assume that Thm. 1 is true for the reduced networks represented by t_kj (recall that these subnetworks are of size N − 1 since the i^th state is withheld by definition from t_path and thus t_kj). This substitution yields the expression

$${\text{CV}}_{ij}^2\ge \frac{{\langle t_{i+l}\rangle }^2+\frac{1}{N-2}{\langle {\langle t_{kj}\rangle }^2\rangle }_{\widehat{p}(k)}}{{(\langle t_{i+l}\rangle +\langle t_{\text{path}}\rangle )}^2}.$$ (49)

We can also use the fact that the second moment of a random variable is not less than the square of its mean (i.e. 〈x²〉 ≥ 〈x〉²) to perform an additional inequality step:

$${\text{CV}}_{ij}^2\ge \frac{{\langle t_{i+l}\rangle }^2+\frac{1}{N-2}{{\langle \langle t_{kj}\rangle \rangle }^2}_{\widehat{p}(k)}}{{(\langle t_{i+l}\rangle +\langle t_{\text{path}}\rangle )}^2}.$$ (50)

Finally, recalling that the hitting time 〈t_kj〉 is equivalent to 〈t_path〉 _p(tpath|k), we can use the identity given in Eq. 41 to replace 〈t_kj〉 _p̂(k) and state the following final expression for the ${\text{CV}}_{ij}^2$:

$${\text{CV}}_{ij}^2\ge \frac{{\langle t_{i+l}\rangle }^2+\frac{1}{N-2}{\langle t_{\text{path}}\rangle }^2}{{(\langle t_{i+l}\rangle +\langle t_{\text{path}}\rangle )}^2}$$ (51)

or

$${\text{CV}}_{ij}^2\ge \frac{L^2+\frac{1}{N-2}{P}^2}{{(L+P)}^2},$$ (52)

where, for notational simplicity, we have replaced 〈t_i+l〉 and 〈t_path〉 with L and P respectively.

Our goal is to establish that the ${\text{CV}}_{ij}^2$ is not less than $\frac{1}{N-1}$ for all networks of size N. Since Eq. 52 is true for all networks, if the minimum value of the ratio on the right-hand side of the inequality is greater than or equal to $\frac{1}{N-1}$, the theorem is proved. The network topology affects this ratio through the values of L and P, and so we minimize with respect to these variables ignoring whether or not the joint minimum of L and P corresponds to a realizable Markov chain (i.e. since the unconstrained minimum cannot be greater than any constrained minimum, if the inequality holds for the unconstrained minimum, it must hold for all network structures).

$$\begin{array}{l}{\text{CV}}_{ij}^2\ge \underset{\text{networks}}{min}{\text{CV}}_{ij}^2\\ \ge \underset{L,P}{min}\frac{L^2+\frac{1}{N-2}{P}^2}{{(L+P)}^2}\end{array}$$ (53)

Note that the ratio in Eq. 53 is a Rayleigh quotient as a function of the vector (L, P)^T and thus has known minimum solution (which we derive here for clarity) [Strang, 2003]. Eq. 53 gives rise to a Lagrangian minimization as

$$\mathcal{L}(L,P)=L^2+\frac{1}{N-2}{P}^2-\phi (L+P),$$ (54)

with Lagrange multiplier φ. Differentiating with respect to L and P, gives expressions for these variables in terms of φ as

$$\begin{array}{l}\frac{\partial }{\partial L}\mathcal{L}(L,P)=2L-\phi \\ L_{min}=\frac{\phi }{2}\end{array}$$ (55)

and

$$\begin{array}{l}\frac{\partial }{\partial P}\mathcal{L}(L,P)=\frac{2P}{N-2}-\phi \\ P_{min}=\frac{\phi }{2}(N-2).\end{array}$$ (56)

Substituting these expressions back into Eq. 53 establishes the proof of the theorem:

$$\begin{array}{l}{\text{CV}}_{ij}^2\ge \frac{{\left(\frac{\phi }{2}\right)}^2+\frac{1}{N-2}{\left(\frac{\phi }{2}(N-2)\right)}^2}{{\left(\frac{\phi }{2}+\frac{\phi }{2}(N-2)\right)}^2}\\ =\frac{1+(N-2)}{{(1+(N-2))}^2}\\ =\frac{1}{N-1}.\end{array}$$ (57)

A.1.4 Establishing Theorem 2

In order to prove that an irreversible linear chain with the same forward transition rate between all adjacent pairs of states is the unique topology which saturates the bound on the ${\text{CV}}_{ij}^2$ of the hitting time t_ij given by Thm. 1, we follow a similar inductive approach as in Sec. A.1.3. To derive the inequality expression for the ${\text{CV}}_{ij}^2$ given by in Eq. 52, three successive inequality steps were employed. For Eq. 52 to be an equality—a necessary condition for the bound in Thm. 1 to also be an equality—each of those steps must be lossless. If the steps are lossless only for the linear chain architecture, then the theorem is proved.

Consider the second inequality step (the inductive step) in Sec. A.1.3 which results in Eq. 49. Recall that the hitting times t_kj represent subnetworks of size N − 1 starting in some set of states where every k ∈ is reachable by a single transition from state i. For Eq. 49 to be an equality, the ${\text{CV}}_{kj}^2$ must be equal to $\frac{1}{N-2}$ for all k ∈ . By assuming the inductive hypothesis that, for networks of size N −1, constant-rate linear chains are the only topologies which saturate the bound, then, for Eq. 49 to be an equality, all the states in set must be start states of linear chains of length N − 1. This is clearly possible only if the set consists of a single state k.

This constraint, that there is a single state k reachable by direct transition from state i and that this state is the start state of a constant-rate linear chain of length N − 1, forces the other two inequality steps in Sec. A.1.3 (Eqs. 48 and 50) to also be equalities. The mean number of loops 〈R〉 is zero since no loops are possible (i.e. after transitioning from state i to k the system follows an irreversible linear path to j which never returns to i), and so the first term of Eq. 45 is zero. Furthermore, the variance of 〈t_kj〉 is zero since there is only one k ∈ , and so the first term of Eq. 47 is also zero. Thus the substitutions comprising the first inequality step (Eq. 48) are lossless. Similarly, since there is only one k ∈ , the second moment of 〈t_kj〉 equals the square of its mean, which makes the substitution resulting in the final inequality (Eq. 50) also lossless.

Therefore, if and only if the network topology is such that state k is the only state reachable from state i and state k is the start state of a constant-rate linear chain of length N −1, then the following holds:

$${\text{CV}}_{ij}^2\ge \frac{{\langle t_{i+l}\rangle }^2+\frac{1}{N-2}{\langle t_{\text{path}}\rangle }^2}{{(\langle t_{i+l}\rangle +\langle t_{\text{path}}\rangle )}^2}.$$ (58)

We can simplify this expression by noting (1) that R = 0 and so 〈t_i+l〉 = 〈w_i〉 = 1/λ_ki where λ_ki is the transition rate from state i to state k, (2) that there is only one k ∈ and so 〈t_path〉 = 〈t_kj〉, and (3) that t_kj represents a constant-rate linear chain of length N − 1 and so its mean hitting time will be the number of transitions divided by the constant transition rate (i.e. $\langle t_{kj}\rangle =\frac{N-2}{\lambda }$ for constant rate λ):

$$\begin{array}{l}{\text{CV}}_{ij}^2=\frac{{\left(\frac{1}{{\lambda }_{ki}}\right)}^2+\frac{1}{N-2}{(\frac{N-2}{\lambda })}^2}{{\left(\frac{1}{{\lambda }_{ki}}+\frac{N-2}{\lambda }\right)}^2}\\ =\frac{{\lambda }^2+(N-2){\lambda }_{ki}^2}{{(\lambda +(N-2){\lambda }_{ki})}^2}.\end{array}$$ (59)

As in Sec. A.1.3, to determine the relative values of λ_ki and λ that minimize the ${\text{CV}}_{ij}^2$, we can define the following Lagrangian:

$$\mathcal{L}(\lambda ,{\lambda }_{ki})={\lambda }^2+(N-2){\lambda }_{ki}^2-\phi (\lambda +(N-2){\lambda }_{ki}).$$ (60)

Differentiating by each variable and substituting out the Lagrange multiplier φ establishes the theorem:

$$\begin{array}{l}\frac{\partial }{\partial \lambda }\mathcal{L}(\lambda ,{\lambda }_{ki})=2\lambda -\phi \\ \phi =2\lambda ,\end{array}$$ (61)

$$\begin{array}{l}\frac{\partial }{\partial {\lambda }_{ki}}\mathcal{L}(\lambda ,{\lambda }_{ki})=2(N-2){\lambda }_{ki}-\phi (N-2)\\ {\lambda }_{ki}=\frac{\phi }{2}\\ {\lambda }_{ki}=\lambda .\end{array}$$ (62)

All transition rates are equal and so the uniqueness proof is complete. An N-state Markov chain saturates the bound given in Thm. 1 if and only if it is an irreversible linear chain with the same forward transition rate between all pairs of adjacent states. Furthermore, the bound is only saturated for the hitting time from the first to the last state in the chain (Fig. 1b).

A.2 The moments of t_ij

For clarity, we give a derivation of the explicit formula for the n^th moment of the hitting time t_ij from state i to j for the Markov chain given by the transition rate matrix A_j. The subscript j in A_j is used to denote the fact that the j^th column of the matrix is a vector of all zeros (i.e. j is a collecting state). For the purposes of this derivation, we assume that the underlying transition rate matrix A, without the connections away from j removed, represents a Markov chain for which all states are reachable from all other states in a finite amount of time. In other words, A is assumed to be ergodic (although the resulting formulae still hold if this assumption is relaxed). Substituting t for t_ij to simplify notation and using the expression for the probability distribution of t_ij given in Eq. 6, we have

$$\begin{array}{l}\langle t^n\rangle ={\int }_0^{\infty }{t}^{n}p(t)dt\\ ={\int }_0^{\infty }{t}^n{\mathbf{e}}_j^T{\mathbf{A}}_j{e}^{{\mathbf{A}}_{j}t}{\mathbf{e}}_{i}dt\\ ={\mathbf{e}}_j^T{\int }_0^{\infty }{t}^n{e}^{{\mathbf{A}}_{j}t}dt{\mathbf{A}}_j{\mathbf{e}}_i,\end{array}$$ (63)

where we have used the fact that a matrix commutes with the exponentiation of itself.

In order to evaluate this integral, it is convenient to construct an identity matrix defined in terms of A_j and a pseudoinverse of A_j, P_A. If the eigenvalue decomposition of A_j is RDL (with L = R⁻¹), then P_A ≡ RP_DL where P_D is a diagonal matrix composed of the inverse eigenvalues of A_j except for the j^th entry which is left at zero (the j^th eigenvalue of A_j is zero). In matrix notation, P_D is given as

$${\mathbf{P}}_{\mathbf{D}}\equiv {(\mathbf{D}+{\mathbf{e}}_j{\mathbf{e}}_j^T)}^{-1}-{\mathbf{e}}_j{\mathbf{e}}_j^T,$$ (64)

which gives P_A as

$$\begin{array}{l}{\mathbf{P}}_{\mathbf{A}}\equiv \mathbf{R}{\mathbf{P}}_{\mathbf{D}}\mathbf{L}\\ =\mathbf{R}\left[{(\mathbf{D}+{\mathbf{e}}_j{\mathbf{e}}_j^T)}^{-1}-{\mathbf{e}}_j{\mathbf{e}}_j^T\right]\mathbf{L}\\ ={[\mathbf{R}(\mathbf{D}+{\mathbf{e}}_j{\mathbf{e}}_j^T)\mathbf{L}]}^{-1}-\mathbf{R}{\mathbf{e}}_j{\mathbf{e}}_j^T\mathbf{L}\\ ={({\mathbf{A}}_j+{\mathbf{e}}_j{\mathbf{1}}^T)}^{-1}-{\mathbf{e}}_j{\mathbf{1}}^T,\end{array}$$ (65)

where, in the final step, we have used the fact that the j^th column of R (the j^th right eigenvector of A_j) is e_j (since the j^th column of A_j is 0) and the fact that the j^th row of L (the j^th left eigenvector) is 1^T ≡ (1, …, 1) (since the columns of A_j all sum to 0). Thus, Re_j = e_j and ${\mathbf{e}}_j^T\mathbf{L}={\mathbf{1}}^T$.⁹

To construct an appropriate identity matrix, we calculate the product of A_j and its pseudoinverse as

$$\begin{array}{l}{\mathbf{A}}_j{\mathbf{P}}_{\mathbf{A}}=\mathbf{RDL}·\mathbf{R}{\mathbf{P}}_{\mathbf{D}}\mathbf{L}\\ =\mathbf{R}(\mathbf{D}{\mathbf{P}}_{\mathbf{D}})\mathbf{L}\\ =\mathbf{R}(\mathbf{I}-{\mathbf{e}}_j{\mathbf{e}}_j^T)\mathbf{L}\\ =\mathbf{I}-{\mathbf{e}}_j{\mathbf{1}}^T,\end{array}$$ (66)

where we have used the fact that DP_D is an identity matrix except for a zero in the j^th diagonal entry (due to the non-inverted zero eigenvalue). Furthermore, it is trivial to show that ${\mathbf{A}}_j^n{\mathbf{P}}_{\mathbf{A}}^n={\mathbf{A}}_j{\mathbf{P}}_{\mathbf{A}}$ for any positive integer n (since A_je_j = 0), and so we have derived the following expression for the identity matrix:

$$\mathbf{I}={\mathbf{A}}_j^n{\mathbf{P}}_{\mathbf{A}}^n+{\mathbf{e}}_j{\mathbf{1}}^T.$$ (67)

Finally, this allows us to restate the transition rate matrix as

$$\begin{array}{l}{\mathbf{A}}_j={\mathbf{A}}_j·\mathbf{I}\\ ={\mathbf{A}}_j({\mathbf{A}}_j^n{\mathbf{P}}_{\mathbf{A}}^n+{\mathbf{e}}_j{\mathbf{1}}^T)\\ ={\mathbf{A}}_j^{n+1}{\mathbf{P}}_{\mathbf{A}}^n,\end{array}$$ (68)

where again we have used the fact that e_j is the eigenvector of A_j associated with the zero eigenvalue.

Substituting Eq. 68 and the eigenvalue decomposition of A_j into Eq. 63 gives

$$\begin{array}{l}\langle t^n\rangle ={\mathbf{e}}_j^T{\int }_0^{\infty }{t}^n{e}^{{\mathbf{A}}_{j}t}dt{\mathbf{A}}_j^{n+1}{\mathbf{P}}_{\mathbf{A}}^n{\mathbf{e}}_i\\ ={\mathbf{e}}_j^T{\int }_0^{\infty }{t}^n{e}^{\mathbf{RDL}t}dt{(\mathbf{RDL})}^{n+1}{\mathbf{P}}_{\mathbf{A}}^n{\mathbf{e}}_i\\ ={\mathbf{e}}_j^T{\int }_0^{\infty }{t}^n{\mathbf{R}e}^{\mathbf{D}t}\mathbf{L}dt\mathbf{R}{\mathbf{D}}^{n+1}\mathbf{L}{\mathbf{P}}_{\mathbf{A}}^n{\mathbf{e}}_i\\ ={\mathbf{e}}_j^T\mathbf{R}{\int }_0^{\infty }{t}^n{e}^{\mathbf{D}t}{\mathbf{D}}^{n+1}dt\mathbf{L}{\mathbf{P}}_{\mathbf{A}}^n{\mathbf{e}}_i.\end{array}$$ (69)

The off-diagonal elements of the integral portion of Eq. 69 are zero as is the j^th diagonal element (i.e. the zero eigenvalue of A_j associated with eigenvector e_j). The k^th diagonal element of the integral for k ≠ j is given by

$${\left[{\int }_0^{\infty }{t}^n{e}^{\mathbf{D}t}{\mathbf{D}}^{n+1}dt\right]}_k={\eta }_k^{n+1}{\int }_0^{\infty }{t}^n{e}^{{\eta }_{k}t}dt,$$ (70)

where η_k is the k^th eigenvalue. These integrals are analytically tractable:

$$\begin{array}{l}{\left[{\int }_0^{\infty }{t}^n{e}^{\mathbf{D}t}{\mathbf{D}}^{n+1}dt\right]}_k={\eta }_k^{n+1}{\int }_0^{\infty }\frac{d^n}{d{\eta }_k^n}{e}^{{\eta }_{k}t}dt\\ ={\eta }_k^{n+1}\frac{d^n}{d{\eta }_k^n}{\int }_0^{\infty }{e}^{{\eta }_{k}t}dt\\ ={\eta }_k^{n+1}\frac{d^n}{d{\eta }_k^n}\left(-\frac{1}{{\eta }_k}\right)\\ ={\eta }_k^{n+1}{(-1)}^{n+1}\frac{n!}{{\eta }_k^{n+1}}\\ ={(-1)}^{n+1}n!,\end{array}$$ (71)

where we have used the fact that all of the eigenvalues of A_j except the j^th are strictly negative, which is a result of the following argument. Since A_j is a properly structured transition rate matrix for a continuous time Markov chain, there exists a finite, positive dt such that I + A_jdt is a properly structured transition probability matrix for a discrete time Markov chain. We can rewrite this probability matrix as R (I + Ddt) L and use the Perron-Frobenius theorem, which states that the eigenvalues of transition probability matrices (i.e. the entries of I + Ddt) are all less than or equal to one [Poole, 2006]. Furthermore, since we assumed that the underlying Markov chain A is ergodic, the Perron-Frobenius theorem asserts that exactly one of the eigenvalues is equal to one. Thus, it is clear that one of the entries of D is equal to zero and the rest are negative.

Substituting the result from Eq. 71 back into Eq. 69, gives the final expression for the moments of the hitting time:

$$\begin{array}{l}\langle t^n\rangle ={(-1)}^{n+1}n!{\mathbf{e}}_j^T\mathbf{R}(\mathbf{I}-{\mathbf{e}}_j{\mathbf{e}}_j^T)\mathbf{L}{\mathbf{P}}_{\mathbf{A}}^n{\mathbf{e}}_i\\ ={(-1)}^{n+1}n!{\mathbf{e}}_j^T(\mathbf{I}-{\mathbf{e}}_j{\mathbf{1}}^T){\mathbf{P}}_{\mathbf{A}}^n{\mathbf{e}}_i\\ ={(-1)}^{n}n!{(\mathbf{1}-{\mathbf{e}}_j)}^T{\mathbf{P}}_{\mathbf{A}}^n{\mathbf{e}}_i.\end{array}$$ (72)

As an alternative to the preceding somewhat cumbersome algebra, it is also possible to use an intuitive argument to find the analytic expression for the first moment (mean) of the hitting time [Norris, 2004]. With the expression for the first moment known, the higher order moments can then be derived using Siegert’s recursion [Siegert, 1951, Karlin and Taylor, 1981].

A.3 The gradients of the mean, variance, and energy cost functions

From Sec. A.2, the expressions for the mean and variance of the hitting time t_1N are given as

$$\langle t_{1N}\rangle =-{(\mathbf{1}-{\mathbf{e}}_N)}^T{\mathbf{P}}_{\mathbf{A}}{\mathbf{e}}_1$$ (73)

and

$$var(t_{1N})=2{(\mathbf{1}-{\mathbf{e}}_N)}^T{\mathbf{P}}_{\mathbf{A}}^2{\mathbf{e}}_1-{\langle t_{1N}\rangle }^2.$$ (74)

The definition of P_A (Eq. 65) and the expression for the derivative of an inverse matrix (∂M⁻¹ = −M⁻¹ (∂M) M⁻¹) give the following:

$$\begin{array}{l}\partial {\mathbf{P}}_{\mathbf{A}}=\partial \left[{({\mathbf{A}}_N+{\mathbf{e}}_N{\mathbf{1}}^T)}^{-1}-{\mathbf{e}}_N{\mathbf{1}}^T\right]\\ =-{({\mathbf{A}}_N+{\mathbf{e}}_N{\mathbf{1}}^T)}^{-1}\partial \mathbf{A}{({\mathbf{A}}_N+{\mathbf{e}}_N{\mathbf{1}}^T)}^{-1}\\ =\left[{({\mathbf{A}}_N+{\mathbf{e}}_N{\mathbf{1}}^T)}^{-1}-{\mathbf{e}}_N{\mathbf{1}}^T\right]\partial \mathbf{A}\left[{({\mathbf{A}}_N+{\mathbf{e}}_N{\mathbf{1}}^T)}^{-1}-{\mathbf{e}}_N{\mathbf{1}}^T\right]\\ =-{\mathbf{P}}_{\mathbf{A}}\partial \mathbf{A}{\mathbf{P}}_{\mathbf{A}},\end{array}$$ (75)

where we have defined ∂A as the derivative of A_N with respect to the variable of interest, and have used the fact that e_N and 1^T are the right and left eigenvectors of A_N associated with the zero eigenvalue and thus that both (∂A) e_N and 1^T∂A are zero. Therefore, the gradients of the mean and variance with respect to the optimization parameters θ_ij (where θ_ij ≡ − ln λ_ij for transition rate λ_ij) can be shown to be

$$\frac{\partial }{\partial {\theta }_{ij}}\langle t_{1N}\rangle ={(\mathbf{1}-{\mathbf{e}}_N)}^T{\mathbf{P}}_{\mathbf{A}}\partial {\mathbf{A}}^{ij}{\mathbf{P}}_{\mathbf{A}}{\mathbf{e}}_1,$$ (76)

and

$$\frac{\partial }{\partial {\theta }_{ij}}var(t_{1N})=2{(\mathbf{1}-{\mathbf{e}}_N)}^T{\mathbf{P}}_{\mathbf{A}}\left\{\left[{\mathbf{e}}_1{(\mathbf{1}-{\mathbf{e}}_N)}^T-\mathbf{I}\right]{\mathbf{P}}_{\mathbf{A}}\partial {\mathbf{A}}^{ij}-\partial {\mathbf{A}}^{ij}{\mathbf{P}}_{\mathbf{A}}\right\}{\mathbf{P}}_{\mathbf{A}}{\mathbf{e}}_1,$$ (77)

where the element in the k^th row and l^th column of the differential matrix ∂A^ij is given by

$${[\partial {\mathbf{A}}^{ij}]}_{kl}=\{\begin{array}{l}-{\lambda }_{ij},k=i\text{and}l=j\hfill \\ {\lambda }_{ij},k=j\text{and}l=j\hfill \\ 0,\text{otherwise}\hfill \end{array}.$$ (78)

Energy cost function I (Sec. 4.2), given as

$$E_{\text{tot}}=\sum _{i,j}\left|ln\frac{{\lambda }_{ij}}{{\lambda }_{ji}}\right|,$$ (79)

has a gradient of

$$\frac{\partial }{\partial {\theta }_{ij}}{E}_{\text{tot}}=\{\begin{array}{r}\hfill 1,{\lambda }_{ij}<{\lambda }_{ji}\\ \hfill -1,{\lambda }_{ij}>{\lambda }_{ji}\\ \hfill 0,{\lambda }_{ij}={\lambda }_{ji}\end{array},$$ (80)

while energy cost function II (Sec. 4.3), given as

$$E_{\text{tot}}=\sum _{i,j}-ln{\lambda }_{ij}+ln({\lambda }_{ij}+1),$$ (81)

has a gradient of

$$\frac{\partial }{\partial {\theta }_{ij}}{E}_{\text{tot}}=\frac{1}{1+{\lambda }_{ij}}.$$ (82)

A.4 Derivation of pure diffusion solution

At E_tot = 0 under the energy function given in Eq. 13, it is possible to analytically solve for the transition rates which minimize the CV² of the hitting time. First, note that all pairs of reciprocal rates must be equal (since the energy is zero), and furthermore, that all pairs of rates between nonadjacent states are equal to zero. Thus, to simplify notation, we shall only consider the rates λ_i for i ∈ {1, …, M} where λ_i ≡ λ_i,i+1 = λ_i+1,i and M ≡ N − 1. This yields the following transition rate matrix:

$${\mathbf{A}}_N\equiv \left(\begin{array}{cccccc}-{\lambda }_1& {\lambda }_1& 0& \cdots & 0& 0\\ {\lambda }_1& -{\lambda }_1-{\lambda }_2& {\lambda }_2& \cdots & 0& 0\\ 0& {\lambda }_2& -{\lambda }_2-{\lambda }_3& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& \cdots & -{\lambda }_{M-1}-{\lambda }_M& 0\\ 0& 0& 0& \cdots & {\lambda }_M& 0\end{array}\right).$$ (83)

From our general definitions of the moments of t_1N for abitrary Markov chains (Eq. 72), we have, respectively,

$$\langle t_{1N}\rangle =-{(\mathbf{1}-{\mathbf{e}}_N)}^T{\mathbf{P}}_{\mathbf{A}}{\mathbf{e}}_1$$ (84)

and

$$\begin{array}{l}var(t_{1N})=\langle t_{1N}^2\rangle -{\langle t_{1N}\rangle }^2\\ =2{(\mathbf{1}-{\mathbf{e}}_N)}^T{\mathbf{P}}_{\mathbf{A}}^2{\mathbf{e}}_1-{\langle t_{1N}\rangle }^2,\end{array}$$ (85)

where P_A ≡ (A_N + e_N 1^T)⁻¹ − e_N 1^T (Eq. 65) as before. For the specific tridiagonal matrix A_N given in Eq. 83, P_A can be shown to be

$${\mathbf{P}}_{\mathbf{A}}=\left(\begin{array}{cccccc}-{\sum }_{i\ge 1}\frac{1}{{\lambda }_i}& -{\sum }_{i\ge 2}\frac{1}{{\lambda }_i}& -{\sum }_{i\ge 3}\frac{1}{{\lambda }_i}& \cdots & -\frac{1}{{\lambda }_M}& 0\\ -{\sum }_{i\ge 2}\frac{1}{{\lambda }_i}& -{\sum }_{i\ge 2}\frac{1}{{\lambda }_i}& -{\sum }_{i\ge 3}\frac{1}{{\lambda }_i}& \cdots & -\frac{1}{{\lambda }_M}& 0\\ -{\sum }_{i\ge 3}\frac{1}{{\lambda }_i}& -{\sum }_{i\ge 3}\frac{1}{{\lambda }_i}& -{\sum }_{i\ge 3}\frac{1}{{\lambda }_i}& \cdots & -\frac{1}{{\lambda }_M}& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ -\frac{1}{{\lambda }_M}& -\frac{1}{{\lambda }_M}& -\frac{1}{{\lambda }_M}& \cdots & -\frac{1}{{\lambda }_M}& 0\\ {\sum }_{i\ge 1}\frac{i}{{\lambda }_i}& {\sum }_{i\ge 2}\frac{i}{{\lambda }_i}& {\sum }_{i\ge 3}\frac{i}{{\lambda }_i}& \cdots & \frac{M}{{\lambda }_M}& 0\end{array}\right),$$ (86)

from which, with a bit more manipulation, we can give expressions for the mean and variance as follows:

$$\begin{array}{l}\langle t_{1N}\rangle =\sum _{i=1}^M\frac{i}{{\lambda }_i}\\ ={\mathbf{x}}^T\mathbf{z}\end{array}$$ (87)

and

$$\begin{array}{l}var(t_{1N})=\sum _{i=1}^M\frac{1}{{\lambda }_i}\sum _{j=1}^M\frac{min{(i,j)}^2}{{\lambda }_j}\\ ={\mathbf{x}}^T\mathbf{Zx},\end{array}$$ (88)

where we have defined the vectors x and z as $x_i\equiv \frac{1}{{\lambda }_i}$ and

z_i ≡ i respectively, and the matrix Z as Z_ij ≡ min (i, j)².

Finding x, and thus the rates λ_i, that minimizes the CV² of t_1N is equivalent to employing Lagrangian optimization to minimize the variance while holding the mean constant at 〈t_1N 〉. This gives the following simple linear algebra problem:

$${\mathbf{x}}_{min}=arg\underset{\mathbf{x}}{min}({\mathbf{x}}^T\mathbf{Zx}-\alpha {\mathbf{x}}^T\mathbf{z}),$$ (89)

where x_min is guaranteed to be the unique optimum since Z is positive definite (Sec. A.4.1) and the constraint is linear. Thus the solution can be found by setting the gradient to zero:

$$\begin{array}{l}0={{\nabla }_{\mathbf{x}}({\mathbf{x}}^T\mathbf{Zx}-\alpha {\mathbf{x}}^T\mathbf{z})|}_{\mathbf{x}={\mathbf{x}}_{min}}\\ 0=\mathbf{Z}{\mathbf{x}}_{min}-\alpha \mathbf{z}\\ {\mathbf{x}}_{min}=\alpha {\mathbf{Z}}^{-1}\mathbf{z}.\end{array}$$ (90)

Note that we did not enforce that the elements of x (and thus the rates λ_i) be positive under this optimization. However, if the solution x_min has all positive entries, as will be shown, then this additional constraint can be ignored.

Some algebra reveals that Z⁻¹ is a symmetric tridiagonal matrix with diagonal elements

$${[{\mathbf{Z}}^{-1}]}_{ii}=\{\begin{array}{l}\frac{4i}{4i^2-1},i<M\hfill \\ \frac{1}{2M-1},i=M\hfill \end{array},$$ (91)

and subdiagonal elements

$${[{\mathbf{Z}}^{-1}]}_{i,i+1}={[{\mathbf{Z}}^{-1}]}_{i+1,i}=-\frac{1}{2i+1},i<M.$$ (92)

Substituting this inverse into the expression for the minimum above (Eq. 90) yields, for i < M,

$$\begin{array}{l}{[{\mathbf{x}}_{min}]}_i=\alpha {[{\mathbf{Z}}^{-1}\mathbf{z}]}_i\\ =\alpha \left(-\frac{1}{2i-1}\frac{4i}{4i^2-1}-\frac{1}{2i+1}\right)\left(\begin{array}{c}i-1\\ i\\ i+1\end{array}\right)\\ =\frac{2\alpha }{4i^2-1},\end{array}$$ (93)

and, for i = M,

$$\begin{array}{l}{[{\mathbf{x}}_{min}]}_M=\alpha {[{\mathbf{Z}}^{-1}\mathbf{z}]}_M\\ =\alpha \left(-\frac{1}{2M-1}\frac{1}{2M-1}\right)\left(\begin{array}{c}M-1\\ M\end{array}\right)\\ =\frac{\alpha }{2M-1}.\end{array}$$ (94)

For positive values of α—corresponding to positive values of 〈t_1N 〉—all of the elements of x_min are positive and thus this solution is reasonable. Therefore, the following rates minimize the processing time variability for a zero energy, purely diffusive system:

$$\frac{1}{{\lambda }_i}=\{\begin{array}{l}\frac{2\alpha }{4i^2-1},i\ne M\hfill \\ \frac{\alpha }{2M-1},i=M\hfill \end{array}.$$ (95)

To determine α from 〈t_1N 〉, we substitute the solution (Eq. 95) into the expression for the mean given by Eq. 87:

$$\begin{array}{l}\langle t_{1N}\rangle =\sum _{i=1}^M\frac{i}{{\lambda }_i}\\ =\left(\sum _{i=1}^{M-1}\frac{2\alpha i}{4i^2-1}\right)+\frac{\alpha M}{2M-1}+\left(\frac{2\alpha M}{4M^2-1}-\frac{2\alpha M}{4M^2-1}\right)\\ =\alpha \left[\left(\sum _{i=1}^M\frac{2i}{4i^2-1}\right)+\frac{M}{2M+1}\right]\\ =\alpha \left[\left(\sum _{i=1}^M\frac{2i}{4i^2-1}\right)+\left(\sum _{i=1}^M\frac{1}{4i^2-1}\right)\right]\\ =\alpha \left(\sum _{i=1}^M\frac{2i+1}{4i^2-1}\right)\\ =\alpha \left(\sum _{i=1}^M\frac{1}{2i-1}\right)\\ =\alpha \xi (M),\end{array}$$ (96)

where we have defined $\xi (M)\equiv {\sum }_{i=1}^M\frac{1}{2i-1}$ and have taken advantage of the following series identity (which can easily be shown by induction):

$$\frac{M}{2M+1}=\sum _{i=1}^M\frac{1}{4i^2-1}.$$ (97)

Our introduced function, ξ(M), can be shown to have the following closed-form solution [Abramowitz and Stegun, 1964]:

$$\xi (M)=\frac{1}{2}(\mathrm{\Psi }(M+\frac{1}{2})+\gamma )+ln2,$$ (98)

where Ψ(x) is the digamma function defined as the derivative of the logarithm of the gamma function (i.e. $\mathrm{\Psi }(x)\equiv \frac{d}{dx}ln\mathrm{\Gamma }(x)$) and γ is the Euler–Mascheroni constant.

From Eq. 96 we see that

$$\alpha =\frac{\langle t_{1N}\rangle }{\xi (M)},$$ (99)

which can be substituted back into Eq. 95 to give the optimal rates in terms of 〈t_1N 〉 rather than α:

$$\frac{1}{{\lambda }_i}=\{\begin{array}{l}\frac{2\langle t_{1N}\rangle }{\xi (M)(4i^2-1)},i\ne M\hfill \\ \frac{\langle t_{1N}\rangle }{\xi (M)(2M-1)},i=M\hfill \end{array}.$$ (100)

It is now possible to find an expression for the CV² in terms of M and 〈t_1N 〉. From the derivation of Eq. 90, we have

$$\mathbf{Z}{\mathbf{x}}_{min}=\alpha \mathbf{z},$$ (101)

which can be substituted into Eq. 88 to get

$$var(t_{1N})=\alpha {\mathbf{x}}_{min}^T\mathbf{z}.$$ (102)

Finally, using the expressions for the mean and for α (Eqs. 87 and 99), we obtain the following result:

$$\begin{array}{l}{\text{CV}}^2=\frac{\alpha \langle t_{1N}\rangle }{{\langle t_{1N}\rangle }^2}\\ =\frac{1}{\xi (M)}\\ =\frac{1}{\xi (N-1)},\end{array}$$ (103)

where we revert to a notation using the number of states N.

A.4.1 The matrix Z_ij ≡ min(i, j)² is positive definite

The M × M matrix Z introduced in Sec. A.4, where Z_ij ≡ min (i, j)², is positive definite. First, note the following identity:

$$n^2=\sum _{i=1}^{n}2i-1,$$ (104)

which can be easily proven inductively. Now let us define a set of vectors $\sqrt{\mathbf{2}\mathbf{i}-\mathbf{1}}$ for i = 1, …, M where vector $\sqrt{\mathbf{2}\mathbf{i}-\mathbf{1}}$ consists of i−1 zeros followed by M −i+1 elements all having the value $\sqrt{2i-1}$. For example,

$$\mathbf{1}\equiv {\left(1,\dots ,1\right)}^T,$$ (105)

$$\sqrt{\mathbf{3}}\equiv {\left(0,\sqrt{3},\dots ,\sqrt{3}\right)}^T,$$ (106)

and

$$\sqrt{\mathbf{5}}\equiv {\left(0,0,\sqrt{5},\dots ,\sqrt{5}\right)}^T.$$ (107)

From the identity given in Eq. 104, Z can be rewritten as the following sum of outer products:

$$\mathbf{Z}=\sum _{i=1}^M\sqrt{\mathbf{2}\mathbf{i}-\mathbf{1}}{\sqrt{\mathbf{2}\mathbf{i}-\mathbf{1}}}^T.$$ (108)

Now consider x^TZx for arbitrary nonzero x. We have

$$\begin{array}{l}{\mathbf{x}}^T\mathbf{Zx}={\mathbf{x}}^T\left(\sum _{i=1}^M\sqrt{\mathbf{2}\mathbf{i}-\mathbf{1}}{\sqrt{\mathbf{2}\mathbf{i}-\mathbf{1}}}^T\right)\mathbf{x}\\ =\sum _{i=1}^M{\mathbf{x}}^T\sqrt{\mathbf{2}\mathbf{i}-\mathbf{1}}{\sqrt{\mathbf{2}\mathbf{i}-\mathbf{1}}}^T\mathbf{x}\\ =\sum _{i=1}^M{\left({\sqrt{\mathbf{2}\mathbf{i}-\mathbf{1}}}^T\mathbf{x}\right)}^2,\end{array}$$ (109)

which must be nonnegative since it is a sum of squares. Furthermore, the $\sqrt{\mathbf{2}\mathbf{i}-\mathbf{1}}$ vectors are linearly independent and, since there are M of them, they form a basis. Since the projection of an arbitrary nonzero vector on at least one basis vector must be nonzero, one of the terms in the sum in Eq. 109 must be positive. Thus we have

$${\mathbf{x}}^T\mathbf{Zx}>0,$$ (110)

and so Z is positive definite.