Axons Pull on the Brain, But Tension Does Not Drive Cortical Folding

Abstract

During human brain development, the cerebral cortex undergoes substantial folding, leading to its characteristic highly convoluted form. Folding is necessary to accommodate the expansion of the cerbral cortex; abnormal cortical folding is linked to various neurological disorders, including schizophrenia, epilepsy, autism and mental retardation. Although this process requires mechanical forces, the specific force-generating mechanisms that drive folding remain unclear. The two most widely accepted hypotheses are (1) folding is caused by differential growth of the cortex and (2) folding is caused by mechanical tension generated in axons. Direct evidence supporting either theory, however, is lacking. Here we show that axons are indeed under considerable tension in the developing ferret brain, but the patterns of tissue stress are not consistent with a causal role for axonal tension. In particular, microdissection assays reveal that significant tension exists along axons aligned circumferentially in subcortical white matter tracts, as well as those aligned radially inside developing gyri (outward folds). Contrary to previous speculation, however, axonal tension is not directed across developing gyri, suggesting that axon tension does not drive folding. On the other hand, using computational (finite element) models, we show that differential cortical growth accompanied by remodeling of the subplate leads to outward folds and stress fields that are consistent with our microdissection experiments, supporting a mechanism involving differential growth. Local perturbations, such as temporal differences in the initiation of cortical growth, can ensure consistent folding patterns. This study shows that a combination of experimental and computational mechanics can be used to evaluate competing hypotheses of morphogenesis, and illuminate the biomechanics of cortical folding.

Introduction

In humans, cortical folding begins during the 26th week of gestation [1]. This process occurs after proliferation and migration of neural precursor cells and is largely concomitant with neuronal differentiation [2]. Disruptions in any of these developmental events can cause folding abnormalities, which are associated with various genetic perturbations and neurological disorders [3-5]. Folding is fundamentally a mechanical process that is intrinsic to the brain [2], and researchers have speculated for decades on specific folding mechanisms [2,6]. Data supporting these hypotheses are sparse and indirect, however, and the mechanisms that drive cortical folding remain poorly understood.

Two hypotheses have dominated thinking on this topic. The first is the intracortical differential growth hypothesis [7], whereby differences in growth rate between cortical layers cause the surface to buckle or fold (Fig. 1a). Using a mathematical model of buckling on an elastic foundation, Richman et al. [7] found reasonable agreement between computed and experimental results for the wavelength of the folding pattern in both normal and abnormal brains. The differential growth model also is supported by the finding that fetal brains in which most of the tissue below the cortex is surgically ablated prior to folding develop, at term, essentially normal folds, suggesting that folding depends largely on intracortical events [8]. While this model can reasonably reproduce small random folds found in normal, microgyric, and lissencephalic human fetuses, it does not predict the spatially consistent patterns of large primary folds [7]. In addition, the model predictions are based on the assumption that cortical grey matter is much stiffer (by an unrealistic factor of ten) than underlying tissue.

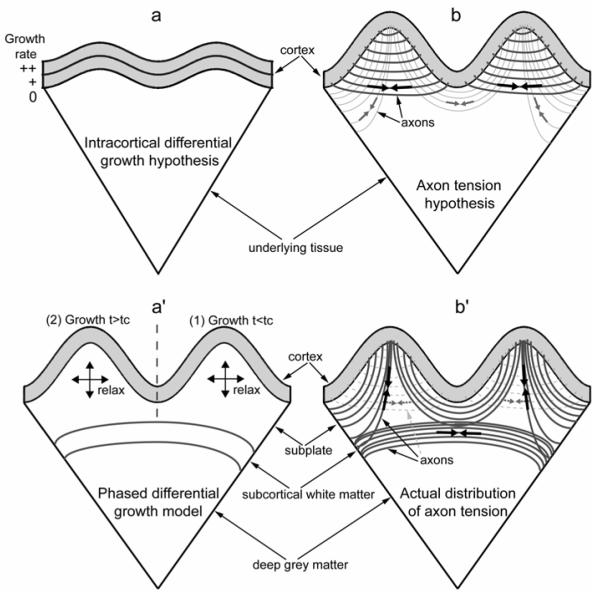
Figure 1. Schematics of postulated models for brain cortical folding.

(a) Intracortical differential growth model (Richman et al., 1975). Brain cortex is roughly divided into two layers with the outer layer growing faster (indicated by “++”) than the inner layer (“+”). All other underlying tissue is treated as a softer elastic foundation without any growth (“0”). Differential growth results in cortical buckling. (b) Axon tension hypothesis (Van Essen, 1997). Tension (black arrows) in axons that strongly interconnect two cortical regions pulls them closer to each other to form an outward fold. An inward fold forms between two outward folds to separate weakly interconnected cortical regions (grey arrows). (a’) Phased differential growth model. Cortical growth in region 1 (t < t_c) followed by cortical growth in region 2 (t > t_c) produces two folds. The underlying subplate grows to provide stress relaxation in response to the cortical growth. (b’) Actual distributions of axon tension based on present dissection and histology data. Axons are under tension (black arrows), and the majority of them are located circumferentially in the subcortical white matter tract and radially in the subplate or the cores of outward folds (from around P18). No circumferential tension (grey arrows) or axons (grey dotted lines) was detected in the cores (subplate) of outward folds.

The other, more recent hypothesis is the tension-based theory of cortical folding [9]. According to this model, tension generated by axons drives folding by pulling strongly interconnected cortical regions together (Fig. 1b). This hypothesis, which has gained increasing acceptance [10], is supported by the finding that axons sustain measurable tension both in culture [11,12] and in vivo [13], and by the observation that tension-driven shortening of axonal connections can create compact wiring of neural circuitry [9]. However, the tension-based hypothesis has not yet been tested directly.

In the present study, we test these hypotheses using a combination of experiment and computation. Microdissection assays reveal that axons are indeed under considerable tension in the developing ferret brain, but the patterns of tissue stress are not consistent with a causal role for axonal tension (Fig. 1b’). On the other hand, using computational (finite element) models, we show that differential cortical growth accompanied by remodeling of the subplate leads to outward folds and stress fields that are consistent with our microdissection experiments, supporting a mechanism involving differential growth (Fig. 1a’).

Experimental Methods

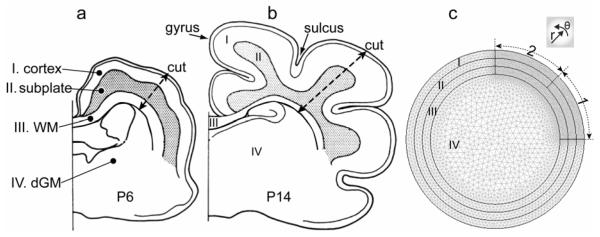
The brain is composed of white matter (primarily axons) and grey matter which contains axons, dendrites, neuronal cell bodies, and glial cells [14]. During folding, the ferret brain consists of four major layers (Fig. 2): cortex (cortical grey matter), subplate (becomes white matter in mature brains), subcortical white matter tract, and deep grey matter. The subcortical white matter contains the highest concentration of axons.

Figure 2. Schematic and model geometry of the developing ferret brain.

(a,b) Schematic of coronal section of ferret brain at postnatal day 6 (a) and 14 (b). Drawings were modified based on the tracings of ferret brain sections in Smart and McSherry (1986b). The ferret brain consists of four major layers: (I) cortex, (II) subplate, (III) subcortical white matter (WM), and (IV) deep grey matter (dGM). (c) Representative 2-D finite element model for a brain section before folding. The geometry is partitioned into the four major layers I-IV, each composed of triangular mesh elements. To simulate phased differential growth, a quarter of the cortex and corresponding subplate regions are further divided into two regions (labelled 1 and 2).

In the ferret, cortical folding occurs primarily during first three weeks after birth [15-18]. The ferret brain is smooth (lissencephalic) at birth (P0, postnatal day 0). Curvature changes that signify incipient folds are visible at P6 (Fig. 2a), and the folding pattern, consisting of outward folds (gyri) and inward folds (sulci), is nearly complete around P14-P18 (Fig. 2b). In general, folds develop initially from P6-P11 and substantially from P15-P21.

Tissue dissection

Dissection techniques are commonly used to reveal the stress state in living tissues [13,19,20]. The procedure used in this work follows published methods [13]. Briefly, whole brains were extracted from male ferrets (Marshall BioResources, North Rose, NY) on postnatal days P6, P18, and adult (9- and 12-month old) immediately after sacrifice (two animals at each age). Similar tests were also conducted on brains of other ages, e.g. P11, P15, and P21. The results shown in this article are representative observations from all these brains. Using a vibratome, we cut 600-μm-thick (800 μm for adult brains) coronal slices from brains submerged in ice-cold artificial cerebrospinal fluid (aCSF) [21]. Slices containing the subcortical white matter with corpus callosum were collected (2-4 slices from each animal) and allowed to recover for about 15 min at room temperature (~22°C) in aCSF. To eliminate potential artifacts caused by surface tension, all brain sections were fully submerged in aCSF during the experiments.

To probe the circumferential stress in different layers of cerebral gyri and sulci, a razor blade was used to make radial cuts completely through the slice thickness at different levels of depth into the brain: (1) through the cerebral cortex and the subplate, and (2) deeper into the subcortical white matter tract (Fig. 2a,b). The degree of opening at the cutting site served as an indicator of the magnitude of the stress perpendicular to the cutting line [13]. Tensile stress directed perpendicular to the cut causes local opening, while compressive stresses keep the cut closed. To minimize tissue damage by the blade and ensure a straight cut, only one cut at a specified depth was made at each gyrus or sulcus. In addition, to probe the stress in the radial direction, circumferential cuts of limited lengths were made with a surgical blade.

Diffusion tensor imaging (DTI)

Although major fiber architecture in the developing human brain has been well studied [22], less is known about the developing ferret brain. To correlate the stress field with tissue anisotropy and the distribution of fiber tracts, diffusion weighted images of brains fixed at P6, P21, and adult were acquired with a DTI protocol on a 4.7T Varian imaging system [15]. DTI detects anisotropic diffusion, which is a distinguishing feature of white matter tracts [23] and developing cortex [24,25] and thus provides a global view of the structure of the brain. Briefly, the animal was deeply anesthetized with sodium pentobarbital, and the brain perfusion-fixed with 4% paraformaldahyde. The brain was imaged ex vivo in fixative (P6, P21) or Krytox™ perfluorinated ether (adult), allowing long stable scans for enhanced signal-to-noise and spatial resolution. Imaging parameters were optimized based on age: TE=35-67ms; TR=3.5-4s; 250-350 μm isotropic voxels; 25 diffusion-weighting directions, b = 200-12,100 s/mm² (P6, P21); 22 directions, b = 2700 s/mm² (adult).

The local diffusion tensor was estimated by fitting the decay in signal amplitude to the exponential function predicted for ideal diffusion in an anisotropic medium (governed by the generalized Fick’s Law). Relative anisotropy (RA) was calculated from the eigenvalues of the diffusion tensor at each voxel. RA is the ratio of the standard deviation to the mean of the eigenvalues (RA=0 corresponds to isotropic diffusion). “Whisker” plots were generated by plotting the major eigenvector of the diffusion tensor at each voxel. Each vector was scaled in intensity and length by its corresponding RA value.

Immunohistochemistry

Histology was used to further confirm dominant axon orientations indicated by DTI. Animals were anesthetized and perfused transcardially with a fixative composed of 4% paraformaldehyde in 0.1M phosphate buffer (pH 7.4). Brains were postfixed for 24 hrs in the same fixative. Floating vibratome sections (50 μm thick) were washed in 0.01M PBS, quenched for 10 min in a solution of methanol containing 3% hydrogen peroxide, and incubated at room temperature for 1 hr in blocking solution (2% BSA/0.2% non-fat dry milk/0.4 % Triton X-100 in PBS) before incubation with primary antisera. Axon processes were labeled with monoclonal antiserum to SMI312 (Covance, 1:1000). Polyclonal MBP antibody (Sigma, 1:1000) was also used to detect myelinated axons. Following overnight incubation in primary antisera at 4°C, sections were thoroughly rinsed in PBS and incubated for 1 hr in complementary secondary antibodies (Vector Laboratories, Burlingame, CA, 1:200 dilution in 1% BSA in 0.01M PBS at pH 7.4). Sections were then rinsed and reacted in the dark with streptavidin-peroxidase reagent (standard Vectastain ABC Elite Kit, Vector Laboratories, Burlingame, CA). Finally immunoreactive product was visualized by VIP kit (Vector). Stained sections were mounted on glass slides, air-dried, dehydrated and coversilpped. Observations were made using a Nikon microscope.

Microindentation tests

Regional mechanical stiffness was measured on 800-μm-thick coronal brain slices using a custom-made microindentation device. The design of our tissue-level device is based on that of the cell indenter [26], which was originally developed for measuring cell stiffness and was the precursor of atomic force microscopy. Force is computed from the measured deflection of a thin glass cantilever beam (about 66 μm in diameter) of known stiffness. Indentation depth is recorded directly from the motion of a tip attached to the end of the beam. All experiments were conducted at room temperature, with the brain slice glued to the bottom of a dish filled with aCSF.

The slope of a linear regression fit to the approximately straight force-indentation curve (up to 10 μm) yielded the stiffness of the brain at the tested region. For small indentation depths, the material shear modulus (G) is proportional to the measured tissue stiffness (k) and can be estimated as [27]

$$G=\frac{k(1-\nu )}{2d},$$ (1)

where d the indenter diameter and ν is Poisson’s ratio. For example, for an incompressible material (ν = 0.5) with a 1 mdyn/μm stiffness measured by a 66-μm cylindrical indenter, the shear modulus is approximately 38 Pa. However, it is the relative modulus between regions, not the actual modulus, that is critical to the behavior of growth models for cortical folding [7].

At each developmental age, two brain slices were probed from the two animals used in the dissection experiments. In general, 3-16 locations were chosen for each designated region and three consecutive indentations were analyzed at each location. Hence, the mean and standard deviation of the stiffness are based on 9-48 data points for each region. To compare stiffness among different regions at a certain age or among different ages for a certain region, one-way ANOVA tests were used, followed by Tukey’s all-pairwise comparison. The significance level was taken as P < 0.05.

Computational Methods

Brain model

To explore the differential growth hypothesis, we created a nonlinear plane-stress finite element model for a brain slice using the software COMSOL Multiphysics (V.3.4, COMSOL AB, Providence, RI). As a first approximation, the slice is taken as an initially circular disk composed of four layers representing cortex, subplate, subcortical white matter (WM), and deep grey matter (dGM) (Fig. 2c). To simulate phased differential growth, a quarter of the cortex and corresponding subplate regions are further divided into two regions (labeled 1 and 2 in Fig. 2c). The model geometry is partitioned into triangular mesh elements, with the sufficiency of the mesh density confirmed by solving the problem for increasing densities.

Growth theory

Volumetric growth is modelled using the theory of Rodriguez et al. [28]. Briefly, the total deformation gradient tensor F is written in the form F = F^*·G, where G is the growth tensor and F^* is the elastic deformation gradient tensor that enforces geometric compatibility. The zero-stress configuration of each material element grows according to G, but stress depends only on F^*. In this formulation, therefore, the geometric and equilibrium equations are expressed in terms of F, but the constitutive equations are written in terms of F^*. The Cauchy stress tensor is given by the constitutive relation

$$\sigma ={\mathrm{J}}^{\ast -1}{\mathbf{F}}^{\ast }\cdot \partial \mathrm{W}∕\partial {\mathbf{F}}^{\ast \mathrm{T}},$$ (2)

where W is the strain-energy density function and J^* = det F^* is the elastic volume ratio.

For this two-dimensional problem, the growth tensor is written in the form G = G_rr e_re_r + G_θθ e_θe_θ + G_rθ e_re_θ + G_θr e_θe_r, where the G_ij are growth components relative to the undeformed cylindrical polar coordinates (r, θ), and e_i are the corresponding local unit vectors [29]. Depending on the region, the G_ij are either specified functions of time or determined through a mechanical growth law. Further details on the implementation of growth in COMSOL are given in Taber [30].

Material Properties

Our microindentation tests have revealed that the mechanical properties of white and grey matter are similar throughout the post-natal ferret brain (see the Results section). As a first approximation, both grey matter and white matter are assumed to be isotropic, nearly incompressible, pseudoelastic materials characterized by the modified neo-Hookean strain-energy density function

$$\mathrm{W}=\frac{1}{2}\mu ({\mathrm{I}}^{\ast }{\mathrm{J}}^{\ast -\frac{2}{3}}-3)+\mathrm{p}(1-{\mathrm{J}}^{\ast }-\frac{\mathrm{p}}{2\kappa }),$$ (3)

where μ and κ are the shear and bulk modulus, respectively, I^* = tr(F^*T· F^*) is a strain invariant, and p is a penalty variable introduced for nearly incompressible materials.

Stresses presented in the Results section are normalized relative to the shear modulus (e.g., the normalized circumferential stress is σ_θθ^*= σ_θθ/μ, where μ on average is about 40 Pa based on our microindentation tests). For numerical stability of simulations involving nearly incompressible material, we took κ to be three orders of magnitude larger than μ.

Simulation

The simulation for cortical folding is based on our measured stress distributions and the following lines of experimental observations: (1) during development, sulci and gyri form along a lateral to medial gradient, corresponding to regional differences in cortical growth [16,24]; (2) relative to the subcortical white matter tract, the bases of sulci move relatively little in the radial direction [17,18]; and (3) axonal tension is approximately the same order of magnitude as the shear modulus [13]. The major steps of the simulation are:

1. Differential growth is specified in the initially smooth brain disk. We set G_rr = G_θθ = 1 in subcortical white matter (Fig. 2c, layer III), while G_rr and G_θθ increase from 1 to 1.3 for all other regions. This induces tensile stress in the subcortical white matter tract that is similar in magnitude to the shear modulus [13].

2. One region of the cortex (Fig. 2c, layer I of region 1) grows circumferentially (G_rr remains at 1.3 from the previous step and G_θθ increases from 1.3 to 1.625), accompanied by underlying subplate growth (Fig. 2c, layer II of region 1) governed by the growth laws [28]

   $$\begin{array}{cc}\hfill & \mathrm{d}{\mathrm{G}}_{\mathrm{r}\mathrm{r}}∕\mathrm{d}{\mathrm{t}}^{\ast }=\mathrm{A}{{\sigma }_{\mathrm{r}\mathrm{r}}}^{\ast }{\mathrm{G}}_{\mathrm{r}\mathrm{r}}\hfill \\ \hfill & \mathrm{d}{\mathrm{G}}_{\theta \theta }∕\mathrm{d}{\mathrm{t}}^{\ast }=\mathrm{A}{{\sigma }_{\theta \theta }}^{\ast }{\mathrm{G}}_{\theta \theta }\hfill \\ \hfill & \mathrm{d}{\mathrm{G}}_{\mathrm{r}\theta }∕\mathrm{d}{\mathrm{t}}^{\ast }=\mathrm{d}{\mathrm{G}}_{\theta \mathrm{r}}∕\mathrm{d}{\mathrm{t}}^{\ast }=\mathrm{A}{{\sigma }_{\mathrm{r}\theta }}^{\ast },\hfill \end{array}$$ (4)

   where t^* is nondimensional time and A = 10 is a growth coefficient. The initial conditions are G_rr = G_θθ = 1.3 (from step i) and G_rθ = G_θr = 0 at t^* = 0. According to these relations, growth ceases when all stresses are zero. The value for A ensures relatively fast relaxation of subplate stresses caused by cortical expansion (consistent with the experimental results).

3. After growth from the previous step is complete, the other region of the cortex (Fig. 2c, layer I of region 2) grows circumferentially, accompanied by underlying subplate growth (Fig. 2c, layer II of region 2). The values of the regional parameters are the same as those used in (ii).

After growth is complete, radial cuts are simulated by freeing boundaries from the cortical surface to the subcortical white matter tract on half of the geometry.

Results

Stress distributions

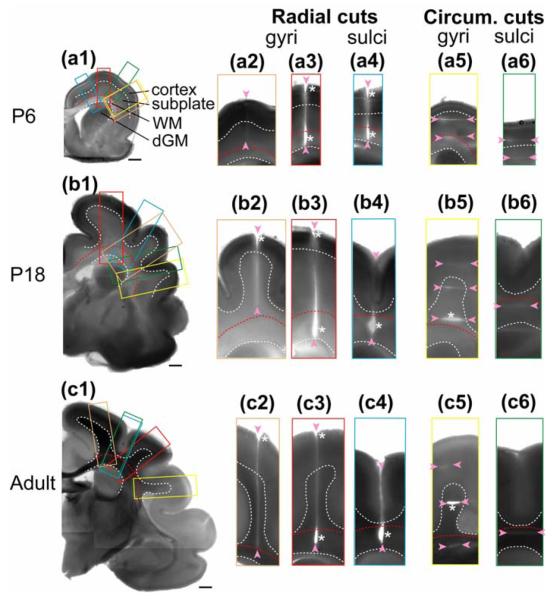
We used multiple cuts in different directions to map stress distributions during folding in the ferret brain. Radial cuts made through the cortex and subplate layers of gyri usually opened at the extreme outer cortical surface, but consistently remained closed in the core of the gyrus (Fig. 3-a2-c2). When radial cuts were extended into the subcortical white matter, however, the cuts opened and extended back into the subplate (Fig. 3-a3-c3). These results indicate that, during folding, significant circumferential tension (tension tangential to the original cortical surface) exists at the outer (pial) surface and in the subcortical white matter but not in the interior of the developing gyri.

Figure 3. Microdissection assay of developing ferret brain.

(a1-c1) Coronal brain sections at postnatal day (P) 6, 18 and adult. Dashed curves outline the boundaries between cortex, subplate, subcortical white matter (WM), and deep grey matter (dGM). Scale bars represent 1 mm. Color-coded rectangles indicate the regions shown in the close-ups to the right of each section. Cuts of various ranges (indicated by pairs of arrowheads) are made either radially (a2-a4, b2-b4, and c2-c4) or circumferentially (a5-a6, b5-b6, and c5-c6) on developing gyri and sulci as marked. Significant openings are indicated by asterisks.

Radial cuts into sulci produced opening patterns similar to those found in gyri (Fig. 3-a4-c4). The primary difference was that the outer region of the cortex did not open after P6 (Fig. 3-b4, c4), indicating the development of tangential compression at the outer surface of sulci.

At all ages, circumferential cuts in the cortex of both gyri and sulci did not open, revealing little or no radial tension (Fig. 3-a6,b5,c5). Circumferential cuts in the subplate region of sulci also did not open at any age (Fig. 3-a6-c6). Similar cuts through the cores (subplate) of incipient gyri of P6 ferrets also did not open (Fig. 3-a5), but the trend changed in older brains. At P18, circumferential cuts in gyral cores near the subcortical white matter opened considerably (Fig. 3-b5), and similar cuts in the fiber-rich interiors of mature gyri consistently sprang open at all locations (Fig. 3-c5).

Taken together, our dissection data indicate that considerable circumferential tension is present in subcortical white matter and at the pial surface of gyri at all ages studied. At the surfaces of sulci, an initial circumferential tension at P6 later becomes compression. In the subplate, radial tension begins to develop by P18 near the subcortical white matter and spreads throughout this region by maturity. Elsewhere, either compressive stresses, or very small tensile stresses are present in both directions at all ages.

Axon distributions

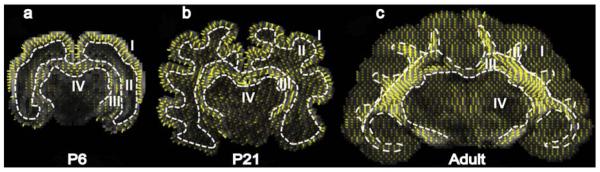
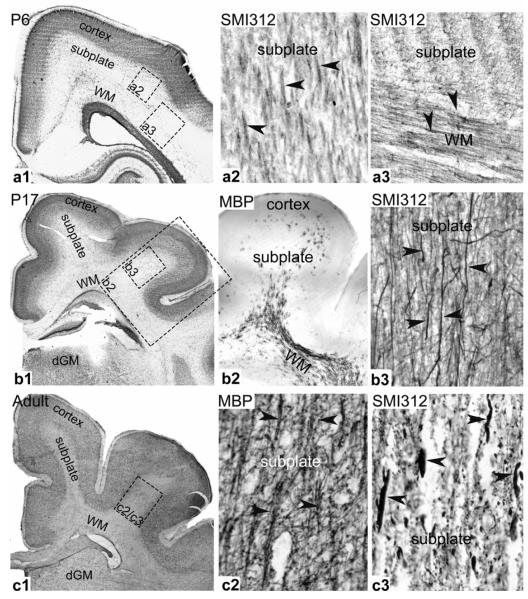
DTI images of the P6 brain indicate the presence of circumferential fibers in the subcortical white matter, and radially-directed fibrous structure in the cortex (Fig. 4a). Immunostaining reveals that the circumferential fibers are axons (Fig. 5-a3), as expected, but the radial cortical fibers are glial cells [31]. During folding, DTI indicates increased anisotropy in the subcortical white matter, as fiber density and myelination increase. Anisotropy in the cortex decreases (Fig. 4b,c), however, as the dendrites of cortical neurons extend and arborize (key processes underlying tangential cortical growth), and radial glia transform into astrocytes [24,31]. Hence, the main concentrations of axons are located in the subcortical white matter (Fig. 5).

Figure 4. Structural anisotropy of developing ferret brain measured by diffusion tensor imaging (DTI).

White dashed curves outline the boundaries between (I) cortex, (II) subplate, (III) subcortical white matter, and (IV) deep grey matter. Data were acquired ex vivo at postnatal day (P) 6, 21, and adult. Directions of yellow “whiskers” correspond to the direction of maximal diffusivity (the first eigenvector of the local diffusion tensor), which is indicative of fiber orientation in white matter, and radial glial orientation in immature grey matter. Whisker length and intensity are proportional to the local relative anisotropy (RA) of the tissue.

Figure 5. Histology of developing ferret brain.

Coronal brain slices were obtained and selectively stained at postnatal day (P) 6, 17 and adult. Neuronal cell bodies were marked by Nissl staining (darker areas in a1, b1, and c1), while myelinated and unmyelinated axons (indicated by arrowheads) were stained by MBP (myelin based protein) and SMI312 (neurofilament marker) immunoreactivity, respectively. Indicated rectangles are relative regions where axon staining is shown. Regions of cortex, subplate, subcortical white matter (WM), and deep grey matter (dGM) are labelled.

The subplate region initially has very low anisotropy, but DTI detects an increase in radially directed fibers in the core of gyri from age P21 onward (Fig. 4). Histology is consistent with these results, as organized fiber tracts are absent in the subplate at P6 (Fig. 5-a2), but myelinated axons in the core of P17 gyri start to emerge from the subcortical white matter and extend radially towards the cortex (Fig. 5-b2, b3). In the adult, myelinated axonal tracts are fully developed in the core of gyri with a predominant radial orientation (Fig. 5-c2, c3).

Taker together with the dissection results, these data indicate that the circumferential tension in the white matter tract, as well as the radial tension that develops near the tract by P18 and spreads throughout the gyral core in the mature brain, is associated with axons in the same orientations.

Mechanical stiffness

Regional stiffness of the brain tissue at each developmental age was measured by microindentation. Despite some statistically significant differences between regions (marked in Fig. 6), the stiffness at each developmental age is similar for the cortex, subplate, subcortical white matter (WM), and deep grey matter (dGM). During postnatal development between P6 and P18, significant changes in stiffness occurred only in the cortex (P < 0.05). During this period, the stiffness of all regions of the ferret brain was around 1 mdyn/μm, corresponding to a shear modulus of about 40 Pa (see Methods). The stiffness of each region in adult brains (around 2 mdyn/μm) was significantly larger than those at P6 and P18 (P < 0.0001) (Fig. 6). In our model for cortical folding, therefore, we assume that the mechanical properties of white and grey matter of different regions are the same throughout the post-natal ferret brain.

Figure 6. Regional stiffness of developing ferret brain.

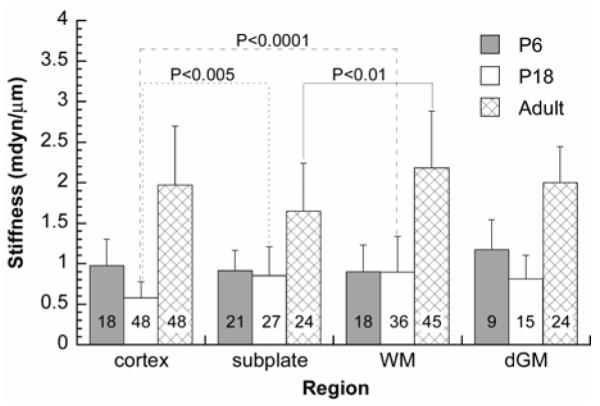
Indentation stiffness is reported as mean ± standard deviation. The total number of indentations for each case is shown in the corresponding column. Temporal differences: Between P6 and P18, significant changes in stiffness occurred only in the cortex (P < 0.05). The stiffness of each region in adult brains was significantly larger than those at P6 and P18 (P < 0.0001). Spatial differences: Despite some statistically significant differences between regions (shown in the figure), the stiffness at each developmental age is similar for the cortex, subplate, subcortical white matter (WM), and deep grey matter (dGM).

Computational results

Our computational model was used to explore the differential growth hypothesis. Prior to the onset of folding, isotropic growth in layers I, II, and IV (see Fig. 2c) relative to the subcortical white matter (layer III) introduces circumferential tension along the white matter tract and compression in the other regions of the brain (Fig. 7a). Cortical growth in region 1 of Fig. 2c, followed by growth in region 2 then produces two outward cortical folds (Fig. 7b,c). These outward folds are separated by an inward fold with a base that moves relatively little in the radial direction during the folding process.

Figure 7. Finite element model for cortical folding caused by phased differential growth.

(a-c) Model geometry and stress distribution after each major simulation step (i-iii, see Methods), leading to the formation of two gyri in designated regions. (d-g) A section of the model shown in (c) was used to simulate the effects of subsequent radial cuts within a gyrus (d,e) and a sulcus (f,g). The simulated cuts from the cortical surface through the subcortical white matter tract are indicated by pairs of arrowheads, and resulting openings are indicated by asterisks. (Panels e and g are close-ups of the dashed regions in d and f, respectively.) Colors indicate circumferential stress (σ_θθ^*) normalized relative to the material shear modulus.

After growth, the outer cortical surfaces of gyri and sulci are under circumferential (tangential) tension and compression, respectively, primarily due to bending of the expanding cortex, while the subplate sustains relatively little tension (Fig. 7c). Correspondingly, simulated radial cuts open only at the gyral surface and the subcortical white matter tract, but not at the sulcal surface and the subplate region (Fig. 7d-g).

Discussion

In this study, we tested two competing hypotheses for brain cortical folding. One is the axon tension hypothesis [9] and the other is the differential cortical growth hypothesis [7].

In testing the tension-based theory for cortical folding, we found that axons are indeed under considerable tension in the developing ferret brain. However, most of that tension is located along axons bundles in the subcortical white matter tract, which is too deep to significantly affect folding taking place near the surface of the brain (see Fig. 1b’). Furthermore, in the cores of developing gyri there is no significant axonal tension, or any other tension, in the circumferential direction (i.e., between the walls of gyri. These results suggest that axonal tension does not play a major role in initiating (around P6), sustaining (around P18), or maintaining (in adult) cortical folding by pulling on interconnected cortical regions. Our finding directly contradicts the tension-based hypothesis of cortical folding [9], which speculates that axon tension inside a gyrus pulls the gyral walls together (see Fig. 1b).

Nevertheless, axonal tension still may play a role in shaping the cortical surface. For example, the radial tension within gyri may limit expansion of the cortex, thereby helping to shape the cortical surface [32]. Moreover, the magnitude of this tension may be regulated by stress-dependent axon growth, as indicated by experiments with single axons [11], suggesting that regional variations in tension can affect brain shape [10]. Thus, although it may not directly drive cortical folding, axonal tension may mediate brain growth and morphology.

On the other hand, our computational model shows that, given realistic assumptions and parameter values, forces generated by differential growth can initiate and drive folding patterns that are consistent with observed folding geometry, as well as with directly measured stress distributions (Fig. 7). The distributions of circumferential stress in the model after growth were further confirmed by simulated radial cuts (Fig. 7d-g) that are in reasonable agreement with those found from the dissection experiments (Fig. 3). In our model, intercortical “phased” growth is the key to establishing a specific folding pattern, as a sulcus is created between two gyri when a slowly growing region of the cortex first constrains the deformation of an adjacent faster growing region to give one bulge, and then the growth rates switch regions to generate a second bulge (see Figs. 1a’ and 7a-c). Without this constraint, our model would generate arbitrarily located folds, similar to the model of Richman et al. [7] (see Fig. 1a). This mechanism also is fundamentally different than previous speculation whereby rapidly growing regions of the cortex (gyri) are separated by slowly growing regions (sulci) [2]. Although our results support differential growth as the primary folding mechanism, this idea warrants further testing in the laboratory.

Several other mathematical models for growth-driven cortical folding have been proposed previously [32-35]. These models, however, focus mainly on folding geometry and do not present stress distributions that can be compared to experiment. Direct comparison of experimental stress measurements to model predictions helps us distinguish between multiple solutions that often characterize nonlinear problems such as brain cortical folding.

In conclusion, although we did not find significant circumferential tension between the walls of gyri, relatively small tensions may be present that could not be detected using tissue dissection (see light grey lines in Fig. 1b’). Although these small forces would be too small to drive cortical folding by direct mechanical deformation, they may provide regional mechanical signals that trigger the patterns of growth that fold the cortex. This type of mechanical feedback is consistent with Beloussov’s mechanical theory of morphogenesis [36]. In addition, as mentioned above, radial axon tension may limit gyral expansion. Consequently, the mechanism for cortical folding may involve differential growth in a primary role and axon tension in a distinctly secondary role.