A New Approach to Account for the Correlations among Single Nucleotide Polymorphisms in Genome-Wide Association Studies

Abstract

In genetic association studies, such as genome-wide association studies (GWAS), the number of single nucleotide polymorphisms (SNPs) can be as large as hundreds of thousands. Due to linkage disequilibrium, many SNPs are highly correlated; assuming they are independent is not valid. The commonly used multiple comparison methods, such as Bonferroni correction, are not appropriate and are too conservative when applied to GWAS. To overcome these limitations, many approaches have been proposed to estimate the so-called effective number of independent tests to account for the correlations among SNPs. However, many current effective number estimation methods are based on eigenvalues of the correlation matrix. When the dimension of the matrix is large, the numeric results may be unreliable or even unobtainable. To circumvent this obstacle and provide better estimates, we propose a new effective number estimation approach which is not based on the eigenvalues. We compare the new method with others through simulated and real data. The comparison results show that the proposed method has very good performance.

Introduction

In a multiple-comparison setting, a certain statistical test is applied to each individual variable. Tests with p values less than a preset threshold will be claimed statistically significant. It is important but usually difficult to set the cutoff values in advance. With a large cutoff value, there will be so many false-positive results due to chance only; on the other hand, with a too stringent cutoff, many true-positive results will not pass the threshold and therefore be overlooked. Šidák [1] and Bonferroni [2, 3] corrections are two commonly used methods to control experiment-wise error rate.

In a multiple testing problem, if the individual tests are not independent, the Šidák and Bonferroni corrections are conservative in the sense that the actual experiment-wise error rate will be lower than the given nominal value. In recent genome-wide association studies, the number of variables (e.g. single nucleotide polymorphisms, SNPs), which are often densely genotyped, can be up to hundreds of thousands. Due to linkage disequilibrium (LD), many SNPs are highly correlated. Giving this situation, neither Šidák nor Bonferroni correction should be used since they are only appropriate for independent tests. An alternative method based on permutation has been proposed [4]. This method shuffles the cases and controls in each permutation; then it calculates the p values (or the corresponding statistics) for all variables. For each permutation, the smallest p value (or the statistic with the largest absolute value) is recorded. After a large number of permutations, say M, have been conducted, the q-th quantile of the M-smallest p values (or the largest absolute statistics) is then the estimated point-wise cutoff p value (or statistic) to control the experiment-wise error rate at level q[4]. Usually, the cutoff p values from this approach control the experiment-wise error rates quite well and it has been served as the gold standard method. However, it is a computation-intensive approach that requires many permutations to get accurate estimates. With large number of variables, it could take time from several days to many years [5].

Some methods that are less computation dependent have been proposed [5, 6, 7, 8, 9, 10, 11, 12, 13, 14]. We assume there exist N_eff independent tests which are equivalent to those N correlated tests in the sense that the cutoff value based on these independent tests will control the experiment-wise error rate at the given nominal level. N_eff is called the effective number of independent tests. Cheverud [6] is the first person who proposed the idea of effective number of independent tests and developed a simple method to estimate this number based on the eigenvalues of the correlation matrix. However, studies have shown that Cheverud's method is too conservative [5, 8, 9, 10]. Several other eigenvalue-based methods have also been proposed to improve the performance [5, 7, 8, 9, 10]. One should notice that although the method proposed by Dudbridge and Gusnanto [12] also utilized the eigenvalues; the correlation matrix used in their method was different from those used in the above methods. Unfortunately, those eigenvalue-based methods have limitations which are associated with eigenvalue calculation. When the dimension of the correlation matrix is large, the numerical results are either unreliable or difficult to get. In order to circumvent these difficulties and provide better estimates, we propose a new approach that does not require calculating the eigenvalues of the correlation matrix. Instead, we use the correlation coefficients themselves to estimate the effective number. To evaluate the performance of the new approach, we compare it with other methods through simulated and real data by using the permutation-based method as the gold standard. Our comparisons show that the proposed method performs better than existing eigenvalue-based methods.

Methods

Effective Number and Its Estimation

In a multiple comparison problem that controls the experiment-wise error rate, the Šidák point-wise cutoff p value is defined as

$${\alpha }_p\hspace{0.17em}=\hspace{0.17em}1\hspace{0.17em}-\hspace{0.17em}{\left(1\hspace{0.17em}-\hspace{0.17em}{\alpha }_e\right)}^{1/N}$$ (1)

where α_e is the experiment-wise threshold and N is the total number of comparisons in the study [1]. The Bonferroni point-wise cutoff p value is an approximation for that of Šidák and is given by [2, 3]:

$${\alpha }_p\hspace{0.17em}=\hspace{0.17em}{\alpha }_e\hspace{0.17em}/N$$ (2)

Both Šidák and Bonferroni corrections are conservative and only appropriate for independent comparisons (tests). In a genome-wide association study (GWAS), it is very common that some SNPs are highly correlated due to LD. Observing that ‘higher correlation among the traits leads to higher eigenvalue variance’, Cheverud proposed the following formula to estimate the effective number [6]:

$$N_{Chev}\hspace{0.17em}=\hspace{0.17em}N\left[1\hspace{0.17em}+\hspace{0.17em}\frac{\left(1\hspace{0.17em}-\hspace{0.17em}N\right)V_{\lambda obs}}{N^2}\right]$$ (3)

where

$${\text{V}}_{\lambda obs}\hspace{0.17em}=\hspace{0.17em}\sum _{i\hspace{0.17em}=\hspace{0.17em}1}^N{\left({\lambda }_i\hspace{0.17em}-\hspace{0.17em}1\right)}^2\hspace{0.17em}/\hspace{0.17em}\left(N\hspace{0.17em}-\hspace{0.17em}1\right)$$

is the observed variance of the eigenvalues λ_i (i = 1, 2, …, N) of the correlation matrix of all SNPs. N_Chev has the following properties [6, 8]:

Property 1

When all tests are completely independent, the N eigenvalues are all equal to 1 and Vλ_obs = 0, therefore N_Chev = N.

Property 2

When all the tests are perfectly correlated, except for one which is equal to N, all other eigenvalues are equal to 0, Vλ_obs = N, and hence N_Chev = 1.

Replacing N by N_Chev in (1) or (2), we can get the Cheverud's point-wise cutoff p value. This method is usually very conservative in the sense that the actual experiment-wise error rates are much smaller than the preset value [5, 8, 9, 10, 15]. Nyholt [10] tried to improve Cheverud's method by excluding all SNPs in perfect LD except one before using formula (3). However, Nyholt's method is still overly conservative [5].

Li and Ji [8] pointed out that the effective number should also have the third property:

Property 3

If the N tests can be composed of c(1 ≤ c ≤ N) copies of N/c independent tests, then the effective number is N/c.

N_Chev does not possess this property since in this situation N/c of the N eigenvalues are equal to c and the remainder equal to 0. The estimated effective number from (3) is then N − 1 + c, not N/c[8]. Observing this limitation of Cheverud's method, Li and Ji [8] proposed an improved version of N_Chev which satisfies property 3:

$$N_{LJ}\hspace{0.17em}=\hspace{0.17em}\sum _{i\hspace{0.17em}=\hspace{0.17em}1}^{N}f\hspace{0.17em}\left(\left|\hspace{0.17em}{\lambda }_i\hspace{0.17em}\right|\right)$$ (4)

where f(x) = I(x ≥ 1) + (x − [x]) for x ≥ 0 and [x] is the floor function which gives the largest integer less than or equal to x.

Recently, Gao et al. [5, 7] proposed another eigenvalue-based method to estimate the effective number through principal component analysis:

$$N_{Gao}\hspace{0.17em}=\hspace{0.17em}min\left\{M:\frac{\sum _{i\hspace{0.17em}=\hspace{0.17em}1}^M{\lambda }_i}{\sum _{j\hspace{0.17em}=\hspace{0.17em}1}^N{\lambda }_i}>C\right\}$$ (5)

where λ₁ ≥ λ₂ ≥ … ≥ λ_N are the ordered eigenvalues of the correlation matrix and C is a parameter, which is typically set as 99.5% [5, 7]. Obviously, N_Gao does not possess property 2. When all the tests are completely independent, N_Gao will always underestimate the effective number for any C < 1.

New Method to Estimate Effective Number N_Chen

Step 1. For the i-th (i = 1, 2, …, N) SNP, estimate the absolute composite LD (CLD) coefficient between this SNP and any other SNP ∣r_ij∣, j ≠ i;

Step 2. Calculate

$${\text{R}}_i\hspace{0.17em}=\hspace{0.17em}\sum _{j\hspace{0.17em}=\hspace{0.17em}1}^N|r_{ij}{|}^k,i\hspace{0.17em}=\hspace{0.17em}1,2,\dots ,N,$$

where k is a positive constant number;

Step 3. Estimate the effective number:

$$N_{Chen}\hspace{0.17em}=\hspace{0.17em}\sum _{i\hspace{0.17em}=\hspace{0.17em}1}^N\frac{1}{R_i}$$ (6)

The constant k is a statistical test-dependent parameter. In this paper, the Cochran-Armitage trend test is used to test associations between the phenotype and the genotype [16, 17]. It is easy to verify that our new method satisfies properties 1–3 mentioned above.

Once we obtain the effective number, we can estimate the point-wise cutoff p value by using Šidák or Bonferroni correction with the total number of tests N being replaced by the estimated effective number in (1) and (2), respectively. In this paper, we use N_P, N_Chev, N_LJ, N_Gao and N_Chen to denote the estimated effective number from the permutation-based method, the methods of Cheverud, Li and Ji, Gao et al. and our new method, respectively. We actually do not need to estimate the effective number if the permutation-based method is used; however, in order to use it as a standard in method comparisons, we will estimate N_P by α_e/α_p, where α_p is the estimated point-wise cutoff p value from the permutation-based method.

For our proposed method, we estimate the effective number based on the correlation matrix. As suggested by Gao et al. [5], we use the CLD coefficient to estimate the correlation coefficient between each pair of SNPs since it has certain advantages over the LD correlation [5, 18, 19, 20, 21]. For example, the expectation-maximization algorithm-based estimate of LD correlation makes a strong assumption of the Hardy-Weinberg equilibrium [22], which may not meet in practice [21, 23, 24]. Some researchers have shown that CLD can capture the relationship among SNPs comparable to those of gametic LD without requiring the Hardy-Weinberg equilibrium [5, 18, 19, 20, 21]. In addition, the CLD coefficient can be easily estimated. The calculation of the CLD coefficient is simple: code the wild-type homozygote, heterozygote and variant homozygote as 2, 1 and 0, respectively, for each individual genotype and then calculate the correlation coefficient in the usual way [e.g. R function cor()] for each pair of SNPs. For more details, see Gao et al. [5].

Simulation Settings

The R package ‘popgen’ (version 0.0-4; http://cran.r-project.org/src/contrib/Archive/popgen/) is used to generate phenotype data. We simulate data sets with the settings similar to those used in Gao et al. [5, 25]. More specifically, we simulate two different data sets. For simulation 1, we simulate 8 cold regions (each 10 kb long) separated by hotspots (each 1 kb long). For simulation 2, we simulate 4 cold regions (each 10 kb long) separated by hotspots (each 15 kb long). The mutation rate is θ = 4N_eμ, where the effective population size N_e and the mutation rate per base pair per generation μ are set to be 10,000 and 1.4 × 10⁻⁸, respectively. The recombination rate is r = 4N_eδ, where the recombination rate per base pair per generation δ are chosen to be 2.5 × 10⁻⁸ and 9 × 10⁻¹⁰ for cold regions in simulation 1 and 2, respectively, to get patterns similar to those observed in the SeattleSNP database [5, 25]. For the hot regions, the recombination rates per base pair per generation are set to be 100 times greater than those in the cold regions. For both simulations, 100 experiments will be generated, each with 200 cases and 200 controls. To see whether sample sizes affect the outcomes, we also simulate data sets with 1,000 cases and 1,000 controls. The lowest minor allele frequency (MAF) will be set as 0.05, as commonly chosen in practice; SNPs with MAF <0.05 will be removed. Gao et al. [5] used 0.1 as the MAF cutoff in their simulations. In the permutation-based method, we use chran-Armitage trend tests with 10,000 permutations to estimate the point-wise cutoff p values and the corresponding estimated effective numbers N_P with experiment-wise levels 0.05 and 0.01. Regarding the method of Gao et al. [5], we use 99.5% for the parameter C; in our new approach, we use k = 7.

Real Data

A real SNP data set is also used to compare the methods [26]. In this data set, we use the data from the 167 Eastern Asian Chinese people. There are 1,272 SNPs across 16 regions of chromosome 21; among them 226 SNPs with MAF <5% are removed, resulting in 1,046 SNPs in the final analysis. Among the 167 samples, 83 are assumed as hypothetical cases and 84 as controls in the permutation-based test.

Results

Simulation Results

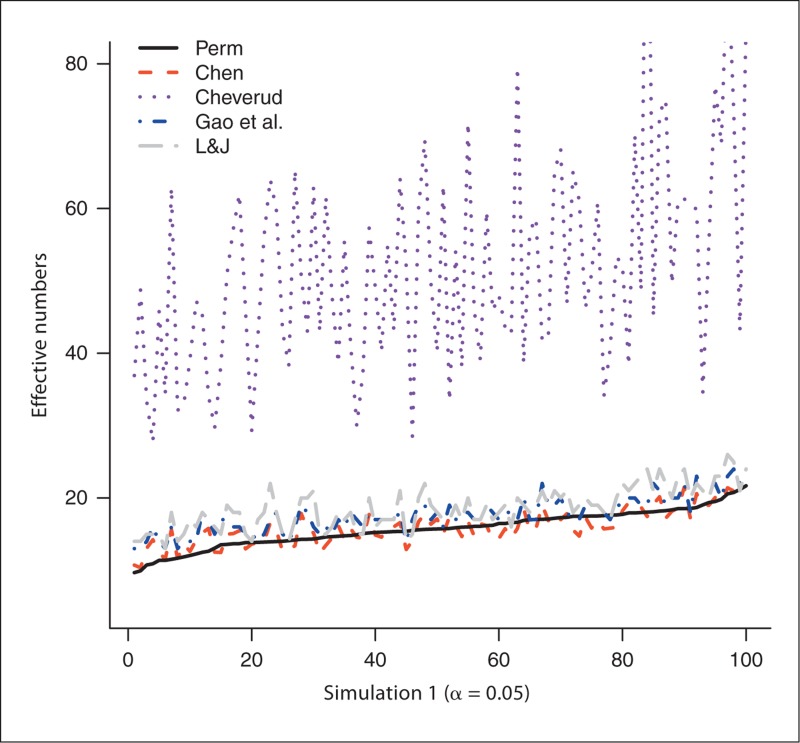
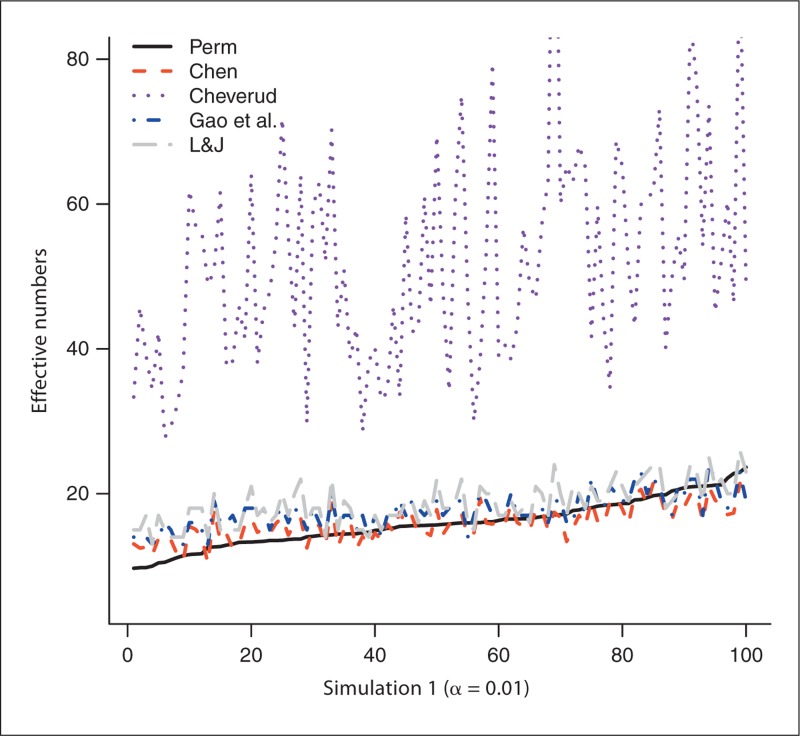
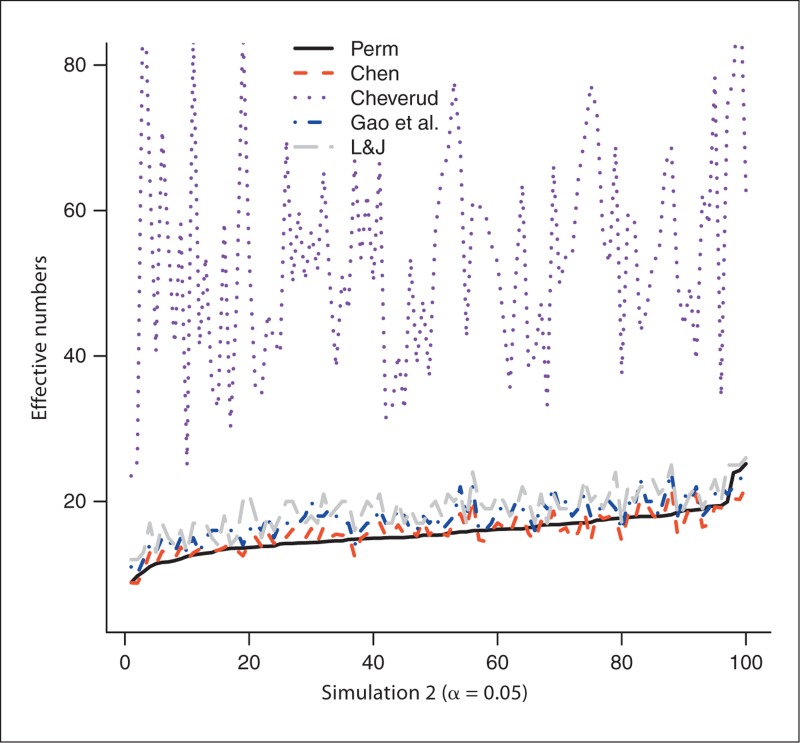
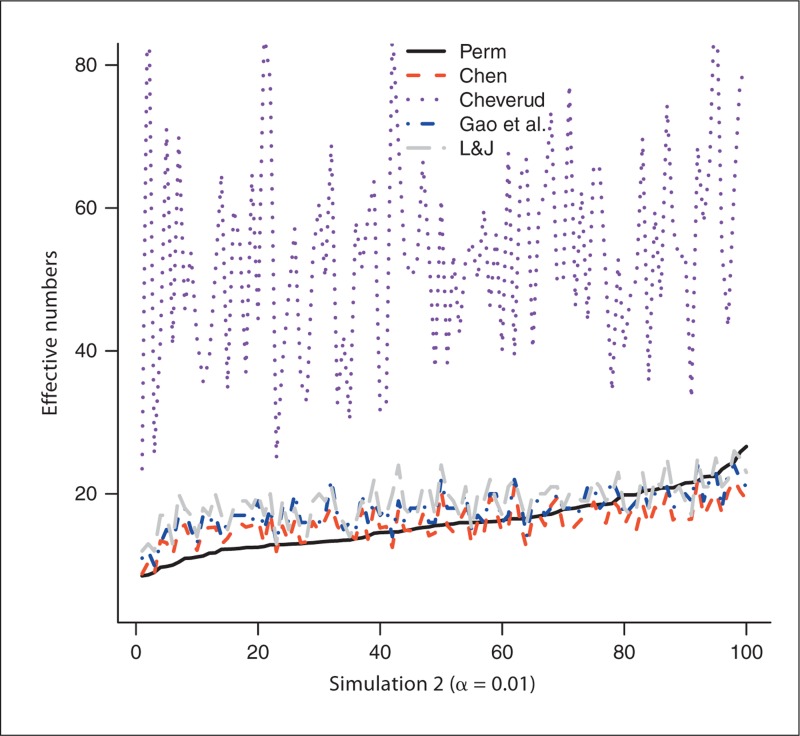
The number of SNPs generated from the 100 experiments in simulation 1 varies from 33 to 184 with a mean of 69.1 and a median of 65.5. Similarly, the number of SNPs in simulation 2 is between 30 and 170, with a mean of 74.4 and a median of 75.5. We first use the permutation-based method to estimate N_P, which is then served as the gold standard: the closer the estimated effective number to N_P, the better the method performs. Figure 1 plots the estimated effective numbers N_Chev, N_LJ, N_Gao and N_Chen by the methods of Cheverud, Li and Ji, and Gao et al., and our new method, respectively, in simulation 1, with N_P estimated from trend test with experiment-wise level 0.05. The effective numbers are sorted by N_P before they are plotted to give better visualization (this applies to all figures). Figure 2 compares those estimated effective numbers in simulation 1 with N_P estimated with experiment-wise level 0.01. Figures 1 and 2 clearly show that regardless of the experiment-wise levels used, most of the time, N_Chen performs better than N_LJ and N_Gao, which are close to each other and both perform better than N_Chev. Figures 3 and 4 plot the effective numbers estimated in simulation 2 with N_P estimated with experiment-wise levels 0.05 and 0.01, respectively. Again the overall performance of our new method is better than the methods of Li and Ji and Gao et al., which both are better than the Cheverud method.

Fig. 1.

The estimated effective numbers from various methods in simulation 1 (1, 2) and in simulation 2 (3, 4) with N_P estimated at experiment-wise level 0.05 (1, 3) and 0.01 (2, 4). Perm = Permutation; L&J = Li and Ji.

Fig. 2.

The estimated effective numbers from various methods in simulation 1 (1, 2) and in simulation 2 (3, 4) with N_P estimated at experiment-wise level 0.05 (1, 3) and 0.01 (2, 4). Perm = Permutation; L&J = Li and Ji.

Fig. 3.

The estimated effective numbers from various methods in simulation 1 (1, 2) and in simulation 2 (3, 4) with N_P estimated at experiment-wise level 0.05 (1, 3) and 0.01 (2, 4). Perm = Permutation; L&J = Li and Ji.

Fig. 4.

The estimated effective numbers from various methods in simulation 1 (1, 2) and in simulation 2 (3, 4) with N_P estimated at experiment-wise level 0.05 (1, 3) and 0.01 (2, 4). Perm = Permutation; L&J = Li and Ji.

Tables 1 and 2 summarize the statistics of the estimated effective numbers from various methods in simulations 1 and 2, respectively. It is noticeable that our new method N_Chen has very similar characteristics as the permutation-based method. For example, in simulation 1 the estimated overall effective numbers are 1,574 and 1,592 from N_P with experiment-wise level 0.05 and 0.01, respectively, which are very close to the 1,594 obtained by our new method. The estimated overall effective numbers from N_LJ and N_Gao are both greater than those from N_P.

Table 1.

Summary statistics of the estimated effective numbers from various methods in simulation 1

Method	Min	Max	Mean	Median	SD	Sum
Trend (αe = 0.05)	9.7	21.7	15.7	15.7	2.49	1,574
Trend (αe = 0.01)	9.7	23.6	15.9	15.7	3.24	1,592
Chen (k = 6)	10.0	20.6	15.2	15.1	2.32	1,523
Chen (k = 7)	10.4	21.5	15.9	15.8	2.42	1,594
Chen (k = 8)	10.7	22.2	16.5	16.3	2.51	1,649
Cheverud	27.7	123.8	51.7	48.9	15.5	5,172
Gao et al.	13	24	17.6	17	2.44	1,763
Li and Ji	13	26	18.6	18	2.89	1,855

Table 2.

Summary statistics of the estimated effective numbers from various methods in simulation 2

Method	Min	Max	Mean	Median	SD	Sum
Trend (αe = 0.05)	8.8	25.2	15.7	15.4	2.73	1,567
Trend (αe = 0.01)	8.5	26.6	16.0	15.7	3.98	1,596
Chen (k = 6)	8.3	21.2	15.2	15.0	2.44	1,519
Chen (k = 7)	8.8	22.0	15.9	15.6	2.55	1,590
Chen (k = 8)	9.0	22.8	16.5	16.2	2.63	1,646
Cheverud	23.5	96.7	53.5	53.2	15.1	5,351
Gao et al.	10	24	17.8	18	2.73	1,778
Li and Ji	12	26	19.0	19	2.95	1,897

We also perform statistical tests to compare N_Chev, N_LJ, N_Gao and N_Chen with N_P. A one-sample test (e.g. a paired t test or a signed-rank test) is applied to the effective numbers estimated by each pair of methods of the 100 experiments within the same simulation. Tables 3 and 4 report the p values from a one-sample t test for simulations 1 and 2, respectively. For both simulations (1 and 2), the estimated effective numbers from our new method and the permutation-based method are not statistically significantly different. For any other methods, their estimated effective numbers are always highly statistically significantly different than those from the permutation-based method. We also applied the Wilcoxon signed-rank test and obtained very similar results. When we increase the numbers of cases and controls to 500 or 1,000 each, we have very similar results to those with 200 cases and 200 controls; this is consistent with the findings from Gao et al. [5].

Table 3.

p value from the comparison of the estimated effective numbers in simulation 1

	Chen	Cheverud	Gao et al.	Li and Ji
Trend (αe = 0.05)	0.16	<2.2 × 10−16	<2.2 × 10−16	<2.2 × 10−16
Trend (αe = 0.01)	0.92	<2.2 × 10−16	1.6 × 10−11	<2.2 × 10−16

Table 4.

p value from the comparison of the estimated effective numbers in simulation 2

	Chen	Cheverud	Gao et al.	Li and Ji
Trend (αe = 0.05)	0.13	<2.2 × 10−16	<2.2 × 10−16	<2.2 × 10−16
Trend (αe = 0.01)	0.85	<2.2 × 10−16	2.9 × 10−9	<2.2 × 10−16

For SNP data, it is very common to have missing values, methods based on principal component analysis, such as N_G, cannot be applied directly to this kind of data [5]. Although some data imputing strategies can be used, this will bring some errors as well. Another problem with principal component analysis is that it becomes inefficient with a large number of SNPs (>1,000) [5]. The new proposed method is not sensitive to missing value since it only needs the correlation coefficient between each pair of SNPs.

When the number of SNPs becomes very large, many effective number estimation methods need to group the SNPs into subsets. However, we may not know exactly which SNPs should be grouped together in practice. It is desirable to know how the subset size affects the effective number estimation. To this purpose, we treat the generated SNP data from the 100 experiments within the same simulation as one single data set; then choose different subset sizes (e.g. 100, 200, …, 1,000) to separate the single data set into several subsets with equal numbers of SNPs (only the last subset may have more SNPs). The overall estimated effective number is assumed the sum of the effective numbers estimated from each individual subset. Tables 5 and 6 report the results for simulations 1 and 2, respectively. It can be seen that our new method is not sensitive to the subset size. With subset sizes between 500 and 1,000, our new method gives reliable, effective numbers, which are very close to those from the permutation-based method.

Table 5.

Estimated effective numbers with different size (n) and number of subsets (G) in simulation 1

n (G)	Chen (k = 6)	Chen (k = 7)	Chen (k = 8)	Cheverud	Gao et al.	Li and Ji
−a(100)	1,523	1,594	1,649	5,172	1,763	1,855
100 (69)	1,850	1,926	1,984	5,891	1,765	1,926
200 (34)	1,681	1,754	1,811	6,298	1,565	1,731
300 (23)	1,609	1,680	1,736	6,452	1,480	1,638
400 (17)	1,596	1,667	1,723	6,573	1445	1,597
500 (13)	1,607	1,680	1,737	6,650	1,420	1,581
600 (11)	1,559	1,630	1,685	6,674	1,367	1,520
700 (9)	1,573	1,645	1,701	6,724	1,333	1,493
800 (8)	1,549	1,620	1,675	6,733	1,299	1,458
900 (7)	1,546	1,617	1,672	6,754	1,264	1,427
1,000 (6)	1,566	1,638	1,694	6,774	1,220	1,398

^aNumber of SNPs from each experiment.

Table 6.

Estimated effective numbers with different size (n) and number of subsets (G) in simulation 2

n (G)	Chen (k = 6)	Chen (k = 7)	Chen (k = 8)	Cheverud	Gao et al.	Li and Ji
−a(100)	1,519	1,590	1,646	5,351	1,778	1,897
100 (74)	1,824	1,900	1,959	6,025	1,731	1,930
200 (37)	1,662	1,735	1,792	6,576	1,543	1,756
300 (24)	1,624	1,698	1,755	6,848	1,485	1,686
400 (18)	1,589	1,661	1,718	6,977	1,440	1,631
500 (14)	1,575	1,647	1,703	7,082	1,400	1,597
600 (12)	1,570	1,643	1,699	7,120	1,383	1,568
700 (10)	1,543	1,615	1,670	7,162	1,333	1,521
800 (9)	1,559	1,631	1,687	7,193	1,336	1,526
900 (8)	1,551	1,623	1,679	7,222	1,308	1,498
1,000 (7)	1,538	1,609	1,665	7,242	1,267	1,456

^aNumber of SNPs from each experiment.

To see how those methods work for large SNP data, we combine the data from the two simulations into one single data set with 14,453 SNPs in total. Due to the limit of the memory of R, we need to divide the whole data set into four subsets with almost equal size. The running time values (in seconds) using R are 274, 631, 628, 630 and 1,086,961 (about 302 h) for our new method, and the methods of Cheverud, Gao et al., and Li and Ji, and the permutation method with trend test and 10,000 replicates, respectively. The estimated effective numbers by those methods are 3,198, 14,225, 1,405, 2,030 and 3,359, respectively. The estimated effective number by Cheverud is too large, while those by Gao et al. and Li and Ji are too small. Our proposed method and the permutation method obtained very similar results.

Results from Real Data

From the real data, the estimated effective numbers from the permutation-based method with experiment-wise level 0.05 and 0.01 are 354 and 349, respectively. The effective number from our new method is 348, which is very close to those from the permutation-based method. The estimated effective numbers from Gao et al., Li and Ji, and Cheverud methods are 361, 371, and 859, respectively. Again we can see that the Cheverud method is too conservative.

Discussion

In multiple-comparison problems with highly correlated tests, such as GWAS using SNPs, statistical methods that account for the dependence and give reasonable cutoff p values are highly desirable. Some of these methods have been proposed and successfully applied to genetic association studies. The concept of effective numbers of independent tests is simple but very useful.

Like constant C in the method of Gao et al., the parameter k in our new method needs to be chosen in advance. This constant may vary among different situations. Although we used k = 7 for our new method when the statistical tests were Cochran-Armitage trend tests, we found that, unlike the method of Gao et al. [5], our method was not sensitive to the parameter k. For example, if we replace 7 by any value between 6 and 8, we will have very similar results as those from our new method with k = 7. From both simulation and real data, we have shown that the estimated effective numbers from our new method with k = 7 were very close to those from the permutation-based method; we feel that k = 7 is appropriate for most situations. If other association tests are used, another constant k should be chosen. For example, we find that if Pearson's χ² test with 2 degrees of freedom (d.f.) is used, k = 3 is more appropriate (data not shown). In GWAS, one may want to adjust some covariates, e.g. age and gender. Under this situation, a logistic regression model with genotype and several other covariates as independent variables is more appropriate. As the statistical method changes, we would expect that a different constant k needs to be chosen. We do not have such data to give our suggestion about choosing k for this situation, however, in principle, we may estimate this constant based on the permutation method with a small portion of the data. Although based on the results from our simulations and real data, k = 7 is suitable for both significance levels 0.05 and 0.01, this constant k may also depend on the significance level used, as pointed out by other researchers [11, 14].

For the methods of Gao et al., and Li and Ji, it is important to find a suitable group size to divide a large data set into some subsets as the grouping effects are not negligible for those methods. However, for our proposed method, the grouping effect is limited based on our simulations.

It should be noticed that the method proposed by Moskvina and Schmidt [11] also utilizes the correlation coefficients among SNPs, although in a different way, to estimate the effective number. In general, the estimated effective numbers by their method are conservative since their r_js are usually underestimated, resulting in overestimated k_js and therefore the effective numbers. Furthermore, Moskvina and Schmidt's method is independent of the association tests used. This may be a limitation of their method. Recently, Han et al. [13] proposed another correction method based on the observation that the covariance of their test statistics from two markers was the sample correlation coefficient of the two markers. However, the test they used was related to the allelic χ² test (Pearson's χ² test with 1 d.f. for a 2 × 2 contingency table); it was neither the trend test nor the χ² test with 2 d.f. for a 2 × 3 contingency table. It is unclear how this method works if we choose the commonly used trend test.

We have proposed a new simple method to estimate the effective number to account for the correlations among SNPs in genetic association studies. It is less computation dependent and easy to implement. Through simulation and real data, we have shown that the proposed method outperforms existing effective number estimation methods.