Glucose Interactions with a Model Peptide

Abstract

Molecular dynamics simulations have been conducted of the helical polypeptide melittin, in concentrated aqueous solutions of the alpha and beta anomers of D-glucopyranose. Glucose is an osmolyte, and is expected to be preferentially excluded from the surfaces of proteins. This was indeed found to be the case in the simulations. The results indicate that the observed exclusion may have a contribution from an under-representation of hydrogen bonding interactions between glucose groups and exposed side chains, compared to water. However, glucose was found to bind quite specifically to melittin by stacking its hydrophobic face, consisting of aliphatic protons, against the flat hydrophobic face of the indole group of the tryptophan-19 side chain. While the binding site for this interaction is localized, the binding is weak for both anomers, with a binding free energy estimated as only ~0.5 kcal/mol, (i.e. near k_BT). The face of the sugar stacked against the Trp indole ring is different for the two anomers of glucose, due to the disruption of the H1-H3-H5 hydrophobic triad of the beta anomer by the axial C1 hydroxyl group in the alpha anomer. The measurable affinity of the sugar for the Trp side chain is consistent with the very frequent occurrence of this group in the binding sites of proteins that complex with sugars.

Introduction

The presence of co-solutes can significantly affect the properties of biological molecules in aqueous solutions. Such effects are important, since virtually all biological solutions are complex mixtures of many species. Co-solute effects are perhaps best known for the case of various common electrolytes, which can be ordered into Hofmeister series depending on their influence at high concentrations on the solubility and conformational stability of proteins. Some ions raise the melting temperature of proteins, while simultaneously decreasing their solubility, while other ions denature proteins while making them more soluble. The origins of such effects have been much discussed since Hofmeister first introduced these ordered series.¹ Explanations generally assume either a change in solvent quality or direct interactions with proteins, or a combination of both.^2–6 It seems unlikely that a common explanation covering all possible co-solutes exists, and different species may operate through different mechanisms. In some cases, such as monatomic cations, the ordering correlates strongly with the ionic effects on solution surface tension.⁷ For polyatomic solutes, earlier explanations often invoked the possibility that the co-solutes affect the long-range structuring of water, as cosmotropes or chaotropes. Little experimental support for such models has been found, however, and more recent studies have focused on short-range water structuring and direct interactions between the co-solutes and protein functional groups. For example, recent work suggests that in solutions of proteins and the denaturant guanidinium chloride, the guanidinium ions interact directly with planar non-polar amino acid side chains by stacking against their flat faces, displacing waters into the bulk solvent.⁸ Perhaps more surprisingly, guanidinium ions were also found to stack against the flat faces of the guanidinium groups of arginine side chains,⁸ just as they stack against one another in pure solutions of GdmCl.⁹ This curious result arises because the distribution of charge density on the large Gdm ion frustrates hydrogen bonding to the central carbon atom, which cannot serve as a donor, while the three NH₂ groups can hydrogen bond to water molecules or other hydrogen bond acceptors in the plane of the ion. It is generally considered that interactions with the peptide backbone dominate many co-solute effects on proteins, and Gdm⁺ has been proposed to make stacking interactions with the peptide amide groups of the backbone,¹⁰ similar to guanidinium-side chain amide stacking interactions observed in simulations.⁸

Neutral species can also affect protein stability and solubility. The denaturant urea is perhaps the best studied of such co-solutes.^11–14 Urea interacts directly with proteins, accumulating at the surface,¹⁵ and competitively hydrogen bonding to peptide backbone groups.^10,16 Sugars are also important neutral co-solutes in biological systems, and are classified as osmolytes in a Hofmeister sense. They generally stabilize protein conformations,^2,17 and are known to have cryoprotective effects not only for protein conformations at very low temperatures, but also for lipid bilayer membranes.^18,19 With their numerous polar hydroxyl groups, simple sugars are quite hydrophilic and very soluble in water. As osmolytes, in aqueous protein solutions sugars are expected to be less abundant in the immediate vicinity of a protein solute than in bulk solution, unlike urea and guanidinium.

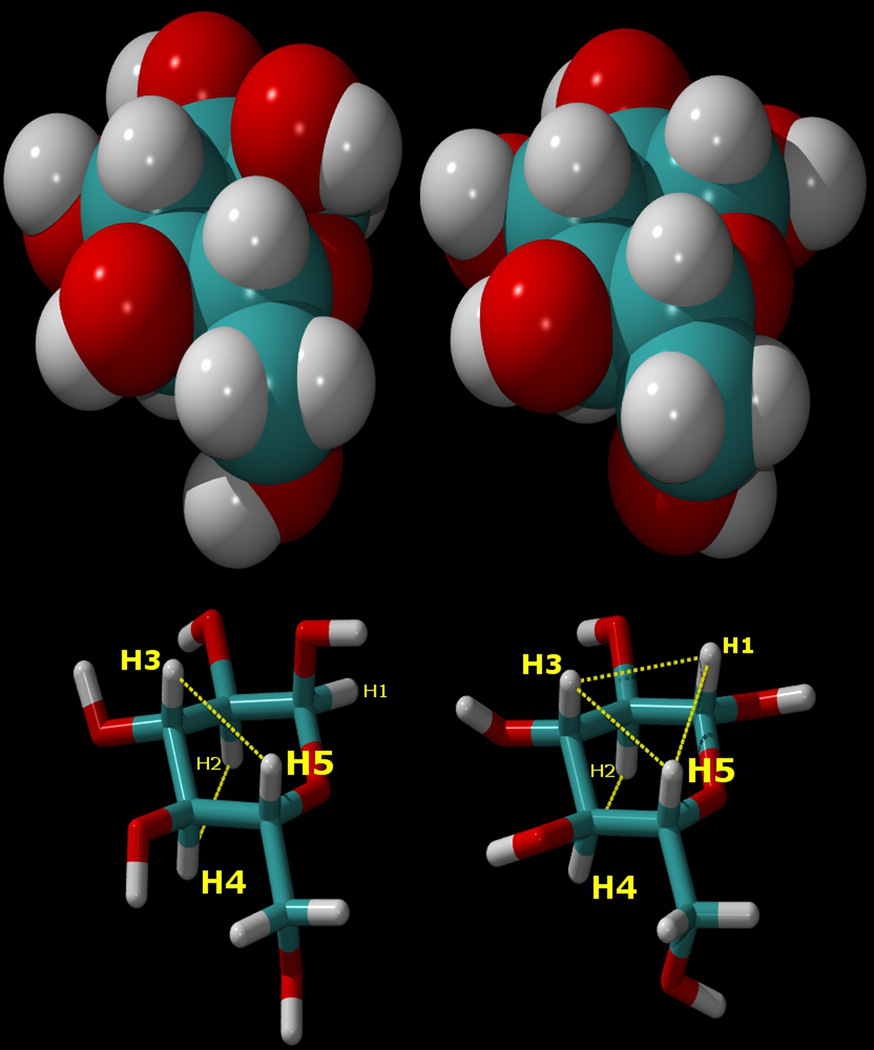
Like most biological solutes, however, sugar molecules consist of a number of functional groups, including not only polar hydroxyl groups but also hydrophobic aliphatic C-H groups, juxtaposed in close proximity by their molecular topology. The hydration of sugar molecules is therefore more complex than that of simple monatomic ions.^20–22 Probably the most important biological sugar is the prototypical monosaccharide glucose. In aqueous solution, glucose occurs primarily in a dynamic equilibrium between two different pyranose ring forms, α and β, that differ only in their anomeric configurations (Figure 1). In the more abundant β-D-glucopyranose anomer, all of the hydroxyl groups of carbons 1 through 4 are in equatorial positions directed around the periphery of the relatively rigid sugar ring, while the aliphatic protons of carbons 1 through 5 are all in axial positions, directed “up” or “down”, creating a situation in which the “tops” and “bottoms” of the sugar rings are actually hydrophobic, while the equatorial peripheries are hydrophilic (hydrogen bonding), with an overall disc-like topology (Figure 1).

Figure 1.

Top: van der Waals surface representations of α-D-glucopyranose (left), and β-D-glucopyranose (right). Bottom: the atomic numbering for the atoms in these sugars, shown as “liquorice” drawings in the same orientations, and with the axial aliphatic protons connected by dotted lines to indicate their hydrophobic regions. As can be seen, the H1–H3–H5 “underside” of the β anomer is completely hydrophobic. In the α anomer (left), the positions of the hydroxyl group and proton on the C1 atom are interchanged, disrupting the aliphatic proton triad.

Nature exploits this dual character of glucose in designing the binding sites of sugar binding proteins such as glucose binding proteins (GBP),^23,24 as is shown in Figure 2. In these proteins, the binding site must have a significant affinity for the sugar in order to outweigh the strong hydrophilicity of the solute. This is achieved in part by offering the sugar ligand precisely-positioned alternate hydrogen bond partners in the binding site, such as glutamine and glutamic acid side chains. In addition, the binding sites of sugar binding proteins contain planar hydrophobic side chains such as tryptophan and phenylalanine, against which the hydrophobic faces of glucose can stack. As can be seen from Figure 2, for example, in GBPs the glucose ligand is stacked against a tryptophan residue side chain.

Figure 2.

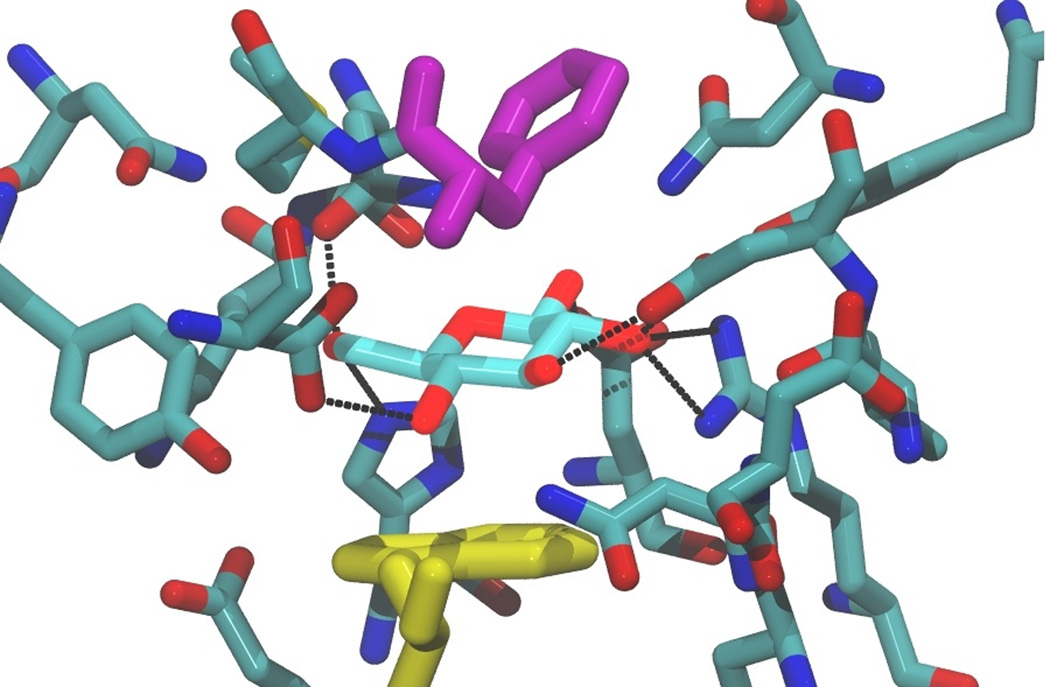
The binding site of E. coli glucose/galactose binding protein, Protein Data Bank ID: 2HPH, with a bound glucose ligand, illustrating stacking of the sugar against the lower tryptophan indole group (shown in yellow). The ligand is also sandwiched by a phenylalanine residue side chain, shown in purple. Residues within 4.5 Å of the ligand are shown, with hydrogen bonds between the sugar ligand and the protein shown as black dashed lines.

The affinity of guanidinium ions for planar hydrophobic functional groups, and the evidence from the crystal structures of proteins that bind glucose, suggest that there may also be a specific affinity of glucose for planar hydrophobic amino acid side chains. Such an affinity was recently confirmed for the case of tryptophan in a calculation of the potential of mean force for the interaction of glucose with indole, the side chain of the amino acid tryprophan.²⁵ We report here a molecular dynamics simulation of a model peptide, melittin, in a concentrated solution of glucose, to further test whether there is any tendency for glucose to directly interact with side chains of a peptide, and in particular whether it has any affinity for the indole side chain group of tryptophan when part of a larger polypeptide molecule.

The 26 amino acid melittin has the sequence (Gly Ile Gly Ala Val Leu Lys Val Leu Thr Thr Gly Leu Pro Ala Leu Ile Ser Trp Ile Lys Arg Lys Arg Gln Gln-amide). The present simulations are not intended to model the behavior of the alpha helical melittin, which only exists as a helix in water when associated into a tetrameric complex.²⁶ Melittin has been the subject of several computational and theoretical studies in recent years, primarily relating to the wetting behavior of its surface, and the role that hydration plays in its association into a tetrameric complex.^27,28 It was selected for the present study since it has a relatively simple amino acid composition, with a mix of hydrophobic and hydrophilic side chains, and as an alpha helix, presents the side chains of these amino acids to the solvent in a way that facilitates the examination of their individual hydration behaviors. This last feature is particularly relevant, since partially or fully buried tryptophan residues would not provide a good test of the affinity of the indole group for glucose.

The present study consisted of two simulations of single melittin chains in periodic boxes containing 120 independent glucose molecules. Since the β anomer of glucopyranose is essentially disc-like with approximately planar faces, while the α anomer, with an axial C1 hydroxyl group, is less disc-like, separate solutions of both anomers were modeled. In real solutions of glucose, however, these two forms are constantly interchanging via the open chain aldehyde form, so that both anomers would be present in the approximate ratio 33/67 (α/β in glucose, the furanoid tautomers are present in negligible amounts).²⁹

Materials and Methods

Separate identical simulations were performed for both the alpha and beta anomers of D-glucopyranose in solution with a single melittin chain. The MD simulations employed the CHARMM program,³⁰ with the TIP3P water^31,32 model and a time step of 1 fs. In these simulations a periodic cubic system was created containing a single helical melittin molecule and a number of independent glucose molecules surrounded by explicit water molecules. The melittin starting coordinates were taken from the protein data bank (accession # 2MLT), using only one of the two chains, and were modeled with the CHARMM22 protein force field parameters. The backbone atoms of the peptide were constrained to this structure using the CHARMM dihedral constraint function with a force constant of 2 kcal/mole/radian/radian. The simulations employed the same carbohydrate potential energy function used in our previous studies.³³ The protein has an amidated C terminus and a protonated N terminus, giving it a formal charge of +6; this was balanced by the inclusion of six chloride counterions. Chemical bonds to hydrogen atoms were kept fixed using SHAKE.³⁴ Arbitrary starting coordinates were generated by randomly placing and orienting one melittin molecule and 120 glucose molecules in a cubic box with sides of ~46.5Å. These coordinates of the sugars and peptide were superimposed on a previously-equilibrated box of water molecules, and those which overlapped any solute heavy atom were discarded. By design this procedure produced a solution containing 2406 TIP3P water molecules, 3.00 molal in glucose and 23 mmolal in melittin. Finally, the box length was rescaled on a molecular basis to ~46.5 Å; this yielded the correct physical number density (0.105 atoms Å⁻³). The resulting concentration of glucose is about 1000 times higher than those found in metabolic systems, but corresponds to the denaturing concentrations used in a previous simulation of melittin in a guanidinium chloride solution,⁸ to which the present results are compared.

All van der Waals interactions were smoothly truncated on an atom-by-atom basis using switching functions³⁰ from 10.5 to 11.5 Å, while electrostatic interactions were treated using the Particle Mesh Ewald method^35,36 with a real space cutoff of 12.5 Å, κ = 0.3 Å⁻¹. The simulation was run at a constant temperature of 300 K, using a Hoover constant pressure/temperature algorithm, at a constant pressure of 1 atm, maintained using a Hoover piston with a mass of 2000 amu.³⁷ Initial velocities were assigned from a Boltzmann distribution at 300 K and the trajectories were then run for 50.0 ns. The first 1 ns was taken as equilibration (approximately the time required for the glucose molecules to diffuse significantly from their starting positions relative to the protein), and the remaining 49 ns were used for analysis.

Results and Discussion

During the course of each simulation, the interactions of the sugar anomers with the polypeptide were monitored to determine if any affinity between these solutes existed. The most significant qualitative observation that can be made from the analysis of the calculated trajectories is that, averaged over the simulations, glucose is preferentially excluded from the surface of the peptide (Figure 3), out to a distance of about 15 Å, or approximately 2 glucose diameters, as can be seen from the averaged probability of finding glucose ring atoms as a function of distance from the peptide. In calculating this distribution function, the distance to the nearest protein heavy atom was calculated for each glucose ring atom. This probability versus distance function was then divided by r² and linearly normalized such that at the high r limit the data converged to unity. This distribution gives the relative probability of finding a glucose ring atom at a given distance from the nearest protein heavy atom relative to the bulk density of glucose ring atoms.

Figure 3.

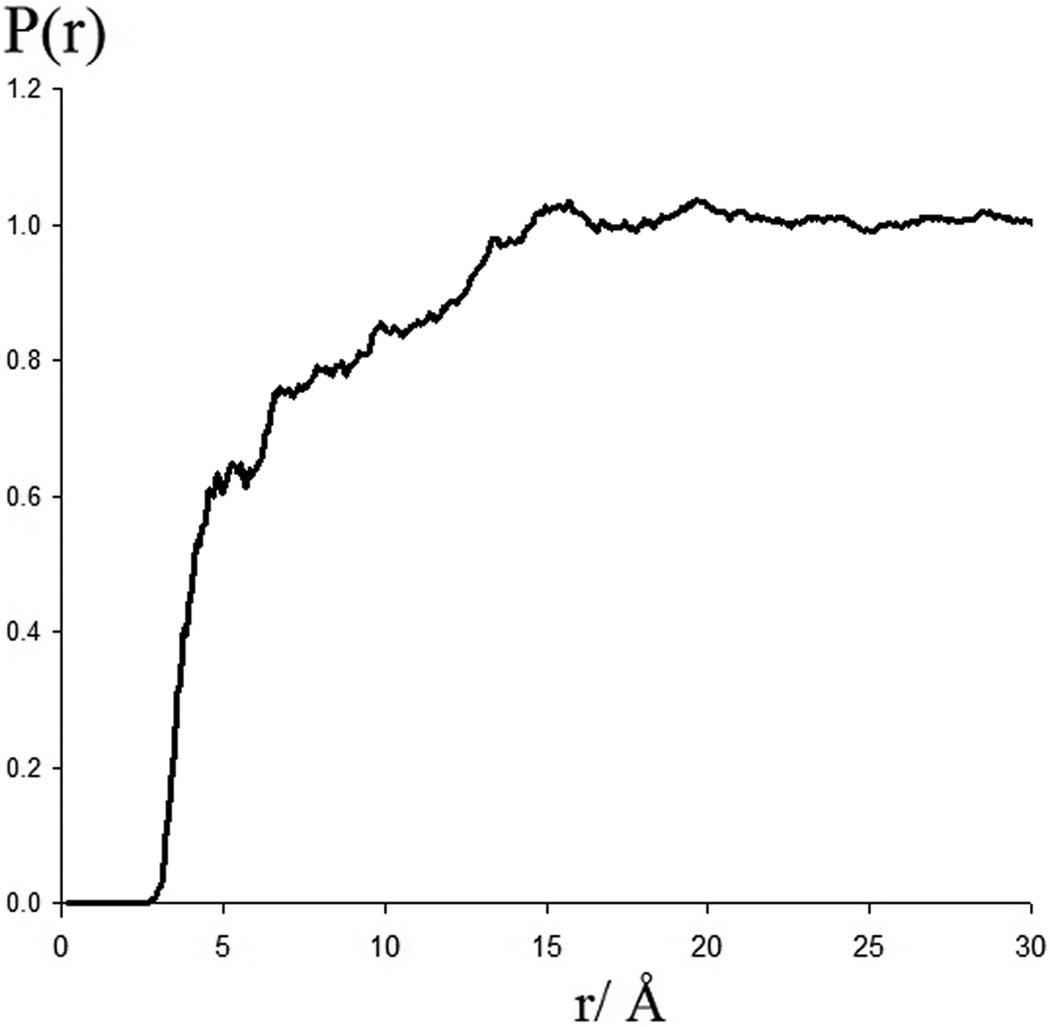
The normalized radial probability of finding glucose ring atoms a given distance from the nearest heavy atoms of the protein as calculated from the simulations.

However, in both the α and β anomer simulations, an accumulation of glucose molecules on the surface of the peptide was observed adjacent to specific residues (Figure 4). This accumulation resulted in an initial decrease in the number of water molecules hydrating the melittin. Figure 5 displays the history of the hydration of the polypeptide, as defined by its coordination number to water, in both of the glucose simulations. The average hydration number was 216 in the α-D-glucopyranose case and 209 in the β-D-glucopyranose. As can be seen, while exhibiting large very short fluctuations, the average hydration is stable throughout the simulation after the initial 2–3 ns, indicating the results are satisfactorily converged. This decrease in hydration number is paralleled over the same interval by an increase in glucose coordination number, which also then exhibits long-term stability.

Figure 4.

A representative “snapshot” of the melittin monomer, shown as a green helix, and the glucose co-solutes, colored red if they are within 4.5 Å of a peptide heavy atom, and grey otherwise. This example is for the α anomer. The Trp19 side-chain is shown in yellow.

Figure 5.

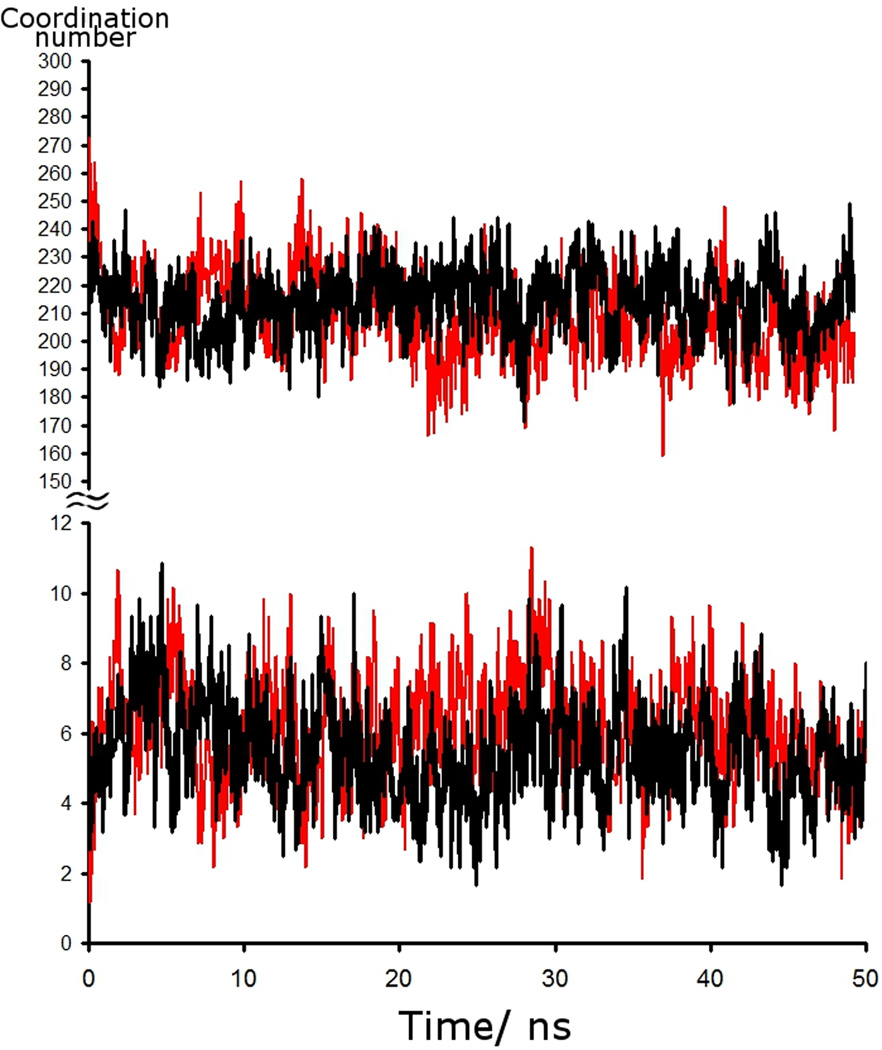
The time series for water coordinated to melittin as calculated from MD simulations. A water molecule is defined as coordinated if its oxygen atom is within 4.5 Å of a heavy atom of the peptide. Black is α-D-glucopyranoside, and red is β-D-glucopyranoside. The bottom panel displays the coordination number to glucose.

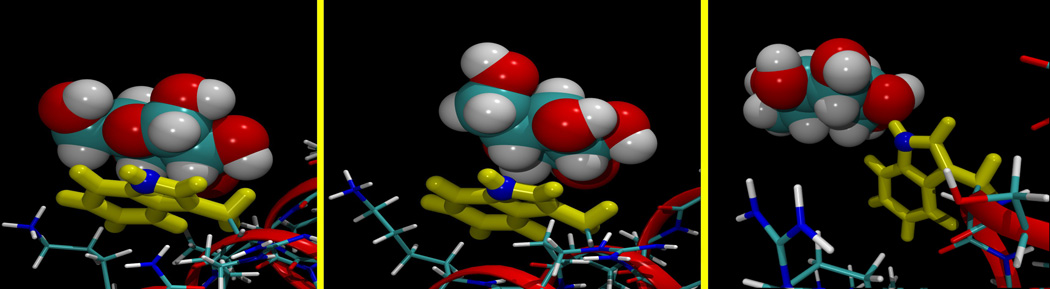
In spite of the overall depletion of sugar molecules at the peptide surface, in the simulations the glucose rings were observed to spend significant periods of time stacked against the planar face of the Trp 19 indole side chain group, consistent with X-ray crystal structures of sugar-binding proteins.^23,24 Figure 6 illustrates examples of such an interaction, as “snapshots” of a β-, or α-D-glucopyranose molecule binding to the Trp 19 side chain indole group. This association is primarily hydrophobic in character, with some complementary electrostatics arising from the partial charge distribution in the glucose and indole groups,³⁸ but does not prevent the hydroxyl groups of the glucose molecule from making hydrogen bonds to water molecules. It thus resembles the previously observed interaction of planar guanidinium ions with this same residue in simulations of melittin in guanidinium chloride solution.⁸

Figure 6.

Left: a snapshot from the simulation of melittin in an α-D-glucopyranose solution, showing a representative example of this sugar molecule adjacent to the Trp 19 residue, shown in yellow and blue. The C6 group is on the left in this panel, directing a third aliphatic proton into van der Waals contact with the indole ring. Middle: a snapshot from the simulation of melittin in β-D-glucopyranose solution, showing a representative example of a sugar molecule interacting with the Trp 19 residue in the predominant arrangement for this anomer, with the face consisting of the three hydrophobic aliphatic protons in contact with the indole ring.. Right: An example from the β-D-glucopyranose simulation of a sugar molecule hydrogen bonding through its O2 hydroxyl group acting as an acceptor with the N-H group of the Trp indole ring.

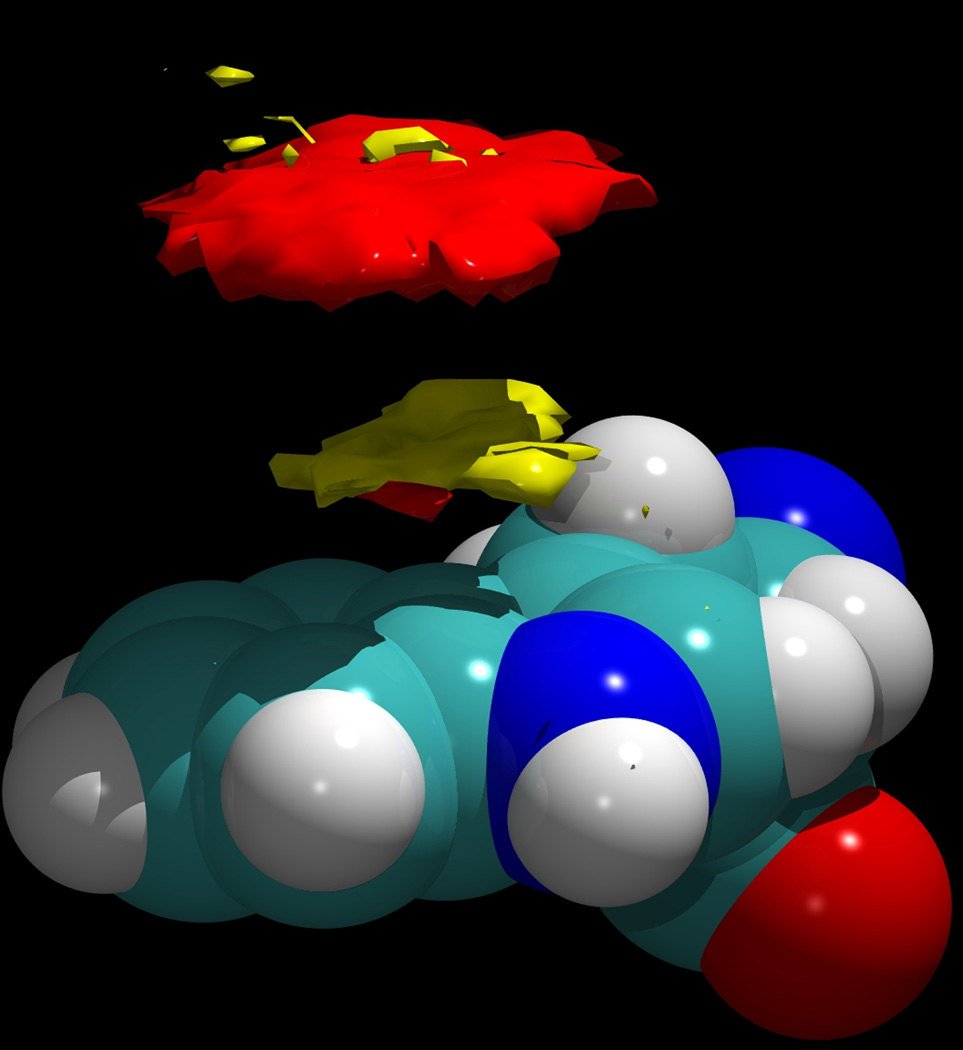
In the present simulations the indole sidechain lay against the peptide, exposing only one face to the solution. However, the sidechain was observed to flip over about 10 times during the course of each simulation; in all cases the transition was rapid, and except for these very brief transitions, only one face of the aromatic group was exposed to the solution. As these states are effectively energetically degenerate, in the present analysis these two states were symmetrized along the mirror plane of this group to more accurately represent the behavior of a tryptophan side chain exposed to the solution. Figure 7 displays a three dimensional contour plot of the calculated density of the H2 and H4 protons around the Trp 19 residue for both the β and α anomers (shown in red and yellow, respectively), averaged over the two separate simulations, but displayed in the same figure to emphasize the difference in their binding geometries. In each case, the mesh of the density map used cubes with sides of length 0.32 Å. The density contours displayed in Figure 7 enclose those regions of space with an atomic number density greater than 0.017 atoms·Å⁻³, approximately 7 times bulk density. As can be seen, the β anomer tends to bind with its H1-H3-H5 surface in contact with the indole group, so that its H2 and H4 protons are further away. Note that while the β anomer is hydrophobic on both of its faces, and particularly on its H1-H3-H5 face, this hydrophobic triad is somewhat disrupted by the axial O1 hydroxyl group in the α anomer (see Figure 1). Thus, it would not stack as optimally against the center of the hydrophobic planar face of tryptophan, as that would require the sacrifice of at least one hydrogen bond by this hydroxyl group. Thus, while both anomers interact with the Trp 19 group, the geometries of their interactions differ. The α anomer interacts with this residue “flipped” over, with its axial H2 and H4 residues pointing toward the tryptophan. These orientational preferences are statistically meaningful, since the contours in Figure 3 are averaged over approximately 70 exchanges of the glucose ligand for each of the anomers. In addition to stacking against the hydrophobic face of the indole, both anomers of glucose in principle can interact with the NH group of this side chain via hydrogen bonding as an acceptor. An example of such an interaction is shown in Figure 6 for the β anomer.

Figure 7.

The density of the H2 and H4 aliphatic protons of α-D-glucopyranose around the Trp 19 residue of melittin (yellow) and for β-D-glucopyranose (red). The difference in distance from the Trp ring occurs because the α anomer is oriented “upside down” compared to the orientation of the β anomer. In both cases, the ring heavy atoms would lie in the empty region between these two clouds. The density contour in both cases is 0.017 atoms Å⁻³.

The fractional occupancy of the binding site adjacent to the tryptophan side chain can be calculated from the simulations and used to estimate an approximate binding energy for the glucose molecules to the indole group, by comparing this to the occupancy of the same volume in the bulk, where the solutes should be randomly distributed. Density map contour levels such as those shown in Figure 7 can be used to define a “bound state”, and the enclosed densities can then be integrated to give the fraction of time that indoles are bound to a glucose molecule, and thus the fractions of free and bound groups. These concentrations can be used to calculate a host-guest type equilibrium constant $K=\frac{[\mathit{\text{glucose}}•\mathit{\text{indole}}]}{[\mathit{\text{glucose}}][\mathit{\text{indole}}]}.$ This equilibrium constant can be used to calculate the binding free energy $\mathrm{\Delta }G=-\mathit{\text{RT}}\text{ln}\frac{K}{K^o},$ with the standard state defined as the binding site volume occupied by bulk density glucose.

Table 1 lists these calculated occupancies, equilibrium constants, and binding energies. The calculated binding energy will depend to some extent upon the definition of the binding site, which in this case means the density contour interval selected to define the occupied volume. However, since the glucose density in this site is so much higher than the bulk density, and falls off so steeply, the binding energy is only weakly dependent on this definition, as can be seen from Table 1, which uses four different definitions for each anomer. Thus, a meaningful qualitative estimate of the binding affinity can be made from the average data of the simulations. These binding energies are on the order of ~0.5 kcal/mole, or approximately equal to kT at the simulation temperature of 300K. This binding affinity is roughly equal for the two anomers, but consistently slightly lower for the α anomer. With such a weak magnitude, these sugar molecules could not be considered to be “bound” in the conventional sense, which is borne out by the observation of frequent escapes and exchanges. From these 70 exchange events the average residence time is estimated to be ~100ps. Nonetheless, the calculated energies illustrate the clear preferential affinity of the glucose molecules for this position adjacent to the protein, relative to bulk solution. These binding energy estimates are of a similar order to those determined experimentally by Waters and co-workers for a system of a simple carbohydrate (including glucose) interacting with a tryptophan residue in a small β-hairpin peptide.³⁸

Table 1.

The calculated binding energies for the association of both anomers of glucose with the Trp 19 residue of melittin as calculated from the simulations.

	Density Cutoff (atoms/Å3)	Calculated coordination number	Coordination number of an equivalent volume of bulk	Keq	Binding energy, ΔG (kcal/mol)
β-D-glucopyranose	0.030	0.0600	0.0082	7.68	−0.53
	0.024	0.0904	0.0139	7.06	−0.51
	0.019	0.1189	0.0206	6.42	−0.48
	0.016	0.1421	0.0272	5.91	−0.46
α-D-glucopyranose	0.030	0.0004	0.0001	6.28	−0.48
	0.024	0.0044	0.0008	5.26	−0.43
	0.019	0.0192	0.0043	4.50	−0.39
	0.016	0.0386	0.0099	4.00	−0.36

As might be surmised from Figure 4, glucose makes weak interactions with other surface groups that constitute representative side chain moieties of proteins. Figure 8 displays a snapshot of the peptide interacting with α-D-glucopyranose molecules in comparison with a similar snapshot from a previous study of melittin in a guanidinium chloride solution;⁸ at a concentration of 3 m glucose the peptide surface appears to be highly “decorated” with glucose. However, only in the case of the Trp indole is the interaction with glucose sufficiently strong that significant density is observed in atom density plots relative to bulk density (Figure 7), consistent with the conventional view of glucose as an osmolyte, which is supported by the data in Figure 3. Thus, whereas glucose exhibits similar stacking interactions with the tryptophan indole group as does guanidinium (Figures 6 and 7),⁸ glucose does not stack significantly against the planar π-bonded guanidine group of arginine, nor the planar π-bonded side chain amide of glutamine. These observations indicate significant differences in side chain interactions between the denaturant guanidinium and the osmolyte and protein stabilizer glucose.

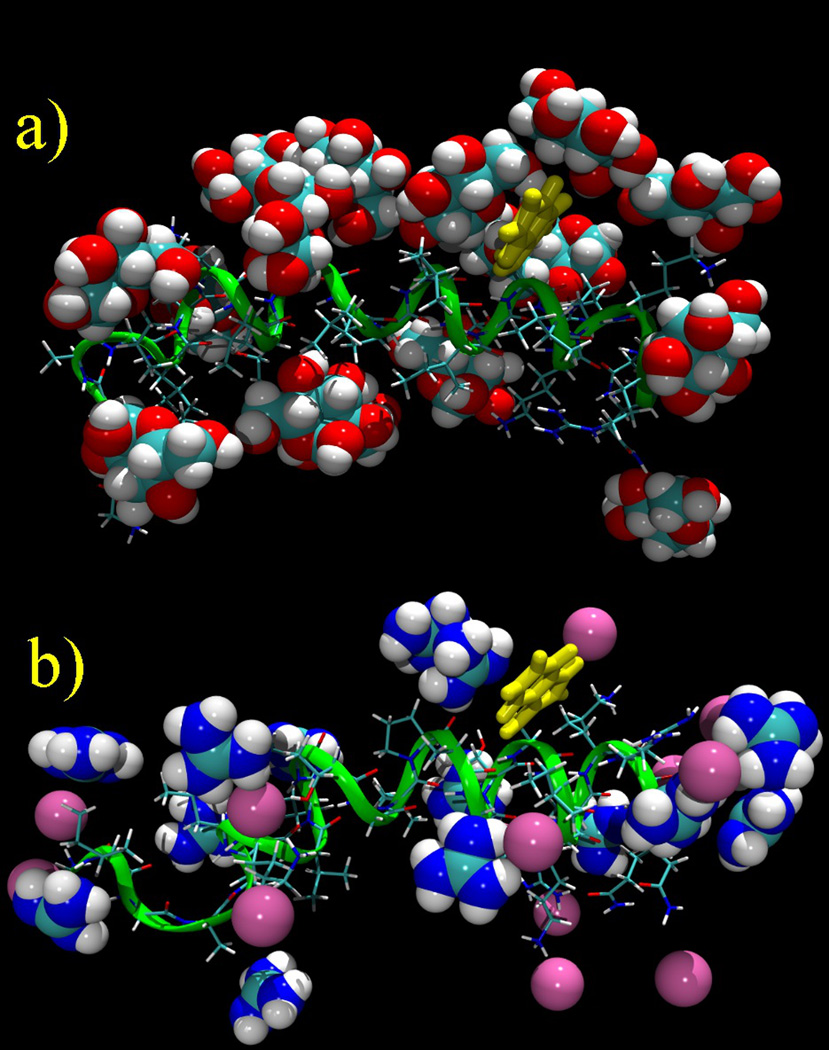
Figure 8.

a) A snapshot of the glucose molecules interacting directly with the melittin peptide in the simulation of the α anomer; b) A comparable snapshot of the guanidinium and chloride ions interacting with melittin in a 3 m soution. The melittin helix is oriented N-terminus (left) to C-terminus (right). In both cases the bulk molecules are not shown.

The glucose-side chain hydrogen bond interactions were analyzed by averaging hydrogen bond populations over the α-anomer simulation, using as the definition for a hydrogen bond, a heavy atom separation of 3.5 A or less, and an X-H…O angle greater than 120° (where X is N or O). These data (Table 2) show that glucose makes marginally more hydrogen bonds as a hydrogen donor to the neutral hydroxyl and amide groups of Ser (but not Thr), and Gln, respectively, than expected from its mole fraction of hydrogen bonding groups relative to water, whereas hydrogen bonding involving glucose oxygens as hydrogen bond acceptors is under-represented relative to that expected based on mole fractions of hydrogen bonding groups. Overall, water slightly “out-competes” glucose in its interaction with neutral hydrogen bonding groups on this protein surface, as would be expected in the case of an osmolyte. The marginal preference of either glucose or water for hydrogen bond interactions with neutral groups may be partly due to steric considerations, since the additional methyl group on Thr compared to Ser reduces each of the hydrogen bond populations involving glucose; i.e. both as a hydrogen bond donor and (especially) as a hydrogen bond acceptor. Likewise all hydrogen bond interactions involving glucose oxygens as hydrogen bond acceptors are under-populated compared to water. This is consistent with the expectation that the bulky glucose molecule may be less able to make the close approaches to the surface required to present its oxygen atoms as hydrogen bond acceptors. These conclusions also apply to hydrogen bond interactions between glucose and the positively charged side chains of arginine and lysine. In each case the oxygen atoms of glucose are under-represented as hydrogen bond acceptors in relation to their mole fractions, compared with water.

Table 2.

The fraction of H bonds from the alpha anomer of glucose and water, to the donor and acceptor groups of neutral peptide sidechains of Gln 25 & 26 (average), Thr 10 & 11 (average), Ser 18, Lys 21 & 23 (average), and Arg 22 & 24 (average), expressed as fractional populations. The fractional populations of H bond donors and acceptors on both water and glucose are shown in bold italic text. The estimated error based on the spread of the data from splitting the simulation into 10 equal parts is ~ 6%.

	Fraction of HO donors on water and glucose	Fraction of O donors on water and glucose
fraction HO/O groups water	0.88	0.76
fraction HO/O groups glucose	0.12	0.24
	O on peptide-OH on glucose or water	XH on peptide-O on glucose or water
	O(Gln) - HO	NH2(Gln) - O
Gln - water	0.86	0.83
Gln - glucose	0.14	0.17
	O(Thr) - HO	OH(Thr) - O
Thr - water	0.90	0.88
Thr- glucose	0.10	0.12
	O(Ser) - HO	OH(Ser) - O
Ser - water	0.88	0.85
Ser - glucose	0.12	0.15
	N(Lys) - HO	NH(Lys) - O
Lys - water	-	0.86
Lys - glucose	-	0.14
	N(Arg) - HO	NH(Arg) - O
Arg - water	-	0.84
Arg - glucose	-	0.16

Conclusions

These simulations have found significant binding of glucose molecules to specific sites on a peptide in aqueous solution, with some similarities to the denaturant guanidinium. Like guanidinium, glucose molecules were found to pair their hydrophobic surfaces with the indole side chain of the Trp 19 residue in a manner similar to that seen in sugar binding proteins,^39–41 and in enzymes such as cellulases^42,43 which have glucosic substrates. The strength of this binding was largely independent of the anomer, and is topologically dependent on the geometry of the glucose anomers, with a different binding face preferred for the two anomers. Overall, however, the glucose molecules were found to essentially behave as osmolytes, with the specific affinities for some groups balanced by a relative avoidance of others, producing an overall net depletion of the sugar at the peptide surface. The observed tryptophan affinity was the only interaction that resulted in a substantially enhanced and localized atom density consistent with a specific molecular interaction. Unlike guanidinium, glucose showed no significant tendency to make stacking interactions with the planar π-bonded guanidine or amide groups of the side chains of arginine and glutamine, respectively. Glucose makes hydrogen bond interactions with the side chain amide of glutamine, the serine and threonine hydroxyl groups, and the charged side chains of arginine and lysine, but overall these are marginally under-represented (for neutral hydrogen bonding groups) or more significantly under-represented (for positively charged groups), based on the relative mole fractions of hydrogen bonding groups in glucose compared to water, again consistent with the general behavior of glucose overall as an osmolyte.

Focusing on glucose-tryptophan indole interactions, the present observations are consistent with the experimental study of Laughrey et al,³⁸ who used thermodynamic cycles to quantitate the free energy contributions to conformational stability afforded by carbohydrate-aromatic interactions in a designed β-hairpin peptide. These authors attributed small stabilizing contributions specifically to carbohydrate aromatic π-interactions, as has been previously asserted.⁴⁴ Although π orbitals are not explicitly represented in molecular mechanics simulations, the simulations are expected to represent both the geometry and polarity of the molecular species as well as their charge distributions, and each of these is likely to contribute to the interactions observed experimentally and in simulations. Thus, a similar small free energy contribution of the order of −0.37 (Laughrey et al.)³⁸ or −0.5 kcal•M⁻¹ (this study) is not unexpected. These observations are broadly consistent with the expectation that a molecule presenting a planar non-polar surface (glucose or guanidinium) is likely to interact favorably with planar aromatic surfaces in exposed protein side chains.⁴⁵ The source of this favorable interaction, however, is not necessarily due to π orbital effects, since it could equally be due to hydrophobic association of the two weakly hydrated faces.

These simulations have implications both for the interactions of glucose in the binding sites of carbohydrate binding proteins and the general effects of glucose on protein stability. In the first case, the simulations support the conclusion that the interaction of glucose with aromatic surfaces provides a small favourable contribution to the binding energy, as well as orienting the sugar for optimal hydrogen bond interactions with side chains in the binding site. In the second case, the simulations may give some insight into the mechanisms by which glucose stabilizes folded protein states. The simulations find a significant depletion of glucose from the protein surface for this specific peptide, as might be expected for a stabilizing osmolyte,⁴⁶ and the sugar is slightly under-represented in its hydrogen bond interactions with hydrogen bonding side chain groups. In addition, glucose does not make stacking interactions with the side chain amide of glutamine. If the observations with the side chain primary amide of glutamine are representative of the peptide backbone amide, then glucose is not expected to interact productively with backbone peptide groups exposed upon polypeptide unfolding. This is likely to be exacerbated by steric restrictions on the access of the bulky glucose molecule to the secondary amide of the peptide backbone, which recent evidence supports as the dominant site for solute interactions that modulate folded state stability of proteins.⁴⁶ This prediction could be addressed by simulation studies of the interaction of glucose with unfolded polypeptide chains.