Polarizing Agents and Mechanisms for High-Field Dynamic Nuclear Polarization of Frozen Dielectric Solids

Abstract

This article provides an overview of polarizing mechanisms involved in high-frequency dynamic nuclear polarization (DNP) of frozen biological samples at temperatures maintained using liquid nitrogen, compatible with contemporary magic-angle spinning (MAS) nuclear magnetic resonance (NMR). Typical DNP experiments require unpaired electrons that are usually exogenous in samples via paramagnetic doping with polarizing agents. Thus, the resulting nuclear polarization mechanism depends on the electron and nuclear spin interactions induced by the paramagnetic species. The Overhauser Effect (OE) DNP, which relies on time-dependent spin-spin interactions, is excluded from our discussion due the lack of conducting electrons in frozen aqueous solutions containing biological entities. DNP of particular interest to us relies primarily on time-independent, spin interactions for significant electron-nucleus polarization transfer through mechanisms such as the Solid Effect (SE), the Cross Effect (CE) or Thermal Mixing (TM), involving one, two or multiple electron spins, respectively. Derived from monomeric radicals initially used in DNP experiments, bi- or multiple-radical polarizing agents facilitate CE/TM to generate significant NMR signal enhancements in dielectric solids at low temperatures (< 100 K). For example, large DNP enhancements (~300 times at 5 T) from a biologically compatible biradical, 1-(TEMPO-4-oxy)-3-(TEMPO-4-amino)propan-2-ol (TOTAPOL), have enabled high-resolution MAS NMR in sample systems existing in submicron domains or embedded in larger biomolecular complexes. The scope of this review is focused on recently developed DNP polarizing agents for high-field applications and leads up to future developments per the CE DNP mechanism. Because DNP experiments are feasible with a solid-state microwave source when performed at <20 K, nuclear polarization using lower microwave power (< 100 mW) is possible by forcing a high proportion of biradicals to fulfill the frequency matching condition of CE (two EPR frequencies separated by the NMR frequency) using the strategies involving hetero-radical moieties and/or molecular alignment. In addition, the combination of an excited triplet and a stable radical might provide alternative DNP mechanisms without the microwave requirement.

1. Introduction

Dynamic nuclear polarization (DNP) has emerged as an important technique to enhance nuclear magnetic resonance (NMR) signals as illustrated by the many significant contributions to protein structural characterization [1*; 2*], investigation of the interface of polymer mixtures [3; 4], nanomaterials [5; 6*] and surface catalytic functional groups [7*]. In DNP, the greater polarization of electron spins (see Fig. 1 for examples of stable radicals) is perturbed by microwave fields and is subsequently transferred to bulk nuclear spins, leading to nuclear hyperpolarization. Conventional DNP enhancement, ε, is defined as:

$$\epsilon \equiv \frac{I_{on}}{I_{\mathit{off}}},$$ (1)

where I_on and I_off stand for the NMR signal intensities with and without microwave irradiation (which induces DNP effects), respectively. Figure 2 shows the combination of ¹H-DNP with a simple cross polarization (CP), magic-angle spinning (MAS), proton-decoupled ¹³C-NMR experiment. This NMR signal enhancement can be obtained in general sample systems and has also had significant impact on magnetic resonance image (MRI) contrasting techniques [8; 9; 10; 11]. While many recent DNP applications are demonstrated with hyperpolarized solutions, these applications are primarily based on initial DNP approaches in cryogenic solids, followed by a rapid dissolution or rapid melting process [12*; 13*]. Therefore, the polarizing agents discussed in this review article are designed and utilized for DNP in dielectric solids. There is no limitation on the type of nuclei for direct polarization transfer to occur as long as the specific nuclei interact with the electron spins [14; 15; 16; 17]. However in biological or polymer solids, proton spins are often polarized more rapidly, and then the other low-γ nuclei (e.g., ¹³C and ¹⁵N) can be polarized through CP using the enhanced polarization of protons [18; 19*; 20; 21; 22*]. The enhancement factor from DNP (compared to the thermal nuclear polarization obtained without microwave irradiation) can be as much as 660 for ¹H, 2600 for ¹³C and 6600 for ¹⁵N using Boltzmann electron spin polarization. If electron spin polarization is non-Boltzmann (e.g., resulting from photoexcited triplets or optical pumping) [23; 24; 25], nuclear spin polarization could be increased close to the limit of 100 percent. Significant DNP enhancements for magic-angle spinning (MAS) NMR have benefited structural characterization in samples with submicron domains (e.g., nanocrystals [6*] or mono-molecular layers [7*]) and of more complex biomolecular systems (e.g., membrane proteins [2]).

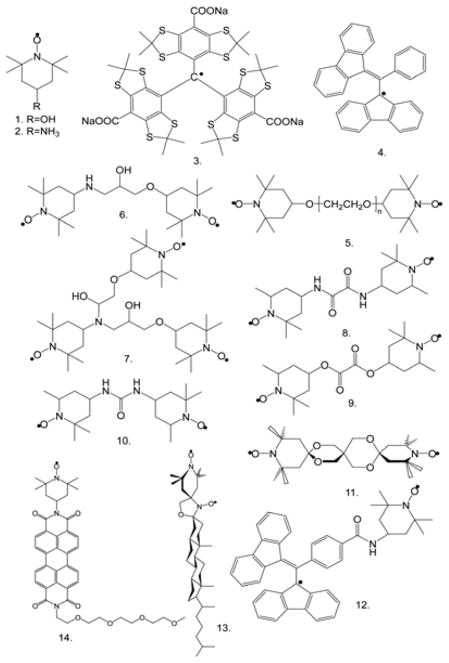
Figure 1.

Polarizing agents: (1) 4-hydroxy-TEMPO, (2) 4-amino-TEMPO, (3) trityl [154], (4) BDPA [104], (5) BTnE, n=2, 3 or 4 [49*], (6) TOTAPOL [50], (7) DOTOPA-TEMPO [52*], (8) BTOXA [22*], (9) BTOX [22*], (10) BTurea [22*], (11) bTbk [48], (12) BDPA-TEMPO [81], (13) BTcholesterol [99], (14) pyrelene-TEMPO. What is illustrated includes the commonly used radicals for high-field DNP (1–12) and future designer polarizing agents for aligned membranes (13) and photoexcited DNP (14).

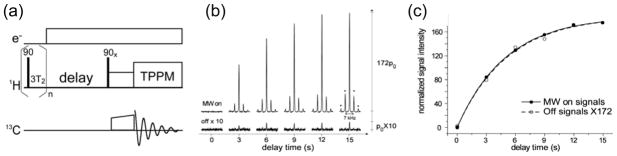
Figure 2.

(a) Illustrative pulse sequence for a general DNP-NMR SSNMR experiment. The saturation prior to the experiment ensures the same initial NMR signals regardless of the microwave irradiation mode, which is either continuous or intermittent for NMR pulsing and detection periods. (b) Typical DNP buildup under MAS conditions, such as the results shown for polarized ¹³C-urea signals from DNP using BT2E in d₆- DMSO/D₂O/H₂O (6:3:1 w/w/w) at 90 K and 5 T. The enhancement factor was assessed by comparing NMR signals with and without microwave irradiation and showed little dependence on microwave irradiation time under MAS. (c) The DNP buildup time constant was similar to T_1n because the polarizing agents were well-diluted against the concentration of bulk protons. Figures are reprinted from [22*].

For sample volumes of tens of microliters that are incompatible with most of the resonating geometries for millimeter waves, DNP experiments often involve continuous-wave (CW) microwave irradiation in a non-resonating structure (quality factor Q~1 for microwave delivery) [20; 26; 27; 28*; 29], as opposed to a cavity resonator (Q>1000) required by pulsed-microwave EPR experiments [30; 31*]. Thus, higher microwave power (~10 W) is required for typical DNP as opposed to lower power (~10 mW) for routine EPR. The DNP polarizing mechanisms at work under CW microwave irradiation depend on the electron paramagnetic resonance properties of the utilized unpaired electrons, which are either endogenous or exogenous in the NMR sample [32*; 33; 34]. Without intrinsic paramagnetic species, stable radicals (Fig. 1 for examples) or transition metal ions are often employed as ‘polarizing agents’ as a source of electron spin polarization, which is defined by the thermal equilibrium. The concentration of unpaired electrons in NMR samples has to be dilute to reduce the paramagnetic broadening of NMR [35*]. Thus, the rate of polarization transfer from electrons to bulk nuclei is slow and often regulated by the nuclear spin-lattice relaxation time (T₁). Figure 2c indicates that typical NMR signals from DNP grow with a time constant similar to nuclear T₁. Meanwhile, optimal electron T_1e and T_2e (spin-spin relaxation times) are required to be in the range of micro- to milliseconds to simultaneously facilitate efficient microwave saturation of electron spin polarization (which prefers long T_1e) essential for DNP mechanisms and fast turnover rates (which require small T_1e) in multiple polarization transfers [36]. Moreover, homonuclear spin diffusion that assists polarization transfer from dilute electron spins to bulk nuclei is more effective with a long nuclear relaxation time [6*]. For all of the aforementioned reasons, DNP experiments are frequently performed at cryogenic temperatures maintained by liquid helium or nitrogen. In addition, while partial reduction of the proton concentration (by deuteration) helps increase the observed DNP enhancements [37], a minimum proton concentration is required to maintain nuclear spin diffusion for efficient DNP. Over the past two decades, high-field DNP experiments have involved high-frequency (100–700 GHz), high-power (5–25 W) microwave irradiation from gyrotron devices [21; 27; 38; 39; 40*; 41; 42; 43; 44; 45; 46; 47] and have produced ever increasing NMR signal enhancements at liquid nitrogen temperatures. Valuable, 50- to 300-fold NMR signal enhancements have resulted from efficient polarization mechanisms (vide infra) facilitated by designer polarizing agents [13*; 22*; 33; 48; 49*; 50]. At helium temperatures (<20 K), significant DNP enhancements can be obtained with low microwave power provided by solid state sources [31*; 51]. In particular, using polarizing agents composed of three nitroxide radicals, DNP enhancements of ~80 can be obtained at 16 K and 9 T using a 30 mW diode multiplier source [52*].

Throughout their 60-year history of DNP[53*], CW-microwave polarization mechanisms have been categorized as belonging to the Overhauser Effect (OE), the Solid Effect (SE), the Cross Effect (CE) or Thermal Mixing (TM) [32*; 54]. OE occurs with mobile electrons in gases and liquids and in conducting solids. Polarization transfer in OE relies on electron-nuclear cross relaxation, and the efficiency depends on the correlation time of the underlying stochastic modulation of electron-nuclear interactions. Within frozen solutions, the time dependence of spin interactions favors polarization processes, such as SE, CE and TM that utilize the residual Hamiltonian terms of electron-electron and electron-nucleus spin interactions [35*].

It is noteworthy to know that DNP can occur in the liquid state at high magnetic fields (3–9 T) [55; 56; 57]. For example, OE DNP enhancements with factors of > 100 at 5 T and room temperatures were observed in a low-dielectric solvent with solutes undergoing transient contacts with BDPA that modulate the scalar electron-nuclear interactions [58*]. Recent DNP experiments in aqueous solutions have shown unexpected but significant OE enhancements at 3–9 T using nitroxides in aqueous systems [57; 59; 60; 61; 62; 63], in which the electric field of the microwave irradiation was attenuated by appropriate resonator designs [64]. An enhancement factor of −20 was measured from Fremyl salt, Na₂(SO₃)₂NO· and typical nitroxide radicals (Fig. 1, 1 and 2) in water. Molecular dynamics simulations of nitroxide and explicit water molecules showed unexpectedly short correlation times (< 5 ps) involving NO^• … H-O-H contacts [60; 65; 66]. While high-field OE remains challenging, low-field (< 1 T) OE experiments have often been performed using nitroxide radicals [67; 68] for applications such as probing molecular motion (e.g., in amyloid fibril growth and membrane optimization) [69*; 70; 71; 72; 73] and contrasting magnetic resonance images [74; 75; 76]. Enhanced nuclear polarization at low field can be transferred to high field for measurements with better resolution and detection sensitivity [77; 78; 79; 80].

Returning to the main focus on frozen solutions, various polarization mechanisms, such as SE, CE and TM, are primarily distinguished by the EPR linewidth of the utilized paramagnetic species. SE involves a narrow EPR line shape compared to the nuclear Larmor frequency (ω_0I), and either CE or TM involve an EPR linewidth larger than the target ω_0I due to either inhomogeneous or homogenous broadening, respectively. Figure 3 shows that field-dependent DNP enhancement profiles are determined by the EPR line shape, especially the linewidth, of the relevant paramagnetic species [33]. In contrast to the idea that efficient DNP should result from convenient microwave excitation of a narrow EPR line that facilitates SE, CE and TM resulting from partial microwave saturation of a broad EPR line shape appeared to be very efficient for DNP at high fields due to their favorable dependence on the external magnetic field. Therefore, Hu et al. introduced biradicals, two nitroxides tethered by a molecular linker, to facilitate CE and obtain significant NMR signal enhancements (~175 fold) at 5 T and 90 K under 3.5 kHz MAS conditions [49*]. The compounded improvement of DNP (judged by the improved DNP enhancements and reduced unpaired electron concentrations) using biradicals was ~16 fold in the initial work. Results that confirmed that CE is more efficient at high fields and can be improved by tethering stable radicals of the same or different kind opened a new avenue for the latest developments of DNP agents [22*; 48; 50; 81].

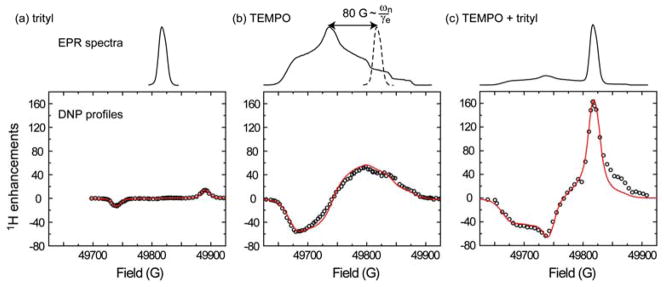
Figure 3.

High-field DNP polarizing mechanisms depend on the total EPR line shape of the utilized polarizing agents. (a) SE driven by 40 mM trityl radicals; (b) CE/TM driven by 40 mM monomeric 4-hydroxy-TEMPO; (c) CE/TM driven by radical mixture with 20 mM 4-hydroxy-TEMPO and 20 mM trityl radicals. The experiments were performed in solutions with 2 M ¹³C-urea in 6:3:1 w/w/w d₆-DMSO/D₂O/H₂O doped with TEMPO and/or trityl radicals. Note that the CE/TM mechanism was enhanced by the appropriate g-value separation between TEMPO and trityl (~80 G or 224 MHz) as shown by the dashed EPR line shape for trityl in (b). The experimental data points are shown in open circles, and theoretical curves are drawn in red lines. Figures are reprinted from [33].

Classical DNP theories based on spin-temperature thermal dynamics [32*; 82; 83] could not fully explain the discovery of biradical polarizing agents that are operative at low concentrations at which inhomogeneous line broadening dominates the linewidth. Therefore, a number of quantum mechanical explanations of DNP were reported [84; 85; 86; 87; 88; 89]. In addition, a sound explanation of high-field DNP using biradicals required new theories based on spin quantum mechanics. Along with the long history of DNP experiments, several review articles have helped clarify the developments and applications of contemporary high field DNP implementations [28*; 32*; 34; 90; 91]. Hence, this review will focus on the latest developments of polarizing agents for high-field DNP that have drastically sensitized modern NMR spectroscopy. The discussion here will be focused on polarizing agents involved in various polarizing methods and on future efforts in finding new compounds and experimental conditions that best facilitate polarization transfer to achieve the full nuclear polarization defined by the involved electron spins.

2. Polarizing agents for DNP in dielectric solids

High-field DNP based on CW-microwave irradiation enjoys a higher efficiency in frozen solids because the polarizing of liquid samples in high fields suffers from a shorter skin depth of microwave irradiation and the lack of fast molecular motions comparable to high EPR frequencies (> 100 GHz) [58*]. Polarizing mechanisms in dielectric solids include SE, CE and TM [35*; 92]. SE dominates the polarization mechanisms when the EPR linewidth (δ and Δ for homogeneous and inhomogeneous broadenings, respectively) is less than the nuclear Larmor frequency (ω_0I). Microwave irradiation at ω_0S ± ω_0I, where ω_0S is the EPR frequency, drives the ‘forbidden’ electron-nuclear mutual flip-flop transitions, derived as double quantum and zero quantum spin operators, resulting in positive and negative NMR enhancements, respectively (for nuclei with positive gyromagnetic ratios). Because the off-resonance electron-nuclear transition relies on level mixing by electron-nuclear dipolar interactions, its transition moment scales with B₀⁻² as does the resulting DNP enhancement. When Δ>ω_0I, both positive and negative SE enhancements can occur simultaneously and thus cancel each other to attenuate the SE efficiency. Consequently, CE emerges as the dominating polarizing mechanism with larger Δ. In CE, spin polarization transfers in a dipole-coupled electron-electron-nucleus three-spin system, in which the optimal transfer efficiency requires |ω_0S1 − ω_0S2|=ω_0I (Fig. 4a) and an appropriate electron-electron and electron-nuclear dipolar interaction [35*]. The essential electron-electron dipolar interaction can be prepared by a molecular tether between two electron spin moieties. Moreover, the CE enhancements scale with B₀⁻¹ due to the EPR frequency-matching requirement rather than the transition moments involved.

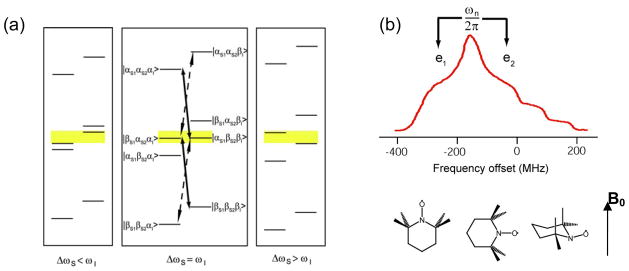
Figure 4.

(a) Illustration of the correct EPR frequency separation for efficient CE that requires that the |β_S1α_S2α_I> and |α_S1β_S2β_I> product spin states are degenerate, where S1 and S2 denote two electron spins and I denotes the nuclear spin. Without the degeneracy, the level mixing becomes ineffective due to level separation, as indicated by the yellow shading. (b) The EPR spectrum (shown in MHz) of TEMPO at 5 T with the corresponding TEMPO orientations shown roughly below the EPR frequencies. The anisotropic g-tensor of nitroxide permits the required EPR frequency matching (ω_0e2−ω_0e1=ω_0n) via appropriate nitroxide molecular orientations with respect to the external magnetic field (pointing up in the figure).

The figure of merit for designing polarizing agents for efficient high-field DNP is the enhancement factor, which is a ratio between NMR signals with and without microwave irradiation at the same delay time from saturation of the nuclear polarization (Eq. 1). Although the DNP buildup time matters for the polarization efficiency, its equivalence with the nuclear spin-lattice relaxation time (T_1n) makes it inappropriate for optimization because a shorter T_1n (as a result of paramagnetic doping) implies a stronger paramagnetic broadening of the NMR line shapes and of the less detectable NMR signals. Nevertheless, along with an increasing DNP enhancement, the buildup time often decreases and thus supports a more efficient polarization process. The following sections describe common polarizing agents for high-field DNP for various experimental demands.

2.1. Efficient CE/TM using biradicals for high-field DNP

The requirement of electron-electron dipolar interaction for CE has been proven experimentally by better DNP enhancements from the biradicals with shorter linkers as shown in the results from BTnE (Fig. 5) [22*; 49*]. In addition, the required frequency separation in a biradical is known to be fulfilled by the correct g-tensor orientations, occurring independently due to a flexible linker when the whole biradical molecule is randomly oriented in a powder system. Whether the correct molecular orientations can be constrained by a rigid tether is nontrivial, but it was easily shown that CE was suppressed when the two EPR frequencies were locked around the same value by a planar linker with a centered symmetry, as shown by the worst DNP enhancement from BTOXA (vide infra). The optimal pair of EPR frequencies for CE is obtained with one EPR frequency defined by the microwave irradiation and the other matching frequency from a g-anisotropy-broadened EPR line shape (Δ >ω_0I) (see illustrations of TEMPOs in Fig. 4b) [93]. Thus, the probability of frequency matching scales with B₀⁻¹ as for the CE DNP enhancements, assuming the field dependence of the DNP transition moment is compensated by appropriate electron-electron dipolar interactions. For example, using similar concentrations of TOTAPOL, the DNP enhancements in a variety of biological samples measured at ~9 T falls in the range of 30–100 [45], approximately 50% less than what is obtainable at 5 T and at similar temperatures of ~ 90 K [50].

Figure 5.

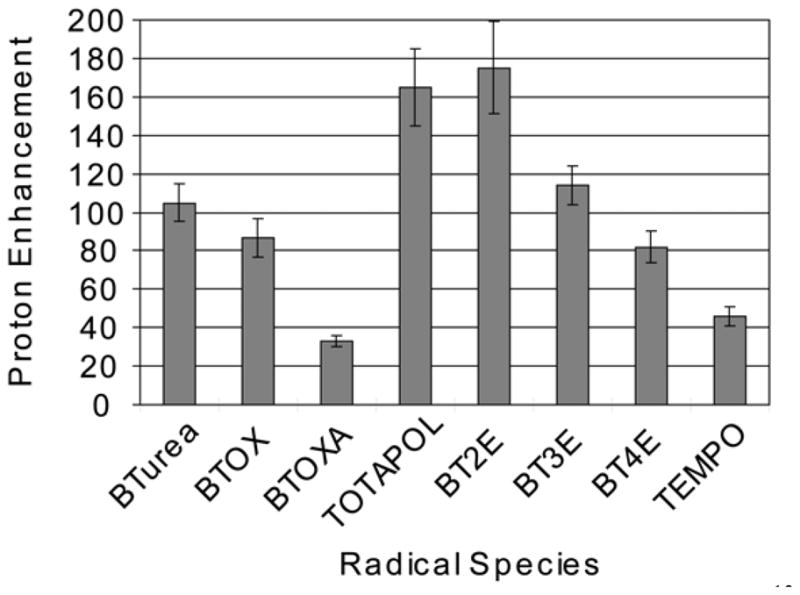
DNP enhancements in standard solutions (2 M ¹³C-urea, 6:3:1 w/w/w d₆- DMSO/D₂O/H₂O in a 4 mm o.d. sapphire rotor) doped with electron spins totaled at 10 mM and measured at 90 K and 5 T. Considering uncertainty, the best-performing polarizing agents are BT2E and TOTAPOL, the latter of which is biologically compatible and yields higher enhancement with sufficient microwave power (i.e., irradiated in a 2.5 o.d. mm sapphire rotor). Also interestingly, the worst DNP enhancement from BTOXA manifested the requirement of EPR frequency matching for CE. The figure is reprinted from [22*].

TM involves a similar mechanism to that which drives CE. The major difference between TM and CE is to incorporate more dipole-coupled electron spins. Classical explanations of TM were based on a ‘spin temperature’ theorem [32*; 82; 83] but become less relevant when DNP is performed in a high magnetic field and at a low radical concentration, for which inhomogeneous EPR line broadening dominates the homogeneous broadening. A modified TM theory by Farrar et al. for high-field DNP better addressed these issues by dividing the whole electron spin ensemble into several bins at different EPR frequencies included in the EPR line shape [94]. Each of the bins forms a spin temperature bath. With microwave excitation of specific bins, the perturbed spin temperatures can equilibrate (accompanying spin polarization transfers) with the bins possessing adjacent EPR frequencies. The energy bandwidth of the connected electron spin baths has to be greater than the nuclear Larmor frequency to make the polarization transfer from the connected electron dipolar baths to the nuclear spin bath. While the classical TM-DNP theories are described by phenomenological master equations on the spin temperature baths involved, TM can be described from a purely quantum mechanical point of view by extending a newly developed quantum mechanical CE theory (vide infra) to include more electron spins in order to understand, for example, a tri-radical polarizing agent (DOTOPA-TEMPO) utilized in stationary samples at 16 K and 9.4 T [52*]. These results indicate that large polarizations can be achieved with low-power microwave sources at low temperatures because an enhancement factor of 20 at 20 K is the same as a factor of 100 at 100 K. DNP experiments at low temperatures with low microwave powers might be improved with different polarizing agents than experiments at higher temperatures with higher microwave powers. One specific example is the Haupt effect, in which the nuclear polarization is induced by tunneling rotational quanta of methyl groups [95; 96; 97; 98] as the sample temperature is perturbed by microwave irradiation.

A sound quantum mechanical theory for CE was developed based on the Hamiltonian:

$$H=\sum _i{\omega }_{0S_i}{S}_{iz}+\sum _{i,j>i}[d_{ij}(3S_{iz}{S}_{jz}-S_i·S_j)-2J_{ij}{S}_i·S_j]-{\omega }_{0I}{I}_z+\sum _i(A_i{S}_{iz}{I}_z+B_i{S}_{iz}{I}_x),+\sum _i{\omega }_{1S_i}cos({\omega }_{MW}t)S_{ix},$$ (2)

where the electron and nuclear Larmor frequencies are denoted by ω_0Si (ω_0Sj) and ω_0I, respectively, d_ij and J_ij are the electron-electron dipolar and scalar (J-coupling) interactions, respectively, A_i and B_i represent the secular and semi-secular electron-nuclear dipolar interactions, respectively, and ω_iSi and ω_MW denote the microwave field strengths (for each electron spin) and the microwave frequency, respectively. Microwave-driven polarization transfers in DNP result from electron-electron and electron-nuclear dipolar interactions (especially the semi-secular electron-nuclear dipolar terms of the Hamiltonian). In particular, the oscillating microwave-field Hamiltonian in Eq. (2) is converted into a DNP-transition Hamiltonian, such as those coupling |α_S1β _S2α_I> and |α_S1α_S2β _I> and coupling |β _S1α_S2β _I> and |β _S1β _S2α_I> (Fig. 4a) [35*] in a tilted and rotating frame. Two, sequential unitary transformations were applied to the sub-product spin bases in order to emphasize the perturbation of the electron-electron dipolar interaction D₀, leading to a second-order coupling ~|B₁ − B₂| · D₀/|ω_0S1 − ω_0S2|. This second-order coupling became important when |ω_0S1 − ω_0S2|~ω_0I and resulted in strong mixing of the product spin states, aforementioned in Fig. 4a. As a result, the enhancement of nuclear spin polarization can be derived as a function of either

$$\frac{1}{2}{\epsilon }_{max}(1-cos\frac{{\omega }_{1S}t}{\sqrt{2}})$$

or

$${\epsilon }_{max}{sin}^2\frac{{\stackrel{\sim }{\stackrel{\sim }{\mathrm{\Omega }}}}_t}{2}{sin}^2\frac{{\omega }_{1S}t}{2},$$

where ε_max denotes the maximal DNP enhancement, and $\stackrel{\sim }{\stackrel{\sim }{\mathrm{\Omega }}}$ is a second-order variable derived from electron-electron and electron-nuclear dipolar interactions [35*]. This spin quantum dynamics picture without relaxation helps us understand the exact frequency-matching condition involving EPR and NMR frequencies. In addition, the time-dependent DNP enhancement elaborates nuclear polarization growth under conditions of weak and strong microwave fields. When dipolar interactions are strong, the DNP process is mainly microwave power-dependent, and the external field dependence is limited from the perturbation point of view. In this limit, the external field dependence is mainly described by the frequency matching using the g-anisotropy properties of electron spins. In the other limit of rapid microwave saturation of one of the coupled electron spins, a second-order Hamiltonian that couples |α_S1β _S2α_I> and |β _S1α_S2β _I> (three-spin mutual flips) can be derived from the dipolar interactions involved and leads to the subsequent polarization of the nucleus.

Enhancements as multiples of γ _e/γ _n ranging from ¼ to 1 could be obtained depending on the frequency-matching condition with |ω_0S1-ω_0S2| ~ ω_0I. The frequency matching is assisted by a broader excitation bandwidth resulting from microwave phase uncertainty and stronger microwave fields. Following the analytical derivation of the spin dynamics in DNP, a stochastic Liouville equation was employed to numerically calculate the Zeeman order transfer from electron spins to a nucleus in an electron-electron-nucleus three spin system, where the relaxation effects can be assessed [36]. The frequency-matching conditions for both SE and CE were simulated, and the conditions for more efficient polarization transfer in CE than in SE were demonstrated. Appropriate electron-electron dipolar interaction is desirable for optimal polarization transfer efficiency because an exceedingly strong electron-electron interaction prefers the singlet-triplet configuration of two coupled electron spins over the simple product spin states and complicates the frequency-matching condition. From these simulations, electron spin relaxation helps the frequency-matching condition by broadening the matching bandwidth. In addition, a longer T_1n is required for complete accumulation of transfer electron spin polarization in bulk nuclei when the polarization transfer needs to be repeated multiple times. Furthermore, whereas T_1e had a limited impact on the SE results, longer T_1e and T_2e facilitated microwave saturation in CE, but the DNP turnover rate (for multiple polarization transfers) decreased with longer T_1e, which was not favored in the case of dilute electron spins. In theory, a biradical polarizing agent with two different radical moieties can provide the benefits of long and short T_1e simultaneously. The optimal DNP results when microwave irradiation is tuned to the electron spin with longer T_1e, and the other electron spin with shorter T_1e will rapidly recover its spin polarization after performing one round of polarization transfer to the coupled nucleus.

Experimentally, biradicals were designed and examined as polarizing agents for high-field DNP. Specifically, polyethylene glycol (PEG_n, n=4,3 and 2) was used as a molecular linker to tether two TEMPO radicals, resulting in biradicals – bis-TEMPO tethered by n ethylene glycol units (a.k.a. BTnE) [22*; 49*]. DNP was verified from the enhanced ¹³C-urea signal in d₆-DMSO/D₂O/H₂O (6:3:1 w/w), and the largest DNP enhancement was measured from sample solutions doped with BT2E. Although a shorter PEG chain implies a more rigid biradical conformation, all BTnE series present no orientation constraints on TEMPOs according to their EPR spectra [22*], and thus, the two TEMPOs are oriented randomly with respect to each other, despite the distance constraints due to the PEG linker. With the frequency-matching condition satisfied by independent powder orientation of the two TEMPOs, the required electron-electron dipolar interaction is maintained within a biradical, and experimentally larger electron-electron coupling constants (as large as 22 MHz) result in greater DNP enhancements. Overall, measurable DNP enhancements were improved 4 fold, and the utilized electron spin concentration decreased 4 fold. A DNP enhancement of ~175 was obtained from 5 mM BT2E at 90 K under 3.5 kHz MAS at 5 T (211 MHz ¹H NMR).

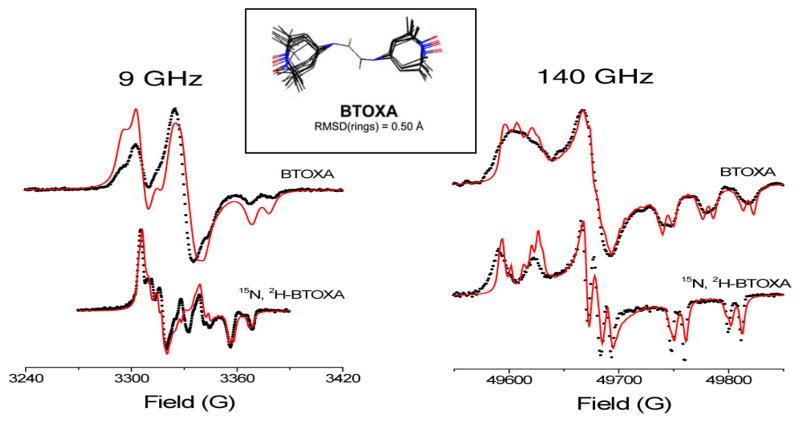
In addition, several shorter and rigid biradicals were designed, synthesized and examined in DNP experiments. Those include BTOX, BTOXA, BTurea and TOTAPOL for the purpose of constrained TEMPO orientations that possibly generate EPR frequencies satisfying the matching condition for CE [22*]. However, despite shorter electron-electron distances than in BT2E, most of these rigid biradicals did not yield larger DNP enhancements. In particular, BTOXA performed worse than monomeric TEMPO at the same electron spin concentration. According to the analysis of multiple EPR-frequency line shapes using 9 and 140 GHz microwaves (0.33 and 5 T fields), the underlying molecular conformation depicted symmetric g-, hyperfine- and dipolar-tensor orientations in BTOXA, and thus the two EPR frequencies in BTOXA were generated around the same value, regardless of the molecular orientation. Failure in the frequency matching for CE resulted in poor DNP enhancements from BTOXA. For BTOX and BTurea, the constrained TEMPO orientations did not necessarily support good frequency separation in powder distributions. The smaller enhancements compared to BT2E indicated a more beneficial effect from two independently oriented TEMPOs in BTnE. Nevertheless, the smaller enhancements might have resulted from a complicated polarization mechanism due to a stronger electron-electron dipolar interaction and emerging J-couplings in shorter biradicals. Finally, a semi-rigid and water-soluble biradical 1-(TEMPO-4-oxy)-3-(TEMPO-4-amino)propan-2-ol (a.k.a. TOTAPOL) was synthesized and found to generate similar enhancement to BT2E [50]. Greater DNP enhancements from TOTAPOL (than BT2E) were obtained with higher microwave-irradiation power density in a smaller sample rotor. The requirement of higher microwave power to yield higher DNP enhancements reflected a stronger electron relaxation effect due to the stronger electron-electron dipolar interactions compared to the average interaction in BT2E. Furthermore, the larger plateau enhancement extrapolated from the microwave-power dependence of enhancement might have resulted from a higher probability of having the correct TEMPO orientation in TOTAPOL for frequency matching as evidenced by EPR characterization [22*].

A recent success in improving CE in terms of the correct TEMPO orientation was demonstrated [48] with a newly synthesized, rigid biradical bTbk. A DNP enhancement factor of 250 (as opposed to 175 from BT2E) in DMSO/ethanol in a 4 mm rotor was obtained at 90 K, 3.5 kHz MAS and 5 T. Improved DNP enhancements resulted from constrained TEMPO orientations that increased the probability of g_yy and g_zz components (whose difference in EPR matched the ¹H Larmor frequency) when the biradical molecules were randomly oriented in a powder system. To unambiguously prepare the two correct EPR frequencies, one might place bTbk in an oriented state, such as aligned in a host diamagnetic crystal, which is then rotated for the desirable EPR frequencies. Another plausible approach to the correct EPR frequencies is to attach a rigid biradical to a cholesterol molecule [99] inserted in biological membranes or lipid bilayer disks that can be aligned mechanically or magnetically [100]. Moreover, to better facilitate CE in either powder or aligned systems, relative g-tensor orientations of potential rigid biradical candidates have been assessed from the three-dimensional molecular structures obtained by computer calculations [101]. Although bTbk is not soluble in water, it could be employed as a polarizing agent in membrane systems in which it has produced a DNP enhancement of 18 in an oriented membrane polypeptide system [102].

Hitherto, the CE frequency-matching condition is ideally fulfilled by two radicals with sharp EPR lines (i.e., with small g-anisotropy) separated by the exact nuclear Larmor frequency. Initially, this effect was demonstrated in frozen solutions with TEMPO and Trityl mixtures that generated larger enhancements compared to those from an identical amount of TEMPO or trityl radicals (Fig. 3) [33]. The enhancement profile as a function of the microwave irradiation frequency (shown in Gauss in Fig. 3) is asymmetric, with a larger enhancement from microwave saturation of the trityl EPR signal. The improvement primarily resulted from EPR frequency separation between the TEMPO g_yy component and the isotropic g-value of trityl radicals. In addition, an asymmetric enhancement profile indicated optimal DNP that required microwave saturation of the trityl signal, followed by conversion of the polarization difference between a dipolar coupled TEMPO and the excited trityl to the coupled nucleus in a three-spin flip-flop process. The longer T_1e and T_2e relaxation times of trityl-facilitated microwave saturation and the shorter T_1e of TEMPO ensured a quick turnover rate for multiple polarization transfers to bulk nuclei through spin diffusion.

The above experimental evidence describes a potential benefit of using heterogeneous radical moieties for two reasons: (1) direct frequency matching and (2) optimal relaxation times simultaneously facilitate microwave saturation and polarization turnover. Consequently, the syntheses of TEMPO-trityl [103] and TEMPO-BDPA with the requirement of water solubility have been attempted [81; 104]. It is important to know that the reported biradicals composed of TEMPO and trityl contain relatively strong J-couplings and significant dipolar interactions, which in turn strongly perturb the frequency-matching condition for CE. A different theoretical understanding should be applied to these biradicals as described in the latest DNP theory based on spin quantum dynamics [35*].

Early DNP applications using monomeric TEMPOs showed possible sample systems compatible with DNP experimental conditions, including detection of ¹⁵N of proteins and ³¹P of genetic materials outside and inside phage particles, respectively [105], ¹⁵N and ¹³C of the bacteria Rhodopsin (bR) proton pumping center [106], ¹⁷O-water[107] and biological solutes [108]. Enhancement factors of ~50 were obtained in those systems at 5 T. For example, phage-DNP indicated the penetration of polarization into inner DNA materials of the phage when ¹H-¹H spin diffusion was efficient between domains separated by phage protein shells. DNP-NMR measurements on bR drastically contrasted the signal-to-noise ratio of non-DNP experiments and time-saving for investigations of enzymatic reaction centers. Furthermore, ¹H-¹H spin diffusion was essential when the NMR system of interest is not accessible to polarizing agents. In ¹⁷O CP experiments, a short CP contact time between ¹H and ¹⁷O was desirable to maintain undistorted quadrupolar NMR line shapes, and the reduced sensitivity due to fractional CP transfer benefited from DNP enhancements.

The advent of the biologically compatible biradical, TOTAPOL, has permitted many applications of high-field DNP. Successful applications include: (1) enhancement of the proton pumping center of the membrane protein bR [1*; 2*; 109], in which the NMR system of interest is very dilute due to the complexity of bR and the present of the lipid membrane, (2) enhancement of a nanocrystal of a fibril peptide GNNQQNY [5; 6*] although the utilized polarizing agents TOTAPOL could not penetrate the crystals. Apparently, the polarization transfer has to be relayed by proton spin diffusion as evidenced by the differential DNP buildup times of the glassy medium and the crystals, (3) enhancement of the ¹⁴N signal of model peptides that facilitated the ¹³C-¹⁴N correlation spectra for ¹⁴N quadrupolar coupling parameters [110], (4) the successful polarization of a protein complex of tubline and kinesin proteins, which should be published soon from Oschkinat’s group in Berlin, Germany, and (5) new, DNP-enhanced NMR results of surface chemistry of porous catalytic materials [7]. Specifically in protein structural characterization, a typical issue with severe NMR line broadening, possibly due to phase transitions or inhomogeneous environments as a result of water arrangement around the protein, was not observed in the DNP applications to bR and protein complexes [111]. Moreover, problems arising from the limited concentration of species of interest in the above protein systems were solved by DNP enhancements. Furthermore, efficient ¹H-¹H spin diffusion permits separation of the nuclear spins of interest from the doped electron spins to maintain resolution of the enhanced NMR spectra.

In addition to indirect polarization (mediated by ¹H spins) of ¹³C, ¹⁵N and other low-γ nuclei through cross polarization in biological systems, it is plausible to directly polarize relevant nuclei, such as ²H, ¹⁷O, ¹⁴N and ³¹P, at longer microwave irradiation times [14; 15; 21]. Despite issues with line broadening due to closer electron-nuclear distances (for sufficient electron-nuclear interaction in DNP), direct polarization generalizes DNP to a sample system without sufficient proton density or to the relevant sites within a short distance from the paramagnetic species. This is particularly important when endogenous electron spins, such as reaction metal centers or local spin labels residing in or attaching to a region of the investigated protein, were utilized for DNP [112].

2.2. Regaining efficiency of SE-DNP using tri-aryl-based radicals

Tri-aryl radicals, including trityl and BDPA, yield narrow EPR line shapes with small g-anisotropy [33; 104; 113]. In ¹H DNP, nuclear polarization from trityl or BDPA occurs primarily through SE because Δ < ω_0I. In early DNP experiments approximately two decades ago, SE was assumed to be improved by polarizing agents with a narrower EPR line shape, which could be fully utilized for off-resonance excitation by high-power microwave irradiation [21]. For example, Wind and Yanoni used endogenous paramagnetic centers to polarize ¹³C spins in charcoals and diamonds via SE [114; 115]. Schaefer used BDPA to polarize ¹³C spins across polymer interfaces, in an attempt to use SE-DNP to assess the domain thickness at nanometer scales [3; 4; 116]. Nevertheless, the forbidden transition in SE makes the enhancement scale with B₀⁻² and significantly hinders its efficiency in high fields, where high-power, high-frequency microwave sources are very expensive. Initial high-field DNP (5T) was demonstrated in polarized polystyrene doped with BDPA [21]. With sufficient microwave power to overcome the unfavorable field dependence, SE can generate large DNP enhancements as shown in a trityl-doped solution in a capillary tube held in a cylindrical microwave resonator [31*]. Despite unfavorable field dependence, the option of SE can be exclusive to highly diluted paramagnetic species, such as naturally occurring electron centers in diamonds [117; 118; 119; 120], γ-ray irradiated organic solids [121] and sparsely dye-doped systems in which non-Boltzmann electron spin polarization can be obtained from photoexcited triplets [122; 123].

For DNP using isolated electron spins with narrow EPR line shapes, polarization transfer using limited microwave power should take the route analogous to cross polarization between spins with different gyromagnetic ratios. However, the huge difference between the gyromagnetic ratio of the electron spin and that of a nucleus (such as ¹H) presents difficulties to the Hartmann-Hahn condition (i.e., an electron microwave field has to be on the MHz scale in order to cover the smallest EPR linewidth, whereas the strongest ¹H radio-frequency field is less than 0.5 MHz). While new pulse sequences are being developed for effective Hartmann-Hahn frequency matching using pulsed microwave and radio-frequency fields, it is still more convenient to perform SE using continuous microwave irradiation. The adverse field dependence of SE enhancements due the off-resonance microwave irradiation in laboratory-frame spin dynamics can be alleviated by matching the nutation frequency of electron spins in the rotating frame defined by the microwave field with the resonance offset of the nuclear spins (the laboratory frame of the nuclear spin), because the ‘energy gap’ defined by the microwave field strength is smaller. This concept was realized by Weis et al. who developed the dressed-state-solid-effect (DSSE) to indirectly demonstrate the DNP effect using trityl radicals [86]. A similar electron spin echo-detection was used to demonstrate SE using gadolinium in aqueous media [124]. The central EPR transition in the high spin center in gadolinium experiences an effective field strength multiple of the delivered microwave field. Such increased SE-DNP transition moments in high-spin transition metal ions were utilized in a recent demonstration of DNP at 5 T and 90 K using ~2 W microwave irradiation from a 140 GHz gyrotron [125]. Finally, TM polarization of ¹H using trityl in frozen solutions can be implemented in ¹H rotating frame [94].

2.3. Solution NMR enhancements from low-temperature DNP followed by melting or dissolution of the polarized solids

Recently hyperpolarized nuclear polarization in high fields has been obtained from dissolved or melted solutions that were polarized in cryogenic conditions. Trityl is a popular polarizing agent recommended for dissolution DNP experiments in commercial polarizing devices [12*; 126; 127; 128; 129; 130; 131]. Despite the relatively narrow EPR linewidth (Δ) of trityl, the frequency-matching conditions for CE/TM can be satisfied for low-γ nuclei, such as ¹³C and ¹⁵N, and thus, direct polarization can generate high nuclear polarization at 1.2 K and 3.35 T [12*]. The polarization efficiency can be improved by trityl biradicals [132] and nitroxide radicals [133]. Subsequent dissolution by hot steam converts the high nuclear polarization in a frozen solution into hyper nuclear polarization in liquid states. A dissolution approach dilutes both the polarizing agents and the solutes involved, and it moves the sample solution away from the polarizing chamber. Thus, the resulting nuclear hyperpolarization is restricted to one-shot NMR acquisition, such as fractional detection of the nuclear polarization, which is only possible in simple flip-acquisition experiments, or in the recently developed single-scan multidimensional NMR methods involving sophisticated field gradients [134; 135]. To reproduce the freezing-polarization-melting cycles, a DNP-NMR sample was placed in a sapphire rotor (slowly rotated for uniform microwave irradiation) and mounted on a DNP-NMR probe that permitted IR-laser (10.6 μm) melting in < 1 s [13*]. The melting approach utilizes TOTAPOL and high-power microwave irradiation from a gyrotron and produces enhanced liquid-state NMR signals that are stable for multidimensional NMR experiments [136] and are more compatible with conventional NMR pulse sequences. Notice that the enhancements in dissolution DNP usually refer to NMR signal-intensity gains compared to room-temperature signals and can easily be a factor of tens of thousands. When the Boltzmann factor is excluded, the DNP-only enhancement, assessed at the polarization temperature ~4 K, is approximately 130, which reflects the DNP efficiency of the utilized polarizing agent (i.e., trityl) and the polarization scheme (i.e., direct ¹³C polarization). Enhanced liquid NMR signals from melted, hyper-polarized, frozen solutions are widely applied to MRI in contrasting and metabolic imaging techniques [8; 137; 138; 139; 140; 141; 142]. In addition, preservation of the polarized signal over a long time (through melting and liquid transfer to target organs) was attempted by storing nuclear spin orders in long-lived spin states [143; 144; 145].

3. Paramagnetic species for prospective photoexcited-DNP

In some photoexcited systems, hyper nuclear polarization can be obtained through a number of mechanisms involving time-dependent electron-nuclear interactions [146]. The attractiveness of these phenomena is the intermediate, non-Boltzmann electron spin polarization resulting from photoexcitation, such as excited triplets and optical pumping (using circularly polarized photons) [25]. Interestingly, photoexcited chemically induced DNP (photo-CIDNP) in condensed protein systems (e.g., the reaction center of a photosynthesis system or a photo-activated signal transduction protein) could result from a three-spin process similar to that which drives CE [147; 148; 149]. Furthermore, the CE mechanism can involve a photoexcited triplet or optically pumped electron spin order that is non-Boltzmann (much greater than thermo-equilibrated spin polarization), and the new polarization methods may be performed by linking a stable radical to a dye moiety (such as 14 in Fig. 1) that absorbs specific photons [150; 151; 152]. Because the electron spin polarization gradient between the excited dye and the stable radical is obtainable without microwaves, DNP without microwave irradiation is speculated.

4. Concluding remarks

After reviewing the recent progress in polarizing agents, we have discerned an apparent trend that efficient high-field DNP using CW microwave irradiation relies on the CE mechanism. The essential parameters for CE (EPR frequency separation and dipolar interactions) can be optimized through molecular designs, such as designer rigid molecular linkers that constrain both the relative tensor orientations and the interradical distance. To move beyond thermal spin polarization that requires perturbation by microwave fields, non-Boltzmann spin polarization can be prepared through photoexcitation and spin-state sorting through a magnetic semiconducting membrane [153]. Beyond the DNP operation with CW microwaves, stronger microwave fields improve SE or permit spinlock polarization transfer, and polarizing agents with narrow EPR linewidths and long relaxation times would be desirable. New polarizing agents derived from the above concepts will be examined further in the future.

Figure 6.

Line shape fitting of the EPR spectra (simulations in solid lines and experimental data in dots) of BTOXA measured with 9 and 140 GHz microwave frequency. The multi-frequency spectra were simultaneously fitted with a set of spectral parameters that helped constrain the underlying biradical conformations. For example, possible molecular structures of BTOXA refined from the fitting are shown in the inset. A planar BTOXA molecule yields close EPR frequencies of the tethered nitroxides, regardless of the molecular orientation and thus impedes the efficiency of CE. Figures are reprinted from [22*].

• Overview of polarization mechanisms for high-field DNP in frozen solids.

• Emphasis on the most efficient high-field polarization mechanism, the Cross Effect.

• Review of biradical polarizing agents that improve the Cross Effect.

• Speculation of future polarization methods with less or without microwave power.

Biography

Kan-Nian Hu received a B.A. degree (1996) and a M.S. degree (1998) in chemistry from National Taiwan University. In 2000, he joined Dr. Robert G. Griffin’s research group as a research assistant in Francis Bitter Magnet Laboratory at Massachusetts Institute of Technology, worked in areas of high resolution solid state NMR and high field dynamic nuclear polarization, and subsequently earned a Ph.D. degree (2006) in physical chemistry from MIT. He was a Visiting Fellow (2006 to 2011) with Dr. Robert Tycko in National Institute of Diabetes, Digestive and Kidney Diseases at National Institutes of Health, working on structural characterization of folding and misfolded proteins. Since June 2011, he joined Vertex Pharmaceuticals, Inc in Cambridge, Massachusetts, working on solid state characterization and controls of drug substance and drug product from early discovery to clinical trials and to the final commercial stage.