Abstract
Biological tissues have unique mechanical properties due to the wavy fibrous collagen and elastin microstructure. In inflation, a vessel easily distends under low pressure but becomes stiffer when the fibers are straightened to take up the load. The current microstructural models of blood vessels assume affine deformation; i.e., the deformation of each fiber is assumed to be identical to the macroscopic deformation of the tissue. This uniform-field (UF) assumption leads to the macroscopic (or effective) strain energy of the tissue that is the volumetric sum of the contributions of the tissue components. Here, a micromechanics-based constitutive model of fibrous tissue is developed to remove the affine assumption and to take into consideration the heterogeneous interactions between the fibers and the ground substance. The development is based on the framework of a recently developed second-order homogenization theory, and takes into account the waviness, orientations, and spatial distribution of the fibers, as well as the material nonlinearity at finite-strain deformation. In an illustrative simulation, the predictions of the macroscopic stress-strain relation, and the statistical deformation of the fibers are compared to the UF model, as well as finite-element (FE) simulation. Our predictions agree well with the FE results, while the UF predictions significantly overestimate. The effects of fiber distribution and waviness on the macroscopic stress-strain relation are also investigated. The present mathematical model may serves as a foundation for native as well as for engineered tissues and biomaterials.
Keywords: Tissue, Fibers, Collagen, Microstructure, Vessel
1. INTRODUCTION
The mechanical properties of blood vessels are fundamental for understanding hemodynamics, wave propagation, distensibility of arteries and veins, plaque stability and rupture, and vascular growth and remodeling which are strongly affected by the stress or strain of the cells. The model prediction of mechanical response of blood vessels subjected to physiological or pathological loads may help clarify the initiation, progression, and clinical treatment of diseases such as atherosclerosis (Vito and Dixon, 2003). The mechanical properties of the vessels largely stem from microstructural components such as elastin and collagen fibers, cells and ground substance (Azuma and Hasegawa, 1971; Azuma and Oka, 1971; Oka, 1967, 1972; Oka and Azuma, 1970). Thus, the relation between the microstructure and macroscopic mechanical properties of the vessel is essential in tissue engineering, biomedical research and clinical practice. Accurate prediction of microstructural deformation and evolution, and in turn the function, will result in a new level of understanding of biological tissue in health and disease and for tissue engineering of new biomaterials.
The vast majority of constitutive models of vascular tissue are phenomenological in nature. In the pseudo-elastic models, blood vessels are modeled using constitutive relations to describe the repetitive loading and unloading behaviors separately. Hyperelasticity theory, in which the stress is calculated as the derivative of the strain energy function (SEF), has been adopted to further simplify the stress-strain relation. Fung et al. (1979) introduced a 2-D exponential SEF and later generalized it into a 3-D form (Chuong and Fung, 1983), in which the formulation applied to axisymmetric deformation of the vessel where the principal directions of the stress and strain tensors coincide with the radial, circumferential and axial directions. This leads to zero shear terms in their formulas. Deng et al. (1994) extended the formulation by adding a radial-circumferential strain to analyze axial torsion experiment and to determine the respective shear parameter. Humphrey proposed a general form of Fung-type SEF for arbitrary 3-D deformations (Humphrey, 1995). Other forms of hyperelastic constitutive models include the four-parameter logarithmic SEF of Takamizawa and Hayashi (1987), and the polynomial SEFs developed by Vaishnav et al. (1973) with three, seven or twelve parameters. Collectively, these models consider the vessel wall as a homogeneous material and are strictly phenomenological. Due to their simple analytic form, they have been used as a basis for investigating many vascular mechanics problems (Chuong and Fung, 1983). However, the parameters in these models have no physical meaning, and cannot be directly related to the vascular microstructure in health or disease.
There has been much effort to derive the constitutive model of the soft tissue from the geometry, distribution and the mechanical properties of the individual microstructures such as collagen and elastin fibers. There have been two major classes of micromechanical models, due to different consideration of the matrix material (cells and ground substance) in the tissue. The first class of models proposed by Lanir (1979, 1983) considers the tissue as a composite of elastin and collagen fibers embedded in a fluid-like matrix. Thus, the fibers are the only constituent phases that sustain non-hydrostatic loading such as tension and shear, while the contribution of the fluid-like matrix is a hydrostatic pressure. This assumption leads to a simplification that all the microstructures deform identically to the macroscopic deformation of the tissue since no fiber interactions are considered, such that the macroscopic SEF is the volumetric sum of fibers’ SEF. On the basis of this assumption and thermodynamic consideration, Lanir developed a general multiaxial theory for the constitutive relations in fibrous connective tissues (Lanir, 1979, 1983). Similarly, Decraemer et al. (1980) proposed a parallel wavy fibers model for soft biological tissues in uniaxial tension, followed by Wuyts et al. (1995). More recent developments of fluid-like matrix based models can be referred to in Refs. (Dahl et al., 2008; Humphrey and Yin, 1987; Lokshin and Lanir, 2009).
A second class of micromechanical theories assume the tissue as a collagen fiber reinforced composite, whose matrix is a solid-like material that can take up loading. This assumption is motivated by the fact that the elastin, which is part of the matrix, becomes straightened and starts to take the load in the early deformation of the tissue. For example, the experimental study of Gundiah et al. (2007) suggested that the elastin can be described with a neo-Hookean constitutive model. Based on this solid-like matrix assumption, Holzapfel et al. (1998, 2000) modeled the arterial wall as a two-layer fiber-reinforced composite where the macroscopic SEF of soft tissue stems from two sources: 1) an isotropic part associated with the mechanical response of the non-collagenous matrix material (elastin fibers, cells and ground substance), and 2) an anisotropic part due to the deformation of two classes of collagen fibers symmetrically disposed with respect to the axis of the vessel. Successive developments can be found in Refs. (Kroon and Holzapfel, 2008; Li and Robertson, 2009; Zulliger et al., 2004). Specifically, Zulliger et al. (2004) made further refinement to account for the distribution of the waviness of collagen fibers and different SEF of the matrix and collagen fibers. These models assume affine deformation; i.e., the deformation of the collagen fibers and the matrix are identical to the macroscopic deformation of the tissue. Consequently, the microstructural information considered in most of these models is the volume fraction and orientation of the fibers.
There have been significant developments in the past decades to bridge the nonlinear macroscopic properties of heterogeneous non-biological media with the geometry and mechanical properties of the functional microstructures (Kailasam et al., 1997; Lebensohn et al., 2004; Liu, 2003; Liu et al., 2003; Liu and Ponte Castañeda, 2004a, 2004b; Lopez-Pamies and Ponte Castañeda, 2004, 2007; Ponte Castañeda, 2002; Willis, 1977). For example, the recent second-order estimate (SOE) theory of Ponte Castañeda et al. (Lopez-Pamies and Ponte Castañeda, 2004; Ponte Castañeda, 2002) considers the microstructural interactions, finite-strain deformation and strong material nonlinearity and heterogeneity within a framework of minimum energy principle. Applications of the model have been made to predict the macroscopic stress-strain relation and microstructural deformation of porous rubber, and show significant improvements over the previous micromechanics models when compared to finite-element (FE) simulations.
In this work, the SOE theory will be implemented to model the wavy fibrous microstructure in soft biological tissue such as vessel wall. In comparison to the affine models with a solid matrix, the present development enable consideration of full set of microstructural geometries; i.e., fiber orientation, aspect ratio, statistical spatial distribution and waviness, as well as their nonlinear interactions. The model can predict the statistically average strains in the fiber and matrix, which are heterogeneous but assumed uniform in the affine approach. This is an important feature since the accurate description of the stresses and strains in the ground substance (matrix) is important for loading-induced remodelling of the tissue. Illustrative results will be presented along with FE for validation.
2. METHODS
2.1. The geometry and mechanics of wavy fibers
The mechanical properties of a tissue stem from the microstructural constituents. In the adventitia, dense and wavy collagen fibers form an interwoven network that tangles with some elastin fibers (Rhodin, 1979; Wolinsky and Glagov, 1967). Histologically, a collagen or elastin fiber is well described as a bundle of loosely bounded fibrils (Fratzl et al., 1997; Ottani et al., 2001). In an undulating state, such a fiber can deform with very little stress. When straightened, it can sustain a significant amount of axial stress. At low strain level, elastin fibers gradually extend (Lu et al., 2004) and straighten to take up load together with the fibroblasts and ground substance. Since the axial stiffness of elastin fibers is not significantly higher than the matrix fibroblasts and ground substance, the stress-strain behavior of the tissue exhibits only weak nonlinearity. When the artery is distended beyond a certain stretch ratio, the collagen fibers are gradually straightened and begin to take up the increasing loads (Lu et al., 2004), in a manner which depends on the deformation of the network. Since the collagen fibers have much higher tensile stiffness than elastin fibers and ground substance, and gradual engagement of the collagen fibers leads to the highly nonlinear overall mechanical properties of the adventitia (i.e., increase in tangent stiffness which protects the media layer from over stretch).
Thus, the first approximation is that the fibrous tissue is considered as a composite, in which the elastin, fibroblasts and ground substance make the effective matrix and the collagen fibers are considered as the reinforcing phases. This approximation is consistent with the framework of Holzapfel et al. (1998, 2000).
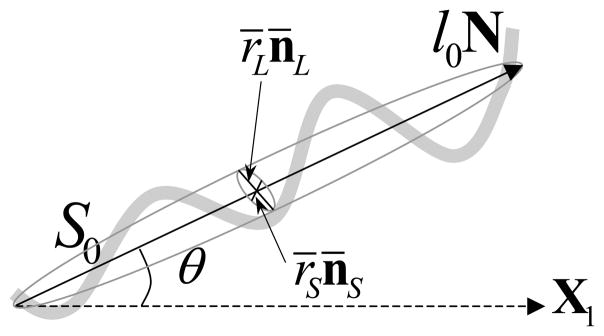
The waviness of a single undeformed fiber, denoted as λ0, is defined as the ratio of the end-to-end distance S0 and the straight length l0 (Fig. 1), as λ0 = S0/l0. This is also called straightening stretch ratio, meaning that the fiber is straightened when it is stretched along the fiber direction with a ratio > λ0. The orientation of the fiber is described by the overall direction N as shown in Fig. 1. The shape of the fiber can be described by a geometric tensor (⊗: dyadic product), where (r̄L, n̄L) is the cross-sectional long axis and (r̄S, n̄S) is the short axis, such that Zs · (X − Xc)≤1 (X is the spatial coordinate vector, and Xc is the geometric center of the fiber) defines an ellipsoidal material region that the fiber occupies (Willis, 1977).
Figure 1.
The geometry of an undulated collagen fiber with total length S0 and straight length l0. The overall fiber direction is N, which is described by the overall orientation angle θ for 2-D problem. The undeformed cross-sectional area is described by the long axis r̄L/n̄L and short axis r̄Sn̄S.
For convenience, the collagen fibers are categorized into N phases in the present homogenization modeling, such that the r-th phase has the same geometric properties (λ0, Zs) and occupies a volume fraction c(r) in the composite. Correspondingly, the volume fraction of the matrix, denoted as phase 0, is . Furthermore, we use an elliptical two-point (joint) distribution function P(rs) (X, X′) to describe the probability of simultaneous occurrence of the geometric centers of an r-th phase fiber at X and an s-th phase fiber at another point X′. Under the approximation of elliptical symmetry in micromechanics (Ponte Castaneda and Willis, 1995; Willis, 1977), the spatial distribution of fibers centers is characterized by a tensor , in which Nk are the principal directions of fiber distribution, ak is the characteristic distance between the centers of two neighboring fibers in direction Nk. A description of P(rs) (X, X′) and Zd and their effects on the macroscopic behaviors of composite is given by Ponte Castaneda and Willis (1995).
According to Holzapfel et al. (1998, 2000) and Gundiah et al (2007), the effective matrix material (elastin, fibroblasts and ground substance) is assumed to be isotropic, and is described by an approximate incompressible (κ ≫ μ) neo-Hookean SEF, as:
| (1) |
where F is the deformation gradient, I1 = tr C (C= FT · F) and are the first and the third invariants of the right Cauchy-Green deformation tensor, respectively.
As the second approximation, the constitutive SEF for the fibers is assumed to have the form:
| (2a) (2b) |
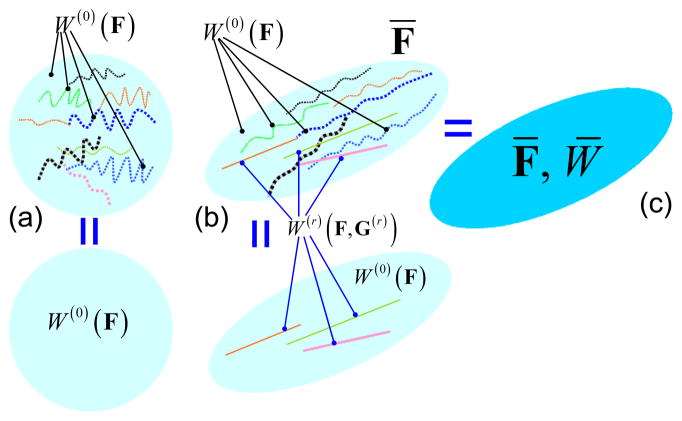
where is the stretch of the fiber along the fiber direction N(r), and is the straightening stretch ratio of the r-th phase. This approximation implies that a fiber deforms the same as the soft matrix before straightening, and becomes stiffer with additional deformation energy W (r)(λ) when straightened. Correspondingly, when the tissue is at the reference state without macroscopic deformation gradient F̄ = I, all the r-th phase fibers are wavy (since ) so that the term W (r) (λ) is not present in the model (Fig. 2a). When F̄ increases, some of fibers are straightened and will be treated as straight fibers, and the tissue is considered as a composite with straight fibers (Fig. 2b), whose macroscopic SEF is W̄ (F̄) (Fig. 2c) as will be derived below. This approximation is consistent with Holzapfel et al. (1998, 2000), in which an exponential function is assumed to describe the strain energy function of collagen fibers. It should be noted that although the SEF of fibers is approximately zero under the assumption of exponential form before the fibers are straightened, a similar results is approximated in the present model since the fibers: 1) are thin and 2) occupy a low volume fraction in the tissue and 3) the SEF of matrix is small as compared to that of straightened fibers.
Figure 2.
Conceptual demonstration of homogenization method. (a) A representative volume element of a fibrous tissue at reference state. All the fibers are undulated and exhibit the same property as the matrix with strain energy function (SEF) W0; (b) When subjected to a macroscopic F̄, some fibers are straightened and show stiffer property with SEF W (r) as in Eq. (2b). (c) The effectively homogeneous material with macroscopic SEF W̄.
2.2. Finite-strain homogenization framework
From a thermodynamic consideration, the microscopic stress field in the tissue can be derived from the heterogeneous hyperelastic SEF W (X, F) under isothermal and adiabatic (det (F) =1) conditions as:
| (3) |
where χ(r)=1 when X ∈ Ω(r) (the volume occupied by phase r), and 0 otherwise. The hydrostatic stress p is due to the incompressibility of the soft tissue. S is the transpose of the first Piola-Kirchhoff stress; i.e., it is related to the Cauchy stress σ by S = σ · F−T. The classical works of Hill (1972), Hill and Rice (1973) and Ogden (1978) proved that the macroscopic constitutive property for a microscopically inhomogeneous hyperelastic material can be described with macroscopic or effective SEF W̄ (F̄):
| (4) |
where κ(F̄) denotes all admissible deformation gradient field in the representative volume element (RVE) of the composite such that the displacement u on the boundary ∂Ω of RVE is u(X)= (F̄ − I) · X (where rigid-body motion is excluded). The notation 〈 · 〉 denotes volumetric average in the RVE, and 〈 · 〉(r) denotes volumetric average in the r-th phase. Equation (4) represents the principle of minimum strain energy in micromechanics. In general, the rigorous minimization solution for Eq. (4) is difficult to obtain for a random heterogeneous material whose microstructural information is complex and incomplete. The efforts to seek an approximate minimizing field F(X) have resulted in several classes of finite-strain micromechanics models including the following uniform-field upper bound and the second-order estimate.
2.3. Uniform-field upper bound based on solid-like matrix
The current homogenization models of soft tissue assume a uniform deformation field in the RVE, as F(X)= F̄. Thus, the macroscopic SEF W̄ (F̄) is simply the volumetric sum of the constituents, as in (Holzapfel and Gasser, 2000; Holzapfel and Weizsacker, 1998; Kroon and Holzapfel, 2008; Li and Robertson, 2009; Zulliger et al., 2004):
| (5) |
Since F(X)= F̄ is an admissible deformation field that does not minimize the total strain energy, W̄U (F̄) is an upper bound of the exact W̄ (F̄). Consequently, the stress S̄U =∂W̄U/∂F̄ is the upper bound of the exact macroscopic stress for a given F̄. A number of works (Holzapfel and Gasser, 2000; Holzapfel and Weizsacker, 1998; Kroon and Holzapfel, 2008; Li and Robertson, 2009; Zulliger et al., 2004) employ this uniform field approximation F(X)= F̄ in various forms, and thus are all upper bounds. As indicated by Eq. (5), the only geometric information considered in this previous approach is the volume fraction c(r), and the information that are included in W (r) such as the fiber orientations. The interactions between constitutive phases are also neglected.
2.4. Second-order microstructural model
In order to consider the statistical microstructural geometry of the tissue and provide a better constitutive model than the uniform-field upper bound W̄U (F̄), a recently developed SOE homogenization method (Lopez-Pamies and Ponte Castañeda, 2004a; Ponte Castañeda, 2002) for composites in finite-strain deformation was implemented. Unlike linear infinitesimal-strain composites where all the constituent phases are linearly elastic, finite-strain homogenization methods face challenges from the inherent nonlinearities of deformation and material properties (Ogden, 1978).
The key premise of SOE method is to introduce a linear thermoelastic comparison composite (LTCC) that has the same microstructures as the nonlinear composites, but each of the phases is linearly thermoelastic with SEF (Lopez-Pamies and Ponte Castañeda, 2004a;Ponte Castañeda, 2002):
| (6) |
in which the reference modulus L(r) and virtual residual deformation gradient F*(r) are to be determined later for conditional minimization of Eq. (4), and ρ*(r) = (∂W (r)/∂F)F=F*(r). Analogous to the derivation in (Ponte Castañeda, 2002) for infinitesimal-strain nonlinear composites, it can be shown that the following inequality holds for arbitrary choice of {F*(r), L(r)}:
| (7) |
with . By relaxing the constraint F ∈ κ(F̄) in the second term on the right hand side and defining , it is shown that the exact macroscopic SEF in Eq. (4) can be approximated by, as in (Ponte Castañeda, 2002),
| (8) |
where is the effective strain energy for the LTCC. The same formula can be derived by means of generalized Legendre transform of the strain energy as in (Lopez-Pamies and Ponte Castañeda, 2004a; Ponte Castañeda, 2002). The significance of this derivation is that it translates the optimization over continuous deformation field F ∈ κ(F̄) to that of respective tensors L(r) and F*(r). In theory, the field F ∈ κ(F̄) must satisfy continuity and compatibility conditions, while L(r) and F*(r) can be arbitrary within the physically meaningful ranges. It is further noted that Eq. (8) is identical to the principle of minimum energy, provided that L(r) and F*(r) are allowed to change from point to point in the material. In standard nonlinear micromechanics (Lopez-Pamies and Ponte Castañeda, 2004a; Ponte Castañeda, 2002; Willis, 1977), as well as here, we make the approximation that L(r) and F*(r) are uniform for the r-th phase to reduce the computational cost, so that Eq. (8) is an estimate of the exact SEF.
As has been derived in (Kailasam et al., 1997; Liu, Y., 2003), W̄T is estimated for the LTCC by taking into account the shape and distribution tensors and Zd, as
| (9) |
where L̃ is the effective stiffness of LTCC, s̃ and g̃ are the macroscopic residual stress and energy. These quantities all depend on the phase modulus L(r), residual deformation gradient F*(r) as well as geometric property Zs and microstructural spatial distribution function Zd. Here, we have extended the generalized finite strain Hashin-Shtrikman theory that considers the two-point material distribution (Kailasam et al., 1997; Liu, Y., 2003):
| (10a) |
| (10b) |
| (10c) |
| (10d) |
in the above relations, ΔL(r)= L(r) − L(0), L(0) is the reference stiffness of the matrix, A(r) is the deformation concentration tensor and a(r) is residual deformation gradient induced by F*(r). Furthermore, we have local residual stress s(r)= ρ(r) − L(r) (F–I), s*(r) = s(r) − s(0) and s̃*= s̃ − s(0). The fourth-order tensor P(r) is defined by the shape tensor Z(r) of the r-th fiber phase via integration over a unit spherical surface:
| (11) |
where H(Ξ) is a tensor with components , and . As mentioned previously, the geometry of the r-th phase fibers does not play role during homogenizing before it is straightened, such that the fibers behave the same as the matrix with ΔL(r) = 0. After the r-th phase fibers are straightened, ΔL(r) ≠ 0 and the shape Z(r) of the fibers begins to take effect. The tensor Pd in Eqs. (10) is calculated using the same formula for P(r) in Eq. (11), but with Z(r) replaced by the two-point microstructural distribution tensor Zd.
Finally, the stationary procedures involved in the above derivation, maximization of V(r) and the minimization in Eq. (8), yield a set of nonlinear tensorial equations for determination of the unknown reference modulus L(r) and reference deformation gradient F*(r) (Lopez-Pamies and Ponte Castañeda, 2004a, 2004b, 2006;Ponte Castañeda, 2002). These equations have multiple solutions that lead to various estimations of the macroscopic SEF W̄ (F̄). In this work, we employ a tangent solution (Ponte Castaneda and Tiberio, 2000), as:
| (12) |
i.e., the reference deformation gradient F*(r) is taken to be the average deformation gradient F̄(r) in the r-th phase of the LTCC, and L(r) is the tangent stiffness tensor evaluated at F̄(r). This solution leads to V(r) (F*(r), L(r))= 0 and an estimation of the macroscopic SEF, as:
| (13) |
In the above relations, the tensor F̄(r) is determined in the framework of the generalized finite-strain Hashin-Shtrikman theory as
| (14) |
As indicated by Eqs. (10), the tensor A(r) and a(r) are determined by reference stiffness tensors L(s) (s =0, 1, …,N), as well as the geometry and spatial distribution of the phases through the fourth-order tensors P(s) (s = 1, 2, …,N) and Pd. Thus, Eqs. (12) constitutes a system of nine nonlinear algebraic equations for the nine components of F̄(r) for each phase.
3. APPLICATIONS
As an illustrative example, the above tangent second-order micromechanics model is applied to 2-D tissue-like material with distributed collagen fibers. The tissue undergoes macroscopic deformation with gradient:
| (15) |
The tissue stretches along the principal direction e1 of the fibers with stretch ratio λ̄, but shrinks in the transverse direction e2 to maintain material incompressibility. This mimics a deformation of inflated vessel without axial pre-stretch, where the tissue stretches circumferentially and shrinks radially. Correspondingly, the fourth-order tensor P(r) in Eq. (11) is defined by the shape tensor Z(r) of a planar needle-like fiber showed in Appendix A.
3.1. Discretization of fiber phase
In general, the shape, orientation, waviness of the collagen fibers distribute randomly with continuous distribution functions (Lanir, 1979, 1983), as well as their spatial distributions. To simplify the present simulation, all the fiber centers are assumed to be isotropically distributed in space (Zd= I), and have the same undeformed cross-sectional geometry with r̄L = r̄S = 0.05l0 (i.e., the fiber aspect ratio = 10, see Fig. 1).
The fiber orientation is assumed to follow a Beta-distribution (Sacks, 2003), which can be skewed or symmetric and bounded in a finite interval (xmin, xmax):
| (16) |
where x is a random variable, Δ is the span of x; i.e., Δ= xmax − xmin. The span Δ and two parameters α, β characterize the Beta-distribution. In 2-D, the orientation vector N of the fiber is quantified by an orientation angle θ that is Beta-distributed with the span Δ= 60° and α = β = 6, which assures that most collagen fibers orient along the principal direction of the tissue, i.e., θ = 0°.
In line with tissue ultrastructure (Brown, 1973) and following Sverdlik and Lanir (2002), the waviness of collagen fibers λ0 can be assumed to be Beta-distributed, but the span Δ is considered to be direction-dependent. Thus, the span of collagen undulation is Δ = λ0max (θ) − λ0min (θ), where λ0min and λ0max are the θ-dependent minimal and maximal values of straightening stretch, respectively. Lokshin and Lanir (2009) recently developed a general constitutive model of planar tissues by incorporation of such undulation distribution of fibers and estimated a set of parameters α= 6.11, β = 6.0 and Δ for collagen fibers. The θ-dependent minimal and maximal values of straightening stretch are adopted in Ref. (Lokshin and Lanir, 2009):
| (17) |
where λ11min = 1.4, λ22min = 1.07 and λ11max = 1.8, λ22max = 1.34 are the lowest and highest reference straightening stretch in the two principal directions. Finally, the θ-dependent span Δ of collagen waviness is determined.
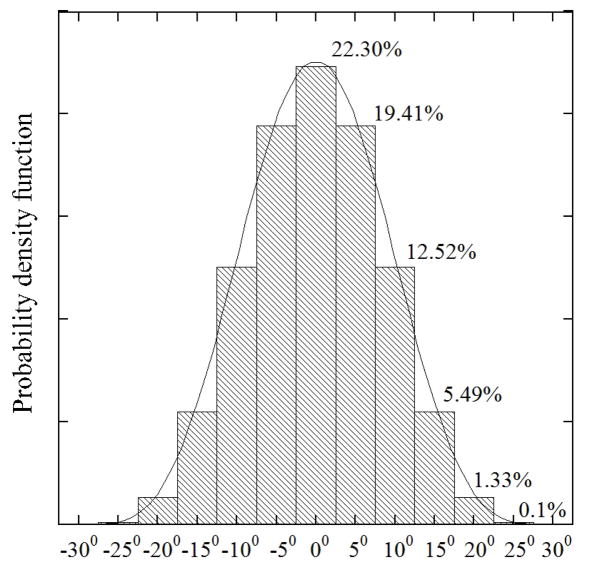
In the simulation, the orientation space is discretized into 13 regions as shown in Fig. 3, indicating the mean values and cumulative probabilities of these regions. Similarly, the waviness space is discretized into 5 regions. It is noted that the cumulative probabilities for them depend on orientation angle θ, and the waviness of collagen fibers become low as they align off the macroscopic loading axis. Thus, the composite material involves a total number of 65 phases of collagen fibers (phases 1–65), and a matrix phase (phase 0). In this work, the volume fraction of the matrix is taken as c0 =0.80 and the total volume fraction of all the fibers is cfiber =0.2, which is distributed to the 65 fiber phases according to their cumulative probabilities of the orientation and waviness (Table 1). For example, c(r) of the fiber phase with mean orientation angle θ = 10° and waviness λ0 = 1.6 is 0.15% (=0.2×17.65%). Note that .
Figure 3.
Discretization of the Beta-distribution of fiber orientation θ. The corresponding cumulative probability D(x) is given for each region. The span of Beta-distribution is Δ = 60°, and α = β = 6. The continuous cumulative probability D(x) is discretized by rounding method: D(x)= p(x+ h/2) − p(x−h/2), in which h is interval between regions.
Table 1.
The cumulative probabilities (×100%) of sixty-five fiber phases, discretized by orientation angle θ and waviness λ0.
| θ | 0° | ±5° | ±10° | ±15° | ±20° | ±25° | ±30° |
|---|---|---|---|---|---|---|---|
|
λ0 | |||||||
| 1.4 | 0 | 0 | 0 | 0.02 | 0.02 | 0.003 | 0 |
| 1.5 | 3.32 | 3.11 | 2.44 | 1.42 | 0.48 | 0.05 | 0 |
| 1.6 | 13.38 | 11.74 | 7.65 | 3.32 | 0.74 | 0.05 | 0 |
| 1.7 | 5.51 | 4.50 | 2.40 | 0.72 | 0.09 | 0.002 | 0 |
| 1.8 | 0.09 | 0.06 | 0.03 | 0.01 | 0.0003 | 0 | 0 |
3.2. Constitutive models
The parameter μ in the neo-Hookean type SEF W(0) (Eq. 1) is directly taken from Holzapfel and Gasser (2000), and the bulk modulus is set as k ≫ μ in our simulation to account for the material incompressibility (Table 2). The anisotropic term in the SEF of fibers (Eq. 2) is selected as:
| (18) |
Table 2.
The parameters in the strain energy function for each of the constitutive phases in the tissue. The data are fitted to the constitutive models in Holzapfel and Gasser (2000).
| Strain energy function | Holzapfel and Gasser (2000) | Present model | ||
|---|---|---|---|---|
| Matrix W(0) | μ(I1 − 3)/2 | μ(I1 − 3)/2 − μ ln I3 + (κ/2 − μ/3) (I3 − 1)2 | ||
| Collagen fibers |
|
|
||
| Parameters | μ = 0.300kPa | μ = 0.375kPa, κ ≫ μ | ||
| k1 = 0.562kPa | E1 = 5.0 kPa | |||
| k2 = 0.7112 | E2 = 45.0kPa |
This is a generalization of the linear model employed in other works (Decraemer et al., 1980; Lanir, 1979, 1983; Wuyts et al., 1995) where only the first term was included. This model is consistent with the experimental observation (Gentleman et al., 2003; Gosline et al., 2002) and analysis (Annovazzi, 2010) that the axial stress-strain relation of single straightened collagen fibers is somewhat nonlinear. In the study of Holzapfel and Gasser (2000), features an exponential form and is thus strongly nonlinear, which can be interpreted as a phenomenological description of the fiber behavior starting from undeformed state (λ = 1) to post-straightening (λ > λ0). To determine the material parameters E1 and E2, we fit the present to the exponential form in (Holzapfel and Gasser, 2000) with λ0 =1.6 (the mean value of Beta-distribution of the waviness), and the results are given in Table 2. Figures 4 show the SEF and stress-stretch curves of the matrix and fibers. Note that the homogenization model employed in this work, in principle, can use any well-defined constitutive model of the matrix and fibers. Moreover, it should be emphasized that the collagen fiber is transversely isotropic here; i.e., the random spatial distribution (Zd= I) of collagen fibers will lead to an isotropic macroscopic-tissue statistically. The macroscopic-tissue will become anisotropic, however, when the collagen fibers have a preferred direction in space.
Figure 4.
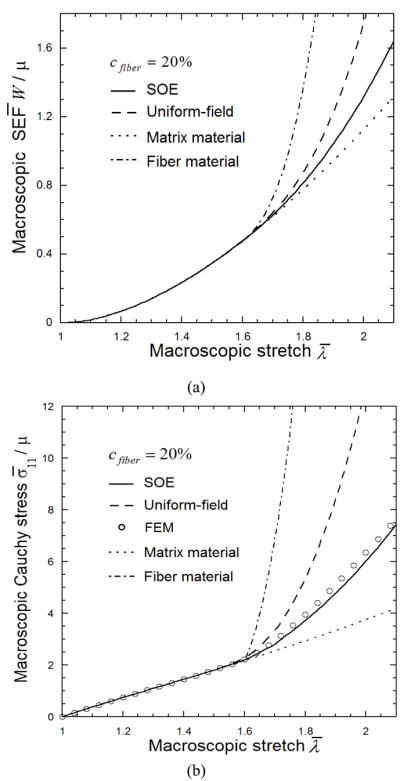
The macroscopic strain energy function (a) and Cauchy stress-stretch relation (b) of fibrous tissue with 20% randomly distributed collagen fibers. Values are normalized with material parameter μ. The reference fiber material has waviness λ0 =1.6.
3.3. Finite-element validations
FE simulations were used for the purpose of model validation, as a golden standard. The FE model contains ~200 randomly distributed fibers whose orientation angle θ and straightening stretch ratio λ0 were randomly assigned according to the Beta-distribution. The material models and parameters were identical to the homogenization model. A typical FE mesh contained ~30000 quadratic elements. Boundary displacement was applied on the FE model according to Eq. (15). The average Cauchy stress was outputted and compared with the micromechanics prediction.
4. RESULTS AND DISCUSSION
The tangent SOE model prediction of the macroscopic SEF W̄ and the tensile Cauchy stress σ̄11 of the above described fibrous tissue are plotted in Figs. 4 as functions of the applied tensile stretch λ̄, in comparison with the uniform-field (UF) predictions (dashed line) and FE computational results (circle). Note that the macroscopic Cauchy stress is determined from S̄ (Eq. 4) by the relation σ̄ = F̄S̄ since d e t (F̄) = 1. The SEF W̄ and stress σ̄11 of a pure matrix material and a collagen fiber (with θ= 0°, λ0 = 1.6) that undergo macroscopic deformation are shown for reference. For deformation λ̄ < 1.6 where most fibers are still undulated or have just been straightened, the predictions by the present SOE and FE are very similar and close to that of pure matrix material, while UF estimates are consistent with them. When the macroscopic deformation λ̄ is >1.6, the UF prediction shows rapid increase with higher macroscopic loading, and much higher than FE and SOE predictions (Table 3), while all show similar shape. Unlike UF model, the present model statistically accounts for the heterogeneous deformation of the matrix and fibers, which is due to the heterogeneities of microstructural geometries and material properties, as well as the interactions denoted by the second terms of the concentration tensor A(r) and residual deformation gradient a(r) in Eq.(10). Thus, the statistical deformation field employed by SOE is more realistic than UF theory, and in principle, leads to lower estimates of the macroscopic SEF and stress than the UF upper bounds. Table 3 shows error estimates for macroscopic Cauchy stress of both UF and SOE predictions in reference to the FE results as a gold standard. It is seen that the error estimate for UF predictions can reach up to 100% at high macroscopic loading, while the corresponding error for SOE is 5.4%, which implies that the SOE stress-strain curve is in excellent agreement with FE.
Table 3.
The error estimates for both SOE and UF predications considering FE results as a gold standard. error%= |* − FE|/FE × 100%,
| error% | Macroscopic stretch λ̄ | |||||
|---|---|---|---|---|---|---|
| 1.0 | 1.2 | 1.6 | 1.8 | 2.0 | 2.2 | |
| SOE | 0.0 | 0.0002 | 0.0012 | 1.0 | 6.2 | 5.4 |
| UF | 0.0 | 0.0001 | 0.001 | 2.6 | 34.8 | 100 |
denotes SOE and UF results respectively.
The statistical average deformation in the matrix phase and the fibers are plotted in Figures 5. Figure 5(a) gives the axial stretch of the collagen fibers that are parallel to the loading axis (θ= 0°) and with waviness λ0= 1.5, 16, 1.7 and 1.8, as well as the stretch of the matrix phase in the loading direction. In UF method, the deformation gradient of the matrix and all fibers are identical to the applied macroscopic deformation, such that the stretch of matrix and all the fibers (with θ= 0°) are identical and equal to λ̄ regardless of the straightening of the fibers, as plotted with the dashed line. In the SOE model, the microscopic deformation is non-affine once some fibers are straightened and become stiffer to take up the load. As the second approximation of this study and the constitutive SEF of the fibers, Eqs. (2), a fiber deforms identically to the matrix before it is straightened. Once straightened, it becomes increasingly stiffer and deforms much less than the matrix. For a small amount of fibers with a low waviness, such as λ0= 1.5, their stretch show a tendency of becoming saturated or flat at large macroscopic deformation λ̄. As a result, the matrix phase must deform slightly more to accommodate the applied macroscopic deformation, as indicated by the solid line in the plot, which is noticeably higher than the UF prediction. Consequently, SOE model predicts earlier engagement of the fiber than the UF method.
Figure 5.
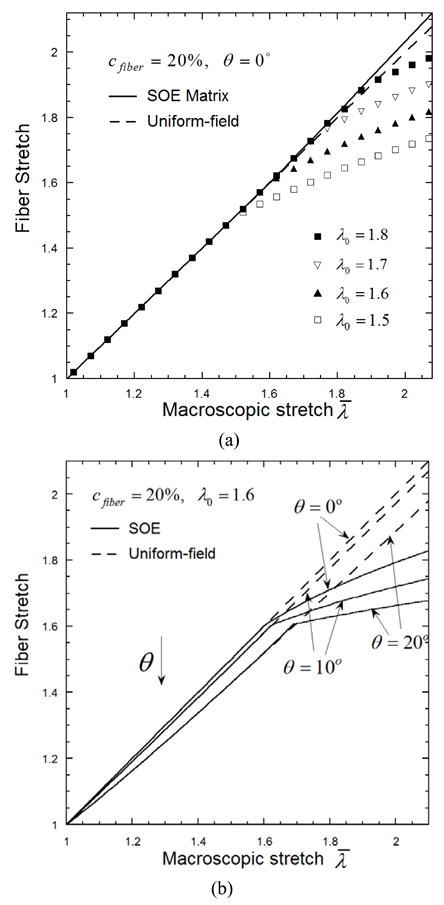
The influence of waviness λ0 and orientation angle θ on the statistical average microscopic stretch of the fibers. (a) The microscopic stretch of matrix phase (solid line) and collagen fibers (symbols) with waviness λ0 = 1.5, 1.6, 1.7 and 1.8, and orientation angle θ= 0°, while the uniform-field prediction (dashed line) is independent of the waviness; (b) The microscopic stretch of collagen fibers with orientation angle θ= 0°, 10° and 20°, and waviness λ0 =1.6.
We further investigated the influence of the orientation angle θ on the statistical average microscopic stretch of the fibers. Figure 5(b) shows the stretch of fibers with orientation angle θ= 0°, 10° and 20°, and waviness λ0= 1.6. The UF predictions depend on the orientation but not the waviness, as:
| (19) |
which indicates decrease of stretch as the fibers align off the macroscopic loading axis. The SOE predictions also show similar trend that larger orientation angle θ leads to later engagement of the fiber. For all the cases, the SOE predictions of fiber stretch are slightly and consistently higher than the corresponding UF prediction prior to fiber engagement, and become much lower when the fibers deform slightly beyond the straightening stretch. Thus, for the fibers with given orientation angle θ and waviness λ0, the SOE model predicts earlier engagement than the UF.
To further illustrate this, we plot (in Fig. 6) the macroscopic stretch λ̄ that straightens the fibers with θ= 0°, 15° and 25°, and λ0 from 1.4 to 1.8, denoted as the macroscopic straightening stretch. The UF estimate (dashed lines) can be directly obtained from Eq. (19). The macroscopic straightening stretches predicted by SOE model are consistently lower than the UF predictions, indicating earlier engagement of the fibers. The difference is more significant for fibers with larger angle and/or higher waviness. As discussed above, the earlier fiber engagement is due to the heterogeneous microscopic deformation predicted by SOE method.
Figure 6.
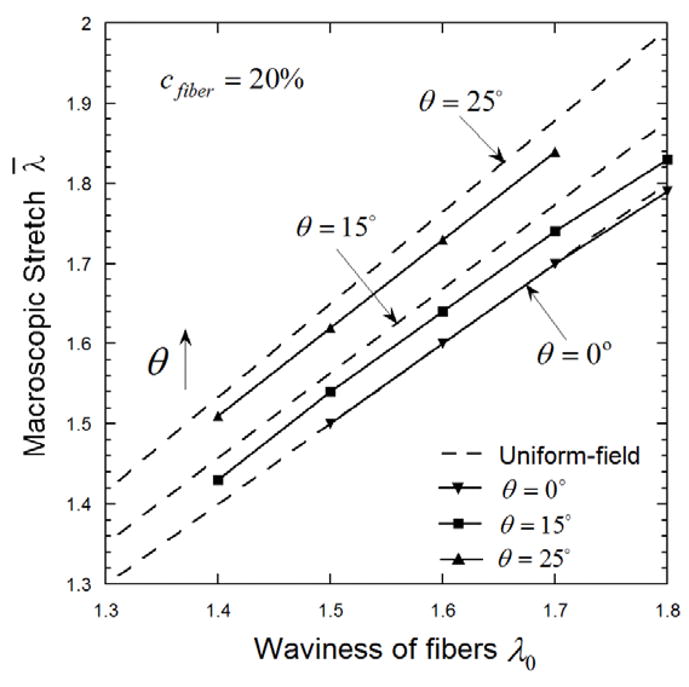
The macroscopic stretch that straightens the undulated collagen fibers with orientation angle θ= 0°, 15° and 25°. The uniform-field predictions (dashed line) are consistently higher than SOE predictions (symbols).
It is worth highlighting that the differences in the model predictions of macroscopic stress stem from the basic assumption of the microscopic deformation field, as indicated by Eq. (4) for the principle of minimum strain energy. The assumption of uniform deformation field requires that all fibers in the same orientation must deform with the same axial stretch despite that straightened fibers are much stiffer than undulated fibers, as shown in Figs. 5–6, which is inconsistent with the notion that soft phases deform more than hard phases in a composite. In contrast, SOE allows more flexible deformation: once a fiber is straightened, it deforms less than those undulated fibers and the macroscopic deformation, due to the engagement of higher SEF . To accommodate the applied macroscopic deformation, SOE model thus requires the matrix phase and undulated fibers to deform more, which results in earlier engagement of the fibers, in particular for those with large orientation angles (Fig. 6). This mechanism prevents over stretch of the fibers with low waviness λ0 in the tissue under large macroscopic deformation (Figs. 5). Since there is limit for the collagen fibers to stretch beyond the straightening value (Mohanaradhakrishnan et al., 1970), this prediction is qualitatively consistent with the protective role of the fibers in the tissue.
The most significant advantage of the UF method is the lower computational cost; i.e., it only requires a simple summation as in Eq. (5). In comparison, the SOE method requires higher computational expense, albeit it is much more efficient than direct FE simulation. Therefore, it is useful to investigate the condition in which the UF predictions are accurate. We conducted UF, SOE and FE simulation of two tissues in which the span of the fiber orientation distribution was Δ= 0° and 60°, respectively, while Δ of the waviness was zero; i.e., all fibers have the same waviness λ0=1.6. The predicted macroscopic stress curves for these two tissues are plotted in Fig. 7 which shows that while Δ= 60°, the UF estimates are significantly higher than both SOE and FE. The UF estimates, however, are similar to both FE and SOE results for Δ= 0°. Both SOE and FE predications dramatically decease with increase of Δ, while UF predications become only slightly lower. It is clear that Δ of the fiber orientation plays an important role in FE and SOE prediction, while it is much less significant for the UF upper bound. Thus, for the tissue with distribution of fiber orientations, Δ= 60° for this case, the UF overestimates the macroscopic stress. For the tissue with aligned fibers, the UF macroscopic stress is close to both FE and SOE results. Thus, the UF upper bound of the macroscopic stress is considered accurate for tissue with very narrow distribution of fiber orientation. This comparison suggests the need for accurate measurements of fiber orientation to justify the model used.
Figure 7.
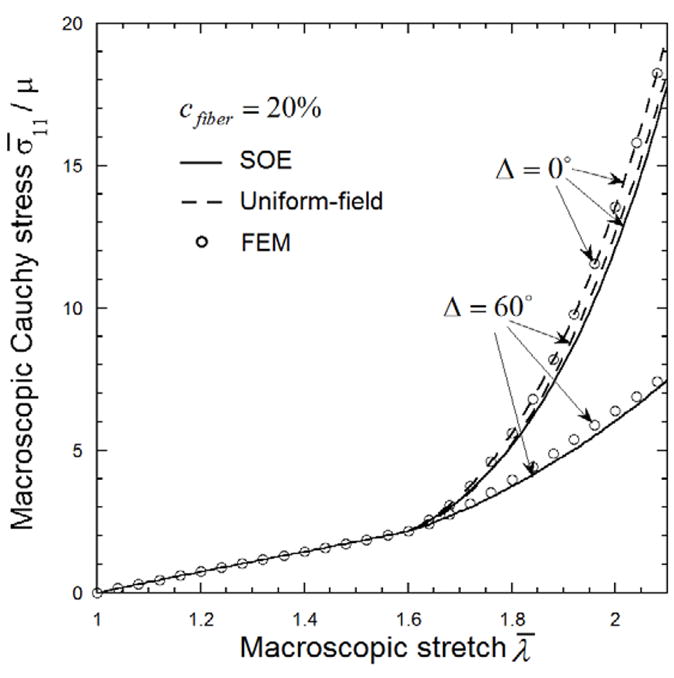
The macroscopic tensile stress-strain curve of fibrous tissues with 20% randomly distributed collagen fibers. The Beta-distribution of the fiber orientation angle θ has mean M= 0° and span Δ= 0° and 60°, respectively. All the fibers are assumed to have the same waviness λ0 =1.6.
There are some simplifications that require mention. Firstly, the material parameters E1 and E2 of the fibers were determined from the study of Holzapfel and Gasser (2000) (see Section 3.2), and then used in all the models for the illustrative example: SOE, UF and FE models. Thus, given the same morphological data of the fibers, the present UF model should closely reproduce the homogenization model in Holzapfel and Gasser (2000), whose parameters were fitted to experimental data. On the other hand, in the SOE and FE models, these parameters are simply assigned for demonstration of the predictive capability of the models, rather than fitting experimental data. Since the model in (Holzapfel and Gasser, 2000) is a UF upper bound, the parameters for the model to fit experimental data are expected to underestimate actual values. Thus, these parameters give a lower stress curves than the UF prediction in FE and SOE method. Since the material model and parameters of collagen fibers are found to be highly variable in the literature (Holzapfel and Gasser, 2000; Zulliger et al., 2004), mechanical tests on individual fibers such as in (Gentleman et al., 2003; Gosline et al., 2002; Mohanaradhakrishnan et al., 1970) are necessary to unify the material model and narrow the physical range of the parameters.
Secondly, the geometric information used in the present illustrative simulation is idealized due to the lack of direct experimental measurements of the fiber structures. The SOE model can take into consideration a full set of statistical microstructural geometric information including the shape, orientation and distribution of the fibers, and those microstructural geometries such as the orientation angle have shown important implications on microscopic deformation and the macroscopic constitutive relation. With advances of imaging technique such as multi-photon microscopy (MPM), direct measurements of the 3-D fiber structures in vascular tissue have recently become available (Zoumi et al., 2004), and the statistical data can be extracted and imported into the homogenization model such as UF and SOE methods.
Finally, the present model takes into consideration two functional microstructures in the vascular tissue: an effective matrix and distributed collagen fibers. The elastin fibers, which are also undulated, are considered as part of the effective matrix. This simplification is motivated by the fact that the elastin, while being stiffer than the ground substance and cells, are much softer than the collagen fibers and become straightened in the early deformation of the tissue. Thus, W(0) (F) in Eq. (1) should be considered as a macroscopic SEF of the effective matrix, and thus the presently employed neo-Hookean form of W(0) is phenomenological. For more microstructural modeling of W(0) and accurate description of the deformation of the cells and elastin, a multiscale homogenization method is needed. In such a multiscale approach, the present effective matrix is considered as an elastin-fiber reinforced composite, with the ground substance and cells as the ground material. Lanir (1983) and Lokshin and Lanir (2009) employed this approach while considering both collagen and elastin as fibrous entities embedded in a fluid-like matrix. When considering solid-like matrix, the SEF W(0) of the effective matrix is first estimated with use of homogenization methods which takes into account the constitutive relation, geometries and distributions of the elastin. Once W(0) is known, the effective SEF W̄ of the entire tissue is estimated as illustrated here.
Additionally, the homogenization approaches for W(0) of the effective matrix should be adjusted to reflect the microstructures of soft tissue. For example, in the media layer of the vessel, the elastin forms a complex network connected to the cells that can sustain non-hydrostatic loading such as tension and shear. Therefore, the assumption of solid-like matrix may be an accurate description. In the adventitial layer, the non-fiber constituents are fibroblasts and amorphous gel-like ground substances (Holzapfel and Gasser, 2000) that do not take much non-hydrostatic loading. Thus, the fluid-like matrix as employed in the models of Lanir et al. (1979, 1983) is appropriate. The in situ microscopic images of elastin and collagen fibers in the adventitia layer of coronary artery show that large collagen fiber bundles are seldom cross-linked, while the much thinner elastin fibers show network-like structures (unpublished observations). These observations support the affine deformation of collagen fibers in adventitia if the ground substance is considered fluid-like.
6. CONCLUSION
The recently developed second-order micromechanics method for nonlinear composites has been extended here to estimate the macroscopic constitutive model and microscopic deformation of tissue with undulated collagen fibers. The method is an integration of the Hashin-Shtrikman theory of the finite-strain linear thermoelastic comparison composite that takes into consideration a full set of statistical microstructural geometries and the interactions, and a variational principle to approach the nonlinearity of the constituent phases. As such, the present method overcomes the shortcomings of the classical uniform-field theory to enable more realistic predictions of the macroscopic stress and the statistical deformation of the wavy collagen fibers, and compares favorably with direct FE numerical simulations.
Acknowledgments
This work was supported by the National Institute of Health-National Heart, Lung, and Blood Institute Grant 1R01 HL087235-02.
APPENDIX A: THE TENSOR P FOR A PLANAR ELLIPTICAL FIBER
For a planar elliptical fiber, the shape tensor can be written as the diagonal matrix with respect to the principal axes of fiber as:
| (A.1) |
where a1, a2 are planar long and short axes respectively, and ε=1/a3 denotes the length of the principal axis of the ellipsoidal inclusion in the e3 direction (ε → 0 corresponds to the inclusion becoming infinitely long in that direction). Since fiber orientation is defined by a rotation angle φ, the shape tensor of the fiber in fixed laboratory frame can be written as:
| (A.2) |
where R(φ) is rotation matrix. It should be noted that this expression is consistent with geometric tensor Zs.
In polar cylindrical coordinates, tensor P(r) (Eq. 11) takes the form:
| (A.3) |
and
| (A.4) |
where A = |(Z(r))−1 Ξ|2. By changing variables to z′ = z/ε, the integral is rewritten as
| (A.5) |
If we consider the limit ε → 0, we obtain:
| (A.6a) |
| (A.6b) |
If we integrate on z′, the tensor P(r) for a planar elliptical fiber yields the desired result:
| (A.7) |
in which ω= a1/a2 is the fiber aspect ratio. For a needle-like fiber, the aspect ratio ω is much greater than one.
References
- Annovazzi L, Genna F. An engineering, multiscale constitutive model for fiber-forming collagen in tension. J Biomed Mater Res Part A. 2010;92(1):254–266. doi: 10.1002/jbm.a.32352. [DOI] [PubMed] [Google Scholar]
- Azuma T, Hasegawa M. A rheological approach to the architecture of arterial walls. Japan J Physiol. 1971;21:37–47. doi: 10.2170/jjphysiol.21.27. [DOI] [PubMed] [Google Scholar]
- Azuma T, Oka S. Mechanical equilibrium of blood vessel walls. Am J Physiol. 1971;221:1310. doi: 10.1152/ajplegacy.1971.221.5.1310. [DOI] [PubMed] [Google Scholar]
- Brown IA. A scanning electron microscope study of the effect of uniaxial tension on human skin. Br J Dermatol. 1973;89:383–93. doi: 10.1111/j.1365-2133.1973.tb02993.x. [DOI] [PubMed] [Google Scholar]
- Chuong CJ, Fung YC. Three-dimensional stress distribution in arteries. ASME J Biomech Eng. 1983;105:268–274. doi: 10.1115/1.3138417. [DOI] [PubMed] [Google Scholar]
- Dahl SL, Vaughn ME, Hu JJ, Driessen NJ, Baaijens FP, Humphrey JD, Niklason LE. A Microstructurally motivated model of the mechanical behavior of tissue engineered blood vessels. Ann Biomed Eng. 2008;36(11):1782–1792. doi: 10.1007/s10439-008-9554-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Decraemer WF, Maes MA, Vanhuyse VJ. An elastic stress-strain relation for soft biological tissues based on a structure model. J Biomech. 1980;13:463–468. doi: 10.1016/0021-9290(80)90338-3. [DOI] [PubMed] [Google Scholar]
- Deng SX, Tomioka J, Debes JC, Fung YC. New experiments on shear modulus of elasticity of arteries. Am J Physiol. 1994;266:1–10. doi: 10.1152/ajpheart.1994.266.1.H1. [DOI] [PubMed] [Google Scholar]
- Fratzl P, Misof K, Zizak I. Fibrillar structure and mechanical properties of collagen. J Struct Biol. 1997;122:119–122. doi: 10.1006/jsbi.1998.3966. [DOI] [PubMed] [Google Scholar]
- Fung YC, Fronek K, Patitucci P. Pseudoelasticity of arteries and the choice of its mathematical expression. Am J Physiol. 1979;237:620–631. doi: 10.1152/ajpheart.1979.237.5.H620. [DOI] [PubMed] [Google Scholar]
- Gentleman E, Lay AN, Dickerson DA, Nauman EA, Livesay GA, Dee KC. Mechanical characterization of collagen fibers and scaffolds for tissue engineering. Biomaterials. 2003;24:3805–3813. doi: 10.1016/s0142-9612(03)00206-0. [DOI] [PubMed] [Google Scholar]
- Gosline J, Lillie M, Carrington E, Guerette P, Ortlepp C, Savage K. Elastic protein: biological roles and mechanical properties. Phil Trans R Soc Lond B. 2002;357:121–132. doi: 10.1098/rstb.2001.1022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gundiah N, Ratcliffe MB, Pruitt LA. Determination of strain energy function for arterial elastin: Experiments using histology and mechanical tests. J Biomech. 2007;40:585–594. doi: 10.1016/j.jbiomech.2006.02.004. [DOI] [PubMed] [Google Scholar]
- Hill R. On constitutive macro-variables for the heterogeneous solids at finite strain. Proc R Soc Lond A. 1972;326:131–147. [Google Scholar]
- Hill R, Rice J. Elastic potentials and the structure of in elastic constitutive laws. SIAM J Appl Math. 1973;25:448–461. [Google Scholar]
- Holzapfel GA, Gasser TC. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elasticity. 2000;61:1–48. [Google Scholar]
- Holzapfel GA, Weizsacker HW. Biomechanical behavior of the arterial wall and its numerical characterization. Comput Biol Med. 1998;28:377–392. doi: 10.1016/s0010-4825(98)00022-5. [DOI] [PubMed] [Google Scholar]
- Humphrey JD. Mechanics of arterial wall: review and directions. Crit Rev Biomed Eng. 1995;23:1–162. [PubMed] [Google Scholar]
- Humphrey JD, Yin FC. A new constitutive formulation for characterizing the mechanical behavior of soft tissue. Biophys J. 1987;52(4):563–570. doi: 10.1016/S0006-3495(87)83245-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kailasam M, Ponte Castaneda P, Willis JR. The Effect of Particle Size, Shape, Distribution and Their Evolution on the Constitutive Response of Nonlinearly Viscous Composites. I Phil Trans R Soc Lond A. 1997;355:1835–1852. [Google Scholar]
- Kroon M, Holzapfel GA. A new constitutive model for multi-layered collagenous tissues. J Biomech. 2008;41:2766–2771. doi: 10.1016/j.jbiomech.2008.05.033. [DOI] [PubMed] [Google Scholar]
- Lanir Y. A structural theory for the homogeneous biaxial stress-strain relationship in flat collagenous tissues. J Biomech. 1979;12:423–436. doi: 10.1016/0021-9290(79)90027-7. [DOI] [PubMed] [Google Scholar]
- Lanir Y. Constitutive equations for fibrous connective tissues. J Biomech. 1983;16:1–12. doi: 10.1016/0021-9290(83)90041-6. [DOI] [PubMed] [Google Scholar]
- Lebensohn R, Liu Y, Ponte Castañeda P. Macroscopic properties and field fluctuations in model power-law polycrystals: full-field solutions versus self-consistent estimates. Proc R Soc Lond Ser A. 2004;460:1381–1405. [Google Scholar]
- Li D, Robertson AM. A structural multi-mechanism constitutive equation for cerebral arterial tissue. Int J Solids Struct. 2009;46:2920–2928. [Google Scholar]
- Liu Y. PhD Thesis. University of Pennsylvania; U.S.A: 2003. Macroscopic behavior, field fluctuations and texture evolution in viscoplastic polycrystals. [Google Scholar]
- Liu Y, Gilormini P, Ponte Castañeda P. Variational self-consistent estimates for texture evolution in viscoplastic polycrystals - Application to titanium. Acta Mater. 2003;51:5425–5437. [Google Scholar]
- Liu Y, Ponte Castañeda P. Second-order estimates for the effective behavior and field fluctuations in viscoplastic polycrystals. J Mech Phys Solids. 2004a;52:467–495. [Google Scholar]
- Liu Y, Ponte Castañeda P. Homogenization estimates for the effective behavior and field heterogeneity in cubic and HCP polycrystals. J Mech Phys Solids. 2004b;52:1175–1211. [Google Scholar]
- Lokshin O, Lanir Y. Micro and macro rheology of planar tissues. Biomaterials. 2009;30:3118–3127. doi: 10.1016/j.biomaterials.2009.02.039. [DOI] [PubMed] [Google Scholar]
- Lopez-Pamies O, Ponte Castañeda P. Second-order estimates for the macroscopic response and loss of ellipticity in porous rubbers at large deformations. J Elasticity. 2004a;76:247–287. [Google Scholar]
- Lopez-Pamies O, Ponte Castañeda P. Second-Order Homogenization Estimates Incorporating Field Fluctuations in Finite Elasticity. Math Mech Solids. 2004b;9:243–270. [Google Scholar]
- Lopez-Pamies O, Ponte Castañeda P. On the overall behavior, microstructure evolution, and macroscopic stability in reinforced rubbers at large deformation: I-theory. J Mech Phys Solids. 2006;54:807–830. [Google Scholar]
- Lopez-Pamies O, Ponte Castañeda P. Homogenization-based constitutive models for porous elastomer and implications for macroscopic instabilities. I - Analysis J Mech Phys Solids. 2007;55:1677–1701. [Google Scholar]
- Lu X, Pandit A, Kassab GS. Biaxial incremental homeostatic elastic moduli of coronary artery: two-layer model. Am J Physiol Heart Circ Physiol. 2004;287:1663–1669. doi: 10.1152/ajpheart.00226.2004. [DOI] [PubMed] [Google Scholar]
- Mohanaradhakrishnan V, Ramanathan N, Nayudamma Y. Strength of collagen fibers obtained from different sources. Biorheology. 1970;7:119–124. doi: 10.3233/bir-1970-7204. [DOI] [PubMed] [Google Scholar]
- Ogden R. Extremun principles in nonlinear elasticity and their application to composites: Part I. Int J Solids Struct. 1978;14:265–282. [Google Scholar]
- Oka S. Theoretical studies on hemorheology. The 16th Rheology Symposium; Sapporo. 1967. [Google Scholar]
- Oka S. Some theoretical studies on hemorheology. In: Kotani M, editor. Advances in Biophysics. Univ. of Tokyo Press; Tokyo: 1972. p. 97. [PubMed] [Google Scholar]
- Oka S, Azuma T. Physical theory of tension in thick walled blood vessels in equilibrium. Biorheology. 1970;7:109–117. doi: 10.3233/bir-1970-7203. [DOI] [PubMed] [Google Scholar]
- Ottani V, Raspanti M, Ruggeri A. Collagen structure and functional implications. Micron. 2001;32:251–260. doi: 10.1016/s0968-4328(00)00042-1. [DOI] [PubMed] [Google Scholar]
- Ponte Castañeda P. Second-order homogenization estimates for nonlinear composites incorporating field fluctuations. I Theory and II Applications. J Mech Phys Solids. 2002;50:737–782. [Google Scholar]
- Ponte Castañeda P, Tiberio E. A second-order homogenization procedure in finite elasticity and applications to black-filled elastomers. J Mech Phys Solids. 2000;48:1389–1411. [Google Scholar]
- Ponte Castañeda P, Willis JR. The effect of spatial distribution on the effective behavior of composite materials and cracked media. J Mech Phys Solids. 1995;43:1919–1915. [Google Scholar]
- Rhodin JAG. Architecture of the vessel wall. In: Berne RM, editor. Handbook of Physiology American Physiology Society, Sect 2. Vol. 2. 1979. pp. 1–31. [Google Scholar]
- Sacks MS. Incorporation of experimentally derived fiber orientation into a structural constitutive model for planar collagenous tissues. J Biomech Eng. 2003;125(2):280–287. doi: 10.1115/1.1544508. [DOI] [PubMed] [Google Scholar]
- Sverdlik A, Lanir Y. Time-dependent mechanical behavior of sheep digital tendons, including the effects of preconditioning. J Biomech Eng. 2002;124(1):78–84. doi: 10.1115/1.1427699. [DOI] [PubMed] [Google Scholar]
- Takamizawa K, Hayashi K. Strain energy density function and uniform strain hypothesis for arterial mechanics. J Biomech. 1987;20:7–17. doi: 10.1016/0021-9290(87)90262-4. [DOI] [PubMed] [Google Scholar]
- Vaishnav RN, Young JT, Patel DJ. Distribution of stresses and of strain-energy density through the wall thickness in a canine aortic segment. Circ Res. 1973;32:577–583. doi: 10.1161/01.res.32.5.577. [DOI] [PubMed] [Google Scholar]
- Vito RP, Dixon S. Blood vessel constitutive models-1995–2002. Ann Rev Biomed Eng. 2003;5:413–39. doi: 10.1146/annurev.bioeng.5.011303.120719. [DOI] [PubMed] [Google Scholar]
- Willis JR. Bounds and self-consistent estimates for the overall moduli of anisotropic composites. J Mech Phys Solids. 1977;25:185–202. [Google Scholar]
- Wolinsky H, Glagov S. A lamellar unit of aortic medial structure and function in mammals. Circ Res. 1967;20:99–111. doi: 10.1161/01.res.20.1.99. [DOI] [PubMed] [Google Scholar]
- Wuyts FL, Vanhuyse VJ, Langewoutters GJ, Decraemer WF, Raman ER, Buyle S. Elastic properties of human aortas in relation to age and atherosclerosis: a structural model. Phys Med Biol. 1995;40:1577–1597. doi: 10.1088/0031-9155/40/10/002. [DOI] [PubMed] [Google Scholar]
- Zoumi A, Lu X, Kassab GS, Tromberg BJ. Imaging coronary artery microstructure using second-harmonic and two-photon fluorescence microscopy. Biophysical J. 2004;87:2778–2786. doi: 10.1529/biophysj.104.042887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zulliger MA, Fridez F, Hayashi K, Stergiopulos N. A strain energy function for arteries accounting for wall composition and structure. J Biomech. 2004;37:989–1000. doi: 10.1016/j.jbiomech.2003.11.026. [DOI] [PubMed] [Google Scholar]