Refinement of the Cornell et al. Nucleic Acids Force Field Based on Reference Quantum Chemical Calculations of Glycosidic Torsion Profiles

Abstract

We report a reparameterization of the glycosidic torsion χ of the Cornell et al. AMBER force field for RNA, χ_OL. The parameters remove destabilization of the anti region found in the ff99 force field and thus prevent formation of spurious ladder-like structural distortions in RNA simulations. They also improve the description of the syn region and the syn–anti balance as well as enhance MD simulations of various RNA structures. Although χ_OL can be combined with both ff99 and ff99bsc0, we recommend the latter. We do not recommend using χ_OL for B-DNA because it does not improve upon ff99bsc0 for canonical structures. However, it might be useful in simulations of DNA molecules containing syn nucleotides. Our parametrization is based on high-level QM calculations and differs from conventional parametrization approaches in that it incorporates some previously neglected solvation-related effects (which appear to be essential for obtaining correct anti/high-anti balance). Our χ_OL force field is compared with several previous glycosidic torsion parametrizations.

Introduction

The relevance of sampled structures and conformational dynamics of molecules in molecular dynamics (MD) simulations critically depends on the quality and accuracy of the applied empirical force fields. Among force-field terms, the torsion parameters are known to strongly influence the molecular structures. This creates a considerable problem since the torsions are the least “physics-based” parameters in the sense that they cannot be directly derived from either experimental data or quantum mechanics (QM). Further, the sampled torsions depend not only on the values of all of the other parameters but also on the applied simulation methods (for example, whether or not all bonds, only bonds with hydrogen atoms, or no bonds are constrained). Bond and angle parameters can be straightforwardly derived from crystal data, IR and microwave spectroscopy, and/or high-level QM. Relatively straightforward procedures or protocols are also available to determine intermolecular parameters, such as van der Waals radii and well depths by matching experimental densities and atomic charges through fits to QM-derived electrostatic potentials or energetics. In contrast, fitting of the torsional parameters is largely an art and often rather ad hoc. The results strongly depend on the choice of model systems and approach, including the means used to fit the QM data, the level of QM calculations, the QM optimization methodology, and inclusion of solvation. For nucleic acids, a particularly difficult problem is parametrization of the flexible and anionic sugar–phosphate backbone, as the force field must simultaneously reproduce properties of canonical nucleic acid forms and numerous noncanonical topologies.¹⁻⁷

Most of the current generation of nucleic acid force fields were initially designed to reproduce properties of isolated nucleosides in vacuo. This residue-based parametrization approach relies on investigations of small molecule model systems under the assumption that the parameters are transferable and applicable to nucleosides and larger nucleic acid structures in solution.^8,9 A significant issue at the time of writing is that these model systems were primarily studied in the early 1990s when higher level QM investigations of full models representative of the nucleotides or nucleotides were not possible. Understanding the deficiencies, the initial nucleic acid force fields were then tweaked—arguably with limited success—through a series of designed, automated, or ad hoc torsional potential modifications aiming to reproduce B-DNA and A-RNA helix structures in solution. Other target properties included (inter alia) the subtle balance of the A–B DNA conformational equilibrium and the B-DNA helical twist.¹⁰⁻²⁰

Despite improvements, cryptic deficiencies remained and tend to remain undiscovered except through prolonged MD or enhanced sampling simulations and investigations of larger numbers of noncanonical structures, such as various G-DNA and RNA structures. For example, although unexpected and persistent γ = trans backbone conformational transitions in B-DNA simulations were reported in the early 2000s,²¹⁻²³ it took time (and longer simulations) to convince the research community that the most widely used nucleic acid force field, the AMBER force field (ff94) presented by Cornell et al.,(8) and its basic variants ff98(17) and ff99(20) (collectively termed the AMBER ff9X force fields) significantly overstabilized the γ = trans backbone state. As a result, the initially infrequently populated γ = trans state sampled in α/γ conformational transitions becomes the global minimum in B-DNA. Given sufficiently long MD simulations this overstabilization leads to complete degradation of the B-DNA structure. To overcome this deficiency, several approaches based on high-level QM calculations of larger and more representative model systems were applied to improve mapping of the α/γ energy surfaces, leading to the bsc0 refinement of the AMBER ff9X force fields.^24,25 The ff99bsc0 force field is the best currently available for modeling B-DNA,^26,27 but it still has potential inaccuracies. For example, the B-DNA helical twist remains underestimated, the occasional γ = trans flips in B-DNA simulations are still probably too frequent,(28) and for modeling DNA hairpin loops, although the refinement improves the overall force-field performance, an experimentally known γ = trans state is incorrectly eliminated.(29) On the other hand, all of the AMBER ff9X force fields, with or without bsc0 modifications, provide similar simulations of the behavior of RNA helices, since in all cases the γ = trans backbone flip is reversible.(30) This indicates that force-field modifications for DNA and RNA simulations might be pursued independently, in contrast to earlier perceptions that the parameters should be transferable across the nucleic acids.

Considerably more challenging than simply maintaining canonical helical structure is achieving a balanced description of the various noncanonical and/or unfolded nucleic acid structures, which are especially important in analyses of RNA functions, catalysis, dynamics, and drug targeting.³¹⁻³⁵ Although simulations of such structures may be improved by straightforward adjustment of a particular parameter (as for the γ = trans backbone states), some problems will likely require simultaneous or concerted modification of numerous parameters, which is demanding. Finally, considering the severity of the overall physical approximations of the pairwise additive force fields, some problems might be entirely beyond the capabilities of simple force-field approximations. Thus, it is not surprising that different force fields often provide remarkably different descriptions of the same structure, a phenomenon termed “force-field-dependent polymorphism”.³⁶⁻⁴⁰ A large part of this undesirable variability can likely be attributed to the inaccurate or nonoptimal description of the torsion space. Hence, the torsion parameters used in the various force-field treatments have been continuously refined.^{8,19,20,24,41,42}

In nucleic acids one of the most distinctive torsions is the glycosidic torsion, χ, describing rotation about the bond that links the base to the sugar moiety and determines the relative orientation of the nucleobase and sugar moieties in DNA and RNA (Figure 1). It is believed to be involved in the equilibrium of the A and B forms of DNA as well as the C2′-endo and C3′-endo equilibrium. The χ torsion is linked to many base pair and helical parameters that are modeled rather inaccurately by current force fields, including the helical twist (underestimated),(17) base pair propeller twist (also underestimated), and size of the DNA grooves. Recent work also suggests that it is important for the correct description of complex RNA folds.(43) In the two most widely used sets of biomolecular force fields for nucleic acids, AMBER and CHARMM, several reparameterizations of the χ torsion have appeared in recent years,^{7,17,19,41,42,44,45} indicating that deriving its torsion potential is a particularly difficult task.

Figure 1.

Chemical structures and atom-naming conventions for the model ribonucleosides used in our derivation of χ torsion parameters for cytosine (C), adenine (A), guanine (G), and uracil (U). The dihedral angle χ is defined by the O4′–C1′–N1–C2 atoms for C and U and by the O4′–C1′–N9–C4 atoms for A and G (this definition is used throughout this work). Note, however, that in ff94, ff98, and ff99 force fields the χ parameters are actually assigned to the complementary angle, specifically O4′–C1′–N1–C6 for C and U and O4′–C1′–N9–C8 for A and G.

The focus of this work is on the χ torsion in the Cornell et al. ff9X force-field family. Before reviewing previous parametrizations, we should note that the χ angle is tightly coupled to sugar puckering. Therefore, when corrections to the χ parameters are made in a particular force field they are often accompanied by adjustments to the ribose/deoxyribose parameters. The parameters for χ and sugar pucker in the most commonly used force field for NA simulations, AMBER ff94, originally presented by Cornell et al.,(8) have already been revised at least four times. In the AMBER ff98 force field(17) both the χ torsion and sugar puckers were changed, followed by minor readjustments of the sugar pucker parameters in the AMBER ff99 force field.(20) Although not fully described in the literature, these modifications were largely based on ad hoc changes to the parameters with assessment by relatively long (for the time) MD simulations to ascertain their influences on the DNA structure, twist, and sugar puckering. This contrasts with a more physically based approach involving better QM calculations based on more relevant model systems. The main aim of the rather subtle tunings in ff98 was to reduce the ff94 force field’s quite pronounced underestimation of helical twist in B-DNA. However, the improvement afforded by the reparameterization was modest, and all the ff9X force fields are usually assumed to have similar strengths, weaknesses, and ranges of applicability. While the ff94 force field underestimates χ values, sugar pucker, and helical twist(17) in B-DNA simulations, the ff98 twist is closer to experimental values. Even with the latest ff99 force field, the description of the structural parameters coupled to the χ angle is not fully satisfactory. For DNA, the helical twist is still somewhat underestimated, and the average χ and pucker values are probably still too far from values obtained from X-ray and solution analyses. We emphasize that this assessment concerns primarily B-DNA, which has been the main target of the force-field parametrization efforts. Assessment and validation of the performance of force fields for other types of nucleic acid structures has been much less systematic, and the results have often been difficult to interpret due to a lack of both unambiguous target experimental structures and published or disseminated data regarding simulation failures.^{29,38,43,46−49} The above-mentioned critical α/γ torsional reparameterization (bsc0) was primarily designed as a complement to ff99.(24)

In 2008 Ode et al. attempted a new χ parametrization based on QM calculations.(44) This parametrization can be combined with either ff99 or ff99-parmbsc0, but assessing the effects of the new parameters on the performance of these force fields is difficult since the original testing was limited to analysis of the progression of rmsd values in a few very short MD trajectories. More recently, we tested the modifications in simulations of guanine quadruplex (G-DNA) loops, which are known to be described poorly with standard ff9X parametrizations. However, the Ode et al. modifications did not have any clear advantages with respect to the original force fields for the G-DNA loops; the simulation outcomes were not significantly influenced by the choice of χ potential but were strongly influenced by the choice of ff99 versus ff99-parmbsc0.(29) Recently, another χ reparameterization was presented by Yildirim et al.(45) This reparameterization (tested solely in combination with ff99, in RNA simulations) was shown to improve the concordance of syn–anti populations of isolated RNA nucleosides with NMR data, but no simulations of nucleic acids were presented.

In simulations of RNA, a major failure of the ff99 force field recently reported by Mlynsky et al.(43) is the generation of large “ladder-like” structural distortions in one stem of the hairpin ribozyme.(43) These distortions are characterized by a shift of χ toward the region typical for the B form (high-anti, ∼270°), loss of helical twist, a change of the sugar pucker from C3′-endo to C2′-exo, and increases in slide and P–P distances in their radial distribution function. According to our experience, deformations of this type are actually fairly common in MD simulations of smaller RNA fragments.(46) Hence, they may have appeared in some previously published investigations, including RNA tetraloop folding studies, and results of these simulations should be viewed with care.

It should be noted that the “ladder-like” artifact would not have appeared in most previous RNA simulation studies, since it usually takes at least several tens of nanoseconds to emerge, depending on the system (for several examples see our recent study, in which we found that between 20 and 95 ns is required for some RNA tetraloop structures(46)). However, collectively through the large sets of RNA simulations performed by the collaborating groups we accumulated quite strong evidence that the “ladder-like” structure is preferentially favored over traditional A-RNA helices by both the ff99 and the ff99bsc0 force fields. Thus, we expect the ladder-like structure artifact to appear, eventually, in all sufficiently long RNA MD simulations. In other words, we hypothesize that the “ladder-like” structure is the global RNA minimum and its appearance (and accompanying structural changes in the simulated RNA molecule) is solely dependent on the simulation time scale, even for folded RNAs. Finally, we note that deficiencies in the χ potential are not unique to the AMBER force fields since χ parameters of the CHARMM all22 and all27 force fields have been revised,^19,50 and subsequent studies suggest that further revision is required.^7,41

Since transition to the ladder-like structures is accompanied by a large shift of the χ value toward the high-anti region, the distortions could be attributed to the χ torsion parametrization. Removing the tendency of force fields to generate unnatural ladder-like structures in RNA simulations through reparameterization of the glycosidic torsion was one of the main motivations of the work presented here.

To derive new χ torsion parameters, we decided to base the parametrization procedure on better quantum-chemical (QM) reference data obtained from more relevant model systems. Here, we compare the most frequently used QM methods, including HF/6-31G*, MP2/6-31G*, DFT-based computations, etc., with the best available reference QM method, here denoted CBS(T). CBS(T) is the MP2 method extrapolated to the complete basis set (CBS) limit of atomic orbitals with a correction by the CCSD(T) method using a smaller basis set.(51) Further, we carefully evaluate errors arising from other commonly applied methodological assumptions. The first is the choice of the geometries for deriving the parameters, namely, the assumption that the same QM-optimized geometries can be used for both the QM and the MM single-point calculations. The second assumption is that solvation effects can be ignored, i.e., that in vacuo parameters for torsion can be reliably applied. Hypothesizing that both approximations may lead to substantial errors, we suggested a new protocol that takes both effects into account, derived new χ torsion parameters, and compare them here to other available parametrizations, in terms of the shape of the torsion profiles with regard to the A/B form equilibrium, syn/anti relative energies, and transition barriers. In addition, we tested various χ profiles in MD simulations of a B-DNA helical structure and three A-RNA structures. Finally, after the preliminary tests, we ran extensive MD simulations (dozens of microseconds) of numerous other systems with various force fields. The results of these more extensive simulations are briefly mentioned here and described (or will be described) in more detail in separate publications, such as our recent study of RNA tetraloops.(46)

Methods

Selection of Model Molecules

In our attempts to improve modeling of the χ potential, we used almost complete ribo- and deoxyribonucleoside models with the 5′-OH group replaced by a hydrogen (Figure 1; only the ribo compounds are shown). We omitted the 5′-OH group to avoid its contacts with the nucleobases (for instance, the contact of 5′-OH with H6 of pyrimidines), which would bias the parameters. Note that the value of the pseudorotation angle was fixed in all calculations (see below), and therefore, neglect of the anomeric effect of the missing 5′-OH group should not influence our results. We refer to the compounds in Figure 1 as ribo/deoxyribonucleosides or simply dN/rN hereafter to facilitate discussion, noting that in this work these terms always refer to the nucleosides with the 5′-OH replaced by a hydrogen. These molecules are probably the smallest models that could be reasonably used for our purpose as they include all the intramolecular contacts that occur upon rotation about the torsion angle. The intramolecular contacts are very important because they make major contributions to the torsion energy. For instance, the repulsive O4′···O2 and O4′···N3 contacts in purines and pyrimidines, respectively, correspond to the highest rotation barriers on the potential energy surface. Note also that increasing the complexity of the model beyond certain limits does not necessarily improve the quality of the results as some long-range interactions and contacts might introduce considerable additional problems.^25,52 As described below, to assess the influence of the sugar pucker, the calculations were performed for two sugar conformations in deoxyribonucleosides, C2′-endo and C3′-endo. For the ribonucleosides only the C3′-endo conformation was considered.

Levels of Theory

The single-point calculations were performed at various levels of theory. The most accurate are the MP2/CBS + ΔCCSD(T) calculations, which approximate CCSD(T)/CBS quality and are denoted CBS(T) hereafter. The complete basis set (CBS) extrapolations were obtained through the scheme of Helgaker and Halkier^53,54 (HF and MP2 energies were extrapolated separately) using cc-pVTZ and cc-pVQZ basis sets. Turbomole 5.10^55,56 was used to calculate the MP2 energies with the RI approximation. The correction term for higher order correlation effects, ΔCCSD(T), was calculated using the cc-pVDZ basis set in Molpro 06.(57) For more details, see Jurecka and Hobza.(51) To derive the DFT-based parameters we used the PBE density functional, 6-311++G(3df,3pd)⁵⁸⁻⁶¹ basis set (LP hereafter), and empirical dispersion corrections (DFT-D, 1.06-23).(62) For some of the geometry optimizations described below we also used smaller basis sets, TZVP and TZVPP.(63)

Geometry Optimizations and Constraints

In the QM calculations, the starting structures corresponding to either C2′-endo or C3′-endo forms were first relaxed at the PBE/TZVPP level with the continuum solvent model COSMO(64) in the TurboMole 5.10^55,56 software suite (water, ε_r = 78.4). Then, several constraints were applied in the TurboMole program. The O4′–C4′–C3′–C2′ angle was constrained at the value taken from the PBE/TZVPP/COSMO optimal structure to keep the sugar pucker close to C2′-endo or C3′-endo, i.e., for dA, dT, dG, and dC at 28.1°, 26.0°, 25.2°, and 25.4° and for rA, rU, rG, and rC at −34.7°, −38.9°, −39.6°, and −39.2°, respectively. The C4′–C3′–O3′–H3T angle was constrained at −60° to prevent H bonding with the O2′ oxygen, and for ribonucleosides, the C3′–C2′–O2′–HO′2 torsion was constrained at −120° to prevent any sugar···base H-bond formation or intramolecular H-bond formation with O2′. Then, the χ angle was increased with 10° increments and the geometries relaxed using the PBE DFT functional and the LP basis set (see above) in the COSMO continuum solvent. The same constraints were applied in the MM optimizations, which were performed in the Gaussian software suite(65) using the “external” function and the ff99 force field. The external program for MM geometries was the sander module of AMBER(66) and a Poisson–Boltzmann (PB) continuum solvent was used.

Solvent Models

The COSMO continuum solvent model(64) was used in the QM calculations, while a Poisson–Boltzmann (PB) continuum solvent model^67,68 was applied in the MM calculations. The COSMO calculations were performed with TurboMole 5.10^55,56 with default scaled Bondi radii (scaling factor, 1.17) and default water parameters (ε_r = 78.4). The PB calculations were carried out with Gaussian 03 software using the “external” function and in-house scripts linking Gaussian to the sander module of AMBER 9.(66) In sander the grid spacing was set to 0.2 Å, while default water parameters (ε_r = 78.4) and default radii were used (see also refs (67) and (68)). The nonpolar terms were included in the PB optimizations, but only the PB electrostatic component was considered in dihedral parameter development (see discussion below).

Obtaining the Torsion Profiles

Usually the torsion angle parameters (E_dih,χ^vac here) are determined by the difference between the MM single-point energy (E_–χ^MM//QM,vac) and QM single-point energy (E^QM//QM,vac) obtained in vacuo using the same (QM) geometry for both the MM and the QM calculations (eq 1):

Here, we use a different scheme that takes into account certain solvation-related effects (eq 2). In this approach, the geometry optimizations are carried out at the QM and MM levels separately (see below) in continuum solvents (COSMO and PB, respectively) and are followed by single-point calculations including solvation energies (E^QM//QM,COSMO and E_–χ^MM//MM,PB, respectively). Note that similar techniques have been used before. For instance, independent relaxation of the QM and MM structures is used in CHARMM (see, e.g., ref (69) and references therein). Solvation by the IEFPCM model (QM calculation only) was used, e.g., in ref (70).

With this approach, only the difference between the COSMO and the PB solvation energies enters the resulting torsion parameters (not the total solvation energy). In this way double counting of solvation energy is prevented, while some desirable terms (such as solute polarization) are included. The force field can subsequently be used in simulations with explicit solvent molecules. Our approach can also be justified by the observed improvements in the performance of the force field. Note that for consistency we use full solvent treatment in all our calculations, i.e., for both MM and QM and for both optimizations and single-point energy evaluations. In the PB calculations (single point) only the electrostatic component is considered, in accordance with the COSMO calculations.

Derivation of χ Parameters

In the Cornell et al. force field, the force-field energy (without the PB solvation energy) is a sum of the bond stretching (E_bond), angle bending (E_angle), dihedral (E_dih), nonbonded electrostatic (E_elst), and nonbonded van der Waals (E_vdW) terms (eq 3).

The dihedral term is described as a cosine series (eq 4), where n is the periodicity of the torsion, V_n is the rotational barrier, ϕ is the torsion angle, and γ is the phase angle.

The QM-MM difference obtained in eq 2 is approximated (fitted) by eq 4 (V_n and γ are varied). Upon torsion rotation all force-field components (eq 3) contribute to torsion potential energy, not only the dihedral term (eq 4). To differentiate between the total energy of the torsion and the dihedral contribution to the torsion energy we call the former the “χ torsion profile” and the latter the “χ dihedral term” hereafter. To better understand the various contributions to the χ parameters two parametrizations were derived and tested.

(1) χ_OL-DFT: The first parametrization, χ_OL-DFT, was fully based on the DFT-D QM profile. Only the deoxyribonucleosides (dA, dT, dC, and dG) in a C2′-endo conformation were considered. After DFT optimization (PBE/LP in continuum solvent) the single-point calculations were performed at the DFT-D level (PBE-D-1.06-23/LP). Solvent effects were introduced according to eq 2. In the fitting procedure, double weight factors were assigned to the five points around the important χ values of 200° and 260° to improve the fit in the anti and high-anti regions. The total χ dihedral term was distributed among three of the six torsions contributing to χ (C2–N1–C1′–X in pyrimidines and C4–N9–C1′–X in purines). Since χ dihedral parameters derived for dA and dG were quite similar, only one set of parameters was fitted (i.e., both dG and dA curves were used in a single fitting). This parametrization is presented only for comparison and is not intended to be used for NA simulations. However, although the χ_OL-DFT parameter set is not recommended for simulations, we provide the respective parameters in the Supporting Information. The abbreviation “OL” in the force-field name stands for the city of Olomouc (see affiliations).

(2) χ_OL: In the second parametrization, χ_OL, the MP2/CBS data were taken as a reference. The MP2/CBS method was used instead of CBS(T) because both methods provide very similar profiles (see below) but MP2/CBS is much less computationally demanding. Both the deoxyribonucleosides (C2′-endo) and ribonucleosides (C3′-endo) were considered. For the deoxyribonucleosides single-point calculations were also carried out at the DFT-D (PBE-D-1.06-23/LP) level. The difference between the MP2/CBS and PBE-D-1.06-23/LP calculations for deoxyribonucleotides was then added to the PBE-D-1.06-23/LP results for ribonucleosides to save computer time (assuming that the MP2/CBS correction is similar for ribonucleosides and deoxyribonucleosides). Then, continuum solvent terms were introduced according to eq 2 using the PBE-D-1.06-23/LP method. The final QM values were then obtained as combinations of the COSMO PBE-D-1.06-23/LP data adjusted by the above-mentioned MP2/CBS correction. The reference curve for the fit was obtained by combining the data for the ribo- and deoxyribonucleosides. For the region between 210° and 330°, we took the reference curve for the deoxyribonucleosides (C2′-endo) while the ribonucleoside (C3′-endo) curve was used for the remaining χ range. Double weights were assigned to χ values of 180°, 190°, 200°, 210°, and 220° and 240°, 250°, 260°, 270°, and 280° to improve the accuracy of the fit in the important anti and high-anti regions, respectively. The parameters obtained in this manner (our final parameters) are listed in Table 1.

Table 1. Dihedral Parameters for χ_OL Parameterization^a.

		χOL parameter
nucleoside	torsion (atom types)	n	Vn/2	ϕ
A	O4′–C1′–N9–C8	1	0.9656	68.79
	(OS-CT-N*-C2)	2	1.0740	15.64
		3	0.4575	171.58
		4	0.3092	19.09
G	O4′–C1′–N9–C8	1	0.7051	74.76
	(OS-CT-N*-CK)	2	1.0655	6.23
		3	0.4427	168.65
		4	0.2560	3.97
C	O4′–C1′–N1–C6	1	1.2251	146.99
	(OS-CT-N*-C1)	2	1.6346	16.48
		3	0.9375	185.88
		4	0.3103	32.16
U(T)	O4′–C1′–N1–C6	1	1.0251	149.88
	(OS-CT-N*-CM)	2	1.7488	16.76
		3	0.5815	179.35
		4	0.3515	16.00

^aC1 and C2 are new atom types for C introduced to distinguish A from G and C from U (T). The parameters can be downloaded from http://fch.upol.cz/en/rna_chi_ol/.

MD Simulations of RNA and DNA Duplexes

Initial structures of RNA and DNA duplexes were taken from X-ray data. The ions and water molecules were removed from the original PDB files. The 1RNA tetradecamer duplex r(U(AU)₆A)(71) and 1BNA dodecamer duplex d(CGCGAATTCGCG)(72) were taken without any further modifications. In the brominated tridecamer r(GCGUU-5BUGAAACGC) (PDB ID 2R20)(73) the brominated uracil was replaced with uracil, and this structure is hereafter denoted 2R20′. The decamer r(GCACCGUUGG) was excised from the 1QC0(74) structure and is hereafter denoted 1QC0′. In all simulations the total charge was neutralized by Na⁺ ions.(75) A TIP3P(76) water box was used to solvate the nucleic acid molecules (equilibrium box sizes 59 × 68 × 65 Å with 8428 water molecules for 1RNA, 51 × 55 × 68 Å with 6145 water molecules for 1BNA, 65 × 60 × 60 Å with 7502 water molecules for 2R20′, and 54 × 51 × 58 Å with 5121 water molecules for 1QC0′). Simulations were carried out with the pmemd code from the AMBER 9 program suite(66) under NPT conditions with default temperature and pressure settings (tautp = 1.0 ps and taup = 1.0 ps), a 2 fs time step, a 9 Å nonbonded cutoff, and SHAKE on bonds to hydrogen atoms with default tolerance (0.00001). Nonbonded pairlist was updated every 25 steps. PME was used with default grid settings and default tolerance (dsum_tol = 0.00001). Default scaling factors were used to scale nonbonded and Coulomb interactions (scnb = 2.0 and scee = 1.2, respectively).

Averages of several structural parameters were taken from the last 20 ns of 100 ns simulations, and snapshots were stored every 1 ps. In the case of B-DNA simulation we ran only 50 ns simulations (the last 20 ns were taken for analysis), because this was enough to demonstrate the large deviations for the χ_OL parametrization. Two terminal base pairs at both ends of the modeled structures were omitted from the analyses. All analyses were performed using X3DNA code.(77) For the 2R20′ structure, the base pair parameters of the noncanonical GG pair and base pair step parameters of the steps including this noncanonical pair were filtered off in order to focus solely on the canonical base pair geometries (and thus avoid averaging of bimodal distributions). Mass-weighted rmsd values were calculated with respect to the initial structure (all atoms), again omitting the two terminal base pairs at both ends.

Further force-field assessments included very extensive simulations of numerous other RNA species, including UUCG and GNRA RNA tetraloops (up to 1 μs trajectories), short A-RNA duplexes, and reverse kink-turns (see below). Simulations of sarcin-ricin domains of 23S rRNA, ribozymes, riboswitch, kink-turns, C-loops, and other selected molecules are in progress. A detailed report of the RNA tetraloop calculations has already been published.(46)

Results and Discussion

Choice of the Method for Geometry Optimization

In order to derive reliable data for force-field parametrization, it is first necessary to determine the level of computations required. Several levels of theory for geometry optimization were tested for the dC nucleoside with the C2′-endo pucker. The dC nucleoside has the largest steric clashes of all nucleosides (the highest rotational barrier) and thus should theoretically be the most sensitive probe regarding the level of theory.

We used DFT-based methods for geometry optimizations, due to their advantageous balance between quality and speed. The utility of HF and MP2 methods for deriving geometries has not been specifically tested for the following reasons. The HF method is highly unreliable due to the lack of electron correlation, and the MP2 method is known to exhibit very large intramolecular basis set superposition errors (BSSEs) when manageable basis sets are used.⁷⁸⁻⁸⁰ The following DFT functional/basis set combinations were tested: BLYP/TZVP, B3LYP/TZVP, PBE/TZVP, PBE/TZVPP, and PBE/LP. All optimizations were carried out in COSMO implicit solvent(64) (water, ε = 78.4). We assumed that the last combination, the PBE functional with the largest LP basis set, would be the most reliable because it is known to provide the best results for polar molecular complexes(62) (note that the potential energy surface is shaped mainly by the polar contacts in dC). The other optimization methods were judged according to rmsd values of 36 optimized geometries (χ profiles) with respect to the PBE/LP geometries. The BLYP/TZVP and PBE/TZVP combinations yielded the largest rmsd values (1.26 and 0.91 Å, respectively, all atoms) relative to the PBE/LP geometries, and the RSMD between the geometries they generated was also large (1.48 Å). The B3LYP/TZVP gave a better rmsd of 0.76 Å. These results are consistent with the results found for molecular complexes.(62) To test whether a smaller basis set could be used, PBE results were also calculated using the TZVP and TZVPP basis sets. While the results for TZVPP were very close to the PBE/LP results (total rmsd 0.48 Å), the PBE/TZVP optimization exhibited rather large structural deformations for several geometries (rmsd 0.76 Å).

Considering these results we decided to use the largest LP basis set (6-311++G(3df,3pd)) together with the PBE density functional in all optimizations carried out in this study to ensure quality of the results. The LP basis set is already fairly efficient at eliminating intramolecular BSSE, while the large BSSE of smaller basis sets could compromise the results. Hence, we strongly recommend use of large basis sets for geometry derivation in force-field parametrization. Although the lower level methods, such as the popular HF/6-31G* method (used for example by Yildirim et al.(45) to derive their χ parametrization), may sometimes provide acceptable results based on fortuitous error cancellation, in general they are likely to introduce bias. The HF/6-31G* method for geometry derivation was justified in the mid-1990s, when better methods were not feasible, but it does not reflect contemporary standards in the field.

Brief comment is needed regarding the use of the empirical dispersion correction for the DFT optimizations. We did not use the dispersion correction for the DFT optimizations carried out in solvent to avoid an imbalanced description of the solute–solute and solute–solvent interactions. However, it is possible that when larger and more compact molecules are modeled the intramolecular dispersion correction of DFT might become necessary. Note, however, that it is still necessary to include dispersion correction in the single-point QM calculations in eq 2.

Choice of Method for Single-Point Calculations

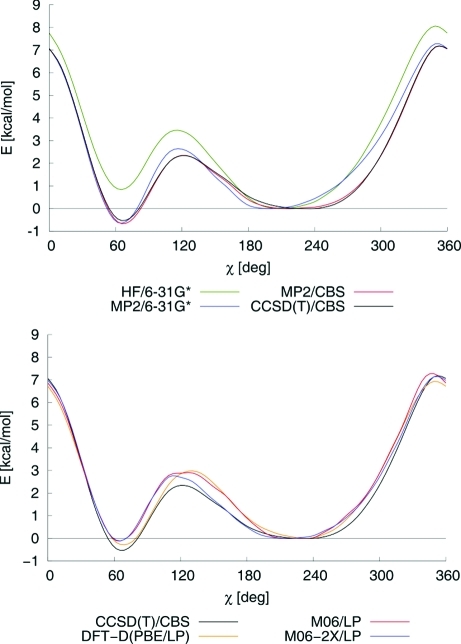
As mentioned in the Introduction, even very small changes in the torsion potential can cause substantial discrepancies in MD simulations. Therefore, it is important to determine the sensitivity of the torsion profile to the level of theory. The best available reference method for systems containing tens of atoms is the CCSD(T)/CBS (coupled clusters singles and doubles with perturbative treatment of triple excitations/complete basis set limit) method.(51) However, since CCSD(T)/CBS calculation is not tractable, we used the MP2/CBS level with CCSD(T)/cc-pVDZ correction, here denoted CBS(T). Figure 2 compares profiles obtained with several frequently used methods with the CBS(T) reference profile for nucleosides.

Figure 2.

Torsion profiles for guanine nucleoside (dG) calculated at various levels of theory in vacuo. The reference method is CBS(T). (Top) Profiles obtained with the wave function methods: CBS(T) (black), HF/6-31G* (green), MP2/6-31G* (blue), and MP2/CBS (red). (Bottom) Profiles obtained with the DFT methods: DFT-D (PBE/6-311++G(3df,3pd)/1.06-23) (orange), M06 (red), M06-2X (blue), and the reference CBS(T) profile (black). Energies are offset to the anti minimum structure.

Although the torsion profiles presented in Figure 2 may seem fairly similar at first sight, differences from the reference CBS(T) curve are often greater than 1 kcal/mol, especially those obtained using less computationally demanding methods. For instance, the MP2/6-31G* method predicts the modeled structure to be significantly less stable (by about 0.6 kcal/mol) than does the reference CBS(T) method at the key energy minimum in the high-anti region (χ = 250°). Furthermore, MP2/6-31G* yields an incorrect balance of the anti and high-anti regions (torsion angles 210° and 250°) and somewhat overestimates the height of the lower barrier. Given the requirements for the χ profile discussed in this paper, we conclude that use of MP2 with a small basis set would not yield sufficiently accurate data for parameter development.

The data shown in Figure 2 also suggest that the DFT description of the χ profile is quite inaccurate. Although the profile generated using the PBE-D-1.06-23 method with a large LP basis set is somewhat closer to the reference curve than the MP2/6-31G* profile around the anti minimum, it still exhibits sizable errors around the energy barriers. As we show below, such deviations in the χ potential lead to substantial deviations of certain structural parameters in MD simulations of RNA duplexes (compare the results for χ_OL-DFT and χ_OL below). Similar conclusions can also be drawn regarding the M06 and M06-2X DFT functionals recently presented by Zhao and Truhlar,(81) both of which are overly repulsive in the high-anti region, overestimate the lower transition barrier, and provide inaccurate balances between the syn and the anti minima (note, the LP basis set used here is similar to the basis set used for the M06 functional development). Given the accuracy required for the χ dihedral parameters, none of the applied DFT-based methods can be recommended for their derivation. This is an important methodological finding of our study, which is corroborated by our recent benchmark study of another model of nucleic acid backbone, in which a broader set of DFT methods was tested.(52)

In contrast, the MP2/CBS level provides results that are very close to those obtained using the reference CBS(T) method, with differences of merely ca. 0.1 kcal/mol around the minima. We hypothesize that the MP2/CBS method is sufficiently accurate to serve as a reference level of theory, and our final parameters (χ_OL, presented below) are based on MP2/CBS data because they are significantly less computationally demanding to handle than CBS(T) reference data. We do not recommend using any level of theory lower than MP2/CBS for torsion profile derivation.

Dependence of the χ Profile and Dihedral Term on Sugar Conformation and Type

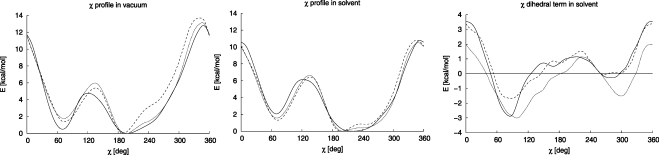
To assess the effect of sugar pucker on the derived dihedral parameters we calculated the χ torsion profiles for two different puckers of the A, T, C, and G deoxyribonucleoside models (C2′-endo and C3′-endo) and for the C3′-endo pucker of the A, U, C, and G ribonucleoside models. Figure 3 displays results of the PBE-D-1.06-23/LP calculations both in vacuo (left panel) and in COSMO continuum solvent (middle panel) for cytosine. The χ dihedral term contributions (i.e., the QM profile minus the MM profile without the respective χ terms) derived from the continuum solvent data are shown on the right. The results for the other nucleosides are similar and can be found in the Supporting Information (Figure S3).

Figure 3.

Torsion profiles for cytosine calculated in vacuo (left), with COSMO continuum solvent (middle), and the χ dihedral term’s contribution to the torsion derived from the continuum solvent data (right) of the cytosine 2-deoxyribonucleoside with C2′-endo and C3′-endo sugar puckers and the ribonucleoside with C3′-endo sugar pucker (full, dotted, and dashed lines, respectively).

To differentiate between the total potential energy of the torsion (as in eq 3, including PB solvation energy for calculations in solvent) and the dihedral contribution to the total torsion energy (E_dih only, eq 4) we call the former the “χ torsion profile” and the latter the “χ dihedral term” hereafter.

The results presented in Figure 3 suggest that in vacuum the χ torsion profile is quite strongly modulated by the sugar conformation and the presence of the 2′-OH group. Comparing the deoxy C2′-endo and ribo C3′-endo compounds, the maximum difference is almost 3 kcal/mol, and around the anti minimum the differences are as large as 2 kcal/mol.

When a COSMO continuum treatment of the solvation energy is included, the χ profiles differ from those obtained in vacuum. The higher energy barrier is lowered, the lower barrier increases, and both the syn/anti equilibrium and the shape of the profile in the anti minimum region are also affected. Profiles obtained at the force-field level with PB continuum solvent show very similar patterns in these respects (see Supporting Information, Figure S3). Clearly, the in vacuo and in-solvent profiles of the torsion potentials differ markedly. Consequently, comparing, for instance, the relative stability of two minima in vacuum and in solvent can lead to quite different conclusions. We hypothesize that in-solvent profiles are more likely to be representative of NAs in solution than corresponding profiles obtained in vacuo because the continuum mimics the screening of the electrostatic component that occurs with hydrated nucleoside structures in solution. If so, in-solvent profiles rather than in vacuo profiles should be considered (although the latter are commonly used) in attempts to link torsion curves to the outcomes of in-solvent MD simulations.

Interestingly, when solvation is included, the profiles show less dependence on the pucker or presence of the 2′-OH and overall become strikingly more similar. The maximum difference between the deoxy C2′-endo and the ribo C3′-endo compounds drops to less than 1.5 kcal/mol, and around minima the differences are smaller than 1 kcal/mol. These differences are mainly due to variation of the van der Waals (vdW) and electrostatic interactions of the sugar and base atoms as the χ torsion rotates. For different sugar puckers the interacting parts of the sugar and base moieties approach each other at different distances, thus providing different energy profiles. However, the major components of this variation cancel out when the MM single-point energies (with χ dihedral terms set to zero) are subtracted from the QM energies; see the χ dihedral terms derived from these data (Figure 3, right).

The derived χ dihedral terms (Figure 3, right) display a maximum difference between the curves corresponding to the different puckers/2′-hydroxylation of about 2 kcal/mol. If we consider only the two most relevant dC C2′-endo and rC C3′-endo conformations, the maximum difference drops to about 1 kcal/mol and around the minima it is even smaller. When average parameters are used as a compromise, the corresponding errors drop to about one-half of the averaged differences between the curves (if two conformations are considered, as in the case of χ_OL). This gives an estimate of the errors intrinsic to our parametrization. These errors cannot be eliminated if a universal set of torsion parameters is required for DNA and RNA. Note, however, that there is still the possibility of reducing the errors by simultaneously adjusting another (coupled) component of the force field, for instance, the torsions determining the sugar pucker, but this was not attempted in the work presented here.

Effects of Geometry Relaxation

The effects of geometry relaxation on the resulting torsion parameters are rarely discussed. Usually, the following procedure is used to obtain new parameters. First, a model molecule with constrained dihedral angle is relaxed at the QM level and the QM energy, E^QM//QM, is obtained. Then single-point MM energy is calculated, based on the QM geometry with the parametrized torsion set to zero, E_–χ^MM//QM, and the torsion parameters are determined according to eq 5.

However, more adequate parameters may be obtained when a MM optimization is also carried out and the MM energy, E_–χ^MM//MM, is calculated based on the MM relaxed geometry rather than the QM geometry. Then, the resulting parameters are determined according to eq 6. This scheme is used, for instance, in the CHARMM force field (see, e.g., ref (69) and references therein), and a very similar scheme was applied by Ode et al.(44)

The rationale underlying eq 6 is that the MM potential energy surface (PES) derived in this manner is more similar to the QM PES than when eq 5 is used, in terms of the relative energies of key PES regions, such as minima and transition states. The relative energies of minima and transition states are of primary interest in empirical modeling; hence, they need to be as similar as possible to reference QM values on the QM PES. The key to understanding which of the approaches (eq 5 or 6) is more adequate in this sense is to realize that eq 6 corresponds to situations where the system samples the MM geometries and acquires MM energies, as in molecular dynamics, while eq 5 corresponds to situations where the system samples the QM geometries but acquires MM energies. The latter is clearly artificial, critically dependent on the other intra- and intermolecular MM force-field parameters, and may substantially bias parametrization of force fields. Thus, the former approach (i.e., eq 6) is preferable.

Equation 5 can also be understood as an approximation to eq 6, which can be reasonably justified in two cases: (i) when the optimal QM and MM geometries are very similar, especially in terms of distances between the 1–4, 1–5, etc. atoms or (ii) when the remaining force-field contributions, namely, the Coulombic and wdW terms, and the bond, angle, and other dihedral angle terms do not contribute significantly to the torsion profile. Note that the Coulomb and vdW terms codetermine the 1–4 distances. This also holds for the bond, angle, and other dihedral terms that may be deformed when the given torsion is rotated. Many of those terms are quite inaccurate in the force fields (and likely parametrized for different geometries than the QM-optimized geometries). Using eq 6 can partially correct for these inaccuracies by including them in the parametrized torsion.

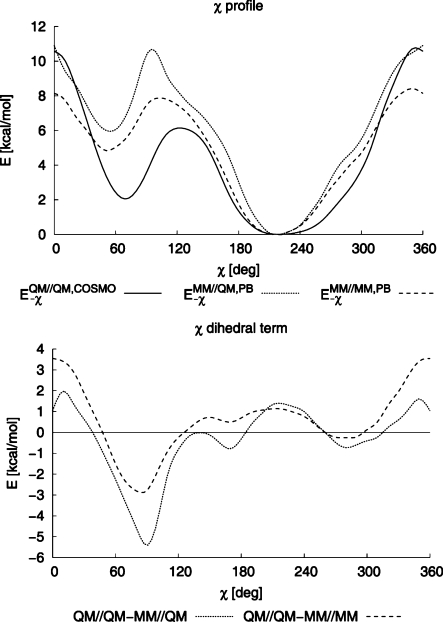
To illustrate the differences between relaxed and nonrelaxed conditions we show torsion profiles calculated using the QM method based on QM-optimized geometries (E^QM//QM,COSMO, full line) and compare them with the MM_–χ profiles based on QM-optimized geometries (E_–χ^MM//QM,PB, dashed line) and MM-optimized geometries (E_–χ^MM//MM,PB, dotted line) for dC in Figure 4 (top). The derived χ parameters correspond to the differences between the dashed and full lines (eq 5) and dotted and full lines (eq 6) and are also shown in Figure 4 (bottom). Clearly, the resulting dihedral terms differ markedly. For example, consider the torsion barrier (around 360°) between the high-anti and syn regions. When dihedral parameters are derived from eq 5 (illustrated by the difference between the full and dotted lines), they will be positive for the transition region but much smaller (by about 2.5 kcal/mol) compared to those derived from eq 6 (illustrated by the difference between the full and dashed lines). In a MD simulation the molecule will follow the MM PES on its way from the high-anti region to the syn region. If we added the underestimated dihedral penalty obtained from eq 5 to the MM energy, the total barrier would be underestimated as well. Similar errors appear in other parts of the PES and influence the relative stability of the anti and syn forms, the low-anti to syn transition barrier, and the shape of the resulting MM potential curve.

Figure 4.

(Top) Torsion profiles for dC calculated as QM energy based on QM-optimized geometry (E^QM//QM,COSMO, full line), MM_–χ energy based on MM-optimized geometry (E_–χ^MM//MM,PB, dashed line), and MM_–χ energy based on QM-optimized geometry (E_–χ^MM//QM,PB, dotted line). (Bottom) χ dihedral terms E_dih,χ^solv derived from E^QM//QM,COSMO – E_–χ^MM//MM,PB (QM//QM-MM//MM, dashed line) and E^QM//QM,COSMO – E_–χ^MM//QM,PB (QM//QM-MM//QM, dotted line) normalized to χ = 250°. The ff99bsc0 force field was used in all cases, and energies are in kcal/mol.

It is important to note that the magnitude of the errors associated with using the QM geometries for the MM single-point calculations is not marginal; the differences in this case reach almost 3 kcal/mol, comparable to the amplitude of the dihedral torsion itself. Deviations are significant for both the barrier heights (∼2.5 and 0.7 kcal/mol for the lower and upper barriers, respectively) and the region around χ ≈ 70° characteristic of the Z-form of DNA and many nucleotides in folded RNA structures (∼1 kcal/mol). Interestingly, in the context of this study, there are also differences in the shape of the curves in the anti region, which might contribute to the relative stability of the A and B forms of nucleic acids (see also the ΔE_{anti/high-anti,dih} criterion described below).

Regarding the origin of the observed differences, we can hypothesize that they are mainly due to the short-ranged vdW contacts that occur upon dihedral rotation. For instance, in the cytosine nucleoside the O4′ and O2 oxygen atoms approach each other closely (this contact corresponds to the higher torsion barrier, χ = 0°) and upon rotation the O2 and H2′ atoms also approach each other (the lower barrier, χ = 120°). The optimal QM distances for these interactions differ from the optimal MM distances. For instance, in dC the distances between the O4′ and O2 atoms for χ = 0° are 2.72 Å in QM and 2.66 Å in MM and those between the O2 and H2′ atoms for χ = 120° are 2.31 Å in QM and 2.44 Å in MM. Since the vdW and Coulomb energies depend strongly on distance, especially at short separations,(82) the associated errors may be significant. Other geometry differences between the QM and MM structures are probably less important. In MM structures the pseudorotation angle P (for definition see below, section MD Simulations of A-RNA Duplexes) is systematically underestimated by about 5° compared to QM, and this underestimation somewhat increases for χ = 0°, 90°, and 180° (note that only the O4′–C4′–C3′–C2′ angle was constrained, therefore the ribose was partly flexible). The next difference is the slightly different value of pyramidalization on the N1 atom in QM and MM (around the anti minimum they differ by less than 3°). In other parameters the MM and QM structures are very similar.

For the above reasons we recommend using relaxed MM geometries for calculating MM single-point energies in attempts to derive torsion parameters that perform well in MD simulations. However, it is possible that relaxation of the MM geometries may lead to a significantly different structure than QM relaxation (due to differences between the MM and the QM PES). If so, using suitable constraints to keep the MM geometry close to expectations would probably cause a smaller error than using eq 5.

Finally, we compare the fully relaxed structures of rA, rG, rC, and rU obtained with the ff99bsc0 and ff99bsc0 χ_OL force fields with the QM reference geometries (PBE with LP basis set). All optimizations are carried out in solvent (COSMO in QM and PB in MM) without any constraints. The OH group on C2′ is oriented such that it forms a hydrogen bond with the OH group on C3′ atom in order to prevent formation of hydrogen bonds with the NA bases. The optimal χ values are 201° (QM), 217° (ff99bsc0), and 194° (ff99bsc0χ_OL) for rC and 201° (QM), 204° (ff99bsc0), and 196° (ff99bsc0χ_OL) for rU. These values are quite similar, and the small differences between the QM reference and the ff99bsc0χ_OL force field can be attributed to geometry constraints used in parameter derivation and to inaccuracies of the fit. For purines the optimal χ values are 200° (QM), 266° (ff99bsc0), and 189° (ff99bsc0χ_OL) for rG and 198° (QM), 261° (ff99bsc0), and 183° (ff99bsc0χ_OL) for rA. Here, the ff99bsc0χ_OL values are again quite similar to the QM reference; however, the ff99bsc0 values are significantly higher, closer to the high-anti region. The relatively large shift in the minimum position of rG and rA is in line with the observed propensity to formation of the ladder-like structures in the ff99bsc0 force field.

Comparing χ Parameters

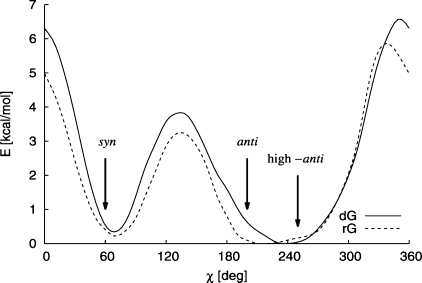
Before comparing effects of various parametrizations on the behavior of modeled systems in the anti region we discuss relevant experimental data. In crystal structures,(83) RNA is typically found in the A form with the χ population peaking at around 200° (anti). For DNA the B form is prevalent with χ ≈ 250° (high-anti), but in DNA χ can also adopt values characteristic of the A and Z forms. In the Z form χ is in the syn region (χ ≈ 60°) for dG and the high-anti region (χ ≈ 250°) for dC. Typical values of χ are indicated and compared with the χ torsion profiles of dG and rG nucleosides, calculated at the PBE/LP level (including COSMO continuum solvation energy to improve comparability with nucleic acids in real environments), in Figure 5.

Figure 5.

χ torsion profiles for dG (full line) and rG (dashed line), indicating typical average X-ray values for A-RNA, B-DNA, and Z-DNA. PBE/LP data including solvent effects.

The data displayed in Figure 5 show that in the anti region the energy minimum of the dG potential is shifted more toward the high-anti (χ ≈ 250°) while the rG minimum is closer to the anti configuration (χ ≈ 200°). The same trend is also found for other nucleosides (see Figure S1 in the Supporting Information). Therefore, it seems that the shape of the χ potential profile drives the ribo- and deoxyribonucleosides toward their typical A and B forms (anti and high-anti configurations, respectively). Note, however, that in the X-ray structures of B-DNA (for instance) the χ distribution is relatively broad and very high values of χ may also appear, much higher than those corresponding to the energy minima in Figure 5. This indicates that either our theoretical potentials are still inaccurate, or the environment (surrounding bases and the sugar–phosphate backbone) contribute strain to the χ torsion and significantly influence the actual values of χ.

Here it is worth noting that the MM-derived χ profiles exhibit the same systematic anti/high-anti propensities for dN/rN compounds as the QM profiles (compare Figure 6 below and Figure S2 in Supporting Information), although the same χ dihedral parameters were used for both dN and rN nucleosides. Therefore, the A/B propensities of ribo/deoxyribo compounds must come partially from the nonbonded interactions or dihedral contributions associated with the 2′-OH group of ribose and not from the χ parametrization.

Figure 6.

Torsion profiles for the χ angle (on the left, ff99-optimized geometries) and the χ dihedral terms (on the right) of ff99 (black), Ode et al. (blue), Yildirim et al. (green), and parameters derived herein (χ_OL-DFT orange, χ_OL red) for ribonucleosides. The dihedral term was offset to χ = 250°, and idealized geometries were used to calculate the χ dihedral terms on the right to facilitate comparison with published data (see also text).

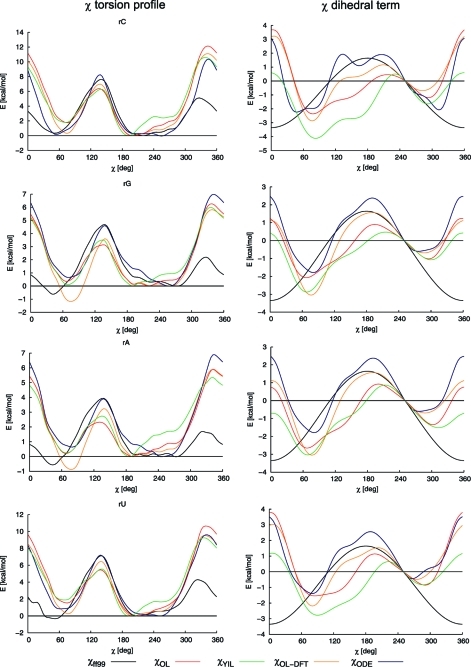
In the following text we compare the available χ parametrizations and discuss their influence on the main features of χ torsion profiles. Figure 6 compares χ torsion profiles (on the left) and the corresponding dihedral terms (on the right) calculated using ff99 (black), Ode et al. (blue), and Yildirim et al. (green) parametrizations and parameters derived herein, i.e., χ_OL-DFT (orange) and the final χ_OL parameters (red). All energies were calculated using the same force-field-optimized geometry (ff99), and only the profiles for ribonucleosides are shown (for dN profiles see Supporting Information, Figure S2). In order to make the profiles as comparable as possible to those of hydrated NA structures, PB solvation energy (identical for all parametrizations) was included in the calculations.

It should be noted that the differences between the χ torsion profiles (on the left) do not fully correspond to the differences between the derived dihedral terms (on the right). This is because the latter were calculated using cosine formulas assuming idealized geometries (i.e., C1′ was assumed to be an ideal tetrahedron, the O4′–C1′–N1–C6 dihedral was assumed to be O4′–C1′–N1–C2 + 180°, etc.), whereas MM-optimized geometries were used to generate the profiles on the left. The MM-optimized geometries slightly differ from the idealized geometries because all the nonconstrained dihedrals and angles deform upon torsion rotation, for example, the C1′ is not perfectly tetrahedral. Consequently, differences in energy are found mainly for the χ torsion parametrizations that involve terms including C2′ and H1′ of ribose, such as χ_OL-DFT, χ_ODE, and χ_YIL. This also means that the ΔE_{anti/high-anti,dih} values (see below) that would be obtained from the right part of Figure 6 differ somewhat from those given in Table 2, because the latter were determined using optimized geometries. The dihedral terms are presented for the idealized geometries to facilitate their comparison with published data.

Table 2. χ Contribution to Anti/High-Anti Relative Stability, ΔE_{anti/high-anti,dih} = E_dih(χ = 210°) – E_dih(χ = 250°), for Several χ Parameterizations^a.

	ΔEanti/high-anti,dih [kcal/mol]
parameterization	A	G	C	U(T)	average
ff94	1.9	1.9	1.9	1.9	1.9
ff98/99	1.3	1.3	1.3	1.3	1.3
χODE	2.0	2.0	1.8	1.8	1.9
χYIL	0.8	0.5	0.0	0.5	0.5
χvacb	1.8	1.7	1.1	1.9	1.6
χOL-DFT	0.5	0.5	0.8	1.2	0.8
χOL	0.9	0.8	0.4	0.9	0.8

^aThe more positive the anti/high-anti value, the stronger the stabilization of the high-anti conformation. Results with and without bsc0 correction are identical.

^bThe χ dihedral term was derived in the same way as in χ_OL-DFT, but based on gas phase QM data; see text.

Anti Minimum and Relative Anti/High-Anti Stability

Figure 6 shows that the profiles generated using the compared parametrizations differ significantly in the anti minimum region. While the minima of curves obtained using the parametrization of Yildirim et al. are located strictly in the anti region, the parameters presented by Ode et al. shift the minimum to the high-anti region. Minima of profiles generated using the ff99, χ_OL (and χ_OL-DFT) parameters appear somewhere between those two extremes but closer to the anti region. Further, the profiles differ not only in the position of the minimum but also in its shape. This is also very important because the distribution of the χ angle in real NA structures is usually quite broad; thus, the steepness of changes in the potential across a wide range of angles matters.

χ Contribution to Relative Anti/High-Anti Stability and Ladder-Like Structures

The link between emergence of the ladder-like structures in RNA simulations and the glycosidic angle χ was first pointed out by Mlynsky et al.(43) Since the transition to the ladder-like structure is accompanied by a significant shift of the χ angle from the anti region (χ ≈ 210°) toward the high-anti region (χ ≈ 250°), the χ potential must clearly affect the simulated behavior of RNA (the values of χ ≈ 210° and 250° were chosen arbitrarily and provide stable results for our purposes). In order to assess the contribution of χ to formation of the ladder-like structures quantitatively, we need a suitable measure. A convenient one could be the energy difference between anti (χ = 210°) and high-anti (χ = 250°) orientations, ΔE_{anti/high-anti} = E(χ = 210°) – E(χ = 250°). However, this would also incorporate electrostatic, vdW, and other contributions to high-anti propensity. An alternative measure is the χ dihedral term’s contribution to the anti/high-anti equilibrium, ΔE_{anti/high-anti,dih} = E_dih(χ=210°) – E_dih(χ = 250°). This measure enables assessment of the available χ parametrizations—ff94, ff98/99, χ_YIL, χ_ODE, χ_OL-DFT, and χ_OL—with regard to their propensity to lead to high-anti conformation (Table 2).

Table 2 shows ΔE_{anti/high-anti,dih} values for all nucleosides and all parametrizations shown in Figure 6 plus the ff94 parametrization. All values in Table 2 are positive, which means that all dihedral terms considered destabilize the anti (χ ≈ 210°) region typical for RNA. However, they do so to varying extents. We suggest that decreasing the stability of the anti region will increase the likelihood of formation of high-anti ladder-like structures in MD simulations. Thus, the propensity of the parametrizations to lead to formation of ladder-like structures should increase in the following order: χ_YIL < χ_OL-DFT ≈ χ_OL < ff99 < χ_ODE. If so, the bottom three parametrizations in Table 2 (χ_YIL, χ_OL-DFT, and χ_OL) have the potential to eliminate (or at least reduce) formation of ladder-like structures in RNA simulations because they destabilize the anti orientation less than ff98/99. In contrast, the parametrization of Ode et al. should promote laddering behavior more than ff99.

Extensive testing of different force fields has confirmed this expectation.^46,84 The ff99 and χ_ODE parametrizations lead to predictions of the ladder-like structure as the global minimum of the A-RNA stem, the latter actually accelerating its formation in simulations, while the χ_YIL, χ_OL-DFT, and χ_OL parametrizations appear to eliminate ladder formation.(46) However, the χ_YIL parametrization seems to do so excessively, which introduces other irregularities into the simulations (see below). Note that the particularly large anti/high-anti value for χ_YIL stems from significant destabilization of the high-anti region connected with the rapid onset of the high-anti penalty manifested in the “bumps” in the profiles in Figure 6 (left). In part this could be attributed to use of the insufficiently large 6-31G* basis set of atomic orbitals in the MP2 calculations, which contributes to destabilization in the high-anti region (e.g., by about 0.6 kcal/mol in the case of guanine, see Figure 2).

It should be noted that solvation-related effects also contribute to the relative anti/high-anti stability. To assess the magnitude of this contribution we derived another set of parameters in the same way as for χ_OL except that solvation was not included (using eq 1 instead of eq 2). Comparison of these vacuum-derived parameters (denoted χ_vac in Table 2) with χ_OL shows that including the solvation effects destabilizes the high-anti region by about 0.8 kcal/mol on average, thus increasing preference for the anti conformation typical for A-RNA. Thus, neglecting the solvation effects may introduce substantial bias in the χ potential. Note that the lack of solvent-induced stabilization is also apparent when the χ_ODE parameters (which were also derived in vacuo) are used. Interestingly, the same effect is not found in the χ_YIL modification, probably as a result of the error compensation (χ_YIL parameters represent a compromise between four structures with rather different torsion profiles; therefore, substantial uncertainties connected with the fitting procedure are to be expected).

Note that the ΔE_{anti/high-anti,dih} values presented in Table 2 were derived using the relaxed geometries with fixed χ angle value, while plots in the right part of Figure 6 were derived using idealized geometries (assuming a perfect tetrahedron on C1′ and planarity of the bases). Therefore, the results shown in Figure 6 may not fully correspond with the values in Table 2.

At this point, one might question the assumption that such small differences (on the order of tenths of a kcal/mol) between the parameters could be responsible for major structural distortions. However, such energy contributions may have strong cumulative effects since they reflect interactions that are present at numerous sites in regular DNA and RNA structures.(85) Furthermore, the dihedral terms are “hard wired” in the force fields and are not diminished by competing interactions with water, unlike Coulomb and vdW interactions. Therefore, even small errors can have profound consequences. The strong effects of small changes to torsional potentials have also been considered and addressed in parametrizations of the ϕ/ψ parameters of proteins, for example, in both the AMBER ff99SB(86) modifications of ff99 and the CMAP corrections to the CHARMM all22 force field.(87) It is also worth noting that the position of the energy minimum and the anti/high-anti criterion are not sufficient to fully characterize the anti minimum; the detailed shape and derivatives of the χ profile around the anti and high-anti regions are also probably very important for correctly describing nucleic acid structure, as also pointed out by Bosh et al.(41)

To conclude, the χ_OL parameters provide greater stabilization of the anti region than the ff99 force-field parameters. This is desirable as it helps to avoid the known tendency for ladder-like structures to form in RNA simulations. χ_YIL stabilizes the anti region even more than χ_OL-DFT and χ_OL. The χ_YIL parameters also stabilize the anti region, even more than χ_OL-DFT and χ_OL parameters, but probably excessively. Our tests (see also ref (46)) suggest that the χ_OL parameters perform best for RNA structures.

Syn Region

The local minimum in the syn region, around χ ≈ 70°, is mainly associated with guanosine residues in Z-DNA but also occurs in the stems of antiparallel DNA quadruplexes. It is also often populated in RNA structures, UNCG hairpin tetraloops, for example,(46) and various other recurrent RNA motifs. Figure 6 clearly shows that use of the available torsion parameters leads to quite significant differences in the syn region and that these differences are not always systematic among different nucleosides. Let us first consider the position of the syn minima. Our best references are the QM/COSMO curves shown in Figure S1 in the Supporting Information. Compared to the QM reference, ff99 shifts the minimum to low angles, around 50°, while the other force fields mostly tend to shift it to higher angles, around 70–75°, that are more consistent with the QM data. As we have shown in reference simulations of the UUCG RNA tetraloop,(46) the imbalanced ff99 syn region destabilizes the tetraloop structure while the reparameterized χ torsions are apparently able to maintain the stable structure of the tetraloop over at least the ∼100+ ns time scale, with the χ force-field modifications in combination with the parmbsc0 α/γ correction providing the best performance in this respect. In fact, the advantages of the parmbsc0 modifications over ff99 for RNA simulations can only be fully appreciated after tuning the χ profile.

Regarding the energy of the syn minimum relative to that of the anti minimum, the χ_YIL and χ_OL parametrizations provide similar results, both of which agree fairly well with our QM data. The χ_YIL parametrization has been tested against syn/anti populations of C and U ribonucleosides as detected in NMR experiments and shows notable improvement compared to ff99, which tends to overstabilize syn conformation for C and U.(45) Because χ_OL parametrization is similar to χ_YIL in this respect, we can expect the same improvement for χ_OL as well. Note that our preliminary χ_OL-DFT version also exhibits certain tendency to overstabilize syn, mainly because ribonucleosides were not included in the χ_OL-DFT fitting.

Torsion Barriers

Figure 6 shows that various χ parametrizations differ considerably in the resulting torsion barrier heights, most obviously ff99 gives a reversed order of torsion barrier heights, relative to those in the QM profile. Since our best estimates for the torsion barrier heights are the latter, we suggest that ff99 gives qualitatively incorrect descriptions of the torsion energetics. The other parametrizations appear to be more accurate, but the spread of the torsion barriers is still quite wide. Compared to the QM data, χ_YIL and χ_OL seem to provide the best agreement.

MD Simulations of A-RNA Duplexes

Several A-RNA MD simulations were carried out to compare the available χ parametrizations: ff99, ff99χ_YIL, ff99χ_OL-DFT, ff99χ_OL, and the corresponding χ combinations with bsc0. The χ_ODE parametrization was not included in this comparison as it accelerates formation of “ladder-like” structures and is thus not applicable to A-RNA.(46) The main conclusions are best illustrated by the bsc0-corrected simulations, since the bsc0 α/γ correction reduces the number of α/γ “γ-trans” flips and thus keeps the structures closer to X-ray reference structures.(37) We have also shown recently that the ff99bsc0 force field improves the behavior of RNA tetraloops relative to ff99.(46) Although the reduction of α/γ flipping in A-RNA simulations by bsc0 may be excessive, ff99 likely overpopulates the α/γ flips.(37) While the bsc0 modifications are currently essential for B-DNA simulations, their use is also starting to prevail over ff99 in RNA simulations.

We monitored mainly average values of the χ angle, sugar pucker (pseudorotation angle P according to Altona and Sundaralingam(88)), size of the major and minor grooves, and several base pair and interbase pair (base-pair step) parameters, considering them to be most relevant to A-RNA helix description. Only parameters that appeared to be sensitive to the χ angle are presented here, and the A-RNA results are summarized in Table 3 and Tables S2 and S3 in the Supporting Information. Standard deviations are shown to illustrate the distribution width.

Table 3. Average Structural Parameters (last 20 ns of 100 ns simulations) for the A-RNA Duplex 1QC0′ (r(GCACCGUUGG)) Obtained Using the ff99bsc0 Force Field with Various χ Corrections (values with ff99 force field in italics)^a.

parameter	X-ray	no χ correction	χYIL	χOL-DFT	χOL
χ/deg	197.1 ± 4.4	203.1 ± 9.2	196.0	197.4	199.1
		209.4 ± 12.7	194.0	196.3	196.7
P/deg	17.7 ± 6.0	19.3 ± 13.5	15.4	19.2	17.4
		27.5 ± 16.9	13.4	17.5	17.1
minor groove width/Å	15.4 ± 0.1	15.3 ± 0.6	15.2	15.3	15.3
		15.0 ± 0.6	14.9	15.1	14.8
major groove width /Å	14.7 ± 1.5	15.9 ± 2.9	19.0	17.5	17.9
		18.9 ± 3.2	22.1	19.8	22.3
slide/Å	–1.70 ± 0.25	–1.69 ± 0.50	–2.07	–1.94	–1.90
		-1.89 ± 0.57	-2.35	-2.11	-2.30
roll/deg	8.1 ± 4.1	9.7 ± 6.1	4.6	7.1	6.7
		8.5 ± 6.2	3.0	6.4	4.0
propeller/deg	–12.5 ± 4.5	–13.7 ± 8.5	–6.3	–10.7	–9.7
		-12.5 ± 8.7	-4.3	-9.8	-7.4
X-displ./Å	–4.45 ± 1.18	–4.85 ± 1.60	–5.01	–5.07	–4.95
		-5.35 ± 2.18	-5.50	-5.49	-5.91
inclination/deg	15.2 ± 8.3	18.0 ± 11.0	8.8	13.4	12.7
		16.3 ± 11.7	5.5	12.2	8.0
helical twist/deg	32.3 ± 3.6	31.7 ± 4.1	29.7	30.5	30.4
		31.1 ± 4.9	28.6	29.8	28.6
rmsd/Å		1.04	1.21	1.06	1.07
		1.36	1.85	1.43	1.90

^aStandard deviations are shown for the unmodified force fields for orientation, and they are very similar for the other force fields. RMSD is mass weighted for all atoms.

Sensitivity of the A-RNA Structure to χ Potential

Table 3 and Tables S2 and S3 in the Supporting Information show that several structural characteristics of the A-RNA duplexes have substantial sensitivity to the shape of the χ torsion profile. Among the most sensitive parameters for A-RNA are the inclination, roll, major groove width, and propeller twist. Inclination and roll are key descriptors of the A-RNA shape and mathematically interrelated.^89,90 The magnitude of the impact of varying the χ parametrization on the structural parameters is rather unsettling; in several cases even very small changes in the χ profile, on the order of a fraction of a kcal/mol, significantly influence the simulated structure, as already noted in ref (41).

Basic Sampling of the A-RNA Conformational Space

One of the most important parameters characterizing A-RNA structure is the inclination of base pairs with respect to the A-RNA helix. In A-RNA the base pair planes are significantly inclined (typically by more than 10°) with respect to the helical axis, while in B-DNA the base pair planes are almost perpendicular to the helical axis and the inclination is close to zero. As we recently noted, the experimental values of A-RNA inclination in X-ray structures vary quite widely and do not depend on the sequence.^37,91 The average inclination value for the 1QC0′ X-ray structure is 15.2°. The ff99 and ff99bsc0 simulations give fairly similar values (18.0° and 16.3°, respectively). The χ_YIL parametrization, which quite strongly stabilizes the anti region, reduces the inclination to as low as 5.5° in combination with ff99 (the combination suggested by Yildirim et al.(45)) and to 8.8° when ff99bsc0 is used. This is a considerable deviation from the experimental reference. The new χ_OL parametrization gives values of 8.0° with ff99 and 12.7° with ff99bsc0, which represents a noticeable but still acceptable reduction of inclination, the ff99bsc0χ_OL combination being superior in this respect. Since the χ_OL-DFT parametrization consistently gives values that are quite similar to those obtained using χ_OL, only the latter is discussed in the following text. As noted above, the base pair parameter roll is mathematically related to inclination; thus, the roll trend mirrors that of inclination; the experimental value is 8.1°, while ff99bsc0, ff99, ff99bsc0χ_OL, and ff99χ_YIL give values of 9.7°, 8.5°, 6.7°, and 4.6°, respectively.

Another A-RNA parameter that is quite sensitive to χ parametrization is the major groove width. Major groove width varies considerably in experimental X-ray structures (it ranges from 8 to 20 Å) and seems to depend not only on the sequence but also on the crystallization conditions, as discussed in detail in refs (37) and (91). Even larger variations have been observed in published NMR studies, but these are mainly due to inaccuracies in the NMR structural refinement protocols; recent work has shown that application of the highest quality NMR methods leads to very good agreement between X-ray and NMR geometries of both A-RNA(92) and B-DNA.(93) Despite the uncertainty in target values for the major groove width it seems that it is usually overestimated by simulations. There is a marked difference in this respect between the ff99 and the ff99bsc0 force fields, primarily due to a 10–20% population of short-lived γ-trans substates with ff99, which reduce inclination and widen the major groove of A-RNA.(37) For 1QC0′ the X-ray determined major groove width is 14.7 Å, while we obtained values of 15.9, 18.9, 17.9, and 22.1 Å in simulations using ff99bsc0, ff99, ff99bsc0χ_OL, and ff99χ_YIL, respectively. Clearly, the ff99χ_YIL value is not only significantly larger than in the starting X-ray structure but also outside the experimentally observed ranges, while the ff99bsc0χ_OL values are closer to the reference.

The general trends are also well illustrated by the results obtained for the AU-rich 1RNA structure (Table S3 in Supporting Information). For inclination, the experimental value is 18.8°, while ff99bsc0, ff99, ff99bsc0χ_OL, and ff99χ_YIL give values of 25.8°, 21.4°, 19.4°, and 10.3°, respectively. In this case, the ff99bsc0χ_OL value is closest to the experimental data. The ff99χ_YIL inclination is again likely too low. The inclination trend is mirrored by roll values: experimental value is 9.96°, while ff99bsc0, ff99, ff99bsc0χ_OL, and ff99χ_YIL values are 14.1°, 12.1°, 11.1°, and 5.7°, respectively. The experimental value for major groove width is 12.3 Å, while ff99bsc0, ff99, ff99bsc0χ_OL, and ff99χ_YIL give 15.3, 17.1, 14.8, and 18.1 Å, respectively.

The trends in the structural parameters described above indicate that when the χ parameters are modified in a manner that prevents the ladder-like degradation of RNA structure associated with the original (ff99 or ff99bsc0) χ profile, A-RNA inclination and base pair roll are systematically reduced while the major groove width expands. Note that inclination, roll, and narrowing of the major groove characterize how deeply the duplex enters A-RNA conformational territory. In other words, stabilization of the anti χ region seems to counter the tendency of the simulated molecule to adopt highly compact A-RNA geometries (see Tables 3 and Tables S2 and S3 in the Supporting Information). For the sake of completeness, let us add that the anti stabilization also reduces the absolute value of propeller twist; the experimental value for this variable of 1QC0′ is −12.5°, and we obtained values of −13.7°, −12.5°, −9.7°, and just −4.3° using ff99bsc0, ff99, ff99bsc0χ_OL, and ff99χ_YIL, respectively.

Another important structural parameter is helical twist. The data presented in Table 3 and Tables S2 and S3 in the Supporting Information show that the force fields provide values for this parameter that are reasonably close to the experimental value. However, ff99bsc0 simulations usually show larger helical twists than ff99-based simulations, as the ff99 γ-trans flips, especially those with longer lifetimes, tend to reduce helical twist.(30) Note that the helical twist in RNA molecules is not as crucial as when describing the fine structure of B-DNA.

In conclusion, when suppression of the ladder-like structures formation is of primary concern, we suggest that ff99bsc0χ_OL is the best combination of parameters currently available for A-RNA. Its use eliminates emergence of the ladder-like structures but still allows A-RNA to adopt significant inclination, roll, and propeller twist. (The preliminary ff99bsc0χ_OL-DFT version provides similar results for A-RNA but overstabilizes the syn region.)

MD Simulation of B-DNA

Table 4 compares structural parameters obtained from X-ray analysis of a B-DNA dodecamer (1BNA) and simulations using the four χ parametrizations considered above in the discussion of parametrization effects on A-RNA simulations (ff99bsc0, ff99, ff99bsc0χ_OL, and ff99χ_YIL) and the parameters of Ode et al.(44) Clearly, the three new χ variants are in many respects worse than the original ff99bsc0 force field for modeling B-DNA. They reduce helical twist, which is underestimated even with ff99bsc0. Underestimation of helical twist is a notorious problem in B-DNA simulations. Another problem appears in coupling of the χ torsion with the sugar pucker. The new χ parametrizations seem to “push” the sugar pucker pseudorotation value (136° in X-ray structures) more to the east: while with ff99bsc0 the average pucker is 130°, it drops to 116° with ff99bsc0 χ_OL and even to 106° with χ_YIL. As can be seen in Table 4, these changes are reflected by shifts in other structural parameters, mostly away from the X-ray and ff99bsc0 values. The groove sizes, slide, and X-displacement increase, while propeller and helical twist slightly decrease. Both χ_OL and χ_OL-DFT parametrizations seem to provide structures that are closer, overall, to the X-ray structure than the χ_YIL parametrization, which also shows the largest rms error. This again indicates that χ_YIL overestimates the high-anti penalty, which disturbs the balance with the other force-field parameters somewhat.

Table 4. Average Structural Parameters (last 20 ns of 50 ns simulations) for the B-DNA Duplex 1BNA^a.

parameter	X-ray	ff99bsc0	ff99bsc0 χYIL	ff99bsc0 χODE	ff99bsc0 χOL-DFT	ff99bsc0 χOL
χ/deg	243.6 ± 14.7	243.3 ± 18.2	223.1	244.4	229.1	231.4
P/deg	129.2 ± 26.7	130.4 ± 31.6	105.1	133.5	118.4	115.6
minor groove width /Å	10.3 ± 1.0	11.5 ± 1.1	12.6	11.4	11.7	12.3
major groove width /Å	17.3 ± 0.7	19.1 ± 1.9	21.5	18.7	20.5	20.2
slide/Å	0.07 ± 0.53	–0.41 ± 0.58	–1.20	–0.36	–0.90	–0.83
roll/deg	1.98 ± 3.41	3.64 ± 5.22	2.76	3.53	3.03	4.24
propeller/deg	–13.3 ± 5.94	–12.5 ± 7.9	–8.5	–11.5	–11.1	–11.0
X-displ./Å	–0.23 ± 0.53	–1.65 ± 1.73	–2.82	–1.44	–2.19	–2.33
inclination/deg	4.0 ± 7.2	7.8 ± 10.3	5.4	6.9	5.7	8.0
helical twist/deg	35.6 ± 5.2	33.5 ± 5.7	31.5	34.2	33.0	32.6
rmsd/Å		1.58	2.52	1.46	1.95	2.15

^aStandard deviations are only shown for the ff99bsc0 force fields because they are very similar for the other force fields. RMSD is mass weighted for all atoms.

In conclusion, χ_OL does not improve upon the original ff99bsc0 force field for the B-DNA duplex. The same holds also for χ_OL-DFT, which was parametrized based on DNA nucleosides. We would like to reiterate that the χ angle and sugar pucker are fine tuned to complement each other in ff99bsc0 and ff99, and suitable adjustment of the sugar pucker torsions may also be beneficial for B-DNA description with the new χ parameters presented herein. This, however, is beyond the scope of this study. Our groups have attempted several times in the past to improve modeling of the helical twist of B-DNA in various ways, including pucker modification, but no convincing solution has been found to date.

Conclusions

The χ torsion angle is a challenging parameter to accurately model in the various empirical force fields for nucleic acids. Many variants of χ parametrization have been suggested in recent few years, but none of them seems to provide a fully satisfactory description. Here, we investigated whether reliable force-field parameters can be obtained based on accurate QM calculations. We studied the influence of both the level of theory on the χ profile and the applied methodology (the effects of geometry relaxation and solvation). We suggest that when deriving the torsion parameters the following three points should be considered.

• (i)Using the same (usually QM-optimized) geometry for deriving the torsion parameters as differences between the QM and MM χ energies may introduce significant errors in the resulting profiles. Instead, geometry for the MM single-point calculations should be optimized at the MM level.
• (ii)Solvation-related effects considerably influence the resulting χ torsion profile. For instance, their inclusion results in stabilization of the anti region typical for A-RNA with respect to the high-anti region typical for B-DNA. It appears that appropriate balance of the anti and high-anti structures in RNA systems can only be obtained when the solvation effects are considered.
• (iii)The χ torsion profile is quite sensitive to the level of theory. On the basis of comparisons with estimated reference CCSD(T)/CBS data, we suggest that the MP2/CBS method provides results of sufficient accuracy in this case, while using small basis sets such as 6-31G* with the MP2 method introduces significant errors. The PBE DFT functional does not provide sufficiently accurate results, even when a large (6-311++G(3df,3pd)) basis set is used and a dispersion correction (D-1.06-23) is applied. Results obtained with M06 and M06-2X functionals of Zhao and Truhlar are of similar quality to the PBE-D-1.06-23/LP results and also insufficiently accurate for force-field derivation. Thus, it appears that despite the impressive recent progress in DFT methodology, DFT-based calculations cannot currently match the accuracy of high-quality wave function theory calculations for modeling DNA and RNA backbone segments.

Using our parametrization model we derived new parameters for the glycosidic torsion angle, χ_OL (“OL” stands for the city of Olomouc in the Czech Republic), intended for use in RNA simulations. Our main goal was to correct the undesirable destabilization of the anti region with respect to the high-anti region observed with the ff99 and ff99-parmbsc0 force fields, which leads to formation of “ladder-like” structures in MD simulations of RNA molecules. The χ_OL parameters successfully achieve this goal.^46,84

The ability of the χ_OL parameters to suppress formation of the ladder-like structures has been verified in refs (46) and (84). In these works we carried out a broad set of extended RNA simulations of UNCG and GNRA tetraloops, short A-RNA stems, and a reverse kink-turn motif with a total length of more than 15 μs. It has been shown that while use of the original ff99 and ff99bsc0 force fields leads to frequent formation of the ladder-like structures, the ff99bsc0χ_OL potential suppresses their emergence and keeps simulations closer to the native conformations.

In addition, in a study of UUCG tetraloop(46) we have shown that the χ_OL modification in connection with the ff99bsc0 force field leads to stabilization of some signature interactions present in the X-ray and NMR structures of this tetraloop. This improvement is most likely due to improved description of the syn region of χ potential, which is of key importance in this structure.

In this work we show that the χ_OL adjustment modestly affects helical parameters of A-RNA duplexes; nevertheless, the simulations remain in good agreement with X-ray structures. We also demonstrate that overstabilization of the anti χ region leads to excessive reductions of inclination, roll, and propeller twist in A-RNA and substantially impairs the performance of B-DNA simulations. This problem appears to occur with another recent parameter set, ff99χ_YIL.

We do not recommend use of the reparameterized force field for B-DNA, as adjusting the anti–high-anti balance to stabilize RNA somewhat impairs description of B-DNA. Despite substantial efforts, we have not as yet found any means, based solely on modifying the χ torsion, to stabilize A-RNA simulations while not adversely affecting B-DNA simulations. However, the χ_OL refinement might be useful in simulations of DNA molecules containing syn nucleotides.

Although the χ_OL torsion refinement can be combined with both ff99 and ff99bsc0 force-field variants, in all cases our simulations indicate that it provides better results when combined with ff99bsc0. Nevertheless, the parmbsc0 α/γ and χ_OL modifications are entirely independent refinements of the Cornell et al. force-field torsion space.

In summary, we recommend use of the χ_OL force field for RNA simulations, preferably in combination with the ff99bsc0 α/γ refinement. The main advantage of the new force field is that it eliminates formation of ladder-like structures, spurious artifacts generated by older versions of the force field. Since elimination of the ladder-like structures is a basic requirement for stabilizing RNA in simulations, the χ_OL parameters probably provide better RNA descriptions than other currently available parameter sets. The χ_OL + ff99bsc0 force field gives satisfactory descriptions of A-RNA duplexes and improves simulations of some other RNA systems, such as UNCG and GNRA tetraloops. We would like to note that although the χ_OL + ff99bsc0 force-field refinement brings a substantial improvement of extended RNA simulations, further reparameterizations still may be necessary.

Supporting Information Available

Torsion profiles of the studied ribo- and deoxyribonucleosides in vacuo and in COSMO and PB solvent models, χ_OL-DFT torsion parameters, and tables of structural parameters for 1RNA and 2R20′ structures. This material is available free of charge via the Internet at http://pubs.acs.org.

Funding Statement

National Institutes of Health, United States