Proton evolved local field solid-state nuclear magnetic resonance using Hadamard encoding: Theory and application to membrane proteins

Abstract

NMR anisotropic parameters such as dipolar couplings and chemical shifts are central to structure and orientation determination of aligned membrane proteins and liquid crystals. Among the separated local field experiments, the proton evolved local field (PELF) scheme is particularly suitable to measure dynamically averaged dipolar couplings and give information on local molecular motions. However, the PELF experiment requires the acquisition of several 2D datasets at different mixing times to optimize the sensitivity for the complete range of dipolar couplings of the resonances in the spectrum. Here, we propose a new PELF experiment that takes the advantage of the Hadamard encoding (HE) to obtain higher sensitivity for a broad range of dipolar couplings using a single 2D experiment. The HE scheme is obtained by selecting the spin operators with phase switching of hard pulses. This approach enables one to detect four spin operators, simultaneously, which can be processed into two 2D spectra covering a broader range of dipolar couplings. The advantages of the new approach are illustrated for a U-¹⁵N NAL single crystal and the U-¹⁵N labeled single-pass membrane protein sarcolipin reconstituted in oriented lipid bicelles. The HE-PELF scheme can be implemented in other multidimensional experiments to speed up the characterization of the structure and dynamics of oriented membrane proteins and liquid crystalline samples.

INTRODUCTION

Dipolar couplings (DCs) and anisotropic chemical shifts are of central importance in the structure determination of membrane proteins by oriented solid-state NMR spectroscopy.^{1, 2} These parameters are directly measured by using 2D separated local field (SLF) experiments³ that resolve the chemical shift (CS) of the S spin (¹⁵N or ¹³C) and DC between I (¹H) and S spins in two dimensions. The oscillatory nature of these anisotropic NMR parameters can give a semi-quantitative view on the secondary structure and relative orientation of the domains in membrane proteins.^{4, 5, 6, 7, 8, 9} More importantly, if the chemical shift anisotropy tensor of the S spin and the distance between the I and S spins are known, these observables are easily converted into orientation-dependent restraints for structure determination.¹⁰

SLF experiments have been widely used by chemists and biophysicists to characterize the structures of liquid crystals as well as membrane proteins in mechanically or magnetically aligned lipid bilayers.^{11, 12, 13, 14, 15, 16, 17, 18} Since the introduction of the SLF experiment, several variants have emerged, such as PISEMA,^{19, 20, 21} SAMPI4,²² HIMSELF,²³ and more recently the sensitivity-enhanced and constant time versions.^{24, 25, 26, 27} These experiments are also known as rotating frame SLF (R-SLF) experiments and take advantage of the heteronuclear DC evolution under Hartmann-Hahn matching of RF fields for I and S spins and homonuclear decoupling for the abundant I spins. The proton evolved local field (PELF) experiment, or as previously described proton detected local field (PDLF) experiment, is another outstanding example of SLF pulse schemes. The PELF experiment has several advantages over R-SLF experiments. First, the PELF is less demanding in terms of RF power for the low-γ nuclei, since it has only one refocusing π pulse on the S spin during the t₁ dipolar evolution period.^{28, 29} Second, the PELF experiment is sensitive to both short- and long-range DCs. Finally, the PELF experiment is not dependent on¹H offset, as for the R-SLF experiments.¹⁹

Recently, Ramamoorthy and co-workers reported an elegant application of the PELF pulse scheme to analyze the topology and dynamics of single-pass membrane proteins oriented in magnetically aligned lipid bicelles.¹⁸ Parallel studies demonstrated the utility of the PELF pulse sequence to detect ¹³C-¹H dipolar couplings of membrane proteins and lipid bilayers.³⁰ All of these studies concluded that while the R-SLF experiments provide better resolution for DC in rigid solids and motionally restricted domains of membrane proteins, the PELF experiments offer superior resolution and sensitivity for dynamic molecules and mobile regions of membrane proteins. Although, several groups have optimized the performance of the PELF experiment,^{31, 32} varying homonuclear decoupling schemes during t₁ and cross-polarization schemes during the mixing period, the main drawback of the experiment remains the strong dependence of the peak intensities on the DC values and mixing period used. As a result, the acquisition of multiple 2D experiments at different mixing times is needed to cover the entire range for all the DC values.^{18, 31, 32} This approach is very time consuming and cumbersome, especially for the analysis of membrane proteins oriented in lipid membranes. In fact, these samples are notoriously insensitive due to the low protein-to-lipid ratio, which is necessary to maintain the biological activity and homogeneous sample preparations.³³

In this paper, we present a Hadamard-encoded PELF experiment (or HE-PELF), which can achieve the optimum sensitivity for a wide range of DC values using a single 2D experiment. The advantages of the HE-PELF over the original PELF pulse sequence are demonstrated for a ¹⁵N labeled NAL single crystal and uniformly ¹⁵N labeled sarcolipin oriented in lipid bicelles.

THEORY

Separation of DC and CS in the conventional PELF experiment is achieved using the pulse sequence in Figure 1a. During t₁ evolution, the frequency switched Lee-Goldberg (FSLG) homonuclear decoupling scheme³⁴ is applied on protons to suppress homonuclear DCs, and two π pulses placed in the middle of t₁ evolution refocus the proton chemical shifts while retaining ¹⁵N-¹H heteronuclear DCs. The initial 90° pulse aligns the I-spin magnetization perpendicular to the direction of the effective field defined by the FSLG scheme, which is evolved under heteronuclear DC during t₁ evolution. A 35° pulse brings the magnetization into the X-Y plane. Subsequently, the I-spin magnetization is transferred to S spin via cross polarization using the windowless isotropic mixing (WIM) scheme.³⁵ The evolution of the I-S spin system under PELF sequence is given by

(1)

Figure 1.

Pulse sequences of (a) PELF and (b) HE-PELF (Hadamard-encoded PELF) experiments. In both pulse sequences, a two step phase cycle is applied for an initial 90° pulse and receiver phases. In HE-PELF, (ϕ₁, ϕ₂) is set to (y, y), (y, −y), (−y, y), and (−y, −y) in four interleaved acquisitions, where the number of scans for each (ϕ₁, ϕ₂) data set is one fourth of total number of scans used in PELF.

In Eq. 1, during acquisition time t₂ only the detectable S spin operators are retained. The effective Hamiltonians during t₁ and τ periods are given by

$$\begin{array}{ccc}\hfill H_{\mathrm{FSLG}}& =& s_{\mathrm{FSLG}}{\omega }_{\mathit{IS}}2I_z^{\prime }{S}_z,\hfill \\ \hfill H_{\mathrm{WIM}24}& =& s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}(I_x{S}_x+I_y{S}_y+I_z{S}_z),\hfill \\ \hfill I_x^{\prime }& =& e^{i{\theta }_m{I}_y}{I}_x{e}^{-i{\theta }_m{I}_y},I_y^{\prime }=I_y,I_z^{\prime }=e^{i{\theta }_m{I}_y}{I}_z{e}^{-i{\theta }_m{I}_y},\hfill \\ \hfill {\omega }_{\mathit{IS}}& =& 2\pi D_{\mathit{IS}},s_{\mathrm{FSLG}}=0.57,\mathrm{and}{s}_{\mathrm{WIM}24}=0.66,\hfill \end{array}$$ (2)

where s_FSLG and s_WIM24 are scaling factors of FSLG and WIM24 pulse sequences, respectively, and D_IS is the heteronuclear dipolar coupling. Note that the two-spin order term 2I_zS_z does not evolve under the H_WIM24 Hamiltonian. During t₂ acquisition and under heteronuclear decoupling, the two-spin order terms become undetectable. The resulting density matrix for the PELF experiment acquired with four scans for each t₁ increment is given by

$$\begin{array}{ccc}\hfill {\rho }_{\mathrm{PELF}}& =& 4{\mathrm{c}}_1{S}_y\cos \left(s_{\mathrm{FSLG}}{\omega }_{\mathit{IS}}{t}_1\right)e^{i{\omega }_s{t}_2},\hfill \\ \hfill {\rho }_{\mathrm{PELF}}\left({\omega }_1,{\omega }_2\right)& =& 4c_1\rho \left({\omega }_1,{\omega }_2\right),\hfill \\ \hfill {\mathrm{where}\mathrm{c}}_1& =& {\sin }^2(s_{\mathrm{wim}24}{\omega }_{\mathit{IS}}\tau ∕2).\hfill \end{array}$$ (3)

The HE-PELF experiment is obtained by phase switching of the hard pulses. The pulse sequence of HE-PELF is shown in Figure 1b. For each t₁ increment, four interleaved scans are acquired with phases (ϕ₁, ϕ₂) defined as (y, y), (y, −y), (−y, y) and (−y, −y), respectively. The resultant density matrix for phases (y, y) is derived as follows:

(4)

where 1.16s_FSLG is equal to s_WIM24. The derivation of the density matrices for the remaining pairs of phases (y, −y), (−y, y) and (−y, −y) is similar, and the final density matrices are

$$\begin{array}{ccc}\hfill {\rho }_2& =& \left[-S_x{\sin }^2(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau ∕2)+\frac{1}{2}\left(S_y\right){\sin }^2\left(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau \right)\right]\hfill \\ & & \times \cos \left(s_{\mathrm{FSLG}}{\omega }_{\mathit{IS}}{t}_1\right)e^{i{\omega }_s{t}_2}\hfill \\ & & +\left[-S_y{\sin }^3(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau ∕2)-\frac{1}{2}\left(S_x\right)\sin \left(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau \right)\right]\hfill \\ & & \times \sin \left(s_{\mathrm{FSLG}}{\omega }_{\mathit{IS}}{t}_1\right)e^{i{\omega }_s{t}_2},\hfill \end{array}$$ (5)

$$\begin{array}{ccc}\hfill {\rho }_3& =& \left[S_x{\sin }^2(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau ∕2)-\frac{1}{2}\left(S_y\right){\sin }^2\left(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau \right)\right]\hfill \\ & & \times \cos \left(s_{\mathrm{FSLG}}{\omega }_{\mathit{IS}}{t}_1\right)e^{i{\omega }_s{t}_2}\hfill \\ & & +\left[S_y{\sin }^3(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau ∕2)+\frac{1}{2}\left(S_x\right)\sin \left(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau \right)\right]\hfill \\ & & \times \sin \left(s_{\mathrm{FSLG}}{\omega }_{\mathit{IS}}{t}_1\right)e^{i{\omega }_s{t}_2},\hfill \end{array}$$ (6)

$$\begin{array}{ccc}\hfill {\rho }_4& =& \left[-S_x{\sin }^2(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau ∕2)-\frac{1}{2}\left(S_y\right){\sin }^2\left(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau \right)\right]\hfill \\ & & \times \cos \left(s_{\mathrm{FSLG}}{\omega }_{\mathit{IS}}{t}_1\right)e^{i{\omega }_s{t}_2}\hfill \\ & & +\left[S_y{\sin }^3(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau ∕2)-\frac{1}{2}\left(S_x\right)\sin \left(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau \right)\right]\hfill \\ & & \times \sin \left(s_{\mathrm{FSLG}}{\omega }_{\mathit{IS}}{t}_1\right)e^{i{\omega }_s{t}_2}.\hfill \end{array}$$ (7)

Each density matrix in Eqs. 4, 5, 6, 7 consists of four terms, whose signs correspond to the four rows of a four-dimensional Hadamard matrix (H):^{36, 37}

$$H=\left(\begin{array}{cccc}+& +& -& +\\ -& +& -& -\\ +& -& +& +\\ -& -& +& -\end{array}\right).$$ (8)

The phase modulation for the four terms in Eqs. 4, 5, 6, 7 is not the same in either direct or indirect dimensions. Hence, the Fourier transformation of the time domain data will give mixed line shapes in the frequency domain. However, since the four terms are Hadamard-encoded, it is possible to retrieve each of the terms by the Hadamard decoding of the time domain data. The decoding is obtained by transposing the H matrix. The resultant density matrices from the Hadamard decoding of the time domain data (ρ₁ to ρ₄) are given by

$$\begin{array}{ccc}\hfill {\rho }_{\mathrm{H}1-\mathrm{PELF}}& =& {\rho }_1-{\rho }_2+{\rho }_3-{\rho }_4\hfill \\ & =& 4{\mathrm{c}}_1{S}_x\cos \left(s_{\mathrm{FSLG}}{\omega }_{\mathit{IS}}{t}_1\right)e^{i{\omega }_s{t}_2},\hfill \end{array}$$ (9a)

$$\begin{array}{ccc}\hfill {\rho }_{\mathrm{H}2-\mathrm{PELF}}& =& {\rho }_1+{\rho }_2-{\rho }_3-{\rho }_4\hfill \\ & =& 4{\mathrm{c}}_2{S}_y\cos \left(s_{\mathrm{FSLG}}{\omega }_{\mathit{IS}}{t}_1\right)e^{i{\omega }_s{t}_2},\hfill \end{array}$$ (9b)

$$\begin{array}{ccc}\hfill {\rho }_{\mathrm{H}3-\mathrm{PELF}}& =& -{\rho }_1-{\rho }_2+{\rho }_3+{\rho }_4\hfill \\ & =& 4{\mathrm{c}}_3{S}_y\sin \left(s_{\mathrm{FSLG}}{\omega }_{\mathit{IS}}{t}_1\right)e^{i{\omega }_s{t}_2},\hfill \end{array}$$ (9c)

$$\begin{array}{ccc}\hfill {\rho }_{\mathrm{H}4-\mathrm{PELF}}& =& {\rho }_1-{\rho }_2+{\rho }_3-{\rho }_4\hfill \\ & =& 4{\mathrm{c}}_4{S}_x\sin \left(s_{\mathrm{FSLG}}{\omega }_{\mathit{IS}}{t}_1\right)e^{i{\omega }_s{t}_2},\hfill \end{array}$$ (9d)

where

$$\begin{array}{ccc}\hfill {\mathrm{c}}_1& =& {\sin }^2(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau ∕2),\hfill \\ \hfill {\mathrm{c}}_2& =& \frac{1}{2}{\sin }^2\left(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau \right),\hfill \\ \hfill {\mathrm{c}}_3& =& {\sin }^3(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau ∕2),\mathrm{and}\hfill \\ \hfill c_4& =& \frac{1}{2}\sin \left(s_{\mathrm{WIM}24}{\omega }_{\mathit{IS}}\tau \right).\hfill \end{array}$$ (9e)

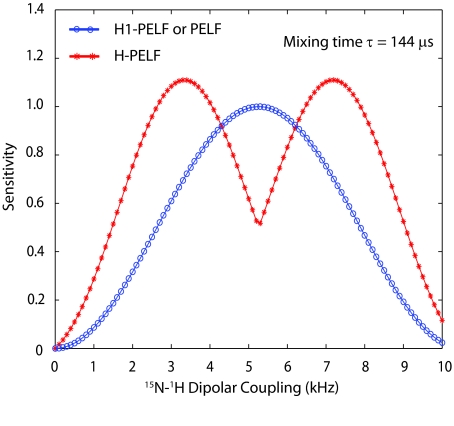
In order to obtain the absorptive line shapes, a relative 90° zeroth-order phase correction is applied in the direct dimension for ρ_{H2 − PELF} and ρ_{H3 − PELF} with respect to ρ_H1-PELF and ρ_H4-PELF. Similarly, in the indirect dimension, a relative 90° zeroth-order phase correction for ρ_H3-PELF and ρ_H4-PELF is applied with respect to ρ_H1-PELF and ρ_H2-PELF. The coefficients c₁ to c₄ determine the intensity of each resonance and depend on the value of the DC for a given mixing time. As an example, Figure 2 shows the theoretical values of the four coefficients for a 144 μs mixing time. ρ_H1-PELF and ρ_H2-PELF correspond to the cosine-modulated dipolar coherences, which give a positive dipolar doublet with the c₁ and c₂ coefficients having positive values for all DC values. In this case, the Fourier transformation gives positive peaks for all DC values. In contrast, ρ_H3-PELF and ρ_H4-PELF correspond to the sine-modulated dipolar coherences, which give an anti-phase dipolar doublet (positive and negative peaks) with the c₃ and c₄ coefficients having positive and negative values according to the DC values in Figure 2. If c₃ and c₄ are negative, the negative peak of the dipolar doublet for ρ_H3-PELF and ρ_H4-PELF becomes positive. Correspondingly, if c₃ and c₄ are positive, the positive peak of the dipolar doublet for ρ_H3-PELF and ρ_H4-PELF remains positive.

Figure 2.

Simulations of the relative sensitivities of Hadamard decoded data sets (H1-PELF, H2-PELF, H3-PELF, and H4-PELF) obtained by plotting the coefficients c1, c2, c3 and c4 of Eq. 9e for a mixing time of 144 μs. Note that the sine-modulated dipolar coherence coefficients c3 and c4 are odd functions, therefore can assume positive and negative values.

Therefore, for all DC values, each of the components in Eqs. 9a, 9b, 9c, 9d consists of at least one positive peak for each doublet, which is added up constructively (positive phase). In the resulting spectrum, the intensities of the dipolar doublet will be asymmetric, i.e., one peak of each dipolar doublet will have a higher intensity than the other. To avoid these discrepancies, it is convenient to process the spectra in magnitude mode after the second Fourier transformation. This process inverts the negative peaks of all of the components in Eqs. 9a, 9b, 9c, 9d, which are then added to obtain a final spectrum ρ_H-PELF(ω₁, ω₂). Using this procedure, both peaks of the dipolar doublet will have equal intensity. For ρ_H1-PELF and ρ_H2-PELF, the magnitude mode processing does not affect the sign of the peaks, which are already positive. For consistency, all of the spectra (ρ_H1-PELF to ρ_H4-PELF) after the second Fourier transformation are processed in magnitude mode. This also ensures that the baseline of each spectrum coincides, avoiding artifacts in summing the spectra.

$$\begin{array}{ccc}\hfill {\rho }_{\mathrm{H}-\mathrm{PELF}}({\omega }_1,{\omega }_2)& =& \left|{\rho }_{\mathrm{H}1-\mathrm{PELF}}({\omega }_1,{\omega }_2)\right|+\left|{\rho }_{\mathrm{H}2-\mathrm{PELF}}({\omega }_1,{\omega }_2)\right|\hfill \\ & & +\left|{\rho }_{\mathrm{H}3-\mathrm{PELF}}({\omega }_1,{\omega }_2)\right|+\left|{\rho }_{\mathrm{H}4-\mathrm{PELF}}({\omega }_1,{\omega }_2)\right|\hfill \\ & =& 4\left[\left|{\mathrm{c}}_1\right|+\left|{\mathrm{c}}_2\right|+\left|{\mathrm{c}}_3\right|+\left|{\mathrm{c}}_4\right|\right]\rho \left({\omega }_1,{\omega }_2\right).\hfill \end{array}$$ (10)

Adding two 2D spectra with a relative 90° zeroth-order phase correction in both dimensions is equivalent to summing two 2D spectra: a Fourier-transformed spectrum set and a Hilbert-transformed spectrum. This operation increases the rms noise of the resultant spectrum by $\sqrt{2}$.^{38, 39} Analogously, adding the four 2D spectra |ρ_H1-PELF(ω₁, ω₂)| to |ρ_H4-PELF(ω₁, ω₂)| after relative zeroth-order phase corrections will increase the rms noise of the resulting spectrum by $\sqrt{4}$.⁴⁰ Each of the four spectra |ρ_H1-PELF(ω₁, ω₂)| to |ρ_H4-PELF(ω₁, ω₂)| is obtained from Hadamard decoding of four single scan data sets (Eqs. 4, 5, 6, 7); hence the rms noise of each of these spectra is identical to four scans, i.e., ρ_PELF(ω₁, ω₂) spectrum in Eq. 3. The signal-to-noise ratio of H-PELF and PELF spectra can be written as follows:

$$\begin{array}{ccc}& & {\left(\frac{S}{N}\right)}_{\mathrm{H}-\mathrm{PELF}}\propto \frac{4\left[\left|{\mathrm{c}}_1\right|+\left|{\mathrm{c}}_2\right|+\left|{\mathrm{c}}_3\right|+\left|{\mathrm{c}}_4\right|\right]}{\sqrt{4}},\hfill \\ & & \mathrm{and}{\left(\frac{S}{N}\right)}_{\mathrm{PELF}}\propto {4\mathrm{c}}_1.\hfill \end{array}$$ (11)

In Eq. 11, relative rms noise of H-PELF is $\sqrt{4}$ times the PELF rms noise. HE-PELF requires a number of scans multiple of 4. The Hadamard decoded dataset ρ_H1-PELF (Eq. 9a) is identical to ρ_PELF (Eq. 3), i.e., they both have the same signal-to-noise ratio.

$${\left(\frac{S}{N}\right)}_{\mathrm{H}1-\mathrm{PELF}}={\left(\frac{S}{N}\right)}_{\mathrm{PELF}}.$$ (12)

Figure 3 shows the comparison of theoretical sensitivity of H-PELF and PELF (or H1-PELF) spectra. H-PELF gives higher sensitivity for a wide range of dipolar couplings (in the ranges of 0–4.2 and 6.2–10 kHz). On the other hand, PELF and H1-PELF give higher sensitivity in the range of 4.2–6.2 kHz. Although Figures 23 are obtained for τ = 144 μs, the relative shapes of the curves are similar for any mixing time. Thus, the HE-PELF pulse sequence alleviates the need of repeating the 2D PELF experiments at several mixing times for measuring all of the DC values.

Figure 3.

Comparison of the relative sensitivities of H-PELF and PELF (or H1-PELF) spectra obtained by plotting 2(|c₁| + |c₂| + |c₃| + |c₄|) and 4c₁, respectively (Eq. 11) for a mixing time of 144 μs. The sensitivity of the H1-PELF is identical to the conventional PELF (Eq. 12). The HE-PELF pulse sequence results in two 2D spectra (H1-PELF and H-PELF) covering the dipolar couplings in the ranges defined by the blue and red curves in a single 2D experiment.

EXPERIMENTAL

Sample preparation

U-¹⁵N SLN (31 residues) was expressed as a fusion protein with maltose binding protein in Escherichia coli, cleaved with tobacco etch virus and purified as reported previously.^{33, 41, 42} Approximately 1.3 mg of SLN was carefully dissolved in an NMR buffer containing 6.9 mg D6PC (1,2-caproyl-sn-glycero-3-phosphocholine), 20 mM HEPES, 30 mM CaCl₂ and 0.02% NaN₃ at pH 7.0. Bicelles were formed after adding the D6PC-solublized protein to 33.1 mg DMPC (1,2-ditetradecanoyl-sn-glycero-3-phosphocholine) suspended as vesicles in water. YbCl₃ was added to a final concentration of 5 mM to flip the bicelle orientation.

NMR spectroscopy

All NMR experiments were carried out on a 700 MHz VNMRS spectrometer equipped with a low-E bicelle probe built by the RF program at the National High Magnetic Field Laboratory (NHMFL) in Florida.⁴³ The spectra of sarcolipin in flipped bicelles were acquired at 38 °C, whereas a temperature of 28 °C was used for the NAL single crystal. Both the 90° and 180° pulse lengths on ¹H and ¹⁵N are 4 and 8 μs, respectively, which correspond to a field strength of 62.5 kHz RF (γB₁). PELF and HE-PELF use a two step phase cycle with the initial 90° pulse on ¹H with (x, −x) and receiver phase (x, −x). The cycle time of FSLG was 28 μs with ¹H RF field strength of 58.3 kHz that corresponds to an effective field of 71.4 kHz. In our experiments, FSLG is obtained by ramping the phase of ¹H RF field from 0 to 206.9 for +LG and 28.39 to 181.49 for −LG, with a total of 280 phase steps. The t₁ dwell time was 56 μs, which consists of two FSLG cycles, resulting in a dipolar spectral width of 313 28 Hz with a dipolar scaling factor of 0.57. During WIM24, 4 μs 90° pulses were applied on ¹H and ¹⁵N simultaneously with phases: −y, x, −y, −y, x, −y, y, x, y, y, x, y, −y, −x, −y, −y, −x, −y, y, −x, y, y, −x. The cycle time of the WIM24 was 96 μs. Note that for certain mixing times it is possible to use the combination of WIM24 and WIM12 pulse schemes. For example, a mixing time of 144 μs is obtained by a WIM24 followed by a WIM12, whereas 192 μs can be obtained by two WIM24 cycles. During t₂ acquisition, a SPINAL heteronuclear decoupling⁴⁴ was applied on ¹H with 50 kHz RF field strength. PELF and HE-PELF experiments on sarcolipin were acquired with 15 t₁ increments (4400 scans per t₁ increment), with an acquisition time of 4 ms and a recycle delay of 4s. For the NAL single crystal, PELF and HE-PELF were acquired with 64 t₁ increments (8 scans per t₁ increment), with an acquisition time of 7 ms and a recycle delay of 4 s. The HE-PELF was recorded as four interleaved data sets with four sets of (ϕ₁, ϕ₂) values, where each interleaved data set is recorded with one fourth of the total number of scans. HE-PELF time domain data was Hadamard decoded to obtain H1-PELF, H2-PELF, H3-PELF, and H4-PELF (see Eqs. 9a, 9b, 9c, 9d), which were Fourier transformed with the appropriate zeroth-order phase corrections (see Sec. 2) followed by the magnitude processing to obtain positive intensities for all peaks. The resulting H-PELF spectrum was obtained by adding the four frequency domain spectra of H1-PELF, H2-PELF, H3-PELF, and H4-PELF. The PELF experiment was processed in real mode in the t₁ dimension and magnitude mode was applied after the second Fourier transformation. All spectra were processed with cosine shifted sine bell window function in both dimensions and base line correction is applied in the direct dimension using NMR pipe.⁴⁵

RESULTS AND DISCUSSION

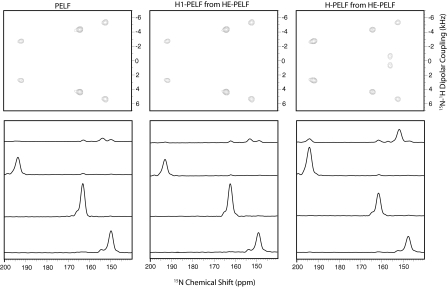
Top panel of Figure 4 shows the ¹⁵N-NAL single crystal spectra of PELF, H1-PELF, and H-PELF, where H1-PELF and H-PELF spectra were obtained from HE-PELF data using Hadamard decoding procedures as explained in Secs. 2, 3. For this experiment, we used a mixing time of 144 μs. All the spectra are drawn at the same noise level so that the intensity of a peak is a measure of sensitivity. Bottom panel of Figure 4 shows the dipolar cross sections of respective 2D spectra in the top panel. The relative sensitivity of PELF, H1-PELF, and H-PELF obtained from normalized peak heights from the 2D spectra in Figure4 are reported in Table 1. As expected, the sensitivity of H1-PELF is within ±5 % of the conventional PELF experiment. The intensities of the peaks resonating at 164.5 and 153 ppm in the PELF and H1-PELF are higher than H-PELF. In contrast, the other two resonances are substantially more intense in the H-PELF spectrum. Table 1 also shows the comparison of the peak intensity of the 2D spectra obtained with mixing times (τ) of 240 μs and 336 μs. While most of the values observed are close to the theoretical values, slight deviations are present and may reflect relaxation phenomena occurring during the 1.16τ period and/or deviation of FSLG and WIM24 scaling factors resulting in an incomplete ¹H-¹H decoupling. Since the S-spin operator of H1-PELF is along the Z direction during a 1.16τ period, we do not expect any signal loss of the H1-PELF component in the HE-PELF experiment.

Figure 4.

(Top panel) PELF, H1-PELF, and H-PELF spectra acquired at τ = 144 μs of ¹⁵N-NAL single crystal at an arbitrary orientation with respect to external magnetic field. H1-PELF and H-PELF spectra are obtained by processing the HE-PELF data as described in the text. (Bottom panel) (top to bottom) dipolar cross sections at 0.7, 2.8, 4.3, and 5.4 kHz, respectively. Dipolar spectral widths were corrected with an FSLG scaling factor of 0.57. All the spectra are drawn at the same noise floor, so that the peak intensity is a direct measure of sensitivity. For the peaks at 164.5 and 156.1 ppm, PELF and H1-PELF are slightly more sensitive than H-PELF; whereas for the peaks at 192.2 and 156.1 ppm, the sensitivity in H-PELF spectra is, respectively, 1.82 and 3.82 times that of the PELF spectra (Table 1).

Table 1.

Relative sensitivities of H1-PELF and H-PELF with respect to the conventional PELF for ¹⁵N-NAL resonances shown in Figure 4 at mixing times 144 μs, 240 μs, and 336 μs. The theoretical sensitivity of H1-PELF is identical to PELF. Bold numbers indicate higher sensitivity of H-PELF with respect to PELF and H1-PELF.

	τ = 144 μs				τ = 240 μs				τ = 336 μs
				H-PELF				H-PELF				H-PELF
15N-Chemical shift (ppm)	PELF	H1-PELF	H-PELF	(theoretical)	PELF	H1-PELF	H-PELF	(theoretical)	PELF	H1-PELF	H-PELF	(theoretical)
192.2	1	0.98	1.85	1.95	1	0.99	0.80	0.88	1	0.97	0.95	1.00
164.5	1	1.00	0.95	0.99	1	0.98	1.50	1.56	0.0	0.0	5.00	5.02
156.1	1	1.05	3.82	4.01	1	1.08	2.82	3.00	1	1.05	2.20	2.63
153.0	1	0.97	0.70	0.56	1	0.96	2.30	2.70	1	0.99	1.90	2.33

The superior performance of the HE-PELF over the conventional PELF experiment is demonstrated for a U-¹⁵N single-pass membrane protein sarcolipin^{42, 46, 47} reconstituted in magnetically aligned DMPC∕D6PC bicelles. Top panel of Figure 5 shows the PELF, H1-PELF, and H-PELF spectra plotted at the same noise level. Bottom panel of Figure 5 shows the dipolar cross sections of respective 2D spectra reported in the top panel. H1-PELF and H-PELF spectra were obtained by Hadamard decoding of the HE-PELF time domain data, and processed accordingly as described in Sec. 2. As predicted from the theoretical behavior (Figure 3), the DC cross section at 5.2 kHz is more intense for PELF and H1-PELF compared to H-PELF, whereas the DC cross section at 1.5 kHz is more intense in the H-PELF spectrum. Remarkably, the intensity of all the other peaks follows the theoretical trend reported in Figure 3. Both PELF and H1-PELF spectra give more sensitivity than H-PELF for DC values ranging from 4.2 to 6.2 kHz, which is very narrow compared to the DC obtained for sarcolipin (1 to 8 kHz). In fact, the peaks at the dipolar cross sections for 3.5 and 7.5 kHz located within the polarity index slant angle wheel (PISA)^{4, 7} are more intense for H-PELF compared to both PELF and H1-PELF. The integrated intensity of peaks between 140 to 220 ppm and 1 to 10 kHz is 1.10 times (10%) higher for PELF and H1-PELF than for H-PELF. Whereas the integrated intensity of H-PELF between 60 to 120 ppm and 0 to 5 kHz is 2.2 times (120%) higher than that for the PELF and H1-PELF spectra. As expected from the theoretical trend in Figure 3, H1-PELF spectrum is similar to PELF spectrum, and H-PELF is more intense in the DC region of 0 to 3.5 kHz and 7 to 8 kHz. These data clearly demonstrate advantages of HE-PELF pulse sequence over PELF in achieving optimal sensitivity for broad range of DC values.

Figure 5.

(Top panel) PELF, H1-PELF, and H-PELF spectra of U-¹⁵N sarcolipin in DMPC/D6PC bicelles with bilayer normal parallel to B_o magnetic field. H1-PELF and H-PELF spectra are obtained by processing the HE-PELF data as described in the text. (Bottom panel) (top to bottom) dipolar cross sections at 1.0, 2.1, 3.2, 5.9, and 8.2 kHz, respectively. Dipolar spectral widths were corrected with an FSLG scaling factor of 0.57. The integrated intensities of the peaks between 140 to 220 ppm and 1 to 10 kHz is 1.10 times (10%) higher for PELF and H1-PELF compared to H-PELF; whereas the intensities between the 60 to 120 ppm and 0 to 5 kHz of H-PELF is 2.20 times (120%) that of the PELF spectrum. Total acquisition time for both the PELF and HE-PELF data was 74 h using 4400 scans for each t₁ increment.

Although we used a 144 μs mixing time, the relative shapes of the curves in Figure 3 are similar for all the mixing times. Of course, at very long mixing times, H-PELF sensitivity will decrease due to the relaxation during 1.16τ period. However, it is not necessary to use very long mixing times in HE-PELF since τ = 144 μs already gives reasonable sensitivity for a wide range of dipolar couplings. Note that for conventional PELF and its analogous sequences one must use multiple 2D experiments at different mixing times to optimize the sensitivity when applied to membrane proteins. On the contrary, the new HE-PELF pulse sequence does not require multiple 2D experiments, since one experiment is sufficient to optimize the detection of a wide range of DC values using a single mixing time.

CONCLUSIONS

In summary, we demonstrate the performance of the new HE-PELF experiment for measuring DCs in strongly aligned molecular systems. To achieve this in the HE-PELF experiment, the signs of the spin operators are Hadamard-encoded in such a way that the time domain data can be decoded to get individual 2D spectra for each of the operators. The data obtained with the HE-PELF pulse scheme can be processed to get two 2D spectra: H1-PELF similar to a conventional PELF spectrum and H-PELF, which has higher sensitivity for broad range of DC values. Therefore, the HE-PELF experiment avoids repeating the PELF experiment at several mixing times for the optimal detection of dynamically averaged dipolar couplings, an important detail for flexible or weakly aligned molecular systems. We demonstrated the performance of the PELF for a uniformly ¹⁵N labeled membrane protein. We anticipate that the combination of the sensitivity enhanced methods with the HE-PELF will speed up the acquisition of multidimensional data for aligned membrane proteins.