Diffusion-influenced ligand binding to buried sites in macromolecules and transmembrane channels

Abstract

We consider diffusion-influenced binding to a buried binding site that is connected to the surface by a narrow tunnel. Under the single assumption of an equilibrium distribution of ligands over the tunnel cross section, we reduce the calculation of the time-dependent rate coefficient to the solution of a one-dimensional diffusion equation with appropriate boundary conditions. We obtain a simple analytical expression for the steady-state rate that depends on the potential of mean force in the tunnel and the diffusion-controlled rate of binding to the tunnel entrance. Potential applications of our theory include substrate binding to a buried active site of an enzyme and permeant ion binding to an internal site in a transmembrane channel.

INTRODUCTION

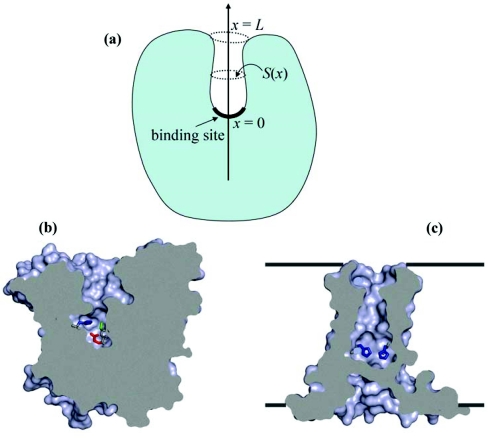
Substrate binding sites in enzymes are often buried.¹ In many cases they are accessible from the surface of the macromolecule by a narrow tunnel as shown schematically in Fig. 1a. In order to reach the active site, a ligand must diffuse into and then through the crevice leading to the site. A classic example is acetylcholinesterase (see Fig. 1b).² Transmembrane channels also can have binding sites that are produced either by a deep minimum in the potential of mean force³ or by a pore-lining residue that can covalently bind a permeant ion or molecule. For example, a histidine or glutamate residue within the pore can bind a proton.^{4, 5, 6} When binding is due to a pore-lining residue, then there is a chance that the permeant species can pass through without binding. However, when the channel is sufficiently narrow, the binding site cannot be bypassed and the enzyme and channel problems are essentially the same. The His37 tetrad in the influenza M2 proton channel (see Fig. 1c) appears to be such an obligatory binding site for a permeant proton.^{6, 7, 8}

Figure 1.

(a) Schematic representation of a biding site buried in a tunnel of length L and varying cross-section S(x). (b) The tunnel leading to the active site of acetylcholinesterase. The active-site residues are shown as stick. (c) The M2 proton channel with an internal binding site, consisting of a histidine tetrad. Only two of the four histidines are shown, as stick. In this structure the channel is blocked so proton can access the internal site from just one side of the membrane. Channel activation allows proton release to and binding from the other side of the membrane.

Studies of binding to a buried site were initiated by Samson and Deutch,⁹ who obtained an approximate steady state rate for binding to a site located at the bottom of a conical tunnel within a spherical macromolecule. Zhou¹⁰ considered a more general problem where the binding site is located in a crevice connected to the bulk by a narrow tunnel. A rigorous solution of this problem requires that both the ligand-site pair distribution function and the corresponding flux be continuous across the tunnel entrance. To make this problem tractable, Zhou assumed that the flux over the entrance is constant and that the pair distribution is continuous only when averaged over the entrance surface. This is analogous to the constant flux approximation¹¹ (which is equivalent¹² to the Wilemski-Fixman approximation) for the diffusion-controlled ligand binding. In solving this problem, rather than requiring the pair distribution function to vanish on the binding surface, one assumes that it vanishes only on the average and that the flux is the same everywhere on the surface of the site. Assuming a constant flux over the tunnel entrance, the steady-state rate to a buried site can be expressed in terms of (1) the constant-flux diffusion-controlled rate of binding to the entrance and (2) the rate of binding to the site for an auxiliary problem where the pair distribution function on the entrance is kept at its equilibrium value for all times. He then obtained a simple analytic expression for the steady-state rate in the special case of an active site located at the end of a cylindrical tunnel.⁶

In this paper, we do not invoke the constant flux approximation and obtain a general expression for the steady-state rate constant for all geometries where the dynamics in the interior region can be described, to a good approximation, as one-dimensional diffusion (e.g., the site is at the end of a narrow tunnel). Under the single assumption of fast equilibration over the tunnel cross section, the calculation of the time-dependent rate coefficient is reduced to a solution of a one-dimensional diffusion equation with a novel boundary condition that involves the exact diffusion-controlled rate coefficient for binding to the tunnel entrance. We then use this formalism to obtain explicit results for a case of practical interest: a cylindrical tunnel in the presence of a linear potential of mean force. Finally, we derive a simple general expression for the steady-state rate constant that involves the exact diffusion-controlled rate of binding to the tunnel entrance and the potential of mean force in the tunnel. After applying this formula to several special cases, we conclude by discussing future applications and extensions.

THEORY

Consider the irreversible binding of a ligand to a site buried at the end of a tunnel as shown in Fig. 1a. Suppose that at t = 0 an empty binding site is surrounded by an equilibrium distribution of non-interacting ligands with bulk concentration c. Then according to Smoluchowski, the probability that the binding site remains empty at time t satisfies

$$dB\left(t\right)∕dt=-k\left(t\right)cB\left(t\right),$$ (2.1)

where k(t) is the time-dependent rate coefficient. It can be calculated from the ligand-site pair distribution function, g(r, t), according to

$$\begin{array}{ccc}\hfill k\left(t\right)& =& D\underset{S\left(0\right)}{\int \int }{e}^{-\beta U\left(\mathrm{r}\right)}\frac{\partial }{\partial x}\left[e^{\beta U\left(\mathbf{r}\right)}g(\mathbf{r},t)\right]dS\hfill \\ & =& {\kappa }_0\underset{S\left(0\right)}{\int \int }\mathrm{g}(\mathrm{r},\mathit{t})\mathit{dS},\hfill \end{array}$$ (2.2)

where β = (k_BT)⁻¹, r = (x, y, z) is the displacement vector between the ligand and the binding site, U(r) is the potential of mean force [U(r) → 0 as r ≡ |r| → ∞], D is the diffusion constant of the ligands, κ₀ is the intrinsic binding rate to the surface of the binding site, S(x) denotes the tunnel cross section at a fixed value of x. The distribution function g(r, t) satisfies the Smoluchowski equation,

$$\frac{\partial g}{\partial t}=\nabla ·D{e}^{-\beta U\left(\mathbf{r}\right)}\nabla \left[e^{\beta U\left(\mathbf{r}\right)}g\right],$$ (2.3)

subject to the equilibrium initial condition

$$g(\mathbf{r},0)=e^{-\beta U\left(\mathbf{r}\right)}$$ (2.4)

and the boundary condition

$$\begin{array}{c}\hfill D{e}^{-\beta U\left(\mathbf{r}\right)}\frac{\partial }{\partial x}\left[e^{\beta U\left(\mathbf{r}\right)}g(\mathbf{r},t)\right]={\kappa }_{0}g(\mathbf{r},t),\mathbf{r}\in S\left(0\right).\end{array}$$ (2.5)

In addition, we require that g(r, t) approaches 1 as r → ∞ and satisfies the reflecting boundary condition on all inert surfaces.

These equations completely specify the mathematical problem but have not been solved exactly when the binding site is buried. Here we consider a class of such problems when the binding site occurs at the end of a narrow tunnel (0 ⩽ x ⩽ L, see Fig. 1a). We assume that the dynamics of ligands is sufficiently fast so that local equilibrium on the tunnel cross section is maintained. This amounts to assuming that within the tunnel the three-dimensional pair distribution function g(r, t) is related to the one-dimensional (and hence the subscript “1”) distribution function g₁(x,t)≡∫∫_S(x)g(r,t)dS by

$$g(\mathbf{r},t)=\frac{e^{-\beta U\left(\mathbf{r}\right)}{g}_1(x,t)}{\underset{S\left(x\right)}{\int \int }{e}^{-\beta U\left(\mathbf{r}\right)}\mathit{dS}}=\frac{e^{-\beta U\left(\mathbf{r}\right)}{g}_1(x,t)}{\sigma \left(x\right)e^{-\beta V\left(x\right)}}$$ (2.6)

at all times. Here we have defined the one-dimensional potential of mean force V(x) via σ(x)e^−βV(x)=∫∫_S(x)e^−βU(r)dS, where σ(x) is the area of the tunnel cross section at a fixed value of x, σ(x)=∫∫_S(x)dS. With this single approximation we now show that the problem of calculating k(t) can be rigorously reduced to the solution of a one-dimensional equation with a novel boundary condition that involves the time-dependent rate coefficient k_E(t) that describes diffusion-controlled binding by the tunnel entrance.

To obtain the partial differential equation satisfied by g₁(x, t), we substitute g(r, t) in Eq. 2.6 into Eq. 2.3 and integrate both sides over the surface S(x). In this way we find that

$$\frac{\partial g_1}{\partial t}=\frac{\partial }{\partial x}D\sigma \left(x\right)e^{-\beta V\left(x\right)}\frac{\partial }{\partial x}\frac{g_1}{\sigma \left(x\right)e^{-\beta V\left(x\right)}}.$$ (2.7)

The initial and boundary conditions as well as the expression for k(t) can be found the same way, namely, by substituting g(r, t) in Eq. 2.6 into Eqs. 2.4, 2.5, 2.2, respectively, with subsequent integration over the cross section. This leads to

$$g_1(x,0)=\sigma \left(x\right)e^{-\beta V\left(x\right)},$$ (2.8)

$$k\left(t\right)=D\sigma \left(0\right)e^{-\beta V\left(0\right)}{\left.\frac{\partial }{\partial x}\frac{g_1(x,t)}{\sigma \left(x\right)e^{-\beta V\left(x\right)}}\right|}_{x=0}={\kappa }_0{g}_1(0,t).$$ (2.9)

To make the problem of finding g₁(x, t) well posed, we need a boundary condition at x = L. We derive this boundary condition by matching the flux at the boundary separating the tunnel from the bulk. The flux into the tunnel depends on the derivative of g(r, t), which satisfies the three-dimensional diffusion equation, Eq. 2.3, subject to the initial condition given by Eq. 2.4. On the tunnel entrance it satisfies (see Eq. 2.6)

$$g(\mathbf{r},t)=\frac{e^{-\beta U\left(\mathbf{r}\right)}{g}_1(L,t)}{\sigma \left(L\right)e^{-\beta V\left(L\right)}},\mathbf{r}\in S\left(L\right),$$ (2.10)

and on the rest of the surface it satisfies the reflecting boundary condition. We now show that the solution to this problem can be found in terms of the pair distribution function h(r, t) for an auxiliary problem, namely, that of diffusion-controlled binding to the tunnel entrance. In this way, we will express the required boundary condition in terms of the diffusion-controlled rate k_E(t) of binding to the tunnel entrance. A similar idea has been used in a study of the particle number fluctuations in a cylindrical channel.¹³ The distribution function h(r, t), defined in the bulk, satisfies the same differential equation and initial condition as g(r, t), Eqs. 2.3, 2.4. The crucial difference is that h(r, t) satisfies the absorbing boundary condition on the tunnel entrance

$$h(\mathbf{r},t)=0,\mathbf{r}\in S\left(L\right),$$ (2.11)

while g(r, t) satisfies the boundary condition in Eq. 2.10.

Since g(r, t) and h(r, t) obey the same partial differential equation, it is natural to try to find a relation between them. It turns out to be convenient to work in the Laplace space. [We denote the Laplace transform of a function f(t) as $\widehat{f}\left(s\right)$; $\widehat{f}\left(s\right)={\int }_0^{\infty }{e}^{-st}f\left(t\right)dt$.] Since when r ∈ S(L), h(r, t) = 0 while g(r, t) is given by Eq. 2.10, we try the ansatz

$$\widehat{g}(\mathbf{r},s)=A\left(s\right)\widehat{h}(\mathbf{r},s)+\frac{e^{-\beta U\left(\mathbf{r}\right)}{\widehat{g}}_1(L,s)}{\sigma \left(L\right)e^{-\beta V\left(L\right)}}.$$ (2.12)

Since g(r, t), h(r, t), and e^−βU(r), all approach unity as r → ∞, it follows that

$$A\left(s\right)=1-\frac{s{\widehat{g}}_1(L,s)}{\sigma \left(L\right)e^{-\beta V\left(L\right)}}.$$ (2.13)

The flux continuity condition at the tunnel entrance is

$$\begin{array}{ccc}& & D\sigma \left(L\right)e^{-\beta V\left(L\right)}{\left.\frac{\partial }{\partial x}\frac{g_1(x,t)}{\sigma \left(x\right)e^{-\beta V\left(x\right)}}\right|}_{x=L}\hfill \\ & & =\underset{S\left(L\right)}{\int \int }D{e}^{-\beta U\left(\mathrm{r}\right)}\frac{\partial }{\partial x}\left[e^{\beta U\left(\mathbf{r}\right)}g(\mathbf{r},t)\right]\mathit{dS}.\hfill \end{array}$$ (2.14)

Substituting g(r, t) in Eq. 2.12 with A(s) in Eq. 2.13 into the Laplace transform of Eq. 2.14, we find

$$\begin{array}{ccc}& & D\sigma \left(L\right)e^{-\beta V\left(L\right)}{\left.\frac{\partial }{\partial x}\frac{{\widehat{g}}_1(x,s)}{\sigma \left(x\right)e^{-\beta V\left(x\right)}}\right|}_{x=L}=\left(1-\frac{s{\widehat{g}}_1(L,s)}{\sigma \left(L\right)e^{-\beta V\left(L\right)}}\right)\hfill \\ & & \times \underset{S\left(L\right)}{\int \int }D{e}^{-\beta U\left(\mathrm{r}\right)}\frac{\partial }{\partial x}\left[e^{\beta U\left(\mathbf{r}\right)}\widehat{h}(\mathbf{r},s)\right]\mathit{dS}.\hfill \end{array}$$ (2.15)

We note that the integral over S(L) on the right-hand side of Eq. 2.15 is simply the Laplace transform of the rate coefficient that describes diffusion-controlled binding to the tunnel entrance from the outside, ${\widehat{k}}_{\mathrm{E}}\left(s\right)$. Thus we have

$$\begin{array}{ccc}& & D\sigma \left(L\right)e^{-\beta V\left(L\right)}{\left.\frac{\partial }{\partial x}\frac{{\widehat{g}}_1(x,s)}{\sigma \left(x\right)e^{-\beta V\left(x\right)}}\right|}_{x=L}\hfill \\ & & =\left(1-\frac{s{\widehat{g}}_1(L,s)}{\sigma \left(L\right)e^{-\beta V\left(L\right)}}\right){\widehat{k}}_{\mathrm{E}}\left(s\right),\hfill \end{array}$$ (2.16)

which is the desired boundary condition at x = L that makes the one-dimensional problem in the tunnel well posed. In the time domain our boundary condition,

$$\begin{array}{ccc}& & D\sigma \left(L\right)e^{-\beta V\left(L\right)}{\left.\frac{\partial }{\partial x}\frac{g_1(x,t)}{\sigma \left(x\right)e^{-\beta V\left(x\right)}}\right|}_{x=L}\hfill \\ & & =-{\int }_0^t{k}_{\mathrm{E}}(t-t^{\prime })\frac{\partial }{\partial t^{\prime }}\frac{g_1(L,t^{\prime })}{\sigma \left(L\right)e^{-\beta V\left(L\right)}}d{t}^{\prime },\hfill \end{array}$$ (2.17)

has an interesting non-Markovian structure.

TIME-DEPENDENT RATE COEFFICIENT FOR A CYLINDRICAL TUNNEL IN THE PRESENCE OF A CONSTANT FORCE

As an illustration of the above formalism we consider a cylindrical tunnel of radius a and length L in the presence of a linear potential, βV(x) = βV₀(x − L)/L, 0 ⩽ x ⩽ L. In this case σ(x) = σ = πa² is independent of x. Again it is convenient to work in Laplace space. The Laplace transforms of the rate coefficient, Eq. 2.9, and the Smoluchowski equation, Eq. 2.7, respectively, are

$$\widehat{k}\left(s\right)={\kappa }_0{\widehat{g}}_1(0,s)$$ (3.1)

and

$$\begin{array}{ccc}& & s{\widehat{g}}_1(x,s)-\sigma e^{-\beta V_0(x-L)∕L}\hfill \\ & & =D\frac{d^2{\widehat{g}}_1(x,s)}{d{x}^2}+\frac{D\beta V_0}{L}\frac{d{\widehat{g}}_1(x,s)}{dx}.\hfill \end{array}$$ (3.2)

The general solution to this equation is

$${\widehat{g}}_1(x,s)=\frac{\sigma }{s}{e}^{-\beta V_0(x-L)∕L}+e^{-\beta V_{0}x∕2L}\left(B_1{e}^{-\lambda x∕L}+B_2{e}^{\lambda x∕L}\right),$$ (3.3)

where

$$\lambda =\sqrt{{\left(\beta V_0∕2\right)}^2+s{L}^2∕D}.$$ (3.4)

The unknown coefficients, B₁ and B₂, are determined by inserting Eq. 3.3 into Eqs. 2.9 (in Laplace space) and 2.16. The Laplace transform of the rate coefficient is then determined from Eq. 3.1. In this way we find that

$$\begin{array}{c}\hfill \frac{1}{s\widehat{k}\left(s\right)}=\frac{1}{k_0}+\frac{e^{-\beta V_0}\left[\lambda \coth \lambda +\beta V_0∕2+s{\widehat{k}}_{\mathrm{E}}\left(s\right)L∕\left(D\sigma \right)\right]}{s{\widehat{k}}_{\mathrm{E}}\left(s\right)\lambda \coth \lambda +s\sigma L-\beta V_{0}s{\widehat{k}}_{\mathrm{E}}\left(s\right)∕2},\end{array}$$ (3.5)

where k₀=κ₀σe^βV₀. If the potential is zero outside the tunnel, and the inert surface around the tunnel entrance is flat, then¹⁴

$${\displaystyle \frac{s{\widehat{k}}_{\mathrm{E}}\left(s\right)}{4Da}=1+\frac{\pi }{4}\sqrt{{\displaystyle \frac{s{a}^2}{D}}}+\frac{\left({\displaystyle \frac{\pi }{4}-1}\right)\sqrt{{\displaystyle \frac{s{a}^2}{D}}}}{{\displaystyle \frac{\pi (4-\pi )}{({\pi }^2-8)}+\sqrt{{\displaystyle \frac{s{a}^2}{D}}}}}}$$ (3.6)

is an excellent approximation.

STEADY-STATE RATE CONSTANT

The time-dependent rate coefficient can be obtained analytically only for special cases of σ(x) and V(x). We will now show that the steady-state rate constant can be found in general as

$$\frac{1}{k_{\mathrm{ss}}}=\frac{1}{k_{\mathrm{E}}^{\mathrm{ss}}}+\frac{1}{k_0}+{\int }_0^L\frac{e^{\beta V\left(x\right)}dx}{D\sigma \left(x\right)},$$ (4.1)

where k₀ = κ₀σ(0)e^−βV(0) is the “chemical” rate constant and $k_{\mathrm{E}}^{\mathrm{ss}}$ is the steady-state rate constant for ligands outside the tunnel to be absorbed by the entrance of the tunnel. If the entrance surface area and perimeter are σ and P, respectively, and the reflecting surface around the entrance is effectively infinite and flat, then to an excellent approximation $k_{\mathrm{E}}^{\mathrm{ss}}$ is given by¹⁵

$$k_{\mathrm{E}}^{\mathrm{ss}}=D{\left(32\sigma P∕{\pi }^2\right)}^{1∕3}.$$ (4.2)

For a planar disk of radius a this reduces to the exact result $k_{\mathrm{E}}^{\mathrm{ss}}=4Da$.¹⁶

To derive Eq. 4.1 we take the t → ∞ limit of Eq. 2.9 and find k_ss to be given by

$$k_{\mathrm{ss}}={\kappa }_0{g}_1^{\mathrm{ss}}\left(0\right)=D\sigma \left(0\right)e^{-\beta V\left(0\right)}{\left.\frac{d}{dx}\frac{g_1^{\mathrm{ss}}\left(x\right)}{\sigma \left(x\right)e^{-\beta V\left(x\right)}}\right|}_{x=0},$$ (4.3)

where $g_1^{\mathrm{ss}}\left(x\right)$ is the steady-state limit of g₁(x, t): $g_1(x,t)\to g_1^{\mathrm{ss}}\left(x\right)$ as t → ∞. The corresponding limit in Laplace space is $s{\widehat{g}}_1(x,s)\to g_1^{\mathrm{ss}}\left(x\right)$ as s → 0. From Eq. 2.7 it follows that $g_1^{\mathrm{ss}}\left(x\right)$ satisfies

$$\frac{d}{dx}\sigma \left(x\right)e^{-\beta V\left(x\right)}\frac{d}{dx}\frac{g_1^{\mathrm{ss}}\left(x\right)}{\sigma \left(x\right)e^{-\beta V\left(x\right)}}=0.$$ (4.4)

Multiplying both sides of Eq. 2.15 by s and taking the s → 0 limit, we find that the boundary condition at x = L takes the form

$$\begin{array}{ccc}& & D\sigma \left(L\right)e^{-\beta V\left(L\right)}{\left.\frac{d}{dx}\frac{g_1^{\mathrm{ss}}\left(x\right)}{\sigma \left(x\right)e^{-\beta V\left(x\right)}}\right|}_{x=L}\hfill \\ & & =\left(1-\frac{g_1^{\mathrm{ss}}\left(L\right)}{\sigma \left(L\right)e^{-\beta V\left(L\right)}}\right)k_{\mathrm{E}}^{\mathrm{ss}}.\hfill \end{array}$$ (4.5)

Integrating Eq. 4.4 from zero to x twice and using Eq. 4.3, the boundary condition at x = 0, we find that

$$\frac{g_1^{\mathrm{ss}}\left(x\right)}{\sigma \left(x\right)e^{-\beta V\left(x\right)}}=k_{\mathrm{ss}}\left(\frac{1}{k_0}+{\int }_0^x\frac{e^{\beta V\left(y\right)}dy}{D\sigma \left(y\right)}\right).$$ (4.6)

Using this result in Eq. 4.5 and solving the resulting linear equation, we obtain the formula for k_ss given by Eq. 4.1. It is interesting to note that this equation could have been derived using the formalism of Zhou,¹⁰ albeit with the constant flux approximation for $k_{\mathrm{E}}^{\mathrm{ss}}$.

We will now use Eq. 4.1 to derive a variety of the results that have been previously obtained in different ways.^{6, 10, 17} We begin with a cylindrical tunnel of radius a in the presence of a linear potential, βV(x) = βV₀(x − L)/L. For such a tunnel σ(x) = σ = πa², and k₀=κ₀σe^−βV₀. In addition, we assume that there is no potential outside the tunnel, so that $k_{\mathrm{E}}^{\mathrm{ss}}=4Da$. In this case Eq. 4.1 leads to

$$\frac{1}{k_{\mathrm{ss}}}=\frac{1}{4Da}+\frac{1}{k_0}+\frac{L\left(1-e^{-\beta V_0}\right)}{\pi a^{2}D\beta V_0}$$ (4.7)

that agrees with the s → 0 limit of Eq. 3.5.

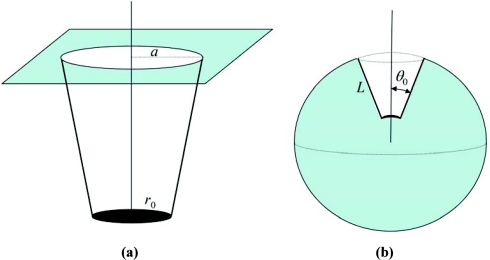
Next we consider a conical tunnel schematically shown in Fig. 2a, which is embedded in an essentially infinite inert plane, in the absence of potential both inside and outside the tunnel, i.e, U(r) = 0 everywhere. The x dependence of the cross-section area of such a tunnel is given by σ(x) = π[r₀ + (a − r₀)x/L]², where r₀ and a are the smallest and largest radii of the tunnel (Fig. 2a). The rate constants $k_{\mathrm{E}}^{\mathrm{ss}}$ and k₀, respectively, are $k_{\mathrm{E}}^{\mathrm{ss}}=4Da$ and $k_0={\kappa }_0\sigma \left(0\right)=\pi r_0^2{\kappa }_0$, and Eq. 4.1 leads to

$$\frac{1}{k_{\mathrm{ss}}}=\frac{1}{4Da}+\frac{1}{k_0}+\frac{L}{\pi a{r}_{0}D}.$$ (4.8)

Figure 2.

(a) Schematic representation of a binding site located in a conical tunnel of length L with the smallest and the largest tunnel radii equal to r₀ and a, respectively. (b) Schematic representation of a binding site located at depth L in a sphere of radius R; tunnel sides are specified by the polar angle θ₀.

When r₀ = a, the tunnel becomes cylindrical with a uniform radius a, and Eq. 4.8 reduces to Eq. 4.7 with V₀ = 0, as to be expected.

Finally we consider the model originally studied by Samson and Deutch,⁹ in which the entrance to the tunnel and the reactive site are spherical “caps” (not planar surfaces as above). In this model, a spherical protein of radius R contains a perfectly absorbing (κ₀ = ∞) curved binding site located at distance L from the surface as shown in Fig. 2b. The tunnel cross section is a spherical cap with radius R − L + x, 0 ⩽ x ⩽ L; hence σ(x) = 2π(1 − cos θ₀)(R − L + x)². Using this in Eq. 4.1 we find

$$\frac{1}{k_{\mathrm{ss}}}=\frac{1}{k_{\mathrm{E}}^{\mathrm{ss}}}+\frac{L}{2\pi (1-\cos {\theta }_0)R(R-L)D},$$ (4.9)

where $k_{\mathrm{E}}^{\mathrm{ss}}$ is the diffusion-controlled steady-state binding rate to a spherical “cap” of radius R and semi-angle θ₀. This is identical to the result of Samson and Deutch⁹ when $k_{\mathrm{E}}^{\mathrm{ss}}$ is approximated by their analytical expression. When angle θ₀ is small Eq. 4.9 becomes identical to Eq. 4.8 with k₀ = ∞ since a ≈ Rθ₀ and r₀ ≈ (R − L)θ₀.

CONCLUDING REMARKS

We have considered the diffusion-influenced ligand binding to a buried site that is connected to the surface by a narrow tunnel. Assuming fast equilibration over the tunnel cross section, the ligand motion can be modeled as one-dimensional diffusion under the influence of the potential of mean force. Based on this assumption alone we were able to analytically express the steady-state rate of the ligand binding to a binding site in terms of the potential of mean force and the diffusion-controlled rate of the ligand binding to the tunnel entrance. Using our formalism, we obtained an analytical expression for the Laplace transform of the time-dependent rate coefficient for a simple model where the tunnel is cylindrical and the potential of mean force is linear. Although we have focused here on irreversible binding, the time-dependent rate coefficient plays a central role in theories of reversible binding.¹⁸ Thus our work opens the way to modeling reversible diffusion-influenced binding to buried active sites.

The work presented here can be extended in several directions. The influence of rotational diffusion of the macromolecule^{19, 20} and/or ligand binding to the surface of the macromolecule^{21, 22, 23} can be handled by simply using the appropriate diffusion-controlled rates to the tunnel entrance, as long as these complications do not influence the dynamics in the tunnel. When the tunnel cross section is variable and/or the tunnel is winding, an improved description of the binding can be obtained by using a position-dependent diffusion coefficient [i.e, D(x)]^{24, 25, 26, 27} to describe ligand dynamics in the tunnel. Our result for the steady-state rate can be generalized to this case by simply replacing D by D(x) in Eq. 4.1. In addition, as a result of protein dynamics, the shape of the tunnel can fluctuate. For example, the entrance to the tunnel can switch between open and closed conformations.¹⁰ The influence of such stochastic gating on the rate coefficient can be determined from a straightforward extension of our formalism.