Hemodynamic Signals Not Predicted? Not so: A comment on

Abstract

In their 2009 Nature article: “Anticipatory haemodynamic signals in sensory cortex not predicted by local neuronal activity,” Yevginiy Sirotin and Aniruddha Das suggest that hemodynamic signals, the basis of functional MRI (fMRI), can arise without any measurable neuronal activity. They report that hemodynamic signals in visual cortex were associated with and time-locked to the anticipation of a visual stimulus, and importantly, without any associated neuronal activity as measured with direct electrophysiological recordings. In this commentary, we demonstrate, using an assessment of their own data, that their claims are not strongly supported. In fact, we found that specific LFP frequency ranges predicted with a high degree of accuracy, the “dark” or “anticipatory” hemodynamic response. For other frequency ranges, we found differences in phase but not magnitude of the measured and predicted hemodynamic response. Importantly, when comparing simply the magnitude as well as the time series standard deviation of the electrophysiological recordings with those of the measured hemodynamic responses, we found a direct correspondence of the dark/stimulated magnitude and standard deviation between the electrophysiological recordings and the hemodynamic responses. All of these analyses strongly imply that anticipatory hemodynamic responses are, in fact, accurately predicted in phase and magnitude by several LFP frequency bands, and are predicted in standard deviation and magnitude by the standard deviation and magnitude of even a wider range of LFP frequencies. We argue that rather than casting doubt on fMRI signal changes, these studies open up an interesting window into exploring more subtle neurovascular relationships.

Yevginiy Sirotin and Aniruddha Das published an article (Sirotin and Das 2009) suggesting that hemodynamic signals, the basis of functional MRI (fMRI), can arise without any measurable neuronal activity. They report that hemodynamic signals in visual cortex were associated with and time-locked to the anticipation of a visual stimulus, and importantly, without any associated neuronal activity as measured with direct electrophysiological recordings. While the related commentary of Kleinschmidt and Muller focuses on reasons the technique of Sirotin and Das might successfully record hemodynamic activity while missing neuronal activity, we decided to focus on the authors’ presented data to determine whether the claim of observing a hemodynamic response in the absence of neuronal activity is justified. A secondary point that we would like to make is that questioning the entire basis of interpretation of the fMRI signal with every reported inconsistency or with every hypothesized or simulated alternative explanation for various BOLD dynamics does not advance the field. The current models of neurovascular coupling are imperfect. Inconsistencies are expected and regularly observed. Merely mentioning an inconsistency has limited scientific value. Reports that emphasize and examine possible variations on what is known about the fMRI signal and the hemodynamic response are interesting windows into understanding more subtle and complex relationships between neuronal activity, hemodynamics, and measured signal. In fact, while we argue that the key conclusions of Sirotin and Das are mostly unsupported by the analyses presented within the paper, we secondarily note some extremely interesting observations in their data that contradict their conclusions, but could open new areas of research.

Sirotin and Das write: “Haemodynamic signals… are assumed to reflect metabolic demand generated by local neuronal activity, with equal increases in haemodynamic signal implying equal increases in the underlying neuronal activity.” They claim to identify a hemodynamic component that “that entrains to task structure independently of visual input or of standard neural predictors of hemodynamics.” It is always difficult to support a claim of independence. It requires examining multiple aspects of data using multiple methods that all show no relationships between the signals. They provide very little data supporting this statement. The only presented evidence to support this statement is shown in Figure 2a and supplementary Figure 3 of their article (Sirotin and Das 2009). During stimulation, there is strong spiking as well as clear local field potential activity and hemodynamic response. In the dark condition, when the two alert behaving monkeys were anticipating a stimulus, it is reported that they observed no spiking, weak LFP activity, but a fairly large hemodynamic response. The authors claim this shows vascular responses in the absence of standard neural predictors. We show here that this is simply not supported by the presented data.

As also noted in the related commentary by Kleinschmidt and Muller, a qualitative look at the LFP images in Figure 2a shows that there is, in fact, clearly some LFP response during rest. For example, one can easily see a band of reduced activity across all frequencies during the anticipatory period. Supplementary Figure 3b claims to show that the fit of the LFP to the hemodynamics is poor in the dark condition, but the authors only compare the average of 66–130Hz LFP to hemodynamics. There are no references explaining why they averaged over this range of frequencies and they presented no data over other frequency ranges. In addition, it is not clear what exactly the authors are trying to demonstrate with their fitting kernel method for matching hemodynamics to the data. Different kernel shapes might show a noisy or poorly characterized system, but this is weak evidence that the hemodynamic and LFP are independent. To show independence, one would need to demonstrate a lack of relationship between the time series and not just variation in the convolution kernels used to test that relationship. A poor fit for a kernel could be an artifact of the fitting algorithm or the boundary conditions of the fit. If the best fit is outside of the boundary conditions, the fitted kernel might merely be showing the location of a noisy local minimum. In addition, the logic behind the authors’ approach to kernel fitting is that we are expecting a strictly linear relationship between LFP and hemodynamic responses. If this linearity were violated, the implications would be interesting and perhaps open up new research questions, but certainly should not be used as support to the claim that the hemodynamics are independent of neuronal activity.

Except for the kernel variations shown in Supplementary Figure 3c-e, the authors present no data across their population supporting the key observation of independence between hemodynamics and LFP activity. In fact, except for the kernel variations, the authors present only a few trials of data from a single recording in a single animal to support their conclusions. Again, the argument of non-dependence from a lack of good fit to a sparse amount of data appears to be intrinsically weak.

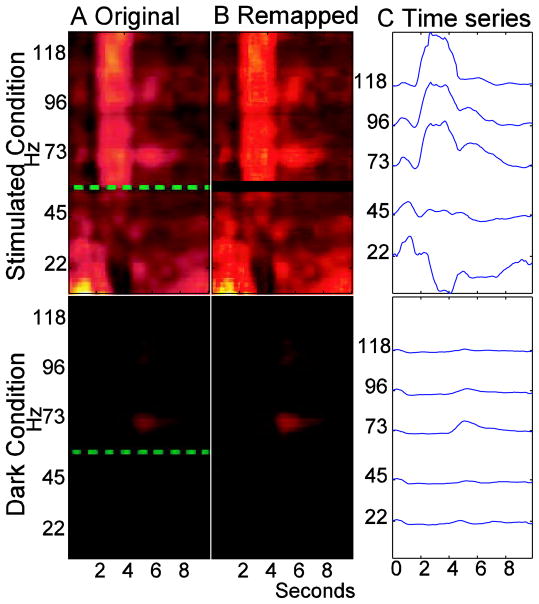
In a further step, we decided use the authors’ data to reconstruct the times series from the single trial presented in Sirotin and Das’ Figure 2a to quantitatively test if the authors’ own data support their claim that equal increases in neural and hemodynamic responses don’t occur during the dark condition. For the hemodynamic data, we extracted the green curves between the vertical dashed black lines (as shown in Sirotin and Das’ Figure 2a). We assumed the y-axis markings for this figure ranged from 0–2.5%. Although not clearly stated, we assumed the presented trial has a 10s duration. Other durations would affect the x-axis on our plots and the precise hemodynamic fitting parameters, but not our conclusions. The times series for the LFP data were generated from the single trial marked by the beginning of the green box until the beginning of the next green box in their Figure 2a. The image contained three red/green/blue values defining the color in each pixel. We converted each pixel to a single magnitude with a range from −50 to 400 using the “hot” color map in Matlab (www.mathworks.com). Due to jpeg image compression we needed to make assumptions to convert the triplets of values to single magnitudes that could be used to calculate time series. This conversion didn’t affect the overall appearance of the image. In this manuscript, Figure 1A shows the original images of the single trial and 1B shows our images.

Figure 1.

(A) The LFP data from the stimulated and dark conditions in Sirotin and Das 2009 (B) The same data after remapping the red/green/blue pixel values onto single values. (C) Time series generated from the data in B using approximately 23Hz frequency bands centered on the listed frequencies.

For the LFP data, frequencies were assumed to range from 10Hz to 130Hz with 0.3046 steps. The section from 57–61Hz was excluded because of the dashed green line on the image. For calculations across bands of frequencies, we averaged the time series within specified bands and then performed calculations on that data. Figure 1C shows the LFP time series averaged over multiple bands of approximately 23Hz in width that are centered on the listed frequencies. While the selection of 23Hz bands are arbitrary, they help show some variation of the time series at different frequencies.

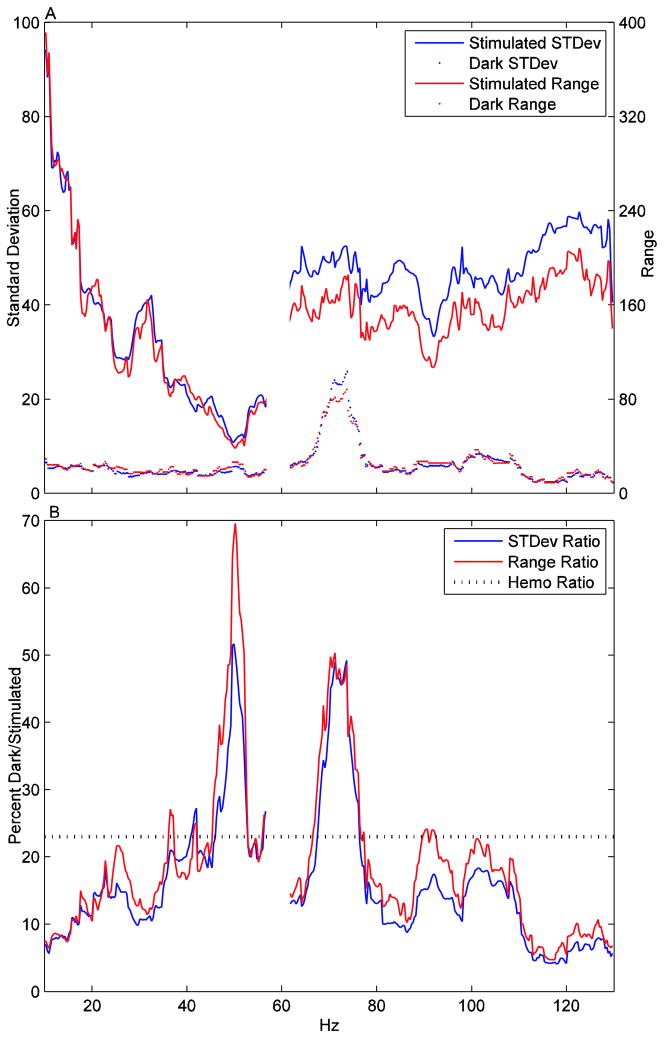
Since the key finding in question is whether the LFP during the dark condition contains measured activity relevant to the hemodynamics, we decided to initially ignore shape fitting and focus on the most basic measure that would show a relationship: Is the ratio of the magnitude of the hemodynamic signal changes during the stimulated relative to dark conditions similar to the ratio of the magnitude of LFP signal changes during the same conditions? If we had more data to work with, it would be possible to use causality metrics to see if the LFP trace could predict the hemodynamics over a longer period of time. To limit method selection bias, we chose two metrics of magnitude: (1) The standard deviation of the time series across the trial and (2) The signal range from the maximum to the minimum values in the time series. Figure 2A shows these standard deviation and range values for the stimulated and dark conditions at every frequency. The 57–61Hz band is excluded since no data were available. The hemodynamic stimulated and dark values have standard deviations of 1.02 and 0.24 respectively and ranges of 2.93 and 0.68 respectively. Figure 2B shows the dark/stimulated ratio (percentages are 100*(dark/stimulated)) of the standard deviations and ranges for the LFP signals. In comparison, the hemodynamic dark/stimulated ratio of standard deviation and ranges are 23.0% and 23.2% respectively – meaning that the hemodynamic signal power during the dark condition, was about 23% of the hemodynamic signal power during the stimulation time series. This is well within the ranges of this ratio as measured across LFP frequency. Figure 2B clearly shows that these LFP percentages for the range of 35–75Hz are about the same or considerably greater than those for the hemodynamic dark/stimulated ratio, The ratio rarely drops below 10% from 20–110Hz. While in some of the less than 60Hz frequencies, the large ratios are due to decreased magnitudes in the stimulated condition, they are due to increased magnitudes in the dark condition in the 60–80Hz range. Niessing et al observed that LFP frequencies in the 50–90Hz band have a relationship to hemodynamics (Niessing et. al. 2005). For this range, the dark/stimulated percentage is 20.6% for standard deviation and 23.2% for range.

Figure 2.

(A) The magnitudes measured by standard deviation and range for the stimulated and dark conditions across all frequencies. (B) 100*(dark magnitude)/(stimulated magnitude) across all frequencies. The dotted line shows the magnitude from the hemodynamic response. The hemodynamic standard deviation and range values are so visually close that only a single line is used. This shows that dark/stimulated response in the supposedly inactive LFP data is larger or roughly equal to the hemodyanmic response.

It is impossible to look at this data and conclude that the magnitudes of hemodynamic changes vary independently from the measured electrical activity. It is important to stress that we are only analyzing a single trial of data from the author’s manuscript, but, that trial is the only complete trial of data presented in the manuscript and it shows almost the opposite of what the authors claim, a clear magnitude relationship between LFP and hemodynamics in the absence of spiking. Sirotin and Das might have additional data to support their conclusions, but that data is not presented in their manuscript.

In order to better understand the authors’ kernel fitting results, we performed a second analysis, which involved convolving a hemodynamic response function derived from the stimulation condition data with the LFP time series from the dark condition. This approach showed interesting variations in the relationship between the LFP and hemodynamic responses across the two conditions.

Specifically, we convolved the LFP time series with a kernel (the sum of two Gamma functions) to fit the authors’ hemodynamic data. This approach is similar to that shown in their Supplementary Figure 3. We focused on fitting the stimulated LFP’s to the stimulated hemodynamic signal and subsequently convolved that same fitted kernel and the same amplitude with the LFP data from the dark condition. Since temporal delays of a hemodyanamic response might make it last longer than a single trial, it is impossible to fit the hemodynamic kernel to a single trial of data. Therefore, we took the single trial of LFP data and replicated it over time to create a series of identical trials. This data was convolved with the kernel. It took several trials until the transient effects of a hemodynamic delay ended and the convolved time series reached a steady state. We compared the single-trial hemodynamic data to a portion of the convolved LFP time series that was in a steady state. We calculated a separate optimal kernel using the stimulated data for every tested LFP frequency band. The fitting was performed using a discrete sampling of the entire search space within boundary conditions for time-to-peak, peak width, and post-stimulus undershoot magnitude.

We had some trouble defining an optimal kernel for this data. Sometimes, the fit between the LFP and hemodynamic data during the stimulated condition kept improving for later or wider peaks with no clear local minima. For the presented fits, we set a maximum time-to-peak of 9s. While the reasons for this issue are not clear, it helped highlight to us that the authors’ chose an exceedingly rapid hemodynamic kernel template. It peaked at 1.7s while the fitted kernels peak around 2.5s. The template and most of the fitted kernels also returned to baseline in less than 10s. From our experience, the kernel chosen by the authors is short for hemodynamic responses.

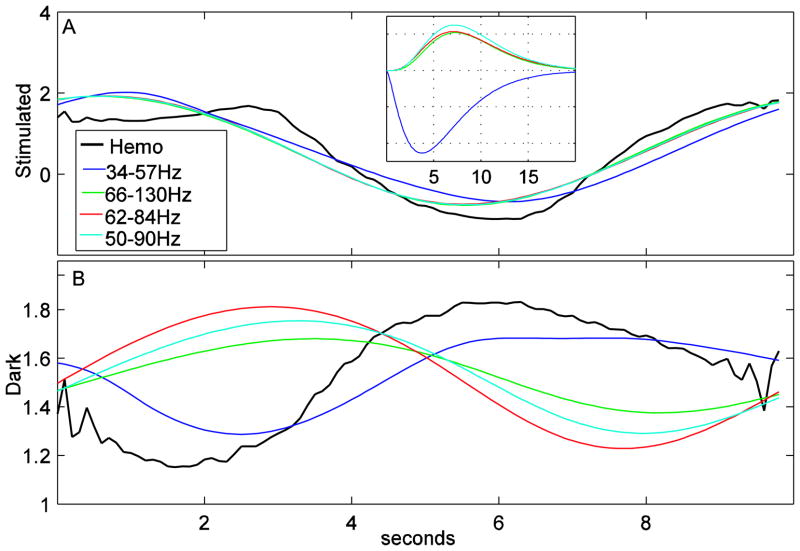
Figure 3A shows these the fits of different LFP frequency bands fits during the stimulated condition to the hemodynamic response during the stimulated condition. We present 50–90Hz because that is the band suggested by Niessing et al and 66–130Hz because that is the band presented by Sirotin and Das. The 34–57Hz and 62–84Hz are arbitrary, but roughly corresponded to frequency bands in figure 2B that had similar or larger percentages than the hemodynamic response. The inset in Figure 3A shows the shape of the hemodynamic kernels for each band. Figure 3B is created by taking same kernels scaled to the same magnitudes, and convolving them with LFP data from the dark condition. The mean is set to equal the mean of the dark hemodynamic response in the same figure. As expected, for the frequency bands with similar ratios in figure 2B (34–57HZ, 62–84Hz and, to a lesser extent, 50–90Hz), the magnitudes of the LFP responses in Figure 3B are similar to the hemodynamic responses. Interestingly, the greater than 60Hz LFP responses seem to have a large temporal phase shift from the hemodynamic response. A similar phase difference is also visible by comparing the blue (the fit based on the simulated condition) and green (the hemodynamic response) lines in the dark trials plot in Sirotin and Das’ Supplementary Figure 3 using their 66–130Hz frequency band. Thus, this observation might be more than an outlier from the single trial we analyzed. We feel that it would be an over-interpretation to say a phase difference means no relationship between LFP and hemodynamics during the dark condition, but, if replicable, the causes of this phase change when there is LFP activity, but no spiking could be a very interesting area for future research.

Figure 3.

The hemodynamic % signal changes (black) from Figure 2A in Sirotin and Das 2009 overlaid with the LFP data for different frequency bands convolved with a kernel. (A) The stimulated condition. The kernels are fitted for each of these frequency bands. These kernels are shown as an inset in this figure. (B) The dark condition. The kernel shapes and magnitudes from the stimulated condition were convolved with the LFP data from the dark condition to make the LFP plots.

It is also clear from our analyses that the dark hemodynamic response is closely predicted in phase and magnitude from convolution of the hemodynamic kernel with the 34 to 57 Hz neuronal signal. As shown in Figure 1C, these bands have a similar shape in the stimulated and dark conditions. The inset in figure 3A shows that the fitted kernel to this band looks very different from the higher frequency bands. It is possible that the fit to this band is being dominated by the small blip at the beginning of the trial that appears across all frequencies. Still, even if the nature of this fit is different from other frequencies, it leaves the question why it exists in the dark trials when Sirotin and Das state there is no LFP response. If replicable, this observation may also shed further light on more subtle details of neuronal-hemodynamic coupling during activation and rest.

In conclusion, Sirotin and Das claim that the LFP and hemodynamic responses are independent during the dark condition. The evidence in their manuscript that they try to use to support this claim is lacking, and the data they include in the manuscript actually shows a clear relationship between LFP and hemodynamic responses even without spiking. If the authors have data that support their claim, they were not presented in this manuscript. Due to the potential importance of this data, we would be very happy to analyze the full pre-processed data set if the authors are willing to share it with us and we think it would benefit the community if Sirotin and Das made their data available to others. Still, the authors present a novel task design that was able to generate LFP activity in the absence and presence of spiking in awake, behaving animals. There seem to be interesting variations in the temporal profile of the hemodynamic response depending on the presence of spiking. If replicable, this task design could be extremely useful for future study into the complex relationship between spiking, LFP, and hemodynamic responses.