Abstract
Purpose: The authors developed an iterative image-reconstruction algorithm for application to low-intensity computed tomography projection data, which is based on constrained, total-variation (TV) minimization. The algorithm design focuses on recovering structure on length scales comparable to a detector bin width.
Methods: Recovering the resolution on the scale of a detector bin requires that pixel size be much smaller than the bin width. The resulting image array contains many more pixels than data, and this undersampling is overcome with a combination of Fourier upsampling of each projection and the use of constrained, TV minimization, as suggested by compressive sensing. The presented pseudocode for solving constrained, TV minimization is designed to yield an accurate solution to this optimization problem within 100 iterations.
Results: The proposed image-reconstruction algorithm is applied to a low-intensity scan of a rabbit with a thin wire to test the resolution. The proposed algorithm is compared to filtered backprojection (FBP).
Conclusions: The algorithm may have some advantage over FBP in that the resulting noise level is lowered at equivalent contrast levels of the wire.
Keywords: CT image reconstruction, iterative methods, low dose CT, compressive sensing
INTRODUCTION
Motivated by the desire to reduce dose1 and the ever-climbing availability of cheap computation power, much effort has been directed to developing iterative image reconstruction (IIR) for application in x-ray computed tomography (CT).1, 2, 3, 4 When considering a fixed total x-ray dose for a given scan, there is a trade-off between intensity-per-view and number-of-views. Much of the recent work on IIR based on a constrained, ℓ1 or total-variation (TV) optimization problem has explored the sparse-view end of this trade-off.4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 While the low-intensity∕many-views end of this spectrum is generally dealt with by employing filtered backprojection (FBP) with regularization or IIR based on a maximum-likelihood (ML) principle, the use of the ML principle is motivated by the high noise levels in low-intensity CT. While practical IIR on low-intensity CT data will certainly need to incorporate some form of ML methods, we point out in this work that it may also be important to consider angular undersampling, especially when the structures of interest are comparable in size with the detector bins. To address potential angular undersampling, we extend IIR based on constrained, TV minimization to handle CT data with many projections and low-intensity (high noise) per projection.
The use of constrained, TV minimization is derived from recent theory in compressive sensing (CS),15, 16, 17 where certain sparsely sampled linear systems can be inverted accurately when the underlying object has an approximately sparse gradient magnitude image. The CS-motivated optimization problem appears to be effective for accurate image reconstruction from sparse-view data as evaluated by many image quality metrics.18 The obvious question now is why would we want to extend constrained, TV minimization to CT data with many projections? The answer is that no matter how many projections a CT data set contains, there may always be an issue with view-angle undersampling. Particularly in diagnostic x-ray CT, the bar for image quality is quite high; it is often expected that detail on the scale of a single detector bin (0.1–0.25 mm) will be visible. At such scales, images of structures are often degraded due to the fact that standard CT scans—even with 1000 projections—contain too few views. Further evidence of undersampling in CT practice is that industry has developed a hardware solution, which is a x-ray source with a flying focal-spot to effectively double the number of projections.19, 20 The reason for the need to push for higher sampling rates in CT is that the underlying object function contains edge discontinuities at the interface of different tissues and at the object boundaries. As such, any CT data set may benefit from the TV-minimization approach for image reconstruction. For the present case of many views and low x-ray intensity, the application of TV minimization requires some technical modification to be able to handle the noise level in the individual projections and to be able to recover object structures on the scale of a detector bin.
The main goal of this article is to report a constrained, TV-minimization IIR algorithm for low-intensity∕many-view CT projection data. The algorithm is derived from a framework we have been developing where constrained, TV minimization is solved with a combination of steepest-descent (SD), to reduce image TV, and projection onto convex sets (POCS), to enforce data error and other image constraints. As the step size of the SD component of the algorithm is adaptively adjusted, the algorithm framework is referred to as adaptive SD-POCS (ASD-POCS). The particular flavor of ASD-POCS presented here is designed to solve constrained, TV minimization accurately in a reasonable number of iterations (100 iterations). This ASD-POCS algorithm is demonstrated with an XCounter CT scan of a rabbit with a thin wire taped to the outside of the sample holder. The data are of low intensity and contain 1878 projections with a 2266×64 bin detector at a resolution of 0.1 mm. The thin wire provides a good test for the image-reconstruction algorithm because this object has a width similar to the detector bin size. For our purpose, we take the middle row on the detector from this data set and focus on 2D fan-beam CT reconstruction with 1878 projections on a 2266-bin linear detector array. This small object forces the use of a super-resolution grid, which increases the ill-posedness of the image-reconstruction problem. This ill-posedness and the high noise level are dealt with by the present implementation of ASD-POCS. In Sec. 2, we discuss a fundamental issue of sampling for IIR in detail; in Sec. 3, we present the ASD-POCS algorithm for low-intensity CT; and in Sec. 4, the algorithm is applied to the rabbit scan.
SAMPLING AND IMAGE REPRESENTATION FOR HIGH-RESOLUTION CT IMAGING
For FBP, which is an analytic-inverse-based image-reconstruction algorithm, the data sampling requirements are guided by the fact that one needs a good estimate of the continuous projection data. Whether or not done explicitly, the discretely sampled x-ray transform is interpolated to a continuous function and then fed into an analytic-inverse formula for the x-ray transform. In the theory for CT sampling, there is much discussion about satisfying a Nyquist sampling condition for the data, but, in practice, this condition is used only as an estimate of resolution for a given CT system. Often objects being scanned in CT have edge discontinuities, which violate the band-limited requirement of Nyquist sampling. Furthermore, most implementations of FBP use linear interpolation in the filtering and backprojection integrals instead of the sinc-interpolation called for by the sampling theorem. In any case, the CT sampling issue boils down to how well the interpolated data function matches the continuous projection of the underlying object function. The FBP image can be displayed on a grid of any size because FBP provides a closed-form expression for the image in terms of the data. The accuracy of this image, however, depends on the accuracy of the interpolation of the data function.
For IIR, which uses a discrete data model, the image resolution depends on two things: (1) The expansion set used to represent the image and (2) the number of measurements available to determine the expansion coefficients. The first step is to design an expansion set for the underlying object function. For the present work, we choose image pixels as this expansion set. Fixing the expansion set, the next step to understanding the sampling is to determine if there are enough ray-integration measurements to specify the expansion coefficients. The required amount of data to determine a unique image depends on the number of expansion elements. To explain this sampling issue for IIR more concretely, we use the configuration of the XCounter CT of a rabbit-plus-wire.
The projection of the rabbit is confined to the middle 1266 bins of the detector so the data size is effectively 1878 views by 1266 bins with each bin measuring 0.1 mm in width. We would like to resolve structure within a (0.1mm)2 region, and as a result, the pixels representing the image must be much smaller than this 0.1 mm square.21 Say, we choose pixels of size 0.025 mm so that the 0.1 mm square has 16 subelements. It turns out that the support of the rabbit can be covered by a 4096×4096 array of pixels of size (0.025mm)2. With this choice of parameters, the number of pixels is much larger than the number of measurements. If instead we had decided to use (0.1mm)2pixels, the discrete data model would not be an underdetermined linear system. It is clear, however, that the data model will always be underdetermined if the pixel size is chosen to be smaller than the detector bin width. Using alternative basis functions does not resolve this dilemma; whenever it is desirable to recover structure on the scale of a detector bin, there will be many more expansion elements than measurements.
Within the framework of optimization-based image reconstruction, such undersampling problems are resolved by the exploitation of some kind of prior knowledge. One possible choice is to exploit sparsity in the gradient magnitude image and employ constrained, TV minimization. Mathematically, the constraints of having to agree with the data and image non-negativity yield a multiplicity of images. However, there will, in general, be one image, with in this feasible subset, that has a minimum image TV. While constrained, TV minimization has proved useful for angular undersampling, it may not be as effective when both the scanning angle and the detector bin direction are undersampled, as is the case here.
A possible solution to the problem of how to employ a super-resolution grid of pixels comes from analyzing the sampling for FBP. CT sampling is not uniform and the limiting factor is usually the angular sampling rate. As a prior on the system, we can assume that the sampling along the projection does satisfy the Nyquist sampling condition. If this is the case, we can generate more samples by Fourier interpolation, zero-padding the projection’s Fourier transform, to augment the data set to 1878 views by 5064 (4×1266) bins. With this set of data, we are no longer undersampled on the direction along the detector. Now, we can exploit sparsity in the gradient magnitude image by basing the IIR algorithm on constrained, TV minimization. Moreover, we can expect this strategy to be successful, as constrained, TV minimization has been demonstrated to be effective against angular undersampling. Although we have chosen a factor of 4, the method can be extended to even larger subsampling factors because, under the assumption of Nyquist sampling along the detector, the number of samples per projection can scale with the pixel grid size. Another extension of this idea is to use other methods to interpolate the projections, for example, linear interpolation.
THE ASD-POCS ALGORITHM FOR LOW-INTENSITY CT
The main new idea of this article is to employ upsampling on the individual CT projections in combination with constrained, TV minimization, which we now briefly describe. The specific data model for our system is a linear equation,
| (1) |
where represents the augmented projection data, in this case a vector of length 1878×5064; is a vector of pixel values on the super-resolution grid, here 4096×4096; and X is the ray-driven model of the x-ray transform where system matrix element is the intersection length of a given ray through a given pixel. An IIR algorithm based on constrained, TV minimization aims at solving
| (2) |
where is the sum over the gradient magnitude image and ɛ is a data error tolerance parameter. Because there will be no image that exactly reproduces the data, due to noise and other physical factors, there will be a nonzero minimum data error tolerance ɛmin. The optimization problem in Eq. 2 has been studied extensively recently, and much literature has been devoted to algorithms for solving it, see for example.22 We would also like to highlight POCS-type algorithms described in Refs. 23, 24, which could be potentially adapted to our system and which could have the necessary computational efficiency. For the present application, any of these algorithms could benefit from upsampling the CT projection data.
The remainder of this section describes how we adapted our ASD-POCS algorithm for the present CT sampling conditions. We do not claim that ASD-POCS is better than other algorithms designed to solve Eq. 2. We continue to develop ASD-POCS because algorithm efficiency continues to be a concern in CT as the data set sizes are typically quite large. As a result, IIR algorithms developed for x-ray tomography are often run at very low iteration numbers. This is demonstrated in literature on digital breast tomosynthesis, an x-ray tomographic modality where IIR is applied in practice.10, 25, 26 The iteration number for this application is typically 10 or less.
Up until now, we have not addressed the issue of the high noise level at each projection. In this work, we do not explicitly incorporate a noise model into the design of the IIR algorithm. Instead, the consideration of noise is more of a practical issue in that it turns out to be difficult to solve the constrained, TV-minimization problem with a large number of views and a high noise level per view. The optimization problem [Eq. 2] can be difficult to solve for our system; especially, because we are interested in values of ɛ near ɛmin. An alternate version of ASD-POCS can be designed to solve this problem efficiently by converting Eq. 2 to an equivalent least-absolute-shrinkage-and-selection-operator (LASSO) optimization problem.27 In the LASSO form, the term representing the data error goes into the objective function and the image TV is swapped out as a constraint,
| (3) |
where the parameter t0 is the maximum allowed image TV. This parameter replaces ɛ from Eq. 2. To solve Eq. 2, one selects a t0 and then solves Eq. 3. The value of ɛ corresponding to t0 is found by simply evaluating the objective function for . This optimization problem is more amenable for algorithm design for a few reasons: (1) We are interested in low ɛ that corresponds to high t0 —thus the feasible set of images is large; (2) the initial estimate of a zero image has zero image-TV and is thus in the feasible set from the beginning; and (3) it is efficient to project images into the feasible set because the constraints can be evaluated quickly for a given image estimate. The optimality conditions for Eq. 3 fall into two cases: First, if t0 is chosen too large, then the image-TV constraint is satisfied with a strict inequality; the image is non-negative; and the gradient of the data-residual objective function, masked by the image estimate support, has zero length. The masking by the image support comes from the non-negativity constraint.9 Second, the more useful case, which is equivalent to Eq. 2, is when the image-TV constraint is active and is therefore satisfied with equality. In this case, we define an angle α between the gradient of the data residual, masked by the image support, and the gradient of the image TV, also masked by the image support. At optimality, this angle should be 180° or cosα=-1 and, of course, the image should be non-negative. This condition is derived and described in more detail in Ref. 9. The condition cosα=-1 is a very sensitive test and is therefore quite useful for the present purposes because we aim at solving Eq. 3 accurately. The use of a data error plot with iteration number, as is often done, does not indicate convergence because we are solving an underdetermined problem and there is a large multiplicity of images for a given data residual.
For readers interested in the algorithm design, we present its details here; otherwise, one can skip to Sec. 4. The algorithm designed to solve Eq. 3 is an ASD-POCS algorithm in that SD with an adaptive step size is used to lower image TV and POCS is employed to lower the data-residual objective function. The pseudocode is
| 1: | β:=1.0;βred:=0.7;βmin:=10-5 |
| 2: | ρmin:=1.1;ρmax:=2.0; |
| 3: | γred:=0.8 |
| 4: | |
| 5: | while β≥βmin do |
| 6: | |
| 7: | for j=1, Nd do |
| 8: | |
| 9: | |
| 10: | |
| 11: | ρ:=min(ρ,ρmax) |
| 12: | |
| 13: | if and ρ<ρmin then |
| β:=β*βred | |
| 14: | |
| 15: | |
| 16: | if then |
| 17: | |
| 18: | |
| 19: | |
| 20: | |
| 21: | γ:=1.0 |
| 22: | while do |
| 23: | γ:=γ*γred |
| 24: | |
| 25: | |
| 26: | end while |
| 27: | |
| 28: | end if |
| 29: | end while |
| 30: | return |
The general idea of the algorithm is to start with a zero image estimate, which obviously satisfies non-negativity and the image TV constraints. A POCS step is computed, which reduces the data error while maintaining non-negativity. This step is scaled so that the image estimate goes to the boundary of the feasible space . A single SD step on the image TV is then taken with a line search to ensure that the image TV is reduced, taking the image estimate to the interior of the TV constraint. The image estimate after a single loop of POCS and SD will, on the average, have a lower data residual and will remain in the interior of the TV constraint. Repetition of this loop will slide the image along the boundary of the TV constraint, maintaining non-negativity, until a minimum data error is reached.
The data error reduction happens at line 7 with the standard algebraic reconstruction technique (ART) loop, where is the row of the system matrix yielding an estimate for the ray integration corresponding to the data element gj and Nd is the number of ray measurements in the augmented data set; for the results below, Nd=1878×5064. Line 8 enforces non-negativity with the function Pos(·), which puts zeros in any component of the argument that are negative; lines 7 and 8 together are POCS. The relaxation factor β at line 7 starts at a value of 1.0 and is reduced aggressively by a factor βred defined at line 1. Termination of the program is based on testing β against a minimum value at line 5. The program is designed so that the current image estimate before ART at line 7 satisfies the image TV constraint, , with inequality. A POCS step is then computed at lines 7 and 8, and this step is scaled at line 10 so that the image estimate satisfies the TV constraint with equality. (The function solves the nonlinear equation in the first argument of S[·,·] for ρ, the second argument of S[·,·].) It is here where the LASSO form enters into the algorithm design. It is much more efficient to solve the equation for ρ than it would be to perform the equivalent on a data error constraint (data error computation requires a forward projection which is time-consuming).
If there is no solution at line 10, the value of ρ is selected that minimizes the difference magnitude on the left-hand side; if this is the case, the resulting image TV will be less than t0 instead of greater. The scale factor ρ is needed to bring the TV of the image estimate to t0. This factor is bounded above at line 11 by the value 2 in order that the ART step does not increase the data error. The ART step with a scale factor is added to the image estimate at line 12. There are two conditions for reducing the relaxation factor at line 13. The first condition checks if the POCS step with scaling could successfully bring the image estimate to the boundary of the feasible space. This check is necessary because it is possible that the relaxation factor is reduced too fast. If this is the case the image estimate will remain in the interior of the TV constraint after POCS, and in this case, we do not want to reduce the relaxation factor further. The second checks if the scale factor ρ is below a minimum value. This test effectively adjusts the ART-step size quickly to the problem at hand. The image estimate is stored in at line 14; this will be the final image on the termination of the program. The magnitude of the image change due to POCS, dp, is computed at line 15 for use in the adaptive SD on the image TV. The SD portion of the program at lines 16–28 are executed only if the POCS step successfully reached an image TV of t0. If this is not the case, the image TV will be less than t0 and we do not want to reduce it further. The adaptive aspect of the SD step is seen at line 20 where the step search is started with the value of dp. The choice of algorithm parameters at lines 1–3 are what we used in Sec. 4.
The critical parameters are βred and ρmin. If βred is chosen too small, then the program terminates too quickly, well before convergence. Likewise, higher values of ρmin cause the relaxation factor to be reduced more often. A value of ρmin should be greater than or equal to 1.0, with higher values reducing the number of iterations. Critical is the cosα=-1 test. A good strategy is to start with aggressive parameters, where it will be clear whether or not convergence can be achieved within 10–20 iterations. If not, then βred can be increased or ρmin can be reduced. cosα will, in general, not reach −1.0, but values below −0.5 generally indicate proximity to the solution. Because of the high dimensionality of the image coefficient vector, cosα<-0.5 indicates a small error per pixel, if the error is distributed evenly over all pixels.
We stress that this form of the ASD-POCS algorithm is designed for IIR in the situation where the desired operating range for image regularization is relatively weak and the data error tolerance is near its minimum possible value. Qualitatively, the resulting images will still have speckle noise, albeit at a lower level. If images are desired, which are regularized to the point where the speckle noise is removed, then it is better to use the basis pursuit [Eq. 2] optimization problem to design an algorithm because the feasible region for the LASSO problem shrinks while that of the basis pursuit expands.
Finally, because the goal of the algorithm is an accurate solution to Eq. 3, the resulting images can be regarded as a function of only the scanning parameters and t0. The details of the algorithm, both particular parameter settings of methods for reducing data error or image TV, are only important for algorithm efficiency and they do not affect the final image. On the other hand, this means we must take the optimality conditions seriously. In Sec. 4, we give a sense of image dependence on cosα to demonstrate that the error in solving the LASSO equation is well below the visual threshold of detecting a difference in the image. A question arises on how to choose t0. As the application here is to perform image reconstruction, which has a lower noise level than that obtained by standard FBP, the FBP image itself provides a reference value for t0. In Sec. 4, we show images for different values of t0, and the optimal value will depend on imaging task.
RESULTS: LASSO-FORM ASD-POCS APPLIED TO A RABBIT SCAN WITH A THIN WIRE
We use the rabbit scan with a thin wire to demonstrate the LASSO form of the ASD-POCS algorithm on finely sampled projection data with low x-ray intensity. The first set of results is aimed at illustrating various points about the algorithm itself; we discuss algorithm convergence and the need to perform upsampling in the projection data. The second set of results compares the LASSO-form ASD-POCS algorithm with a standard FBP algorithm over a range of image regularizations.
Illustration of the LASSO-form ASD-POCS IIR algorithm: Convergence and upsampling
As noted above, the size of the reconstruction problem solved here is relatively large for a 2D CT system. The image array consists of 4096×4096pixels and the upsampled data contain 1878×5064 measurements resulting in a system matrix of size ≈107×(1.6×107). Fortunately, computations on a commodity graphics processing unit (GPU), originally introduced to the medical imaging community by Xu and Mueller,28 make possible a substantial acceleration by approximately a factor of 10, for our case. Even though we have implemented the ART step of line 7 in CUDA using a Tesla C1060 GPU, this step still takes a few minutes of computation time. Thus, efficiency of the ASD-POCS algorithm itself is still important.
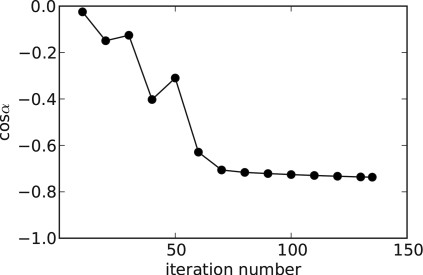
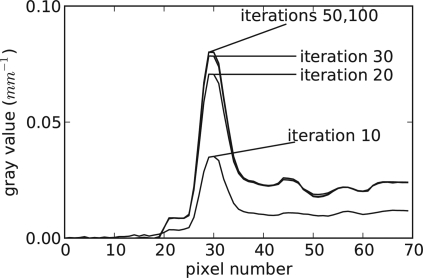
To demonstrate convergence of one of the ASD-POCS reconstructions, we show cosα as a function of iteration number in Fig. 1. We point out that all other constraints of Eq. 3, positivity and the TV bound, are satisfied. Within tens of iterations cosα drops below −0.5, a value which on the face of it seems rather far from the truly converged value of −1.0. However, the image space here is large— 16×106pixels. With such high dimensionality, a value of −0.5 results in a fairly accurate image. For example, suppose that the error from the true solution is a random image following an independent uniform Gaussian distribution. One can show that the average deviation per pixel from the true solution is 0.04% for cosα=-0.5. Of course, we do not expect that the error image follows this model, but at least this gives a sense of the meaning of cosα. As an independent demonstration of convergence, we show a series of one dimensional profiles, through the wire object, corresponding to different iteration numbers in Fig. 2. The difference in the profiles between 50 and 100 iterations is imperceptible, even though cosα drops from −0.31 to −0.74 over this range. The difference images as a function of iteration seems to agree with the Gaussian error model. Although we show only one example here, we have verified similar convergence properties for this version of ASD-POCS for numerous scanning conditions. Thus, we claim that the images shown in this article are visually indistinguishable from the true solution of Eq. 3 for the grayscale ranges shown.
Figure 1.
Evolution of cosα with iteration number for an example run of the LASSO-form ASD-POCS algorithm.
Figure 2.
Profile through wire for different iteration numbers of an example run of the LASSO-form ASD-POCS algorithm.
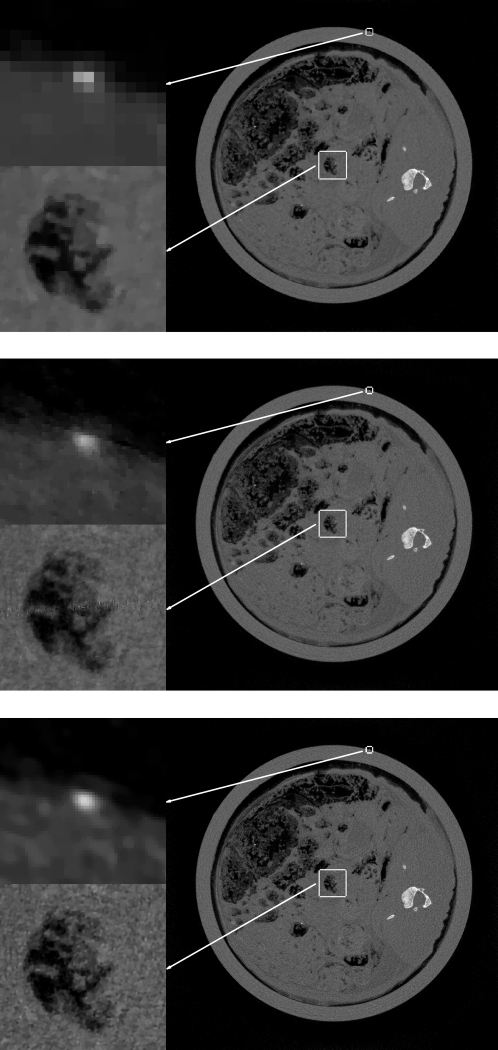
To demonstrate the importance of the projection data upsampling to squeeze out the resolution contained in the data, we compare images for three cases shown in Fig. 3. First, we show the ASD-POCS image obtained when the image array is 1024×1024 at a pixel size is (0.1mm)2, the same as the detector bin size, and no upsampling of the data is performed. Second, we increase the image array to 4096×4096, or, equivalently, decrease the pixel size to (0.025mm)2, and no upsampling of the data is performed. Finally, the 4096×4096 image array is employed with each projection being upsampled by a factor of 4. All computations are done at equivalent t0. The small image array is clearly not up to the task as the wire appears as a single square. Moreover, the overall impression of the image appears blotchy—a criticism that has been leveled against the use of TV in many articles. Going to the larger array, without data upsampling, improves the image, but the reconstruction is a difficult inversion problem in this case because the undersampling factor is not small and both dimensions of the data space are undersampled relative to the pixel array. Inspection of the image shows some peculiarities in the noise pattern, where widely spaced, large-amplitude, salt-and-pepper noise appears, and artifacts are clearly visible in the lower left panel where gaps between the measurement rays cause some striping. High values of the noise pattern could be mistaken as tiny microcalcifications. Finally, the high resolution array combined with the upsampled data appears to properly reconstruct the wire while not introducing a strange noise pattern or artifacts. We reiterate here that the upsampling strategy is not only useful for ASD-POCS; it should help for other algorithms which aim at solving Eq. 2.
Figure 3.
Top: ASD-POCS reconstruction from 1878×1266 data set to a 1024×1024 image array. Middle: ASD-POCS reconstruction from same data set to a 4096×4096 image array. Bottom: ASD-POCS reconstruction from 1878×5064 upsampled data set to a 4096×4096 image array. For each image, the grayscale is [0,0.06]mm-1 except for the top, left ROI containing the cross section of the wire, which is displayed in a window of [0,0.1]mm-1.
We also point out here that the strategy of upsampling the data is not the only possibility of improving the condition number of the discrete imaging model. A strip integration model for the projection data, where the extended x-ray source-spot and detector bin are taken into account, would likely yield decent image quality with the large image array. However, this seemingly more realistic model does not necessarily model the CT system better than the present upsampling approach because an accurate model of the physics would include a nonlinear averaging of the rays in the strip and not just straight summation of the rays contributing to a single measurement.29 We leave the investigation of alternate projection models to future work.
Image regularization through varying t0
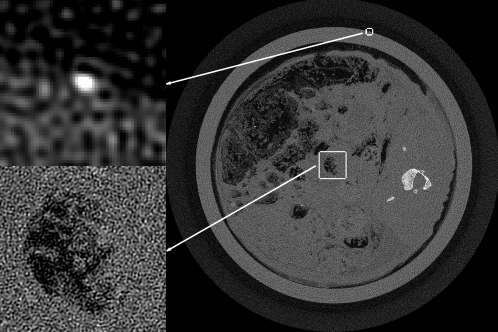
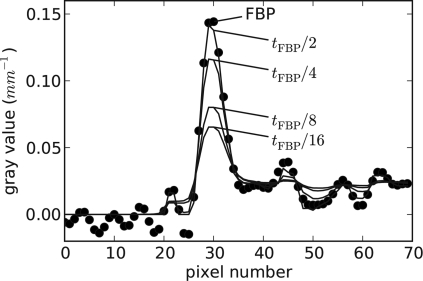
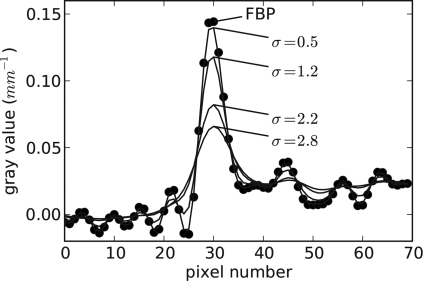
The main practical impact of the present ASD-POCS algorithm comes if there is some potential advantage over standard fan-beam FBP. Recall that the sampling here is of high density. Because the sampling is so fine, we do not expect a dramatic improvement in image quality in going from FBP to an IIR algorithm similar to what is seen with CS-style image reconstruction with sparse views (see, e.g., Ref. 9). A word about FBP is in order here. The fan-beam FBP algorithm employed involves no rounding of the ramp filter, and the corresponding unregularized image is shown in Fig. 4. The TV of this fan-beam FBP reconstruction, denoted by tFBP, is computed as a reference value for the ASD-POCS algorithm. Image reconstruction with ASD-POCS is performed for values t0=tFBP∕2, tFBP∕4, tFBP∕8, and tFBP∕16. As t0 is decreased, one can expect that the noise level in the image will be lower. To find a counterpart FBP image, we smoothed the unfiltered image with a Gaussian kernel, where the kernel width is selected so that the wire amplitude matches the corresponding ASD-POCS image. The widths of the Gaussian kernels found in this way turn out to be σ=0.5, 1.2, 2.2, and 2.8, respectively, in units of pixel widths. (The corresponding full width half maximum values are 1.18, 2.35, 5.18, and 6.59 pixel widths). The comparison with smoothed FBP is done because it is a standard processing technique, but we point out that FBP reconstruction followed by TV denoising30 is an interesting alternate approach.
Figure 4.
Unregularized FBP image reconstructed onto a 4096×4096 image array.
In Figs. 56, we show comparisons between the ASD-POCS images with the corresponding regularized FBP image for the least and greatest, respectively, amount of regularization. Additionally, for more quantitative comparison, we show a series of ASD-POCS profiles through the wire in Fig. 7 and the corresponding FBP profiles in Fig. 8.
Figure 5.
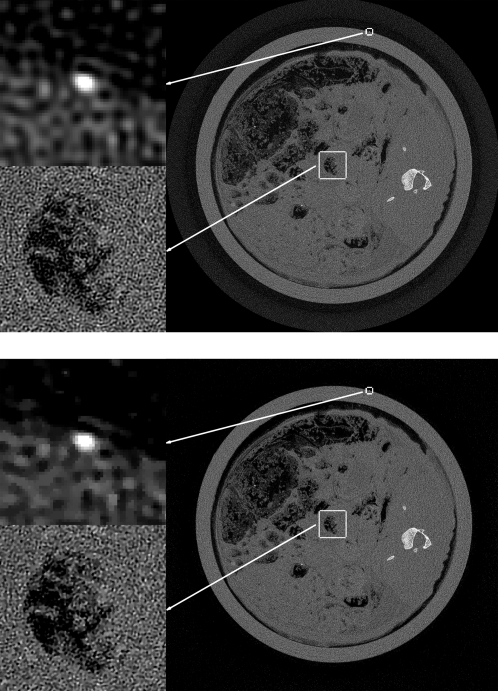
Top: FBP image convolved with a Gaussian of width σ=0.5. Bottom: ASD-POCS reconstruction for t0=tFBP∕2. For each image, the grayscale is [0,0.06]mm-1 except for the top, left ROI containing the cross section of the wire, which is displayed in a window of [0,0.1]mm-1.
Figure 6.
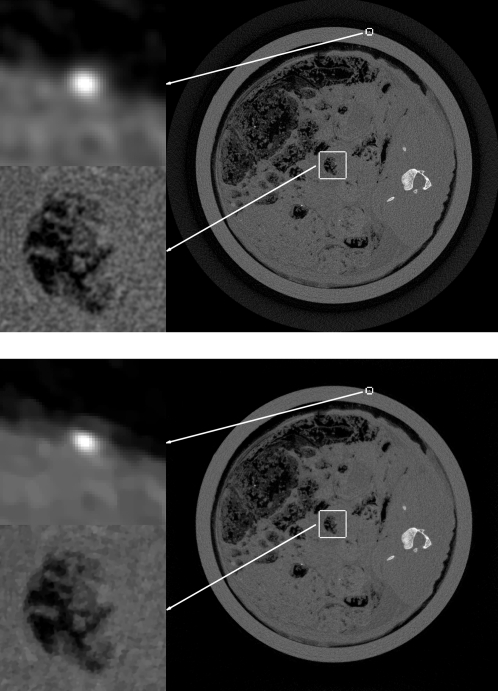
Top: FBP image convolved with a Gaussian of width σ=2.8. Bottom: ASD-POCS reconstruction for t0=tFBP∕16. For each image, the grayscale is [0,0.06]mm-1 except for the top, left ROI containing the cross section of the wire, which is displayed in a window of [0,0.1]mm-1.
Figure 7.
The solid curves represent the wire profile for ASD-POCS images for different values of t0. The dotted curve is the same profile for the unregularized FBP image.
Figure 8.
The solid curves represent the wire profile for FBP images smoothed by a Gaussian of various widths. The dotted curve is the same profile for the unregularized FBP image.
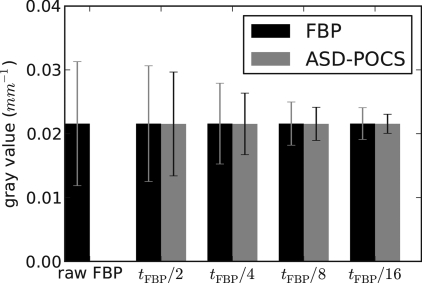
We discuss the possible advantage of IIR with the present ASD-POCS algorithm. We point out again and it is clear from the images that potential advantages will be small as we are trying to squeeze out more information from a very finely sampled system. Nevertheless, there appears to be some advantage. Comparing Figs. 45, one can see that the level of FBP regularization is negligible as both FBP images appear very similar. The corresponding ASD-POCS image has some visible advantage as the noise level is lower; this is most easily seen in the lower left ROIs in the dark regions of the images. For all the image pairs, the noise level of the ASD-POCS image is perceptibly lower than the corresponding FBP image. This can be seen quantitatively by computing the mean and standard deviation of pixel values in a 200×200 square just above and to the right of the bone, where the subject’s gray value is uniform. The resulting values are displayed in a bar chart shown in Fig. 9. The profile plots in Figs. 78 illustrate another possible advantage to the ASD-POCS algorithm. For ASD-POCS, the wire profiles maintain their width as image TV is decreased, while the Gaussian smoothed FBP profiles show spreading with increasing regularization. This trend in the wire profile is also apparent in the 2D image of Fig. 6. In all the ASD-POCS images the smallest ROI containing the wire cross section still has some perceptible graininess. This graininess can be effectively removed by further upsampling the data and reconstructing onto an 8192×8192 image array. We found, however, that the resulting gain in image quality is minimal for our purpose.
Figure 9.
Mean and standard deviation over a 200×200pixel region, where the subject is uniform. The first column shows values for the unregularized FBP image of Fig. 4. The subsequent columns are labeled by the t0 value used in the ASD-POCS reconstruction. The corresponding regularized FBP result is obtained by Gaussian smoothing where the kernel width is selected by matching the amplitude of the wire in the ASD-POCS image, as explained in the text. In each case, the ASD-POCS yields a standard deviation lower than that of the FBP image with equivalent contrast of the wire object.
CONCLUSION
We have developed a CS-style image-reconstruction algorithm for finely sampled projection data obtained with a low-intensity x-ray beam. The main goals of the IIR algorithm are to provide control over the image regularity and to image small objects of width comparable to the detector bin. The technical points to achieve these goals are (1) an upsampling scheme for the projection data, which takes advantage of the asymmetry in data sampling, namely, that recognizes that the bin direction of the data is sampled more finely than the angular direction, and (2) conversion of the constrained, TV-minimization problem to a LASSO formulation for the purpose of deriving an alternate ASD-POCS algorithm, which efficiently solves the corresponding optimization problem to a high degree of accuracy. The resulting algorithm appears to achieve the above mentioned goals.
Anecdotally, there have been complaints from radiologists that IIR images yield unrealistic looking images, which has been blamed on the different noise patterns from IIR and FBP algorithms. We speculate that the real issue is that IIR algorithms implemented on commercial scanners reduce the image resolution to gain in noise reduction in a way that is difficult to control. Objects of size on the order of the detector bin are highly distorted in standard IIR implementations. The presented ASD-POCS algorithm allows for more control over this trade-off. We point out that the upsampling idea can be used in conjunction with any IIR algorithm—a subject for future investigation. Another direction which the current work can be extended is the inclusion of more physics of the imaging process in the LASSO optimization problem; for example, a data error term could be designed to more closely match the noise model of this CT system. After accounting for a realistic noise model in the data divergence term, we will validate the ASD-POCS algorithm on a series of computer-simulated data sets, where the impact of noise model and angular undersampling can be unambiguously quantified.
Addressing now the main practical issue of dose reduction while maintaining image quality, we have developed an IIR algorithm for the extreme where IIR should have the least impact—namely, fine sampling in the projection angle. Fixing the overall dose, but decreasing the number of views should result in equal or better image quality for ASD-POCS as it is originally designed for sparse-view sampling. Thus, for a given image task, there is a potential not only to reduce dose but also to eliminate the need for expensive flying focal-spot technology on the x-ray source.31 This point, however, is presently speculation as it requires a more in-depth study on data sets with similar exposure and different numbers of projections and there may be an additional practical issue from blurring if the x-ray source moves at a constant rotation rate with fewer sampling intervals.
ACKNOWLEDGMENTS
This work was supported, in part, by NIH R01 Grant Nos. CA120540 and EB000225, and a Pilot Project Award from NIH SPORE Grant No. P50CA090386. The contents of this article are solely the responsibility of the authors and do not necessarily represent the official views of the National Institutes of Health.
References
- McCollough C. H., Primak A. N., Braun N., Kofler J., Yu L., and Christner J., “Strategies for reducing radiation dose in CT,” Radiol. Clin. North Am. 47, 27–40 (2009). 10.1016/j.rcl.2008.10.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erdogan H. and Fessler J. A., “Ordered subsets algorithms for transmission tomography,” Phys. Med. Biol. 44, 2835–2852 (1999). 10.1088/0031-9155/44/11/311 [DOI] [PubMed] [Google Scholar]
- Qi J. and Leahy R. M., “Iterative reconstruction techniques in emission computed tomography,” Phys. Med. Biol. 51, R541–R578 (2006). 10.1088/0031-9155/51/15/R01 [DOI] [PubMed] [Google Scholar]
- Pan X., Sidky E. Y., and Vannier M., “Why do commercial CT scanners still employ traditional, filtered back-projection for image reconstruction?,” Inverse Probl. 25, 123009-1–123009-36 (2009). 10.1088/0266-5611/25/12/123009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M., Yang H., and Kudo H., “An accurate iterative reconstruction algorithm for sparse objects: Application to 3D blood vessel reconstruction from a limited number of projections,” Phys. Med. Biol. 47, 2599–2609 (2002). 10.1088/0031-9155/47/15/303 [DOI] [PubMed] [Google Scholar]
- Sidky E. Y., Kao C.-M., and Pan X., “Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT,” J. X-Ray Sci. Technol. 14, 119–139 (2006). [Google Scholar]
- Chen G. H., Tang J., and Leng S., “Prior image constrained compressed sensing (PICCS): A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets,” Med. Phys. 35, 660–663 (2008). 10.1118/1.2836423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song J., Liu Q. H., Johnson G. A., and Badea C. T., “Sparseness prior based iterative image reconstruction for retrospectively gated cardiac micro-CT,” Med. Phys. 34, 4476–4483 (2007). 10.1118/1.2795830 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidky E. Y. and Pan X., “Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization,” Phys. Med. Biol. 53, 4777–4807 (2008). 10.1088/0031-9155/53/17/021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidky E. Y., Pan X., Reiser I. S., Nishikawa R. M., Moore R. H., and Kopans D. B., “Enhanced imaging of microcalcifications in digital breast tomosynthesis through improved image-reconstruction algorithms,” Med. Phys. 36, 4920–4932 (2009). 10.1118/1.3232211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidky E. Y., Anastasio M. A., and Pan X., “Image reconstruction exploiting object sparsity in boundary-enhanced x-ray phase-contrast tomography,” Opt. Express 18, 10404–10422 (2010). 10.1364/OE.18.010404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia X., Li R., Song W. Y., Jiang S. B., and Lou Y., “GPU-based fast cone beam CT reconstruction from undersampled and noisy projection data via total variation,” Med. Phys. 37, 1757–1760 (2010). 10.1118/1.3371691 [DOI] [PubMed] [Google Scholar]
- Choi K., Boyd S., Wang J., Xing L., Zhu L., and Suh T.-S., “Compressed sensing based cone-beam computed tomography reconstruction with a first-order method,” Med. Phys. 37, 5113–5125 (2010). 10.1118/1.3481510 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergner F., Grimmer R., Ritschl L., Kachelriess M., Berkus T., Oelhafen M., Kunz P., and Pan T., “An investigation of 4D cone-beam CT algorithms for slowly rotating scanners,” Med. Phys. 37, 5044–5054 (2010). 10.1118/1.3480986 [DOI] [PubMed] [Google Scholar]
- Candès E. J., Romberg J., and Tao T., “Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information,” IEEE Trans. Inf. Theory 52, 489–509 (2006). 10.1109/TIT.2005.862083 [DOI] [Google Scholar]
- Candès E. J., Romberg J. K., and Tao T., “Stable signal recovery from incomplete and inaccurate measurements,” Commun. Pure Appl. Math. 59, 1207–1223 (2006). 10.1002/cpa.20124 [DOI] [Google Scholar]
- Candès E. J. and Wakin M. B., “An introduction to compressive sampling,” IEEE Signal Process. Mag. 25, 21–30 (2008). 10.1109/MSP.2007.914731 [DOI] [Google Scholar]
- Bian J., Siewerdsen J. H., Han X., Sidky E. Y., Prince J. L., Pelizzari C. A., and Pan X., “Evaluation of sparse-view reconstruction from flat-panel-detector cone-beam CT,” Phys. Med. Biol. 55, 6575–6599 (2010). 10.1088/0031-9155/55/22/001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flohr T., Stierstorfer K., Raupach R., Ulzheimer S., and Bruder H., “Performance evaluation of a 64-slice CT system with z-flying focal spot,” RoFo., Fortschr. Geb. Rontgenstr. Nuklearmed. 176, 1803–1810, ISSN 1438-9029 (2004). 10.1055/s-2004-813717 [DOI] [PubMed] [Google Scholar]
- Kachelriess M., Knaup M., Penssel C., and Kalender W. A., “Flying focal spot (FFS) in cone-beam CT,” IEEE Trans. Nucl. Sci. 53, 1238–1247 (2006). 10.1109/TNS.2006.874076 [DOI] [Google Scholar]
- Zbijewski W. and Beekman F. J., “Characterization and suppression of edge and aliasing artefacts in iterative X-ray CT reconstruction,” Phys. Med. Biol. 49, 145–157 (2004). 10.1088/0031-9155/49/1/010 [DOI] [PubMed] [Google Scholar]
- Vogel C. R., Computational Methods for Inverse Problems (Society for Industrial and Applied Mathematics, Philadelphia, PA, 2002). 10.1137/1.9780898717570 [DOI] [Google Scholar]
- Combettes P. L. and Pesquet J.-C., “Image restoration subject to a total variation constraint,” IEEE Trans. Image Process. 13, 1213–1222 (2004). 10.1109/TIP.2004.832922 [DOI] [PubMed] [Google Scholar]
- Byrne C. L., Applied Iterative Methods (AK Peters, Wellesley, MA, 2008). [Google Scholar]
- Wu T., Moore R. H., Rafferty E. A., and Kopans D. B., “A comparison of reconstruction algorithms for breast tomosynthesis,” Med. Phys. 31, 2636–2647 (2004). 10.1118/1.1786692 [DOI] [PubMed] [Google Scholar]
- Zhang Y., Chan H.-P., Sahiner B., Wei J., Goodsitt M. M., Hadjiiski L. M., Ge J., and Zhou C., “A comparative study of limited-angle cone-bean reconstruction methods for breast tomosynthesis,” Med. Phys. 33, 3781–3795 (2006). 10.1118/1.2237543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Figueiredo M. A. T., Nowak R. D., and Wright S. J., “Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems,” IEEE J. Sel. Top. Signal Process. 1, 586–597 (2007). 10.1109/JSTSP.2007.910281 [DOI] [Google Scholar]
- Xu F. and Mueller K., “Accelerating popular tomographic reconstruction algorithms on commodity PC graphics hardware,” IEEE Trans. Nucl. Sci. 53, 1238–1247 (2006). 10.1109/TNS.2006.880974 [DOI] [Google Scholar]
- Zou Y., Sidky E. Y., and Pan X., “Partial volume and aliasing artefacts in helical cone-beam CT,” Phys. Med. Biol. 49, 2365–2375 (2004). 10.1088/0031-9155/49/11/017 [DOI] [PubMed] [Google Scholar]
- Chan T. F., Osher S., and Shen J., “The digital TV filter and nonlinear denoising,” IEEE Trans. Image Process. 10, 231–241 (2001). 10.1109/83.902288 [DOI] [PubMed] [Google Scholar]
- Xia D., Bian J., Han X., Sidky E. Y., and Pan X., “An investigation of compressive-sensing image reconstruction from flying-focal-spot CT data,” IEEE Medical Imaging Conference Record, Orlando, FL, pp. 3458–3462, 2009. [DOI] [PMC free article] [PubMed]