Nanoparticle Brownian motion and hydrodynamic interactions in the presence of flow fields

Abstract

We consider the Brownian motion of a nanoparticle in an incompressible Newtonian fluid medium (quiescent or fully developed Poiseuille flow) with the fluctuating hydrodynamics approach. The formalism considers situations where both the Brownian motion and the hydrodynamic interactions are important. The flow results have been modified to account for compressibility effects. Different nanoparticle sizes and nearly neutrally buoyant particle densities are also considered. Tracked particles are initially located at various distances from the bounding wall to delineate wall effects. The results for thermal equilibrium are validated by comparing the predictions for the temperatures of the particle with those obtained from the equipartition theorem. The nature of the hydrodynamic interactions is verified by comparing the velocity autocorrelation functions and mean square displacements with analytical and experimental results where available. The equipartition theorem for a Brownian particle in Poiseuille flow is verified for a range of low Reynolds numbers. Numerical predictions of wall interactions with the particle in terms of particle diffusivities are consistent with results, where available.

INTRODUCTION

A significant aspect of modeling nanoparticle motion in an incompressible fluid is the accurate evaluation of the associated momentum transport with or without bulk fluid flow. The modeling should account both for the Brownian motion and the hydrodynamic interactions and resolve the translational and rotational motions that arise. Effects of particle locations in the flow domain and of the presence of the wall must be delineated. The effects on particle diffusivity must be resolved.

The theory of non-equilibrium statistical mechanics indicates that the influence of thermal fluctuations on a mechanical system can typically be represented through the addition of thermal forcing terms to the equations governing the system. The thermal forcing terms following the statistics of a white nose rapidly decorrelate in time. The related hydrodynamics, however, involves a non-trivial structure of correlations between the state variables. In order to achieve thermal equilibrium, the correlations should be such that there is an energy balance between the thermal forcing and the dissipation of the system as required by the fluctuation-dissipation theorem.^{1, 2}

In Brownian simulations, there exist two different approaches to couple the thermal fluctuations with the hydrodynamic interactions. These are Langevin approach³ and fluctuating hydrodynamics approach.⁴ In the present study, we adopt the fluctuating hydrodynamics approach. This essentially consists of adding stochastic stresses to the stress tensor (random stress) and stochastic fluxes to the heat flux (where an energy equation is present in the formulation).⁵

Over the past decades, numerical simulations of the fluctuating hydrodynamics approach have been carried out employing the finite volume method,^{6, 7} lattice Boltzmann method (LBM),^{8, 9, 10, 11, 12, 13, 14} and stochastic immersed boundary method.¹⁵ A coarse-graining methodology has been developed to bridge molecular dynamics and fluctuating hydrodynamic simulations.^{16, 17} Serrano and Español¹⁸ and Serrano et al.¹⁹ have solved the fluctuating hydrodynamic Navier-Stokes equations without a particle using the finite volume Lagrangian discretization in a moving Voronoi grid. They have ensured that their discretized governing equations cast in the general equation for non-equilibrium reversible∕irreversible coupling (GENERIC) formalism^{20, 21} satisfies the fluctuation-dissipation theorem. The GENERIC formalism proposed by Grmela and Öttinger²⁰ and Öttinger and Grmela²¹ ensures the correct treatment of thermal fluctuations and fluctuating hydrodynamics. Patankar has simulated the thermal motion of two dimensional particles in a stationary medium with the finite element method (FEM).¹¹ Sharma and Patankar⁶ have employed a distributed-Lagrangian multiplier (DLM) based finite volume method to simulate the thermal motion of particles. The computational domain is periodic in all directions and the thermal fluctuations are included in the fluid equations using random stress tensor. They have validated the numerical results by comparison with analytical expressions. Nie and Lin¹⁴ have employed the fluctuating LBM to simulate Brownian motion of particles and have validated their numerically obtained velocity autocorrelation function (VACF) by comparison with theoretical predictions. It is shown that the temperature characterizing translational motion of the particle in three coordinate directions agrees with each other after a lapse of time, but the predicted particle temperature is 15% lower than the effective temperature of the fluid fluctuations. This is in accord with the earlier findings of Ladd,¹⁰ who first proposed the use of fluctuating LBM. Adhikari et al.¹² have established agreement between fluctuation and dissipation by introducing ghost noise to the fluctuating LBM in the formulation (see Dünweg and Ladd¹³ for further discussions of Ref. 12).

In this paper, we employ a direct numerical simulation (DNS) based on arbitrary Lagrangian-Eulerian (ALE) FEM (Refs. ^{22, 23, 24, 25}) to accurately resolve the complicated fluid-particle interfacial motions. Both translational and rotational motions of a nanoparticle in a (i) stationary fluid medium and (ii) Poiseuille flow are investigated. Heat flux (energy equation) is not considered. An unstructured finite element mesh, generated by the Delaunay-Voronoi method,²⁶ has enabled a significantly higher number of mesh points in the regions of interest (i.e., close to the particle and wall surfaces compared to the regions farther away). This feature also keeps the overall mesh size computationally reasonable even with a nanoparticle moving in a very large domain.^{22, 23, 27, 28, 29} Thermal fluctuations are included in the equations of linearized hydrodynamics by adding stochastic components to the stress tensor as white noise in space and time.^{4, 30} As noted in Español et al.,³⁰ “even though the original equations of fluctuating hydrodynamics are written in terms of stochastic partial differential equations, at a very fundamental level, the inclusion of thermal fluctuations requires always the notion of a “mesoscopic cell” in order to define the fluctuating quantities.” In Español et al.,³⁰ it is shown that fluctuating hydrodynamic equations discretized in terms of finite element shape functions based on the Delaunay triangulation satisfy the fluctuation-dissipation theorem. The numerical schemes for the implementation of thermal fluctuations in the Landau-Lifshitz Navier-Stokes equations are expected to perform very delicate tasks^{31, 32} and obtaining accurate numerical results is a challenging endeavor.

It has been extensively discussed in the literature that the relation between fluctuation and dissipation is impacted by the compressibility of the fluid.^{33, 34, 35, 36} However, our objective is to keep the numerical model within the frame work of an incompressible liquid assumption. To account for compressibility, following Zwanzig and Bixon,³⁴ we modify the numerically predicted results to take into account the energy carried by sound waves. For real liquids of technological interest, such as water, blood etc., a numerical route to simulate the hydrodynamics is only practical by invoking this feature. With a finite element model, the accounting for the compressibility in the liquid medium would be very complicated, even if we knew the highly non-trivial equation of state. Furthermore, the approach employed in this paper is easily extendable to several biological applications.^{37, 38}

The chief motivation for the present study is the simulation of a nanoparticle thermal motion in a fluid flow that occurs in targeted drug delivery (TDD) and microparticle flows, such as the motion of a particle through a nanochannel.^{39, 40} In TDD, the drug carrying nanocarriers are intravascularly introduced into the vasculature.^{41, 42, 43} The drug-laden nanocarriers are functionalized with ligands (e.g., antibodies) and recognize specific determinants (receptors) expressed by endothelial cells.^{38, 44} The receptor-ligand binding interactions at the involved sites define the efficacy of nanocarrier arrest by the targeted cell. Since the drug-laden nanocarrier, essentially neutrally buoyant, is delivered to a therapeutic target via the vasculature, its motion in a bloodstream has to be determined accurately. In order to achieve this goal, as a first step, it is necessary to determine the motion of a nanocarrier (due to thermal and hydrodynamic effects) in an incompressible Newtonian fluid. The numerical methodology developed in this study is aimed at that objective.

The paper is organized as follows. Section 2 describes the mathematical formulation of the problem. Section 3 explains the Galerkin finite element formulation of the momentum equations and the generation of random stress tensor for a tetrahedron finite element mesh. Numerical results and discussions along with the validations are presented in Sec. 4, and the conclusions are in Sec. 5.

FORMULATION OF THE PROBLEM

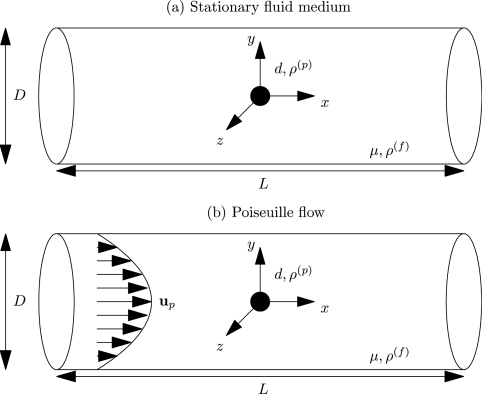
The Brownian motion of a nanoparticle in an incompressible Newtonian fluid contained in a horizontal circular vessel is considered. The fluid and particle equations are formulated in an inertial frame of reference with the origin coinciding with the center of the vessel (Figure 1). The diameter, D, and the length, L, of the vessel (tube) are very large compared to the particle size, d, the diameter of the particle. Two different cases are considered: a fluid at rest in a cylindrical vessel and a fully developed Poiseuille flow in a circular tube. Initially, a nanoparticle is introduced either at the vessel (tube) centerline or at suitably chosen locations away from the center line towards the bounding wall. In the numerical simulation for Poiseuille flow, the particle is initially fixed at the starting location and the flow is allowed to evolve until the flow is fully developed in the entire domain.²⁸ Then, the particle is released and allowed to move. This way, the velocity profiles in the flow cases are fully developed in the domain of interest, and the calculations are effected in the fully developed regime. No body force is considered either for the particle or for the fluid domain. At time t=0, the nanoparticle is subjected to Brownian motion in each case. The motion of the nanoparticle is determined by the hydrodynamic forces and torques acting on the particle and the wall interactions.

Figure 1.

Schematic representation of a nanoparticle in a cylindrical vessel (tube) (not to scale). Diameter of the tube: D=10 μm; length of the tube: L=10 μm; diameter of the nanoparticle: d(500 nm≤d≤1000 nm); viscosity of the fluid: μ=10^-3 kg∕ms; density of the fluid and the nanoparticle: ρ^(f)=10³ kg∕m³ and 990 kg∕m³≤ρ^(p)≤1010 kg∕m³. Particle locations away from the center are not displayed in this figure.

Governing equations and boundary conditions

The motion of an incompressible Newtonian fluid satisfies the conservation of mass and momentum given by

$$\nabla ·\mathbf{u}=0,$$ (1)

$${\rho }^{(f)}\frac{D\mathbf{u}}{\mathit{Dt}}=\nabla ·\mathbf{\sigma },$$ (2)

where u and ρ^(f) are the velocity and density of the fluid, respectively, and σ is the stress tensor. The material derivative of the velocity in Eq. 2 is given by

$$\frac{D\mathbf{u}}{\mathit{Dt}}=\frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u}·\nabla )\mathbf{u}.$$ (3)

For a Newtonian fluid, the stress tensor is given by

$$\mathbf{\sigma }=-p\mathbf{J}+2\mu \mathbf{D}[\mathbf{u}]+\mathbf{S};\mathbf{D}[\mathbf{u}]=\frac{1}{2}[\nabla \mathbf{u}+{(\nabla \mathbf{u})}^T],$$ (4)

where p is the pressure, J is the identity tensor, μ is the dynamic viscosity, D[u] is the rate of deformation tensor, and S is the random stress tensor. S is assumed to be a Gaussian with

$$〈S_{\mathit{ij}}(\mathbf{x},t)〉=0〈S_{\mathit{ik}}(\mathbf{x},t)S_{\mathit{lm}}({\mathbf{x}}^{}\mathit{\prime },t^{}\prime )〉=2k_{B}T\mu ({\delta }_{\mathit{il}}{\delta }_{\mathit{km}}+{\delta }_{\mathit{im}}{\delta }_{\mathit{kl}})\delta (\mathbf{x}-{\mathbf{x}}^{}\prime )\delta (t-t^{}\prime ),$$ (5)

where 〈〉 is the ensemble average, k_B is the Boltzmann constant, T is the absolute temperature, δ_ij is the Kronecker delta, and the Dirac delta function δ(x-x^′) denotes that the components of the random stress tensor are spatially uncorrelated (Markovian). The right hand side of Eq. 5 shows that the mean and variance of the thermal fluctuations are chosen to be consistent with the fluctuation-dissipation theorem^{4, 20, 21, 45} for an incompressible fluid. By including this stochastic stress tensor due to the thermal fluctuations in the governing equations, the macroscopic hydrodynamic theory is generalized to include the relevant physics of the mesoscopic scales ranging from tens of nanometers to a few microns.

For a rigid particle suspended in an incompressible Newtonian fluid, the translational motion of the particle satisfies Newton’s second law,

$$m\frac{d\mathbf{U}}{\mathit{dt}}=\mathbf{F},$$ (6)

and the rotational motion satisfies the Euler equation,

$$\frac{d(\mathbf{I}\mathbf{\omega })}{dt}=T,$$ (7)

where m is the mass of the particle, I is its moment of inertia, and U and ω are the translational and angular velocities of the particle, respectively. The hydrodynamic force F and the torque T acting on the particle are given by

$$\mathbf{F}=-{\int }_{\partial {\Sigma }_p}\mathbf{\sigma }·\stackrel{\wedge }{\mathbf{n}}\mathit{ds};\mathbf{T}=-{\int }_{\partial {\Sigma }_p}(\mathbf{x}-\mathbf{X})\times (\mathbf{\sigma }·\stackrel{\wedge }{\mathbf{n}})\mathit{ds},$$ (8)

where X is the position of the centroid of the particle, (x-X) is a vector from the center of the particle to a point on its surface, ∂Σ_p denotes the particle surface, and $\stackrel{\wedge }{\mathbf{n}}$ is the unit normal vector on the surface of the particle pointing into the particle.

The initial conditions for the problem are

$$\mathbf{U}(t=0)=0\mathbf{u}(t=0)=0\mathrm{on}{\Sigma }_0-\partial {\Sigma }_i,$$ (9)

and the boundary conditions are given by

$$\mathbf{u}={\mathbf{u}}_p\mathrm{on}\partial {\Sigma }_i,$$ (10)

$$\mathbf{\sigma }·\stackrel{\wedge }{\mathbf{n}}=0\mathrm{on}\partial {\Sigma }_o,$$ (11)

$$\mathbf{u}=\mathbf{U}+\mathbf{\omega }\times (\mathbf{x}-\mathbf{X})\mathrm{on}\partial {\Sigma }_p,$$ (12)

where _up is the prescribed velocity (zero or fully developed Poiseuille flow inlet profile), Σ₀ is the domain occupied by the fluid, and ∂Σ_i and ∂Σ_o are the inlet and outlet boundaries, respectively. The stochastic governing equations 1, 2, 3, 4, 5, 6, 7 along with the initial and boundary conditions 9, 10, 11, 12 are solved numerically. It is assumed that there is no body torque acting at any point in the fluid and the viscous stress tensor, σ, is symmetric. The fluctuation-dissipation theorem for the random stress tensor of the fluid requires that S is symmetric as well.^{21, 46}

COMBINED FLUID-SOLID WEAK FORMULATION

Owing to the complex nature of the shape of the fluid-particle domain, finite-element techniques are particularly useful for discretizing the governing fluid equations. For this purpose, a weak formulation that incorporates both the fluid and particle equations 1, 2, 6, and 7 is considered.^{22, 23, 27, 29}

Let, V be the function space given by

$$\mathbb{V}=\left\{\begin{array}{c}V=(u,U,\text{ω}) | u\in H^1,(U,\text{ω})\in {ℛ}^3,\\ u=U+\text{ω}\times \left(x-X\right) \text{on} \partial {\Sigma }_p \text{on} u=u_p \text{on} \partial {\Sigma }_i.\end{array}\right\}.$$ (13)

Here, Hilbert space H¹ is defined on the fluid domain, and the particle velocities belong to the three dimensional real space ℜ³. The square integrable L2 -functions in an L² space is chosen for the pressure and is denoted by

$$\mathbb{P}=\{p|p\in L^2\}.$$ (14)

The test function V (variation) is considered as follows to derive the weak formulation for the combined fluid-particle system,

$$\tilde{\mathbf{V}}=(\tilde{\mathbf{u}},\tilde{\mathbf{U}},\tilde{\mathbf{\omega }})\in {\mathbb{V}}_0.$$ (15)

Here, the variational space _V0 is the same as V, except that u=0 on ∂Σ_i. Multiplying Eq. 2 by the test function for the fluid velocity, $\tilde{\mathbf{u}}$, and integrating over the fluid domain at time t gives

$${\int }_{{\Sigma }_0}{\rho }^{(f)}\frac{D\mathbf{u}}{\mathit{Dt}}·\tilde{\mathbf{u}}\mathit{dV}+{\int }_{{\Sigma }_0}\mathbf{\sigma }:\nabla \tilde{\mathbf{u}}\mathit{dV}-{\int }_{\partial {\Sigma }_p}(\mathbf{\sigma }·\stackrel{\wedge }{\mathbf{n}})·\tilde{\mathbf{u}}\mathit{ds}=0.$$ (16)

It should be noted that the variations for each variable introduced above are arbitrary except on the particle surface, where the no-slip boundary condition 12 enforces the equality of variations of fluid and particle velocities given by the following relation

$$\tilde{\mathbf{u}}=\tilde{\mathbf{U}}+\tilde{\mathbf{\omega }}\times (\mathbf{x}-\mathbf{X})\mathrm{on}\partial {\Sigma }_p.$$ (17)

Using the equations of motion for the particles 6, 7, the surface integral in Eq. 16 may be rewritten as follows:

$$-{\int }_{\partial {\Sigma }_p}(\mathbf{\sigma }·\stackrel{\wedge }{\mathbf{n}})·\tilde{\mathbf{u}}\mathit{ds}=-\tilde{\mathbf{U}}·{\int }_{\partial {\Sigma }_p}(\mathbf{\sigma }·\stackrel{\wedge }{\mathbf{n}})\mathit{ds}-\tilde{\mathbf{\omega }}·{\int }_{\partial {\Sigma }_p}(\mathbf{x}-\mathbf{X})\times (\mathbf{\sigma }·\stackrel{\wedge }{\mathbf{n}})\mathit{ds}=\tilde{\mathbf{U}}·\left[m\frac{d\mathbf{U}}{\mathit{dt}}\right]+\tilde{\mathbf{\omega }}·\left[\mathbf{I}\frac{d\mathbf{\omega }}{\mathit{dt}}\right].$$ (18)

Substituting for stress tensor σ from Eqs. 4, 18 into Eq. 16, the combined fluid-particle momentum equation for the fluctuating hydrodynamics method is given by

$${\int }_{{\Sigma }_0}{\rho }^{(f)}\frac{D\mathbf{u}}{\mathit{Dt}}·\tilde{\mathbf{u}}\mathit{dV}-{\int }_{{\Sigma }_0}p(\nabla ·\tilde{\mathbf{u}})\mathit{dV}+{\int }_{{\Sigma }_0}\{\mu [\nabla \mathbf{u}+{(\nabla \mathbf{u})}^T]+\mathbf{S}\}:\nabla \tilde{\mathbf{u}}\mathit{dV}+\tilde{\mathbf{U}}·\left[m\frac{d\mathbf{U}}{\mathit{dt}}\right]+\tilde{\mathbf{\omega }}·\left[\mathbf{I}\frac{d\mathbf{\omega }}{\mathit{dt}}\right]=0.$$ (19)

The weak formulation for the mass conservation equation is obtained in a similar fashion. Let, $\tilde{p}$ be the variation of pressure p such that $\tilde{p}\in \mathbb{P}$. Here, the function space for both $\tilde{p}$ and p are chosen to be the same. The weak form of Eq. 1 is then given by

$${\int }_{{\Sigma }_0}\tilde{p}(\nabla ·\mathbf{u})\mathit{dV}=0.$$ (20)

The domain movement is handled by an ALE scheme. The details of mesh, its movement techniques, temporal discretization of time derivatives, and spatial discretization of the domain are described below.

Random stress tensor for the tetrahedral finite element mesh

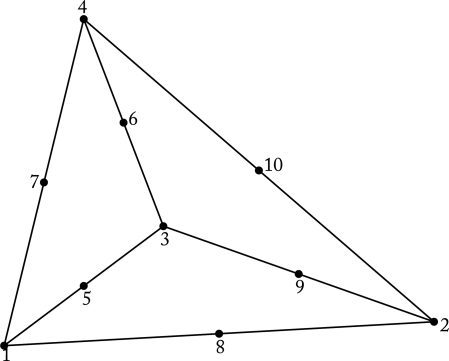
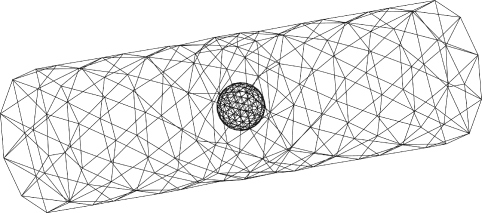
Following Hu,²² Hu et al.,²³ and Hughes et al.,⁴⁷ the computational domain is covered by a finite element mesh generated using Delaunay-Voronoi methods. In this study, the fluid domain is discretized by quadratic irregular tetrahedral elements. Since the stochastic stresses in Eq. 19 are fundamental to this problem, we now describe the procedure for numerical simulation of the random stresses associated with the unstructured tetrahedron mesh while conserving the volume. A typical element is shown in Figure 2. Figure 3 shows a triangular mesh discretizing the surface of the fluid domain (cylinder) and the surface of the nanoparticle. The discretization of the fluid domain changes at each time step of the simulation due to the motion of the nanoparticle.

Figure 2.

Representation of a 10-node tetrahedron.

Figure 3.

Finite element surface mesh of a cylindrical tube with one spherical nanoparticle.

Let V be the total volume of the system. The volume of each quadratic tetrahedral element V_e depends on the state of the mesh. The variance of the random stress tensor (Eq. 5) depends on this volume element. The random stress tensor is generated per tetrahedral element based on its volume such that total volume of the system

$$V\approx \sum _{i=1}^{N_e}{V}_e^{(i)}$$ (21)

is conserved, where $V_e^{(i)}$ represents the volume of the ith tetrahedral element and N_e is the number of elements in the finite element mesh. Each quadratic tetrahedron element has four vertices (numbered 1-4 in Figure 2) and six middle nodes (numbered 5-10 in Figure 2).

The random stress tensor S from Eq. 5 in each tetrahedral element becomes

$$\begin{array}{c}\multicolumn{1}{c}{〈S_{\mathit{xx}}〉=〈S_{\mathit{yy}}〉=〈S_{\mathit{zz}}〉=0,〈S_{\mathit{xy}}〉=〈S_{\mathit{yz}}〉=〈S_{\mathit{zx}}〉=0,〈S_{\mathit{xx}}^2〉=〈S_{\mathit{yy}}^2〉=〈S_{\mathit{zz}}^2〉=\frac{4k_{B}T\mu }{V_e\Delta t},〈S_{\mathit{xy}}^2〉=〈S_{\mathit{yz}}^2〉=〈S_{\mathit{zx}}^2〉=\frac{2k_{B}T\mu }{V_e\Delta t},}\end{array}$$ (22)

where Δt is the time step for the numerical simulation. Recall that the random stress tensor S is present in Eq. 19. As stated earlier, an unstructured finite element mesh enables a significantly higher number of mesh points near the nanoparticle and wall surfaces compared to regions far away. As a result, the volume of the tetrahedral elements closer to the particle is much smaller than the elements far away.

Mesh movement: ALE technique

When a nanoparticle moves in a fluid medium, the domain of interest occupied by the fluid is irregular and changes with time. An ALE technique has been used to handle the movement of this domain. The material derivative of u(x,t) in an ALE formulation is given as

$$\frac{D\mathbf{u}}{\mathit{Dt}}(\mathbf{x},t)=\frac{\delta \mathbf{u}}{\delta t}+[(\mathbf{u}-{\mathbf{u}}_m)·\nabla ]\mathbf{u},$$ (23)

where

$$\frac{\delta \mathbf{u}}{\delta t}={\frac{\partial }{\partial t}\mathbf{u}(\mathbf{x}(\varphi ,t),t)|}_{\varphi \mathit{is}\mathit{fixed}}\mathrm{and}\frac{d}{\mathit{dt}}\mathbf{x}(\varphi ,t)={\mathbf{u}}_m$$ (24)

are, respectively, the referential time derivative and the mesh velocity (domain velocity). The function x(ϕ,t) is the mapping from the fixed referential frame to the spatial domain Σ₀(t), domain occupied by the fluid at a given time instant t. When the referential and spatial domains coincide at the current instant, u_m=0, the referential time derivative in Eq. 23 reduces to the local Eulerian time derivative. When the mesh velocity coincides with the particle velocity, _um=u, the referential time derivative in Eq. 23 regains the Lagrangian time derivative.

The mesh velocity in Eq. 24 is arbitrary in the interior of the domain. The mesh velocity on the boundaries has to follow the motion of the particle and the motion of the confining fluid geometry. The movement of all the interior vertices is computed using the Laplace’s equation

$$\nabla ·({\varepsilon }_e\nabla {\mathbf{u}}_m)=0\mathrm{in}\Sigma (t),$$ (25)

$${\mathbf{u}}_m=\mathbf{U}+\mathbf{\omega }\times (\mathbf{x}-\mathbf{X})\mathrm{on}\partial {\Sigma }_p,$$ (26)

$${\mathbf{u}}_m=(\mathbf{U}·\stackrel{\wedge }{i})\stackrel{\wedge }{i}\mathrm{on}\partial {\Sigma }_i\partial {\Sigma }_o,$$ (27)

$${\mathbf{u}}_m=(\mathbf{U}·\stackrel{\wedge }{i})\stackrel{\wedge }{i}\mathrm{on}\partial {\Sigma }_w,$$ (28)

where ∂Σ_w denotes the tube wall and $\stackrel{\wedge }{i}$ is a unit vector along the axis of the tube. The volume of the tetrahedral elements closer to the particle is much smaller than the elements far away. Here, function ɛ_e controls the deformation of the mesh, such that the regions away from the particle absorb most of the deformation, while the region close to the particle is relatively stiff. We choose ɛ_e=1∕V_e, where V_e is the volume of the quadratic tetrahedral element. Similarly, the acceleration field, a_m(x,t), of the mesh vertices is chosen to satisfy

$$\nabla ·({\varepsilon }_e\nabla {\mathbf{a}}_m)=0\mathrm{in}\Sigma (t),$$ (29)

$${\mathbf{a}}_m=\frac{d\mathbf{U}}{\mathit{dt}}+\frac{d\mathbf{\omega }}{\mathit{dt}}\times (\mathbf{x}-\mathbf{X})-\mathbf{\omega }\times \mathbf{U}\mathrm{on}\partial {\Sigma }_p,$$ (30)

$${\mathbf{a}}_m=(\frac{d\mathbf{U}}{\mathit{dt}}·\stackrel{\wedge }{i})\stackrel{\wedge }{i}\mathrm{on}\partial {\Sigma }_i\partial {\Sigma }_o,$$ (31)

$${\mathbf{a}}_m=(\frac{d\mathbf{U}}{\mathit{dt}}·\stackrel{\wedge }{i})\stackrel{\wedge }{i}\mathrm{on}\partial {\Sigma }_w.$$ (32)

This mesh acceleration field is used for the second order mesh movement scheme. The position of the particle and the nodal points of the mesh are updated explicitly. Particle and fluid velocities are calculated semi-implicitly. This explicit-implicit scheme is numerically unconditionally stable. The weak formulations for Eqs. 25, 29 are obtained in a way similar to that outlined in Sec. 3.

Spatial and temporal discretization

A numerical simulation at a mesoscopic scale involving a particle in a fluid could be based on a discretization of the Eqs. 1, 2, 3, 4, 5, 6, 7. However, the discrete forms have to satisfy the fluctuation-dissipation theorem.^{6, 18, 19, 20, 21, 48, 49} Español and Zúñiga⁵⁰ and Español et al.³⁰ have shown that a well behaved set of discrete equations obtained in terms of the finite element shape functions based on the Delaunay triangulation conserves mass, momentum, and energy while ensuring thermodynamic consistency. Furthermore, Español et al.³⁰ have cast their discrete hydrodynamic equations in the GENERIC structure and observed that the resulting reversible matrix does not satisfy the Jacobi identity and the degeneracy conditions of GENERIC structure.^{20, 21} But, these conditions are of the order of the cell size and vanish in the continuum limit.³⁰ In effect, Español et al.³⁰ have shown that the finite element discretization procedure based on Delaunay triangulation is an appropriate procedure for discretizing the compressible fluctuating Navier-Stokes equations. In the present study, we obtain the discrete hydrodynamic equations using finite element shape functions based on the Delaunay-Voronoi tetrahedrizations.

The fluid domain is discretized by quadratic tetrahedral finite-elements (10 nodes defined per tetrahedron with 10 basis functions that are second-order polynomials; see Figure 2). The discrete solution for the fluid velocity is approximated in terms of piecewise quadratic functions and is assumed to be continuous over the domain (P2 elements). The discrete solution for the pressure is taken to be piecewise linear and continuous (P1 element). This P1∕P2 element for the pressure and the velocity is consistent with the Ladyzhenskaya-Babuska-Brezzi (LBB) or inf-sup condition and yields convergent solutions.^{22, 23} The pressure and the velocities of the fluid are associated with each node in the system, and the thermal noise (random stresses) is associated with each subelement in the system. The white noise property of stochastic stress tensor is implemented as an absence of correlations between different subelements.³⁰

The time derivatives in the combined fluid-solid weak formulation are discretized using a finite difference second-order Crank-Nicolson scheme. The time derivatives in Eq. 19 are replaced by the following expressions:

$$\frac{D\mathbf{u}}{\mathit{Dt}}(\mathbf{x},t_{n+1})\approx 2\frac{\mathbf{u}(\mathbf{x},t_{n+1})-\mathbf{u}(\mathbf{x}\prime ,t_n)}{\Delta t}-\frac{\delta \mathbf{u}}{\delta t}({\mathbf{x}}^{}\prime ,t_n)+[(\mathbf{u}(\mathbf{x},t_{n+1})-{\mathbf{u}}_m(\mathbf{x},t_{n+1}))·\nabla ]\mathbf{u}(\mathbf{x},t_{n+1}),$$ (33)

$$\frac{d\mathbf{U}}{\mathit{dt}}(t_{n+1})\approx 2\frac{\mathbf{U}(t_{n+1})-\mathbf{U}(t_n)}{\Delta t}-\frac{d}{\mathit{dt}}\mathbf{U}(t_n),$$ (34)

$$\frac{d}{\mathit{dt}}\left(\mathbf{I}\mathbf{\omega }\right)(t_{n+1})\approx 2\frac{\left(\mathbf{I}\mathbf{\omega }\right)(t_{n+1})-\left(\mathbf{I}\mathbf{\omega }\right)(t_n)}{\Delta t}-\frac{d}{\mathit{dt}}\left(\mathbf{I}\mathbf{\omega }\right)(t_n),$$ (35)

where Δt=t_n+1-t_n and $\mathbf{x}=\mathbf{x}\prime +{\mathbf{u}}_m(\mathbf{x}\prime ,t_n)\Delta t+{\mathbf{a}}_m(\mathbf{x}\prime ,t_n)\frac{{(\Delta t)}^2}{2}$. In order to prevent the distortion of the shape of the rigid particle during simulation, the nodes on the particle surface are reset to the surface at each time step.

The translational and rotational motions of the particle are updated using a second order explicit method as

$$\mathbf{X}(t_{n+1})=\mathbf{X}(t_n)+\Delta t\mathbf{U}(t_n)+\frac{{(\Delta t)}^2}{2}\frac{d\mathbf{U}}{\mathit{dt}}(t_n),$$ (36)

$$\mathbf{\Theta }(t_{n+1})=\mathbf{\Theta }(t_n)+\Delta t\mathbf{\omega }(t_n)+\frac{{(\Delta t)}^2}{2}\frac{d\mathbf{\omega }}{\mathit{dt}}(t_n).$$ (37)

For a given finite element mesh and with the finite element interpolation functions as described above, the combined fluid-solid weak formulations 19, 20 would reduce to a nonlinear system of algebraic equations, which is solved by a Newton-Raphson algorithm. Similarly, the weak formulations for the mesh velocity 25 and the mesh acceleration 29 are also reduced to linear systems of algebraic equations. These linear system of algebraic equations are solved using a biconjugate gradient stabilized algorithm.⁵¹

Time scales

The time scale for the computation of the Brownian motion of the particle may be derived from evaluating the various time scales (macroscopic and mesoscopic) governing the problem. The different time scales involved in this study are (i) hydrodynamic time scale, τ_ν=a²∕ν (the time scale for momentum to diffuse over a distance equal to the radius of the nanoparticle); Brownian time scales, (ii) τ_b=m∕ζ^(t) (Brownian relaxation time over which velocity correlations decay in the Langevin equation), and (iii) τ_d=a²ζ^(t)∕k_BT (Brownian diffusion time over which the nanoparticle diffuses over a distance equal to its radius). Here, a is the radius of the nanoparticle, ν is the kinematic viscosity, and ζ^(t)=6πμa is the Stokes dissipative friction force coefficient for a sphere.

It is noted that the time scales encountered in this problem are such that τ_b<τ_ν<τ_d. For a nanoparticle of radius 250 nm, τ_b≈1.38×10^-8 s, τ_ν≈6.25×10^-8 s, and τ_d≈6.88×10^-2 s. As a consequence, the relevant time scales for the Brownian motion of a nanoparticle in an incompressible fluid can span many orders of magnitude. In this study, the time step for the numerical simulation Δt has been chosen such that the combined fluid-particle system reproduces the expected Brownian behavior (equipartition theorem, algebraic decay of VACF) arising due to thermal fluctuations. It is required that Δt be smaller than the smallest of all the physical time scales. The simulations presented in this study have been carried out for long enough durations to allow for the temperature of the particle to equilibrate—i.e., if N is the number of simulated time steps then N·Δt=t>>τ_ν.

NUMERICAL RESULTS AND DISCUSSION

In this section, we numerically predict (i) the translational and rotational temperatures of the nanoparticle with and without bulk flow; the temperature calculation is carried out till thermal equilibration is obtained between the particle and the fluid medium; (ii) the translational and rotational temperatures of nearly neutrally buoyant Brownian particles, thermally equilibrated, in a quiescent fluid; (iii) the translational and rotational velocity distributions of the nanoparticle motion with and without bulk flow; (iv) the translational and rotational VACFs in a quiescent fluid; (v) the translational and rotational mean square displacements (MSD) of the particle in a quiescent fluid, both for ballistic and diffusive regimes; (vi) the effects of the presence of the bounding wall on particles of different radii initially placed at various locations are evaluated for several cases with and without bulk flow; and (vii) provide the computational cost for fluctuating hydrodynamics. The various numerical predictions have been compared with analytical and experimental results, where available.

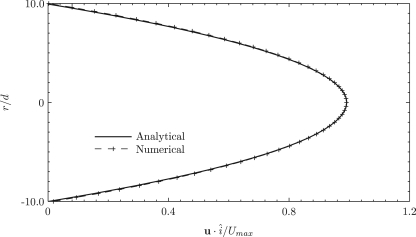
A solid spherical particle of radius a=250 nm is initially placed at the center of a cylindrical tube (R=5 μm) containing a Newtonian fluid. Both, quiescent and fully developed Poiseuille flows are considered. The computational domain moves with the particle, and from the particle location, the ends of the computational domain are at a distance of 20a at any instant of time.²⁷ For a Poiseuille flow, the prescribed velocity ${\mathbf{u}}_p=U_{\mathit{max}}(1-r^2∕R^2)\stackrel{\wedge }{i}$, where U_max is the maximum fluid velocity, and r is the radial distance of the tube from the center line (x-axis). As mentioned earlier, the particle is initially fixed at the starting location and the flow is allowed to evolve until the flow is fully developed in the entire domain.²⁸ The time taken for the flow to fully develop over the entire computational domain is t∕τ_ν=24. Now, the time is reset to zero and the particle is released. Figure 4 shows the fully developed analytical and the numerical profiles for Poiseuille flow in the cylindrical tube. The physical parameters used are k_B=1.3806503×10^-23kg m²∕s²K; μ=10^-3 kg∕ms; ρ^(f)=10³ kg∕m³; and five particle densities in the range, 990 kg∕m³≤ρ^(p)≤1010 kg∕m³. The temperature of the fluid is initially set to T=310 K and the particle at zero Kelvin. The maximum fluid velocities (for Poiseuille flow) presented in this study range from U_max=10^-4 to 10 mm∕s, relevant to some biological applications.³⁷ The flow Reynolds number (Re_f=ρ^(f)RU_max∕μ) ranges from 5×10^-7 to 5×10^-2 for Poiseuille flow. The particle Reynolds number (Re_p=ρ^(f)aU_max∕μ) ranges from 2.5×10^-8 to 2.5×10^-3 for Poiseuille flow. Before the introduction of the nanoparticle, we have ascertained that the solutions to the continuum equations of fluctuating hydrodynamics (Eqs. 1, 2, 3, 4, 5) reproduce the Gaussian field with regard to the distribution of fluid velocities in confirmation with results of Donev et al.⁷

Figure 4.

Analytical and computational profiles for Poiseuille flow in the xy slice. Profiles at inlet, outlet, and in the flow domain, in the absence of the particle are the same as shown here.

For a given nanoparticle of radius a and tube radius R, a “realization” consists of N time steps (approximately 10 s wall clock time for each time step that is generally considered in this study). The number of time steps depends upon equilibration of particle temperature or determination of VACFs and MSD. In order to ensure the uniqueness of the realizations, different initial seeds are chosen for a Gaussian random number generator.

Temperature of the nanoparticle

From the equipartition theorem, at thermal equilibrium, the translational and rotational temperatures of the nanoparticle are given by

$$T^{(t)}=\frac{m〈{\mathbf{U}}^2〉}{3k_B};T^{(r)}=\frac{\mathbf{I}〈{\mathbf{\omega }}^2〉}{3k_B}.$$ (38)

Since we have considered an incompressible fluid, in our simulations, to account for compressibility effects, the particle mass m is augmented by an added mass m₀∕2, where m₀ is the mass of the displaced fluid. In other words, the particle will respond to an imposed force as if its mass were M=m+m₀∕2, where M is the virtual or added mass of the particle.^{33, 34, 36} The rotational motion of the nanoparticle is unaffected by the incompressibility of the fluid. With the incompressibility assumption, the translational and rotational temperatures of the fluctuating nanoparticle are evaluated from

$$T^{(t)}=\frac{M〈{\mathbf{U}}^2〉}{3k_B};T^{(r)}=\frac{\mathbf{I}〈{\mathbf{\omega }}^2〉}{3k_B}.$$ (39)

Figure 5 shows the time evolution of the ensemble average of the mean square translational and rotational velocities of neutrally buoyant particle (a=250 nm), normalized by 3k_BT∕M and 3k_BT∕I, respectively, in a stationary fluid medium. These are obtained from five different realizations in each coordinate direction. Each realization consists of N=20000 time steps. Thus, to evaluate the equilibration of the particle temperature with the preset fluid temperature, we have employed 3×5×20000=300000 time steps. The temperatures characterizing translational and rotational motion of the particle agree with the preset temperature of the fluid within 5% error, after an initial transient. Furthermore, the number of realizations case has been arrived such that any further increase in the number of realizations does not significantly change the prediction of temperature equilibration.

Figure 5.

Time evolution of the mean square translational and rotational velocities of neutrally buoyant particle (a=250 nm) normalized by 3k_BT∕M and 3k_BT∕I, respectively, in a stationary fluid medium.

Figure 6 shows the translational and rotational temperatures of the particle in a stationary medium as a function of the normalized surface mesh length (mesh length divided by particle radius) for two different values of the step size Δt. The error bars have been plotted from standard deviations of the temperatures obtained with 15 different realizations (5 realizations in each direction). For a given Δt, convergence is noted as the normalized mesh size is decreased. Furthermore, for the appropriately chosen values of Δt, the convergence in the temperature is also noted. It is observed that translational and rotational temperatures of the nanoparticle agree with the preset temperature to within 5% error.

Figure 6.

Translational and rotational temperatures of the nanoparticle as a function of the normalized surface mesh length (mesh length divided by particle radius) for two different values of the computational time Δt in a stationary Newtonian fluid medium. The preset temperature is 310 K, and Δt∕τ_ν=0.0016,0.0008, ρ^(p)∕ρ^(f)=1.

Figure 7 shows that translational and rotational temperatures of nearly neutrally buoyant Brownian particles, thermally equilibrated, in a quiescent fluid medium are independent of the density of the particle in relation to that of fluid. This has been discussed in Hauge and Martin-Löf,⁴⁵ although no quantitative results specific to this issue are provided there.

Figure 7.

Translational and rotational temperatures of a nearly neutrally buoyant nanoparticle (a=250 nm) in a stationary fluid medium using fluctuating hydrodynamics approach as a function of the particle density normalized with fluid density.

Figure 8 shows the translational and rotational temperature equilibration of a nanoparticle initially placed at the center of a cylindrical tube as a function of the particle Reynolds number for Poiseuille flow. A convergence in the observed temperature is achieved for Δt=0.0016. It is observed that the calculated temperature of the nanoparticle in the Poiseuille flow is essentially independent of the fluid velocity for the range of Reynolds numbers investigated and agrees with the preset temperature (<5% error).

Figure 8.

Translational and rotational temperatures of the nanoparticle (a=250 nm) initially placed at the center of a cylindrical tube as a function of particle Reynolds number in Poiseuille flow. The preset temperature is 310 K and ρ^(p)∕ρ^(f)=1.

Velocity of the nanoparticle

At thermal equilibrium, the probability distribution of the velocity of the fluctuating nanoparticle follows the Boltzmann distribution. The equilibrium statistics of the three components of U and ω along the three coordinate directions are independent of each other.

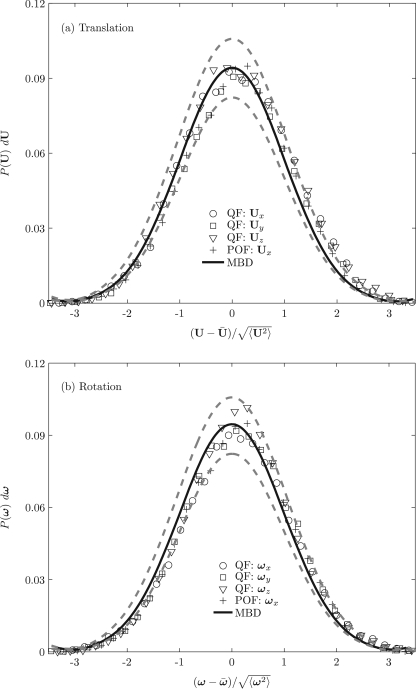
The apparent translational and rotational velocities of the nanoparticle are determined as $(\mathbf{U}-\stackrel{-}{\mathbf{U}})$ and $(\mathbf{\omega }-\stackrel{-}{\mathbf{\omega }})$, where $\stackrel{-}{\mathbf{U}}$ and $\stackrel{-}{\mathbf{\omega }}$ are the average translational and rotational velocities of the particle in the flowing incompressible fluid. For determining the velocity distribution of the nanoparticle, 5 realizations in each coordinate direction consisting of 5×20000=100000 time steps have been computed. Thus, a total of 300000 time steps have been computed. For the Poiseuille flow in the flow direction, 100000 time steps have been computed (5 realizations). In Figure 9, the numerically simulated components of $(\mathbf{U}-\stackrel{-}{\mathbf{U}})$ (Figure 9a) and $(\mathbf{\omega }-\stackrel{-}{\mathbf{\omega }})$ (Figure 9b) (represented by three different symbols) of the nanoparticle with radius a=250 nm are compared with the analytical Maxwell-Boltzmann distribution with a zero mean and variance of k_BT∕M and k_BT∕I, respectively. It is observed that each degree of freedom individually follows a Gaussian distribution. In particular, the mean and the variance calculated by using the fluctuating hydrodynamics approach agrees within 5% error (see dotted line in Figure 9) with that of the analytical Maxwell-Boltzmann distribution. This validates the numerical procedure employed in this study.

Figure 9.

Equilibrium probability of the (a) translational and (b) rotational velocities of the nanoparticle (a=250 nm) in a Newtonian fluid using fluctuating hydrodynamics for ρ^(p)∕ρ^(f)=1. QF: Quiescent fluid; POF: Poiseuille flow; MBD: Maxwell-Boltzmann distribution.

We have also computed that (i) the average velocity of the particle initially placed at the center of the tube in a Poiseuille flow with velocity U_max=0.01 m∕s (_up|_r=0=(0.01,0.0,0.0)m∕s) is equal to $\stackrel{-}{\mathbf{U}}∕\sqrt{k_{B}T∕M}=(1.49\pm 0.05,0.05\pm 0.05,0.004\pm 0.03)$ and $\stackrel{-}{\mathbf{\omega }}∕\sqrt{k_{B}T∕\mathbf{I}}=(0.001\pm 0.01,0.006\pm 0.004,0.004\pm 0.004)$, where the ± quantity denotes standard deviation calculated from five different realizations. The average translational velocity, $\stackrel{-}{\mathbf{U}}∕\sqrt{k_{B}T∕M}$, obtained here is consistent with ${\mathbf{u}}_p∕\sqrt{k_{B}T∕M}=(1.51,0.0,0.0)$; (ii) the average velocity of the particle initially placed at r=2R∕5 in a Poiseuille flow with velocity U_max=0.01m∕s (_up|_r=2R∕5=(0.0084,0.0,0.0)m∕s) is equal to $\stackrel{-}{\mathbf{U}}∕\sqrt{k_{B}T∕M}=(1.27\pm 0.02,0.03\pm 0.04,0.04\pm 0.02)$ and $\stackrel{-}{\mathbf{\omega }}∕\sqrt{k_{B}T∕\mathbf{I}}=(0.001\pm 0.01,0.005\pm 0.03,0.005\pm 0.146)$. When the particle is placed at r=2R∕5 in a Poiseuille flow, the average translational velocity, $\stackrel{-}{\mathbf{U}}∕\sqrt{k_{B}T∕M}$, obtained here is consistent with ${\mathbf{u}}_p{|}_{r=2R∕5}∕\sqrt{k_{B}T∕M}=(1.27,0.0,0.0)$ and the average rotational velocity of the particle is consistent with the average angular velocity, Ω(=1∕2(dU∕dr)|_r=2R∕5), of the particle in Stokes flow, $\Omega ∕\sqrt{k_{B}T∕\mathbf{I}}=(0.0,0.0,0.03)$.

VACF of the nanoparticle

A nanoparticle experiencing Brownian motion in a fluid is influenced by the hydrodynamic interactions. The fluid around the particle is dragged in the direction of motion of the particle. On the other hand, the motion of the particle is resisted by viscous forces arising due to its motion relative to the surrounding fluid. The momentum of the fluid surrounding the particle at any instant is related to its recent history. The friction coefficient is time dependent and is no longer given by the constant Stokes value.

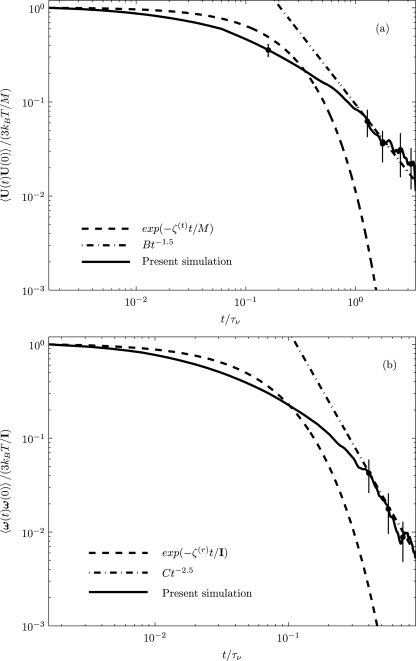
Figure 10 shows the VACF of the translational and rotational motions of a nanoparticle (a=250 nm) in a quiescent fluid medium in a circular vessel as obtained from our numerical simulations. For determining the VACF of the nanoparticle, 45 (15×3=45) realizations have been employed with total computation of 45×100000=4500000 time steps. It may be observed that the translational and rotational VACFs of the Brownian particle have power-law decays over long times that are ~t^-3∕2 and ~t^-5∕2, respectively.

Figure 10.

(a) Translational (B=Mρ^(f)1∕2∕12π^3∕2μ^3∕2) and (b) rotational (C=Iρ^(f)3∕2∕32π^3∕2μ^5∕2) VACFs of a neutrally buoyant Brownian particle (a=250 nm) in a stationary fluid medium in a circular vessel (R=5 μm) using fluctuating hydrodynamics.

In this context, Zwanzig and Bixon³³ have shown that for constant friction coefficient ζ^(t), the VACF of the particle in a simple fluid obeys

$$〈\mathbf{U}(t)\mathbf{U}(0)〉=\frac{3k_{B}T}{M}{e}^{-{\zeta }^{(t)}t∕M};〈\mathbf{\omega }(t)\mathbf{\omega }(0)〉=\frac{3k_{B}T}{\mathbf{I}}{e}^{-{\zeta }^{(r)}t∕\mathbf{I}},$$ (40)

which denote exponential decays, while for the time dependent friction coefficient, the decay of the VACF at long times obeys a power-law:⁴⁵

$$〈\mathbf{U}(t)\mathbf{U}(0)〉\approx \left(\frac{k_{B}T{\rho }^{(f)1∕2}}{4{\pi }^{3∕2}{\mu }^{3∕2}}\right)t^{-3∕2};〈\mathbf{\omega }(t)\mathbf{\omega }(0)〉\approx \left(\frac{3k_{B}T{\rho }^{(f)3∕2}}{32{\pi }^{3∕2}{\mu }^{5∕2}}\right)t^{-5∕2}.$$ (41)

Based on our numerical simulation, for the parameters considered, the translational VACF follows an exponential decay in the range for t≤0.343τ_ν and an algebraic tail for t≥1.202τ_ν. Our simulation also predicts the transitional range. Similarly, the rotational VACF follows an exponential decay, for t≤0.115τ_ν and an algebraic tail for t≥0.495τ_ν. Our computed results are in good agreement with the predictions of the above Eqs. 40, 41 for short and long times, respectively, and also predict the transition between the two. The error bars have been plotted from standard deviations of the decay at particular time instants obtained with 45 different realizations.

Diffusion of the nanoparticle

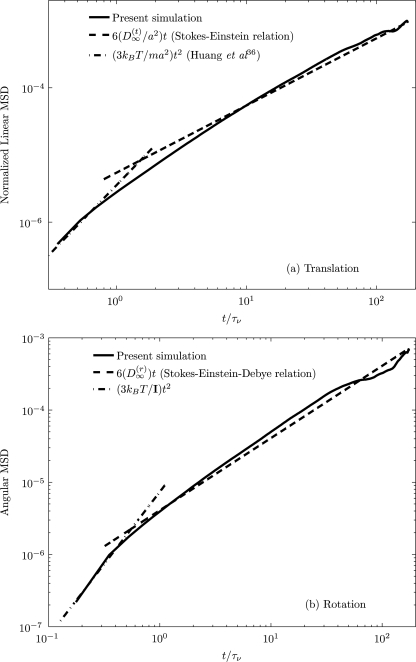
Figure 11 shows the numerically obtained translational and rotational MSDs (measures of diffusion) of a neutrally buoyant nanoparticle (a=250 nm) in a quiescent fluid medium, initially placed at the center of the vessel (R=5 μm), for both short and long times. It is observed that in the regime where the particle’s motion is dominated by its own inertia (ballistic), 0.346τ_ν≤t≤0.63τ_ν (translation), and 0.174τ_ν≤t≤0.316τ_ν (rotation), the translational and rotational motions of the particle follow (3k_BT∕M)t² and (3k_BT∕I)t², respectively. In the diffusive regime, t>>τ_b, and when t≥7τ_ν (translation) and t≥1.2τ_ν (rotation), the translational and rotational MSDs increase linearly in time to follow $6D_{\infty }^{(t)}t$ and $6D_{\infty }^{(r)}t$, respectively, where $D_{\infty }^{(t)}=k_{B}T∕{\zeta }^{(t)}$ and $D_{\infty }^{(r)}=k_{B}T∕{\zeta }^{(r)}$ (ζ^(r)=8πμa³) are the translational and rotational self-diffusion coefficients. The MSDs in an intermediate regime between the ballistic and the diffusive are related to hydrodynamic memory effects, and these are also displayed by our simulation. The above numerical estimates were developed from 45 realizations (3×5=45), each realization computed up to 100 000 time steps.

Figure 11.

The MSD of a neutrally buoyant Brownian particle (a=250 nm) in a stationary fluid medium using fluctuating hydrodynamics.

It is also observed from Figure 11 that in the diffusive regime, the translational and rotational MSDs of the particle follow Stokes-Einstein^{52, 53} and Stokes-Einstein-Debye⁵⁴ relations, respectively. Recently, Huang et al.³⁶ have experimentally investigated the Brownian motion of a single particle in a liquid and provided results for the translational MSDs in both the ballistic and the diffusive regimes corresponding to thermal equilibration. Our numerical predictions of ballistic and diffusive motion of a particle in a fluid are in good agreement with Huang et al.³⁶

Wall effects

As stated earlier, our main motivation for the present study is to simulate a nanoparticle thermal motion in a fluid flow that occurs in TDD and similar microparticle flows. In such flows, the hydrodynamic wall effects on the particle diffusivity are relevant. For a particle initially located at the center of the cylindrical vessel, the wall effects play a minimal role (≤3%, compared to an unbounded fluid domain) on the diffusion coefficient (see Figure 11).⁵⁵ When a particle of radius a is initially placed at a distance h from the tube wall to the center of the particle, h<R, the particle-wall interactions modify the particle diffusivity. For a≪ R, in a quiescent fluid, the Brownian motion near the vessel wall is similar to that of motion in the vicinity of a plane wall (curvature effects may be neglected).^{55, 56} For a particle initially located in the near vicinity of the wall, there is reduced space for the surrounding fluid to negotiate the particle and the corresponding drag force in a direction parallel to the wall is higher. The diffusivity of the particle in the proximity of the wall may be estimated to be $D_w^{(t)}=D_{\infty }^{(t)}{({\zeta }_w^{(t)}∕{\zeta }^{(t)})}^{-1}$ in x, y, and z directions,⁵⁷ while ${\zeta }_w^{(t)}$ depends on the particular direction.

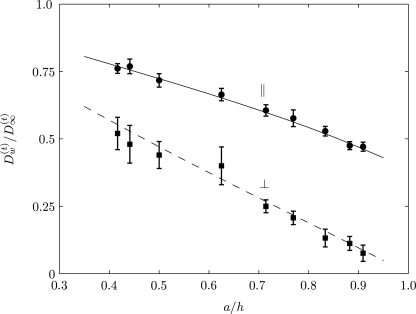
Figure 12 shows the numerically obtained parallel (x direction) and perpendicular (y direction) diffusion coefficients of neutrally buoyant particles of different radii initially placed at various distances from the tube wall, in a quiescent medium. As mentioned earlier, in the diffusive regime, the translational MSD of the particle increases linearly in time. We have numerically evaluated the gradient of the linear profile, normalized by the translational self-diffusion coefficient, $D_{\infty }^{(t)}$, plotted as a function of a∕h. Our numerical results are in agreement with the predictions of Happel and Brenner.⁵⁵

Figure 12.

The translational diffusion coefficient of neutrally buoyant Brownian particles of different radii a initially placed at different locations h from the wall of the circular vessel in a quiescent medium. Solid and dashed lines correspond to the perturbation solutions given in Happel and Brenner (Ref. ⁵⁵).

For the motion of a Brownian particle in shear flows, we have to consider an additional time scale $1∕\stackrel{·}{\gamma }$, where $\stackrel{·}{\gamma }$ is the rate of shear. Where ${\tau }_b\ll t\ll 1∕\stackrel{·}{\gamma }$, the effect of convection due to the shear flow is weak. This is referred to as the diffusive regime for shear flows. The regime where $t>>1∕\stackrel{·}{\gamma }$ is dominated by convection. In this study, we have only explored the diffusive regime. In this regime, for the time scales considered, the MSDs in x, y, and z directions are all $\approx 2D_{\infty }^{(t)}t$.^{58, 59}

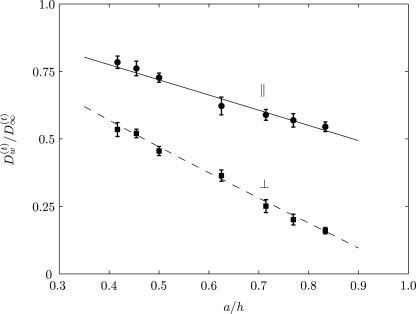
We have numerically evaluated the diffusivity of a particle, $D_w^{(t)}$, initially located close to the wall in Poiseuille flow. The flow and particle Reynolds numbers are Re_f=0.005 and Re_p=0.0025, respectively. Figure 13 shows the parallel (x direction) and perpendicular (y direction) translational diffusion coefficients which have been normalized with $D_{\infty }^{(t)}$ as a function of a∕h. These are for neutrally buoyant particles of different radii a initially placed at various locations h from the tube wall. There are analytical studies which predict the diffusivities, $D_w^{(t)}$, by perturbation theory.^{55, 57, 60} Our numerical predictions show good comparison with the theoretical results. This capability of the simulation is particularly useful in the context of TDD.

Figure 13.

The translational diffusion coefficient of neutrally buoyant Brownian particles of different radii a initially placed at different locations h from the wall of the circular tube in Poiseuille flow, in the diffusive regime ${\tau }_b\ll t\ll 1∕\stackrel{·}{\gamma }$. Solid and dashed lines correspond to the perturbation solutions given in Happel and Brenner (Ref. ⁵⁵) and Goldman et al. (Ref. ⁶⁰).

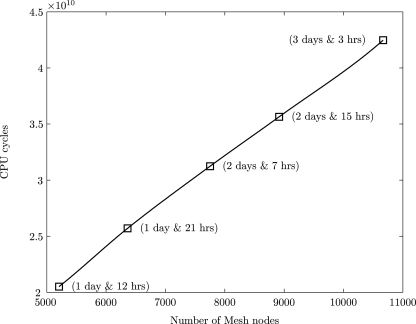
Figure 14 demonstrates the approximate number of CPU cycles required for the computation of a single time step for a particle of radius 250nm in a cylindrical tube of radius 5 μm. All simulations are carried out on a 2.93 GHz processor. Each CPU cycle displayed on the figure corresponds to the average of 300 time steps, spread across three realizations. The number of mesh nodes is displayed on the horizontal axis. Number of days required to complete the simulations with 20 000 time steps are specified inside the brackets and for 100 000 time steps this will be five times higher.

Figure 14.

Computational cost for fluctuating hydrodynamics. Number of days required to complete the simulations with 20 000 time steps are specified inside the brackets.

In regard to mesh nodes, we offer the following estimates from our numerical simulation corresponding to converged solutions. For a particle that is initially located at the center of the circular vessel in a quiescent medium, a small region (1 μm³ cube) around the particle (a=250 nm) is noted to have 34% of total number of mesh nodes in the entire volume, at convergence. For a particle initially located at a distance half way between the vessel center and the vessel wall (h=R∕2), in an equivalent volume, we note there are 35% of total number of mesh nodes. Finally, when h<R∕2, the estimate is 38%. These observations imply that for tracking a nanoparticle Brownian motion in a quiescent fluid, the mesh size has to be considerably smaller even at regions far away from the wall and would have to be finer in the vicinity of the wall. Our numerical simulation has handled these features in a comprehensive way yielding converged solutions to desired levels of accuracy (O(10^-9)).

CONCLUSIONS

A direct numerical simulation based on ALE FEM is employed to simulate the Brownian motion of a nanoparticle in an incompressible Newtonian fluid. Corrections for compressibility effects are introduced. The thermal force from the fluid is incorporated by the fluctuating hydrodynamics approach. Both the translational and rotational motions of a nanoparticle in (i) a quiescent fluid and (ii) a fully developed Poiseuille flow are considered. The thermal fluctuations are modeled as random stress tensors in the fluid equation that depend on the temperature and viscosity of the fluid. At thermal equilibrium, the numerical predictions are validated with analytical results, where available.

We have numerically predicted:

• (a)The translational and rotational temperatures of the particle with and without bulk flow. The temperature calculation is carried out till thermal equilibration is obtained between the particle and the fluid medium. Both for quiescent and Poiseuille flow, in the range of fluid velocities considered, the equipartition theorem is satisfied.
• (b)The translational and rotational temperatures of nearly neutrally buoyant Brownian particles, thermally equilibrated, in a quiescent fluid. These temperatures are noted to be independent of the density of the particle in relation to that of the fluid.
• (c)The translational and rotational velocity distributions of the nanoparticle motion with and without bulk flow.
• (d)The translational and rotational VACFs in a quiescent fluid. Over long times, the decay of the VACF captures algebraic tails for the translational (t^-3∕2) and the rotational (t^-5∕2) motions of the nanoparticle.
• (e)The translational and rotational MSDs of the particle in a quiescent fluid, both for ballistic and diffusive regimes. At short times, translational and rotational MSDs in a quiescent fluid are proportional to t², and in the diffusive regime (t>>τ_b), they agree with the Stokes-Einstein and Stokes-Einstein-Debye theories.
• (f)The effects of the presence of the bounding wall on particles of different radii initially placed at various locations are evaluated for several cases with and without bulk flow. The translational diffusion coefficients for parallel and perpendicular directions have been displayed. Very good agreement with published results, where available.

We have also provided the computational cost for fluctuating hydrodynamics.

In regard to biological applications intended in this study, it is noted that this method may be used to investigate the fluctuating motion of a nanocarrier in a particulate suspension where the dispersion in nanocarrier velocities are athermal in origin caused by collisions with red-blood cells. In such an application, the preset temperature must be replaced by a particulate temperature of blood plasma,³⁷ and this will form a part of our future work.