EMG analysis tuned for determining the timing and level of activation in different motor units

Abstract

Recruitment patterns and activation dynamics of different motor units greatly influence the temporal pattern and magnitude of muscle force development, yet these features are not often considered in muscle models. The purpose of this study was to characterize the recruitment and activation dynamics of slow and fast motor units from electromyographic (EMG) recordings and twitch force profiles recorded directly from animal muscles. EMG and force data from the gastrocnemius muscles of seven goats were recorded during in vivo tendon-tap reflex and in situ nerve stimulation experiments. These experiments elicited EMG signals with significant differences in frequency content (p<0.001). The frequency content was characterized using wavelet and principal components analysis, and optimized wavelets with centre frequencies, 149.94Hz and 323.13Hz, were obtained. The optimized wavelets were used to calculate the EMG intensities and, with the reconstructed twitch force profiles, to derive transfer functions for slow and fast motor units that estimate the activation state of the muscle from the EMG signal. The resulting activation-deactivation time constants gave r values of 0.98 to 0.99 between the activation state and the force profiles. This work establishes a framework for developing improved muscle models that consider the intrinsic properties of slow and fast fibres within a mixed muscle, and that can more accurately predict muscle force output from EMG.

Introduction

The mechanical output of a muscle is dictated by factors such as biochemistry, architecture, fibre composition, and recruitment patterns. Motor units are commonly recruited in an orderly fashion from the slowest to the fastest as stimulus strength increases (eg. Henneman and Olson, 1965; Freund et al. 1975; Hoffer et al., 1987); however, alternative recruitment strategies have been reported for varied mechanical demands (e.g. Grimby et al., 1981; Nardone et al., 1989; Sokoloff and Cope, 1996; Wakeling et al., 2006; Hodson-Tole and Wakeling, 2007). Although twitch properties of different fibre types have been well documented (i.e. Burke et al. 1973; Wakeling & Syme 2002), at present, the factors that influence motor unit recruitment remain unclear.

Several studies have characterized motor unit recruitment by analyzing the time-varying frequency spectra of myoelectric signals (reviews: Hodson-Tole and Wakeling, 2009; Reaz et al., 2006). This study utilizes the differences in spectral content of the signals from slow and fast motor units for their detection (Olson et al., 1968; Wakeling and Rozitis, 2004). Spectral properties of myoelectric signals are traditionally quantified by their mean or median frequency; however, those measures may incorporate factors other than motor unit type by including frequency components throughout the entire spectrum (Wakeling, 2009). Recently, several time-frequency analysis techniques have emerged for characterizing the time-varying frequency spectra of myoelectric signals (Karlsson et al., 2000; von Tscharner, 2000; Kumar et al., 2003). When accompanied with principal component analysis (PCA), these methods can resolve the major features of the intensity spectra and thus distinguish details of spectra shape of the myoelectric signal (von Tscharner, 2002;Wakeling and Rozitis 2004; Hodson-Tole and Wakeling 2007). The methods can be extended by tuning wavelets to the major components of the myoelectric spectra (identified using PCA: von Tscharner and Goepfert, 2006; Hodson-Tole and Wakeling, 2007). By using these optimized wavelets to analyze EMG signals, recruitment of the slow and fast motor units within a signal can be identified, and can be validated against physiological measurements.

Current Hill-type based muscle models calculate muscle force as a function of length, velocity, and activation level (Van Leeuwen, 1992; Epstein and Herzog, 1988). Common simplifying assumptions, such as constant activation-deactivation rates and homogenous fibre-type populations, hinder the development of more advanced models that acccount for known differences in the instrinsic properties of slow and fast fibres. Thus, the main purpose of this study was to derive functions that estimate the activation state of different motor units within muscles of mixed fibre populations using EMG intensities from different fibre types. To do so, we 1) determined a set of optimized wavelets that quantify the EMG intensities from slow and fast motor units, 2) obtained a corresponding set of twitch force profiles from slow and fast motor units, and 3) identified transfer functions that allow the activation state of the different motor units to be derived from their EMG intensities.

To obtain a set of EMG and force data that includes contributions from both slow and fast motor units, we conducted experiments on lateral and medial gastrocnemius (LG and MG) muscles of goats, which are composed of both slow and fast fibres. Goats were studied for two reasons. First, goats use their gastrocnemius muscles for a variety of tasks that may elicit different recruitment patterns, from slow movements such as walking to explosive movement such as jumping. Second, with goats, we were able to attach tendon buckles to the Achilles tendon to measure force; it is very difficult to directly measure muscle or tendon force from humans. Thus, goats were well-suited for this study because they allowed EMG and tendon force to be measured under in vivo and in situ conditions. This was necessary for developing the transfer functions to estimate the activation state of the muscle from EMG.

Methods

Seven African pygmy goats (Capra hircus L; 3 male, 4 female, age 11±5.5 months, mass 23±3.5kg) were tested at Harvard University’s Concord Field Station. EMG and tendon force data were recorded during a series of in vivo and in situ experiments, designed to excite predominantly slow motor units or both slow and fast motor units. The experimental protocol involved four main steps over a three-day period: (1) surgical implantation of transducers, (2) in vivo testing, (3) surgical implantation of nerve cuffs, and (4) in situ testing. All surgical procedures followed IACUC approval.

Surgical implantation of transducers

Animals were initially sedated with a mixed injection of ketamine and xylazine (8mg/kg body mass and 0.05 mg/kg body mass, respectively) into the jugular vein. The animals were then intubated and maintained on a closed system anesthesia machine (Matrix, Orchard Park, NY) at 0.5–1.0% isoflurane.

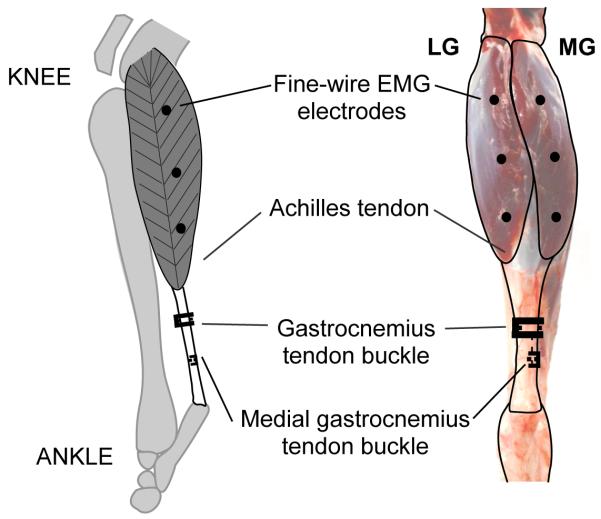
Three to six offset twist-hook bipolar silver-wire electrodes (0.1mm, California Fine Wire Inc., Grover Beach, CA) were implanted into the LG and MG of the left hind limb (Fig.1)(Loeb and Gans, 1986). The electrode tips were bared of 0.5 mm of insulation, separated by 2 mm, and implanted about 3 mm deep in the proximal, mid-belly, and distal portions of each muscle.

Figure 1.

Lateral (left) and posterior (right) view of the goat lower hind limb highlighting the lateral and medial gatrocnemius (LG and MG) muscles. The approximate locations of the EMG electrodes (proximal, mid-belly, and distal) and the common gastrocnemius and MG tendon-buckle force transducers are shown.

A lateral incision proximal to the ankle was made to expose the underlying tendons. An “E”-shaped stainless steel buckle transducer, equipped with a metal foil strain gauge (type FLA-1, Tokyo Sokki Kenkyujo; Biewener and Baudinette, 1995) was attached to the Achilles tendon (Fig.1). Lead wires from all transducers were fed through a subcutaneous tunnel to a connector that was sutured to the skin proximal to the hip. Animals received post-operative analgesia (buprenorphine 0.1 to 0.5mg/kg, subcutaneously) during a 24 hour recovery period. No animals showed signs of post-operative infection (no antibiotics were administered).

In vivo testing

Following the recovery period, tendon-tap reflex trials were performed. Each animal’s body weight was supported such that the hind limbs were relaxed. A custom-made accelerometer-instrumented reflex hammer was used to tap the Achilles tendon. Myoelectric signals were amplified (gain of 100-1000) and recorded with minimal filtering (bandpass 30-3000 Hz, notch filter at 60Hz) (P511J, Grass Technologies, West Warick, RI) (Fig.2). Tendon buckle signals were fed through a bridge amplifier (Vishay 2120, Micro-Measurements, Raleigh, NC). All signals were recorded at 5000 Hz using a 16-channel acquisition device (NI-6259, National Instruments, Austin, TX).

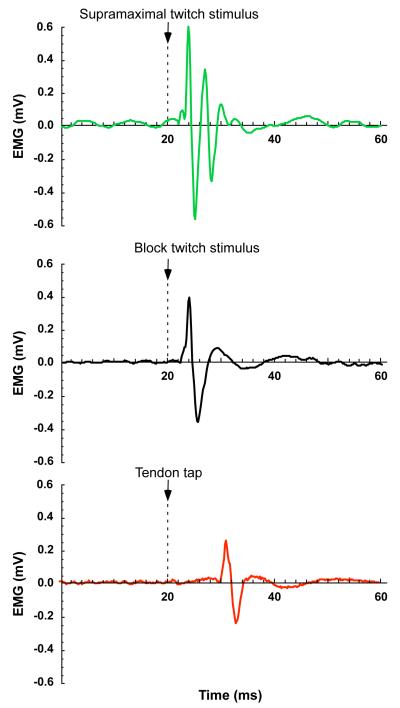
Figure 2.

Action potentials from a supramaximal twitch (green), block protocol twitch (black), and tendon tap stretch reflex (red).

Surgical implantation of nerve cuffs and MG tendon buckle

On the day following in vivo testing, each animal was prepared for surgery as before. An incision was made through the skin and semimembranosus to locate the tibial nerve. One tripolar nerve cuff was placed around the portion of the nerve innervating each muscle, and the proximal end of the nerve was tied and sectioned. The peroneal nerve was also cut to prevent reflex feedback. The lateral incision from the first surgery, proximal to the ankle, was re-opened to expose the Achilles tendon. An incision was made through a portion of the tendon distal to the buckle, and an additional “E”-shaped buckle transducer was attached to the medial portion; this allowed MG forces to be recorded independent from LG forces. A thermocouple was inserted between the muscles to measure the surface temperature, and the temperature was maintained by adjusting a heated pad under the animal.

In situ testing

Animals were tested immediately after the second surgery and maintained on 0.5-1.0% isoflurane anesthesia. Each animal was placed on its right side, while its left hindlimb was secured in a customized stereotactic frame (80/20 Inc, Columbia City, IN) using stainless steel bone pins inserted in the femur and tibia. The tibial nerve was stimulated under direct computer control (Labview 7.1, National Instruments Corp, Austin, TX; A320R, World Precision Instruments, Sarasota, FL). The proximal electrode pair in one of the nerve cuffs was used to deliver single 2 ms pulses. The minimum voltage required to generate the maximum twitch force, termed the “maximum stimulus,” was identified by gradually increasing the stimulus. Tetanic contractions were stimulated with high-frequency trains of pulses at 1.5 times the maximum stimulus. A two-minute rest period between contractions was enforced to ensure that the maximum twitch force did not decline during the experiment. The ankle position corresponding to maximum tetanic force was identified by stimulating the nerve at eight to ten different ankle positions. The ankle was secured at each position, and one of the muscles was stimulated as follows:

1. 1.5 times maximal single pulses to the nerve. This activated all the motor units (slow and fast, Fig.2).

2. 1.5 times maximal pulses delivered simultaneously with a 1000 Hz blocking pulse via the distal electrode in the nerve cuff. The blocking pulse was designed to selectively block the faster motor units (Baratta et al., 1989; Solomonow, 1984; Wakeling and Syme, 2002) such that the contraction was attributable to predominantly slower motor units (Fig.2). The blocking voltage required to allow selective slow motor unit recruitment was determined by ramping the voltage down from the maximum, exciting a series of low-frequency twitches (3 Hz), and identifying the blocking intensity at which action potentials could just be measured. Subsequent twitches were collected while a constant block intensity was implemented.

Five trials of ten twitches each were recorded for each of the tests (a) and (b). Subsequently, the same protocol was completed for the other gastrocnemius muscle.

Following in situ testing, the tendon buckle transducers were calibrated. The distal aponeurosis of the gastrocnemius was cut to free a portion of the Achilles tendon with the buckle intact. The cut end was clamped and frozen with liquid nitrogen, and a series of known cyclical loads were imposed using a force transducer (model 9203, Kistler, Amherst, MA).

EMG analysis

EMG signals from the LG and MG were analyzed using wavelet transformation, similar to previously published wavelet techniques (von Tscharner, 2000; Wakeling and Syme, 2002). The EMG signals were resolved into their intensities in time-frequency space using a filter bank of 19 non-linearly scaled wavelets, 0≤ k ≤23 where k is the wavelet number. Due to low frequency noise (<100 Hz) present in the signal, the first five wavelets were excluded from further analysis so that the remaining wavelets (5≤k≤23) had a total bandwidth of 101 to 1857 Hz. The time resolution and frequency bandwidth of the higher wavelets ranged from 26.4 ms and 49.72 Hz for wavelet k = 5 to 7.6 ms and 206.0 Hz for wavelet k = 23. An intensity, i_k , was calculated for each wavelet, providing an approximation of the power of the signal contained within a given frequency band; thus, an intensity spectrum was constructed for each twitch. We also calculated the mean frequency, f_m:

$$f=\frac{\underset{k}{\Sigma }{f}_c\left(k\right)i_k}{\underset{k}{\Sigma }{i}_k}$$ (1)

where f_c(k) is the centre frequency for wavelet k.

We used PCA to identify the major features of the intensity spectra from all seven goats. We calculated the mean EMG intensity spectra for the twitches and tendon tap reflexes separately, and these mean intensities were compiled into a p×N matrix A, where p=19 wavelets and N=103 spectra. The principal components of the intensity spectra, PC_Is, defined in terms of eigenvector-eigenvalue pairs, were calculated from the covariance matrix B of the data matrix A without prior subtraction of the mean (Wakeling and Rozitis, 2004). This ensured that the whole signal, and not just its variance, was described. The principal component weightings of each PC were given by the eigenvectors ξ of covariance matrix B and the amount of the signal explained by each PC was determined from the eigenvalues. The PC loading scores were calculated from ξ’A, the product of the transpose of the weighting matrix and matrix A. We calculated the angle, θ_I, as the angle formed between the vector of first and second principal component, PC_II-PC_III, loading scores and PC_III loading score axis (Wakeling and Rozitis, 2004). This measure can be used to indicate the contribution of high and low frequency content in the signal. A small θ_I, has a positive contribution of the PC_III loading scores, and indicates a relatively high frequency content. A large θ_I, has a negative contribution of the PC_III loading scores, and indicates a relatively low frequency content.

Each intensity spectrum, i(f), was reconstructed from a linear combination of the principal component weightings:

$$i\left(f\right)\approx {\xi }_{P{C}_I\mathrm{I}}+a{\xi }_{{\mathrm{PC}}_I\mathrm{II}}$$ (2)

where f is a function of k and where a represents the ratio of PC_III to PC_II weightings. Using the constraint that EMG intensity must be positive at all frequencies, the extreme positive and negative values for a that satisfied this constraint were determined, forming two solutions to equation 2. A least-squares minimization of a wavelet function ψ(f) (equation 3) to the intensity spectrum i(f) (equation 2) was used to construct two optimized wavelets, one for each of the two solutions of a: a_slow and a_fast. The value of scale was calculated for which the sum of the squared differences between the intensity and wavelet function for the two different values of a was minimized.

$$\psi \left(f\right)={\left(\frac{f}{f_{\mathrm{c}}}\right)}^{{f_{\mathrm{c}}}^{\ast }\text{scale}}{e}^{\left(\frac{-f}{f_{\mathrm{c}}}+1\right){f_{\mathrm{c}}}^{\ast }\text{scale}}$$ (3)

where scale is the factor that defines the width and shape of the wavelet (von Tscharner, 2000). The two resulting optimized wavelets, ψ_slow(f) and ψ_fast(f), represented the low- and high-frequency bands of the slow and fast motor units respectively. The frequency bandwidth value represented the frequencies at which the magnitudes of these optimized wavelets were 1/e of their maximum values, where e idefined as Euler’s number . The time resolution for each wavelet was calculated as the time at which the intensity was 1/e of the maximum (Von Tscharner, 2000).

The total intensity was calculated as the sum of the intensities determined using each of the original wavelets (5≤k≤23) for each supramaximal twitch. The myoelectric signal of each supramaximal twitch was quantified by (a) its total intensity, and (b) its slow and fast intensities calculated using ψ_slow(f) and ψ _fast (f), respectively.

Muscle force analysis

Twitch responses from the slow and fast fibres were quantified, similar to the EMG signals, using PCA. Force traces from the tendon-tap reflex trials were not included in this analysis due to force artifacts from the tendon tap. All the twitch force traces F(t) from the LG and MG tendon buckles were compiled into a p×N matrix C, where p=500 time divisions and N=525 force traces. The principal components, PCs, defined in terms of eigenvector-eigenvalue pairs were calculated from the covariance matrix D of the data matrix C without prior subtraction of the mean. PCs of the forces, PC_F, were used to reconstruct twitches from a linear combination of the PC weightings:

$$F\left(t\right)\approx {\xi }_{P{C}_F\mathrm{I}}+b{\xi }_{{\mathrm{PC}}_F\mathrm{II}}$$ (5)

where b represents the ratio of PC_FII to PC_FI weightings. Using the constraint that force amplitude must be positive at all times, the extreme positive and negative values for b that satisfied this constraint were determined and used to reconstruct force profiles of slow and fast fibres, respectively. Force rise time was defined as the shortest time between when the force was at its baseline value and at maximum force.

Transfer function derivation

Using the optimized wavelets and the reconstructed twitch force traces, we derived transfer functions that estimated the activation state of each muscle from the EMG intensity. We assumed that activation dynamics could be represented by a series of first-order bilinear differential equations (Eqn. 6, similar to Zajac, 1989), but in a three-step manner where the output of each step is input to the subsequent step. A pattern search algorithm (Matlab Global Optimization Toolbox, The Mathworks, Natick, MA) was used to solve for the constants τ_1,2,3, and β_1,2,3 that minimized a weighted sum of the squared differences between a₃(t) and the twitch force, subject to linear inequality constraints on the values of τ_1,2,3 (τ>0) and β_1,2,3 (0<β<1). A time offset, t_Off, and a non-unity gain factor, C, were allowed.

$$\begin{array}{cc}\hfill & \frac{d}{dt}\left(a_1\right)+\left[\frac{1}{{\tau }_{\mathit{act}1}}\left({\beta }_1+\left[1-{\beta }_1\right]\mathit{EMG}\left(t-t_{\mathit{off}}\right)\right)\right]a_1\left(t\right)=\left(\frac{1}{{\tau }_{\mathit{act}1}}\right)\mathit{EMG}\left(t-t_{\mathit{off}}\right)\hfill \\ \hfill & \frac{d}{dt}\left(a_2\right)+\left[\frac{1}{{\tau }_{\mathit{act}2}}\left({\beta }_2+\left[1-{\beta }_2\right]a_1\left(t\right)\right)\right]a_2\left(t\right)=\left(\frac{1}{{\tau }_{\mathit{act}2}}\right)a_1\left(t\right)\hfill \\ \hfill & \frac{d}{dt}\left(a_3\right)+\left[\frac{1}{{\tau }_{\mathit{act}3}}\left({\beta }_3+\left[1-{\beta }_3\right]a_2\left(t\right)\right)\right]a_3\left(t\right)=C\left(\frac{1}{{\tau }_{\mathit{act}3}}\right)a_2\left(t\right)\hfill \end{array}$$ (6)

Different transfer functions were derived for the total EMG intensity (supramaximal twitches), and for the high- and low-frequency components of the EMG intensity of the supramaximal twitches, obtained using the optimized wavelets.

Statistical analysis

To verify that different motor units were recruited during the different twitch conditions and to determine if the intrinsic spectral features of the EMG intensity were dependent on muscle or location within each muscle, a GLM-ANOVA was conducted with mean frequency, principal component loading scores, and θ_I. as the dependent variables. A similar analysis was conducted on the force data. In both analyses, all factors were fixed with animal as a random factor. When a significant difference was identified from the ANOVAs, post hoc Tukey tests were applied to distinguish which levels within the factor were significantly different.

Pearson product-moment correlations were calculated between the optimized wavelets and the reconstructed spectra and also between the predicted muscle activation levels and the measured twitch forces. Tests were considered significant at the α = 0.05 level.

Results

EMG signals

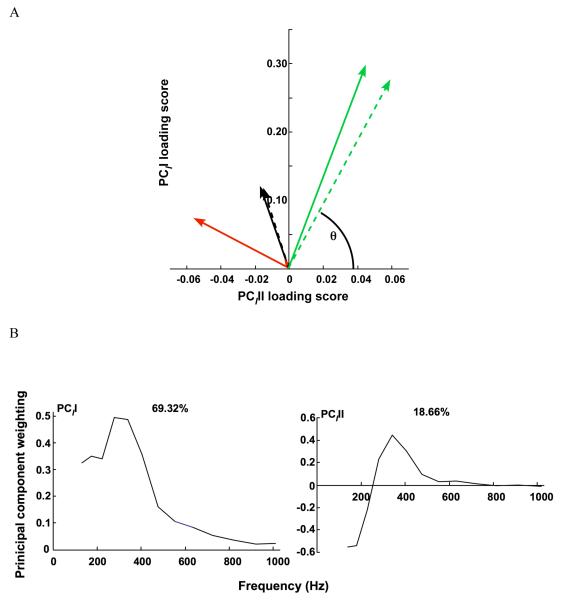
Wavelet analysis of the EMG signals, in combination with PCA, revealed differences in motor unit recruitment during the in vivo and in situ testing. In particular, the PC_II and II scores were significantly different for the tendon-tap reflexes and block stimulation, as compared with the maximal twitches (Table 1, Fig.3a). Also, EMG spectra reconstructed from PC_II and PC_III for the maximal twitches had a higher frequency content than for the tendon-tap reflexes and block stimulation. When comparing the mean frequency for the supramaximal twitches (LG: 313.80 ± 32.35 Hz, N = 21, MG: 307.35 ± 14.10 Hz, N = 18), tendon stretch-reflex twitches (302.51 ± 21.03 Hz N = 21, MG: 319.68 ± 26.33 Hz, N = 11), and block protocol twitches (LG:272.87 ± 11.710 Hz N= 24, MG: 256.42 ± 14.92 Hz, N = 11), the mean frequencies were not significantly different for the three types of twitches. Neither muscle nor location had a significant effect on PC_II or PC_III loading scores (Table 1), but θ_I was significantly smaller in the proximal region than in the distal region of each muscle. θ_I for maximal twitches was significantly different from the block stimulation twitches and tendon taps (p≤0.0001).

Table 1.

Statistical results (p values) for mean frequency, θ_I, and PC_II, PC_III, and PC_IIII loading scores between muscles (lateral and medial gastrocnemius), twitch types (maximal, block, and tendon stretch reflex), and location of electrode (proximal, mid-belly, and distal).

Dependent Variable	Twitch type	Muscle	Location
Mean frequency	0.600	0.817	0.105
θ I	<0.001	0.441	0.026
PCII loading score	<0.001	0.902	0.760
PCIII loading score	0.010	0.780	0.845

Figure 3.

Principal component analysis (PCA) of the myolectric signals. A) PC_II and PC_III loading scores for lateral and medial gastrocnemius (LG, solid; MG dotted) for the maximal twitch (green), block protocol twitch (black), and tendon stretch reflex (red). θ_I is the angle formed between the vector of PC_II and PC_III loading scores and the PC_III loading score axis. B) The first two principal components (PC_II and PC_III) defined from the myoelectric spectra of LG and MG for maximal, block, and tendon tap twitches. The percentage values reflect the percentage of the signal explained by the PC.

From the PCA, the first two principal components explained over 87% of the myoelectric signal (Fig.3b). The PC_II had positive weightings for all frequencies and took a shape that was similar to the mean intensity spectrum; the PC_II loading scores strongly correlated with the total intensity (r=0.97). The second principal component contained positive and negative weightings with a transition occurring at wavelet domain 8 (f_c=218.07Hz).

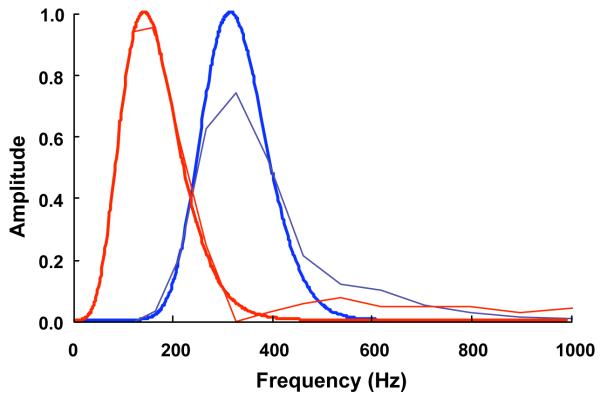
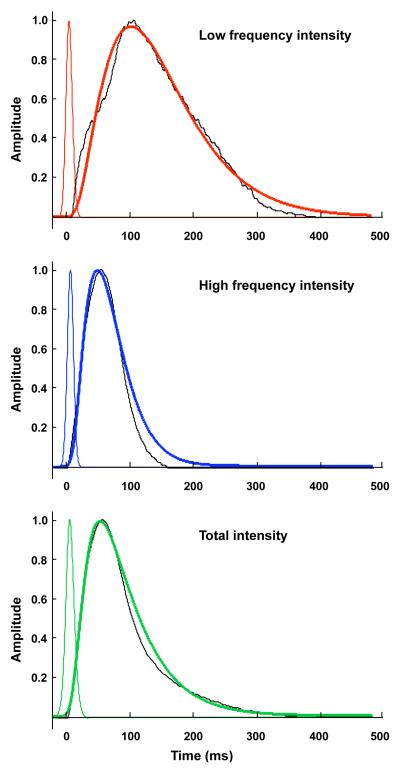
The optimized slow and fast wavelets were strongly correlated with the reconstructed spectra (r=0.996, r=0.983, respectively) (Table 2, Fig.4). The centre frequencies and scale for the slow and fast optimized wavelets were 149.94Hz and 0.045, and 323.13Hz 0.078, respectively (Table 2).

Table 2.

Parameters of optimized wavelets.

Wavelet	Centre frequency fc (Hz)	Frequency bandwidth (Hz)	Time resolution (ms)	scale	r with reconstructed spectra
ψ slow	149.94	165.41	1.98	0.045	0.996
ψ fast	323.13	184.17	3.05	0.078	0.983

Figure 4.

Reconstructed spectra (thin lines) with optimized wavelets (thick lines) for low frequency (red solid) and high frequency (blue dotted).

Tendon force traces and transfer functions

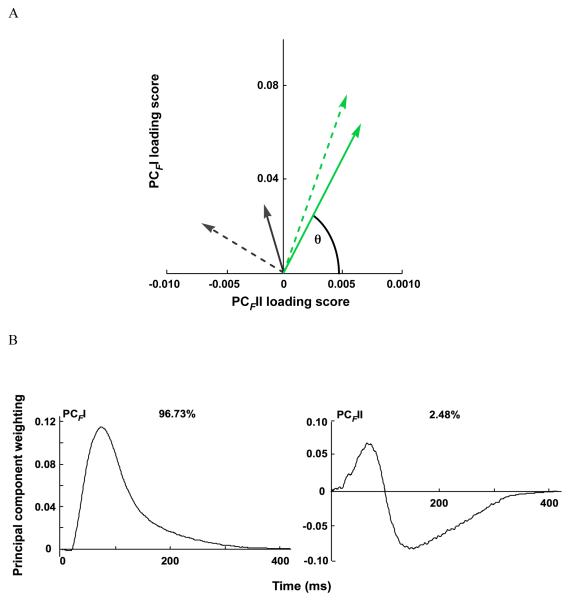
PCA of the force traces revealed differences in force profiles during supramaximal and block protocol twitches. PC_FI and PC_FII loading scores and θ_F were significantly different between the maximal and block twitches and between the LG and MG (p<0.0001, Table 3, Fig.5a).

Table 3.

Statistical results (p values) for θ_F loading scores, and PC_FI, PC_FII, and PC_FIII loading scores between muscles (lateral and medial gastrocnemius) and twitch types (maximal and block).

Dependent Variable	Twitch Type	Muscle
θ F	<0.001	<0.001
PCFI loading score	<0.001	<0.001
PCFII loading score	<0.001	<0.001

Figure 5.

Principal component analysis (PCA) of the tendon forces. A) PC_FI and PC_FII loading scores for lateral and medial gastrocnemius (LG, solid; MG dotted) for the maximal twitch (green) and block protocol twitch (black). θ_F is the angle formed between the vector of PC_FI and PC_FII loading scores and the PC_FII loading score axis. B) The first two principal components (PC_FI and PC_FII) defined from the tendon forces of LG and MG for maximal and block protocol twitches. The percentage values reflect the percentage of the signal explained by the PC.

From the PCA, the first two PCs explained 99.21% of the force traces, with PC_FI explaining 96.73% of the force traces (Fig.5b). PC_FI had all positive weightings with a peak at 75.25 ms. The shape of PC_FI was similar to the mean force trace for the data (r=0.99). Slow and fast twitches were reconstructed that had force rise times of 98.6 and 52.9 ms, respectively (Fig. 6).

Figure 6.

Predicted muscle activation level from the transfer function (thick line), EMG intensity (thin line), and reconstructed forces (dotted black) for A) low frequency component of the EMG intensity (red), B) high frequency component of the EMG intensity, and C) total EMG intensity (green).

Transfer functions derived to describe activation as a function of the EMG intensity showed strong correlations between the activation state and the force-time curves (Table 4, Fig.6 a,b,c).

Table 4.

Transfer function constants and correlation coefficients between estimated activation state and reconstructed slow and fast tendon forces for the total EMG intensity of the supramaximal twitches, and for the high- and low-frequency components of the EMG intensity obtained using the optimized wavelets.

Constants	Total Intensity	Slow Motor Unit	Fast Motor Unit
τ 1	6.37	34.06	18.14
β 1	0.59	0.73	0.90
τ 2	38.05	36.27	20.91
β 2	0.76	0.74	0.99
τ 3	15.89	37.82	20.75
β 3	0.71	0.92	0.98
toff	2.0	6.5	1.5
Correlation (r)	0.993	0.987	0.988

Discussion

Using the experimental and computational methods presented here, we have identified intrinsic properties of slow and fast fibers in the LG and MG muscles of goats. In addition, transfer functions specific to slow and fast fibers have been developed, enabling the activation state of these fibres to be estimated from EMG signals.

Myoelectric signal characteristics and motor unit type

In the present study, no significant difference in mean frequency between twitch types was observed; however, θ_I and PC_III were significantly different between twitch types (Table 1). The main source of variation among the supramaximal, blocking, and tendon reflex twitches analyzed was the recruitment of different motor units within each of the two muscles. The PC analysis was sensitive to this variation in motor unit recruitment. Thus, the PC approach is more sensitive than one based on mean frequency for determining motor unit recruitment patterns (as predicted by Wakeling, 2009). This work also supports use of specified resolution wavelets in intensity analysis of EMG signals (eg. von Tscharner, 2000,2003; Wakeling and Rozitis, 2004;). Power spectra that are derived from Fourier transforms have commonly been used to calculate mean or median frequency values from myoelectric signals. However, these values incorporate signal from the entire spectrum and thus include measurement noise and physiological variations (Wakeling, 2009). Neither muscle (LG versus MG) nor location (proximal, mid-belly, and distal) within each muscle influenced the PC_II and PC_III, loading score, but only θ_I was influenced by location (Table 1). This demonstrates that intrinsic spectral features of the EMG intensity, representing different types of motor unit, can be identified using this approach, and these features are independent of the muscle. However, since θ_I was significantly larger in the distal region of each muscle than the proximal region, this suggests that fiber type population differs within the muscle and supports the idea of compartmentalization (English and Letbetter, 1982).

Optimized wavelets

The fast motor units had about twice the myoelectric frequency of the slower units: the central frequencies of the optimized wavelets were 323.13Hz and 149.94, respectively. The optimized wavelets had a greater bandwidth compared to the original wavelets in the analysis. This illustrates that the original wavelets may over-resolve in frequency for the purpose of determining motor unit recruitment. The time resolution of a wavelet is inversely proportional to its frequency resolution (von Tscharner, 2000), and so the increased bandwidth and thus relaxed frequency resolution of the optimized wavelets results in improved time resolution (Table 2). This allowed better time resolution when calculating the EMG intensities, which was essential for determining the time constants of the transfer function. It should be noted that the optimized wavelets show an overlap at midrange frequencies (Fig.4). Consequently, estimates of slow and fast motor unit recruitment are partially correlated.

Reconstructed forces from slow and fast fibres

The estimated force rise time from baseline to peak of the fast fibres was 1.9 times faster than that of the slow fibres. Using a Q₁₀ of 2.18 (Hodson-Tole, unpublished review) to adjust the twitch rates from the in situ temperature of 34.3°C to the in vivo body temperature of 39°C for goats (Jessen et al., 1984) predicts force rise times of 36.7 and 68.4ms for the fast and slow fibres, respectively at their physiological temperature.

PC_FI loading score was highly correlated with the amplitude of the force and was significantly different between twitch types and muscle. As seen in Figure 5, PC_FII loading scores of block protocol twitches were negative, indicating that the slow fibres had a large contribution to the observed twitch forces. The PC_FII loading scores of the supramaximal twitches fell closer to zero, meaning that both slow and fast fibre types contributed to the force profile of these twitches. The results from the PC analysis suggest that there are differences between the LG and MG twitch force profiles when measured at the Achilles tendon, a result that parallels measurements in humans (100.0 and 113.7ms for the LG and MG: Vandervoort and McComas, 1983). Because prior recordings of forces from the MG and LG during in vivo activities in the goat (McGuigan et al. 2009) did not record forces independently from the two muscles, future studies of in vivo force will benefit from such an assessment.

Transfer function

The transfer functions with constants reported here for slow and fast motor units allow the activation state of the muscle to be estimated from EMG intensity. This provides an important advance in muscle modeling. In Hill-type muscle models commonly used to analyze human movement, activation and deactivation dynamics are often represented by first-order differential equations (Zajac, 1989), where the time constants are not specific to either slow or fast motor units. Another limitation is that the first-order differential equation allows force to rise only when EMG is non-zero. Experimental data reveals, however, that this is not actually the case: action potentials persist for about 3 ms and calculated EMG intensities for 5ms (depending on the analysis and filtering method used) — but the force rise during a twitch can last up to 100 ms. The transfer functions we have calculated here capture both the electromechanical delay and the features of activation that allow it to persist, even after the action potentials have decayed. Furthermore, this analysis incorporates the effect of the EMG processing on the shape of the EMG intensity and thus the transfer function.

The methods described here also have implications for assessing motor unit recruitment. It is often suggested that recruitment order is consistent during voluntary contractions in humans, but there is also evidence that recruitment is different during shortening and lengthening contractions (Nardone et al., 1989) and during cycling (Wakeling et al., 2006). Additionally, recruitment of slow and fast motor units may be altered in individuals with impaired muscle function or impaired neural control of movement. EMG analysis similar to that described in this study has been previously applied to surface EMG in humans (e.g. Wakeling et al., 2009), and thus offers a means of quantifying time-varying patterns of motor unit recruitment in humas. Incorporating these approaches into human muscle models, complemented by the growing availability of software for generating muscle-driven simulations of movement (Delp et al., 2007), could increase the accuracy of muscle force predictions and thus, improve the performance of musculoskeletal models that can be used for clinical populations.

In summary, this work has resulted in novel methods for gaining insight into motor unit recruitment and activation, validated by comparison with in situ measures of tendon force. The need for distinguishing activation of slow and fast motor units is emphasized since muscle performance is primarily determined by force-length and force-velocity relationships, and the activation and deactivation dynamics (Neptune and Kautz, 2001). The methods presented in this paper allow the recruitment of different motor unit types to be identified and provide a crucial step for incorporating activation-deactivation dynamics of different motor unit types to be included in muscle models.

Biography

Sabrina Lee was born in Hong Kong in 1982. She received her BSc in physiology in 2004 at McGill University, Montreal, Canada, and her MSc in 2006 and PhD in 2009 in biomechanics at The Pennsylvania State University, State Colleg, USA. She is currently a post doctorate fellow at Simon Fraser University, Burnaby, Canada in the Department of Biomedical Physiology and Kinesiology.