On the age dynamics of learned societies—taking the example of the Austrian Academy of Sciences

Abstract

In a hierarchical organisation of stable size the annual intake is strictly determined by the number of deaths and a statutory retirement age (if there is one). In this paper we reconstruct the population of the Austrian Academy of Sciences from 1847 to 2005. For the Austrian Academy of Sciences we observe a shift of its age distribution towards older ages, which on the one hand is due to rising life expectancy, i.e., a rising age at death, as well as to an increased age at entry on the other hand. Therefore the number of new entrants has been fluctuating considerably—especially reflecting several statutory changes—and the length of tenure before reaching the age limit has declined during the second half of the last century.

Based on alternative scenarios of the age distribution of incoming members—including a young, an old, the ‘current’ and a mixed-age model—we then project the population of the Austrian Academy and its ageing forward in time. Our results indicate that the ‘optimum policy’ would be to elect either young or old aged new members.

1 Introduction

The logic of population dynamics implies that in a human population closed to migration the only alternative is growing or ageing (ruling out early death). Additionally excluding sustained population growth, a continuing trend towards top-heavy age pyramids is unavoidable. Subpopulations such as learned societies are no exception to this rule. One striking feature of academies of sciences is their increasing “over-ageing”. Faced with rising life expectancy, particularly for older persons, the average age of academy members has increased conspicuously. This trend of over-ageing is enforced by an increase in the age at election.

Currently the Austrian Academy of Sciences (AAS)—similar to other learned societies (Leridon 2004; Matthiessen 1998; van de Kaa and de Roo 2006; Cohen 2003)—is engaged in reforming its policies to rejuvenate its age structure. As recently proposed (ÖAW 2007, p.40), the AAS aims at keeping its number of 90 full members below a statutory “retirement” age¹ but targets a reduction of the latter to 65 years thereby freeing up about 40 seats. Several arguments have been brought forward in favour of a rejuvenation of learned societies. Van de Kaa and de Roo (2006, p.20) argue that an “old” academy might be seen as “… not dynamic enough and no longer well-informed … Hence the repeated efforts of boards or councils to reduce the average ages by creating more vacancies, by creating vacancies more rapidly, and by filling these vacancies with ‘young’ candidates.” In a similar vein, Leridon (2004, p.83) argues that the increase in life expectancy led to the increase in the average age of learned societies and concludes “This is a disadvantage in a field where it is important for an academy to stay in touch with the community of working researchers if it is to continue to play a useful role as an advisory body in society.”

The size and age structure of full membership varies considerably across academies² given international variation in the mortality conditions to which members are exposed to and the age structure of intake, which may be heavily affected by policies governing its size and (to some extent) structure.

In addition to variation in mortality, conditions affecting members in each country and external circumstances potentially affecting the age distribution of intake, such as the age distribution of the pool of potential academicians, there are two broad types of policies that may affect the size and/or composition of intake in more specific ways. First, academies such as the Austrian and the Russian³ have a “corresponding member” status with more limited (e.g., voting) rights previous to full membership. While not all corresponding members get to become full members, the age distribution of those elected to the latter during a given period may be further constrained by the composition of corresponding members.

Second, academies may limit the number of full members to be inducted in a given election period in two ways. On the one hand, elections per period may have a fixed number of new members. Such is the case of the Royal Society, where 44 new fellows have been elected per year in the recent past. Alternatively, intake per election period (typically, yearly) could be linked to a given (but not necessarily fixed) quantity. For instance, the Austrian, Berlin-Brandenburg and Norwegian academies have set the number of elections to match the number of people reaching a statutory retirement age (currently of 70, 68 and 67 years, respectively). This policy has served to maintain the number of full members below statutory retirement age constant (currently to 90, 200 and 220 in Austria, Berlin-Brandenburg and Norway, respectively). As members who are past the age threshold retain all their rights and privileges as full members, this policy has served to restrict membership size nominally, as it were, while permitting the continuous flow of new membership at the same rate as the ageing of academicians close to retirement age.

Either fixing or linking intake may have (contrasting) implications for both the size and age structure of the population of reference, though these consequences also depend on the relative size of intake and its actual age structure. The higher the intake rate and the lower the mean age at election, the larger the rejuvenating effect of intake would be of course.

The issues discussed for learned societies are very much analogous to those in assessing the potential role of immigration in counteracting the effects of ageing in larger, geographically-referenced populations (Blanchet 1988; Espenshade 2001; Schmertmann 1992). As this body of literature has shown, immigration (i.e., age-structured intake) may not be a good solution to the ageing problem as immigrants, albeit young at arrival, naturally tend to age themselves. Or, in other words, a disproportionately higher immigrant inflow would be required to achieve the same rejuvenating results as a given flow of births.

More generally, the question about the sequence of recruitment numbers that generates a given stock trajectory plays an important role not only in demography, but also in person-flow models and manpower planning. In a remarkable paper, Preston (1970) has dealt with an “inverse” problem. Assuming time-invariant mortality and zero net migration, he asked what birth trajectory is required to generate a prescribed population sequence, which is similar to the question “what sequence of recruitment numbers is capable of generating a given stock trajectory” in a more general context of person-flow models (see e.g., Bartholomew 1982, ch. 3). In particular, Feichtinger and Mehlmann (1976) studied the asymptotic behaviour of the recruitment trajectory corresponding to given stock sequences, particularly stationary ones. One of the consequences of moving towards a stationary population is that individual mobility will become more difficult compared with an increasing population. The consequences of the rate of population increase on promotions and career prospects has also been studied—more generally (Keyfitz 1973, 1977) and in the context of universities (Vaupel 1971) as well as for the French civil service (Henry 1971,Henry 1972, 1975).

While Academies of Science are indeed populations subject to analogous conditions as the cases above, they represent a rather particular case of these given their small size and more compact (and significantly older) age structure. Moreover, as the age distribution of intake can in principle be regulated (or at least heavily influenced) by policies and practices, it is worth assessing the past and potential effectiveness of these policies in slowing down ageing.

So far the population of the Austrian Academy of Sciences (AAS) has not been investigated in detail. In this paper we present for the first time an in-depth study of the historical development of the Austrian Academy of Sciences and provide alternative scenarios for its future development. Our focus is on assessing the importance of longevity conditions and academy policies regarding the size and the age composition of intake as well as the statutory retirement age, on the size and age structure of membership. Put differently, the question is: faced with increasing longevity and its fixed membership size, how can the AAS design its recruitment policy and statutory retirement-age rule to avoid excessive ageing.

The following investigations shall provide answers to the above question. After a few formal comments concerning the reconstruction of the data we first look into the historical developments. Chapter 2 is dedicated to full Academy members,⁴ compiling a number of descriptive statistics and illustrations on their development as to numbers, structure and age since the foundation of the Academy. We consider both the group of existing members and that of new entrants as well as the transition from corresponding to full membership, before we go into the mortality of Academy members. A scenario of possible future trends in the development of membership structure is presented in Chapter 3. Here we show several alternative projections that—based on the specific assumptions—yield potential combinations of the total size, age structure and new members of the Academy. We conclude with a discussion of the results and an outlook for further research avenues.

2 Demographic evolution of the Austrian Academy of Sciences 1847–2005

2.1 Reconstructing the data

The data come from the biographic records of the members of the Austrian Academy of Sciences (Hittmair and Hunger 1997). The Austrian Academy of Sciences was founded in 1847 as the “Kaiserliche Akademie der Wissenschaften in Wien” under the auspices of emperor Ferdinand I. The Academy is structured around two sections (termed “Klassen” in German)—the Section for Mathematics and the Natural Sciences (math.nat.) and the Section for the Humanities and the Social Sciences (in German “philosophisch-historische Klasse”, phil.hist.). Membership distinguishes between honorary members, full members and corresponding members. The latter category further distinguishes between corresponding members residing in Austria and corresponding members abroad. Full membership requires residence in Austria. If a full member moves abroad, his or her status changes to that of a corresponding member abroad while living outside of Austria.⁵

The biographic records include date of birth and death, year of election, section membership, membership status and year of change of membership status. Exits from the Academy were mainly through death with few exceptions.⁶ During the Nazi period, several Jewish members were excluded from the Academy: between autumn 1938 and autumn 1940, six full members and 15 corresponding members (including corresponding members abroad) were expelled on ‘racial’ grounds (Matis 1997). After the end of World War II, the excluded members were listed again in the membership directories. Nowadays membership directories do not mention those exclusions. When reconstructing the member population during that time, we decided to keep these excluded members in the Academy population because we did not want to replicate the injustice committed at the time. In 1945 those members of the Academy who had joined the NSDAP (= “Nationalsozialistische Deutsche Arbeiterpartei”) were suspended. With the Amnesty Law of 1948, however, the membership of almost all of them was restored again. Nowadays membership directories do not give any information about these suspensions either.⁷

For the purposes of reconstructing the membership population, we assumed that elections always took place in mid-May each year, which has been the case at least in recent years. If members moved abroad or returned to Austria, we coded the change in membership status to take place in the middle of the year due to lack of information on the actual month of change.

In this way, it is possible to chronologically reconstruct in particular those changes of the Academy’s statutes which led to new section sizes, age limits and rules of election. Table 1 summarises (the amendments of) the byelaws and gives the year in which the relevant change became effective. Apart from the increase of the maximum number of members in 1848, 1925 and 1992, age thresholds were introduced. From 1950 onwards, members who were older than 75 years, no longer counted for the computation of the maximum numbers while still keeping their full membership rights. This age threshold was lowered to 70 years in 1972. Potential candidates who already exceed the age limit may not be nominated for election.

Table 1.

Changes in the byelaws concerning the number of members per section, age limits and rules of elections and the year they became operative

Byelaws	Yeara	Members per section	Specific rules
Statutes, 1st version (1847)	1847	24	24 members per section
- Addendum (1848)	1848	30	Increase by 6 members per section
Byelaws, 1st version (1922)
- Addendum (1925)	1925	33	Increase by 3 members per section
Byelaws, 3rd version (1946)
- Addendum (1949)	1950	33	Age limit of 75 years (see text for details), maximum of five new members elected per year
- Addendum (1960)	1961	33	Restriction on elections dropped
- Addendum (1971)	1972	33	Age limit of 70 years (see text for details)
- Addendum (1991)	1992	45b	Increase by 12 members per section

^aYear of election (in which the change became effective for the first time).

^bInformal agreement to distribute additional elections over three years (Schlögl 1992).

Below we will examine the population of the ‘Austrian Academy of Sciences’ in closer detail, particularly focusing on the full members. Since only these are vested with election rights, they may influence the current member structure by electing new members of a certain age group. We will focus on the Academy as a whole, i.e., considering both sections together, as they have seen a very similar demographic development.

2.2 Population structure and age structure over time

Figure 1 shows the development of full members from 1847 to 2005. The years in which amendments of the byelaws took place are marked. After a rather stable process in the first half of the Academy’s existence, these byelaw amendments led to a continuous rise in membership numbers. Apart from the direct increases in the maximum number of members in the years 1848, 1925 and 1992, the introduction of the 75-years age threshold in 1950 as well as its further reduction to 70 years in 1972 created a considerable space for potential members to be elected. This led to batch-wise growth of the population. Consequently, the Academy started with 39 full members in 1847 and grew to 165 full members in 2005. Among the 165 full members 88 full members belong to the “math.nat.” section, whereas 77 are members of the “phil.hist.” section.⁸

Figure 1. Number of full members over time, 1847–2005 (at mid-year).

Note: The vertical lines indicate those years when changes in the byelaws regarding the number, age limit and rules of election of full members became operative.

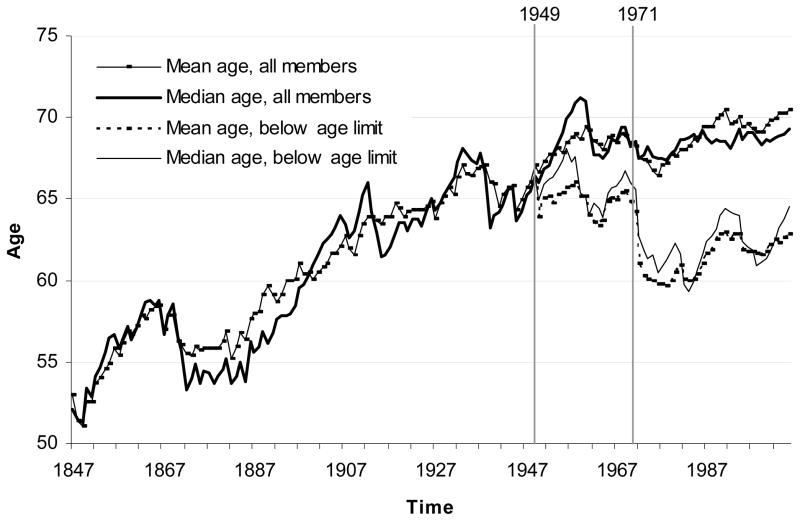
A detailed picture of the age development over time is plotted in Figure 2, which contains the average and median age of full Academy members with and without consideration of the introduction of the age threshold of 75 years in 1950 and its reduction to 70 years in 1972. Starting at 51 years in 1849, the average age rose to 67 years during a time span of one hundred years. With the introduction of the age threshold in 1949 the reference population changed: while the overall average age continued to increase, the average age of those full members below the age threshold decreases with an additional impulse of rejuvenation in 1971. The median age follows a similar pattern as the average age.

Figure 2. Mean age and median age of full members over time, 1847–2005 (at mid-year).

Note: The vertical lines indicate those years when the age limit of 75 years was introduced and lowered towards 70 years, respectively.

Focusing on broader age groups over time shows that the age group of the 60 to 69-year olds dominates, while the 80+ group keeps increasing steadily, which is due to rising life expectancy and also to an increasing age at election (figure not shown).

The duration of membership as a full member (Figure 3), which we calculated for those members who died or reached the age limit in the respective period, is determined by the entrance age on the one hand and by the time of death on the other. In spite of partly strong variations over time—caused by the small sample size—the mean period spent in the population by full members fluctuates around 20 years during the first half of the 20th century. Afterwards, it rose from 16 years in 1946–50 to the recent average of 27 years for all members, while the mean tenure of full members below the age threshold now lasts 12 years.

Figure 3. Average duration of full membership at time of death or voluntary exit and alternatively at reaching the age limit of 75 and 70 years respectively, 1847–2005 (5-year periods).

Note: The vertical lines indicate those years when the age limit of 75 years was introduced and lowered towards 70 years, respectively.

So far the reconstruction of the data clearly shows that an increase in the membership size and a reduction in the statutory retirement age implied an increase in the number of full members over time. To explain the change in the age structure and tenure of the members (as represented in Figure 2 and Figure 3) we need a closer investigation of the age structure of new entrants, their status change (i.e., moving from a corresponding to full member) and their death patterns. In the following two sections we briefly review these developments.

2.3 New entrants

The number of elected members and their age at election since the establishment of the Academy is represented in Figure 4. While the number of elected members for each 5-year period up to the beginning of the 20th century lay around 10–20, this figure gradually rose to over 20–25 later on. The amendments of the byelaws around 1961, 1972 and 1992 allowed to elect a larger number of new members at once, resulting in manifest peaks of the number of new entrants. Hence, 23 new full members were elected during the years 1961–62, 13 new full members in 1972 and 43 new full members from 1992 to 1995.

Figure 4. Number of elected full members (left scale) and mean age of full members (right scale) at time of election, 1847–2005 (5-year periods).

Note: The vertical lines indicate those years when changes in the byelaws regarding the number, age limit and rules of election of full members became operative.

The age at election of full members increased continuously from its lowest value of about 40 years in 1861–65, to above age 60 several times in the second half of the 20th century. In the recent past it has decreased again due to the reduction in the age threshold that led to the election of younger members. Since full members are recruited to a large extent out of the pool of corresponding members it is interesting to investigate whether the increase in the mean age at election of full members is caused by an increase in the mean age at election of corresponding members or a lower transition rate from corresponding to full member. We will discuss this topic in the next section.

2.4 Transition from corresponding to full member

The transition from corresponding to full member represents a key factor since the latter group of members is selected predominantly from the former group and thus the age of corresponding members constitutes an implicit control device to influence the age of full members.

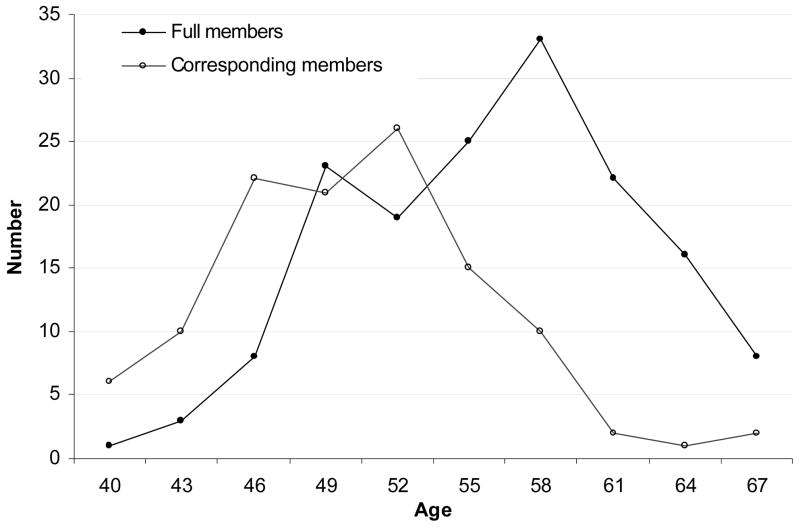
Figure 5 shows the age distribution at the time of election of corresponding and full members elected between 1980 and 2005. Both the age distribution of full members and that of corresponding members exhibit an approximately symmetric distribution. Since the major part of the full members is elected from the pool of corresponding members, the average age at election of full members is higher than that of corresponding members (57 compared to 51 years, respectively). The standard deviation amounts in both cases to approximately 6 years.

Figure 5. Age distribution of corresponding and full members elected in 1980–2005.

Note: 3-year age groups; values plotted above middle of each age group

The proportion of corresponding members ever to become full members has varied quite strongly over time, as shown in Figure 6 (right-hand axis). For instance, among those corresponding members elected in 1976–80, 58% eventually became full members. Meanwhile, the maximum value in the past was about 81% (1866–70), the lowest about 27% (1941–45). Naturally due to right-censoring and the fact that these are cohort measures, the proportion of corresponding members ever to become full members plummets towards the end of the measurement period. The same two arguments (i.e., strong variation and right-censoring issues) hold for the average waiting period (i.e., the number of years that corresponding members “waited”) until election as a full member, also shown in Figure 6 (left scale). However, fluctuations in waiting times did not necessarily mirror those in the lifetime probability of election. That is, long waiting times did not invariably imply a high probability of election. For instance, while 58% of corresponding members elected in the period 1976–80 were eventually elected as full members (after approximately 9 years), those elected in the previous 5-year period had waited only 6 years where their probability of promotion was above 60%.

Figure 6. Mean “waiting period” of corresponding members to become full members (left scale) and share of corresponding members who ever became full members (right scale), 1847–2005 (5-year cohorts).

Note: The dashed lines indicate the decline in the graphs due to right-censoring.

From Figure 4 one may deduce that the increase in members’ mean age shown in Figure 2 was partly caused by the increase in the mean age at election as full member. In addition, to investigate the impact on increasing survival into old age on members’ mean age over time we discuss the mortality development of the members in the following section.

2.5 The low mortality of Academy members

In accordance with general population ageing, Figure 7 confirms that the average age at death—which naturally determines the end of Academy membership—rose continuously within our subpopulation. In 1851–55 a full Academy member died at the average age of 63 years, while the age at death was 74 years in 1931–35 and 82 years in 1996–2000. As a consequence the increasing mean age at death contributed—in addition to the increasing mean age at election—to the rising average age of full members.

Figure 7. Mean age at death of full members, 1847–2005 (5-year periods).

Following the social gradient argument of mortality (e.g., Antonovsky 1967; Kunst 1997), members of a learned society should exhibit much lower death rates than most other social groups. Members of a learned society have not only reached the highest educational level, they also occupy (or have retired from) prestigious positions with high income.⁹

In order to assess whether Academy members indeed exhibit lower death rates than the general population, we compare the mortality of Academy members with the average Austrian mortality. Due to the low number of female members we conduct the mortality comparison only for the male members. Since we did not find any statistically significant differences between the survival functions of full and corresponding members, the following analysis is conducted for full and corresponding members together. This procedure increases our sample size and brings about the potential for stronger statistical significance.

The mortality comparison is based on two measures: (1) the standardised mortality ratio (SMR) and (2) period life expectancy. Applying age-specific reference death rates to the age structure of the members of the Austrian Academy of Sciences (in one or five-year age groups depending on the reference rates), an expected number of deaths is derived; the ratio of actual observed deaths to the latter gives the standardised mortality ratio. Statistical significance of the latter is verified by a score test. Furthermore, by relating age-specific deaths of Academicians to the age-specific person-time spent as Academy member within a certain period yields period death rates, from which period life tables can be constructed. In order to account for the statistical uncertainty due to the small sample size, we compute confidence intervals by applying bootstrapping.

Table 2 shows the comparison of the number of deaths for corresponding and full members in the period 1986–1995 with the life table mortality of the Austrian male population of 1991/92 (Statistics Austria 2005, available through the Human Mortality Database at the Max Planck Institute for Demographic Research 2005). In comparison with the total population the SMR is below 1 for all age groups. This implies that male Academy members register fewer deaths than if they were subject to the average male mortality in Austria. As evident in Table 2, the extent of the mortality difference varies with age: the older the members of the Academy, the larger the SMR, i.e., the difference in the number of deaths shrinks. Declining social differences in mortality with age have been widely reported (Marmot and Shipley 1996; Crimmins 2005). One of the reasons that mortality differentials are lower at older than at younger ages is a selection effect. “As cohorts of persons of different socioeconomic status proceed through life, the force of mortality reduces the number of survivors in each group but at very different rates. Far fewer people in the lowest status group survive to old age; a much higher proportion of high status people survive. Mortality produces a more selected group among those with the lowest status; a group which has been selected against mortality risk.” (Crimmins 2005, p.165–166).

Table 2.

Comparison of the mortality of corresponding and full members in the time period 1986–1995 with the life table of the Austrian male population (and of that with tertiary education) of 1991/92

Age	Observed deaths	Total population		With tertiary education
		Expected deaths	SMR	Expected deaths	SMR
50–69	11	24.4	0.45**	13.0	0.85
70–90	42	71.0	0.59**	57.5	0.73*
total	53	95.3	0.56**	70.5	0.75*

Legend:

^**p<0.01,

^*p<0.05

In summary, from 1986 to 1995, members of the Austrian Academy of Sciences aged between 50 and 90 years registered only about half of the deaths that the Austrian life table for the total population from 1991/92 would have implied. For the period 1996–2005, Academicians show a similar mortality advantage in comparison to the Austrian male life table 2001/02 (Winkler-Dworak 2006).

In a next step, we aim to examine whether mortality differences even persist between members of the Academy and the Austrian population with tertiary education. Otherwise, the mortality difference of the Academy members to the total population could be explained entirely by the higher education level. Therefore, we apply reference death rates of Austrian men with tertiary education, which can be constructed from the number of deaths by educational class reported by Doblhammer et al. (2005)¹⁰. As evident in Table 2, the SMR—although higher than before—is still below unity! Over all age groups considered, corresponding and full Academy members registered about 25% fewer deaths in the years 1986–1995 than would have been expected had they been subject to the age-specific death rates of Austrian men with tertiary education in 1991/92.

Figure 8 compares the period life expectancy of Academy members at the age of 60 with the corresponding figures of the total population available for the Austrian Alpine regions and Cisleithania during the monarchy and later for the Austrian Republic (available through the Human Mortality Database at the Max Planck Institute for Demographic Research 2005). Annual estimates of the life expectancy at age 60 for the Austrian population have been available from 1950 onwards (Statistics Austria 2005)¹¹. For Academy members, life expectancy at age 60 is derived from abridged 10-year period life tables, which are constructed from observed period death rates of the Academicians. With some exceptions, the life expectancy of the Academy members at age 60 is slightly above the corresponding value for the Austrian male population. Starting from the mid-20th century, the life expectancy of Academy members rose more steeply as compared to that of the Austrian population as a whole. Around the turn of the 21st century the difference in the further life expectancy at the age of 60 amounted already to approximately 6 years. For the population with tertiary education, the life expectancy at the age of 60—expectedly—lies between the estimates for the Academy members and for the Austrian male population.¹²

Figure 8. Life expectancy at age 60 of Academy members compared to Austrian life table estimates, 1847–2005.

Widening social gaps of mortality have been also identified by other studies (e.g., Marmot and McDowall 1986; Pamuk 1985). However, most studies on time trends of differential mortality are limited to the second half of the 20th century. In one of the rare studies with different time horizons, Pamuk (1985) studies inequality in mortality by social class in England and Wales from 1921 to 1972. She finds that the social gradient of mortality has been increasing in England and Wales among men for the 1950s, which is consistent with our findings.¹³

3 Projections of the future structure and size of the Academy

According to the reform policies of the AAS (ÖAW 2007), there is an interest in a young age structure and at the same time the aim is to appoint as many excellent scientists as possible without exceeding the maximum number of members below the age threshold of 70 years. Consequently, the Academy is confronted with a trade-off between a “young” society that only allows a small number of vacancies each year and a small number of the total stock of members vs. an “old” society that allows more vacancies and thus a larger stock of members each year. The connection between the annual number of vacancies and the mean age of Academy members is not new. Full member Gerhart Bruckmann summed up this dilemma with an illustration:

With an average age at election of 55 years and ruling out mortality, a member has 15 remaining years until the age threshold. At a maximum number of 90 members, you are bound to see 6 vacancies per year on average. However, if entry at earlier ages were favoured (in order to establish a “younger Academy”), e.g., at 47.5 years, then these new members would stay in the system for 22.5 years until the statutory retirement age—resulting in 90/22.5 = 4 vacancies per year.

This means that the younger the age at election, the longer the tenure in the Academy and thus the lower the rate of rejuvenation. These simple calculations are based on the fundamental identity of a stationary population where the stock equals the number of births multiplied by the life expectancy and in our case:

$$M=RT$$ (1)

where M denotes the total size of the Academy, R the annual intake and T the mean length of tenure. In the Austrian case we have M = 90, 0 ≤ T ≤ 30 (assuming a minimal age at entry of 40 years and an upper age limit of 70 years).

However, the number of recruits and their age structure as well as the length of tenure will vary over the transitional period when policy changes are implemented. Moreover the initial age structure will determine the dynamics during the transition period. Simulations are the adequate tool to capture the development of the population during these transitional periods and to investigate the sensitivity of the age structure and size of the members on changes in policies.

To project the Academy population of full members forward in time we postulate the same mortality development as in the latest forecast of death probabilities by Statistics Austria (Hanika and Klotz 2005), which were derived by employing the Lee-Carter method (Carter and Lee 1992; Lee 2000). The projected death probabilities were converted into death rates under the usual assumption of a uniform distribution of deaths over the age interval. For the age groups above 50, we assumed constant forces of mortality within the age interval instead.

As shown in the last section, Academy members’ have a significantly lower mortality than the general Austrian population. Therefore we adjust the forecasted Austrian death rates according to the standardised mortality ratio for the most recent period (SMR=0.5). Since the mortality differences decline for higher ages, we increase the adjustment factor for increasing age by 2.5 % per year of age starting from age 80. This implies an SMR of about 0.74 at the age of 99 years.

Since the forecasted life table from Statistics Austria (Hanika and Klotz 2005) ends at the age of 99, we extrapolate the mortality for higher ages by assuming a logistic model (Perks 1932) based on the death rates between ages 80 to 99.

For the projection of the development of the AAS age structure, we first project the number of members at the year t surviving until t+1. The difference between the number of survivors below age 70 and the upper limit of 90 members altogether gives the number of vacant posts. The latter are filled according to the postulated age distribution of members at election, where we consider four alternative scenarios (see Figure 9):

Figure 9. Alternative projection scenarios for the age distribution of election.

Status quo: Average age distribution (approximated by a normal distribution) of new entrants observed during the last 25 years, i.e., 1980–2005.

Young: Only persons below age 55 are elected — distributed uniformly.

Old: Only persons aged 55 and above are elected — distributed uniformly.

Bimodal: Persons between age 40 to 49 and 60 to 69 are elected — distributed uniformly.

The average age of new entrants is about 57.2 years for the status quo scenario, 47.5 years for the young scenario, 62.5 years for the old scenario and 55 years for the bimodal scenario. The corresponding standard deviation is 6 years (status quo scenario), 4 years (young and old scenario) and 10 years (bimodal scenario).

Additionally, we consider a fifth scenario (Status quo 65) where we assume the status quo setting and a reduction of the statutory retirement age of 65 (instead of 70), and where the age distribution of elected members used was a re-scaled normal distribution similar to that of the status quo scenario but distributed between ages 40 to 64 (as opposed to 40 to 69).

The projection time horizon runs from 2005 up through 2050 and the initial population consists of 165 members. Among these, 45% are older than 70 years.

The projected number of vacancies over the period 2005–2050 is summarised in Figure 10 for the four scenarios representing the age distribution of new entrants and the fifth scenario where we assume a status-quo age distribution of new entrants but alter the reference population to members below age 65 instead of the current policy of age 70. The initial development is influenced by the actual age structure, i.e., by the number of members who exceed the age threshold of 70 (65 in the fifth scenario).¹⁴ It is after approximately 5 to 10 years that the influence of the observed age structure of 2005 weakens and the differences between the scenarios become visible. Only in the second half of the projection period, however, do the effects of the initial age structure entirely disappear. If the observed age distribution of new entrants over the last 25 years persists (scenario “status quo”), about 6 vacancies are expected per year by 2050. Assuming the “young scenario”, a phase in which none or at most one new member could be elected annually would be reached around 2020! This period would last approximately a decade. Contrary to the status-quo scenario, a stabilisation of the number of vacancies would take longer under the young scenario and amount to about 3 vacancies. This can be explained by the smaller variance and the lower entrance age which implies a longer time interval until the members have passed the age threshold of 70 years and hence open up a vacancy. Under the “old scenario” in which only members of age 55 and above get to be elected the number of vacancies would be highest with 10 seats per year. The “bimodal scenario” of newly elected members would result in a number of annual vacancies similar to the scenario of maintaining the current policy, i.e., the status quo scenario. The scenario that assumes a reduction of the age threshold to 65 years is rather similar to the old scenario. In both scenarios, the mean length of tenure decreases which results in an increase of intakes (see the identity of a stationary population in equation (1)). In the case of the old scenario, the reduction of the mean length of tenure stems from an increase in the mean age at election, while in the status quo 65 scenario the mean length of tenure falls due to the reduction in the age threshold.

Figure 10. Projected number of vacancies for full members, 2005–2050.

The strong differences in the annual number of vacancies under the different scenarios representing the age distribution of new entrants accordingly cause different developments concerning the total number of members over time (Figure 11). With the highest number of vacancies during the initial period, the scenario of a reduced age limit would cause a rapid increase of the number of members from 164 at the end of 2005 up to 306 members in 2050 corresponding to an increase of approximately 87%. A similar pronounced increase can be observed for the old scenario where the number of members would increase up to 291 members in 2050. Under the status quo and bimodal scenarios a more moderate increase of members would result: up to 216 or 200 members in 2050, respectively. Under the young scenario an initial rise would be followed by a decrease in the number of members resulting in only 163 members in 2050 due to the rising tenure as well as the diminishing effect of the initial age structure.

Figure 11. Projected number of full members, 2005–2050.

The development of the members’ mean age is represented in Figure 12. In contrast to the previous two figures, differences between the scenarios are visible right from the beginning of the projection time period. As expected, in the long run, the young (old) scenario implies the lowest (highest) mean age among the four scenarios presented. Clear differences in the members’ mean age are visible, however, between the status quo and bimodal scenario. Under the status quo scenario the mean age would increase continuously while the development under the bimodal scenario would be characterised by phases of shrinking mean ages. In the year 2050 the difference in the average age between the two scenarios would amount to approximately 3 years.¹⁵ In case of reducing the age limit but keeping the age distribution of new members, the mean age would be reduced considerably in the short run. In the long run, however, the mean age of this scenario would be close to the mean age of the status quo scenario.

Figure 12. Projected mean age of full members, 2005–2050.

In summary, as Figures 10 through 12 indicate, the dilemma between a “young” Academy that only allows a small number of vacancies each year and a small number of the total stock of members vs. an “old” Academy that allows more vacancies and a larger stock of members each year becomes obvious. Under the assumption of aiming at a rejuvenation of the Academy and allowing for an increase in the number of new entrants (in comparison to the status quo scenario) the bimodal distribution of the age at entry seems to be a perfect compromise and, as we have shown in a different paper (Dawid et al. 2007), it also constitutes an optimal recruitment policy if the Academy’s goal were to keep its member structure young and to allow a maximum number of recruitments each period. A change in the reference population as in the “status quo 65 scenario” would help to achieve the objective of a high number of vacancies but not the objective of a persistent rejuvenation. Only in the short run would this policy help to reduce the mean age of the members.

4 Discussion

On the basis of a short historical sketch, we have shown that the full membership of the Austrian Academy of Sciences experienced a nontrivial ageing process during the 20th century due to reductions in old-age mortality as well as to increases in the mean age at election. The upward trend in the latter was modulated by an academy policy that links the intake of new members to the number of members reaching a statutory age threshold: 75 years in 1950–1971 and 70 years since 1972. This policy set an effective upper limit to ages at election, thus stabilising to some extent the general ageing trend in mean age at election. In addition, while the policy maintained the number of members below the statutory retirement age at a constant level (currently at 90), remarkable decreases in the old-age mortality of academicians also implied that a growing fraction of standing membership was going to be above that age.

Generally speaking, learned societies will always aim to maintain a delicate balance between being in touch with the community of working researchers while rewarding those who have greatly contributed to their fields of endeavour. In the case of the AAS, the age of members is thus not only a relevant issue to consider as a potential (yet neither unique nor perfect) marker of said quest for balance between contribution and distinction across generations, but it also dictates the number of new members to be inducted in the near future. Another conundrum arises from the fact that a rather low intake may prevent many excellent scientists from ever being elected as they age above the statutory retirement age in the meantime.

Under the premise that the Academy is thus interested in keeping a relatively young age structure, the current intake limits—aimed at keeping membership below the statutory retirement age to 90 persons—seem to be in conflict with the other desirable goal of electing as many new members as possible. Applying standard cohort-component projection methods, we illustrated the trade-off between age at election and size of intake by looking at the effect of new entrants’ age distribution on the number of yearly vacancies and on the age structure of members. A common feature of the various scenarios we posed is that intake would of course invariably depend on the numbers of people close to the retirement age. One of the repercussions of said policy is that—in the transient state and immediate future—intake will inevitably fluctuate in Easterlin-like cycles (see Figure 10), though varying considerably by scenario, from young to old. In turn and as hinted before, a younger/older age structure of intake likewise implies a younger/older academy. In the vast majority of periods and scenarios, the mean age of the academy would in fact be higher than the statutory retirement age, and in some cases considerably so. While maintaining the current election practice would in fact not do a bad job in attempting a fair compromise between the two aforementioned objectives, a bimodal age distribution of new entrants turned out to be optimal with respect to maintaining intake at reasonable levels while yielding a relatively young age structure (for an optimal-control exposition of this same issue, see Dawid et al. 2007).

Our results clearly evidence that age at election is a crucial determinant of the number of vacancies and hence membership renewal. As the stationary population identity indicates, the longer the tenure in the body, the lower the rate of intake. However, a reduction to the stationary case is not appropriate in such relatively small societies where fluctuations in the number of vacancies are very pronounced over the next three decades. Such fluctuations across time within a scenario sometimes exceed the difference of vacancies across scenarios at one point in time (cf. Figure 10). Our results show that the alternative policy of reducing the statutory maximum age to 65, though it would open new vacancies, does not help to limit the ageing of academy members in the long term.¹⁶

As already discussed at the outset, our study is not only relevant for learned societies but also for other subpopulations, whose dynamics (i.e., temporal development and structuring) can be studied with the demographic methods illustrated in this paper. For instance, while geographically referenced (and more generally defined) populations can grow due to fertility and migration, the case of academies constitute an extreme yet informative case of the potential trade-offs that an ageing population (admittedly one that can only grow with one type of age-structured intake) faces if it seeks to limit growth and reduce its own pace of ageing. In addition, the dynamics of an academy may be analogous to those of promotion within organisations such as universities, armies and companies in general. A related research question in personnel management studies is how the career prospects of the members of an organisation would decrease if the system stagnated/shrank after a growth phase (see Feichtinger 1974, 1976; Feichtinger and Mehlman 1976; Henry 1971, 1972, 1975; Keyfitz 1973; Vaupel 1981), and it could also refer to the problem of the transition from corresponding to full member. In future work we will study these dynamics in more detail as corresponding members constitute the “pool” from which the vast majority of full members is elected. We also plan to conduct a comparative study among academies of other countries (Cohen 2003; Leridon 2004; Matthiessen 1999; Van de Kaa and de Roo 2006) in order to look at the results of a wide range of academy policies and, to a lesser extent, mortality conditions in the size and structure of academies, and how optimal recruitment might vary according to those various system characteristics.