Abstract
Flexibility and dynamics are protein characteristics that are essential for the process of molecular recognition. Conformational changes in the protein that are coupled to ligand binding are described by the biophysical models of induced fit and conformational selection. Different concepts are reviewed that incorporate protein flexibility into protein-ligand docking within the context of these two models. Several computational studies will be presented that discuss the validity and possible limitations of such approaches. Finally, different approaches that incorporate protein dynamics, e.g. configurational entropy, and solvation effects into docking will be highlighted.
Keywords: Protein flexibility, protein dynamics, docking, induced fit, conformational selection, entropy, solvation
Molecular recognition between receptors and ligands plays a fundamental role in virtually all biochemical processes in living organisms. In many instances, ligands such as hormones or neurotransmitters are located outside the cell and non-covalently bind to receptors, e.g. G-protein coupled receptors (1-3) or ligand-gated ion channel receptors (4). This association process results in conformational changes that lead to subsequent signaling events inside the cell. Furthermore, environmental signals are also known to bind to receptors and cause downstream signaling events; for example, odors and volatile substances bind to olfactory and taste receptors and trigger down-stream signaling events that are ultimately translated into smells and tastes (5;6).
In addition to molecular recognition leading to downstream signaling effect, substrate recognition by enzymes is a process of central importance that enables the living organism's internal processes as well as interaction with the organisms’ environment. For example, compounds that are absorbed from the environment, including drugs, might have potential adverse effects to the organism. Enzymes such as cytochrome P450 bind and chemically modify these compounds to more water-soluble products that subsequently are excreted from the body (7;8).
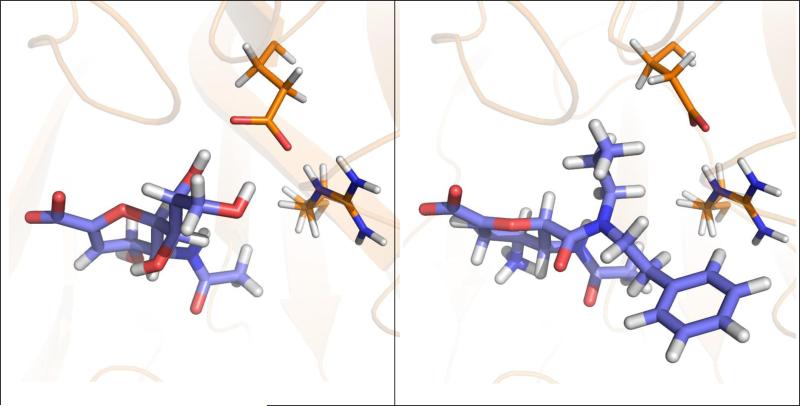
Analyzing examples for molecular recognition as shown in Figure 1 demonstrates that protein flexibility coupled to ligand binding often plays a key role in protein-ligand association (15). Individual residues in the binding site of the protein change their side-chain conformation to bind different ligands (Figure 1, top panel) (9;10). Large-scale loop reorganization is observed upon ligand binding to cytochrome P450 119 (Figure 1, middle panel) (16;17). In the estrogen receptor, the binding of agonists (Figure 1, bottom left) or selective estrogen receptor modulators (SERM) (Figure 1, bottom right) generates different conformations of helix 12 resulting in tissue-specific control of signals (18).
Figure 1.
Three examples of different types of protein flexibility coupled to ligand binding. Top panel: Alternative conformations of the side chain of Glu276 are observed forming inter-molecular hydrogen bonds between influenza A N9 neuraminidase and the inhibitor 2-deoxy 2,3-dehydro-N-acetyl neuraminic acid (PDB-code: 1nnb (9)) and for forming intra-protein hydrogen bonds with Arg224 when 5-acetylamino-4-amino-6-(phenethyl-propyl-carbamoyl)-5,6-dihydro-4h-pyran-2-carboxylic acid is bound (1bji (10)). Middle panel: An extended loop in the apo protein of cytochrome P450 119 (left; 1io9 (11)) adapts a new fold upon binding of 4-phenyl-imidazole (right; 1f4t (12)) stabilizing the ligand. Bottom panel: Binding of the agonist 17β-estradiol (left; 1ere (13)) to the ligand-binding domain of the estrogen receptor causes a different conformation of helix 12 compared to the selective estrogen receptor modulator raloxifene (right; 1err (14)).
In this article, the induced-fit and conformational-selection biophysical models will be discussed to elucidate the role of protein flexibility in ligand binding. Based on this discussion, different approaches that incorporate protein flexibility into docking will be presented. Additional computational studies will be presented that discuss the validity of the different methods that incorporate protein flexibility during docking. Furthermore, three additional important issues will be discussed that need further consideration in the development of future flexible docking methods: The modeling of protein dynamics, i.e. configurational entropy, the modeling of solvation effects, and the precise quantification of the free energy associated with the protein's conformational change coupled to ligand binding.
The mechanism of protein flexibility coupled to ligand binding
The coupling between protein conformational change and ligand binding is commonly explained by one of two different biophysical models, either the induced-fit (19) (or conformational-induction) or the conformational-selection (20) (or population-shift) mechanisms. In a simplified dynamic energy-landscape model (Figure 2) the two mechanisms can be characterized as either a path from the ligand-unoccupied open (UO) state to the ligand-bound closed (BC) state either via the ligand-unoccupied closed (UC) state (in case of conformational-selection mechanism; red path in Figure 2) or via the ligand-bound open (BO) state to the ligand-bound closed (BC) state (induced-fit mechanism; green path in Figure 2). The two different mechanisms of protein flexibility coupled to ligand binding, induced fit and population shift, relate to the models of Koshland-Neméthy-Filmer (KNF) (21) and Monod-Wyman-Changeux (MWC) (22) describing allostery, respectively.
Figure 2.
Scheme representing the two mechanisms of protein conformational change coupled to ligand binding. In the conformational-selection mechanism (red line) the apo form of the protein (unoccupied-open, UO) adapts to a certain probability a closed conformation (UC) to which the ligand binds and stabilizes the conformation (bound-closed, BC). In the induced-fit mechanism (green line) the ligand binds to the apo conformation of the protein (BO). This binding event triggers the conformational change to the final BC state. The top curve shows a model of the free energy of the unbound form of the protein as a function of an arbitrary reaction coordinate describing the conformational change between open and closed form; the bottom curve displays the associated model of the free energy of the bound form.
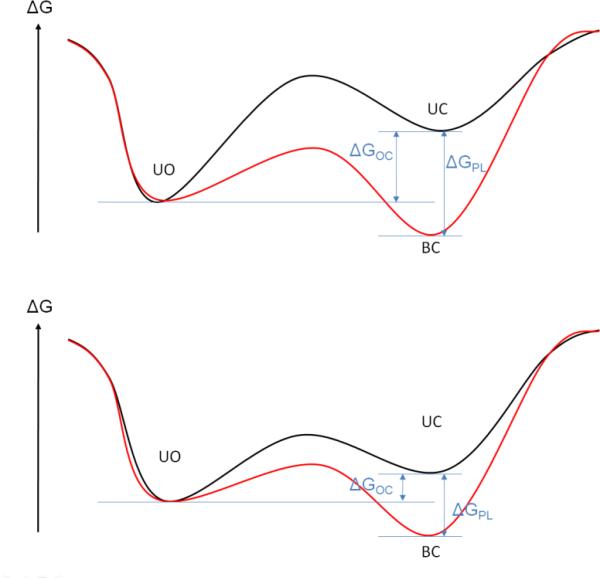
To be able to categorize protein-ligand systems by one of these mechanisms, Okazaki et al. (23) developed a double-basin Hamiltonian quantitatively representing the dynamic energy-landscape model of Figure 2 where two basins of the Hamiltonian describe the open and closed protein state. A ligand-protein interaction term is added to the Hamiltonian that characterizes the influence of the binding of the ligand to the overall Hamiltonian of the system. From simulations using this Hamiltonian with varying strength and range of protein-ligand interactions, the authors deduced that strong and long-range interactions favor the induced-fit mechanism whereas weak and short-range interactions favor the conformational-selection mechanism. The trend between ligand-protein interaction strength and mechanism of conformational change is intuitive and can be interpreted utilizing the free-energy landscape model (Figures 2 and 3). If the free-energy difference between apo and holo conformation ΔGOC of the ligand-free protein is large (Figure 3, top panel), the unbound protein visits the holo form infrequently. For protein systems where this situation occurs, strong protein-ligand interactions ΔGPL are required to induce and stabilize the holo conformation and drive the overall free energy of the protein-ligand complex to a more negative value than the unbound apo conformation. If the energy difference between the apo and the holo protein form is small (Figure 3, bottom panel), the holo conformation is frequently visited by the unbound protein and the ligand can bind to this protein conformation. In this case, a weaker protein-ligand interaction is required to stabilize the holo form of the protein. However, direct interactions between protein and ligand atoms, such as hydrogen bonds or electrostatic interactions, are not always the dominant contributors to ΔGPL. The hydrophobic association between protein and ligand moieties often dominates the free energy of binding (24-27). Until recently, hydrophobic interactions were considered to be always entropically driven (28). In this model water molecules form ordered water shells (29) around hydrophobic ligand moieties or amino acids creating a highly ordered water structure that is entropically unfavorable compared to the structure of bulk water with its highly dynamic hydrogen-bond network. As the ligand binds to the protein, the water molecules in the shell surrounding the hydrophobic moieties of the ligand and the binding site of the protein are released into the bulk solvent and gain translational, rotational, and vibrational entropy thereby lowering the free energy of the protein-ligand complex. However, recent studies (26;27;30;31) demonstrated that hydrophobic interactions can also be enthalpically driven. Using a model system for hydrophobic receptor-ligand association, McCammon and co-workers (26;27) found that disordered water molecules with density smaller than bulk density bind to small but solvent-accessible hydrophobic cavities. Upon ligand binding, these disordered water molecules are released into the bulk solvent and actually loose entropy. The gain of water-water interactions is the major contributor to the net change in enthalpy which over-compensates the loss of entropy.
Figure 3.
Two different free-energy models that characterize protein-ligand systems, likely representing the induced-fit (top panel) and the conformational-selection (bottom panel) mechanisms of binding are shown. The black curve models the free energy of the unbound form of the protein as a function of an arbitrary reaction coordinate that describes the conformational change between the open and closed form of the protein. The red curve displays the associated model of the free energy of the bound form of the protein. ΔGOC is the free-energy difference between the open and closed state of the ligand-free protein, and ΔGPL is the stabilizing free energy of the protein upon ligand binding. The free energy ΔGPL contains many contributions including the direct protein-ligand interactions typically affected by water screening, hydrophobic association, and the conformational and vibrational entropy of protein and ligand.
To separate the two different mechanism of protein-flexibility coupled to ligand binding, experimental techniques such as X-ray crystallography, NMR experiments, and kinetic measurements are utilized to identify holo-like protein conformations pre-existing in the ligand-free state of the protein (32-34) in agreement with the population-shift mechanism, or to identify intermediate states (35) that potentially point towards an induced-fit mechanism. Experiments also suggested the co-existence of both the population-shift and induced-fit mechanisms for ligand binding to a protein (36-39). For example, X-ray crystallography and kinetic measurements on ligand binding to the antibody SPE7 showed that ligands bind to pre-existing conformations of SPE7 followed by induced fit generating the final high-affinity protein-ligand complex (40). Also, single-molecule AFM measurements found that protein-protein binding between a nuclear transport effector, RanBP1, and a nuclear import receptor, importin β, can either follow the population-shift or induced-fit mechanism, depending on which additional substrate binds to importin β (36).
Computational methods to simulate protein-flexibility coupled to ligand binding
Over the past few decades, many computational concepts have emerged that incorporate different levels of protein flexibility into the modeling of protein-ligand association. Many methods are applied to study individual protein-ligand complexes, such as molecular-dynamics (MD) or Monte-Carlo (MC) simulations. Such methods can be used to locally sample energetically accessible substates of the protein-ligand complex's free-energy landscape. Algorithms such as free-energy perturbation (FEP) (41) or thermodynamic integration (TI) (42) in combination with MD or MC simulations can calculate the relative free energy of compounds binding to the same drug target within 1-2 kcal/mol of the experimental value. Unfortunately, the procedures associated with FEP and TI are computationally demanding and are typically limited to the comparison of structurally similar compounds. In addition to being computationally expensive, the application of these techniques requires a priori knowledge of the configuration of the ligand and protein in their bound form.
Recently, standard FEP and TI protocols have been extended to efficiently incorporate conformational changes associated with ligand binding (43;44). Using umbrella sampling in conjunction with the “confine-and-release” framework, Mobley et al. (43) accurately predicted the free energy of a ligand binding to a designed binding site in T4 lysozyme which involves a conformational change of a Val residue. In a separate study, Lawrenz et al. (44) developed an independent-trajectory thermodynamics-integration (IT-TI) method that computes absolute and relative binding free energies using multiple independent trajectories to improve configurational sampling. In their study on peramivir binding to H5N1 avian influenza virus neuraminidase, IT-TI was utilized to extensively sample the phase space accessible to the flexible loop regions that interact with the ligand. IT-TI was designed for use with distributed computing and consequently allows a significantly more rapid computation of absolute free energies of binding compared to standard TI or FEP calculations for a series of ligands.
An alternative method designed to predict in the configuration and binding affinity of a ligand to a specific receptor is receptor-ligand docking. Docking methods are less computationally demanding than simulation-based free energy methods and are used to virtually screen large libraries of existing or hypothetical chemicals with the goal of identifying new potentially active chemotypes that bind to the target receptor. Throughout the docking process, many different ligand orientations and conformations (binding poses) are generated in the binding site of the protein using a search algorithm. The free energy of binding of each pose is subsequently estimated using a scoring function.
For some target proteins, the search algorithm of a docking program may generate bioactive conformations (RMSD < 2 Å) throughout the search process for up to 90% of all ligands; for other proteins this percentage can be as low as 40% (45). However, existing scoring functions used in docking are not accurate enough to reliably estimate the free energy of binding of a protein-ligand complex. Thus, the bioactive pose is not always energetically ranked top among all poses generated throughout the search process (45). The correlation between experimental and predicted binding affinities using scoring functions for a series of compounds binding to the same protein is usually weak and often influenced by considerations of ligand size rather than by the correct modeling of the underlying physico-chemical contributions to binding affinity (46;47).
The above limitations of docking programs originate from the necessity to find a balance between accuracy and speed in order to screen large ligand libraries. Consequently, scoring functions quantify a simplified representation of the full protein-ligand interaction by typically including only elements such as hydrogen bonds and hydrophobic contacts, and typically neglecting effects such as solvation, polarization, and entropy. The individual terms of the scoring function are weighted by pre-factors that are optimized using a training set of protein-ligand complexes. As a consequence of the simplified representation of the physics of protein-ligand interactions and the optimization procedure, the success of scoring functions for binding pose prediction and virtual screening is known to be protein-system dependent (45). In addition to using a simplified scoring function to reduce the computational time required to screen ligand libraries, only critical degrees of freedom of the ligand are considered during the search algorithm to limit the conformational space that must be sampled (i.e. translation, rotation and torsional rotations of ligand). Based on the need to keep the computational costs low, protein flexibility is commonly only partially incorporated into docking, e.g. side-chain flexibility. Only considering side-chain flexibility in the binding site, typically containing between 10-30 residues, there are approximately 20-70 rotatable bonds that represent the protein's degrees of flexibility. The computational cost significantly increases if additional degrees of freedom, representing the backbone motion, of the protein are incorporated.
Concepts that incorporate protein conformational changes into receptor-ligand docking
As several reviews have been published (48-54) that discuss existing methods and software used to model conformational changes during docking, it is not the aim of this article to produce a detailed description of each method. Instead, general concepts that include protein flexibility during docking are highlighted in the context of their relation to the two biophysical mechanism of protein flexibility coupled to ligand binding, the induced-fit versus conformational-selection mechanism.
In general, algorithms can be divided into two categories (Figure 4). The first class of methods generates an ensemble of protein structures (EPS) prior to docking. Based on the ideas of conformational selection, each ligand in the library is then subsequently docked to each member of the EPS. The second category of methods generates alternative protein conformations on-the-fly in parallel to the pose generation of the ligand during docking. In this concept, additional degrees of freedom are selected that describe important contributions of protein flexibility. Variables that characterize the magnitude of the conformational change along the selected degrees of protein flexibility are optimized in parallel to the ligand degrees of freedom, such as translational, rotational and torsional changes. As the accessible conformational space to the protein-ligand system scales, in the worst case, as polynomial with the number of degrees of freedom, the degrees of protein flexibility must be selected very carefully. This approach can be interpreted as an implementation of the induced-fit idea into docking.
Figure 4.
Overview of methods discussed in this article that incorporate protein flexibility in docking simulations. Methods that can be assigned to the conformational-selection mechanism of protein flexibility are colored in red, methods utilizing the induced-fit mechanism in green, and methods that have elements from both mechanisms are colored in yellow. The different sources of protein flexibility for docking are shown in rectangular shapes, the methods to generate these sources as rounded rectangles and the different concepts to use these sources in the docking algorithm are shown as trapezoids. The following abbreviations are used: MD = molecular-dynamics simulations; MC = Monte-Carlo simulations; NMA = normal-mode analysis; ENM = elastic-network model; PCA = principal-component analysis; EPS = ensemble of protein structures.
Docking with conformational change represented by additional degrees of freedom
Many docking programs allow side chains of selected binding-site residues to be flexible throughout the search process. Alternative side-chain conformations are either generated by an exhaustive search (55;56), by selecting states from a pre-generated rotamer library (57-59), or by a minimal change in conformations to resolve steric clashes between protein and the current ligand binding pose (60). The estimation of free-energy changes between different protein conformations is an important issue when including protein flexibility. The energetic cost associated with torsional changes of side chains is typically estimated in one of two ways: The interaction between the flexible residues and the rest of the protein is computed using the same scoring function used to estimate the protein-ligand interactions (61;62) or an empirical energy function is used that is proportional to the size of torsional changes (60). The later estimation assumes that only small changes in the torsion angles are observed.
The question arises as to whether the inclusion of selected side chains is sufficient to accurately model protein flexibility in docking. For protein systems such as neuraminidase (shown in Figure 1, top panel) this may be the case, but for other systems (e.g. HIV protease, cAMP-dependent protein kinase, CYP450 (Figure 1, middle panel) or estrogen receptor (Figure 1, bottom panel)) protein flexibility beyond the side chain level plays a significant role during ligand binding.
To incorporate protein-backbone flexibility into docking, it is possible to include conformational fluctuations of the protein structure in terms of collective motions, or “degrees of freedom”. These collective degrees of freedom are then included as additional searchable variables in the binding-pose optimization procedure. Zacharias and co-workers derived collective degrees of freedom by performing normal-mode analysis (NMA) originally using a full atomistic representation of the protein (63). NMA is based on the assumption that protein motion can be approximated by a combination of harmonic vibrations. In NMA the Hessian matrix containing the partial second derivatives of the potential energy with respect to the atom coordinates is diagonalized. The resulting eigenvectors describing the lowest frequency modes characterize the slow collective or large-scale motions of the protein. To increase the computational efficiency, Zacharias and co-workers later used the collective variables derived from a NMA of an elastic-network model (ENM) (64). In an ENM the residues of the protein are represented by single 3D points that are connected by mechanical springs and the fluctuations of the protein are governed by the difference in local particle density. An alternative approach used to reduce protein dynamics to a few collective degrees of freedom is principle-component analysis (PCA) of a protein trajectory obtained from a MD simulation (65).
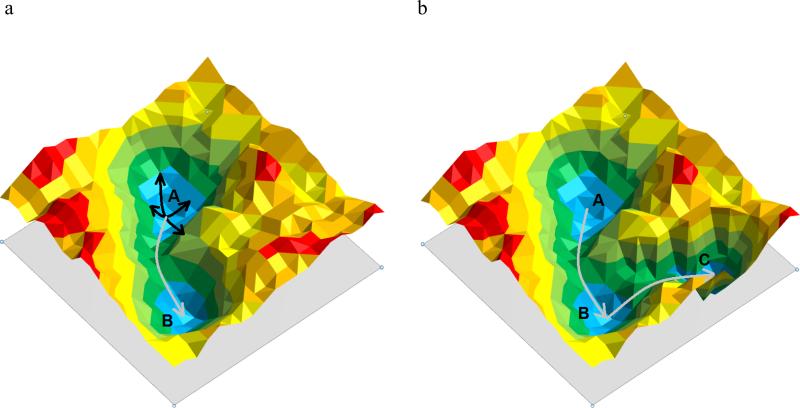
The previously described procedures utilize the potential function of the ligand-free form of the protein to determine the collective degrees of freedom of the protein. Such methods assume that the collective degrees of freedom encode the protein fluctuations necessary for ligand binding to occur. This encoding hypothesis (66-68) is an implication of the conformational-selection model assuming that the fluctuations in the apo protein structure trigger frequent transitions to the holo forms of the protein (Figure 5a). To test this hypothesis, Ikeguchi et al. (69) used linear-response theory where ligand binding was modeled as an external perturbation to the atomic fluctuations of the apo form of the protein. They demonstrated that upon ligand binding, the overall large-scale change (up to 15Å Cα displacement between apo and holo conformations) of three different protein systems (ferric-binding protein, citrate synthase, and F1-ATPase) could be predicted based on five collective modes. However, differences in the order of 2-5Å between the predicted and the experimental holo structure were observed in some portions of each protein system.
Figure 5.
(a) 2D model of a free-energy landscape of a protein system with the apo structure represented by energy minimum A and the holo structure by energy minimum B. Based on the encoding hypothesis, protein motion can be reduced to collective variables (black arrows). A linear combination of these collective variables allows the transition over low energy barriers (gray arrow) to the holo structure of the protein. (b) If holo structure (C) and apo structure (A) are separated by another stable conformation (B) the apo structure may only encode the transition to state B and ligand binding may be necessary to stabilize state B and induce a conformational change to the holo structure C.
In another study to test the encoding hypothesis, Cukier applied PCA analysis to an apo structure of an adenylate kinase known to undergo large-scale conformational changes in the LID and AMP binding domain to form a closed form of the binding site when the substrates AMP and Mg2+-ATP are bound (66). The authors observed that the conformational change of the LID domain was encoded in twelve collective modes of the apo form, whereas the additional AMP-induced conformational change in the AMP binding domain was not encoded in the collective modes. These examples demonstrate that holo-like protein conformations can be generated using collective degrees of freedom from the apo protein for many systems, but that additional induced fit may be necessary to predict a holo-like protein conformation in some protein systems (cf. Figure 5b).
One issue with many of the studies used to validate the ability of the collective mode approach to generate holo protein structures was that the experimental end state of the protein is known a priori (open and closed forms of the protein were obtained beforehand from experimental studies). Without this structural information, we are faced with the question as to how the different collective modes should be weighted and what magnitude of conformational change should be expected.
The weighting of the collective modes and the magnitude of conformational change to be expected from them directly relates to the energy difference required to transition between the apo and holo forms of the protein (represented as ΔGOC in Figure 3). In an attempt to quantify this energy, May et al. (64) estimated the energy needed to transition the protein between states as an empirical fourth-order function of the magnitude of deformation along each collective mode m:
| (1) |
where is the magnitude of conformational change along the m-th collective mode and κm is the square of the eigenvalue of mode m. This empirical quantification approach was successfully applied to cyclin-dependent kinase 2 cross-docking studies. The experimental holo structures for the ligands used in the cross-docking studies differ from the apo form by rather small shifts of secondary structural elements near the binding site (backbone RMSD: 0.7 – 2.2 Å). However, it is not obvious how this quantification of ΔGOC can be applied to protein systems known to undergo large-scale conformational changes between the apo and holo forms and are characterized by two local minima separated by an energy barrier (see Figure 5). In this situation, the energetic penalty used in the study of May et al. (64) would constantly increase with deviation from the apo form in contrast to the free energy profile. In another attempt to quantify the free energy difference associated with conformational shifts in the loop regions Cavasotto et al. (70) used a sophisticated scoring procedure comprised of force-field energies and an implicit solvation model for the protein region of interest, i.e. the residues in close proximity to the binding site. Even more difficult than estimating the free energy associated with conformational shifts of secondary-structure elements is to accurately quantify the relative free energies of large-scale conformations that involve partial refolding of the protein structure, such as unstructured protein regions in the absence of the ligand or significant refolding of loop conformations. As the difficulties of this problem are related to those of ab initio protein structure prediction, an accurate estimation (1-3 kcal/mol) of the free energy of such protein conformational changes is currently unlikely to be achieved with current scoring procedures.
An important question concerning the use of collective variables is the number of degrees of freedom required to generate a holo-like protein structure. The answer to this question certainly depends on the required level of accuracy. Pande and coworkers (71) applied NMA on four different protein systems (myosin, calmodulin, NtrC, and hemoglobin) that undergo significant conformational changes (2.0 Å – 15.1 Å RMSD between experimental apo and holo forms) during ligand binding. Using the 20 most significant normal modes, less than 50% of the observed conformational change (measured by RMSD between the projected and the experimental target structure) was reproduced and deviations between the predicted and the experimental target structure ranged from 2-8Å. To achieve an RMSD of 2Å between the predicted and experimental structures hundreds of normal modes were required. In an attempt to limit the number of additional degrees of freedom required to describe backbone motion, new approaches were recently devised to project the collective variables on important regions of the protein, or individual atoms (66;70) .
Docking into pre-generated ensemble of protein conformations
NMA, PCA or ENM can also be used to generate an ensemble of protein structures (EPS) of alternative templates for docking (Figure 4). The simplest way to include the EPS is to perform sequential docking into all members of the ensemble, linearly increasing the required computational time with the size of the EPS. To speed up the docking process, the EPS alternatively can be integrated in the docking algorithm as alternative states accessible by the protein-ligand system during the pose generation phase (72-74) or can be combined in an average interaction energy grid used throughout docking.(75) A detailed discussion of different means of handling the EPS throughout docking can be found in a review by Totrov and Abagyan (50).
Whereas the previously discussed methods focus on medium to large-scale conformational changes of the protein, it has been recognized that small scale changes (1-2Å RMSD) are often critical for successful docking (76-78). As an alternative to using collective variables to generate EPS, MD simulations can be conducted on the protein system. Whereas large-scale conformational changes are typically missed using a standard MD simulation, this approach has the ability to include small-scale backbone and side-chain fluctuations in the EPS.
In ensemble docking studies (79), it has been recognized that using an EPS with only a few protein conformations can increase the success rate for correctly predicting binding poses and enrichment in virtual screening. Using a very large EPS, however, leads to a reduced performance of docking due to the generation of a large number of false positives, thereby reducing the enrichment rate in virtual screening. Thus, an important consideration when using EPS for docking is how many and which protein conformations should be utilized.
Amaro et al. (80) utilized different approaches, e.g. hierarchical clustering based on pair-wise RMSD between MD snapshots, to reduce the initial EPS generated by MD simulations to a structurally diverse subset of protein structures representing the configurational space sampled by MD. This procedure allowed the authors to reduce the initial size of the EPS by 90-99% without any observable loss of accuracy in virtual screening experiments. Bolstad et al. (81) developed a method for selecting protein conformations from the EPS based on their ability to conserve the relative orientations of a core of amino acids critical for binding. Using dihydrofolate reductase (DHFR) as a test case, atoms of binding site residues that have a conserved relative position in various DHFR co-complexes with ligands were manually identified. Distances between these protein atoms were computed for all MD snapshots and compared with the conserved distances in the X-ray structures. Only MD snapshots that approximately preserve the interatomic distances between the selected protein atoms were chosen as members of the EPS used for docking. This procedure allowed the reduction of the initial EPS by 50-75% increasing the efficiency and ranking accuracy of ensemble docking.
Armen et al. (82) studied the influence of different levels of modeled protein flexibility on cross-docking accuracy using p38α MAP kinase which displays significant side chain and loop flexibility in the binding site. The level of protein flexibility was defined by the number and size of segments of non-restrained atoms or torsions in the MD simulations utilized to generate alternative template structures, ranging from a rigid protein structure over flexible side chains, flexible loop regions to the fully flexible protein for which no restraints on protein atoms or torsions are applied. They found that limiting the modeled protein flexibility to the fewest degrees of freedom necessary to adequately represent the experimentally observed flexibility (i.e. binding-site side chains and two flexible loops in the studied test case) showed superior cross-docking performance compared to using rigid or fully flexible proteins as template structures for docking. The authors reasoned that fully flexible protein models displayed decreased docking performance because incorporating unnecessary degrees of protein flexibility or alternative protein structures into docking increased the potential for generating many non-holo like protein conformations or protein-decoy complex structures that were highly ranked due to insufficient scoring functions.
Independent of the approach used to generate the EPS, each method is based on the conformational-selection model. However, it must be noted that existing computational methods and infrastructure typically only allow the protein to sample a portion of the configurational space accessible to the protein system. In other words, even if the population-shift mechanism is the dominant mechanism of protein flexibility associated with ligand binding, can we actually identify the holo conformation by computational means? Xu et al. (78) recently performed docking to an EPS generated by long MD simulations on two different protein systems that involve only small-scale conformational changes between the apo and the holo structures (RMSD < 1Å). Despite the long simulation time, docking to an EPS generated by short MD simulations with bound ligands clearly out-performed docking to the EPS generated by long MD simulations on the apo form of the proteins. Two possible conclusions were drawn from the results: Either there are too many alternative protein conformations generated by the long MD simulations, making the identification of the relevant holo-like structures difficult and ultimately causing many false positive poses, or ligand binding was required to induce the holo conformation of the protein.
The docking results on the apo MD ensemble led Xu et al. (78) to the development of the ligand-model concept that is capable of sampling protein conformations that are relevant for binding structurally diverse ligands. In this method, MD simulations are preformed with a dynamically changing set of restrained functional groups in the binding site of the protein, essentially representing a large hypothetical ensemble of different chemical species binding to the same target protein. Beginning from an apo structure, the ligand-model approach was used to derive an EPS used for docking and the results outperformed docking to an EPS generated from an apo-MD simulation. Furthermore, the method was only slightly less successful than docking to the experimentally known holo form of each individual protein-ligand complex.
All four previously discussed studies demonstrated that utilizing a large EPS generated from an apo MD simulation significantly increased the required computing time without necessarily improving the docking performance. A reduction of the EPS to a small set of protein structures relevant for ligand binding, or the reduction of protein flexibility to the smallest relevant number of degrees of freedom has been shown to not only increase the efficiency but also the accuracy of ensemble docking.
Concepts that incorporate protein dynamics into receptor-ligand docking
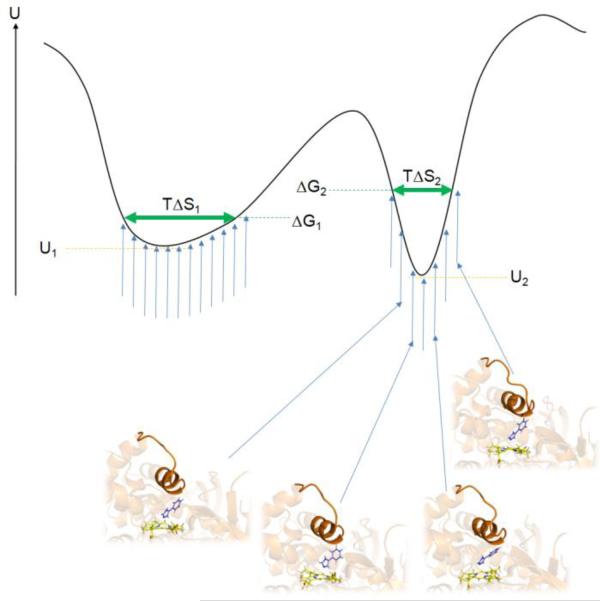
As mentioned previously, a significant problem in current docking protocols is the failure to accurately score the different docking poses and different ligands. Even if the docking study incorporates all inherent conformational changes coupled to ligand binding, for example by retrospective docking using the experimentally determined holo protein structure for each ligand, often no correlation between experimental and predicted binding affinity is observed (46). An important factor contributing to the failure of docking to accurately predict binding affinities is the lack of inclusion of dynamic information of the protein-ligand complex. Even if conformational changes of the protein are included, the docking-predicted free energy of binding is generally based on a single protein-ligand structure. However, in reality the protein-ligand complex samples local substates in the conformational vicinity of a given binding mode (Figure 6).
Figure 6.
Model of the potential energy U of a protein-ligand system of two different binding modes corresponding to the two energy minima. For each binding mode, the protein-ligand system samples slightly different configurations (blue vertical arrows and four selected protein-ligand snapshots of one binding mode). The left local minimum with a shallow shape (minimum potential energy U1) allows for more flexibility of the protein-ligand system and a smaller loss of configurational entropy compared to the steeper right minimum (minimum potential energy U2) and consequently has a lower free energy ΔG1 than the right minimum (ΔG2). Neglecting configurational entropy would cause the binding mode corresponding to the right minimum to be predicted as the top-ranked binding pose in disagreement with the real free-energy values. The vertical blue arrows represent possible protein-ligand conformations at a given temperature T. The horizontal green arrows represent the remaining configurational entropy of the system in the two different binding modes, TΔS1 and TΔS2.
From statistical mechanics, the free energy of binding ΔG0 at standard concentration C0 can be determined by integrating over all configurations accessible to the protein-ligand complex, and the protein and ligand in their unbound state: (83;84)
| (2) |
UPL, UP and UL are the potential energy for protein-ligand, protein and ligand as a function of their internal coordinates. The potential energy includes the solvation of the individual entities. By reformulating equation 2, the free energy of binding can be calculated, for example, using the molecular-mechanics Poisson Boltzmann or generalized Born surface area (MMPBSA/GBSA) (85;86) method to determine the average potential energy of the protein-ligand complex, the free protein, the unbound ligand, as well as the difference in configurational entropy:
| (3) |
The average potential energy terms given in equation 3 are determined using an implicit solvation model, either PBSA or GBSA for example, and thus include a simplified representation of entropic contributions of solvation typically represented by a cavity term ΔGcav that is proportional to the difference in the solvent-accessible surface between the bound and the unbound form of the protein-ligand complex. ΔGcav represents the entropy penalty associated with the reorganization of water molecules around the solutes (86). The ensemble of protein-ligand, free protein, and unbound ligand configurations used in the averaging process are typically sampled by means of MD or MC simulations.
In an attempt to rapidly predict native binding poses and rank libraries of compounds, scoring functions used in docking neglect the averaging process over multiple protein-ligand conformations. Entropic contributions to ligand binding are incorporated into scoring functions in simplified forms. For example, terms describing hydrophobic contacts between the protein and the ligand are used to model changes in solvation entropy upon protein-ligand binding (87;88); a count of the number of rotatable bonds is utilized as measure of conformational restriction of the bound ligand (61;89). Changes in vibrational, translational and rotational entropy upon ligand binding, however, are typically neglected. Furthermore, changes in the configurational entropy of the protein upon ligand binding are typically neglected in standard scoring functions (90;91). Nevertheless, the entropic contributions associated with protein-ligand binding commonly neglected in today's scoring functions are important contributions to the binding affinity and current research tries to develop extensions to current scoring schemes that try to address such factors.
Post-processing of docking poses
One category of methods, named post-processing, incorporates the dynamic information of the protein-ligand system after the docking process has been completed. The top-scored binding pose, or several low-scored poses, are used as input for subsequent MD or MC simulations. In combination with free energy methods such as FEP, TI, MMPBSA/GBSA, or linear interaction energy analysis (LIE) (92) a more accurate estimation of the free energy of binding is possible (93). This post-processing step can significantly improve the successful prediction of binding affinities (93;94). However, this process is relatively time-consuming and therefore requires that the bioactive binding mode is within the top-ranked binding poses for each ligand.
Modeling of configurational entropy in docking
A second category of methods tries to directly estimate the configurational entropy or averages over the predicted free energy of similar protein-ligand configurations generated throughout docking. Chang et al. (95) utilized a simple cluster size method to estimate the configurational entropy of each binding mode. For each pose generated by the docking program, all conformationally related poses (RMSD < 2 Å) are identified. The number of poses within this RMSD range is used as a measure for accessible configurational entropy of the protein-ligand system at a particular local minimum. The underlying assumption is that the search algorithm of the docking software (AutoDock4) more easily identifies binding poses in wide energy wells compared to narrow wells. Based on this assumption, the probability of identifying similar binding poses correlates with the width of the energy well and the accessible configurational entropy of the ligand in the binding site of the protein. A similar estimate of configurational entropy has also been implemented in a knowledge-based scoring function (96).
Ruvinsky et al. (97;98) clustered the ensemble of binding poses based on their pairwise RMSD values to estimate the configurational entropy of each unique binding mode. The entropy of each unique binding mode was calculated by measuring the variance in translational (measured by relative translational coordinate r), the rotational (measured by Euler angles Φ1, Φ2, Φ3), and the torsion (torsion angles Ωk) values among the members of a cluster:
| (4) |
The underlying concept of this method is that binding modes that are restrained within the binding site (i.e. smaller variation in translational, rotational and torsion variables) result in a larger loss of entropy upon binding to the protein than less restrained binding modes (Figure 6) and are energetically less favorable.
Applying the previously described methods to estimate the configurational entropy of 22 ligands binding to APS reductase (95) a significant improvement in identifying native binding poses as the highest ranked was observed for all utilized entropy measures. Whereas the simple cluster-size method relies on the details of the search algorithm throughout docking, the method of Ruvinsky et al. (97;98) was conceptually designed to represent characteristics of the underlying free energy landscape of a given binding mode. However, analysis revealed (95) that the results of the latter method were strongly dependent on the number of poses generated in a binding-mode cluster and therefore primarily correlate with cluster size rather than the underlying free energy landscape.
Unwalla and co-workers (99) derived a scoring method, titled the partition function-based scoring (PFS) method, that includes an estimate for the change in ligand entropy upon binding:
| (5) |
The first term includes estimates for the remaining conformational, positional, and rotational entropy of the bound ligand and the second term estimates the conformational entropy of the unbound ligand; Nbound poses is the number of distinct binding poses identified by the docking program, and Nunbound conformations is the number of ligand conformations within 5 kcal/mol of the lowest identified ligand conformation. An initial study using PFS (99) suggested that this method can improve ranking of compounds with similar number of rotatable bonds, a benefit that is inaccessible to the frequently used approximation that adds a constant entropy penalty per rotatable bond. In addition, the study also suggested that the PFS method would be more accurate if the scoring function accurately mimics the form of the free energy landscape. However, a simple scaling of existing scoring functions (factor f in eq 5) is unlikely to provide such a mimic.
Compared to the previously discussed method for incorporating protein dynamics into docking, the Mining Minima approach (100-103) is computationally more expensive. Mining Minima aims to directly calculate the configurational integrals in eq 2, e.g. for the protein-ligand complex. Local minima corresponding to different binding modes are identified throughout the conformational search procedure. The eigenvectors corresponding to the largest eigenvalues of the Hessian matrix in bond-angle-torsion coordinates are determined. Protein-ligand conformations are generated along the eigenvectors and used to compute the local configurational integral Zi for local minimum i. The overall free energy of a compound is then computed from the sum of local configurational integrals: . This method was successfully applied to binding affinity predictions of ligands binding to HIV-1 protease and phosphodiesterase (103).
Another successful approach that incorporates protein dynamics in docking is the relaxed complex scheme (RCS) (104-106). In this scheme, MD simulations of the apo form of the protein are used to generate an EPS. Sequential docking to the EPS is then performed and for each ligand and similar binding poses are clustered across all EPS protein templates and the score of all members of a cluster is averaged. Using the average score of each unique binding mode was shown to provide a more accurate estimation of binding free energies than using individual scores (106;107). Whereas the original RCS scheme is based on the conformation selection model, Xu et al. (78) extended the RCS approach to allow the incorporation of induced fit contribution to protein flexibility. In combination with the previously discussed ligand-model concept, the RCS scheme was successful applied to predict binding modes and affinities of structurally diverse compounds.
Incorporating solvation effects into docking
As discussed previously in this article, the change in solvation entropy plays a fundamental role in the strength of protein-ligand binding. In empirical scoring functions, desolvation effects are typically represented by a term characterizing hydrophobic contacts between the protein and the ligand (87;88). In scoring functions that are based on physical terms, desolvation of non-polar atoms is often approximated by a function that is proportional to the solvent-accessible surface (61). A similar term has also been utilized for knowledge-based scoring functions (96). The electrostatic component of desolvation that is dominant for polar groups can be approximated using implicit solvation model by means of the Poisson-Boltzmann (PB) or Generalized-Born (GB) methodology. These methods, however, are too time-consuming for use in docking methods applied to virtual screening. To improve the efficiency of implicit solvation models in docking, Mysinger et al. (108) recently developed a concept that computes the fractional desolvation of a ligand atom inside of the protein based on protein's environment surrounding the atom. The energy associated with the atom's transfer from a high- to low-dielectric medium (i.e. water to protein) is then weighted by the fractional desolvation of the atom; this energy estimates the desolvation free energy of each ligand atom. The overall desolvation energy of the ligand is computed by summing over all atomic desolvation contributions.
The previously discussed approaches are based on a continuum approximation of the solvent, and don't include the effects associated with the directionality of water-mediated hydrogen-bonds; the entropic contribution of desolvation is approximated by a solvent accessibility term. Directional hydrogen-bonds, however, can play an important role in mediating polar interactions between solute and solvent (109). Docking programs, e.g. GOLD (109), have been modified to incorporate water-mediated interactions into docking: Water molecules are switched on and off and are allowed to rotate throughout the docking process. To more accurately estimate desolvation energies, Abel et al. (110) have developed the WaterMap concept. Explicit protein-water simulations are performed, water sites are identified based on conserved water positions throughout the MD simulation, and the enthalpy and entropy of each water site relative to bulk water is computed using the MD trajectory and inhomogeneous solvation theory (111;112). The desolvation contribution to the binding free energy has been successfully predicted using WaterMap by considering the excess enthalpy and entropy of the water molecules in the binding site that are replaced by ligand binding (110;113;114).
Concluding remarks
Many methods have been developed in recent years to incorporate conformational changes of the protein in receptor-ligand docking. Most of the methods derive an EPS or collective modes of protein motion from the apo structure of the protein, thus assuming the conformation-selection model of protein flexibility coupled to ligand binding is valid. However, experimental and computational studies have demonstrated that for some systems the induced-fit mechanism of ligand binding plays an important role during protein-ligand recognition. Furthermore, if the conformational-selection model is the dominant mechanism of protein flexibility coupled to ligand binding, elucidating or determining holo-like conformation on the time scale sampled in silico is still challenging. In particular, sampling partial folding or unfolding of segments of the protein associated with ligand binding may not be accessible with current computational methods. For such systems, novel approaches that combine protein folding and ligand binding, may be necessary to accurately predict and quantify ligand binding and is a current area of research (115;116).
Another area of future research is the precise quantification of protein-ligand binding in the context of protein flexibility. Improvement is needed in scoring functions used to quantify the direct interaction between ligand and protein. Improvement is also necessary for the scoring procedure used to estimate the free energy associated with the different conformational states accessible to the protein structure. In general, the inclusion of additional degrees of freedom to simulate protein flexibility adds to the difficulty of accurately predicting the free energy of binding. This difficulty is due to the fact that more contributions to the free energy must be considered that vary between different poses and different ligands, i.e. the interaction between flexible residues and the core of the protein, and typically these additional contributions also introduce additional inaccuracies into the calculated binding affinity. The inaccuracy of scoring protein-ligand complexes in combination with the generation of additional possible binding poses when including protein flexibility contributes to the failure of some virtual screening experiments that incorporate protein flexibility (50;79). To improve the scoring process in docking, it may be necessary to include protein dynamics, for example, by sampling conformational sub-states of a given binding mode or by including an estimate of configurational entropy. This area of research may contribute to a more precise estimation of binding affinities in the future.
ACKNOWLEDGMENT
I thank Matthew Danielson and Jared Thompson for critical reading of the manuscript, and the reviewers for valuable suggestions to improve the manuscript.
FUNDING INFORMATION: This work has in part been supported by the National Institutes of Health (GM085604 and GM092855).
ABBREVIATIONS
- MD
molecular-dynamics simulation
- MC
Monte-Carlo simulation
- NMA
normal-mode analysis
- ENM
elastic-network model
- PCA
principal-component analysis
- FEP
free-energy perturbation method
- TI
thermodynamic integration method
- IT-TI
independent-trajectory thermodynamics integration method
- LIE
linear interaction energy analysis
- MMPBSA
molecular mechanics Poisson Boltzmann surface area method
- MMGBSA
molecular mechanics generalized Born surface area method
- RMSD
root-mean square deviation
- EPS
ensemble of protein structures
- PFS
partition function-based scoring
- KNF
Koshland-Neméthy-Filmer model
- MWC
Monod-Wyman-Changeux model
- SERM
selective estrogen receptor modulators
- DHFR
dihydrofolate reductase
References
- 1.Wess J, Han SJ, Kim SK, Jacobson KA, Li JH. Conformational changes involved in G-protein-coupled-receptor activation. Trends Pharmacol. Sci. 2008;29:616–625. doi: 10.1016/j.tips.2008.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kobilka BK, Deupi X. Conformational complexity of G-protein-coupled receptors. Trends Pharmacol. Sci. 2007;28:397–406. doi: 10.1016/j.tips.2007.06.003. [DOI] [PubMed] [Google Scholar]
- 3.Kobilka BK. G protein coupled receptor structure and activation. Biochim. Biophys. Acta. 2007;1768:794–807. doi: 10.1016/j.bbamem.2006.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hucho F, Weise C. Ligand-gated ion channels. Angew. Chem. Int. Edit. 2001;40:3101–3116. doi: 10.1002/1521-3773(20010903)40:17<3100::AID-ANIE3100>3.0.CO;2-A. [DOI] [PubMed] [Google Scholar]
- 5.Shepherd GM. Discrimination of Molecular Signals by the Olfactory Receptor Neuron. Neuron. 1994;13:771–790. doi: 10.1016/0896-6273(94)90245-3. [DOI] [PubMed] [Google Scholar]
- 6.Rozengurt E, Sternini C. Taste receptor signaling in the mammalian gut. Curr. Opin. Pharmacol. 2007;7:557–562. doi: 10.1016/j.coph.2007.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Denisov IG, Makris TM, Sligar SG, Schlichting I. Structure and chemistry of cytochrome P450. Chem. Rev. 2005;105:2253–2277. doi: 10.1021/cr0307143. [DOI] [PubMed] [Google Scholar]
- 8.Guengerich FP. Cytochrome P450s and other enzymes in drug metabolism and toxicity. AAPS. J. 2006;8:E101–E111. doi: 10.1208/aapsj080112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bossart-Whitaker P, Carson M, Babu YS, Smith CD, Laver WG, Air GM. Three-dimensional Structure of Influenza A N9 Neuraminidase and Its Complex with the Inhibitor 2-Deoxy 2,3-Dehydro-N-Acetyl Neuraminic Acid. J. Mol. Biol. 1993;232:1069–1083. doi: 10.1006/jmbi.1993.1461. [DOI] [PubMed] [Google Scholar]
- 10.Taylor NR, Cleasby A, Singh O, Skarzynski T, Wonacott AJ, Smith PW, Sollis SL, Howes PD, Cherry PC, Bethell R, Colman P, Varghese J. Dihydropyrancarboxamides Related to Zanamivir: A New Series of Inhibitors of Influenza Virus Sialidases. 2. Crystallographic and Molecular Modeling Study of Complexes of 4-Amino-4H-pyran-6-carboxamides and Sialidase from Influenza Virus Types A and B. J. Med. Chem. 1998;41:798–807. doi: 10.1021/jm9703754. [DOI] [PubMed] [Google Scholar]
- 11.Park SY, Yamane K, Adachi S. i., Shiro Y, Weiss KE, Maves SA, Sligar SG. Thermophilic cytochrome P450 (CYP119) from Sulfolobus solfataricus: high resolution structure and functional properties. J. Inorg. Biochem. 2002;91:491–501. doi: 10.1016/s0162-0134(02)00446-4. [DOI] [PubMed] [Google Scholar]
- 12.Yano JK, Koo LS, Schuller DJ, Li H, Ortiz de Montellano PR, Poulos TL. Crystal Structure of a Thermophilic Cytochrome P450 from the Archaeon Sulfolobus solfataricus. J. Biol. Chem. 2000;275:31086–31092. doi: 10.1074/jbc.M004281200. [DOI] [PubMed] [Google Scholar]
- 13.Brzozowski AM, Pike AC, Dauter Z, Hubbard RE, Bonn T, Engstrom O, Ohman L, Greene GL, Gustafsson JA, Carlquist M. Molecular basis of agonism and antagonism in the oestrogen receptor. Nature. 1997;389:753–758. doi: 10.1038/39645. [DOI] [PubMed] [Google Scholar]
- 14.Brzozowski AM, Pike AC, Dauter Z, Hubbard RE, Bonn T, Engstrom O, Ohman L, Greene GL, Gustafsson JA, Carlquist M. Molecular basis of agonism and antagonism in the oestrogen receptor. Nature. 1997;389:753–758. doi: 10.1038/39645. [DOI] [PubMed] [Google Scholar]
- 15.Teague SJ. Implications of protein flexibility for drug discovery. Nat. Rev. Drug Discov. 2003;2:527–541. doi: 10.1038/nrd1129. [DOI] [PubMed] [Google Scholar]
- 16.Park SY, Yamane K, Adachi S. i., Shiro Y, Weiss KE, Maves SA, Sligar SG. Thermophilic cytochrome P450 (CYP119) from Sulfolobus solfataricus: high resolution structure and functional properties. J. Inorg. Biochem. 2002;91:491–501. doi: 10.1016/s0162-0134(02)00446-4. [DOI] [PubMed] [Google Scholar]
- 17.Yano JK, Koo LS, Schuller DJ, Li H, Ortiz de Montellano PR, Poulos TL. Crystal Structure of a Thermophilic Cytochrome P450 from the Archaeon Sulfolobus solfataricus. J. Biol. Chem. 2000;275:31086–31092. doi: 10.1074/jbc.M004281200. [DOI] [PubMed] [Google Scholar]
- 18.Brzozowski AM, Pike AC, Dauter Z, Hubbard RE, Bonn T, Engstrom O, Ohman L, Greene GL, Gustafsson JA, Carlquist M. Molecular basis of agonism and antagonism in the oestrogen receptor. Nature. 1997;389:753–758. doi: 10.1038/39645. [DOI] [PubMed] [Google Scholar]
- 19.Koshland DE. Application of A Theory of Enzyme Specificity to Protein Synthesis. P. Natl. Acad. Sci. U. S. A. 1958;44:98–104. doi: 10.1073/pnas.44.2.98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ma BY, Kumar S, Tsai CJ, Nussinov R. Folding funnels and binding mechanisms. Protein Eng. 1999;12:713–720. doi: 10.1093/protein/12.9.713. [DOI] [PubMed] [Google Scholar]
- 21.Koshland DE, Jr., Nemethy G, Filmer D. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry. 1966;5:365–385. doi: 10.1021/bi00865a047. [DOI] [PubMed] [Google Scholar]
- 22.Monod J, Wyman J, Changeux JP. On the nature of allosteric transitions: A plausible model. J. Mol. Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 23.Okazaki KI, Takada S. Dynamic energy landscape view of coupled binding and protein conformational change: Induced-fit versus population-shift mechanisms. P. Natl. Acad. Sci. U. S. A. 2008;105:11182–11187. doi: 10.1073/pnas.0802524105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tanford C. The hydrophobic effect and the organization of living matter. Science. 1978;200:1012–1018. doi: 10.1126/science.653353. [DOI] [PubMed] [Google Scholar]
- 25.Tanford C. The Hydrophobic Effect. Wiley; New York: 1980. [Google Scholar]
- 26.Baron R, Setny P, McCammon JA. Water in cavity-ligand recognition. J. Am. Chem. Soc. 2010;132:12091–12097. doi: 10.1021/ja1050082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Setny P, Baron R, McCammon JA. How Can Hydrophobic Association Be Enthalpy Driven? J. Chem. Theory Comput. 2010;6:2866–2871. doi: 10.1021/ct1003077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dunitz JD. The entropic cost of bound water in crystals and biomolecules. Science. 1994;264:670. doi: 10.1126/science.264.5159.670. [DOI] [PubMed] [Google Scholar]
- 29.Gao S, House W, Chapman WG. NMR/MRI study of clathrate hydrate mechanisms. J. Phys. Chem. B. 2005;109:19090–19093. doi: 10.1021/jp052071w. [DOI] [PubMed] [Google Scholar]
- 30.Barratt E, Bingham RJ, Warner DJ, Laughton CA, Phillips SE, Homans SW. Van der Waals interactions dominate ligand-protein association in a protein binding site occluded from solvent water. J. Am. Chem. Soc. 2005;127:11827–11834. doi: 10.1021/ja0527525. [DOI] [PubMed] [Google Scholar]
- 31.Bingham RJ, Findlay JB, Hsieh SY, Kalverda AP, Kjellberg A, Perazzolo C, Phillips SE, Seshadri K, Trinh CH, Turnbull WB, Bodenhausen G, Homans SW. Thermodynamics of binding of 2-methoxy-3-isopropylpyrazine and 2-methoxy-3-isobutylpyrazine to the major urinary protein. J. Am. Chem. Soc. 2004;126:1675–1681. doi: 10.1021/ja038461i. [DOI] [PubMed] [Google Scholar]
- 32.Volkman BF, Lipson D, Wemmer DE, Kern D. Two-state allosteric behavior in a single-domain signaling protein. Science. 2001;291:2429–2433. doi: 10.1126/science.291.5512.2429. [DOI] [PubMed] [Google Scholar]
- 33.Boehr DD, Nussinov R, Wright PE. The role of dynamic conformational ensembles in biomolecular recognition. Nat. Chem. Biol. 2009;5:789–796. doi: 10.1038/nchembio.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fraser JS, Clarkson MW, Degnan SC, Erion R, Kern D, Alber T. Hidden alternative structures of proline isomerase essential for catalysis. Nature. 2009;462:669–673. doi: 10.1038/nature08615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dyer CM, Dahlquist FW. Switched or not?: the structure of unphosphorylated CheY bound to the N terminus of FliM. J. Bacteriol. 2006;188:7354–7363. doi: 10.1128/JB.00637-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nevo R, Brumfeld V, Elbaum M, Hinterdorfer P, Reich Z. Direct discrimination between models of protein activation by single-molecule force measurements. Biophys. J. 2004;87:2630–2634. doi: 10.1529/biophysj.104.041889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hammes GG, Chang YC, Oas TG. Conformational selection or induced fit: A flux description of reaction mechanism. P. Natl. Acad. Sci. U. S. A. 2009;106:13737–13741. doi: 10.1073/pnas.0907195106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Weikl TR, von Deuster C. Selected-fit versus induced-fit protein binding: Kinetic differences and mutational analysis. Proteins. 2009;75:104–110. doi: 10.1002/prot.22223. [DOI] [PubMed] [Google Scholar]
- 39.Ma BY, Nussinov R. Enzyme dynamics point to stepwise conformational selection in catalysis. Curr. Opin. Chem. Biol. 2010;14:652–659. doi: 10.1016/j.cbpa.2010.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.James LC, Tawfik DS. Structure and kinetics of a transient antibody binding intermediate reveal a kinetic discrimination mechanism in antigen recognition. Proc. Natl. Acad. Sci. U. S. A. 2005;102:12730–12735. doi: 10.1073/pnas.0500909102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zwanzig RW. High-Temperature Equation of State by A Perturbation Method .1. Nonpolar Gases. J. Chem. Phys. 1954;22:1420–1426. [Google Scholar]
- 42.Kirkwood JG. Statistical mechanics of fluid mixtures. J. Chem. Phys. 1935;3:300–313. [Google Scholar]
- 43.Mobley DL, Chodera JD, Dill KA. The Confine-and-Release Method: Obtaining Correct Binding Free Energies in the Presence of Protein Conformational Change. J. Chem. Theory. Comput. 2007;3:1231–1235. doi: 10.1021/ct700032n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lawrenz M, Baron R, McCammon JA. Independent-Trajectories Thermodynamic-Integration Free-Energy Changes for Biomolecular Systems: Determinants of H5N1 Avian Influenza Virus Neuraminidase Inhibition by Peramivir. J. Chem. Theory. Comput. 2009;5:1106–1116. doi: 10.1021/ct800559d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Warren GL, Andrews CW, Capelli AM, Clarke B, LaLonde J, Lambert MH, Lindvall M, Nevins N, Semus SF, Senger S, Tedesco G, Wall ID, Woolven JM, Peishoff CE, Head MS. A critical assessment of docking programs and scoring functions. J. Med. Chem. 2006;49:5912–5931. doi: 10.1021/jm050362n. [DOI] [PubMed] [Google Scholar]
- 46.Ferrara P, Gohlke H, Price DJ, Klebe G, Brooks CL., III Assessing scoring functions for protein-ligand interactions. J. Med. Chem. 2004;47:3032–3047. doi: 10.1021/jm030489h. [DOI] [PubMed] [Google Scholar]
- 47.Kuntz ID, Chen K, Sharp KA, Kollman PA. The maximal affinity of ligands. Proc. Natl. Acad. Sci. U. S. A. 1999;96:9997–10002. doi: 10.1073/pnas.96.18.9997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Carlson HA. Protein flexibility and drug design: how to hit a moving target. Curr. Opin. Chem. Biol. 2002;6:447–452. doi: 10.1016/s1367-5931(02)00341-1. [DOI] [PubMed] [Google Scholar]
- 49.Teodoro ML, Kavraki LE. Conformational flexibility models for the receptor in structure based drug design. Curr. Pharm. Design. 2003;9:1635–1648. doi: 10.2174/1381612033454595. [DOI] [PubMed] [Google Scholar]
- 50.Totrov M, Abagyan R. Flexible ligand docking to multiple receptor conformations: a practical alternative. Curr. Opin. Struc. Biol. 2008;18:178–184. doi: 10.1016/j.sbi.2008.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Beier C, Zacharias M. Tackling the challenges posed by target flexibility in drug design. Expert Opin. Drug Dis. 2010;5:347–359. doi: 10.1517/17460441003713462. [DOI] [PubMed] [Google Scholar]
- 52.Rao C, Subramanian J, Sharma SD. Managing protein flexibility in docking and its applications. Drug Discov. Today. 2009;14:394–400. doi: 10.1016/j.drudis.2009.01.003. [DOI] [PubMed] [Google Scholar]
- 53.Sotriffer CA. Accounting for Induced-Fit Effects in Docking: What is Possible and What is Not? Curr. Top. Med. Chem. 2011;11:179–191. doi: 10.2174/156802611794863544. [DOI] [PubMed] [Google Scholar]
- 54.Lin JH. Accommodating Protein Flexibility for Structure-Based Drug Design. Curr. Top. Med. Chem. 2011;11:171–178. doi: 10.2174/156802611794863580. [DOI] [PubMed] [Google Scholar]
- 55.Yang AYC, Kallblad P, Mancera RL. Molecular modelling prediction of ligand binding site flexibility. J. Comput. Aid. Mol. Des. 2004;18:235–250. doi: 10.1023/b:jcam.0000046820.08222.83. [DOI] [PubMed] [Google Scholar]
- 56.Meiler J, Baker D. ROSETTALIGAND: Protein-small molecule docking with full side-chain flexibility. Proteins. 2006;65:538–548. doi: 10.1002/prot.21086. [DOI] [PubMed] [Google Scholar]
- 57.Leach AR. Ligand Docking to Proteins with Discrete Side-Chain Flexibility. J. Mol. Biol. 1994;235:345–356. doi: 10.1016/s0022-2836(05)80038-5. [DOI] [PubMed] [Google Scholar]
- 58.Nabuurs SB, Wagener M, De Vlieg J. A flexible approach to induced fit docking. J. Med. Chem. 2007;50:6507–6518. doi: 10.1021/jm070593p. [DOI] [PubMed] [Google Scholar]
- 59.Hartmann C, Antes I, Lengauer T. Docking and scoring with alternative side-chain conformations. Proteins. 2009;74:712–726. doi: 10.1002/prot.22189. [DOI] [PubMed] [Google Scholar]
- 60.Zavodszky MI, Kuhn LA. Side-chain flexibility in protein-ligand binding: the minimal rotation hypothesis. Protein Sci. 2005;14:1104–1114. doi: 10.1110/ps.041153605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Morris GM, Goodsell DS, Halliday RS, Huey R, Hart WE, Belew RK, Olson AJ. Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem. 1998;19:1639–1662. [Google Scholar]
- 62.Morris GM, Huey R, Lindstrom W, Sanner MF, Belew RK, Goodsell DS, Olson AJ. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009;30:2785–2791. doi: 10.1002/jcc.21256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Zacharias M, Sklenar H. Harmonic modes as variables to approximately account for receptor flexibility in ligand-receptor docking simulations: Application to DNA minor groove ligand complex. J. Comput. Chem. 1999;20:287–300. [Google Scholar]
- 64.May A, Zacharias M. Protein-ligand docking accounting for receptor side chain and global flexibility in normal modes: Evaluation on kinase inhibitor cross docking. J. Med. Chem. 2008;51:3499–3506. doi: 10.1021/jm800071v. [DOI] [PubMed] [Google Scholar]
- 65.Amadei A, Linssen AB, Berendsen HJ. Essential dynamics of proteins. Proteins. 1993;17:412–425. doi: 10.1002/prot.340170408. [DOI] [PubMed] [Google Scholar]
- 66.Cukier RI. Apo adenylate kinase encodes its holo form: a principal component and varimax analysis. J. Phys. Chem. B. 2009;113:1662–1672. doi: 10.1021/jp8053795. [DOI] [PubMed] [Google Scholar]
- 67.Lou H, Cukier RI. Molecular dynamics of apo-adenylate kinase: a distance replica exchange method for the free energy of conformational fluctuations. J. Phys. Chem. B. 2006;110:24121–24137. doi: 10.1021/jp064303c. [DOI] [PubMed] [Google Scholar]
- 68.Lou H, Cukier RI. Molecular dynamics of apo-adenylate kinase: a principal component analysis. J. Phys. Chem. B. 2006;110:12796–12808. doi: 10.1021/jp061976m. [DOI] [PubMed] [Google Scholar]
- 69.Ikeguchi M, Ueno J, Sato M, Kidera A. Protein structural change upon ligand binding: linear response theory. Phys. Rev. Lett. 2005;94:078102. doi: 10.1103/PhysRevLett.94.078102. [DOI] [PubMed] [Google Scholar]
- 70.Cavasotto CN, Kovacs JA, Abagyan RA. Representing receptor flexibility in ligand docking through relevant normal modes. J. Am. Chem. Soc. 2005;127:9632–9640. doi: 10.1021/ja042260c. [DOI] [PubMed] [Google Scholar]
- 71.Petrone P, Pande VS. Can conformational change be described by only a few normal modes? Biophys. J. 2006;90:1583–1593. doi: 10.1529/biophysj.105.070045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Claussen H, Buning C, Rarey M, Lengauer T. FlexE: efficient molecular docking considering protein structure variations. J. Mol. Biol. 2001;308:377–395. doi: 10.1006/jmbi.2001.4551. [DOI] [PubMed] [Google Scholar]
- 73.Zhao Y, Sanner MF. FLIPDock: docking flexible ligands into flexible receptors. Proteins. 2007;68:726–737. doi: 10.1002/prot.21423. [DOI] [PubMed] [Google Scholar]
- 74.Ferrari AM, Wei BQ, Costantino L, Shoichet BK. Soft docking and multiple receptor conformations in virtual screening. J. Med. Chem. 2004;47:5076–5084. doi: 10.1021/jm049756p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Knegtel RM, Kuntz ID, Oshiro CM. Molecular docking to ensembles of protein structures. J. Mol. Biol. 1997;266:424–440. doi: 10.1006/jmbi.1996.0776. [DOI] [PubMed] [Google Scholar]
- 76.Erickson JA, Jalaie M, Robertson DH, Lewis RA, Vieth M. Lessons in molecular recognition: the effects of ligand and protein flexibility on molecular docking accuracy. J. Med. Chem. 2004;47:45–55. doi: 10.1021/jm030209y. [DOI] [PubMed] [Google Scholar]
- 77.Kitchen DB, Decornez H, Furr JR, Bajorath J. Docking and scoring in virtual screening for drug discovery: methods and applications. Nat. Rev. Drug Discov. 2004;3:935–949. doi: 10.1038/nrd1549. [DOI] [PubMed] [Google Scholar]
- 78.Xu M, Lill MA. Significant Enhancement of Docking Sensitivity Using Implicit Ligand Sampling. J. Chem. Inf. Model. 2011;51:693–706. doi: 10.1021/ci100457t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Barril X, Morley SD. Unveiling the full potential of flexible receptor docking using multiple crystallographic structures. J. Med. Chem. 2005;48:4432–4443. doi: 10.1021/jm048972v. [DOI] [PubMed] [Google Scholar]
- 80.Amaro RE, Baron R, McCammon JA. An improved relaxed complex scheme for receptor flexibility in computer-aided drug design. J. Comput. Aided Mol. Des. 2008;22:693–705. doi: 10.1007/s10822-007-9159-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Bolstad ES, Anderson AC. In pursuit of virtual lead optimization: pruning ensembles of receptor structures for increased efficiency and accuracy during docking. Proteins. 2009;75:62–74. doi: 10.1002/prot.22214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Armen RS, Chen J, Brooks CL. An Evaluation of Explicit Receptor Flexibility in Molecular Docking Using Molecular Dynamics and Torsion Angle Molecular Dynamics. J. Chem. Theory. Comput. 2009;5:2909–2923. doi: 10.1021/ct900262t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Gilson MK, Zhou HX. Calculation of protein-ligand binding affinities. Annu. Rev. Biophys. Biomol. Struct. 2007;36:21–42. doi: 10.1146/annurev.biophys.36.040306.132550. [DOI] [PubMed] [Google Scholar]
- 84.Gilson MK, Given JA, Bush BL, McCammon JA. The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophys. J. 1997;72:1047–1069. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Kollman PA, Massova I, Reyes C, Kuhn B, Huo S, Chong L, Lee M, Lee T, Duan Y, Wang W, Donini O, Cieplak P, Srinivasan J, Case DA, Cheatham TE., III Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc. Chem. Res. 2000;33:889–897. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- 86.Srinivasan J, Miller J, Kollman PA, Case DA. Continuum solvent studies of the stability of RNA hairpin loops and helices. J. Biomol. Struct. Dyn. 1998;16:671–682. doi: 10.1080/07391102.1998.10508279. [DOI] [PubMed] [Google Scholar]
- 87.Bohm HJ. The development of a simple empirical scoring function to estimate the binding constant for a protein-ligand complex of known three-dimensional structure. J. Comput. Aided Mol. Des. 1994;8:243–256. doi: 10.1007/BF00126743. [DOI] [PubMed] [Google Scholar]
- 88.Eldridge MD, Murray CW, Auton TR, Paolini GV, Mee RP. Empirical scoring functions: I. The development of a fast empirical scoring function to estimate the binding affinity of ligands in receptor complexes. J. Comput. Aided Mol. Des. 1997;11:425–445. doi: 10.1023/a:1007996124545. [DOI] [PubMed] [Google Scholar]
- 89.Huey R, Morris GM, Olson AJ, Goodsell DS. A semiempirical free energy force field with charge-based desolvation. J. Comput. Chem. 2007;28:1145–1152. doi: 10.1002/jcc.20634. [DOI] [PubMed] [Google Scholar]
- 90.Moy FJ, Chanda PK, Chen J, Cosmi S, Edris W, Levin JI, Rush TS, Wilhelm J, Powers R. Impact of mobility on structure-based drug design for the MMPs. J. Am. Chem. Soc. 2002;124:12658–12659. doi: 10.1021/ja027391x. [DOI] [PubMed] [Google Scholar]
- 91.Thielges MC, Chung JK, Fayer MD. Protein dynamics in cytochrome P450 molecular recognition and substrate specificity using 2D IR vibrational echo spectroscopy. J. Am. Chem. Soc. 2011;133:3995–4004. doi: 10.1021/ja109168h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Aqvist J, Medina C, Samuelsson JE. A new method for predicting binding affinity in computer-aided drug design. Protein Eng. 1994;7:385–391. doi: 10.1093/protein/7.3.385. [DOI] [PubMed] [Google Scholar]
- 93.Alonso H, Bliznyuk AA, Gready JE. Combining docking and molecular dynamic simulations in drug design. Med. Res. Rev. 2006;26:531–568. doi: 10.1002/med.20067. [DOI] [PubMed] [Google Scholar]
- 94.Naim M, Bhat S, Rankin KN, Dennis S, Chowdhury SF, Siddiqi I, Drabik P, Sulea T, Bayly CI, Jakalian A, Purisima EO. Solvated interaction energy (SIE) for scoring protein-ligand binding affinities. 1. Exploring the parameter space. J. Chem. Inf. Model. 2007;47:122–133. doi: 10.1021/ci600406v. [DOI] [PubMed] [Google Scholar]
- 95.Chang MW, Belew RK, Carroll KS, Olson AJ, Goodsell DS. Empirical entropic contributions in computational docking: evaluation in APS reductase complexes. J. Comput. Chem. 2008;29:1753–1761. doi: 10.1002/jcc.20936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Huang SY, Zou X. Inclusion of solvation and entropy in the knowledge-based scoring function for protein-ligand interactions. J. Chem. Inf. Model. 2010;50:262–273. doi: 10.1021/ci9002987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Ruvinsky AM, Kozintsev AV. New and fast statistical-thermodynamic method for computation of protein-ligand binding entropy substantially improves docking accuracy. J. Comput. Chem. 2005;26:1089–1095. doi: 10.1002/jcc.20246. [DOI] [PubMed] [Google Scholar]
- 98.Ruvinsky AM. Calculations of protein-ligand binding entropy of relative and overall molecular motions. J. Comput. Aided Mol. Des. 2007;21:361–370. doi: 10.1007/s10822-007-9116-0. [DOI] [PubMed] [Google Scholar]
- 99.Salaniwal S, Manas ES, Alvarez JC, Unwalla RJ. Critical evaluation of methods to incorporate entropy loss upon binding in high-throughput docking. Proteins. 2007;66:422–435. doi: 10.1002/prot.21180. [DOI] [PubMed] [Google Scholar]
- 100.Chang CE, Gilson MK. Free energy, entropy, and induced fit in host-guest recognition: calculations with the second-generation mining minima algorithm. J. Am. Chem. Soc. 2004;126:13156–13164. doi: 10.1021/ja047115d. [DOI] [PubMed] [Google Scholar]
- 101.David L, Luo R, Gilson MK. Ligand-receptor docking with the Mining Minima optimizer. J. Comput. Aided Mol. Des. 2001;15:157–171. doi: 10.1023/a:1008128723048. [DOI] [PubMed] [Google Scholar]
- 102.Kairys V, Gilson MK. Enhanced docking with the mining minima optimizer: acceleration and side-chain flexibility. J. Comput. Chem. 2002;23:1656–1670. doi: 10.1002/jcc.10168. [DOI] [PubMed] [Google Scholar]
- 103.Chen W, Gilson MK, Webb SP, Potter MJ. Modeling Protein-Ligand Binding by Mining Minima. J. Chem. Theory. Comput. 2010;6:3540–3557. doi: 10.1021/ct100245n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Kua J, Zhang Y, McCammon JA. Studying enzyme binding specificity in acetylcholinesterase using a combined molecular dynamics and multiple docking approach. J. Am. Chem. Soc. 2002;124:8260–8267. doi: 10.1021/ja020429l. [DOI] [PubMed] [Google Scholar]
- 105.Lin JH, Perryman AL, Schames JR, McCammon JA. The relaxed complex method: Accommodating receptor flexibility for drug design with an improved scoring scheme. Biopolymers. 2003;68:47–62. doi: 10.1002/bip.10218. [DOI] [PubMed] [Google Scholar]
- 106.Lin JH, Perryman AL, Schames JR, McCammon JA. Computational drug design accommodating receptor flexibility: the relaxed complex scheme. J. Am. Chem. Soc. 2002;124:5632–5633. doi: 10.1021/ja0260162. [DOI] [PubMed] [Google Scholar]
- 107.Kortvelyesi T, Dennis S, Silberstein M, Brown L, III, Vajda S. Algorithms for computational solvent mapping of proteins. Proteins. 2003;51:340–351. doi: 10.1002/prot.10287. [DOI] [PubMed] [Google Scholar]
- 108.Mysinger MM, Shoichet BK. Rapid context-dependent ligand desolvation in molecular docking. J. Chem. Inf. Model. 2010;50:1561–1573. doi: 10.1021/ci100214a. [DOI] [PubMed] [Google Scholar]
- 109.Verdonk ML, Chessari G, Cole JC, Hartshorn MJ, Murray CW, Nissink JW, Taylor RD, Taylor R. Modeling water molecules in protein-ligand docking using GOLD. J. Med. Chem. 2005;48:6504–6515. doi: 10.1021/jm050543p. [DOI] [PubMed] [Google Scholar]
- 110.Abel R, Young T, Farid R, Berne BJ, Friesner RA. Role of the active-site solvent in the thermodynamics of factor Xa ligand binding. J. Am. Chem. Soc. 2008;130:2817–2831. doi: 10.1021/ja0771033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Lazaridis T. Inhomogeneous fluid approach to solvation thermodynamics. 1. Theory. J. Phys. Chem. B. 1998;102:3531–3541. [Google Scholar]
- 112.Lazaridis T. Inhomogeneous fluid approach to solvation thermodynamics. 2. Applications to simple fluids. J. Phys. Chem. B. 1998;102:3542–3550. [Google Scholar]
- 113.Abel R, Salam NK, Shelley J, Farid R, Friesner RA, Sherman W. Contribution of Explicit Solvent Effects to the Binding Affinity of Small-Molecule Inhibitors in Blood Coagulation Factor Serine Proteases. ChemMedChem. 2011;6:1049–1066. doi: 10.1002/cmdc.201000533. [DOI] [PubMed] [Google Scholar]
- 114.Higgs C, Beuming T, Sherman W. Hydration Site Thermodynamics Explain SARs for Triazolylpurines Analogues Binding to the A2A Receptor. ACS Med. Chem. Lett. 2010;1:160–164. doi: 10.1021/ml100008s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Das R, Andre I, Shen Y, Wu Y, Lemak A, Bansal S, Arrowsmith CH, Szyperski T, Baker D. Simultaneous prediction of protein folding and docking at high resolution. Proc. Natl. Acad. Sci. U. S. A. 2009;106:18978–18983. doi: 10.1073/pnas.0904407106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Wong S, Jacobson MP. Conformational selection in silico: loop latching motions and ligand binding in enzymes. Proteins. 2008;71:153–164. doi: 10.1002/prot.21666. [DOI] [PubMed] [Google Scholar]