Understanding the errors of SHAPE-directed RNA structure modeling

Abstract

Single-nucleotide-resolution chemical mapping for structured RNA is being rapidly advanced by new chemistries, faster readouts, and coupling to computational algorithms. Recent tests have shown that selective 2´-hydroxyl acylation by primer extension (SHAPE) can give near-zero error rates (0–2%) in modeling the helices of RNA secondary structure. Here, we benchmark the method on six molecules for which crystallographic data are available: tRNA(phe) and 5S rRNA from E. coli; the P4-P6 domain of the Tetrahymena group I ribozyme; and ligand-bound domains from riboswitches for adenine, cyclic di-GMP, and glycine. SHAPE-directed modeling of these highly structured RNAs gave an overall false negative rate (FNR) of 17% and a false discovery rate (FDR) of 21%, with at least one helix prediction error in five of the six cases. Extensive variations of data processing, normalization, and modeling parameters did not significantly mitigate modeling errors. Only one varation, filtering out data collected with deoxyinosine triphosphate during primer extension, gave a modest improvement (FNR=12% and FDR=14%). The residual structure modeling errors are explained by insufficient information content of these RNAs’ SHAPE data, as evaluated by a nonparametric bootstrapping analysis inspired by approaches in phylogenetic inference. Beyond these benchmark cases, bootstrapping analysis suggests low confidence (<50%) in the majority of helices in a previously proposed SHAPE-directed model for the HIV-1 RNA genome. Thus, SHAPE-directed RNA modeling is not always unambiguous, and helix-by-helix confidence estimates, as described herein, may be critical for interpreting results from this powerful methodology.

The continuing discoveries of new classes of RNA enzymes, switches, and ribonucleoprotein assemblies provide complex challenges for structural and mechanistic dissection [see, e.g., refs. (1–4)]. While crystallographic, spectroscopic, and phylogenetic analyses have led to a deeper understanding of several key model systems, the throughput or applicability of these methods is limited, especially for noncoding RNAs that switch between multiple states in their functional cycles (5–8). In recent years, several laboratories have revisited a widely applicable chemical approach for attaining nucleotide-resolution RNA structural information, variously called “footprinting” or “chemical structure mapping”. Recent advances have included novel chemical modification strategies, faster data analysis software, accelerated readouts via capillary electrophoresis, and multiplexed purification by magnetic beads (9–14).

Despite these advances, chemical mapping data are not expected to generally give structure models accurate at nucleotide resolution. To a first approximation, the protection of an RNA nucleotide from chemical modification indicates that it forms some interaction with a partner elsewhere in the system; but these data, by themselves, do not provide enough information to define the interaction partner. Instead, the mapping data can be used to test, refine, or guide structure hypotheses derived from manual inspection or automated algorithms (15–17). The accuracy of this approach is necessarily limited by uncertainties in the modeling – including incomplete treatment of non-canonical base pairs, base-backbone interactions, and pseudo-knotted folds (17) – and imperfect correlations of chemical modification rates to structural features. Indeed, there are notable historical examples of chemical data giving misleading structural suggestions, including blind modeling work on tRNA (18, 19) and 5S ribosomal RNA (20, 21).

It was therefore exciting when recent studies of 2´-OH acylation (the SHAPE method) coupled to the RNAstructure algorithm reported secondary structure inference with unprecedented sensitivity (98–100% helix recovery) (17). The work acknowledged several uncertainties. Measurements were made on ribosomal RNA without protein partners, which may not form the same structures as crystallized protein-bound complexes. For other test cases, the assumed experimental structures were derived from phylogenetic analysis (P546 domain from the bI3 group I intron), NMR data (HCV IRES), or crystals of constructs with modifications not present in the SHAPE-probed constructs (tRNA^Asp). A “gold-standard” benchmark of SHAPE-directed secondary structure inference on RNAs with corresponding crystallographic models remains unavailable. We present herein SHAPE data, secondary structure inference, and analysis of systematic and statistical errors for six such RNAs containing a total of 661 nucleotides and 42 helices. Our results provide a rigorous appraisal of the strengths and limitations of this promising chemical/computational technology.

Experimental Procedures

Preparation of model RNAs

The DNA templates for each RNA (SI Table S1) consisted of the 20-nucleotide T7 RNA polymerase promoter sequence (TTCTAATACGACTCACTATA) followed by the desired sequence. Double-stranded templates were prepared by PCR assembly of DNA oligomers up to 60 nucleotides in length (IDT, Integrated DNA Technologies, IA) with Phusion DNA polymerase (Finnzymes, MA), and purified with AMPure magnetic beads (Agencourt, Beckman Coulter, CA) following manufacturer’s instructions. Sample concentrations were measured based on UV absorbance at 260 nm measured on Nanodrop 100 or 8000 spectrophotometers. Verification of template length was accomplished by electrophoresis of all samples and 10-bp and 20-bp ladder length standards (Fermentas, MD) in 4% agarose gels (containing 0.5 mg/mL ethidium bromide) and 1x TBE (100 mM Tris, 83 mM boric acid, 1 mM disodium EDTA).

In vitro RNA transcription reactions were carried out in 40 µL volumes with 10 pmols of DNA template; 20 units T7 RNA polymerase (New England Biolabs, MA); 40 mM Tris-HCl (pH 8.1); 25 mM MgCl₂; 2 mM spermidine; 1 mM each ATP, CTP, GTP, and UTP; 4% polyethylene glycol 1200; and 0.01% Triton-X-100. Reactions were incubated at 37 °C for 4 hours and monitored by electrophoresis of all samples along with 100–1000 nucleotide RNA length standards (RiboRuler, Fermentas, MD) in 4% denaturing agarose gels (1.1% formaldehyde; run in 1x TAE, 40 mM Tris, 20 mM acetic acid, 1 mM disodium EDTA), stained with SYBR Green II RNA gel stain (Invitrogen, CA) following manufacturer instructions. RNA samples were purified with MagMax magnetic beads (Ambion, TX), following manufacturer’s instructions; and concentrations were measured by absorbance at 260 nm on Nanodrop 100 or 8000 spectrophotometers.

Chemical probing measurements

Chemical modification reactions consisted of 1.2 pmols RNA in 20 µL with 50 mM Na-HEPES, pH 8.0, and 10 mM MgCl₂ and/or ligand at the desired concentration (see SI Table S1); and 5 µL of SHAPE modification reagent. The modification reagent was 24 mg/ml N-methylisatoic anhydride (NMIA) freshly dissolved in anhydrous DMSO. The reactions were incubated at 24 °C for 15 to 60 minutes, with lower modification times for the longer RNAs to maintain overall modification rates less than 30%. In control reactions (for background measurements), 5 µL of deionized water was added instead of modification reagent, and incubated for the same time. For experiments testing DMSO effects, higher concentrations of NMIA in DMSO were prepared and 2 µL of the modification reagent was added to the 20 µL reaction mixture. Reactions were quenched with a premixed solution of 5 µL 0.5 M Na-MES, pH 6.0; 3 µL of 5 M NaCl, 1.5 µL of oligo-dT beads (poly(A) purist, Ambion, TX), and 0.25 µL of 0.5 mM 5´-rhodamine-green labeled primer (AAAAAAAAAAAAAAAAAAAAGTTGTTGTTGTTGTTTCTTT) complementary to the 3´ end of the RNAs [also used in our previous studies (13, 14)], and 0.05 µL of a 0.5 mM Alexa-555-labeled oligonucleotide (used to verify normalization). The reactions were purified by magnetic separation, rinsed with 40 µL of 70% ethanol twice, and allowed to air-dry for 10 minutes while remaining on a 96-post magnetic stand. The magnetic-bead mixtures were resuspended in 2.5 µL of deionized water.

The resulting mixtures of modified RNAs and primers bound to magnetic beads were reverse transcribed by the addition of a pre-mixed solution containing 0.2 µL of SuperScript III (Invitrogen, CA), 1.0 µL of 5x SuperScript First Strand buffer (Invitrogen, CA), 0.4 µL of 10 mM each dNTPs [dATP, dCTP, and dTTP; and either dGTP or dITP (22)], 0.25 µL of 0.1 M DTT, and 0.65 µL water. The reactions (5 µL total) were incubated at 42 °C for 30 minutes. RNA was degraded by the addition of 5 µL of 0.4 M NaOH and incubation at 90 °C for 3 minutes. The solutions were neutralized by the addition of 5 µL of an acid quench (2 volumes 5 M NaCl, 2 volumes 2 M HCl, and 3 volumes of 3 M Na-acetate). Fluorescent DNA products were purified by magnetic bead separation, rinsed twice with 40 µL of 70% ethanol, and air-dried for 5 minutes. The reverse transcription products, along with magnetic beads, were resuspended in 10 µL of a solution containing 0.125 mM Na-EDTA (pH 8.0) and a Texas-Red-labeled reference ladder (whose fluorescence is spectrally separated from the rhodamine-green-labeled products). The products were separated by capillary electrophoresis on an ABI 3100 or ABI 3700 DNA sequencer. Reference ladders were created using an analogous protocol without chemical modification and the addition of, e.g., 2´-3´-dideoxy-TTP in an amount equimolar to dTTP in the reverse transcriptase reaction.

The HiTRACE software (23, 24) was used to analyze the electropherograms. Briefly, traces were aligned by automatically shifting and scaling the time coordinate, based on cross correlation of the Texas Red reference ladder co-loaded with all samples. Sequence assignments to bands, verified by comparison to sequencing ladders, permitted the automated peak-fitting of the traces to Gaussians.

Likelihood-based processing of SHAPE data

Quantified SHAPE data were corrected for attenuation of longer reverse transcriptase products due to chemical modification, normalized, and background-subtracted. Rather than using an approximate exponential correction and background scaling (25), we used a likelihood framework to determine the final, corrected SHAPE reactivities (see also (26)). Furthermore, a likelihood-derived analysis was implemented to average replicate SHAPE data sets across several experiments. Both of these procedures are described in detail in the SI Methods. The algorithms are available in the functions overmod_and_background_correct_logL.m and get_average_standard_state.m within the freely available HiTRACE software package (24). Final averaged data and errors have been made made publicly available in the Stanford RNA Mapping Database (http://rmdb.stanford.edu). The accession IDs are: TRNAPH_SHP_0001, TRP4P6_SHP_0001, 5SRRNA_SHP_0001, ADDRSW_SHP_0001, CIDGMP_SHP_0001, and GLYCFN_SHP_0001.

Computational modeling

The Fold executable of the RNAstructure package (v5.3) was used to infer SHAPE-directed secondary structures. The entire RNA sequences (SI Table S1), including added flanking sequences, were used for all calculations. The flag “-T 297.15” set the temperature to match our experimental conditions (24 °C). The flags “–sh”, “–sm”, and “–si” were used to input the SHAPE data file, slope m, and intercept b. The latter parameters define the pseudoenergy formula ΔG_i = m log( S_i + 1 ) + b, where S_i is the SHAPE reactivity. In the RNAstructure implementation, these pseudoenergies are applied to each nucleotide that forms an edge base pair, and doubly applied to each nucleotide that forms an internal base pair. Boltzmann probability calculations used the partition executable with the same flags.

Nonparametric bootstrapping analysis was carried out as follows. Given normalized SHAPE data S_i for nucleotides i = 1, 2, .. N, a bootstrap replicate was generated by choosing N random indices i' from 1 to N, with replacement (27, 28) (i.e., some nucleotide positions are not represented and some are present in multiple copies; for the latter, SHAPE pseudoenergies were scaled proportionally). The resulting data sets S_i´ contained the same number of data points and carried any systematic errors present in the original data set. Secondary structure models directed by these data were analyzed in MATLAB to assess the frequency of each base pair arising in the replicates; the maximum bootstrap value across the base pairs of each helix was taken as the boostrap value for the helix. The bootstrapping analysis is being made available on an automated server at: http://rmdb.stanford.edu/structureserver.

Additional calculations were carried out with the fold() routine of the ViennaRNA package (version 1.8.4; equivalent to the ‘RNAfold’ command-lines)(29) extended to accept SHAPE data and calculate pseudoenergies with the same formula used in RNAstructure; calculations were facilitated through Python bindings available through the software’s convenient SWIG (Simplified Wrapper and Interface Generator) interface. Secondary structure figures were prepared with VARNA (30).

Assessment of accuracy

A crystallographic helix was considered correctly recovered if more than 50% of its base pairs were observed in a helix by the computational model. (In practice, 34 of 35 such helices retained all crystallographic base pairs.) Note that, unlike prior work, helix slips of ±1 were not considered correct [i.e., the pairing (i,j) was not allowed to match the pairings (i,j−1) or (i,j+1)].

Results

Accuracy of modeling without experimental data

The benchmark herein (SI Table S1) collects a diverse set of noncoding RNA domains, containing two classic RNA folding model systems, unmodified tRNA^phe from E. coli (31), and the P4-P6 domain of the Tetrahymena group I ribozyme (32); a functional RNA that has been a frequent test case for modeling algorithms, the E. coli 5S ribosomal RNA (15, 16, 20, 21); and three ligand-bound domains from bacterial riboswitches for adenine, cyclic di-GMP, and glycine (33–39). For the last RNA (glycine riboswitch from F. nucleatum), crystallographic data was not available at the time of modeling but released at the time of manuscript submission; it served as a blind test within our benchmark.

As a control, we first applied the RNAstructure (15, 16) algorithm Fold without any experimental data to the benchmark set (SI Fig. S1). Here and below, we discuss modeling errors in terms of false negative rate (FNR; fraction of crystallographic helices that were missed) and false discovery rate (FDR; fraction of predicted helices that were incorrect). The values are summarized, along with the related statistics of sensitivity and positive predicted value, in Table 1. To highlight features of the RNAs’ global folds, we present results in terms of helices rather than individual base pairs. For completeness, FNR, FDR, sensitivity, and positive predictive values at the base-pair level are also compiled in SI Table S2.

Table 1.

Accuracy of secondary structure recovery by RNAstructure with and without SHAPE data.

RNA	Len.	Number of helicesa
		Cryst	RNAstructure		+ SHAPE
			TP	FP	TP	FP
tRNAphe	76	4	2	3	3	1
P4–P6 RNA	158	11	10	1	9	1
5S rRNA	118	7	1	9	6	3
Adenine ribosw.	71	3	2	3	3	1
c-di-GMP ribosw.	80	8	6	2	6	2
Glycine riboswitch	158	9	5	3	8	1
Total	661	42	26	21	35	9
False negative rateb			38.1%		16.7%
False discovery ratec			44.7%		20.5%
Sensitivityd			61.9%		83.3%
Positive predictive valuee			55.3%		79.5%

^aCryst = number of helices in crystallographic model. TP = true positives; FP = false positives.

^bFalse negative rate = 1 – TP/Cryst.

^cFalse discovery rate = FP/(TP+FP).

^dSensitivity = (1 – false negative rate) = TP/Cryst.

^ePositive predictive value = (1 – false discovery rate) = TP/(TP+FP).

Without any data, the RNAstructure algorithm missed 16 of 42 helices, giving an FNR of 16/42 = 38%. The models mispredicted an additional 21 helices, giving an FDR of 21/(26 + 21) = 45% (Table 1). These error rates are significantly worse than their ideal values (0%), and confirm the known inaccuracy of current secondary structure prediction methods without experimental guidance [see, e.g., (16, 17)].

Accuracy of modeling with SHAPE data

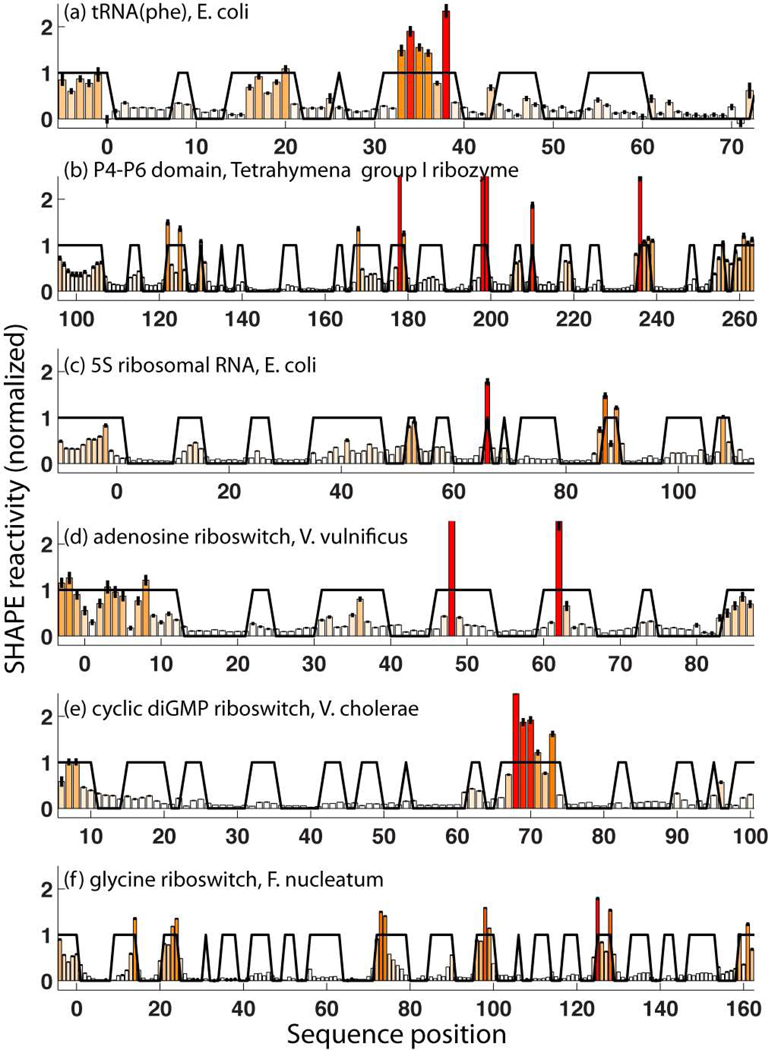
We then acquired SHAPE data for each RNA in 50 mM Na-HEPES, pH 8.0, 10 mM MgCl₂, and saturating concentrations of ligand (for the three riboswitch domains), using the modification reagent N-methylisatoic anhydride (NMIA). Data quantitation for each RNA involved correction for attenuation of long products, background subtraction, and averaging of 12 to 28 replicates (SI Table S1) guided by a likelihood framework (Methods). The data were in excellent agreement with the expected structures [Fig.1 and Fig. 2 (left panels)]. Strong SHAPE reactivities occur mainly at nucleotides that are outside Watson-Crick helices observed in crystallographic models. Based on prior work (17), we expected that inclusion of these data as a pseudo-energy term in the RNAstructure algorithm would substantially improve the accuracy of computational models, with helix-level FNR as low as 0–2 %. The improvement was indeed significant, but not to the expected extent (Fig. 2, right panels; Table 1). The FNR decreased from 38% to 17% (missing 7 of 42 helices), and the FDR decreased from 45% to 21% (misprediction of 9 helices). In five of the six RNAs, the calculations failed to recover all the crystallographic helices.

Figure 1.

SHAPE reactivities measured at single–nucleotide resolution for six non-coding RNAs of known structure. Black lines mark residues that are paired or unpaired in the crystallographic models with values of 0.0 or 1.0, respectively.

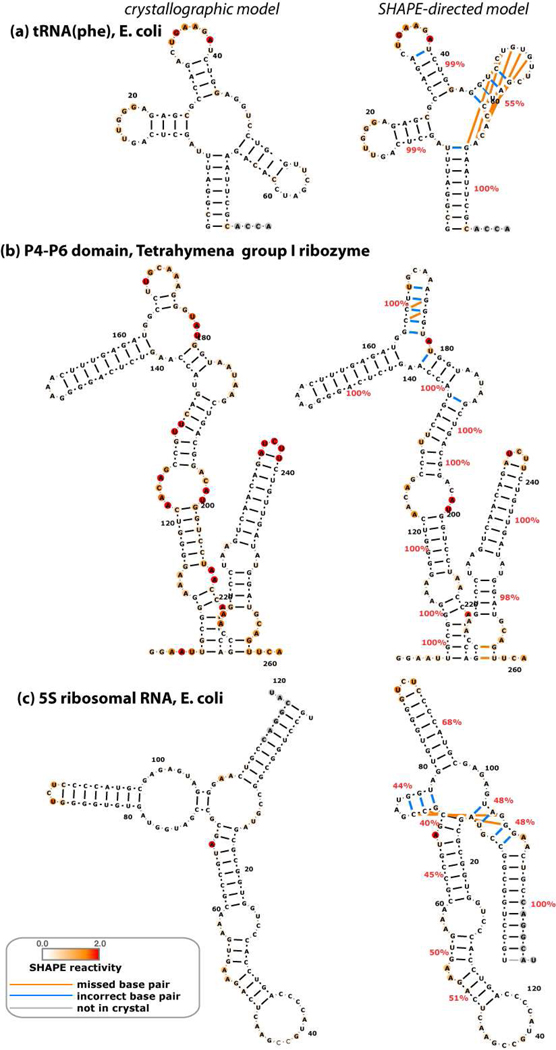
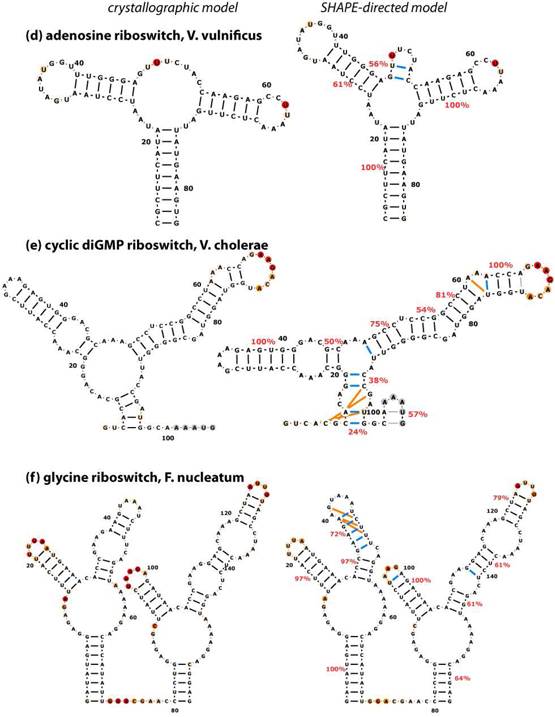
Figure 2.

Crystallographic (left) and SHAPE-directed (right) secondary structure models for a benchmark of non-coding RNAs. SHAPE reactivities are shown as colors on bases, and match colors in Fig. 1. Cyan lines mark incorrect base pairs; orange lines mark crystallographic base pairs missing in each model; gray lines mark base pairs in regions outside crystallized construct. Helix confidence estimates from bootstrap analyses are given as red percentage values. For clarity, flanking sequences (see SI Table S1) are not shown. Figure is in two parts.

Evaluating sources of systematic error

The results above give a somewhat less optimistic picture of SHAPE-directed modeling than previously published measurements (17). The differences between SHAPE benchmarks can be most simply ascribed to different test RNAs. Nevertheless, we investigated several other possible systematic explanations for the error rates (FNR and FDR of 17% and 21%, respectively) in our test set. First, we used herein a more stringent evaluation scheme to define helix recovery than previous work (15–17), which permitted helix register slips by ±1 (see Methods). Using those less stringent criteria gave similar FNR and FDR of 14% and 18%, respectively. Second, we checked for experimental artifacts. Filtering out nucleotides whose SHAPE pseudoenergy errors exceeded 0.4 kcal/mol gave similar FNR and FDR (14% and 18%; Table 2). Third, to test the quality of our lab’s experimental procedures and data processing, we carried out SHAPE measurements on an RNA with a previously published SHAPE-directed model, the hepatitis C virus internal ribosomal entry site domain II. The resulting secondary structure (SI Fig. S2) agreed with prior independent work (17). Fourth, primer extension with dNTPs containing dITP instead of dGTP, reduces errors in quantitating ‘compressed’ bands near G nucleotides (14, 22, 40), but gives added variance at C nucleotides due to reverse transcriptase pausing [SI Fig. S3 and (14)]. Using only data collected with dGTP gave helix-level FNR and FDR of 12% and 14%, respectively (Table 2) – an improvement, but still higher than values of 0–2% achieved for previous test RNAs. The FNR and FDR increased when we used only data collected with dITP (26% and 28%). Fifth, as an additional check on experimental artifacts, we acquired SHAPE data for all the RNAs with the newly developed 2´-OH acylating reagent 1-methyl-7-nitroisatoic anhydride (1M7) (41); the FNR and FDR for models based on these data were identical to the measurements with the more widely used NMIA (Table 2).

Table 2.

Effects of variations of data processing or modeling on accuracy of SHAPE–directed secondary structure modeling.

Variation in modelinga	TPb	FPb	False negative rate	False discovery rate
No SHAPE data (control)	26	21	38.1%	44.7%
SHAPE–directed, default parameters	35	9	16.7%	20.5%
Remove residues with high errorsc	36	8	14.3%	18.2%
Use only data collected with dITP during primer extension	31	12	26.2%	27.9%
Use only data collected with dGTP during primer extension	37	6	11.9%	14.0%
Use 1M7 instead of NMIA reagent	35	9	16.7%	20.5%
Cap outliersd at cutoff value	35	9	16.7%	20.5%
Cap outliersd at 2.0	35	9	16.7%	20.5%
Remove additional 5 residues from 5′ and 3′ end	35	9	16.7%	20.5%
Remove residues with SHAPE <0.5	32	14	23.8%	30.4%
Optimized m and b in pseudoenergy relatione	35	8	16.7%	18.6%
Adjust normalization 2x	35	8	16.7%	18.6%
Adjust normalization 1.5x	35	9	16.7%	20.5%
Adjust normalization 0.75x	34	12	19.0%	26.1%
Adjust normalization 0.5x	31	14	26.2%	31.1%
RNAstructure T=37 °C (not 24 °C)	35	9	16.7%	20.5%
ViennaRNAf instead of RNAstructure	32	10	23.8%	23.8%

^aAll variations are described relative to ‘default conditions’ (in bold) using RNAstructure version 5.3.

^bThe total number of crystallographic helices is 42. TP = true positives; FP = false positives.

^cAny residues whose estimated measurement error of SHAPE reactivity would give errors of more than ±0.4 kcal/mol if included in a base pair, using the SHAPE pseudoenergy relation.

^dOutliers were defined as in the normalization procedure: those with values above a cutoff equal to 1.5 times the interquartile range.

^ePseudoenergy applied to base–paired nucleotides given by m log (1.0 + SHAPE ) + b. Default parameters in RNAstructure are m = 2.6 and b = −0.8. The combinations of m and b gave the same optimal accuracies for this benchmark were m = 3.0 and b = −0.6.

^fViennnaRNA version 1.8.4, using the default parameter set of Matthews et al. (1999) (15).

Sixth, model accuracy might be unduly sensitive to the highest or lowest reactivities in the SHAPE data. However, capping ‘outliers’ (see SI Methods); changing the cutoffs for capping; removing outliers; only including high-reactivity data; and excluding SHAPE data for nucleotides near the 5´ and 3´ ends of the RNA did not improve the accuracy (Table 2). Seventh, the pseudo-energy for base-pairing is derived from SHAPE data by a logarithmic formula [ΔG = m log (1.0 + SHAPE) + b]. Optimizing the parameters m and b did not affect FNR and improved FDR only slightly (from 21% to 18%; Table 2). Eighth, choices in normalizing SHAPE data can affect the modeling; but varying the normalization by factors between 0.5-fold to 2-fold did not significantly improve the accuracy (Table 2). Ninth, we explored whether energy inaccuracies stem from RNAstructure’s thermodynamic parameters, SHAPE data, or both. Comparing energies of crystallographic vs. model structures indicated that both thermodynamic and SHAPE energies are imbalanced to favor incorrect models (by averages of 1.7 and 1.3 kcal/mol, respectively; SI Table S3). Additionally, shifting the Boltzmann weight balances by raising the modeling temperature from 24 °C to 37 °C did not change the error rates (Table 2). Tenth, we additionally tested for algorithm biases by recomputing models in ViennaRNA (29) rather than RNAstructure, but, overall, the FNR and FDR both increased (to 26% and 28%; Table 2).

Evidence against crystal/solution-structure discrepancies

Having found no straightforward explanation for SHAPE-directed modeling errors from systematic errors in experimental data acquisition, data processing, or modeling protocols, we investigated whether there might be differences between these RNA’s secondary structures in available crystals and in our experimental solution conditions, as occurred in prior work on extracted ribosomal RNA (17). Several lines of evidence disfavor this hypothesis in our cases. For tRNA (phe), the P4-P6 domain, the 5S rRNA, and the purine and c-di-GMP riboswitch, independent crystallographic models of several variants indicate that the RNAs’ secondary structures agree with phylogenetic analysis and are furthermore robust to different conditions, binding partners, and crystallographic contexts (SI Table S1). In addition, while flanking sequences added to constructs (SI Table S1) might disrupt the target domains, we designed these sequences to avoid such pairings, and checked this lack of pairings by calculations with and without SHAPE data (SI Fig. S1 & Fig. 2).

Misfolding to kinetically trapped secondary or tertiary structures could lead to differences in solution chemical mapping data compared to those expected from crystallographic structures. To test this possibility, we acquired data for the RNAs after incubating them in 10 mM Na-MES, pH 6.0 and 10 mM MgCl₂ for 30 minutes (‘refolding’ conditions developed for large ribozymes (42, 43)); the resulting reactivities were indistinguishable from RNAs without the refolding treatment (see, e.g., SI Fig. S3 for tRNA data). Similarly, we tested for adverse effects of dimethyl sulfoxide (DMSO, used to solubilize the SHAPE reagent) (44) by repeating measurements in lower DMSO conditions (10% vs. 25% DMSO); SHAPE data were indistinguishable in the two conditions (SI Fig. S3 gives tRNA data).

In addition to these results disfavoring differences in crystal/solution structures, our solution measurements gave positive evidence for the RNAs folding into the correct tertiary conformations. The P4-P6 domain and the 5S rRNA gave changes in their metal core and loop E regions, respectively, upon Mg²⁺ addition, as expected from prior biophysical analysis [e.g, (45–48)]; and the three riboswitches gave SHAPE changes with and without their ligands (SI Fig. S4). Most strongly, we have subjected each of these RNAs to the mutate-and-map method, a two-dimensional extension of chemical mapping (13, 14), and observed near-complete recovery of the crystallographic helices [98% sensitivity; (49)], indicating that the dominant solution structure matches the structure determined by crystallography.

Assessing information content and confidence by bootstrapping

A final explanation for the errors of SHAPE-directed structure models could be that the experimental data have insufficient information content to define the secondary structure. That is, the data, while accurately reflecting each RNA’s solution conformation, are also consistent with non-native secondary structures with similar calculated energy. Indeed, the minimum energy model can be highly sensitive to small changes in the SHAPE data (see tRNA example in SI Fig. S5a-c); and, in some cases, the incorrect lowest-energy SHAPE-directed model is within 1 kcal/mol of the crystallographic structure (see tRNA^phe and the cyclic-di-GMP riboswitch; SI Table S3). Unfortunately, quantitatively interpreting energy differences between models (as well as partition-function-based base pair probabilities, which are skewed to high values; see SI Fig. S5a) is currently complicated by the non-physical nature of the SHAPE pseudoenergies. For example, a useful confidence value should be a good approximation to the actual modeling accuracy. In contrast, the mean base pair probability value over all predicted helices is 88%, suggesting a false discovery rate of 100% – 88% = 12%, substantially underestimating the actual error rate of 21%.

We therefore estimated the helix-by-helix confidence of SHAPE directed models through a nonparametric bootstrapping procedure, inspired by techniques developed to evaluate phylogenetic trees from multiple sequence alignments (27, 28, 50). We generated 400 mock replicates of each data set by resampling with replacement the SHAPE data for individual residues; generating secondary structure models directed by these mock data sets; and evaluating the frequency with which each predicted helix appeared in these replicates (SI Fig. S5b and percentage values in Fig. 2). One quarter of the modeled helices (11 of 44) appeared with bootstrap values under 55%, suggesting insufficient information to confidently determine their structure; 7 of these 11 helices were indeed incorrect. Encouragingly, the 33 helices with bootstrap values above 55% included only two errors, of which one was a single-nucleotide register shift. Further, these bootstrap values are robust to small changes in the SHAPE data (see tRNA example in SI Figs. S6d and e). Finally, the overall mean of the helix bootstrap values was 77%. This result predicts a false discovery rate of 100% – 77% = 23%, in accord with the actual rate of 21%. Bootstrap analysis therefore appears to be well-suited for evaluating confidence in SHAPE-directed models.

Bootstrap analysis of an independent test case: the HIV-1 genome model

As a final demonstration of the utility of bootstrapping confidence estimation, we investigated the information content of an external data set. Recent application of the SHAPE method to the 9173-nucleotide RNA genome extracted from the NL4-3 HIV-1 virion gave a secondary structure hypothesis containing 429 helices (51), and the quantitated SHAPE reactivity data have been published. Employing these data and previously used modeling constraints (including division of the modeled genome into five separated domains), the current version of RNAstructure (5.3) largely recovers the prior working model (Table S4). Furthermore, bootstrapping revealed additional useful information. Several of the model regions, including the 57-nucleotide 5´ TAR element, two helices with lengths greater than 10 bps in the gag-pol region, and the signal-peptide stem at the 5´ end of gp120, have bootstrap values above 95% and are thus highly confident. Overall, however, 236 of 429 helices in the prior SHAPE-directed model have bootstrap confidence estimates lower than 50%. (If base pairs across the five assumed domains are permitted, more helices are found with such low bootstrap values.) The bootstrap value averaged over all predicted helices is 49%; excluding 59 stems in the prior model that are not recovered with the current version of RNAstructure gives a similar value of 55%. These results suggest that much of the HIV-1 secondary structure remains uncertain, even in regions that are strongly protected from SHAPE modification (SI Fig. S7). These low-confidence regions either form single structures that are poorly constrained by the SHAPE data or interconvert between multiple well-formed structures in solution. A tabulation of the helix-by-helix confidence estimates in SI Table S4 should help guide further dissection of these uncertain regions by other chemical and structural approaches.

Discussion

With recent experimental and computational accelerations, nucleotide-resolution chemical mapping permits the characterization of non-coding RNAs at an unprecedented rate. Nevertheless, the resulting data are not always sufficient to determine the molecule’s secondary structure, especially if additional tertiary interactions are present. The helix-level error rates found in this study of six highly structured RNAs (false negative rate and false discovery rate of 17% and 20%, respectively) are significantly better than models generated without data (38% and 45%, respectively), but higher than for prior SHAPE-modeling test cases (FNR of 0–2%). The modeling inaccuracy found herein is similar to error rates (FNR of ~24%) found in benchmarks with other chemical modifiers including dimethyl sulfate, kethoxal, and carbodiimide (16), albeit on different RNAs and with different modeling protocols. Side-by-side tests on the same models RNAs will be necessary to rigorously compare conventional chemical approaches with SHAPE-based methods.

As with all structure characterization methods, SHAPE-directed models cannot be considered “determined structures” but instead are useful hypotheses – especially if accompanied by confidence estimates. This work proposes a bootstrapping analysis for SHAPE-directed modeling that provides such confidence values for novel RNAs. In addition to giving correct predictions for helix accuracy in six crystallized RNAs, bootstrapping analysis of the HIV-1 RNA genome finds numerous regions with high uncertainty in the RNA’s current SHAPE-directed working model. More information-rich multidimensional methods, such as NMR and the mutate-and-map chemical approaches (13, 14), should be able to test these predictions and, more generally, help attain accurate models of non-coding RNAs.