Mutation Rate Distribution Inferred from Coincident SNPs and Coincident Substitutions

Abstract

Mutation rate variation has the potential to bias evolutionary inference, particularly when rates become much higher than the mean. We first confirm prior work that inferred the existence of cryptic, site-specific rate variation on the basis of coincident polymorphisms—sites that are segregating in both humans and chimpanzees. Then we extend this observation to a longer evolutionary timescale by identifying sites of coincident substitutions using four species. From these data, we develop analytic theory to infer the variance and skewness of the distribution of mutation rates. Even excluding CpG dinucleotides, we find a relatively large coefficient of variation and positive skew, which suggests that, although most sites in the genome have mutation rates near the mean, the distribution contains a long right-hand tail with a small number of sites having high mutation rates. At least for primates, these quickly mutating sites are few enough that the infinite sites model in population genetics remains appropriate.

Introduction

Mutation rates vary in a context-dependent fashion (Blake et al. 1992; Hess et al. 1994; Hwang and Green 2004; Walser and Furano 2010), which has necessitated the modification of phylogenetic and population genetic methods to avoid bias (Yang 1996; Hernandez et al. 2007). Significant bias occurs primarily at the upper end of the mutation rate distribution, where the infinite sites model of at most one mutation per site breaks down and sites may be subject to multiple mutations. The dinucleotide CpG, in particular, exhibits a dramatically elevated mutation rate at the C, and, as a result, these sites are often discarded before performing evolutionary analyses. In general, variance from nearest-neighbor nucleotides can be incorporated during inference under a context-dependent model of mutation (Hernandez et al. 2007). However, recent research by Hodgkinson et al. (2009) provided evidence for cryptic variation in the mutation rate at a fine scale that cannot be ascribed to nearest-neighbor effects. This cryptic variation again raises the potential for bias because it, by definition, is not taken into account by current context-dependent models.

Hodgkinson et al. (2009) discovered that a surprising number of human polymorphic sites are also polymorphic in chimpanzees. These coincident single nucleotide polymorphisms (cSNPs) not only occur significantly more frequently than expected under independence but also cannot be easily explained by natural selection, fine-scale context captured by neighboring nucleotides, or large-scale context captured by GC content (Hodgkinson et al. 2009; Hodgkinson and Eyre-Walker 2010). However, they analyzed human and chimpanzee SNPs from the public database dbSNP, which provides no information on ascertainment strategy. Although the majority of the chimpanzee SNPs in dbSNP originate from the chimpanzee genome project, some SNPs stem from smaller studies that may have been guided by knowledge about human polymorphisms. Furthermore, humans and chimpanzees split only 4.1 Ma and had a relatively large ancestral population size (Hobolth et al. 2007), which means a non-negligible number of present-day SNPs would have been polymorphic in the ancestral population (Hobolth et al. 2007). Thus, some of those ancestral SNPs (acSNPs) might also have stayed polymorphic in both populations until today (Clark 1997) to become shared acSNPs.

Here, we revisit this cSNP observation to determine the extent to which the existence of cSNPs can be ascribed to shared ancestral polymorphism, non-independent ascertainment, or other technical artifacts. In addition, we extend the timescale over which this putative mutation rate variation holds by analyzing the frequency of coincident single nucleotide substitutions (cSNSs) between human–chimpanzee and orangutan–rhesus genomes. We define a novel formalization to quantify the excess of cSNPs and cSNSs, use these definitions to develop theory to estimate the extent of mutation rate variation, and conclude by discussing its potential impact on population genetic inference.

Methods

Data

For chimpanzee, we used heterozygous sites from the diploid genome of Clint (The Chimpanzee Sequencing and Analysis Consortium 2005), which we downloaded from http://www.broad.mit.edu/ftp/pub/assemblies/mammals/chimp_SNPs/ and mapped onto the human genome coordinate system using UCSC whole-genome syntenic alignments (Kent et al. 2003).

For human, we used SNPs discovered in low-coverage sequencing of 59 Yoruba individuals as part of the 1000 Genomes Pilot Project (The 1000 Genomes Project Consortium 2010), which we downloaded from ftp://ftp-trace.ncbi.nih.gov/1000genomes/ftp/pilot_data/paper_data_sets/a_map_of_human_variation/low_coverage/snps/YRI.low_coverage.2010_09.sites.vcf.gz. We restricted to biallelic, non-indel SNPs with allele counts between 1 and 117.

We identified 3.6 × 10⁷ human–chimpanzee SNSs by comparing the human and chimpanzee reference sequences via UCSC whole-genome syntenic alignments and requiring ungapped alignment of ±2 bases around the mismatch. We identified 1.4 × 10⁸ orangutan–rhesus substitutions analogously and then mapped the positions of these substitutions onto the human genome coordinate system using UCSC orangutan–human whole-genome syntenic alignments.

For all data, any site that, together with its neighboring nucleotides, matched the pattern N[CT]G or C[GA]N was discarded as a potential CpG site. Neighboring nucleotides were taken from the corresponding genome sequence (e.g., chimpanzee genome if looking at a chimpanzee SNP).

Number of Shared Ancestral Polymorphisms

We wish to calculate the distribution of the number of human–chimpanzee acSNPs that by chance survived genetic drift.

First, we assume a simple population demography for which analytic calculations are feasible. We assume that the human–chimpanzee ancestral population is large enough that splitting it into two populations of size N_e results in identical allele distributions for the two populations. The split happens instantaneously at t generations in the past.

Under this demography, genetic drift operates identically whether moving forward or backward in time. Let y be the present-day allele frequency in humans and x be the present-day allele frequency in chimpanzees. We condition on observing a heterozygous SNP in our chimpanzee sample of size two and allow for 2tN_e generations of drift from chimpanzees to humans:

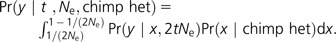Inside the integral, the first term comes from Kimura (1955), who solved the appropriate diffusion equation assuming no mutation to find the probability that an allele starting at frequency x will be segregating at frequency y after 2tN_e generations. The second term captures the process of sampling two chimpanzee chromosomes and can be calculated by applying Bayes theorem: Pr(x|chimp het) ∝ 2x(1 − x) Pr(x), where the chimpanzee population frequency spectrum Pr(x) has form 1/x under neutrality.

Given the human population frequency y, now we need to know the probability of observing both alleles in the 1000 Genomes pilot data, which sampled 118 Yoruba chromosomes at low coverage:

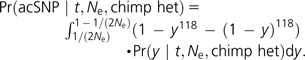(1)

If we further assume that each human SNP represents an independent sample from all possible genealogies, then the number of observed shared ancestral polymorphisms will follow a binomial distribution with Bernoulli probability Pr(acSNP|t, N_e, chimp het).

To obtain more realistic estimates, we simulated data using msms (Ewing and Hermisson 2010). We simulate 3 × 10⁵ fragments of length L = 101 bp with θ = 0.00053/bp (which corresponds to ${\widehat{\theta }}_w$ excluding CpGs for the 1000 Genomes data used in this study) and recombination rate of 1 cM/Mb. These fragments are sampled from two Wright–Fisher populations (“human” and “chimpanzee”) that maintain a constant size until they merge t generations ago, at which point the ancestral population expands to N_a individuals.

Estimating Excess of cSNPs and cSNSs

Intuitively, we clearly observe more cSNPs (or cSNSs) than “background” (i.e., see fig. 1). Now we develop statistics to rigorously quantify the extent to which the number of cSNPs or cSNSs exceeds our expectation under the null hypothesis that mutation rates are independent in different lineages. For all calculations, we assume that the mutation rate at any particular site is independent of the mutation rate at nearby sites.

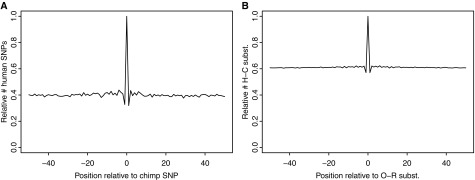
FIG. 1.—

Frequency of observed coincident (position 0) versus expected (position ≠ 0) sites. (A) Relative counts of human SNPs in a window of ±50 bp around a chimpanzee SNP. (B) Relative counts of human–chimpanzee substitutions in a window of ±50 bp around an orangutan–rhesus substitution. The dip at positions ±1 is an artifact of discarding CpG sites (see supplementary material, Supplementary Material online).

First, we must define our notation. Let H be a binary vector of random variables H_i that contains 1 at all genomic positions i that are human SNPs and 0 otherwise. Let C and O be the analogous vectors for chimpanzee SNPs and orangutan–rhesus substitutions, all on the same genomic coordinate system. Lower case versions of these variables (h_i, c_i, and o_i) represent specific values found in a particular data set rather than being random variables.

Define R₂ to be the ratio of the probability of a cSNP to the probability of a human SNP adjacent to a chimpanzee SNP: R₂ = Pr(C_iH_i = 1)/Pr(C_iH_i+1 = 1), where i represents an arbitrary position in the genome. Note that this definition matches our intuitive idea of comparing observed cSNPs to the number expected if the per-site mutation rates were independent in the human and chimpanzee lineages.

We estimate R₂ from our sample by counting the number of cSNPs and dividing by the prediction based on the number of adjacent SNPs. Under our assumption that the mutation rates at nearby sites are independent, ${\Sigma }_{i=1}^L{c}_i{h}_{i+j}$ for small j provides an estimate of the expected number of cSNPs. We can improve this estimate by averaging over the set of neighboring positions within 50 bp, $𝒩=\{-50,\dots ,50\}\backslash \{-1,0,1\}$, which has cardinality $\left|𝒩\right|=98$. Note we exclude immediately adjacent positions from 𝒩 because of CpG effects (see fig. 1).

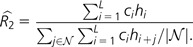An estimate of R₂ can be computed similarly from cSNS data.

Define R₃ to be the ratio of the probability of a site being both a cSNP and an orangutan–rhesus substitution to the probability of an orangutan–rhesus substitution adjacent to a human SNP adjacent to a chimpanzee SNP: R₃ = Pr(C_iH_iO_i)/Pr(C_iH_i+1O_i+2). Similar to R₂, R₃ quantifies the excess of these triply coincident sites relative to the number expected if the per-site mutation rates were independent in human, chimpanzee, and orangutan–rhesus trees. We estimate analogously to R₂:

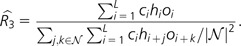Coefficient of Variation

Now we develop theory to connect R₂ with the variance of the mutation rate distribution, f. We ignore the low probability event of an apparent coincident mutation arising from lineage sorting and require that multiple mutations be used to explain the observed data.

For a particular site i, let μ_i denote the per-site mutation rate, which is a random variable drawn with density f(μ_i). We assume that μ_i remains constant over the evolutionary timescale of interest. We begin by calculating the probability that this site is a cSNP (H_iC_i = 1) conditional on the total tree lengths of the chimpanzee lineage, T_c, and of the human lineage, T_h:

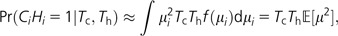(2)

where $\left[{\mathit{\text{μ}}}^2\right]$ represents the second moment of the mutation rate distribution and the approximation requires that the mutation rate be low enough that the chance of more than one mutation within each lineage is negligible. Next we consider two adjacent sites, one of which is polymorphic in chimpanzees (C_i = 1) and the other in humans (H_i+1 = 1). Because these are distinct sites, we assume their mutation rates are independent of each other, μ_i ⊥ μ_i+1:

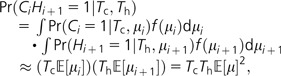(3)

where $[\mu ]$ represents the first moment of the mutation rate distribution.

Now we see R₂ is simply the ratio of equation (2) to equation (3) after integrating each equation over T_c and T_h and canceling: 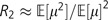. Note that the population sizes of chimpanzees and humans are incorporated into the total tree lengths T_c and T_h; because these factors cancel, R₂ is independent of the population sizes. After a little algebra, we can express the coefficient of variation of f(μ) in terms of R₂:

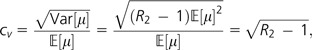which gives us a method of moments estimate, $\widehat{c_{\text{v}}}$, by substituting in the estimated ratio from the data, $\widehat{R_2}$.

Skewness

If a site is both a human/chimpanzee cSNP (H_iC_i = 1) and a substitution between orangutan and rhesus (O_i = 1), then we need three mutations to explain the data. Conditional on the total tree length of the chimpanzee lineage, T_c, human lineage, T_h, and orangutan–rhesus lineage, T_or, we again use our assumption that μ_i remains constant over the entire tree and find:

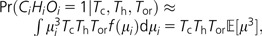(4)

where $𝔼\left[{\mu }^3\right]$ represents the third moment of the mutation rate distribution and the approximation requires that the mutation rate be low enough that the chance of more than one mutation within each lineage is negligible. If the chance of multiple mutations in a single lineage is substantial [e.g., if (μT_or)² > 0.01], then equation (4) will be an overestimate. Next we consider three adjacent sites, one of which differs between orangutan and rhesus, the next is polymorphic in chimpanzees, and the third is polymorphic in humans. As with equation (3) earlier, we assume that the mutation rates of the three sites are independent:

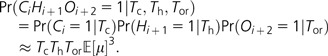(5)

Now taking the ratio of equation (4) to equation (5), we see 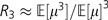. Analogous to the c_v calculation above, we can write the skewness of f(μ) in terms of R₂ and R₃:

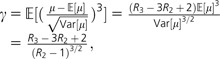which yields a method of moments estimate, $\widehat{\gamma }$, after substituting in $\widehat{R_3}$ and $\widehat{R_2}$ from the data.

Confidence Intervals

We use bootstrap resampling with replacement to generate new lists of sites that are chimpanzee SNPs, human SNPs, and orangutan–rhesus differences. For speed, we restrict the sampling of human SNPs and orangutan–rhesus differences to sites that are within 50 bp of a chimpanzee SNP. When the same site is drawn more than once, we treat it as distinct. Consider a small example: if position 10 were in the chimpanzee SNP list once and the human SNP list contained position 10 twice, then we would count this as two cSNPs. From these three new lists of sites, we estimate $\widehat{R_2}$, $\widehat{{\mathit{R}}_3}$, $\widehat{{\mathit{c}}_v}$, and $\widehat{\gamma }$ and then take the 0.025 and 0.975 quantiles from these sampling distributions as our 95% confidence intervals.

Mutation Rates from Nearest-Neighbor Context

We can also calculate mutation rates under a model of nearest-neighbor context dependence. This model assumes that the mutation rate for a particular site, i, is completely specified by the triplet of nucleotides at positions i − 1, i, and i + 1. Thus, we can estimate mutation rates by simply counting the number of occurrences of each distinct triplet at human SNPs after CpG filtering. Because we do not know which allele is ancestral, each SNP counts toward two triplets: one for each allele. From this distribution of counts, we can directly calculate the coefficient of variation and skewness of the mutation rate distribution because these statistics are scale invariant.

Results

We start with 1.3 × 10⁶ chimpanzee SNPs from the chimpanzee genome project and 1.1 × 10⁷ human SNPs from the 1000 Genomes pilot. Given that CpG sites in primates are known to have a mutation rate ∼30 times higher than other dinucleotide contexts (Hwang and Green 2004), we eliminate these sites from all further results, leaving us with 8.8 × 10⁵ chimpanzee SNPs and 7.1 × 10⁶ human SNPs for a total of 6,452 cSNPs. Similarly, we find 2.4 × 10⁷ substitutions between the human and the chimpanzee genomes after CpG filtering, 1.3 × 10⁶ of which are coincident substitutions (cSNSs) in that these sites also differ between orangutan and rhesus macaque.

Should we be surprised by these numbers?

Excess of cSNPs and cSNSs

We expect some cSNPs to arise due to repeated mutations—one within the human and one within the chimpanzee genealogy. In figure 1A, we plot the number of human SNPs that fall within a window of ±50 bases of a chimpanzee SNP. The observed cSNPs fall at position 0, which shows a clear excess relative to background with $\widehat{R_2}=2.5$ (95% confidence interval of 2.4–2.6). If all sites had the same mutation rate or drew independently from a distribution, then we would expect to see cSNPs as often as we see human SNPs at positions adjacent to chimpanzee SNPs (i.e., R₂ = 1). Note that eliminating chimpanzee CpG SNPs causes spillover effects for human SNPs at adjacent positions −1 and +1. Mutations are generally biased from ancestral C/G to derived A/T, so CpG filtering reduces the number of SNPs at these positions (see also supplementary fig. S2, Supplementary Material online).

Next we follow an analogous procedure to estimate the ratio R₂ for cSNSs (fig. 1B) and find it to be less at 1.638 (95% confidence interval of 1.635–1.641). This difference in estimated R₂ ratios suggests that not all our assumptions hold at both timescales (see Discussion).

Finally, we estimate the relative number of sites that are both a cSNP and an orangutan–rhesus substitution to be $\widehat{R_3}=7.0$ (95% confidence interval of 5.7–8.4). However, the same factors that lead to the substitution $\widehat{R_2}$ being less than the polymorphism $\widehat{R_2}$ also likely depress our estimate of R₃ because this quantity depends on orangutan–rhesus differences as well. Thus, our $\widehat{R_3}$ should be a lower bound on the true R₃.

In all cases, we find a clear excess of observed coincident sites relative to the number expected if mutation rates were independent.

Artifacts that Could Explain the Observation

The excess of cSNPs and cSNSs could arise from either interesting biology or less interesting technical artifacts. Before investigating the former, we must first rule out the latter: ascertainment bias, collapsed duplications in the genome assemblies, or repeated sequencing errors.

Ascertainment bias would lead to cSNPs if the discovery of polymorphisms in one species were influenced by discovery in the other. However, this cannot explain the cSNS results and, regardless, we only use polymorphic sites discovered in full sequence data, which avoids this problem entirely.

Collapsed paralogs in the genome assemblies would create both apparent cSNPs and cSNSs. If these were the case, then coincident sites would fall preferentially into regions that align to multiple locations in the genome and have elevated read coverage in whole-genome shotgun sequencing. We see neither trend. First, we extract ±50 bases of sequence around each SNP and ask what proportion aligns to multiple locations in the human genome with percent identity >92% across a gapped alignment of at least 28 contiguous bases. We find 87% of cSNPs align to multiple locations, 83% of chimpanzee SNPs, and 89% of human SNPs. Second, we examined the raw alignments of Illumina reads from 1000 Genomes Pilot Yoruba individual NA19240 and find the read coverage at cSNPs to be qualitatively similar to the coverage at other chimpanzee SNPs. Quantitatively, cSNPs actually have a slightly lower median coverage (34) relative to the other chimpanzee SNPs (35) due to a very long right tail of the distribution.

If sequencing errors were elevated in a consistent, site-specific fashion, then it would create apparent cSNPs and lead to upward bias in $\widehat{R_2}$. However, this scenario seems implausible given that the results are robust across different sources of human data with varying error profiles (see Discussion). Furthermore, if a significant proportion of cSNPs was due to coincident errors, we would expect the site frequency spectrum (SFS) of cSNPs within humans—that is, the proportion of polymorphic sites within the genome that are found at a given frequency in the population—to differ from that of other SNPs. In particular, the SFS of cSNPs would be more shifted toward rare alleles relative to the SFS of other SNPs. However, the two distributions are very similar, especially in the low frequency range (fig. 3A), which implies that only a minor fraction of the cSNPs could be due to coincident errors.

FIG. 3.—

Folded SFS from 118 Yoruba chromosomes downsampled to 31 chromosomes. (A) SFS of cSNPs compared with simulated acSNPs and background (“linked to chimp SNP”). (B) SFS of sites tightly linked to cSNPs (±50 bp) compared with sites linked to simulated acSNPs and background. In both cases, cSNPs are more similar to background than acSNPs. Because we do not know which allele is ancestral, we fold the spectrum by summing frequencies f and 1 − f. The background SFS is generated using human SNPs found within 50 bp of chimpanzee SNPs; however, using random human SNPs yields the same SFS (results not shown).

On the other hand, if sequencing errors were elevated uniformly across the genome, then it would push $\widehat{R_2}$ toward 1 by increasing the numerator (number of cSNPs) to a lesser degree than the denominator (expected number of cSNPs). Significant bias in $\widehat{R_2}$ requires a relatively high SNP false-positive rate (supplementary material, Supplementary Material online), which would be clearly visible in the SFS (supplementary fig. S1, Supplementary Material online). Furthermore, we would expect the SFS of all SNPs to be shifted even more toward rare alleles than the SFS of cSNPs, which we do not observe (fig. 3A).

After failing to find a convincing explanation for the observed cSNPs on the basis of an artifact, we now turn toward the potential biological explanations of neutral or selected ancestral polymorphisms and mutation rate variation.

Shared Ancestral Polymorphisms versus Mutation Rate Variation

In the following, we test three predictions for shared ancestral polymorphisms that should distinguish them from recurrent mutations:

1. Shared ancestral polymorphisms should have the same two alleles in both species.

2. The number of cSNPs must be compatible with what we know about demography and speciation of humans and chimpanzees.

3. The SFS of very old polymorphisms will no longer exhibit the otherwise characteristic L-shape.

First, a startling number of cSNPs exhibit the same two alleles in both species and a similar, albeit less extreme, pattern holds for cSNSs (table 1). Note that, conditional on the alleles in one species, the typical level of transition/transversion bias (≈2; Zhang and Gerstein 2003) explains only a fraction of this observation because the same set of alleles appear in the other species significantly more than twice as often. Furthermore, we see a bias for the transversion AT to coincide with another AT, both in the cSNP data and, to a lesser extent, in the cSNS data. Thus, these observations immediately suggest the possibility of a single, shared mutation event (i.e., shared ancestral polymorphism) instead of two independent mutation events (i.e., mutation rate variation).

Table 1.

Coincident Mutation Matrices

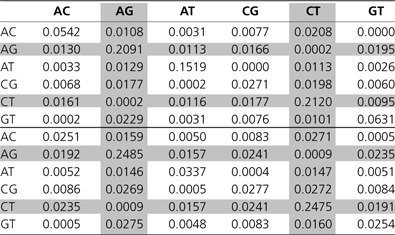Top, cSNPs where rows correspond to human alleles and columns to chimpanzee alleles; bottom, cSNSs where rows correspond to human + chimpanzee and columns to orangutan + rhesus. Transition mutations are shaded and tables are normalized to sum to 1.

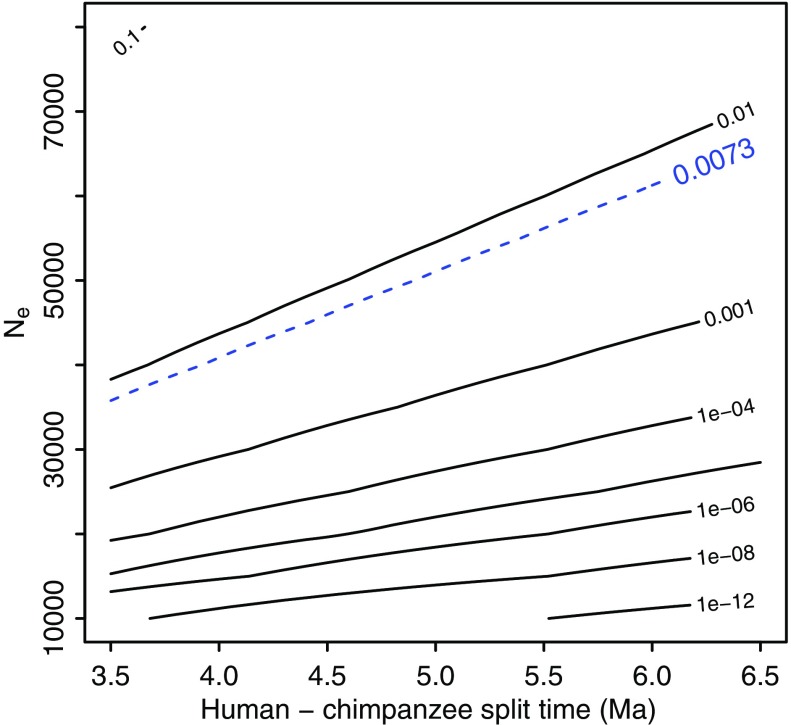
Next, we calculate the expected number of shared polymorphisms. Under simplifying demographic assumptions (see Methods), we can analytically calculate the probability of a shared ancestral polymorphism (acSNP) being maintained since the human and chimpanzee populations split. For this, we need estimates of the split time and the post-split long-term effective population size. In order to attribute all cSNPs to ancestral polymorphism [observed cSNPs/chimp SNPs = 6,452/8.8 × 10⁵ = 0.0073 = Pr(acSNP|chimp SNP, N_e, t)], the long-term N_e would need to be at least 35,000 for both populations and the split time could be no less than 3,500,000/20 generations. (fig. 2, area above dashed line).

FIG. 2.—

Contour plot of the probability of observing an acSNP in a sample of 118 human chromosomes as a function of species split time and population size, conditional on observing a heterozygous SNP in chimpanzees—see equation (1). Dashed contour indicates frequency of observed cSNPs. Both humans and chimpanzees were assumed to have a generation time of 20 years.

In order to relax some of the more unrealistic assumptions of our analytical calculations, we also conducted coalescent simulations. Most importantly, we introduced a finite ancestral population size N_a of humans and chimpanzees, which has been estimated to be between 65,000 and 100,000 (Hobolth et al. 2007; Burgess and Yang 2008). Although we vary N_a, we keep the species split time fixed at t = 4,100,000/20 generations. In agreement with the analytical results, coalescent simulations only yield sufficiently many acSNPs with a long-term post-split N_e ≈ 35,000, at which point the probability of an acSNP conditional on a chimpanzee SNP approaches the observed frequency of cSNPs (0.0083 for N_a = 100,000 and 0.0055 for N_a = 65,000 vs. 0.0073 observed; supplementary table S1, Supplementary Material online).

Third, we examine the SFS of the cSNPs and of sites linked to cSNPs. We begin by comparing the SFS between bi- and triallelic cSNPs, reasoning that only biallelic cSNPs could be ancestral. Indeed, we find that the SFS of triallelic cSNPs is indistinguishable from that of any SNP, although biallelic cSNPs tend to have slightly higher frequencies (fig. 3A). In contrast, theory (Kimura 1955) and simulation predict a near-uniform frequency spectrum for alleles that have been segregating for a long time, so the clear excess of rare variants in both bi- and triallelic cSNPs makes these unlikely to be ancestral polymorphisms maintained either by chance or by balancing selection. In addition, sites linked to a shared ancestral polymorphism will also have a slightly flatter SFS; however, we again see an excess of rare variants at linked sites (fig. 3B). Thus, although it is still possible that some of the observed cSNPs are ancestral polymorphisms, the SFS makes this explanation unlikely for the majority of cSNPs.

Mutation Rate Distribution

After rejecting the above hypotheses, we conclude that the majority of these cSNPs and cSNSs must arise as a result of elevated mutation rate at these sites.

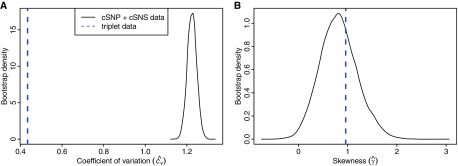
Using the theory developed in Methods and the $\widehat{R_2}$ value from cSNPs, we estimate the coefficient of variation for the mutation rate distribution to be $\widehat{c_{\text{v}}}$ = 1.22 (bootstrap 95% confidence interval of 1.18–1.27). Combining this $\widehat{R_2}$ value with our $\widehat{R_3}$ value, we estimate the skewness of the mutation rate distribution to be $\widehat{\gamma }=0.81$ (bootstrap 95% confidence interval of 0.11–1.61). Skewness grows monotonically as a function of R₃, so, because our estimate of R₃ is a lower bound (see Discussion), our estimate of γ also forms a lower bound. Thus, the distribution has considerable spread and is positively skewed, with the bulk of the distribution mass at lower mutation rates and a long tail reaching into higher mutation rates. Note that, as with all data presented in this paper, these estimates do not include CpG dinucleotides, which would generate additional positive skew.

As expected from the cryptic nature of this variation, our estimate for c_v based on coincident sites is significantly higher than an estimate that assumes nearest-neighbor context explains all variation (fig. 4A). Interestingly, the equivalent comparison of skewness finds our estimate of γ consistent with the nearest-neighbor estimates (fig. 4B), although this may be an artifact of $\widehat{\gamma }$ being a lower bound.

FIG. 4.—

Bootstrap distributions of (A) $\widehat{{\mathit{c}}_v}$ and (B) $\widehat{\gamma }$. Solid curves show distribution of estimates made using coincident sites from 10,000 bootstrap replicates; dashed vertical lines indicate estimates made using nearest-neighbor nucleotide context (triplets). All estimates exclude potential CpG sites.

Discussion

The fundamental observation of an excess of coincident SNPs holds regardless of the underlying source of variable sites. Hodgkinson et al. (2009) used sites retrieved from dbSNP, whereas we used sites identified from the diploid genome of a single chimpanzee (Sanger sequencing) and the 1000 Genomes Yoruba low-coverage pilot (454, Illumina and SOLiD sequencing). Similar estimates for R₂ also arise (results not shown) when we use human SNPs from the Sanger-sequenced diploid genome of a single European individual (Levy et al. 2007), from five Illumina-sequenced, medium-coverage diploid genomes from disparate human populations (Green et al. 2010), from the National Institute of Environmental Health Sciences Environmental Genome Project (http://egp.gs.washington.edu), and from the SeattleSNPs (http://pga.gs.washington.edu).

Each apparent cSNP derives from one of four sources: collapsed paralogs, sequencing error, shared ancestral polymorphism, or coincident (repeat) mutations in each species. Paralogs are ruled out by comparing the alignment and read coverage of cSNPs relative to other SNPs. Sequencing errors are ruled out by comparing the SFS of cSNPs relative to other SNPs. Furthermore, the estimator $\widehat{R_2}$ is relatively robust with respect to sequencing errors and paralogs because, in addition to biasing the observed number of cSNPs, these artifacts also bias the number of adjacent SNPs (the denominator of R₂), leading to little overall change in the ratio (see supplementary material, Supplementary Material online, for analytic analysis of the effect of sequencing error). Thus, the observed excess of cSNPs must arise from one of the two biological sources.

Shared ancestral polymorphisms are polymorphic sites that originated in the ancestral species and have survived genetic drift in both the human and the chimpanzee populations. This survival probability depends strongly on the split time and the post-split effective population size, N_e. Although fairly good estimates exist for the former, relatively little is known about the dynamics of N_e since the split. Any value between 7,000 and 100,000 including our estimate (N_e ≈ 35,000) seems possible (Hobolth et al. 2007; Burgess and Yang 2008; Gutenkunst et al. 2009; Hey 2010). Hence, the bare number of cSNPs cannot exclude shared ancestral polymorphisms. On the other hand, after more than 4N_e generations of genetic drift, all allele frequencies are approximately equally likely for surviving polymorphisms, and hence, the SFS should be flat. Instead, the human SFS for cSNPs is indistinguishable from that of other human SNPs. This observation leaves us with only one viable source for the majority of cSNPs: coincident mutations.

The molecular mechanism underlying this variation remains unknown, although the data contain a couple of tantalizing hints. First, not surprisingly, transition mutations dominate over transversions at coincident sites. More surprisingly, however, we see the transversion A ↔ T dramatically more often than all other transversions in cSNPs (table 1), similar to the findings of Hodgkinson et al. (2009). Second, cSNPs fall in regions of simple sequence repeats and low-complexity sequence as identified by RepeatMasker (Smit et al. 1996–2010) more often than other SNPs (∼15% of cSNPs vs. ∼6% of human or chimpanzee SNPs). These two observations suggest that the signal driving this variation may still lie in the local nucleotide sequence composition.

The excess of coincident substitutions implies that the forces driving this cryptic variation extend to a timescale significantly beyond that of cSNPs. However, the longer timescale of substitutions also provides greater opportunity for the action of potential confounding factors such as variation in the mutation rate of a particular site, which could contribute to the discrepancy between $\widehat{R_2}$ calculated from cSNPs (2.5) and $\widehat{R_2}$ calculated from cSNSs (1.6). Our derivation for $\widehat{R_2}$ and $\widehat{R_3}$ assumes that the mutation rate at a particular site will not change over the timescale of the input data. One potential mechanism for such variation would be self-destruction of mutation hotspots that require a specific nucleotide present at the cSNP. If this was the case, then the very act of mutating would decrease the future mutation rate. Although this mechanism is consistent with the observed tendency to find the same two alleles in both populations (diagonal in table 1), it requires that the elevated mutation rate is not only single-base specific in action but also single-base specific in cause. Regardless of the underlying reason, if the mutation rate at a particular site does change over time, then the numerator of the R₂ and R₃ statistics will decrease to become closer to the denominator. Because the polymorphism timescale encompasses less time for this assumption to be violated, the cSNP data should be closer to the true mutation spectrum than the cSNS data. Thus, we use the polymorphism-based $\widehat{R_2}$ and consider $\widehat{R_3}$ to be a lower bound when calculating $\widehat{\gamma }$.

Given our inferred $\widehat{{\mathit{c}}_v}$ and $\widehat{\gamma }$, we now turn toward the question of whether this cryptic variation will bias typical human population genetic estimates.

The most likely impact of an excess of recurrent mutations on population genetic estimators is that it leads to misidentification of the ancestral allele. The simplest method of identification involves calling the human allele that matches the chimpanzee as ancestral; however, this procedure implicitly assumes that no new mutation at this site occurred in either chimpanzees or the lineage leading to the common ancestor of all humans. The probability of such a mutation happening corresponds roughly to R₂ times the chimpanzee–human divergence (d_ch ≈ 0.9% without CpGs) minus the amount of human diversity (θ ≈ 0.05% without CpGs): R₂·(d_ch − θ) ≈ 0.02. Given this probability, correcting population genetic estimates for ancestral misidentification is straightforward (Hernandez et al. 2007).

Violations of the infinite sites model of mutation within one population, on the other hand, have the potential to be more troublesome, particularly when 4N_eμ ≥ 0.05 (Desai and Plotkin 2008) where μ is the per-site mutation rate. Estimates for the mean human mutation rate are on the order of 10⁻⁸ per site (Lynch 2010), and estimates of the effective population size are around 10⁴. The inferred coefficient of variation ($\widehat{{\mathit{c}}_v}=1.2$) and skewness ($\widehat{\gamma }=0.81$) do not completely specify the underlying mutation rate distribution, but we can examine either a gamma distribution or a worst-case distribution consisting of two point masses, one of which is at μ = 0.05/(4N_e). For these distributions, if we match the mean and our $\widehat{c_{\text{v}}}$, then the skewness will be higher than our lower bound estimate (γ = 2.4 and 103, respectively). If the true mutation rate distributions were to follow the gamma distribution, then the probability of having a mutation rate greater than 0.05/(4N_e) is vanishingly low and the infinite sites assumption works well. In our worst-case scenario, if the true distribution consisted of two point masses, then the probability of having a mutation rate of 0.05/(4N_e) rises to ∼10⁻⁴, which amounts to many sites across the genome.

Thus, although population geneticists studying humans need not worry about cryptic variation causing ancestral misidentification, the infinite sites assumption might still be dangerous, particularly when conducting genome-wide surveys. More broadly, population genetic studies of non-primate species could also be influenced by cryptic variation. Further investigation of this phenomenon lies beyond the scope of this study, but the statistic R₂ and methods to infer c_v can be applied equally well to any pair of closely related species.

Supplementary Material

Supplementary data, figures S1 and S2, and table S1 are available at Genome Biology and Evolution Online (http://www.gbe.oxfordjournals.org/).

Funding

National Science Foundation Award No. DBI-0906041 to P.L.F.J.