Modelling natural and artificial hands with synergies

Abstract

We report on recent work in modelling the process of grasping and active touch by natural and artificial hands. Starting from observations made in human hands about the correlation of degrees of freedom in patterns of more frequent use (postural synergies), we consider the implications of a geometrical model accounting for such data, which is applicable to the pre-grasping phase occurring when shaping the hand before actual contact with the grasped object. To extend applicability of the synergy model to study force distribution in the actual grasp, we introduce a modified model including the mechanical compliance of the hand's musculotendinous system. Numerical results obtained by this model indicate that the same principal synergies observed from pre-grasp postural data are also fundamental in achieving proper grasp force distribution. To illustrate the concept of synergies in the dual domain of haptic sensing, we provide a review of models of how the complexity and heterogeneity of sensory information from touch can be harnessed in simplified, tractable abstractions. These abstractions are amenable to fast processing to enable quick reflexes as well as elaboration of high-level percepts. Applications of the synergy model to the design and control of artificial hands and tactile sensors are illustrated.

1. Introduction

The dichotomy between ‘mens et manus’—or reason and skill, or thought and action—permeates human thinking since the most ancient times: the ancient Greek philosopher Anaxagoras affirmed that ‘man is the most intelligent of animals because he has hands’ [1]; in 1960, the anthropologist Sherwood Washburn wrote in an influential paper for the Scientific American that ‘modern human brain came after the hominide hand’ [2]. That the hand may determine and anticipate cognition is not ‘the innocuous and obvious claim that we need a body to reason; rather, it is the striking claim that the very structure of reason itself comes from the details of our embodiment. The same neural and cognitive mechanisms that allow us to perceive and move around also create our conceptual systems and modes of reason’ [3].

Thus, in order to understand intelligence, we should also understand the details of our hand's sensorimotor system. In robotics, it is quite tempting to think of a similar hypothesis, namely that the design of artificial hands, including the principles of low-level sensing and control, will shape, at least in part, the development of the field of artificial cognitive systems at large.

This paper deals with the hand regarded as a cognitive organ—and how its physical embodiment enables and determines its behaviours, skills and cognitive functions. The paper is in several respects an account of an ongoing research effort, organized in an international cooperation project called ‘THE Hand Embodied’, a title which refers to the ‘hand’ as both the abstract cognitive entity—standing for the sense of active touch—and the physical embodiment of such sense, comprised actuators and sensors that ultimately realize the link between perception and action.

Central to this view is the concept of constraints that are imposed by the embodied characteristics of the hand and its sensorimotor apparatus on the learning and control strategies we use for such fundamental cognitive functions as exploring, grasping and manipulating. From this viewpoint, these constraints are not merely bounds that limit possibilities and performance, but rather are the dominating factors which affected and effectively determined how cognition has developed in the unique, admirable form we are able to observe on the Earth—hence, they really are to be considered ‘enabling constraints’ which organize the hand embodied. The elemental sensorimotor variables that are subject to such organization work together in synergies. The hand embodied hinges about two systems of such enabling constraints, or synergies, respectively, in the hand motor system and in the tactile and kinaesthetic sensory system, and about their interaction. Motor and sensory synergies are also two key ideas for advancing the state of the art in artificial system architectures for the ‘hand’ as a cognitive organ: the ultimate goal of our research being to learn from human data- and hypotheses-driven simulations of how to better design and control artificial hands for robotics, prosthetics and haptic interfaces.

In this paper, we report on recent work in modelling the process of grasping and active touch by natural and artificial hands. Starting from observations made in human hands about the correlation of degrees of freedom in patterns of more frequent use (postural synergies), we consider the implications of a geometrical model accounting for such data, which is applicable to the pre-grasping phase occurring when shaping the hand before actual contact with the grasped object. To extend applicability of the synergy model to study force distribution in the actual grasp, we introduce a modified model including the mechanical compliance of the hand's musculotendinous system. Numerical results obtained by this model indicate that the same principal synergies observed from pre-grasp postural data are also fundamental in achieving proper grasp force distribution. To illustrate the concept of synergies in the dual domain of haptic sensing, we follow with a review of models of how the complexity and heterogeneity of sensory information from touch can be harnessed in simplified, tractable abstractions. These abstractions are amenable to fast processing in order to enable quick reflexes as well as elaboration of high-level percepts.

Finally, applications of the synergy model to the design and control of artificial hands and tactile sensors are illustrated.

2. Modelling hands with synergies

In the long-term perspective of building artificial hands achieving comparable performance with the natural example, the understanding of how the human hand system is organized is clearly fundamental. It should be noticed that, as a corollary of the philosophy expounded above that intelligent behaviours are intrinsic to the physics of the embodiment, it follows that mere mimicry of nature in artificial replicas cannot lead to success. Rather, lessons learned and inspiration taken from the human example need to be translated into a language, which is abstract enough to be understood and applied in a different, artificial, body—a language that, according to the lesson of Galileo, is essentially geometrical.

Indeed, the notion of synergies as ‘enabling constraints’ lends itself very naturally to thinking of synergies in geometrical terms. In the field of motor synergies, such geometrical notions are well entrenched. More than three decades ago, Easton pioneered the idea that particular patterns of muscular activities could form a base set analogous to the concept of basis in the theory of vector spaces: a minimal number of (linearly independent) elements that under specific operations generate all members of a given set, in this case, the set of all movements [4]. As Turvey [5] states it, ‘if synergies could compose such a basis, and if each synergy was self-monitoring, then the duties of other functional levels of the movement system would reduce to orchestrating the specific operations. Patently, the synergies-as-basis hypothesis implies that all movement patterns share the same task-independent synergies.’ Different interpretations on essentially the same geometrical scheme of redundancy resolution have been provided in terms of unconstrained manifold [6] and optimal stochastic control [7].

The complex biomechanical and neural architecture of the hand poses challenging questions for understanding the control strategies that underlie the coordination of finger movements and forces required for a wide variety of behavioural tasks, ranging from multi-digit grasping to the individuated movements of single digits. One striking aspect is that—as in most other functions of the human body—there are many more elemental variables contributing to performance in the motor tasks than absolutely necessary to solve the tasks—e.g. we have five fingers and more than 20 joints, while strictly speaking three fingers and nine joints would be enough for grasping and manipulating objects [8]. This problem of redundancy has been central in the scientific study of motor control since its very beginning [9,10]. In Bernstein's functional hierarchy [11], the level responsible for coordinating large muscle groups and different patterns of locomotion is referred to as the level of muscular-articular links or synergies. The structure of this level is the central problem of movement control and coordination: the problem of degrees of freedom, i.e. the problem of how to compress the movement system's state space of very many dimensions into a control space of few dimensions.

In the domain of hand motor systems, an extensive body of work (reviewed in [12], see also [13]) has revealed the existence of constraints in both the peripheral apparatus and its central control. A number of experimental approaches, from studies of finger movement kinematics to the recording of electromyography and cortical activities, have been used to extend our knowledge of neural control of the hand. Experimental evidence indicates that the simultaneous motion and force of the fingers are characterized by coordination and covariation patterns that reduce the number of independent degrees of freedom to be controlled. Santello et al. [14,15] investigated the hypothesis that ‘learning to select appropriate grasps is applied to a series of inner representations of the hand of increasing complexity, which varies with experience and degree of accuracy required.’ In an experiment, five subjects were asked to shape their hands in order to mime grasps for a set of 57 familiar objects. The hand joint angles were recorded, and principal components analysis of these data revealed that the first two principal components or postural synergies accounted for 84 per cent of the variance, whereas the first three components explained up to 90 per cent of the data. Peripheral and central constraints in the neuromuscular apparatus have been identified that may in part underlie these coordination patterns. These patterns may simplify the control of multi-digit grasping while placing certain limitations on individuation of finger movements. The extent to which such simplification is actually related to neural control of movement is still under debate and the subject of active investigation. Nevertheless, from the perspective of artificial control of a robotic hand, the idea of simplification arises naturally from the ability to control a large number of elements through a smaller number of inputs.

3. Manipulation with synergies

These and other many related experimental observations can contribute a new geometrical insight in grasping and manipulation. The mechanics of articulated hands has been studied intensely in the past three decades or so, starting with Salisbury & Roth [16]. The rather large body of knowledge developed in this field, reviewed in Bicchi & Kumar [17] and more recently in Prattichizzo & Trinkle [18], can be considered to provide a rather exhaustive answer to the issue of modelling mechanics of ‘simple’ robot hands, i.e. hands whose joints are fully and independently controlled, and which manipulate objects using the distal parts of their fingers. Insights have also been given in the literature for more complex problems, such as modelling rolling contacts [19,20], deformable fingertips [21] and networked compliant tendinous actuation [22]. Some of the most mature analysis techniques and models for robotic hands are embedded in the software graspit! [23].

Consideration of synergies introduces a completely new vista on problems that once appeared to be solved. If we denote by p the vector of posture variables at the contact points between the hand and the object, and by q the hand joint angles, let p = k(q) denote the forward kinematic map, and 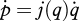the differential kinematics map of the hand. An immediate interpretation of results described in Santello et al. [14] would lead to interpreting the principal components (i.e. the leading eigenvectors) of the covariance matrix of the experimentally observed grasp postures as defining an ordered basis for a subspace of the joint space. In other terms, the generic joint displacement vector q could be represented as a function of fewer elements, collected in a synergy intensity vector σ, as q = q(σ), which effectively would constrain hand configurations in a S dimensional manifold. Synergistic hand velocities would live in the tangent bundle to this manifold, and could be locally described by a linear map as 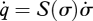. Accordingly, hand velocities can then be expressed locally on the constraint as a function of synergy velocities as 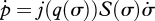. The first column of the synergy Jacobian jS thus dictates the shape of the hand when only the first synergy is used, which is modulated by the intensity σ₁; and analogously for subsequent synergies (figure 1).

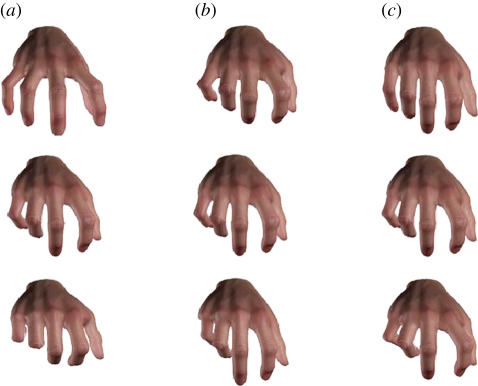
Figure 1.

The three first synergies of the human hand: (a) the first, (b) second and (c) third synergy. Rows (top to bottom) correspond to negative, null (average) and positive intensities.

One of the key problems in manipulation modelling is to study the motion of the manipulated object as a function of the elemental-controlled variables, to understand what object motions are possible for a given grasp and to plan the corresponding degrees of freedom that have to be controlled. Object motions (twists) 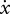would be determined by motion of contact points according to a differential kinematic model written in terms of the so-called grasp matrix G(p) as 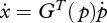. While this problem is solved for fully actuated hands (i.e. when the hand kinematics are injective), the problem is more complex for synergy-based models of hands, both locally (because the constrained Jacobian matrix jS is not full row rank) and globally, i.e. on the nonlinear synergy constraint manifold.

In terms of forces, torques on the joints τ are related to contact forces λ at equilibrium by the equation τ = j^T(q)λ, while the interaction with manipulated object/environment, represented by the wrench w, is represented by the map w = −G(p)λ. When grasping a tool, the hand exchanges contact forces with the tool, which have two main functions: to act on the environment according to the task requirements, and to keep the grasp on the tool, avoiding that it slips or that either the tool or the hand itself gets damaged by excessive forces. Correspondingly, grasping forces are divided into manipulative and internal grasping forces. The fact that the hand embodiment may impose constraints on the kinematics, and hence the hand may have fewer controllable synergies than the number of joints, implies that the classical analysis of internal forces as the annihilator of the grasp matrix G(p) is no longer a valid solution. To realize this, it is sufficient to reckon that the dimension of the kernel of the grasp matrix has the dimension of the range space of the hand Jacobian, while the introduction of synergies reduces drastically the hand degrees of freedom, i.e. the rank of the jS matrix.

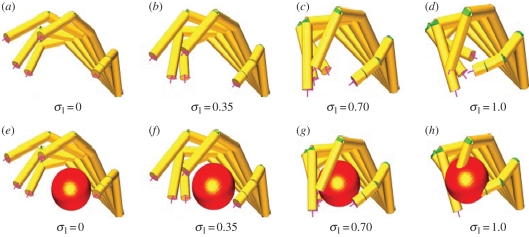
To illustrate which problems are introduced by the application of the model of synergies as motion sub-manifolds, it is convenient to refer to a schematic of a simplified 15 d.f. model of the human hand, depicted in figure 2.

Figure 2.

The inconsistency of a model of synergies as rigid manifolds.

In figure 2a–d, the hand is shown in four configurations corresponding to increasing values of the first synergy intensity σ₁ in a normalized range from 0 to 1. In figure 2e–h, the hand closes on a spherical object. The first contacts occur between the thumb and the index fingertip and the object corresponding to a value of σ₁ = 0.75. If the first synergy is closed further to achieve contact on other phalanges, then the index and thumb phalanges would penetrate the object surface, leading to an unacceptable behaviour of the model.

4. The soft synergy model

The problems raised by the synergistic model of manipulation are new in the robotics literature, and their solution calls for new tools in grasp analysis. Due consideration must be given to the fact that grasping force analysis on a constrained tangent bundle necessitates, for being well-posed, the introduction of a model of elasticity in the system. In the human hand, compliance is introduced by the musculotendinous actuation system. Notably, the redundancy in this apparatus, along with its nonlinear elastic characteristic, is used for changing the compliance of the agonist–antagonist pairs. More generally, it has been recently observed that the brain uses complex co-contraction patterns to vary the impedance of our limbs as seen from the environment, i.e. in a task-reference frame [24], for important functions such as stabilizing and adapting to unknown environment impedance. Much less is known about impedance control in the human hand: however, it can be expected that motor synergies play a fundamental role in selecting what task–space impedance patterns are achievable for manipulated tools, and in controlling them. Although the study of how humans use and control hand impedance in manipulating tools appears to be a problem of daunting complexity, some preliminary hypotheses can be drafted from the proposition of a consistent model of force distribution in artificial systems and its analysis.

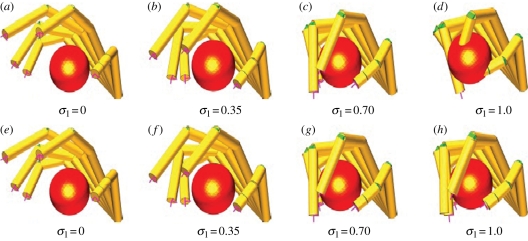
The model, proposed first by Gabiccini & Bicchi [25], consists of considering the synergy manifold to effectively constrain the motion of a reference model for the hand, towards which the physical hand is attracted by forces which are generated by the hand impedance, but from which it can be repelled by interaction forces generated by the contact with the object. In other terms, the physical hand in this model is always in dynamical equilibrium under two force fields: one field is attracting it towards a virtual hand which is shaped on the synergy manifold, and one field is repelling the hand from penetrating the manipulated objects or the environment. The equilibrium between these fields is found depending on the specific pattern of stiffness (and more generally mechanical impedance) of the hand actuation and control systems. The application of this ‘soft synergy’ model to the example above is reported in figure 3.

Figure 3.

In the soft synergy model, the reference hand moves on the synergy manifold (a–d) and represents an attractor for the real hand (e–h), which is repelled by contact forces with the object. The resulting configuration is ultimately dictated by the hand mechanical and control stiffness.

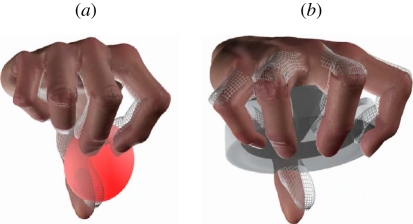
Results of application of the soft synergy model to a computer reconstruction of the human hand exerting a pinch grasp on a cherry-like object and a power (whole-hand) grasp of an ashtray are depicted in figure 4.

Figure 4.

Application of the soft synergy model to the grasp of a cherry-like object (a) and of an ashtray (b). In wireframe is the reference hand, moving according to the constraint manifold corresponding to the first three synergies.

5. Synergies in force distribution

It can be noticed that, in the pre-grasping phase, and whenever the hand is not exerting forces on the manipulated object or the environment, the real hand is at equilibrium in the configuration of the reference hand. Hence, the consideration of hand compliance does not alter the analysis of the pre-grasp phase, which is dominated by postural and kinematic models, and to which most available experimental data for human hands are related.

However, applications of the soft synergy model allow making predictions on force distribution in manipulation, a critical aspect that is intimately related to reflex-driven modulation of grasp forces, slippage avoidance, purposeful control of forces for tool use, etc. The potential usefulness of the models is twofold: on the one hand, predictions generated by these models as applied to the human hand might serve to verify or falsify the synergy models through experiments with subjects; on the other hand, these results could enable the control of artificial synergies in robotic hands and haptic interfaces to characterize which are the feasible manipulation and grasping requirements for a given artificial design, or to design the simplest device that can achieve a given task set.

A first set of preliminary results in the direction of understanding the relevance of the soft synergy model to grasping has been obtained recently by Gabiccini & Bicchi [25]. The goal there was to understand whether or not the first few synergies observed by Santello et al. [14] to generate a large part of pre-grasp postures, could also explain a significant part of distribution patterns for grasp forces. Each postural synergy was associated through a numerical model of hand and object compliance to a contact force pattern. The resulting force synergies were linearly combined with weights, so as to minimize a grasp cost index. The grasp index is used to reflect the capability of the grasp to resist external forces while avoiding slippage of the object in the hand (a property referred to as force-closure), and also weighs factors such as required actuator torques.

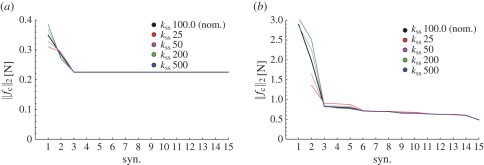
Numerical case studies were used to characterize the role of different postural synergies in the ability of the hand to obtain force-closure grasps. Results of two case studies, addressing the precision and power grasp of a cherry-like object and an ashtray, respectively, are reported in figure 5.

Figure 5.

Grasp cost index variations with increasing number of synergies involved, for different hand compliance values. (a) Grasp of a cherry-like object. (b) Grasp of an ashtray.

From these results, we can observe that the force-closure property of grasps strongly depends on which synergies are used to control the hand. The first few synergies in the ordering suggested by postural data from Santello et al. [14] are sufficient to establish force-closure. A measure of the quality of the grasp is enhanced by increasing the number of actuated synergies, but only to a limited extent. No improvement is observed beyond the first three synergies in the precision grasp case, while continuous but small improvements are obtained in the whole-hand grasp case. On the other hand, other results show that if the first few synergies are not actively controlled, much worse grasp indices are obtained, and force-closure requires many more degrees of freedom (corresponding to high-order synergies) to be actuated.

All the above results are consistently robust, in an extensive numerical case study analysis, with respect to different values of stiffness parameters, which reflect the uncertainty by which these parameters are known in human or robotic hand models, and the fact that stiffness may be changed either voluntarily or not.

6. Synergies in the haptic-sensing domain

Geometrical theories of sensory integration are well established in the scientific literature. As an example, recent models characterize human multi-cue and multi-sensory integration in the presence of uncertainty and noise in terms of Bayesian decision theory, directly linking to concepts in optimal filtering theory such as maximum-likelihood [26] or maximum a posteriori estimates [27]. These concepts have direct geometrical interpretations in terms of projections onto adapted, constraining subspaces. It clearly appears that such geometrical approaches to harnessing the complexity of sensing can be regarded as the dual of the redundancy resolution problem of motor control, and that the vocabulary of synergies, albeit less widespread in this domain, can be usefully adopted here, too.

In the domain of touch, the complexity of the physical phenomena underpinning tactile perception is manifold, as it derives from both the continuous mechanics of stress and strain tensor distributions in the region near contact, and from the wide span of spatial and temporal characteristics of the various receptors contributing kinaesthetic and cutaneous sensing information. Abstractions of contact mechanics into representations that produce functional interpretations are well entrenched in classical mechanics, the most obvious example being Amontons' laws of dry friction. These state that, notwithstanding the complexity and heterogeneity of physical phenomena generating contact tractions at the microscopic scale, and irrespective of both the actual shape and area of the contact region between two bodies, of the actual distribution on the surfaces of contact of the normal and tangential tractions and of the relative velocity, there is a relation between the components of the resultant forces, and between these and the relative velocity. This relationship is geometrically expressed by Coulomb's friction cone which, although insufficient to accurately describe, e.g. a tyre on a road or a fingertip in a grasp, still provide a most useful approximation, and has served well the study of fundamental grasp characteristics (e.g. force-closure) and the synthesis of practically all artificial grasp reflex controllers for robot hands (see Bicchi & Kumar [17] for a review).

One further example of how geometrical constraints can organize complex contact phenomena comes from the method known in robotics as contact-from-force or intrinsic tactile sensing [28]. To introduce it, consider that in a state of static equilibrium, forces and moments which act upon a body—arising from actuators and gravity, and from contacts with other objects—must sum to zero. The contact type establishes constraints on the forces which may be applied through the contact between two bodies: the type that most closely models a fingertip in contact with a relatively stiffer object is the ‘soft finger’ model, whereby the system of distributed contact tractions amounts to a resultant force applied at the contact centroid, and a resultant moment aligned with the normal to the surface at the same point. The contact centroid is a point on the surface of the fingertip (before deformation), which has the important property of being internal to a generalized convex hull of the contact region [28]. If both the geometry of the fingertip surface and the resultant of all forces applied by the finger are known, then the contact centroid can be uniquely determined, along with the total contact force, and moment on the fingertip's surface.

The idea can be simply implemented in robot hands with force/torque sensors (either embedded inside the fingertip surface, or in the joints and actuators), and using the geometrical algorithm in Bicchi et al. [28]. The information elicited by intrinsic tactile sensors¹ is not only geometrical (position of the contact centroid, normal and tangential directions to the object surface), but also dynamic: indeed, it can provide the normal and frictional components of contact forces and torque, and has thus enabled experimental demonstrations of robotic tactile exploration and reconstruction, friction assessment and grasping reflex control [29].

It is natural to draw a similarity between intrinsic contact sensing and the kinaesthetic component of touch information in humans—which basically consists of the processing of force and posture information from musculotendinous, skin-stretch and joint afferents. Indeed, contact information which can be elicited from finger geometry and remote force measurements can be compared with sensory information available to a human subject, when his/her cutaneous sensibility is removed (or drastically constrained), for example when using thick gloves or thimbles. The information about objects being effortfully supported or moved by the body, via mechanoreceptors embedded in the myofascial structure [30], is also apparently related to contact-from-force sensing, and suggests further investigations on how the overall posture and force distribution in a robot structure could be used to elicit useful information about the environment. Extrapolating from these ideas, one could speculate that the effects of gradually increasing the degree of constraints in the manual exploration process—in degrees varying from reducing the number of fingertips, to introducing compliant coverings, rigid finger splints, rigid fingertip sheaths, up to using rigid probes, as described in earlier studies [31,32]—could be regarded as rougher and rougher abstractions (i.e. truncations of the synergy basis of the sensory space) of haptic perception.

Indeed, although contact information from force measurements is very useful in many tasks, it certainly does not exhaust the richness of the sense of touch. In a well-known experiment, Srinivasan & Lamotte [33] showed that the capability of humans to discriminate softness is severely impaired by removal of cutaneous sensibility. While they used local anaesthesia of fingertip sensing, similar results were also shown in normal conditions using suitably conceived specimens, which can produce identical kinaesthetic but different cutaneous cues, or the other way around [34]. These results indicate that kinaesthetic information alone is insufficient to provide good discrimination of softness, and that more elements of tactile information are needed to form a more accurate perception. On the other hand, high-fidelity measurement (or reproduction, if haptic displays are considered) of the tensor state of stress and strain in the fingertip pad is a technologically daunting task. This limitation has prompted the idea of pursuing high-order approximations of tactile perception. The tactile flow equation is one such further constraint along which dynamic (i.e. force-varying) tactile information can be projected. Tactile flow [35] can be regarded as an extension of Marr's model [36] of optic flow to touch, and suggests that what near-surface (extrinsic) contact sensing is mostly about, in dynamic conditions, is the flow of strain energy density (SED) at places where measurements are taken, in the direction perpendicular to iso-SED level surfaces (alternative, but fundamentally equivalent models consider Von Mises stress in place of SED). The tactile flow equation (which generalizes to three-dimensional strain distributions Horn and Schunk's equation [37] for image brightness) generates hypotheses on tactile illusions, which could be verified on human subjects [38]. In its integral version (i.e. analogous to what time-to-contact is for optic flow), the tactile flow hypothesis predicts that objects of different softness, pressed by the same probe (e.g. the fingertip), would deform and warp around the probe at different velocities, thus explaining the experimental fact that the ‘contact area spread rate’ conveys important information for softness discrimination in humans [39]. Consistently with the ‘synergies as a basis’ description, if kinaesthesia (force and posture) is considered as a first synergy and contact area spread rate as a second, results of Scilingo et al. [34] showed that the fidelity by which softness could be artificially rendered increases with the number of synergies employed in rendering. One could further venture to speculate the existence of a complete basis of sensory synergies providing increasingly refined descriptions of the full spectrum of haptic information, i.e. of the ‘plenhaptic function’ presented by Hayward [40].

While a certain amount of knowledge has been accumulated on both sensory and motor synergies, these have been often studied in separation, and the question of how the sensory domain shapes learning and execution of hand synergies is wide open. Not much is known at present as to how the concept of synergies may extend to the interaction of body–task–environment, so that it could be applied to the sensorimotor interaction itself. Recent evidence suggests that, although mostly obtained by studies of grasping and manipulation, postural synergies are not limited to motor tasks. Furthermore, unconstrained haptic exploratory procedures used to identify common objects are also characterized by synergies which, interestingly, are very similar to those associated with grasping [41]. This is a remarkable finding when considering the different goals and neural processes associated with executing a grasp versus acquiring sensory information for feature extraction. One may speculate that the commonality between ‘grasping’ and ‘exploratory’ hand synergies could facilitate or optimize the efficacy of sensorimotor transformations required to translate haptic perception of features of tools and objects into appropriate motor commands.

Understanding the fundamental processes of how humans effectively use multiple sensory representations of the environment (i.e. object shape and/or the consequences that an upcoming set of motor commands will have on that object) for effective (lower dimensional space) control of many muscles and joints of the hand remains a largely unsolved, crucial problem in active touch, which is the object of active ongoing investigations.

7. Synergies for designing artificial systems

The history of robotic hands spans 30 years and millions of Euros in research funding worldwide. Yet, most researchers would frankly acknowledge that the state of the art is not yet any closer to where we would expect it to be: no device has been demonstrated as yet that achieves robust and adaptive grasping in unstructured environments, and even farther is the goal for what concerns dexterous manipulation. Although many advances have been achieved in the mechatronics and computational hardware of hands, the gap that remains between the state of art and a satisfactory functional approximation of the human hand seems to be related to some fundamental issues in the understanding of the organization and control of hands. The role of constraints and synergies in organizing the redundancy of the sensorimotor apparatus of the human hand is bound to have a profound impact on the design of new and improved architectures for artificial embodied cognitive systems, such as robot hands and haptic interfaces. Only very recently, however, has the robotics community realized the potential of the analysis of principal synergistic components to reduce the number of aggregated degrees of freedom, or ‘knobs’, used in programming robot or prosthetic hands [42], or to design hands for basic grasping operations [43].

Studies on human motor and sensor synergies, together with the development of new geometrical synergy-based models of kinematics, dynamics and multi-sensory integration will eventually lead to a much needed solution to the decade-long problem of trading off simplicity and performance in the design of robot hands. The concept, and our long-term goal, is to be able to replicate in the artificial an organized set of synergies, ordered by increasing complexity, so that a correspondence can be made between any specified task set (in terms of a number of different grasps, explorative actions and manipulations) and the least number of synergies whose aggregation makes the task set feasible. For instance, a hand whose goal is to realize basic grasps only could use the first two or three synergies in the basis. However, a manipulative hand with fine motion control of single joints (such as a piano player's hand) may require coordination of many more synergies.

To explore these directions, we have developed a prototypical hand system, which replicates almost exactly the size and kinematics of the model human hand used in Santello et al. [14]. The hand, depicted in figure 6, is a low-cost device realized with fast-prototyping techniques, with 15 d.f., which can be coupled and actuated according to different combinations of synergies. Furthermore, the hand can accommodate selective compliance in the actuation system, which allows experimenting with the soft synergy model described above.

Figure 6.

Five characteristic grasps of The First Hand.

The hand posture must adapt to task requirements and object properties soon after contact is detected and established, so as to capture the task and object geometry, but need not perfectly match either of these. This approximation can be driven by searching not only in the space of feasible hand configurations but also—and maybe primarily—in an ideally reduced space of the task-specific constraints (feasible set of forces and torques, etc.). Humans are very quick and efficient in learning how to choose a suitable mapping between hand configurations, points of force application and forces, in an effortless and effective manner. Further work is needed to capture the key features of sensorimotor integration that allows humans to select and modulate synergies based on sensory feedback of object features as well as intended use of a given object: in this direction, investigations based on geometrical models and artificial implementations will hopefully contribute useful insights.

8. Conclusions

Recent neuroscientific studies on postural synergies of the human hand can inspire decisive advancements in the development of artificial hand systems. In this paper, we have reviewed some of the consequences of considering synergistic couplings between degrees of freedom on the geometry of grasping, and have discussed how the existing models of postural synergies can be extrapolated in the force domain by the introduction of hand impedance. Numerical results suggest that the same synergies which dominate the pre-grasping phase are also crucial in establishing distributions of forces to obtain firm grasps. Finally, we have illustrated some of the possible insights coming from the synergy-based models of manipulation for the design of simpler and more effective robot hands, and have introduced a prototype of an anthropomorphic artificial hand intended to explore these directions.