Radial distance determination in the rat vibrissal system and the effects of Weber's law

Joseph H Solomon; Mitra J Z Hartmann

doi:10.1098/rstb.2011.0166

. 2011 Nov 12;366(1581):3049–3057. doi: 10.1098/rstb.2011.0166

Radial distance determination in the rat vibrissal system and the effects of Weber's law

Joseph H Solomon ¹, Mitra J Z Hartmann ^1,^2,^*

PMCID: PMC3172605 PMID: 21969686

Abstract

Rats rhythmically tap and brush their vibrissae (whiskers) against objects to tactually explore the environment. To extract a complex feature such as the contour of an object, the rat must at least implicitly estimate radial object distance, that is, the distance from the base of the vibrissa to the point of object contact. Radial object distance cannot be directly measured, however, because there are no mechanoreceptors along the vibrissa. Instead, the mechanical signals generated by the vibrissa's interaction with the environment must be transmitted to mechanoreceptors near the vibrissa base. The first part of this paper surveys the different mechanical methods by which the rat could determine radial object distance. Two novel methods are highlighted: one based on measurement of bending moment and axial force at the vibrissa base, and a second based on measurement of how far the vibrissa rotates beyond initial contact. The second part of the paper discusses the application of Weber's law to two methods for radial distance determination. In both cases, Weber's law predicts that the rat will have greatest sensing resolution close to the vibrissa tip. These predictions could be tested with behavioural experiments that measure the perceptual acuity of the rat.

Keywords: vibrissa, touch, tactile, trigeminal, active sensing, shape

1. Introduction

In the past decade, the rodent vibrissal-trigeminal system has become an increasingly important model for the study of the coding and transformation of sensorimotor information at different stages of the nervous system [1–3]. Rats tactually explore objects by rhythmically tapping and brushing their vibrissae (‘whisking’) against them at frequencies between 8 and 25 Hz [4,5], usually accompanied by brief touches with the tip of the nose [6–8]. Using tactile signals from its vibrissae, a rat can extract information about many of an object's spatial properties, including size, orientation and texture, with a resolution that can rival that of the human fingertips [9–11].

The positions of vibrissa/object contact during the rat's tactile exploration are most naturally described in the cylindrical coordinate system [1] shown in figure 1a. In this coordinate system, the vertical location (z) of each point on an object may be coded by the identity of activated vibrissae along each column [1]. This identity-based coding scheme is consistent with the central neural representation of vibrissae in a manner that reflects the regular topographical arrangement of vibrissae on the face [12,13]. The manner in which the rat's nervous system codes information about horizontal angular contact position (θ) and radial object distance (r) is more problematic, as there are no proprioceptors in the muscles that control the vibrissae to provide information about θ [1,14], and there are no sensors along the length of the vibrissae to provide information about r [15,16]. Previous publications have described some possible coding mechanisms for θ [1,3,14,16–18]. In the present work, we focus on the mechanisms by which the rat may estimate the radial distance to an object.

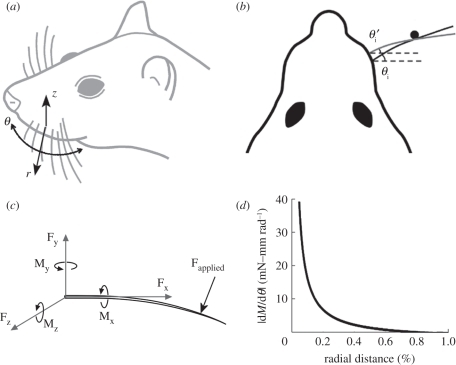
Figure 1. — Vibrissa coordinate system and description of variables relevant to radial distance determination. (a) Cylindrical coordinate system for three-dimensional object localization. (b) Example of the ‘angle-side-angle’ method for radial distance determination. (c) Forces and moments at the vibrissa base induced by contact with an object. (d) dM/d#x03B8; is monotonic with radial distance for the ‘rotational compliance’ method.

When the vibrissa makes contact with an object, the contact force is matched with an equal and opposite force at the vibrissa base, along with a bending moment to achieve equilibrium [15,19]. The force and moment are subsequently transmitted to mechanoreceptors in the follicle, whose responses are integrated in the primary sensory neurons of the trigeminal ganglion [20,21]. Thus, the force and moment at the vibrissal base implicitly contain information about the location of the object. The role of the nervous system is to decode this information in a manner that allows determination of radial object distance, and more generally, object contour and shape.

This paper is divided into two main parts. The first is a survey of different methods by which the rat could determine the radial distance to an object. We highlight two novel methods: one based on measurement of bending moment and axial force at the vibrissa base, and a second based on a balance of moments between the actuating muscles and the reaction forces induced by the object contact. The second part of the paper discusses the application of Weber's law to radial distance determination with vibrissae. We show that for two particular models of radial distance determination, Weber's law predicts that the rat has the greatest sensing resolution close to the tip of the vibrissa. These modelling results could be tested with behavioural experiments that measure the perceptual acuity of the rat.

2. Methods for radial distance determination

In this section, we survey methods by which the rat might determine the radial distance of the object. We note the important adage that the nervous system tends to make use of any and all available information to enhance task performance; thus none of the methods exclude any of the others and the rat could potentially use all the methods simultaneously.

(a). The ‘vibrissa length’ method

The rat could estimate radial object distance based on implicit knowledge about the lengths of each of its vibrissae. Obviously, if the rat ensured that the tip of a particular vibrissa of known linear base-to-tip length made contact with an object, then it could infer that the object was located at a distance equal to that length. This strategy may work particularly well for the most rostral vibrissae, which tend to point concave forward during the course of a whisk, increasing the chances for tip contact [17,22]. Two problems arise with this method for distance determination. First, vibrissae are often damaged and may not maintain the same length from day to day. Second, rats can perform radial distance determination even without touching the tips of their vibrissae to the object [11], so a length-based method alone is not sufficient to explain the capability.

(b). The ‘comparative vibrissa length’ method

The rat could estimate radial object distance by comparing object contact across two or more vibrissae of known length. If a longer vibrissa made contact with an object whereas a shorter vibrissa did not, then the rat could infer that the object was located at a distance intermediate to the two vibrissae. A problem that arises with this method is that rats can perform radial distance determination with a single vibrissa, although their performance does improve as the number of vibrissae increases [11]. A second problem is that the position and orientation of the rat's head, as well as the morphology of the vibrissa array, will strongly influence whether a vibrissa will make contact with an object or not [22–24]. There are several geometric conditions in which a short vibrissa might contact an object, whereas a longer one might not [22]. This means that a cross-vibrissa comparison would provide reliable information about radial object distance only if the rat were able to interpret the signals in the context of a particular head position and orientation, as well as the angle of contact.

(c). The ‘angle-side-angle’ method

If the rat knew the angle θ_i (where i represents impact) at which its vibrissa made first contact with an object, then displaced the vibrissa base through a known distance and then re-determined θ_i, it could determine radial object distance using an ‘angle-side-angle’ (ASA) rule. The ASA rule says that a triangle is unique, given two angles and the enclosed side. The basic geometry of this computation is illustrated in figure 1b, and several variations on the approach are theoretically possible: (i) the vibrissa base could translate between two whisks owing to movement of the head and/or of the mystacial pad, (ii) the rat could make use of contact angles of two different vibrissae with two different base locations, using the inter-vibrissa spacing for the ‘side’ in ASA, (iii) during a single whisk and with the head fixed, the base of a single vibrissa could translate owing to movement of the mystacial pad, such that the angles and base locations of contact and detachment are different, and hence used to determine radial distance in the new head position. The rat could also use any combination of these three methods. A fundamental constraint on the ASA method is that it requires the rat to have an accurate estimate of θ_i before it can determine radial distance.

(d). The ‘vibration’ method

Vibrations at the vibrissa base have been shown to serve as important cues for texture discrimination [25–28]. It is also possible that vibrations could provide information about the radial distance at which the vibrissa made contact with an object.

Although the modes of vibration of the vibrissa (or any mechanical system) will be independent of the location at which the vibration is induced, the relative amplitudes of the modes will change with location. Therefore, it is theoretically possible for information about radial object distance to be coded by the relative amplitudes of two or more modes after a collision. In other words, each radial distance would be represented by a unique spectral ‘signature', involving ratios of two or more frequencies.

To determine whether these types of vibration cues could be uniquely related to radial object distance will require either precisely monitoring these vibrations with a strain gauge, or creating an accurate model of vibrissa dynamics. We recently created a model of vibrissa dynamics using variational integrator techniques [29]. Although this work is still in progress, all preliminary results suggest that there is no simple unique spectral signature associated with a particular radial distance and that it would be difficult for the rat to extract radial distance from such a complicated spectral profile.

(e). The ‘rotational compliance’ method during a vibrissa ‘tap’

Figure 1c illustrates the forces and bending moments that will be induced by contact with an object. We recently demonstrated that the rat could make use of bending near the vibrissa base to determine the radial distance to an object [15,19]. Our method was based on an approach first described by Kaneko et al. [30], and assumes that the vibrissa linearly tapers to a diameter of zero at the tip. When a vibrissa collides with an object, there is a monotonic relationship between the radial distance of object contact and the rate of change of moment 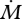Inline graphic for any given vibrissa velocity . Importantly, this means if the rat can keep track of 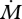and upon object contact, enough information will be present to uniquely determine radial object distance r.

The analytical relation between radial distance and moment for small angles is given by

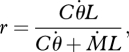2.1

where C is a constant related to vibrissa stiffness and L is the length of the vibrissa.

Importantly, this method can be extended so as to accommodate for the tendency of vibrissae to slip out of the plane of rotation [31], thus permitting radial distance determination while ‘whisking’ in any direction across the object. As will be further described in §2g, sensing moment in two dimensions also permits calculation of a local contour of the object.

(f). The ‘moment and axial force map’ method

The bending moment at the vibrissa base is by definition equal to the cross product of the vector pointing from the vibrissa base to the point of object contact and the force. If the rat were able to measure moment (M_z in figure 1c) and transverse force (F_y in figure 1c) independently, then determination of distance would be straightforward. Accounting for larger rotations, Scholz & Rahn [32] used a large-angle elastic beam model to show that moment and force (both transverse and axial) information can be combined to determine the contact point location for a cylindrical beam.

A problem with this method arises, however, if the rat cannot accurately measure transverse force independently of the bending moment. At the present time, it is not clear from ganglion recordings whether these parameters can be measured independently [16,33]. In contrast, it seems more likely that the rat would be able to measure axial force (F_x in figure 1c) independently of the bending moment [34].

We used numerical simulations to determine whether the rat could combine information about moment and axial force to determine radial distance. All simulations were performed in matlab v. 7.11 and made use of a previously established numerical cantilever beam model that remains accurate for large deflections [15,19,31]. We compared results between a straight linearly tapered vibrissa (r_base/r_tip = 20), and a straight cylindrical vibrissa (r_base/r_tip = 1). The results, shown in figure 2, reveal some important advantages of vibrissa taper.

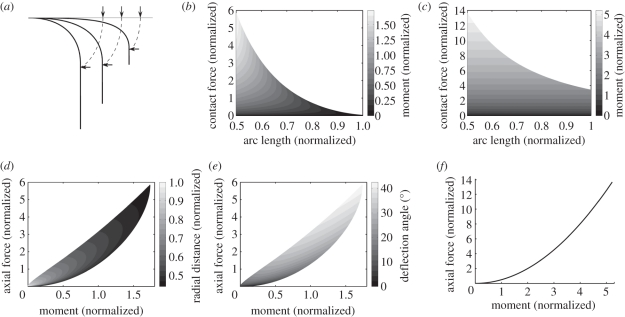
Figure 2a illustrates how simulations of beam bending were performed. We computed the beam shape and resulting forces (axial F_x and transverse F_y) and moment M_z as the beam was gradually deflected by applying increasingly large contact forces F_c at a range of arc length location S. As the beam is bent at each location, the force remains perpendicular to the beam at the point of contact, effectively simulating frictionless contact. The beam was deflected until the angle at the contact point α_c became 90°.

Figure 2b,c compares the bending moments generated for a given applied force for the tapered and cylindrical vibrissae. As expected, the tapered vibrissa (figure 2b) requires smaller applied forces to achieve α_c = 90° than does the cylindrical vibrissa (figure 2c), especially near the tip.

More interestingly, when we plot radial distance and deflection angle θ_d as functions of axial force and moment for the tapered vibrissa (figure 2d and e, respectively), we see that the mappings from (M_z, f_x) to r_c and θ_d are one-to-one (injective). For a particular moment on the x-axis, and a particular axial force value on the y-axis, there is a unique radial distance and deflection angle, indicated by a unique grey-scale value. Note that θ_d (the angle between the line tangent to the vibrissa base and the line from base to contact point) is not the same as contact angle θ_c (the absolute angle of vibrissa–object contact).

On the other hand, for the case of the cylindrical vibrissa shown in figure 2f, no such unique mapping exists. Instead, the mapping between axial force and moment is itself one-to-one, and each possible (M_z, f_x) maps to a range of possible radial distances and deflection angles. In other words, radial distance and deflection angle can be determined using a tapered vibrissa precisely because the relationship between F_x and M_z is not one-to-one.

Although real-world issues such as the intrinsic curvature of vibrissae, contact friction and three-dimensional (out-of-plane) deflections introduce complexities not considered here, the rat may nonetheless be able to exploit consistencies between how the combination of axial force and moment information relates to the position and shape of the object.

(g). ‘Sweeping’ methods

In contrast to ‘tapping’ methods (§2e), which are based on information obtained during only small rotations (θ_d is less than approx. 10°) beyond initial vibrissa–object contact, ‘sweeping’ methods incorporate information obtained as the rat pushes its vibrissae against the object through larger angles. In a previous study we developed a sweeping algorithm that iteratively updates its estimation of contact point location using only moment and pushing angle θ_p (change in θ since contact) information [35]. The algorithm relates changes in moment and pushing angle to changes in radial distance and deflection angle, at all times effectively relying on previous sensor information over the course of a whisk, as opposed to using a static mapping from sensor states to contact point location. The algorithm was developed and shown to work in hardware for cylindrical vibrissae, but could be adapted to tapered vibrissae. Regardless of whether such an algorithm is plausible for the rat, it is notable in its implicit reliance on past sensor information, hinting that recurrent connections may play critical roles in the perception of surface contours.

As mentioned in §2e, lateral sweep is characterized by slip of the vibrissa along the object outside the plane of rotation. This will occur when the object surface at the contact point is not perpendicular to the plane of vibrissa rotation, and the friction cone angle does not exceed the contact angle [31]. Although no explicit method to track the radial distance during lateral sweep has yet been developed, it is possible that the sweeping method described above could be adapted to do this, and we also note that a table-lookup method involving independent measurement of two-dimensional moment, two-dimensional transverse force and axial force (i.e. basically a three-dimensional extension to Scholz & Rahn's ‘brute force’ method [32]) could also work. This form of sweeping contact clearly provides the rat with useful information about surface contours and particularly the local slope of the object [31,36].

(h). The ‘balance of moments’ method

A particularly intriguing possibility is that the rat could determine radial distance from a balance of two bending moments: the moment exerted by the intrinsic muscle that moves the vibrissa and the moment owing to the deflection of the vibrissa. The concept is simple: the muscles can only apply limited moment to the base of the vibrissa. The closer the object is to the base, the faster bending moment will increase as the vibrissa rotates, and the less the vibrissa will be able to rotate past the angle of initial contact. Here, we use a numerical modelling approach to demonstrate how this effect can be exploited to determine radial distance.

During whisking behaviour, the maximum moment that the intrinsic muscle can exert on the follicle is a function of the vibrissa base angle, θ. The relationship between maximum muscle moment and theta is simply a property of the muscle, and is the same during both contact and non-contact whisking. Recent work by Hill et al. [37] has developed a model that can be shown to parametrize the moment–theta curve as:

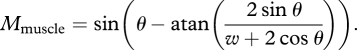2.2

In equation (2.2), θ is the follicle angle and w is a free parameter equal to one-half the ratio of follicle separation to follicle length, found to be about 1.25 at the centre of the pad. Note that the muscle moment at any given time could be under ‘volitional’ control (i.e. sub-maximal), and the balance of moments method could still work, as long that moment is ‘known’. For expository purposes, we consider only the maximum moment curve here.

The relationship between radial distance of object contact and the bending moment at the vibrissa base for small angle deflections was provided in equation (2.1). Rearranging equation (2.1) to solve for M yields:

2.3

Equations (2.2) and (2.3) are valid for small angles, and provide a physical intuition behind the ‘balance of moments’ method. In practice, we used a numerical model analogous to equation (2.3) (the same as was used in §2f) that remains accurate for large deflections, and that can predict when the vibrissa will flick past the object. We simulated the vibrissa to rotate against an object at different radial distances, ranging from 30 per cent of the vibrissa length to the tip.

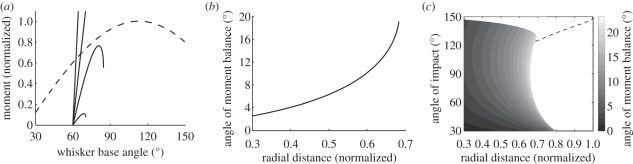
These M_z versus θ curves were then plotted on the same graph as the M_muscle versus θ curve of equation (2.2), as shown in figure 3a for four sample radial distances. The numerical data for M_z were scaled such that the vibrissa tended to flick past the object when contact occurred at around 70 per cent of vibrissa length. For the particular example shown in figure 3a, the vibrissa–object impact angle θ_i was set to 60°. Two of the curves intersected the muscle moment curve, meaning that the object effectively obstructed the movement of the vibrissa, and two curves did not, meaning that the vibrissa flicked past the object. We call the difference in angle between vibrissa–object impact (where the moment starts to ramp up) and the angle of intersection the ‘angle of moment balance’ θ_b. Figure 3b plots θ_b as a function of radial distance, showing that there is a monotonic relationship between r and θ_b. By repeating these steps for a range of impact angles, and assuming the range of whisking is between 30° and 150°, we obtain figure 3c. The final result in figure 3c shows that for any given angle of impact, radial distance can be determined based on how far the vibrissa rotated past initial contact. The method breaks down in the areas indicated by the white space, either because the vibrissa flicked past the object, or because the vibrissa protraction stopped (at 150°) before moment balance was achieved.

3. A role for weber's law in vibrissal sensing

As shown in §2f, the taper of the vibrissa allows determination of radial distance based on measurement of moment and axial force alone. Several other advantages of a tapered vibrissa have been suggested by Williams & Kramer [38], including a finer tip to sense minute surface features, reduced maximum protraction leading to increased spatial acuity during passive deflections, increased ease of movement of the vibrissa tip across surfaces, increased robustness of the resonant frequency to vibrissa breaks, and reduced ambiguity in radial distance caused by object compliance, curvature and friction.

One apparent drawback of vibrissa taper is that it leads to smaller moment and axial force signals, especially when contact is made near the vibrissa tip, as shown in figure 2b,c. When the amount of deflection is small, these small signals would seem to lead to poor resolution in determining radial distance.

However, this line of reasoning ignores Weber's observation that small changes in a stimulus are easier to detect when the absolute value of the stimulus magnitude is small [39].

(a). Weber's law

Weber's law holds that the resolution or ‘just noticeable difference’ (JND) of a stimulus intensity is proportional to the stimulus intensity [40]:

3.1

where I is the stimulus intensity, ΔI is the JND at stimulus intensity I and k_Weber is a constant of proportionality (the ‘Weber fraction’) that relates the two quantities [41]. Importantly, Weber's law applies only to the perception of properties that can be described as having a magnitude [40].

Weber's law is a particularly robust psychophysical phenomenon—having been shown to hold in tasks ranging from sensorimotor judgements of weight [39,41] to cognitive tasks involving estimates of the number of objects in a sample [42].

When testing Weber's law, however, the stimulus is generally assumed to have a relatively unobstructed path to the receptors. The rat vibrissal system is different because there is a purely mechanical transmission stage (the vibrissa) between stimulus and receptors. For the rat vibrissal system, we assume that Weber's law holds for the rat's perception of force and bending moment within the follicle, e.g. due to signal-dependent noise in mechanoreceptors in the follicle [43]. With this assumption, we investigate the effects of sensor mechanics, specifically vibrissa taper, on radial distance determination. We focus on the ‘rotational compliance’ and the ‘moment and axial force map’ methods described in §2e,f.

(b). Weber's law applied to the ‘rotational compliance method’

Before presenting results, it is instructive to anthropomorphize the task of radial distance determination in a manner analogous to one of Weber's original experiments. Weber tested his subjects' ability to discriminate between similar pairs of weights as a function of the weight, and found the results to be consistent with equation (3.1). For example, if the subject could distinguish between 1 and 1.1 kg, and no less, then Weber could reliably predict that the subject could also distinguish between 10 and 11 kg, and no less.

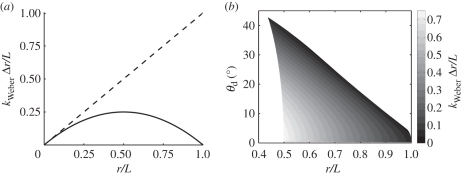
Now consider a similar experiment in which the subject is given two straight, flexible beams of equal length and base diameter, but one is cylindrical and the other is tapered. As the subject rotates the beams against objects at varying distances, s/he is able to feel associated differences in rotational compliance κ, which we define as κ = (dM/dθ)⁻¹ (figure 1d). The subject's task is to distinguish the smallest possible variations (JNDs) in rotational compliance, while blindfolded as the experimenter varies the radial distance to the object, and this is performed for a range of radial distances for both beams.

Given that Weber's law holds true for perception of moment as it does for force [44], we will find that the subject is effectively able to distinguish smaller differences in radial distance with a tapered beam than the cylindrical beam, especially near the tip. Given Weber's law, this result is intuitive: the smaller absolute magnitudes of compliance experienced by the subject as s/he rotates the tapered beam aid the ability to sense small changes in compliance, and hence small changes in radial distance. We will now show this effect analytically.

The key insight is that Weber's law applies to the stimulus that the rat directly measures (the compliance κ or rate of moment change Inline graphic ), but this is different from the variable that the rat wants to estimate (radial distance). In other words, Weber's law tells us , the JND of , but we want to know the JND of radial distance, Δr. The relationship between the two is

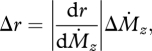3.2

where we take the absolute value of 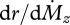Inline graphic because JND is a positive quantity by definition.

Equation (2.3) established the linearized cantilever equations for a tapered beam. Taking the derivative of both sides of equation (2.3) with respect to r yields:

3.3

Weber's law for 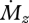Inline graphic states that:

3.4

Combining equations (3.3) and (3.4) with equation (3.2) yields:

3.5

Applying the same steps for the case of the cylindrical beam, we get

3.6

Figure 4a plots equations (3.5) and (3.6). The intuition provided by the anthropomorphized compliant beam experiment is validated by figure 4a, and the overall dependence of Δr on r is particularly noteworthy. Both the tapered and cylindrical beam have a Δr that approaches zero near the base, because the signal for 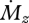Inline graphic becomes infinitely large at the base. Although an infinitely large value for 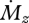is of course physically implausible, the tendency for Δr to approach zero as 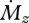increases will hold until either the rat is unable to generate the torque required to whisk past objects, or mechanoreceptors saturate.

The behaviour of Δr near the vibrissa base is similar for cylindrical and tapered vibrissae, but it is quite different near the vibrissa tip. For the cylindrical vibrissa, Δr becomes increasingly large as the signal for 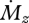Inline graphic approaches zero towards the tip. In contrast, for the tapered vibrissa, Δr decreases to zero near the tip, implying that the rat approaches the ability to sense infinitely small changes in r. Again, infinite resolution is physically impossible, but the tendency for Δr to decrease as 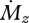Inline graphic decreases could hold down to the minimum response threshold of the mechanoreceptors. Thus, Weber's law predicts a smaller JND closer to the tip of a tapered, but not a cylindrical, vibrissa. Intriguingly, however, a study of haptic perception of torque in humans found that subjects could better localize a stimulus near the tip of a cylindrical rod than closer to the base [45].

(c). Weber's law applied to the ‘moment and axial force map’ method

Weber's law is generally framed as operating in a single dimension, but it can also be conceptualized to operate with a multi-dimensional stimulus magnitude (still mapping to uni-dimensional stimulus perception) [46]. Several of the methods for radial distance determination discussed in §2 depend on sensing two different stimuli, and thus serve as ideal domains to analyse perceptual scaling in two dimensions. Here, we focus on the moment and axial force mapping method.

Unfortunately, it seems there currently is not a widely accepted multi-dimensional version of Weber's law. Relatively few researchers have investigated the subject, and no specific formulations have been empirically shown to hold as general principles of perception [46]. Moreover, the ‘input’ stimuli under consideration will generally have different units of measure, necessitating the use of one or more scaling parameters. In addition, given that we are assuming that Weber's law originates at least in part from signal-dependent noise in the mechanoreceptors [43], an important consideration is the degree to which the noise is (un)correlated across dimensions. In view of these complexities, we limited our investigation to two simple cases in which the rat's sensitivity to changes in radial distance were either (i) dominated by its sensitivity to changes in moment, not changes in axial force, or conversely, (ii) dominated by its sensitivity to changes in axial force, not changes in moment.

Similar results were obtained in both cases, so here we present only the case in which moment sensitivity was dominant. In other words, we assume that regardless of the magnitudes of M_z and F_x at any given time, the JND of M_z, ΔM_z, is much smaller than the JND of F_x, ΔF_x.

The JND of r was computed using an equation very similar to equation (3.2):

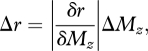3.7

where

3.8

Note that, in contrast to equation (3.2) where there is only one stimulus, we are taking the partial derivative of M_z because we are now dealing with two stimuli, with one (F_x) held constant. Both M_z and δr/δM_z were computed by interpolating the data in figure 2 using matlab's ‘griddata’ function, a triangle-based cubic interpolation algorithm that works with scattered data. Figure 4b displays the results: JND of r as a function of radial distance and deflection angle.

Two interesting trends emerge. First, we see that for any given θ_d, the JND of r becomes smaller as r increases, just as with the ‘rotational compliance’ method. More surprisingly, we see that for any given r, the JND of r decreases as θ_d increases (i.e. during a whisk), despite the fact that moment is concurrently increasing. This occurs because δr/δM_z increases faster than does moment (or ΔM_z in equation 3.7). The implication is that if the rat uses the moment and axial force method to determine radial distance, then the resolution will increase steadily as θ_d increases (depending on the extent of longitudinal slip, i.e. the curvature of the object). In principle, this would allow the rat to accurately determine the object contour with good (and perhaps increasing) resolution.

4. Discussion

When one or more of a rodent's vibrissae make unexpected contact with an object, the animal immediately tends to orient its head towards that object [47]. The animal's ability to perform this orienting movement necessarily implies that it can make use of the mechanical information obtained during contact to localize the object. The present paper is an exposition of the great diversity of possible methods the rat could use for radial distance estimation, several of which are supported by neurophysiological and or behavioural evidence, others of which are, as yet, supported only by plausibility arguments provided by theoretical models. It is important to note that the rat could be using different methods depending on situational context, and/or using any combination of methods simultaneously.

It is also important to note that the mathematical framework of contact points expressed in cylindrical coordinates is a useful construct, but there are many real-world aspects of whisking behaviour that it fails to adequately capture. For example, radial distance determination with a single vibrissa does not address how representations of contact point locations might be integrated into a perception of shape. This type of integrative processing would rely on neurons with multi-vibrissa receptive fields, found as early as the trigeminal nuclei. We also note that some of the analyses performed here assume the vibrissa movement to be occurring within a fixed plane (although not necessarily the horizontal plane), with a fixed base point, and with a monotonically increasing vibrissa base angle. All of these constraints are simplifications of observed whisking patterns [8,17,48]. Although further investigation is needed to quantify how these issues would affect the proposed methods of distance determination in various contexts, it seems unlikely that their potential effectiveness—all statistical correlations between perception and radial distance—would be completely abolished.

It may be useful to view the methods for radial distance determination in the context of Marr's three levels of analysis of the mind/brain: (i) computational theory, a description of the goals of the system; (ii) representation and algorithms, a description of the inputs, outputs and the algorithms underlying the system; and (iii) implementation, how the representations and algorithms are physically instantiated [49]. In this framework, the models presented here are at the level of algorithms. They describe the sensory data potentially available to the rat that at least implicitly contain sufficient information to determine radial distance.

We anticipate that one or more of these models should be instantiated in trigeminal neural circuitry. These models also are beginning to provide some insight into why vibrissae are tapered across species. For example, in §2f, we showed that vibrissa taper allows the determination of radial distance based on measurement of moment and axial force alone.

Importantly, regardless of whether Weber's law is exactly the correct relationship to express the rat's perceptual sensitivity to changes of force and moment, the true relationship is highly unlikely to be linear for the relevant ranges of magnitudes that the rat may experience, and this has important implications on the spatial resolution over the vibrissa array as the rat explores objects. Behavioural studies by Krupa et al. [11] have demonstrated that the rat can discriminate different radial distances, but no attempt has been made to quantify how the sensing resolution depends on radial distance itself. The present results suggest that such investigations could be useful in explaining the morphology of the array, the exploratory behaviours observed in the rat, and perhaps even the particular implementation of radial distance determination and discrimination in the nervous system of the rat.

References

1.Ahissar E., Arieli A. 2001. Figuring space by time. Neuron 32, 185–201 10.1016/S0896-6273(01)00466-4 (doi:10.1016/S0896-6273(01)00466-4) [DOI] [PubMed] [Google Scholar]
2.Diamond M. E., von Heimendahl M., Knutsen P. M., Kleinfeld D., Ahissar E. 2008. ‘Where’ and ‘what’ in the whisker sensorimotor system. Nat. Rev. Neurosci. 9, 601–612 10.1038/nrn2411 (doi:10.1038/nrn2411) [DOI] [PubMed] [Google Scholar]
3.Kleinfeld D., Ahissar E., Diamond M. E. 2006. Active sensation: insights from the rodent vibrissa sensorimotor system. Curr. Opin. Neurol. 16, 435–444 10.1016/j.conb.2006.06.009 (doi:10.1016/j.conb.2006.06.009) [DOI] [PubMed] [Google Scholar]
4.Welker W. I. 1964. Analysis of sniffing of the albino rat. Behaviour 22, 223–244 10.1163/156853964X00030 (doi:10.1163/156853964X00030) [DOI] [Google Scholar]
5.Berg R., Kleinfeld D. 2003. Rhythmic whisking in rat: retraction as well as protraction is under active muscular control. J. Neurophys. 89, 104–117 10.1152/jn.00600.2002 (doi:10.1152/jn.00600.2002) [DOI] [PubMed] [Google Scholar]
6.Brecht M., Preilowski B., Merzenich M. M. 1997. Functional architecture of the mystacial vibrissae. Behav. Brain Res. 84, 81–97 10.1016/S0166-4328(97)83328-1 (doi:10.1016/S0166-4328(97)83328-1) [DOI] [PubMed] [Google Scholar]
7.Hartmann M. J. 2001. Active sensing capabilities of the rat whisker system. Auton. Robot. 11, 249–254 10.1023/A:1012439023425 (doi:10.1023/A:1012439023425) [DOI] [Google Scholar]
8.Sellien H., Eshenroder D., Ebner F. 2005. Comparison of bilateral whisker movement in freely exploring and head-fixed adult rats. Somatosens. Mot. Res. 22, 97–114 10.1080/08990220400015375 (doi:10.1080/08990220400015375) [DOI] [PubMed] [Google Scholar]
9.Carvell G. E., Simons D. J. 1990. Biometric analyses of vibrissal tactile discrimination in the rat. J. Neurosci. 10, 2638–2648 [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Guic-Robles E., Valdivieso C., Guajardo G. 1989. Rats can learn a roughness discrimination using only their vibrissal system. Behav. Brain Res. 31, 285–289 10.1016/0166-4328(89)90011-9 (doi:10.1016/0166-4328(89)90011-9) [DOI] [PubMed] [Google Scholar]
11.Krupa D. J., Matell M. S., Brisben A. J., Oliveira L. M., Nicolelis M. A. L. 2001. Behavioral properties of the trigeminal somatosensory system in rats performing whisker-dependent tactile discriminations. J. Neurosci. 21, 5752–5763 [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Ma P. M., Woolsey T. A. 1984. Cytoarchitectonic correlates of the vibrissae in the medullary trigeminal complex of the mouse. Brain Res. 306, 374–379 10.1016/0006-8993(84)90390-1 (doi:10.1016/0006-8993(84)90390-1) [DOI] [PubMed] [Google Scholar]
13.Woolsey T. A., Welker C., Schwartz R. H. 1975. Comparative anatomical studies of the Sm 1 face cortex with special reference to the occurrence of ‘barrels’ in layer IV. J. Comp. Neurol. 164, 79–94 10.1002/cne.901640107 (doi:10.1002/cne.901640107) [DOI] [PubMed] [Google Scholar]
14.Curtis J. C., Kleinfeld D. 2009. Phase-to-rate transformations encode touch in cortical neurons of a scanning sensorimotor system. Nat. Neurosci. 12, 492–501 10.1038/nn.2283 (doi:10.1038/nn.2283) [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Birdwell J. A., Solomon J. H., Thajchayapong M., Taylor M. A., Cheely M., Towal R. B., Conradt J., Hartmann M. J. Z. 2007. Biomechanical models for radial distance determination by the rat vibrissal system. J. Neurophysiol. 98, 2439–2455 10.1152/jn.00707.2006 (doi:10.1152/jn.00707.2006) [DOI] [PubMed] [Google Scholar]
16.Szwed M., Bagdasarian K., Ahissar E. 2003. Encoding of vibrissal active touch. Neuron 40, 621–630 10.1016/S0896-6273(03)00671-8 (doi:10.1016/S0896-6273(03)00671-8) [DOI] [PubMed] [Google Scholar]
17.Knutsen P. M., Biess A., Ahissar E. 2008. Vibrissal kinematics in 3D: tight coupling of azimuth, elevation, and torsion across different whisking modes. Neuron 59, 35–42 10.1016/j.neuron.2008.05.013 (doi:10.1016/j.neuron.2008.05.013) [DOI] [PubMed] [Google Scholar]
18.Mameli O., Stanzani S., Mulliri G., Pellitteri R., Caria M., Russo A., DeRiu P. 2010. Role of the trigeminal mesencephalic nucleus in rat whisker pad proprioception. Behav. Brain Funct. 6, (doi:10.1186/1744-9081-1186-1169) [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Solomon J. H., Hartmann M. J. 2006. Robotic whiskers used to sense features. Nature 443, 525. 10.1038/443525a (doi:10.1038/443525a) [DOI] [PubMed] [Google Scholar]
20.Ebara S., Kumamoto K., Matsuura T., Mazurkiewicz J. E., Rice F. L. 2002. Similarities and differences in the innervation of mystacial vibrissal follicle-sinus complexes in the rat and cat: a confocal microscopic study. J. Comp. Neurol. 449, 103–119 10.1002/cne.10277 (doi:10.1002/cne.10277) [DOI] [PubMed] [Google Scholar]
21.Zucker E., Welker W. I. 1969. Coding of somatic sensory input by vibrissae neurons in the rat's trigeminal ganglion. Brain Res. 12, 138–156 10.1016/0006-8993(69)90061-4 (doi:10.1016/0006-8993(69)90061-4) [DOI] [PubMed] [Google Scholar]
22.Towal R. B., Quist B., Gopal V., Solomon J. H., Hartmann M. J. Z. 2011. The morphology of the rat vibrissal array: a model for quantifying spatiotemporal patterns of whisker-object contact. PLoS Comput. Biol. 7, e1001120. 10.1371/journal.pcbi.1001120 (doi:10.1371/journal.pcbi.1001120) [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Grant R. A., Mitchinson B., Fox C. W., Prescott T. J. 2009. Active touch sensing in the rat: anticipatory and regulatory control of whisker movements during surface exploration. J. Neurophysiol. 101, 862–874 10.1152/jn.90783.2008 (doi:10.1152/jn.90783.2008) [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Mitchinson B., Martin C. J., Grant R. A., Prescott T. J. 2007. Feedback control in active sensing: rat exploratory whisking is modulated by environmental contact. Proc. R. Soc. B 274, 1035–1041 10.1098/rspb.2006.0347 (doi:10.1098/rspb.2006.0347) [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Diamond M. E., von Heimendahl M., Arabzadeh E. 2008. Whisker-mediated texture discrimination. PLoS Biol. 6, e220. 10.1371/journal.pbio.0060220 (doi:10.1371/journal.pbio.0060220) [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Lottem E., Azouz R. 2009. Mechanisms of tactile information transmission through whisker vibrations. J. Neurosci. 29, 11 686–11 697 10.1523/jneurosci.0705-09.2009 (doi:10.1523/jneurosci.0705-09.2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Ritt J. T., Andermann M. L., Moore C. I. 2008. Embodied information processing: vibrissa mechanics and texture features shape micromotions in actively sensing rats. Neuron 57, 599–613 10.1016/j.neuron.2007.12.024 (doi:10.1016/j.neuron.2007.12.024) [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Wolfe J., Hill D. N., Pahlavan S., Drew P. J., Kleinfeld D., Feldman D. E. 2008. Texture coding in the rat whisker system: slip-stick versus differential resonance. PLoS Biol. 6, e215. 10.1371/journal.pbio.0060215 (doi:10.1371/journal.pbio.0060215) [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Quist B. W., Seghete V., Murphey T. D., Hartmann M. J. Z. 2011. Modeling forces and moments at the vibrissal base during natural motion and collisions. Poster presentation at Royal Society Theo Murphy meeting ‘active tactile sensing’, Chicheley Hall, UK, 31 January–2 February 2011 [Google Scholar]
30.Kaneko M., Kanayama N., Tsuji T. 1998. Active antenna for contact sensing. IEEE Trans. Robot. Aut. 14, 278–291 10.1109/70.681246 (doi:10.1109/70.681246) [DOI] [Google Scholar]
31.Solomon J. H., Hartmann M. J. Z. 2008. Artificial whiskers suitable for array implementation: accounting for lateral slip and surface friction. IEEE Trans. Robot. 24, 1157–1167 10.1109/TRO.2008.2002562 (doi:10.1109/TRO.2008.2002562) [DOI] [Google Scholar]
32.Scholz G. R., Rahn C. D. 2004. Profile sensing with an actuated whisker. IEEE Trans. Robot. Aut. 20, 124–127 10.1109/TRA.2003.820864 (doi:10.1109/TRA.2003.820864) [DOI] [Google Scholar]
33.Leiser S. C., Moxon K. A. 2007. Responses of trigeminal ganglion neurons during natural whisking behaviors in the awake rat. Neuron 53, 117–133 10.1016/j.neuron.2006.10.036 (doi:10.1016/j.neuron.2006.10.036) [DOI] [PubMed] [Google Scholar]
34.Stuttgen M. C., Kullmann S., Schwarz C. 2008. Responses of rat trigeminal ganglion neurons to longitudinal whisker stimulation. J. Neurophysiol. 100, 1879–1884 10.1152/jn.90511.2008 (doi:10.1152/jn.90511.2008) [DOI] [PubMed] [Google Scholar]
35.Solomon J. H., Hartmann M. J. Z. 2010. Extracting object contours with the sweep of a robotic whisker using torque information. Int. J. Robot. Res. 29, 1233–1245 10.1177/0278364908104468 (doi:10.1177/0278364908104468) [DOI] [Google Scholar]
36.Kim D., Möller R. 2007. Biomimetic whiskers for shape recognition. Rob. Auto. Sys. 55, 229–243 10.1016/j.robot.2006.08.001 (doi:10.1016/j.robot.2006.08.001) [DOI] [Google Scholar]
37.Hill D. N., Bermejo R., Zeigler H. P., Kleinfeld D. 2008. Biomechanics of the vibrissa motor plant in rat: rhythmic whisking consists of triphasic neuromuscular activity. J. Neurosci. 28, 3438–3455 10.1523/jneurosci.5008-07.2008 (doi:10.1523/jneurosci.5008-07.2008) [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Williams C. M., Kramer E. M. 2010. The advantages of a tapered whisker. PLoS ONE 5, e8806. 10.1371/journal.pone.0008806 (doi:10.1371/journal.pone.0008806) [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Weber E. H. 1996. E.H. Weber on the tactile senses (eds Ross H. E., Murray D. J.), 2nd edn. Hove: Erlbaum (UK) Taylor & Francis; (Eds Trans.) [Google Scholar]
40.Gescheider G. 1997. Psychophysics: the fundamentals. Mahwah, NJ: Lawrence Erlbaum Associates [Google Scholar]
41.Brodie E., Ross H. 1984. Sensorimotor mechanisms in weight discrimination. Percept. Psychophys. 36, 477–481 10.3758/BF03207502 (doi:10.3758/BF03207502) [DOI] [PubMed] [Google Scholar]
42.Jordan K., Brannon E. 2006. Weber's law influences numerical representations in rhesus macaques (Macaca mulatta). Anim. Cogn. 9, 159–172 10.1007/s10071-006-0017-8 (doi:10.1007/s10071-006-0017-8) [DOI] [PubMed] [Google Scholar]
43.Krueger L. E. 1989. Reconciling Fechner and Stevens: toward a unified psychophysical law. Behav. Brain Sci. 12, 251–267 10.1017/S0140525X0004855X (doi:10.1017/S0140525X0004855X) [DOI] [Google Scholar]
44.Woodruff B., Helson H. 1965. Torque: a new dimension in tactile-kinesthetic sensitivity. Am. J. Psychol. 78, 271–277 10.2307/1420500 (doi:10.2307/1420500) [DOI] [PubMed] [Google Scholar]
45.Wang S., Srinivasan M. A. 2003. The role of torque in haptic perception of object location in virtual environments. In 11th Symp. on Haptic Interfaces for Virtual Environment and Teleoperator Systems (HAPTICS'03), Los Angeles, CA, 22–23 March 2003. pp. 302–309 Los Angeles, CA: IEEE Computer Society. [Google Scholar]
46.Drösler J. 2000. An n-dimensional Weber law and the corresponding Fechner law. J. Math. Psychol. 44, 330–335 10.1006/jmps.1999.1242 (doi:10.1006/jmps.1999.1242) [DOI] [PubMed] [Google Scholar]
47.Benedetti F. 1995. Orienting behavior and superior colliculus sensory representations in mice with the vibrissae bent into the contralateral hemispace. Eur. J. Neurosci. 7, 1512–1519 10.1111/j.1460-9568.1995.tb01146.x (doi:10.1111/j.1460-9568.1995.tb01146.x) [DOI] [PubMed] [Google Scholar]
48.Towal R. B., Hartmann M. J. Z. 2008. Variability in velocity profiles during the free-air whisking behavior of unrestrained rats. J. Neurophysiol. 100, 740–752 10.1152/jn.01295.2007 (doi:10.1152/jn.01295.2007) [DOI] [PubMed] [Google Scholar]
49.Marr D. Vision. A computational investigation into the human representation and processing of visual information. San Francisco, CA:: W.H. Freeman and Company; 1982. [Google Scholar]

[RSTB20110166C1] 1.Ahissar E., Arieli A. 2001. Figuring space by time. Neuron 32, 185–201 10.1016/S0896-6273(01)00466-4 (doi:10.1016/S0896-6273(01)00466-4) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C2] 2.Diamond M. E., von Heimendahl M., Knutsen P. M., Kleinfeld D., Ahissar E. 2008. ‘Where’ and ‘what’ in the whisker sensorimotor system. Nat. Rev. Neurosci. 9, 601–612 10.1038/nrn2411 (doi:10.1038/nrn2411) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C3] 3.Kleinfeld D., Ahissar E., Diamond M. E. 2006. Active sensation: insights from the rodent vibrissa sensorimotor system. Curr. Opin. Neurol. 16, 435–444 10.1016/j.conb.2006.06.009 (doi:10.1016/j.conb.2006.06.009) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C4] 4.Welker W. I. 1964. Analysis of sniffing of the albino rat. Behaviour 22, 223–244 10.1163/156853964X00030 (doi:10.1163/156853964X00030) [DOI] [Google Scholar]

[RSTB20110166C5] 5.Berg R., Kleinfeld D. 2003. Rhythmic whisking in rat: retraction as well as protraction is under active muscular control. J. Neurophys. 89, 104–117 10.1152/jn.00600.2002 (doi:10.1152/jn.00600.2002) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C6] 6.Brecht M., Preilowski B., Merzenich M. M. 1997. Functional architecture of the mystacial vibrissae. Behav. Brain Res. 84, 81–97 10.1016/S0166-4328(97)83328-1 (doi:10.1016/S0166-4328(97)83328-1) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C7] 7.Hartmann M. J. 2001. Active sensing capabilities of the rat whisker system. Auton. Robot. 11, 249–254 10.1023/A:1012439023425 (doi:10.1023/A:1012439023425) [DOI] [Google Scholar]

[RSTB20110166C8] 8.Sellien H., Eshenroder D., Ebner F. 2005. Comparison of bilateral whisker movement in freely exploring and head-fixed adult rats. Somatosens. Mot. Res. 22, 97–114 10.1080/08990220400015375 (doi:10.1080/08990220400015375) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C9] 9.Carvell G. E., Simons D. J. 1990. Biometric analyses of vibrissal tactile discrimination in the rat. J. Neurosci. 10, 2638–2648 [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C10] 10.Guic-Robles E., Valdivieso C., Guajardo G. 1989. Rats can learn a roughness discrimination using only their vibrissal system. Behav. Brain Res. 31, 285–289 10.1016/0166-4328(89)90011-9 (doi:10.1016/0166-4328(89)90011-9) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C11] 11.Krupa D. J., Matell M. S., Brisben A. J., Oliveira L. M., Nicolelis M. A. L. 2001. Behavioral properties of the trigeminal somatosensory system in rats performing whisker-dependent tactile discriminations. J. Neurosci. 21, 5752–5763 [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C12] 12.Ma P. M., Woolsey T. A. 1984. Cytoarchitectonic correlates of the vibrissae in the medullary trigeminal complex of the mouse. Brain Res. 306, 374–379 10.1016/0006-8993(84)90390-1 (doi:10.1016/0006-8993(84)90390-1) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C13] 13.Woolsey T. A., Welker C., Schwartz R. H. 1975. Comparative anatomical studies of the Sm 1 face cortex with special reference to the occurrence of ‘barrels’ in layer IV. J. Comp. Neurol. 164, 79–94 10.1002/cne.901640107 (doi:10.1002/cne.901640107) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C14] 14.Curtis J. C., Kleinfeld D. 2009. Phase-to-rate transformations encode touch in cortical neurons of a scanning sensorimotor system. Nat. Neurosci. 12, 492–501 10.1038/nn.2283 (doi:10.1038/nn.2283) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C15] 15.Birdwell J. A., Solomon J. H., Thajchayapong M., Taylor M. A., Cheely M., Towal R. B., Conradt J., Hartmann M. J. Z. 2007. Biomechanical models for radial distance determination by the rat vibrissal system. J. Neurophysiol. 98, 2439–2455 10.1152/jn.00707.2006 (doi:10.1152/jn.00707.2006) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C16] 16.Szwed M., Bagdasarian K., Ahissar E. 2003. Encoding of vibrissal active touch. Neuron 40, 621–630 10.1016/S0896-6273(03)00671-8 (doi:10.1016/S0896-6273(03)00671-8) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C17] 17.Knutsen P. M., Biess A., Ahissar E. 2008. Vibrissal kinematics in 3D: tight coupling of azimuth, elevation, and torsion across different whisking modes. Neuron 59, 35–42 10.1016/j.neuron.2008.05.013 (doi:10.1016/j.neuron.2008.05.013) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C18] 18.Mameli O., Stanzani S., Mulliri G., Pellitteri R., Caria M., Russo A., DeRiu P. 2010. Role of the trigeminal mesencephalic nucleus in rat whisker pad proprioception. Behav. Brain Funct. 6, (doi:10.1186/1744-9081-1186-1169) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C19] 19.Solomon J. H., Hartmann M. J. 2006. Robotic whiskers used to sense features. Nature 443, 525. 10.1038/443525a (doi:10.1038/443525a) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C20] 20.Ebara S., Kumamoto K., Matsuura T., Mazurkiewicz J. E., Rice F. L. 2002. Similarities and differences in the innervation of mystacial vibrissal follicle-sinus complexes in the rat and cat: a confocal microscopic study. J. Comp. Neurol. 449, 103–119 10.1002/cne.10277 (doi:10.1002/cne.10277) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C21] 21.Zucker E., Welker W. I. 1969. Coding of somatic sensory input by vibrissae neurons in the rat's trigeminal ganglion. Brain Res. 12, 138–156 10.1016/0006-8993(69)90061-4 (doi:10.1016/0006-8993(69)90061-4) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C22] 22.Towal R. B., Quist B., Gopal V., Solomon J. H., Hartmann M. J. Z. 2011. The morphology of the rat vibrissal array: a model for quantifying spatiotemporal patterns of whisker-object contact. PLoS Comput. Biol. 7, e1001120. 10.1371/journal.pcbi.1001120 (doi:10.1371/journal.pcbi.1001120) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C23] 23.Grant R. A., Mitchinson B., Fox C. W., Prescott T. J. 2009. Active touch sensing in the rat: anticipatory and regulatory control of whisker movements during surface exploration. J. Neurophysiol. 101, 862–874 10.1152/jn.90783.2008 (doi:10.1152/jn.90783.2008) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C24] 24.Mitchinson B., Martin C. J., Grant R. A., Prescott T. J. 2007. Feedback control in active sensing: rat exploratory whisking is modulated by environmental contact. Proc. R. Soc. B 274, 1035–1041 10.1098/rspb.2006.0347 (doi:10.1098/rspb.2006.0347) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C25] 25.Diamond M. E., von Heimendahl M., Arabzadeh E. 2008. Whisker-mediated texture discrimination. PLoS Biol. 6, e220. 10.1371/journal.pbio.0060220 (doi:10.1371/journal.pbio.0060220) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C26] 26.Lottem E., Azouz R. 2009. Mechanisms of tactile information transmission through whisker vibrations. J. Neurosci. 29, 11 686–11 697 10.1523/jneurosci.0705-09.2009 (doi:10.1523/jneurosci.0705-09.2009) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C27] 27.Ritt J. T., Andermann M. L., Moore C. I. 2008. Embodied information processing: vibrissa mechanics and texture features shape micromotions in actively sensing rats. Neuron 57, 599–613 10.1016/j.neuron.2007.12.024 (doi:10.1016/j.neuron.2007.12.024) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C28] 28.Wolfe J., Hill D. N., Pahlavan S., Drew P. J., Kleinfeld D., Feldman D. E. 2008. Texture coding in the rat whisker system: slip-stick versus differential resonance. PLoS Biol. 6, e215. 10.1371/journal.pbio.0060215 (doi:10.1371/journal.pbio.0060215) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C29] 29.Quist B. W., Seghete V., Murphey T. D., Hartmann M. J. Z. 2011. Modeling forces and moments at the vibrissal base during natural motion and collisions. Poster presentation at Royal Society Theo Murphy meeting ‘active tactile sensing’, Chicheley Hall, UK, 31 January–2 February 2011 [Google Scholar]

[RSTB20110166C30] 30.Kaneko M., Kanayama N., Tsuji T. 1998. Active antenna for contact sensing. IEEE Trans. Robot. Aut. 14, 278–291 10.1109/70.681246 (doi:10.1109/70.681246) [DOI] [Google Scholar]

[RSTB20110166C31] 31.Solomon J. H., Hartmann M. J. Z. 2008. Artificial whiskers suitable for array implementation: accounting for lateral slip and surface friction. IEEE Trans. Robot. 24, 1157–1167 10.1109/TRO.2008.2002562 (doi:10.1109/TRO.2008.2002562) [DOI] [Google Scholar]

[RSTB20110166C32] 32.Scholz G. R., Rahn C. D. 2004. Profile sensing with an actuated whisker. IEEE Trans. Robot. Aut. 20, 124–127 10.1109/TRA.2003.820864 (doi:10.1109/TRA.2003.820864) [DOI] [Google Scholar]

[RSTB20110166C33] 33.Leiser S. C., Moxon K. A. 2007. Responses of trigeminal ganglion neurons during natural whisking behaviors in the awake rat. Neuron 53, 117–133 10.1016/j.neuron.2006.10.036 (doi:10.1016/j.neuron.2006.10.036) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C34] 34.Stuttgen M. C., Kullmann S., Schwarz C. 2008. Responses of rat trigeminal ganglion neurons to longitudinal whisker stimulation. J. Neurophysiol. 100, 1879–1884 10.1152/jn.90511.2008 (doi:10.1152/jn.90511.2008) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C35] 35.Solomon J. H., Hartmann M. J. Z. 2010. Extracting object contours with the sweep of a robotic whisker using torque information. Int. J. Robot. Res. 29, 1233–1245 10.1177/0278364908104468 (doi:10.1177/0278364908104468) [DOI] [Google Scholar]

[RSTB20110166C36] 36.Kim D., Möller R. 2007. Biomimetic whiskers for shape recognition. Rob. Auto. Sys. 55, 229–243 10.1016/j.robot.2006.08.001 (doi:10.1016/j.robot.2006.08.001) [DOI] [Google Scholar]

[RSTB20110166C37] 37.Hill D. N., Bermejo R., Zeigler H. P., Kleinfeld D. 2008. Biomechanics of the vibrissa motor plant in rat: rhythmic whisking consists of triphasic neuromuscular activity. J. Neurosci. 28, 3438–3455 10.1523/jneurosci.5008-07.2008 (doi:10.1523/jneurosci.5008-07.2008) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C38] 38.Williams C. M., Kramer E. M. 2010. The advantages of a tapered whisker. PLoS ONE 5, e8806. 10.1371/journal.pone.0008806 (doi:10.1371/journal.pone.0008806) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20110166C39] 39.Weber E. H. 1996. E.H. Weber on the tactile senses (eds Ross H. E., Murray D. J.), 2nd edn. Hove: Erlbaum (UK) Taylor & Francis; (Eds Trans.) [Google Scholar]

[RSTB20110166C40] 40.Gescheider G. 1997. Psychophysics: the fundamentals. Mahwah, NJ: Lawrence Erlbaum Associates [Google Scholar]

[RSTB20110166C41] 41.Brodie E., Ross H. 1984. Sensorimotor mechanisms in weight discrimination. Percept. Psychophys. 36, 477–481 10.3758/BF03207502 (doi:10.3758/BF03207502) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C42] 42.Jordan K., Brannon E. 2006. Weber's law influences numerical representations in rhesus macaques (Macaca mulatta). Anim. Cogn. 9, 159–172 10.1007/s10071-006-0017-8 (doi:10.1007/s10071-006-0017-8) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C43] 43.Krueger L. E. 1989. Reconciling Fechner and Stevens: toward a unified psychophysical law. Behav. Brain Sci. 12, 251–267 10.1017/S0140525X0004855X (doi:10.1017/S0140525X0004855X) [DOI] [Google Scholar]

[RSTB20110166C44] 44.Woodruff B., Helson H. 1965. Torque: a new dimension in tactile-kinesthetic sensitivity. Am. J. Psychol. 78, 271–277 10.2307/1420500 (doi:10.2307/1420500) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C45] 45.Wang S., Srinivasan M. A. 2003. The role of torque in haptic perception of object location in virtual environments. In 11th Symp. on Haptic Interfaces for Virtual Environment and Teleoperator Systems (HAPTICS'03), Los Angeles, CA, 22–23 March 2003. pp. 302–309 Los Angeles, CA: IEEE Computer Society. [Google Scholar]

[RSTB20110166C46] 46.Drösler J. 2000. An n-dimensional Weber law and the corresponding Fechner law. J. Math. Psychol. 44, 330–335 10.1006/jmps.1999.1242 (doi:10.1006/jmps.1999.1242) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C47] 47.Benedetti F. 1995. Orienting behavior and superior colliculus sensory representations in mice with the vibrissae bent into the contralateral hemispace. Eur. J. Neurosci. 7, 1512–1519 10.1111/j.1460-9568.1995.tb01146.x (doi:10.1111/j.1460-9568.1995.tb01146.x) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C48] 48.Towal R. B., Hartmann M. J. Z. 2008. Variability in velocity profiles during the free-air whisking behavior of unrestrained rats. J. Neurophysiol. 100, 740–752 10.1152/jn.01295.2007 (doi:10.1152/jn.01295.2007) [DOI] [PubMed] [Google Scholar]

[RSTB20110166C49] 49.Marr D. Vision. A computational investigation into the human representation and processing of visual information. San Francisco, CA:: W.H. Freeman and Company; 1982. [Google Scholar]

PERMALINK

Radial distance determination in the rat vibrissal system and the effects of Weber's law

Joseph H Solomon

Mitra J Z Hartmann

Abstract

1. Introduction

Figure 1.