Human perception of shape from touch

Abstract

In this paper, I focus on the role of active touch in three aspects of shape perception and discrimination studies. First an overview is given of curvature discrimination experiments. The most prominent result is that first-order stimulus information (that is, the difference in attitude or slope over the stimulus) is the dominant factor determining the curvature threshold. Secondly, I compare touch under bimanual and two-finger performance with unimanual and one-finger performance. Consistently, bimanual or two-finger performance turned out to be worse. The most likely explanation for the former finding is that a loss of accuracy during intermanual comparisons is owing to interhemispheric relay. Thirdly, I address the presence of strong after-effects after just briefly touching a shape. These after-effects have been measured and studied in various conditions (such as, static, dynamic, transfer to other hand or finger). Combination of the results of these studies leads to the insight that there are possibly different classes of after-effect: a strong after-effect, caused by immediate contact with the stimulus, that does only partially transfer to the other hand, and one much less strong after-effect, caused by moving over the stimulus for a certain period, which shows a full transfer to other fingers.

1. Perception of shape by touch

The sense of touch is of major importance for the perception of three-dimensional shapes. In actively dealing with objects, both the cuteanous sense (input from receptors in the skin) and the kinesthetic sense (input from receptors located in muscles, tendons, and joints) convey information. Tactual perception originating from such combined inputs is termed haptic perception [1]. The present paper is focused on active haptic perception.

The importance of haptic perception was already recognized by Katz in 1925 [2], but for a long time hardly any quantitative data on haptic perception of shape existed. Gibson [3] was one of the first to conduct a small study on matching and discrimination using 10 unfamiliar sculptured objects and he concluded that subjects were well able to distinguish such objects by touch. In 1985, Klatzky et al. [4] tested subjects on the identification of familiar objects using touch alone, and they concluded that active haptic object recognition can be both rapid and accurate. Comparing this paper with studies on visual perception published around the same time illustrates the difference in the state of the art that existed between the two research fields: haptic perception research had just started, whereas for visual perception of objects advanced theories had already been proposed. Although Roland & Mortensen [5] made a start at modelling somatosensory detection, clearly there was a need for more quantitative research on the haptic perception of shape.

In Utrecht, there existed a long tradition of quantitative visual perception research and in the early nineties, we decided to use this expertise to advance knowledge of haptic perception. We started a line of research using mathematically well-defined shapes, so that the stimulus properties would be known. Being situated in the Department of Physics, we had recourse to a computer-controlled milling machine in the physics' workshop to create stimuli (figure 1). The first study consisted of a shape identification experiment [6], using the shapes in figure 1a. The stimuli were all doubly curved quadric surfaces, such as saddles, cylinders and ellipsoids, which were systematically chosen along a shape-index scale (for further details, see §3a). Such shapes were chosen because mathematically every surface can locally be approximated by one of these shapes. Subjects were first made familiar with this scale, which turned out to be very intuitive and easy to use. Subsequently, subjects were asked to identify shape by active touch alone. The results showed that hyperbolic surfaces (i.e. saddles) were somewhat harder to identify than elliptic ones. Moreover, concave shapes led to a larger spread in answers. As there was a significant interaction between shape and curvature, these two findings were mainly found for the smaller curvatures. Finally, the overall curvature of the shapes had a direct influence on identification performance: the more pronounced the curvatures, the better performance.

Figure 1.

Stimuli used in the various studies. (a) Hand-sized convex and concave paraboloids [6–12]; (b) cupboard full of larger-than-hand-size cylindrical stimuli [13]; (c) zeroth- and first-order stimuli [14] and second-order stimuli [10,14–16]; (d) Gaussian-shaped stimuli of various scales (10, 30, 90 cm) [17]; (e) finger-sized stimuli with spherically curved top [18]; (f) blocks and cylinders with different cross sections but with identical perimeter [19]; (g) stimulus with cylindrically curved sides, index finger-thumb condition [20]; (h) like (g), two index fingers condition [20].

A subsequent study [7] used a subset of the stimuli of the former study in a shape discrimination experiment. Subjects were presented with two shapes simultaneously and by actively exploring the stimuli they had to decide whether or not they were identical in shape. Again, performance was influenced by overall curvature (better performance with higher curvatures), but performance did not depend on the shape of the stimuli. The shape dependence reported in Kappers et al. [6] was found for stimuli with smaller curvatures than those used in Kappers et al. [7], so the outcomes do not contradict each other.

Using another subset of the stimulus set shown in figure 1a, namely the cylindrically curved surfaces, a curvature discrimination experiment was performed [8]. Subjects had to decide which of a pair of curved surfaces had the higher curvature. Again, exploration time and strategy were free. In psychophysical experiments, it is very common to find that discrimination thresholds are constant if expressed in relative differences. This finding is known as Weber's Law. In this experiment, performance was quite good for most curvatures, but for the higher curvatures performance was nearly perfect, resulting in a ceiling effect. Although this was somewhat unfortunate, it did show that curvature discrimination did not follow Weber's Law, as the relative curvature differences used in the experiment were constant. Apparently, performance was relatively better for higher curvatures.

Although these studies gave insights into haptic shape perception, it was felt that more detailed studies using better controlled exploration were needed. The studies were therefore continued along three separate but strongly related lines. First, a series of studies focused on perception of curvature in various conditions. Fundamental knowledge about the haptic perception of curvature is necessary to begin to understand the perception of shapes. Second, in the first few of these curvature discrimination experiments, it was found that bimanual performance was worse than unimanual performance, whereas the opposite was expected [8]. When comparing shapes or curvatures with one hand, there is necessarily a memory component involved, while this is not the case if the stimuli can be compared directly by touching them simultaneously. Knowing more about bimanual or two-finger performance might help in understanding the mechanisms that are involved in haptic perception. Third, coincidentally, it was found that touching a surface has a remarkably strong influence on how the next surface that is touched will be perceived. Curvature experiments in which subjects had to decide whether a shape was concave or convex led to very noisy results. This was only understood when we realized that haptic perception is susceptible to significant after-effects [9]. We therefore decided to investigate this in a separate series of studies. The next three sections will present, compare and discuss this research in detail.

2. Perception of curvature by touch

Hunter [21] was one of the first to study the detection of curvature in a quantitative way (details about the stimuli and exploration method used in this and subsequent studies can be found in table 1). He concluded that what subjects perceived as straight was actually curved and that this effect was more pronounced for sighted than for blind subjects. A similar study was performed by Davidson [22]. His main focus was on comparison of performance of blind and sighted subjects. Like Hunter [21], he concluded that blind observers made more accurate judgements than sighted subjects. However, when sighted subjects were instructed to use the strategies spontaneously used by blind observers, their performance also became more accurate. This conclusion was confirmed in a follow-up study [23].

Table 1.

Curvature discrimination and matching studies. Curvature is expressed in 1 m⁻¹.

study	curvature range	stimulus size	exploration	stimulus	figure
[8]a	−5.7–5.7	20 cm	dynamic	cylinders	1a
[21]b	−2–2	20 cm	dynamic	strips
[22]b	−1.6–1.6	20 cm	dynamic	strips
[23]b	−1.6–1.6	20 cm	dynamic	strips
[24]b	0–19	4 cm	dynamic	plano-convex lenses
[25]	−48.8–694	1 cm	passive	spherically curved
[26]	154–397	0.5 cm	passive	spherically curved
[27]a	−1.8–1.8	20 cm	static	strips	1c (right)
[14]a	−4–4	20 cm	static, dynamic	strips	1c (right)
[10]a	−4–4	20 cm	static	0th, 1st, 2nd order	1c
[10]a	−2.83–2.83	20 cm	static	cylinders	1a
[10]a	−2.83–2.83	20 cm	static	quadrics	1a
[15]	−4–4	20 cm	dynamic	0th, 1st, 2nd order
[19]a	20–46	7−7.3 cm	static, dynamic	cylinders	1e
[17]a		150 µm−24 cm	dynamic	Gaussian strips	1d
[13]a	1.18–4.05	29 cm	dynamic	cylinders	1b
[20]a	20–46	3 cm	dynamic	curved blocks	1g,h

^aStudies done in Utrecht.

^bCurvatures estimated from stimulus description.

Gordon & Morrison [24] used active touch to study curvature detection and discrimination using small stimuli. They showed that if the thresholds were expressed as base-to-peak height divided by half the stimulus length, performance is independent of stimulus length. In other words, the threshold for curvature is determined by the overall gradient of the stimulus. Goodwin et al. [25] decided that the results of the previous studies were too hard to interpret, because in active exploration the roles of sensory and motor afferents cannot be distinguished. Therefore, they used passive touch pressing curved stimuli on immobilized finger pads with a predetermined force. In such an experiment, only cutaneous receptors can play a role. For highly curved stimuli, they found that a 10 per cent difference in curvature could be discriminated (in other words, the Weber fraction was about 0.1). They also reported a correlation between the contact area and estimated curvature. In a subsequent study by Goodwin & Wheat [26], contact area between finger and stimulus was kept constant to exclude that contact area determined the discrimination threshold. Still discrimination thresholds remained about the same, which indicated that the mere stimulation of a skin area was not the factor determining the threshold. Importantly, they also found that discrimination performance improved if the contact area was larger. This latter finding is consistent with the results in Gordon & Morison [24] using active touch: increasing the contact area results in a larger overall gradient, which predicts better performance.

Goodwin et al. [28,29] also studied the neural correlate of curvature. They pressed spherical surfaces on the fingerpads of monkeys and recorded the responses from different types of afferents [28]. The responses of the slowly adapting fibres (SAIs) correlated with both the curvature and the contact force. In a subsequent study, they performed similar experiments using human subjects [29]. Again, responses came mainly from the SAIs. They concluded that the responses of the SAIs contain accurate information about the shape of the sphere, its position of contact and the contact force.

Pont et al. [27] studied haptic curvature discrimination for various regions of the hands (along and across various fingers). Examples of how the stimuli were presented are shown in figure 2a,b. Their main finding was that the discrimination thresholds decrease with contact length. They reached a conclusion similar to that of Goodwin et al. [25], namely that the difference in local attitude (slope) over that part of the stimulus contacted by the hand or finger determines the curvature discrimination threshold. Note, however, that the curvatures and sizes of the stimuli of these two studies cover a quite different range (table 1). As performance with the dorsal side of the hands was much worse than performance with the palmar side, it could also be concluded that the input of cutaneous receptors plays an important role in the perception of curvature. A prediction that followed from Pont et al. [27] was tested in a subsequent study [14]: if local attitude differences determine the curvature discrimination thresholds, then removing this information from the stimulus should result in higher thresholds. Using sets of stimuli (figure 1c) that contained only zeroth-order information (height differences), zeroth- and first-order information (height and attitude), or zeroth-, first- and second-order information (height, attitude and curvature), it could be shown that indeed attitude differences are both necessary and sufficient for curvature discrimination. Figure 2c,d shows how the fingers were placed on the stimuli. In this same study, it was also found that the curvature thresholds for static and dynamic touch were comparable.

Figure 2.

Examples of how the stimuli were presented in the curvature discrimination studies by Pont et al. [14,27]. Subjects were sitting behind a curtain, so that they could not see the stimuli, but did not have to be blindfolded for a long time. (a) Stimulus presented along the middle finger at the palmar side of the hand; (b) stimulus presented across the fingers on the proximal joints, again at the palmar side; (c) fingers on a zeroth-order stimulus containing only height differences; (d) fingers on a curved stimulus containing zeroth-, first- and second-order information. In all these experiments, touch was static.

The finding that attitude differences determine curvature perception has an intriguing consequence: since most human hands are longer than wide, the curvature of a strip presented along the fingers should feel more curved than the same strip presented across the fingers. This was tested in a matching experiment [10] and indeed a significant difference was found for the perceived curvatures along the fingers compared with across the fingers. The same conclusion could be drawn when cylinders instead of strips were used as stimuli [10]. Finally, also in line with these results, it was found that the perceived shape of an ellipsoidal stimulus depended on its orientation [10].

Another study on curvature perception used a device that made it possible to vary zeroth-order stimulus information independently from first-order information, while subjects dynamically explored the stimulus [15]. This would not be possible using solid stimuli. This study confirmed the dominance of local attitude information for the thresholds. The discrimination of curvature did not depend on whether or not height information was included in the stimulus.

In Van der Horst & Kappers [19] subjects were asked to grasp two elliptical cylinders either statically or dynamically and they had to decide which of the two had the circular cross section. These stimuli contained zeroth-, first- and second-order information. Performance with these cylinders was compared with a similar task using rectangular blocks, where subjects had to choose which of two blocks had the square cross section. In this latter condition, subjects had more direct access to the aspect ratio (zeroth-order), but these stimuli lacked first- and second-order information. The thresholds in terms of aspect ratios turned out to be much higher using the rectangular blocks than with the elliptical cylinders. It was concluded that higher order information in the cylindrical stimuli was used for discrimination. Moreover, thresholds expressed in curvature were comparable to those measured in other studies [19,20]. The thresholds for dynamic exploration were slightly lower than those for static exploration.

All of the previous studies used only a limited range of curvatures within an experiment. Moreover, they used different procedures and stimuli, making them hard to compare. Therefore, Louw et al. [17] decided to run an extensive experiment with stimuli over the whole range of haptic spatial scales. They used stimuli with a Gaussian profile, of which the width ranged from 150 to 240 µm. For various widths and both convex and concave stimuli, they determined the threshold height necessary to discriminate the curved stimulus from a flat one. It was found that over the whole range from 1 mm stimulus width on, the threshold height as a function of stimulus width could be described by a power function with an exponent of 1.3. If attitude differences (first-order information) would determine the thresholds, an exponent of 1 should have been found; if curvature (second-order information) would be the sole factor, the exponent should have been 2. An exponent of 1.3 indicates that apart from first-order information that plays a role, there is also a small contribution of curvature information. This finding seems to be somewhat different from previous findings that concluded that only first-order information determines the threshold (e.g. [24,27]), but the results from these other studies expressed threshold height as a function of stimulus width overlap with the thresholds from the Gaussian stimuli. Moreover, the previous studies only compared models with exponents of 0 (height), 1 (attitude) and 2 (curvature) and then an exponent of 1 gave the best fit. Interestingly, whereas exploration varied from making small finger movements for the smallest stimuli to making hand, arm and shoulder movements for the largest stimuli, the dependence of threshold height on stimulus width remained the same [17].

The curvature discrimination studies mentioned so far used unimanual exploration. A study in which cylindrical shells were placed upright showed that bimanual discrimination thresholds were in the same range [13]. The horizontal distance between the two stimuli and the position of the set-up with respect to the subject (shifted to the right or to the left) had no influence on the thresholds. However, they also reported subject-dependent discrimination biases: equal physical curvatures right and left were not always perceived as equal, which was hypothesized to arise from small differences in left and right arm movements.

(a). Discussion and conclusions

The studies described above lead to a consistent picture of the mechanisms involved in curvature discrimination. Zeroth-order information in the stimulus (height or aspect ratio) cannot be processed accurately enough to be responsible for the curvature discrimination thresholds [14,15,19]. On the other hand, removing second-order information (curvature) from the stimuli had no deteriorating effect on the thresholds, indicating that curvature information itself was not necessary [14,15]. The conclusion that follows is that first-order information (local attitude differences) is necessary and sufficient for curvature discrimination [14,15,24,27], although a small contribution of second-order information cannot be excluded [17].

3. One hand/finger versus two hands/fingers performance

Using two hands or two fingers from different hands in a discrimination task has the advantage that both stimuli can be explored simultaneously. Moreover, the task load may be distributed over the two hemispheres [30]. In unilateral performance of such a task, exploration of the stimuli is necessarily sequential and has to involve memory, which might increase discrimination thresholds. On the other hand, processing in just one hemisphere might have a positive effect on thresholds, since the callosum does not have to be passed [30]. Appelle & Countryman [31] investigated the influence of laterality in a task where subjects had to explore bars by dynamic touch. They had to match the orientation of bars and they reported an advantage of unilateral performance. They related this difference between unilateral and bilateral performance to the inherently different scanning movements required in the two conditions. In the following, data from three different discrimination studies will be discussed.

(a). Methods used in the various experiments

In all studies, subjects were seated behind a curtain to block their view of the stimuli. Subjects were asked to move their hand or finger over the stimulus surface, but to avoid systematic exploration of the edges. Exploration time was always unlimited. Subjects never received feedback about the correctness of their response.

In the first study by Kappers et al. [7], a series of hand-sized paraboloids was used, defined by z(x,y) = 1/2(k₁x² + k₂y²). z(x,y) indicates the height of every position (x,y) and thus the shape of the surface. The two principal curvatures (k₁ and k₂) varied in a systematic way along a shape-index scale (see [32] and figure 1a). This shape-index scale ranges from −1 (concave symmetric paraboloids: k₁ = k₂, k₁ < 0, k₂ < 0) via −0.5 (concave cylinder: k₁ = 0, k₂ < 0), 0 (symmetric saddle: k₁ = −k₂), 0.5 (convex cylinder k₁ > 0, k₂ = 0) to 1 (convex symmetric paraboloid: k₁ = k₂, k₁ > 0, k₂ > 0). During each trial, two stimuli that were either identical in shape or differed 0.125 in shape-index were presented simultaneously to a subject. Their task was to decide whether the two shapes were identical or not. In different conditions, they used either their right hand, their left hand or two hands simultaneously.

In the second study by Kappers & Koenderink [8], only cylindrically curved hand-sized stimuli were used (subset of stimuli in figure 1a). Subjects were presented with pairs of stimuli of different curvature and they had to decide which of the two was more convex or concave. Again there were two unimanual (left and right hand) and one bimanual condition.

In the third study by Van der Horst & Kappers [20], the stimuli were much smaller and much more curved (figure 1g,h). There were two two-finger conditions: subjects either had to use their index finger and thumb, or their two index fingers simultaneously. In addition, there were three one-finger conditions: index finger preferred hand, index finger non-preferred hand and thumb preferred hand. In the latter three conditions, the experimenter changed the stimulus in between explorations, so that the exploring finger always touched a stimulus in the same way. In this study, discrimination thresholds were measured and performance is defined here as reference curvature/threshold.

(b). Results

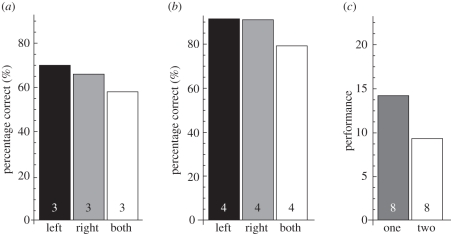
The results of the shape discrimination study by Kappers et al. [7] are presented in figure 3a. Performance is expressed in percentage of correct decisions. The effect of exploration condition was significant: bimanual performance was worse than unimanual performance with either the right or the left hand. This effect could also clearly be seen in the data of the individual (3) subjects.

Figure 3.

Differences between performance in one hand/finger versus two hands/fingers conditions. (a) Discrimination of doubly curved hand-sized surfaces, data from Kappers et al. [7]; (b) Discrimination of cylindrically curved hand-sized stimuli, data from Kappers & Koenderink [8]; (c) discrimination of cylindrically curved finger-sized stimuli (one finger versus two finger exploration), data from Van der Horst & Kappers [20]. Performance is defined as reference curvature/threshold curvature. The numbers in the bars indicate the number of subjects that participated in an experiment. Black is left-hand condition, grey is right-hand condition and white is bimanual condition, dark grey (in c) is averaged over right and left finger conditions.

The results of the curvature discrimination study by Kappers & Koenderink [8] can be seen in figure 3b. Again bimanual performance, expressed in percentage correct, is worse than unimanual performance. In the first section, it was mentioned that in this study, performance was close to perfect resulting in a ceiling effect. However, it can be seen here that the ceiling effect only occurred in the two unimanual conditions and not in the bimanual condition.

The results of the curvature threshold measurement study by Van der Horst & Kappers [20] are presented in figure 3c. In this figure, all one-finger conditions and all two-finger conditions are taken together as the differences between these conditions were not significant. It can be seen that the performance in the one-finger conditions is significantly better (i.e. lower discrimination thresholds) than in the two-finger conditions.

(c). Discussion and conclusions

In the first two studies, performance was expressed in percentage of correct decisions (note that performance is not normalized for task difficulty); in the third study, performance was related to the discrimination threshold, so only the relative performances can be compared. What can be seen is that bimanual or two-finger performance is worse than unimanual or one-finger performance. This is not what was expected when these studies were designed: the expectation was the opposite, because the stimuli could be explored simultaneously. The explanation Appelle & Countryman [31] gave to their finding of worse bilateral performance was the incongruence of scanning movements. That, however, cannot be the explanation of the results from the more recent studies, since in the first two studies, the stimuli were bilaterally symmetric and subjects were allowed to rotate the stimuli and also in the third study, it was possible to make congruent scanning movements.

Another explanation could be that the two hands (or fingers) are calibrated independently, which might result in scaling differences. Such differences might result in biases, which were indeed found [8]. However, matching visually and haptically perceived curvatures did not reveal differences between left and right hands (although there were large-scale differences between the visual and haptic judgements of curvature) [11].

A remaining explanation is that a loss of accuracy during intermanual comparisons is owing to interhemispheric relay [30,33]. Bradshaw et al. [30] reported that different tasks may result in either increased or decreased performance in bimanual conditions compared with unimanual conditions. They argue that this is most likely to do with the difficulty of the task and the related processing load: for difficult tasks, it is advantageous if the processing load can be distributed over the two hemispheres. In the studies presented here, there were no time constraints that would increase work load, so the costs associated with transmitting information to the other hemisphere are apparently relatively high, resulting in worse bimanual performance. Interestingly, performance in the two-finger condition improved when exploration was forced to be sequential instead of simultaneous [20], suggesting that in this way the processing load could be reduced. A magnetic resonance imaging and positron emission tomography scanning study of Bodegård et al. [34] showed that shape discrimination takes place at a level connected to a single hand. As a consequence, it might indeed have been expected that bimanual processing comes with extra costs. On the other hand, Iwamura [35] found a substantial number of neurons with bilateral receptive fields on hand digits, so some processing occurs at a level of two hands simultaneously. However, it remains to be seen whether these neurons are involved in curvature or shape perception and how this finding relates to the current experiments.

4. Haptic after-effect of curved surfaces

Gibson [36] was one of the first to mention the existence of a haptic curvature after-effect. While running the fingers over a curved edge, all subjects stated that the convex curvature seemed to decrease. Moreover, a straight edge touched after 3 min of adaptation along the curved edge was reported to feel as curved in the opposite direction. Although there were some studies on tactual after-effects (e.g. [37–39]), the topic of curvature after-effects was only taken up again in the nineties.

It is also of interest to investigate whether the aftereffect transfers to other fingers or the other hands, as it will indicate possible levels of processing. Kinesthetic after-effects obtained while rubbing a block with thumb and index finger for 1 min were reported to be (partially) transferable to the thumb and ring finger combination [40]. In a sequential tactuomotor learning task, it was also shown that maze tracing experience obtained with one hand transferred to the other hand [41]. They concluded that what is learned takes place at an effector-independent level.

The data of four studies of haptic after-effects will be presented, compared and discussed [9,12,16,18]. As these studies have large parts of their procedures in common, these will be described together. The results, that is, the strength of the after-effects, will be recomputed and expressed in the same manner so that direct comparisons between different studies and conditions become possible.

(a). General methods in after-effect studies

In order to prevent subjects from seeing the stimuli, they were either seated behind a curtain [9,12,18] or blindfolded [16]. In all studies, the adaptation time ranged between 10 and 15 s, as longer periods have hardly any influence on the strength of the after-effect [9,37]. In the static conditions, the subjects were asked to just rest a finger or hand on the adaptation surface. In the dynamic conditions, they had to continuously move their hand or finger tips over the surface. In the active conditions, subjects had to move their finger over the whole stimulus. This condition differs from the dynamic condition in the sense that exploration was necessary to feel the whole stimulus (i.e. the stimulus was much larger than the finger). In the passive condition, the finger was kept at the same location, but the stimulus was moved to and fro under the finger. After this adaptation period, the subject was asked to lift his/her finger or hand and, depending on the condition, to place the same or another hand or finger on the test stimulus. Next, they had to decide immediately whether the test stimulus was convex or concave.

Both convex and concave adaptation surfaces were used, 3.8 m⁻¹ in the active and passive finger conditions (figure 1c) [16], 4 m⁻¹ in the hand conditions (figure 1a) [9,12] and 36 m⁻¹ in the static finger conditions (figure 1e) [18]. The curvatures of the nine test stimuli varied in a range around zero curvature (flat surface). The test stimuli were chosen in such a way that the expected strength of the after-effect (based on pilot experiments) would lie in the middle of the range. Each combination of adaptation surface and test stimulus was presented 10 times in random order.

The data for each subject were analysed separately for the convex and concave conditioning stimuli. The percentage of convex responses was plotted against the curvature of the test stimuli. A psychometric function was fitted to these data. The point where 50 per cent of the responses was convex is the point of subjective equality (PSE), as it is the curvature where subjects just guess whether the test is convex or concave. In order to compare the results from the different studies, the strength of the after-effect is defined as follows: 100% × (PSE resulting from a convex adaptation curvature minus PSE resulting from a concave adaptation curvature)/(convex minus concave adaptation curvatures).

(b). Results

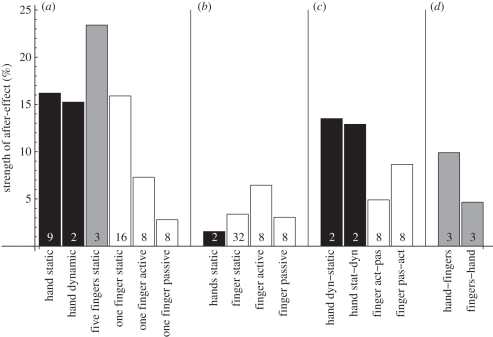
The results from these studies are summarized in figure 4, where similar conditions from the various studies have been combined. Only the after-effect after the transfer from one static hand to the other hand (first bar in figure 4b) was not significant (possibly owing to the small number of subjects); all other conditions led to significant and often quite substantial after-effects.

Figure 4.

Strength of the after-effect is defined as follows: 100 % × (PSE after adaptation to a convex stimulus minus PSE after adaptation to a concave stimulus)/(convex minus concave adaptation curvature). Data from various studies combined and reanalysed: (a) Same hand or finger conditions: hand static [9,12], hand dynamic [12], five fingers static [12], one finger static [18], one finger active [16]; (b) Transfer to other hand or finger: hand static [12], finger static [18], finger active [16], finger passive [16]; (c) Different conditions with the same hand or finger: hand dynamic-static and hand static-dynamic [12], finger active-passive and finger passive-dynamic [16]; (d) From hand to fingers and vice versa [12]. The numbers in the bars indicate the number of subjects that participated in an experiment. Black is hand condition, grey is five fingers condition and white is finger condition.

In figure 4a, all conditions are shown where the exploration of the adaptation stimulus (be it static, dynamic, active or passive) was identical to that of the exploration of the test stimulus. The after-effect is much stronger in the first four conditions than in the last two. Moreover, active exploration with one finger leads to a significantly stronger after-effect than passive stimulation.

In figure 4b, the after-effects after transfer to another hand or finger are shown. Although the after-effect for the hand transfer condition was not significant, given the results for the other conditions, this might be owing to a lack of statistical power. The after-effects for the static hand (if any) and finger are substantially smaller than the same exploration conditions without transfer. However, the after-effect after transfer for the passive and active finger conditions are of the same magnitude as comparable conditions without transfer.

Figure 4c, shows the after-effects for conditions where the adaptation and test stimuli were explored in different ways. It can be seen that for the hand conditions, the after-effects are almost as strong as the original conditions that were not mixed. Owing to the small number of subjects, it cannot be tested whether or not the effect is indeed smaller. For the finger conditions, the effects are as strong as the effects when exploration is not varied. Only when the strength of the after-effect of the finger passive-active condition was compared with the finger-passive condition, was the difference significant; none of the other differences were significant.

Finally, after-effects obtained in static conditions where the way in which the stimulus was touched (either with the whole hand or with the five finger tips) was varied between adaptation and test stimuli are shown in figure 4d. It is of interest that even though the shape of the hand is quite different in the two ways of touching and the skin contact areas are not even overlapping, the after-effects are quite substantial, albeit smaller than in the original conditions that were not mixed.

(c). Discussion and conclusions

The strongest after-effects are found in conditions where the hand or finger(s) are immediately in contact with the whole stimulus at the start of the adaptation period. This is true for the whole hand, the five finger tips and even the one static finger conditions. Interestingly, whether the subjects touch the stimuli statically or dynamically is not of influence, not even if these conditions are mixed over adaptation and test stimuli. In conditions where exploration (active or passive) is necessary to sense the whole stimulus, the after-effects are substantially smaller. This is probably related to the fact that the local curvature in the one finger active and passive conditions is below the curvature perception threshold [14]: movement, either active or passive, is necessary to perceive curvature. The one finger active condition is somewhat similar to the condition tested by Gibson [36], but he used an adaptation period of 3 min. Therefore, it might be that in the active and passive conditions, a 10 s adaptation period is not sufficient to reach the maximum strength of the after-effect. As these experiments always take a long time and are quite boring for both subject and experimenter, this possibility has not (yet) been tested. Unfortunately, Gibson [36] had only one (quite informal) trial per subject and his results consisted of introspective reports, so a quantitative comparison of after-effect strengths is not possible.

Another, possibly additional explanation is that because the representation of curvature has to be built up in the active and passive one finger conditions, other (higher level) brain areas might play a role in comparison with the conditions where a representation of curvature can be obtained directly. An indication that this might indeed be the case is that in these ‘indirect’ conditions there is a complete transfer of the after-effect to other fingers (even to fingers of the other hand), which would be impossible at a peripheral level. In the ‘direct’ conditions, there was also a transfer of after-effects to the other hand or fingers, but these transfers were far from complete. This indicates that the major part of the processing occurs at a level where fingers or hands are represented individually. However, it also indicates that saturation of cutaneous receptors or other peripheral mechanisms cannot be the sole cause of the after-effects.

5. Summary and conclusions

What the research on after-effects has shown convincingly is that the haptic perception of shape or curvature is not veridical. A flat surface will not always be perceived as flat and conversely, a curved surface might feel as flat. Moreover, this percept changes continuously during the day, as the perception of human subjects will be strongly influenced by everything they touch. A few seconds in contact with an object is already sufficient to cause a change in the perception of the next object. It is even the case that what a hand or finger feels is partially influenced by what the other hand or another finger has touched before.

The studies described above seem to point to two distinct, although possibly related, after-effects. When touching the whole stimulus directly, either statically or dynamically, the after-effect is quite strong, but transfer to the other hand or finger is limited. When the local curvature is below the detection threshold and the finger has to move or be moved over the stimulus in order to perceive the shape, the after-effect is much smaller, but transfer to other fingers is almost complete. This difference suggests different processes and probably that different brain areas are involved in the two cases.

The occurrence of after-effects has important consequences for the way experiments should be set up. Asking for absolute judgements (for example, ‘Is this shape convex or concave?’) is only of interest when one is studying the after-effects; in all other cases, it will cause an unwanted variability in the data. Most of the curvature experiments were set up as discrimination studies and although after-effects cannot be ruled out, their influence can then at most be limited.

The curvature discrimination experiments showed that first-order information in the stimulus is the dominant factor determining the threshold. This is true over the whole range of spatial scales, varying from stimuli smaller than a finger tip to stimuli requiring arm movements. This provides a useful insight for the designers of virtual worlds: what subjects cannot feel, does not have to be simulated. Static and dynamic exploration led to identical or very similar curvature discrimination thresholds, but the strength of after-effects is different in these two cases. However, this has not been tested with the use of the same stimuli and that might be essential for drawing conclusions about the levels of processing.

Finally, bimanual or two-finger performance is worse than unimanual or one-finger performance. The most obvious explanation is that transfer of information to the other hemisphere brings extra costs in experiments where time constraints do not play a role. Another possibility is that the state of adaptation is often different for the two hands, causing the unwanted variability mentioned above that should have been avoided.

Although curvature perception, after-effects and unimanual versus bimanual perception have been discussed separately in this paper, all three provide relevant insights into human perception of shape by touch. Still, extensive future studies are needed, as the current state of the art is only the first step in understanding the haptic perception of common objects encountered in daily life.