Abstract

A unique method for quantitative in situ nanotensile testing in a transmission electron microscope employing focused ion beam fabricated specimens was developed. Experiments were performed on copper samples with minimum dimensions in the 100–200 nm regime oriented for either single slip or multiple slip, respectively. We observe that both frequently discussed mechanisms, truncation of spiral dislocation sources and exhaustion of defects available within the specimen, contribute to high strengths and related size-effects in small volumes. This suggests that in the submicrometer range these mechanisms should be considered simultaneously rather than exclusively.
Keywords: In situ tensile testing, transmission electron microscopy (TEM), size effect, strengthening mechanism, dislocation structure
While the observation that size affects the strength of materials in small dimensions and confined volumes is a common conclusion,1−15 the small scale plasticity mechanisms leading to these mechanical size effects are still not fully understood. Room temperature plasticity in single crystal cubic metals is governed by dislocation plasticity,(16) and in smaller samples it is even possible to identify individual bursts of dislocation avalanches using statistical data analysis17,18 or in situ observations in a transmission electron microscope (TEM).14,15,19−21 Currently, there exist two general mechanisms that are considered to be the possible origin of these mechanical size effects—the progressively harder operation of dislocation sources with decreasing size22,23 or the loss of dislocation sources in small volumes due to the more pronounced influence of surfaces,(4) especially in the submicrometer regime(24) (dislocation starvation/exhaustion). Studying these mechanisms theoretically or computationally is hindered by a lack of realistic input structures.25−28 Moreover, there is only limited experimental knowledge on the dislocation sources and involved dislocation mechanisms governing yield and hardening at nanometer scales,14,15,20 as this requires quantitative real time observation of individual crystal defects with nanometer resolution during testing. Here we apply a novel quantitative in situ nanotensile testing technique in the TEM to provide detailed quantitative descriptions of the dislocation source mechanisms controlling strength and hardening for copper single crystals with minimum gauge dimensions of 100–200 nm.
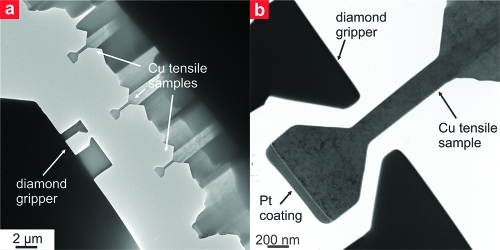
We used copper single crystals with either a (100) or a (2̅34) orientation suited for studying multiple slip or single slip deformation, respectively. A focused ion beam (FIB) microscope operated with Ga+ ions at 30 keV and a final milling current of 10 pA was used to structure nanotensile samples and a corresponding sample gripper from a conductive diamond tip (Figure 1a). This essentially reflects a further miniaturization of what was previously developed for in situ microtensile testing in a scanning electron microscope.(5) Moreover, the wide flat-ended part of the gripper is well suited for performing nanocompression experiments. The nearly rectangular gauge sections of the taper-free tensile samples had minimal dimensions ranging from 128 to 190 nm and high aspect ratios to minimize for deformation constraints5,14,29 during testing and allow for probing relative large volumes under a homogeneous uniaxial stress state, especially compared to tapered pillars.12,14,19 Moreover, a protective Pt coating was applied for minimizing FIB damage during fabrication30,31 without interfering with the subsequent loading process, which is again superior to standard pillar fabrication. Highly precise alignment in the in-plane directions (Figure 1b) is achieved by the outstanding resolution offered by the TEM. Alignment in the out-of-plane direction (electron beam direction) is realized by using a sample gripper with a shaped opening being ∼1 μm deep and therefore multiple times thicker than the tensile specimens. After the tensile sample is aligned in height to the top of the gripper using the TEM focus, it is lowered into the mid of the gripper using the piezo stage.(5) Sample loading was performed under displacement control using a Hysitron Picoindenter PI-95 at nominal strain rates of ∼5 × 10–3 s–1 in situ in a JEOL 3010 TEM at 300 keV, allowing for full insight into the dislocation processes and proper determination of true stresses and strains. In particular, the yield stress was determined by the point at which the first burst of dislocations swept across the sample cross section. This method of data analysis is described in detail in ref (14). Additionally, we derive physically true stresses and strains, thus linking the measured load and sample elongation to the current sample dimensions, instead of the initial ones used commonly to quote technical stresses. This is achieved by simultaneous correlation between the measured load–displacement data and the recorded in situ TEM video to determine the actually smallest sample cross section along the current gauge length, similar to what was introduced recently.(14)
Figure 1.
(a) Low magnification transmission electron micrograph showing several tensile samples and the structured conductive diamond tip to act as gripper. (b) Higher magnification image depicting a sample and the diamond gripper aligned before testing. Notice the rather high defect density resultant of the fabrication process.
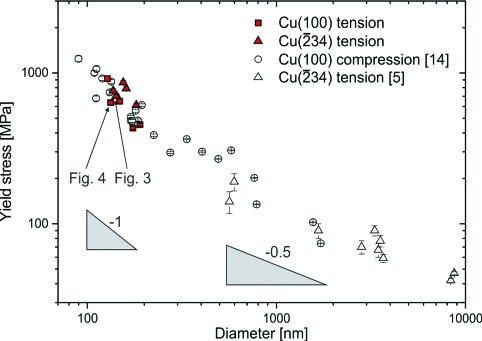
Figure 2 shows the size-dependent yield stresses of the tensile tests (full symbols) for both orientations in comparison to nanocompression(14) and microtensile tests(5) of copper having the same two crystal orientations on a double logarithmic scale. The data sets agree in yield strength, but a change in the scaling behavior along with the scatter in measured yield stresses is evident around 600–800 nm. This potentially indicates a change in the governing deformation mechanism,8,11,14,32 as below this transition length the scaling follows a d–1 behavior indicative of a dislocation source nucleation controlled plasticity.2,8,11,14,32 Above this size scale, strength scaling close to d–0.5 is observed, typically associated with dislocation interaction processes.2,8,11,32 Therefore, it is important to emphasize that the in situ observations discussed below are representative of the small size regime below ∼1 μm and cannot be uncritically applied to larger dimensions.
Figure 2.
Yield stress versus sample size showing the present nanotensile tests (filled symbols) along with nanocompression tests (open circles)(14) and microtensile tests (open triangles).(5) A change in scaling slope and rather large scatter are evident around 600–800 nm.
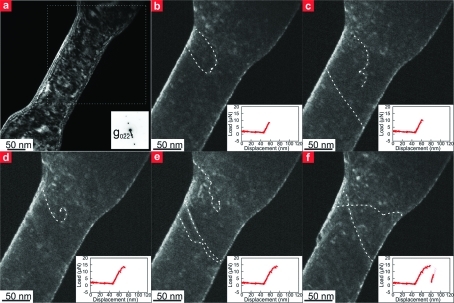
A detailed observation of spiral dislocation sources operating during tensile loading is shown in Figure 3 for a single slip oriented 142 nm thick (2̅34) copper tensile specimen using still images extracted from the recorded in situ dark field video. The full video is available in compressed form as Supporting Information. Figure 3a is a low magnification image of the whole gauge section, indicating the used g02̅2̅ imaging condition and the partial area shown in Figure 3b–f by a dotted box. To facilitate discussion, the concerned dislocations are highlighted by dashed white lines. Supplementary Figure 1 in the Supporting Information depicts the same images without highlights. Moreover, a supporting video showing the whole real time movie of this test and an image sequence (Supporting Figure 2 in the Supporting Information) from this video with correlation of individual frames to Figure 3b–f is provided. Already during what is considered elastic loading, some pre-existing dislocations bow out under the applied external load until they get pinned by defects (Figure 3b). In Figure 3c a straight dislocation on the primary slip plane is released after the lower part of the bowing dislocation reached the sample surface. Plasticity is then generated by revolving of the spiral dislocation source shown in Figure 3d. Dislocations emitted from this source get pinned further down the gauge section and exert a back stress on the spiral dislocation source, which ceases to operate. Instead, a new spiral dislocation source terminated by a different pinning point, and hampered in their operation by other defects as evidenced from the irregular curvature of the dislocation line, is activated at higher loads (Figure 3e). This source finally releases a burst of dislocations, forming a large slip step on the sample surface and a drop in the applied load due to the displacement controlled loading scheme. Upon reloading, besides continued activity on the primary glide plane, a few dislocations were observed on a secondary slip system (Figure 3f). This is presumably the result of changes in the stress state in response to the formation of the large slip step. No dislocation reactions between moving dislocations on different slip planes were observed. Moreover, it is worth mentioning that the pinning points are to some extent mobile, as observed in computational studies,26,27,33 and can be destroyed or unzipped (Figure 3e).
Figure 3.
In situ tensile test of a 142 nm diameter (2̅34) oriented copper sample. (a) Low magnification dark field image showing the whole gauge section and the used g02̅2̅ diffraction condition. A dotted box indicates the section shown in panels b–f. (b) A pre-existing dislocation bows out and gets pinned during elastic loading. (c) Upon further loading a straight dislocation is released from the bowing segment. (d) A spiral dislocation source operating. (e) Dislocations emitted from the spiral dislocation source in (d) get pinned, leading to the activation of another spiral dislocation source on the same slip system. (f) Only after the large load drop, a secondary active glide plane is observed.
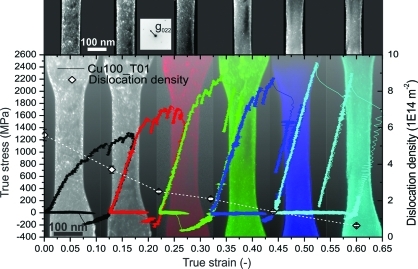
The flow behavior of a repeatedly loaded multiple slip oriented (1 0 0) copper tensile sample with an initial thickness of 133 nm is depicted in Figure 4 in terms of true stresses versus true strains. The yield point was determined at 636 MPa, after which significant hardening set in, reaching true stresses well above 2 GPa when the dislocation density dropped below 2.1 × 1014 m–2 for the last two loading cycles. The negative stresses after unloading emerge from adhesion between the sample head and diamond gripper. As evidenced by the false-color coded dark field TEM images behind the true stress versus true strain data, the sample elongation remained homogeneous up to more than 40% strain, as multiple dislocation sources on different slip systems were activated within the sample volume. This degree of homogeneous deformation was previously reported for qualitative tensile testing of (1 0 0) aluminum(20) but never achieved in miniaturized compression testing due to inhomogeneous boundary conditions and specimen taper.14,19,29 During elongation the sample gets harder and the deformation characteristics become more stochastic. The various dislocation bursts become more and more dramatic, until at 43% strain a larger slip step forms and continues to grow, seen best in the rightmost image of Figure 4. The last loading cycle consists merely of two elastic loadings connected by dislocation bursts and subsequent elastic unloading. The measured elastic slope of ∼35 GPa is lower than the anisotropic directional modulus E100 = 67 GPa calculated using C11 = 168 GPa, C12 = 121 GPa, and C44 = 75 GPa.34,35 This is a common observation for such miniaturized tests, and based on our observations we attribute it to occasionally observed dislocation movement outside the gauge section and the limited stiffness of the load frame, which was not corrected for. Additionally, “mechanical annealing” of near surface defects(19) and any slight misalignment(36) would contribute to a reduced elastic slope. However, a detailed assessment of the contribution of individual aspects is beyond the scope of this paper.
Figure 4.
True stress versus true strain data for repeated loadings of an initially 133 nm diameter tensile sample with (100) orientation. The specimen yields at 636 MPa and shows significant hardening during elongation to 65% true strain. Simultaneously, the dislocation density (defects can be seen as bright features in the upper row of dark field images) as denoted by the white diamond symbols and the right-hand axis of the graph is reduced by an order of magnitude. Correspondingly the deformation characteristics becomes more stochastic as the defect density decreases.
The observed changes in the mechanical behavior can be correlated to the dislocation density determined from dark field micrographs using a g022 imaging condition recorded before and after each individual loading step as shown partially in the upper row of Figure 4. The dislocation density was derived using a classical text book line intercept method and corrected for the fraction of invisible dislocations for the used imaging condition.(16) Error bars are derived from the standard deviation between individual parallel line intercept measurements along the same sample gauge section for a given strain, assuming for simplicity that the expected invisible dislocation fraction will not contribute to the scatter. Moreover, in the initial loading state a discrimination between dislocation lines and dislocation loops was not possible; thus both are accounted for in the quoted dislocation densities. The initial dislocation density is 5.6 × 1014 ± 0.3 × 1014 m–2, well within what was reported previously,19,30,31 but rather high for a single crystal. This is an unfortunate but well-known effect of mostly surface dislocation loops originating from FIB fabrication.19,20,30,31 During elongation of the specimen to 65% true strain, the dislocation density is reduced by an order of magnitude to 6.3 × 1013 ± 0.6 × 1013 m–2, seen by the gradual clearing of the images in Figure 4 from left to right.
Importantly, the initial microstructure for all samples presented in Figures 2–4 is comparable. Still, it clearly shows that the yield strength of smaller samples is higher. The direct observation of a spiral dislocation source (Figure 3 and supporting video) demonstrates that strength can be controlled by the stress required to operate a single source, which as Rao et al.(37) showed is dependent on source length and therefore sample size. Following this approach to evaluate the spiral dislocation source size of the specimen shown in Figure 4 for mixed type dislocations,8,15 the size reduces from ∼20 nm at yield to ∼3 nm for a stress of 2.5 GPa. It is seminal to consider that the average dislocation pinning distance in a bulklike Taylor concept view would increase from ∼40 nm at the beginning of the test to ∼140 nm at the end. This would imply that the material softens, which is obviously not the case, thereby demonstrating that Taylor hardening breaks down in this regime.22,28,38−41 Rather, as shown in Figure 4, the stress level during plastic deformation is controlled by the availability of defects, where lower densities result in higher stresses. This is in accordance with the exhaustion hardening concept,(22) where hardening results from a loss of dislocation sources by source shutdown(14) or a general loss of dislocations (mechanical annealing,(19) dislocation starvation(4)). Therefore, the flow strength in the submicrometer regime and for the range of dislocation densities examined in this study is controlled by the availability, or more precisely the gradual exhaustion, of dislocation sources.
It was generally proposed(42) and shown experimentally for Mo(6) that, starting from a defect-free crystal, there is significant softening when introducing dislocations. The current tensile experiments move the opposite way along this microstructural path: They start with high dislocation densities and rather smooth deformation characteristics at moderate stresses, get gradually more erratic with reduced dislocation content, and end at low densities and strengths in the range of 2.5 GPa, similar to that reported for defect-free (110) oriented Cu whiskers.(43) So far, little is known about the deformation behavior in the low dislocation density regime for nanosized face centered cubic materials.(43) However, a qualitative comparison to body centered cubic Mo is evident. Bei et al.(6) reported rather smooth stress–strain curves for 500 nm Mo fibers being compressively prestrained by 11%, huge scatter for samples containing few dislocations after 4% prestraining,(44) and theoretical strength for defect-free whiskers,(45) in accordance with the deformation characteristics of the present data outlined above. Interestingly, our results show that the dislocation density does not need to equal zero to reach whisker-like strengths. Presumably, emerging surface ledges(46) are more efficient dislocation sources than the few nanometer small FIB created dislocation loops.
Currently, source truncation and exhaustion hardening are usually put forward independently from different studies. We developed a nanotensile testing method well suited for probing the low defect density–high strength regime and observed both phenomena, the operation of spiral dislocation sources at high stresses (Figure 3) and the hardening by a gradual loss of defects (Figure 4), during quantitative in situ TEM tensile testing of ∼100–200 nm thin copper single crystals oriented for single slip as well as multiple slip. Thus, in the submicrometer regime it appears that both mechanisms contribute to higher strengths in smaller volumes and should be considered simultaneously instead of exclusively.
Acknowledgments
This work was supported by the National Center for Electron Microscopy, Lawrence Berkeley National Laboratory, which is supported by the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. D.K. gratefully acknowledges financial support of the Austrian Science Fund (FWF) through the Erwin Schrödinger fellowship J2834-N20. The authors are thankful to R. C. Major from Hysitron, Inc., for his continued support during development of the tensile loading mode.
Supporting Information Available
Still images and video of tensile test for copper sample. This material is available free of charge via the Internet at http://pubs.acs.org.
Author Present Address
§ Department of Materials Physics, University of Leoben & Erich Schmid Institute of Materials Science, Austrian Academy of Sciences, Leoben, Austria.
Supplementary Material
References
- Uchic M. D.; Dimiduk D. M.; Florando J. N.; Nix W. D. Science 2004, 305, 986. [DOI] [PubMed] [Google Scholar]
- Dimiduk D. M.; Uchic M. D.; Parthasarathy T. A. Acta Mater. 2005, 53, 4065. [Google Scholar]
- Wu B; Heidelberg A; Boland J. J. Nat. Mater. 2005, 4, 525. [DOI] [PubMed] [Google Scholar]
- Greer J. R.; Nix W. D. Phys. Rev. B 2006, 73, 1. [Google Scholar]
- Kiener D; Grosinger W; Dehm G; Pippan R. Acta Mater. 2008, 56, 580. [Google Scholar]
- Bei H; Shim S; Pharr G. M.; George E. P. Acta Mater. 2008, 56, 4762. [Google Scholar]
- Uchic M. D.; Shade P. A.; Dimiduk D. Annu. Rev. Mater. Res. 2009, 39, 361. [Google Scholar]
- Dehm G. Prog. Mater. Sci. 2009, 54, 664. [Google Scholar]
- Dunstan D. J.; Ehrler B; Bossis R; Joly S; P’ng K. M. Y.; Bushby A. J. Phys. Rev. Lett. 2009, 103, 4. [DOI] [PubMed] [Google Scholar]
- Zhu T; Li J. Prog. Mater. Sci. 2010, 55, 710. [Google Scholar]
- Kraft O; Gruber P. A.; Mönig R; Weygand D. Annu. Rev. Mater. Res. 2010, 40, 293. [Google Scholar]
- Yu Q; Shan Z-W; Li J; Huang X; Xiao L; Sun J; Ma E. Nature 2010, 463, 335. [DOI] [PubMed] [Google Scholar]
- Dietiker M; Buzzi S; Pigozzi G; Löffler J. F.; Spolenak R. Acta Mater. 2011, 59, 2180. [Google Scholar]
- Kiener D; Minor A. M. Acta Mater. 2011, 59, 1328. [Google Scholar]
- Kiener D; Hosemann P; Maloy S. A.; Minor A. M. Nat. Mater. 2011, 10, 608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirth J. P., Lothe J.. Theory of Dislocations; Wiley: New York, 1982. [Google Scholar]
- Dimiduk D. M.; Woodward C; LeSar R; Uchic M. D. Science 2006, 312, 1188. [DOI] [PubMed] [Google Scholar]
- Csikor F. F.; Motz C; Weygand D; Zaiser M; Zapperi S. Science 2007, 318, 251. [DOI] [PubMed] [Google Scholar]
- Shan Z. W.; Mishra R. K.; Asif S. A. S.; Warren O. L.; Minor A. M. Nat. Mater. 2008, 73, 115. [DOI] [PubMed] [Google Scholar]
- Oh S. H.; Legros M; Kiener D; Dehm G. Nat. Mater. 2009, 8, 95. [DOI] [PubMed] [Google Scholar]
- Minor A. M.; Asif S. A. S.; Shan Z. W.; Stach E. A.; Cyrankowski E; Wyrobek T. J.; Warren O. L. Nat. Mater. 2006, 5, 697. [DOI] [PubMed] [Google Scholar]
- Rao S. I.; Dimiduk D. M.; Parthasarathy T. A.; Uchic M. D.; Tang M; Woodward C. Acta Mater. 2008, 56, 3245. [Google Scholar]
- Weinberger C. R.; Cai W. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 14304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nix W. D.; Lee S.-W. Philos. Mag. 2011, 91, 1084. [Google Scholar]
- Lee S-W; Nix W. D. Mater. Sci. Eng., A 2010, 527, 1903. [Google Scholar]
- Motz C; Weygand D; Senger J; Gumbsch P. Acta Mater. 2009, 57, 1744. [Google Scholar]
- Tang H; Schwarz K. W.; Espinosa H. D. Phys. Rev. Lett. 2008, 100, 185503. [DOI] [PubMed] [Google Scholar]
- Senger J; Weygand D; Motz C; Gumbsch P; Kraft O. Acta Mater. 2011, 59, 2937. [Google Scholar]
- Kiener D; Motz C; Dehm G. Mater. Sci. Eng., A 2009, 505, 79. [Google Scholar]
- Kiener D; Motz C; Rester M; Dehm G. Mater. Sci. Eng., A 2007, 459, 262. [Google Scholar]
- Volkert C. A.; Minor A. M. MRS Bull. 2007, 32, 389. [Google Scholar]
- Kiener D; Rester M; Scheriau S; Yang B; Pippan R; Dehm G. Int. J. Mater. Res. 2007, 98, 1047. [Google Scholar]
- Weinberger C. R.; Cai W. Scr. Mater. 2011, 64, 529. [Google Scholar]
- Gruber P. A.; Böhm J; Onuseit F; Wanner A; Spolenak R; Arzt E. Acta Mater. 2008, 56, 2318. [Google Scholar]
- Armstrong D. E. J.; Wilkinson A. J.; Roberts S. G. J. Mater. Res. 2009, 24, 3268. [Google Scholar]
- Zhang H; Schuster B. E.; Wei Q; Ramesh K. T. Scr. Mater. 2006, 54, 181. [Google Scholar]
- Rao S. I.; Dimiduk D. M.; Tang M; Parthasarathy T. A.; Uchic M. D.; Woodward C. Philos. Mag. 2007, 87, 4777. [Google Scholar]
- Benzerga A. A. J. Mech. Phys. Solids 2009, 57, 1459. [Google Scholar]
- Guruprasad P. J.; Benzerga A. A. J. Mech. Phys. Solids 2008, 56, 132. [Google Scholar]
- El-Awady J. A.; Wen M; Ghoniem N. M. J. Mech. Phys. Solids 2009, 57, 32. [Google Scholar]
- Kiener D; Guruprasad P. J.; Keralavarma S. M.; Dehm G; Benzerga A. A. Acta Mater. 2011, 59, 3825. [Google Scholar]
- Lilleodden E. T.; Nix W. D. Acta Mater. 2006, 54, 1583. [Google Scholar]
- Richter G; Hillerich K; Gianola D. S.; Mönig R; Kraft O; Volkert C. A. Nano Lett. 2009, 9, 3048. [DOI] [PubMed] [Google Scholar]
- Phani P. S.; Johanns K. E.; Duscher G; Gali A; George E. P.; Pharr G. M. Acta Mater. 2011, 59, 2172. [Google Scholar]
- Bei H; Shim S; George E. P.; Miller M. K.; Herbert E. G.; Pharr G. M. Scr. Mater. 2007, 57, 397. [Google Scholar]
- Brochard S; Hirel P; Pizzagalli L; Godet J. Acta Mater. 2010, 58, 4182. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.