A dedicated cone-beam CT system for musculoskeletal extremities imaging: Design, optimization, and initial performance characterization

Abstract

Purpose: This paper reports on the design and initial imaging performance of a dedicated cone-beam CT (CBCT) system for musculoskeletal (MSK) extremities. The system complements conventional CT and MR and offers a variety of potential clinical and logistical advantages that are likely to be of benefit to diagnosis, treatment planning, and assessment of therapy response in MSK radiology, orthopaedic surgery, and rheumatology.

Methods: The scanner design incorporated a host of clinical requirements (e.g., ability to scan the weight-bearing knee in a natural stance) and was guided by theoretical and experimental analysis of image quality and dose. Such criteria identified the following basic scanner components and system configuration: a flat-panel detector (FPD, Varian 3030+, 0.194 mm pixels); and a low-power, fixed anode x-ray source with 0.5 mm focal spot (SourceRay XRS-125-7K-P, 0.875 kW) mounted on a retractable C-arm allowing for two scanning orientations with the capability for side entry, viz. a standing configuration for imaging of weight-bearing lower extremities and a sitting configuration for imaging of tensioned upper extremity and unloaded lower extremity. Theoretical modeling employed cascaded systems analysis of modulation transfer function (MTF) and detective quantum efficiency (DQE) computed as a function of system geometry, kVp and filtration, dose, source power, etc. Physical experimentation utilized an imaging bench simulating the scanner geometry for verification of theoretical results and investigation of other factors, such as antiscatter grid selection and 3D image quality in phantom and cadaver, including qualitative comparison to conventional CT.

Results: Theoretical modeling and benchtop experimentation confirmed the basic suitability of the FPD and x-ray source mentioned above. Clinical requirements combined with analysis of MTF and DQE yielded the following system geometry: a ∼55 cm source-to-detector distance; 1.3 magnification; a 20 cm diameter bore (20 × 20 × 20 cm³ field of view); total acquisition arc of ∼240°. The system MTF declines to 50% at ∼1.3 mm⁻¹ and to 10% at ∼2.7 mm⁻¹, consistent with sub-millimeter spatial resolution. Analysis of DQE suggested a nominal technique of 90 kVp (+0.3 mm Cu added filtration) to provide high imaging performance from ∼500 projections at less than ∼0.5 kW power, implying ∼6.4 mGy (0.064 mSv) for low-dose protocols and ∼15 mGy (0.15 mSv) for high-quality protocols. The experimental studies show improved image uniformity and contrast-to-noise ratio (without increase in dose) through incorporation of a custom 10:1 GR antiscatter grid. Cadaver images demonstrate exquisite bone detail, visualization of articular morphology, and soft-tissue visibility comparable to diagnostic CT (10–20 HU contrast resolution).

Conclusions: The results indicate that the proposed system will deliver volumetric images of the extremities with soft-tissue contrast resolution comparable to diagnostic CT and improved spatial resolution at potentially reduced dose. Cascaded systems analysis provided a useful basis for system design and optimization without costly repeated experimentation. A combined process of design specification, image quality analysis, clinical feedback, and revision yielded a prototype that is now awaiting clinical pilot studies. Potential advantages of the proposed system include reduced space and cost, imaging of load-bearing extremities, and combined volumetric imaging with real-time fluoroscopy and digital radiography.

INTRODUCTION

Current clinical practice in imaging of musculoskeletal (MSK) extremities employs complementary aspects of x-ray CT and MRI for diagnosis, treatment planning, and assessment of treatment response. The former offers high spatial resolution and excellent visualization of bone and joint morphology, and the latter delivers exquisite soft-tissue visibility. Despite the maturity and complementary strengths of these modalities, a variety of limitations can be identified, including: (i) difficulty in examining weight-bearing extremities; (ii) the potential for large cumulative radiation dose in longitudinal studies; and (iii) cost, space, and workflow associated with whole-body scanners applied to extremities imaging. Due in part to these challenges, projection radiography remains widely used in MSK imaging despite the obvious lack of capability for assessing three-dimensional structures. A host of clinical applications would benefit from a system that overcomes these limitations but maintains accessibility and workflow, low patient dose, and the ability to image the extremities in their weight-bearing configuration. Examples of such applications include diagnosis, treatment planning, and treatment evaluation for subtle fractures,¹ arthritis,² impingement syndromes, and abnormal alignment of the extremities.

A number of dedicated extremities imaging systems have been developed in the recent years, partly in response to the limitations of conventional modalities mentioned above. One example is the series of ONI MSK Extreme open MRI scanners (GE Healthcare, Wilmington, MA),³ which provide a relatively small-footprint and low-cost alternative for clinical MR systems at field strengths sufficient for high resolution soft-tissue imaging (1.0 and 1.5 T). Although these compact MR scanners in their current embodiment lack the ability to image load-bearing extremities, their adoption in clinical applications indicates the need for such specialized solutions in MSK imaging. For x-ray imaging, the trend to develop dedicated, compact, low-dose tomographic systems in other clinical applications (e.g., intraoperative imaging,^{4, 5, 6} othoralyngology,⁷ and breast imaging⁸) has employed the paradigm of flat-panel cone-beam CT. Research in novel applications of flat-panel detectors in MSK radiology has initially focused on tomosynthesis.^{2, 9} Only recently have the first dedicated FPD cone-beam CT systems for extremities imaging been introduced, based either on a specialized imaging platform (Planmed Verity, Planamed Oy, Finland)¹⁰ or on an addition of 3D reconstruction capability to existing radiography/fluoroscopy C-arm imagers (Philips MultiDiagnost Eleva, Philips Healthcare, Andover, MA).¹¹ Such scanners illustrate how the low weight, compact form, and inherent high-resolution of FPDs can be leveraged to design a system that allows for imaging both unloaded and weight-bearing extremities, is capable of visualizing fine level of detail in the bony structures, and has a compact footprint suitable for use at the point-of-care. Another attractive advantage of such a paradigm in MSK imaging is the ability to combine digital radiography and real-time fluoroscopy with 3D imaging.

In light of the basic image quality characteristics and broad spectrum of cone-beam CT embodiments developed over the last decade, we posited that a system combining a carefully selected FPD and x-ray source within a knowledgeably selected geometry could address many of the limitations of conventional tomographic modalities in application to MSK extremities. Moreover, a dedicated extremities cone-beam CT scanner has the potential to exceed the image quality and dose characteristics associated with conventional CT for these particular sites, since the system design may be optimized for specific imaging tasks in extremities imaging (rather than accommodating the broad range of imaging tasks in conventional whole-body CT). This goal requires addressing a number of challenging trade-offs that go beyond a direct application of existing CBCT technologies and suggests a novel scanner design. In particular, the system proposed here permits imaging of weight-bearing lower extremities in a natural stance (facilitated by providing a side entry into the gantry), as well as unloaded lower and upper extremities. This involves employing a tilting gantry capable of imaging in both standing and sitting configurations (with ability to image at intermediate tilt angles as well). These design requirements necessitate a compact scanner geometry and a lightweight x-ray source. As a result, the scatter fraction is increased compared to e.g., C-arm imagers, and the source output power is lower than in systems employing standard radiographic tubes. Attaining soft-tissue contrast comparable to clinical CT, maintaining similar (or lower) imaging dose, and maximizing spatial resolution within these constraints requires a multidimensional optimization of system geometry and x-ray spectrum and careful consideration of scatter mitigation techniques.

This paper summarizes the design of the proposed extremities CBCT system and reports quantitative and qualitative studies of the anticipated imaging performance. The scanner was first introduced in an earlier conference proceedings.¹² Here we present a significantly detailed and expanded treatment of methodology employed for system optimization, along with an extended, comprehensive set of results drawing from theoretical and experimental studies of imaging performance. The design process began with clinical requirements and an initial conceptual blueprint of the system, as briefly explained above. In light of the complex interdependencies of factors affecting image quality (e.g., geometric magnification), mechanical constraints (e.g., outer diameter less than ∼100 cm and capability for open side entry), and clinical considerations (e.g., radiation dose), theoretical modeling employing cascaded system analysis (CSA) was performed across a range of x-ray techniques, imaging doses, and system geometries. The results guided the selection of specific system components and optimal mechanical configuration of the scanner, alleviating the need for costly, repeated experimentation. Further system optimization was performed using a flexible imaging test bench, which was also employed to verify image quality in phantoms and cadavers, including a quantitative comparison with conventional CT. Details of the system design and performance assessment are presented in Sec. 2.

MATERIALS AND METHODS

A host of clinical requirements and constraints appropriate to extremities imaging was identified (Sec. 2A). Mechanical system configuration (Sec. 2B) was guided by the clinical requirements and refined through theoretical analysis of imaging performance (Sec. 2C) and experimentation on an imaging benchtop (Sec. 2D).

Clinical considerations and design requirements

The key clinical requirements and constraints provided the starting point for system design and touchstone against, which subsequent theoretical analysis and experimentation would be held. These included: capability to image in a standing configuration (for weight-bearing lower extremities) or a sitting configuration (for nonweight-bearing upper or lower extremities); in the standing configuration, the system should allow the patient a natural stance (estimated as ∼35 cm center-to-center distance between the knees); in either configuration, an open gantry configuration allowing patient setup through the side of the scanner (rather than, for example, pointing the toes and inserting the leg down the bore of the gantry); field of view sufficient to encompass at least ∼16 cm laterally and ∼15–20 cm longitudinally; sub-millimeter isotropic spatial resolution; adequate soft-tissue contrast resolution comparable to (or potentially exceeding) conventional CT; radiation dose no greater than that of conventional CT (∼14–22 mGy, ∼0.03–0.16 mSv, depending on the extremity and site)¹³; a compact footprint (e.g., outer diameter of the gantry less than ∼100 cm); self-shielding for simplified radiation safety site requirements; ability to acquire high-quality isotropic (or nearly isotropic) volumetric images in addition to projection radiography and real-time fluoroscopy within the same setup.

A dedicated cone-beam CT system for extremities imaging

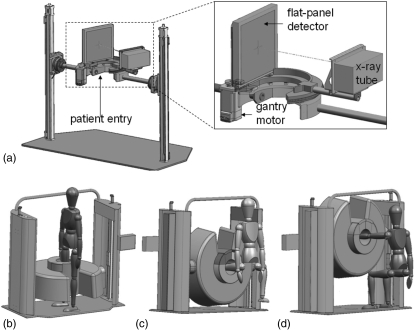
The basic design of the proposed system is illustrated in Fig. 1. As in Fig. 1a, the scanner gantry is mounted on two vertical motion towers to allow height adjustment and may be tilted to allow both a standing configuration [Fig. 1b] and a sitting configuration [Figs. 1c, 1d]. The two configurations allow weight-bearing scans of the lower extremities [Fig. 1b], nonweight-bearing scans of the lower extremities [Fig. 1c], and scanning of the upper extremities [Fig. 1d with or without joint tension applied by an assembly on the opposite side of the scanner].

Figure 1.

Illustration of the extremities scanner. (a) Internal components, including the FPD and x-ray source mounted on a motor-driven sickle arm. A magnified view is shown in the inset. The gantry allows two scanning configurations: (b) a standing configuration for imaging of weight-bearing lower extremities and (c-d) a sitting configuration for imaging of (c) nonweight-bearing lower extremities and (d) tensioned or nontensioned upper extremities.

The hardware components within the gantry are shown in the inset of Fig. 1a, including a sickle-shaped motorized C-arm track onto which the source and FPD are rigidly affixed. The track provides a sliding door side opening for patient entry through the side of the gantry. Following patient setup, the sliding door is closed, so that no moving parts are exposed during the scan. The x-ray source moves along the outer diameter of the gantry and the FPD along the inner diameter. In the standing configuration, the nonimaged leg stands exterior to the gantry in a natural stance, with the FPD traversing between the legs (within the scanner enclosure) during the scan.

Selection of system geometry considered the above clinical requirements in combination with optimization suggested by the theoretical analysis detailed below. The resulting geometry in relation to Fig. 1 is: 550 mm source-detector distance; 420 mm source-isocenter distance; magnification of ∼1.3; reconstruction field of view ∼20 × 20 × 20 cm³. The source and detector traverse a circular orbit covering an angular range of ∼240°, exceeding the short-scan range for this geometry (i.e., 180° + fan ≈ 212°). The inner bore is ∼20 cm diameter and incorporates accessories for patient immobilization, ranging from simple cushions (as in an analogous dedicated MR system³) to more sophisticated devices under development (e.g., an inflatable air bladder). The outer diameter of the gantry is ∼110 cm, and the total footprint is ∼110 × 180 cm², with total weight ∼200 kg. The scanner is self-shielded and can be powered from a standard 120 V, 25 A electrical power outlet.

Selection of the specific detector and source components utilized the theoretical analysis and experimentation detailed below, with the following components identified based on general clinical requirements (e.g., field of view, resolution requirements, etc.). A PaxScan 3030+ FPD (Varian Imaging Products, Palo Alto, CA) with a CsI:Tl x-ray converter is employed, giving a detector format of 1536 × 1536 pixels at 0.194 mm pitch (full resolution, 1 × 1 binning). Lower resolution modes (e.g., 2 × 2 binning at 0.388 mm pitch), as well as dual- and dynamic gain readout modes are available. A fixed anode x-ray tube (Source-Ray XRS-125-7K-P, Source-Ray, Ronkonkoma, NY) with a 0.5 mm focal spot is used. The source delivers techniques up to 125 kVp and 7 mA (corresponding to 0.875 kW) and can be operated at 10–30 fps with a pulse width of 10–30 ms and a duty cycle of up to 50%. For 30 ms pulses (a worst-case scenario), the highest available frame rate is 15 fps. Note that at this relatively slow frame rate, the azimuthal motion blur at the radius of 50 mm from the isocenter (central region of the field of view) is less than ∼0.2 mm for an acquisition with angular step of 0.5°.

Cascaded system analysis of system design and imaging performance

An analytical model based on cascaded systems analysis was used to evaluate the potential imaging performance, power requirements, and radiation dose for the proposed system and to provide assessment and optimization of parameters such as system magnification, kVp selection, and additional filtration. The analysis was intended as a “first-order” guide to design and technique selection with respect to major design parameters (e.g., system geometry and dose), recognizing the likely oversimplification with respect to numerous factors that were assumed negligible in the current analysis (e.g., shift variance of 3D reconstructions, irregular focal spot shape, oblique incidence of x-rays, etc.). Despite such simplifying assumptions, such models have demonstrated an excellent level of agreement with measurements of 2D and 3D noise-power spectrum (NPS) and DQE and have been shown to exhibit basic correspondence with real human observer performance in simple imaging tasks.¹⁴

Cascaded systems model

In cascaded system analysis, the imaging chain is modeled as a sequence of discrete stages, corresponding to various physical processes and image processing operations involved in forming the final image. Typically, the stages represent gain, stochastic spreading, deterministic spreading, or sampling of the signal. The corresponding values of mean gain, gain variance and modulation transfer function determine the mean signal and noise-power spectrum at each stage of the imaging chain. The approach provides a general framework that has been applied fairly broadly for modeling and optimization of 2D imaging systems,^{15, 16, 17, 18} as well as 3D modalities such as CBCT.^{14, 19, 20, 21}

The complete model of a CBCT imaging system^{20, 22} consists of 13 stages, including: a 2D projection cascade describing the physical processes from interaction of x-rays in the converter to sampling and readout of the detector with additive noise (and optional pixel binning²²); and a 3D cascade describing the mathematical processes of filtered backprojection, from log-transform of the projection data to discrete sampling of the 3D reconstruction matrix.²² The studies reported below were limited to an investigation of the resolution (presampling detector MTF) and DQE inherent to the 2D image acquisition component of the proposed system via the 2D projection model. While this approach does not provide a complete picture of 3D imaging performance, it is sufficient for the purpose of guiding the initial stage of system design. Parameters of interest at this stage (e.g., system magnification, x-ray tube voltage, and x-ray filtration) are directly related to projection DQE and MTF, and the 2D model provides a reasonable initial approach for consideration of these variables. A more complete picture of system optimization described by the full 3D reconstruction cascade depends on a number of factors that are not considered in the 2D model (e.g., number of projections, angular range of the acquisition orbit, reconstruction filter, and reconstruction voxel size). These parameters are determined by a combination of mechanical considerations (e.g., the short-scan orbit necessitated by side entry into the gantry) or do not directly pertain to physical scanner design. Their optimization is therefore beyond the scope of this paper, especially taking into account the complexity of multidimensional optimization of the complete parameter space of the reconstruction cascade. Investigation of task-based 3D imaging performance using the full 3D cascaded systems model is the subject of ongoing work, with preliminary results reported previously¹² and a comprehensive analysis presented in an associated paper.²³

The model included an x-ray spectrum computed using the Spektr toolkit²⁴ implementation of the TASMIP model of Boone and Seibert.²⁵ The spectrum calculations were modified empirically to account for variations in anode angle and aging [Tungsten (W) deposition on the exit window] between the actual x-ray tube used in the experimental benchtop emulating the scanner geometry (detailed below) and that implicit in TASMIP (namely, the tube in Fewell and Shupings’ original measurements²⁶). To this end, mR/mAs and HVL were measured at 90 and 120 kVp beams (with added filtration of 0.3 mm Cu and 4 mm Al) using an Accu-Pro 9096 multipurpose exposure meter (Radcal Corp., Monrovia, CA). The Spektr calculations were then adjusted by iteratively adding or subtracting inherent Al and W filtration to yield the best match to measurements, achieved at −0.0014 mm W and 1.1 mm Al. The negative W filtration implies a reduction in tungsten thickness compared to the tube of Fewell and Shupings, consistent with a newer x-ray tube (less anode wear).

The x-ray spectrum transmitted to the FPD included attenuation by an object model roughly approximating a knee and similar to the smaller (16 cm diameter) standard CTDI phantom. For cascaded systems analysis of NPS, DQE, etc., the object model simulated a 16 cm knee including interior bone (detailed in Sec. 2C3), while for calculation and measurement of dose, the object model was a uniform 16 cm diameter cylinder of water or acrylic. The energy-dependent attenuation coefficients of various tissues (detailed below) were adapted from NIST databases²⁷ and ICRU Report 46.²⁸

Details of the 2D projection cascade model were based on previous work for a 250 mg/cm² CsI:Tl converter.²⁹ Pertinent physical parameters were obtained from manufacturer’s data for the PaxScan 3030+ FPD (fill factor of 0.68 and additive electronic noise equal to σ_add = 2000 electrons rms). Unless otherwise mentioned, the detector was assumed to be operated in a 2 × 2 binning mode (pixel pitch at 0.388 mm). The 2D presampling MTF [MTF_FPD(f_u,f_v)] is given by the product of the scintillator and pixel aperture MTF. The NPS associated with quantum noise is denoted by S_Q(f_u,f_v) and the NPS associated with electronic noise (assumed uncorrelated) is denoted by S_E(f_u,f_v). Various parameters of the model (e.g., the x-ray spectrum, exposure level, and pixel pitch) were varied in the studies described below and are summarized in Table Table I. along with their nominal values. The pulse length τ was fixed at its maximum value of 30 ms, based on tube specifications (the worst-case scenario mentioned in Sec. 2A). The number of frames assumed a 0.5° angular step. This value approximately corresponds to the minimum number of projections required to avoid view aliasing artifacts within the central region of the field of view (100 mm diameter) for voxels equal to pixel size demagnified by the nominal magnification. These two variables are subject to future optimization through analysis of images obtained on the clinical prototype and through fully 3D modeling. For the purposes of initial theoretical analysis, the values employed below are expected to provide a sufficient guide to initial system design and performance. They also reflect the settings used in imaging bench experimentation. Note also that the fixed parameters of pulse length and angular increment enter the analysis only as multiplication factors in the calculation of the required source power (pulse length) and total dose (number of projections), and thus the interpretation of the modeling results presented here can be easily extended to include future changes in these variables.

Table 1.

Summary of terms used in cascaded systems analysis of the proposed extremities CBCT scanner. Nominal values were used in the experiments unless mentioned otherwise.

Term	Definition	Nominal value
MTFFPD(fu,fv)	Modulation transfer function for 2D detector cascade	—
MTFspot(fu,fv)	Modulation transfer function associated with focal spot blur	—
SQ(fu,fv)	NPS associated with x-ray quantum noise in the 2D projection	—
SE(fu,fv)	NPS associated with electronic noise in the 2D projection	—
(fu,fv)	Frequency components of the detector Fourier domain (expressed in the detector plane)	—
(fu′,fv′)	Frequency components of the detector Fourier domain (expressed in the imaging plane)	—
${\stackrel{-}{q}}_o$	Mean fluence incident on the detector for a given projection (nominal beam: 90 kVp + 0.3 mm Cu + 4 mm Al; knee model, detector signal=100 × additive noise)	2200 (x-rays/mm2)
$\stackrel{-}{m}$	Mean detector signal	2 00 000 e/pixel
$\stackrel{-}{g_1}$	Quantum detection efficiency (mean fraction of incident photons interacting in the scintillator, imaging conditions as for ${\stackrel{-}{q}}_o$)	0.78
$\stackrel{-}{g_2}$	Mean number of optical photons generated per x-ray interaction	1905
$\stackrel{-}{g_4}$	Coupling efficiency of optical photons to sensor photodiode	0.6
apix	Detector sampling interval	0.194 mm (full-res)
0.388 mm (half-res)
apd	Detector sensitive aperture	0.16 mm (full-res)
0.32 mm (half-res)
σadd	Additive electronics noise	2000 e/pixel
aspot	Focal spot size	0.5 mm
N	Number of projections acquired across circular orbit	480
SDD	Source-detector distance	550 mm
SAD	Source-isocenter distance	420 mm
M	Magnification factor, SDD/SAD	1.3
τ	X-ray pulse length	30 ms

Study I: system MTF and optimal magnification factor

The dependence of system resolution on geometric magnification and size of focal spot is described by the following simple model,³⁰ in which system MTF is given by the product of presampling detector MTF and the focal spot MTF (MTF_spot):

$${\mathrm{MTF}}_{\mathrm{system}}(f_u\text{'},f_v\text{'})={\mathrm{MTF}}_{\mathrm{FPD}}(f_u\text{'},f_v\text{'})·{\mathrm{MTF}}_{\mathrm{spot}}(f_u\text{'},f_v\text{'}),$$ (1)

The 2D MTF is assessed in the Fourier domain (f_u′,f_v′) corresponding to the object plane – i.e., a (coronal) plane located at system isocenter perpendicular to the central ray of the beam, and accounts for system magnification. A simple, first-order model for focal spot blur was assumed as in Johns and Cunningham,³¹ with the focal spot modeled simply as a Gaussian of characteristic width³² (a_spot):

$${\mathrm{MTF}}_{\mathrm{spot}}(f_u\text{'},f_v\text{'})=e^{-\pi {[[(M-1)∕M]a_{\mathrm{spot}}]}^2(f_u{\text{'}}^2+f_v{\text{'}}^2)},$$ (2)

The system MTF was calculated as a function of M (varied from 1.0 to 2.0) and a_spot (varied from 0.2 to 1.5 mm) to assess optimal geometry [i.e., the magnification at which system MTF is maximized through joint optimization of MTF_FPD (improves with increasing M) and MTF_spot (degrades with increasing M)]. Spatial resolution was also characterized summarily in terms of the f₅₀ and f₁₀ values – i.e., the spatial frequency at which MTF_system drops to 0.50 and 0.10, respectively.

Study II: DQE, dose, and power

The detective quantum efficiency (DQE) for the 2D projection FPD imaging chain is computed from cascaded systems analysis as:

$$\mathrm{DQE}(f_u,f_v)=\frac{{\stackrel{-}{m}}^2{\mathrm{MTF}}_{\mathrm{FPD}}{(f_u,f_v)}^2}{{\stackrel{-}{q}}_0[S_Q(f_u,f_v)+S_E(f_u,f_v)]},$$ (3)

where ${\stackrel{-}{q}}_o$ is the mean incident fluence needed to achieve mean detector signal of $\stackrel{-}{m}$:

$$\stackrel{-}{m}=a_{\mathit{pd}}^2{\stackrel{-}{q}}_0{g}_1{g}_2{g}_4,$$ (4)

and a_pd, g₁, g₂, etc. are the cascaded systems parameters defined in Table Table I.. The DQE was computed as a function of x-ray tube voltage (70–140 kVp), added filtration (0–0.5 mm Cu), and mean detector signal (which in turn relates to tube mAs and patient dose). An antiscatter grid was included in the calculations by a simple approximation assuming uniform, energy-independent transmission factor of 70% (equal to the nominal value measured for the custom grid described below across the pertinent range of kVp).

The mean detector signal was varied from 1 to 100 times the electronic noise floor (σ_add) and was computed as the signal in the center of the projection after attenuation by a simple object model representing a knee. The knee model consisted of a 16 cm diameter water cylinder with an 8 cm diameter inner cylinder emulating bone (e.g., the femoral condyles). The inner cylinder consisted of a 0.4 cm thick cortical bone²⁸ surrounding a 7.6 cm diameter cylinder of trabecular bone.²⁸ For the nominal x-ray beam and number of projections (Table Table I.), the range in mAs and radiation dose (to the center of a 16 cm uniform water cylinder) corresponding to the range 1–100 × the noise floor was 0.0008–0.08 mAs and 0.042–4.2 mGy, respectively.

The required tube power was also estimated for each combination of kVp, added filtration, and mean detector signal. The tube power was computed as the product of tube voltage and tube mAs (per projection) needed to achieve the desired detector signal, divided by pulse lengthτ.

Experimental study of imaging performance

In addition to theoretical analysis based on the cascaded systems model, experimental characterization and optimization of the proposed extremities CBCT scanner was performed using a cone-beam imaging test bench. The results of the cascaded systems analysis were used as guidance in the selection of x-ray technique and beam filtration employed in the experimental studies.

CBCT imaging bench

The bench illustrated in Fig. 2 provided a precise, flexible range of source-detector geometry and acquisition techniques and was used as an experimental testbed emulating the prototype scanner. The source and detector are each mounted on 3 DOF translation stages (406XR and HLE60SR linear stages, Parker Hannifin, Cleveland, OH), and the object to be imaged rotates during the scan using a Dynaserv G3 servo drive with a DR1060B motor (Parker Hannifin, Cleveland, OH) with resolution of approx. 0.00055°/step. Motion control is provided by a Compumotor 6k8 (Parker Hannifin, Cleveland, OH), and synchronization of motion, x-ray exposure, and FPD readout is obtained by custom C++ software (VISUAL STUDIO 2008, Microsoft, Seattle, WA). Geometric calibration was performed using the method proposed by Cho et al.³³ For experiments described below, the system geometry was set to that described in relation to Fig. 1.

Figure 2.

Experimental CBCT imaging bench. The flat-panel detector (FPD) and the x-ray source (X) with a collimator (C) are mounted on three translation stages each (T₁–T₃ and T₄–T₆, respectively), allowing for precise motion along the three major axes of the imaging system. The object (Obj) is placed on a rotation stage (θ), which is mounted on another motorized translational axis (T₇) and can thus be moved laterally. The bench is depicted here in a geometric configuration emulating the prototype extremities scanner. The coordinate systems of the detector (u,v) and reconstructed volume (x,y,z) are also illustrated.

The FPD and x-ray source employed on the bench were different from the components specified for the prototype scanner but were believed similar enough to support initial experimentation and characterization of image quality and dose anticipated with the scanner prototype. Specifically, the FPD was a PaxScan 4030CB (Varian Imaging Products, Palo Alto, CA) with a format of 2048 × 1536 pixels at 0.194 mm pitch and a 250 mg/cm² CsI:Tl converter. Aside from the larger lateral FOV (viz., 40 cm instead of 30 cm), the detector is identical to the PaxScan 3030+ on the proposed system. The x-ray tube was a DU694 in EA10 housing (Dunlee, Aurora, IL) with a 14° anode angle, focal spot size of 0.4 or 0.8 mm and maximum tube voltage of 150 kVp powered by an 80 kW generator (Indico, CPI, Mississauga, ON). These capabilities exceed those of the Source-Ray tube proposed for the scanner prototype, so benchtop experiments utilized techniques falling as close as possible to those available with the proposed system. Specifically, a 0.4 mm focal spot size was used throughout (compared to 0.5 mm), and x-ray techniques were limited to 60–120 kVp within the basic power limits (0.8 kW) of the proposed system. The collimator assembly included added filtration appropriate to the scanner prototype, and a bowtie filter was not used in the current work. An additional discrepancy between the benchtop studies and scan techniques envisioned for the prototype is that the bench employs step-and-shoot rotation (with pulsed exposure), whereas the prototype will involve continuous source-detector motion (also with pulsed exposure). The discrepancy is believed to be small, since the prototype will involve pulsed exposures during which motion blur over the duration of each pulse (no longer than 30 ms) is believed to be minor, as mentioned in Sec. 2A. In short, the bench was considered a reasonable emulation of the proposed prototype, with the system geometry closely replicated and small discrepancies associated with focal spot size and system motion.

Nominal acquisition techniques involved 480 projections acquired over 240° (angular step 0.5°) A custom 10:1 antiscatter grid (detailed below) was employed unless otherwise mentioned. Image reconstruction was performed using an in-house implementation of the Feldkamp algorithm³⁴ with a nominal Hann apodization filter with cut-off at the Nyquist frequency. Since the source-detector orbit is slightly greater than 180°+fan, extended Parker weights proposed by Silver³⁵ were used to appropriately reweight the projections.

The acquisition parameters were varied incrementally in kVp and mAs, including three specific, nominal protocols (all 90 kVp + nominal filtration with 480 projections as in Table Table I.): (i) a “Standard” protocol involving 0.1 mAs per projection, with the detector operated in half-resolution mode (2 × 2 binning, 0.388 mm pixel pitch) and 0.5 mm voxels; (ii) a “HighQ” protocol involving 0.25 mAs per projection and half-resolution readout (2 × 2 pixel binning) and 0.5 mm voxels; and (iii) a “Sharp” protocol involving 0.25 mAs per projection, with full-resolution detector readout (1 × 1 binning, 0.194 mm pixels) and 0.15 mm voxels. In each case, the projections were processed prior to reconstruction by dark-flood-defect corrections involving 50 unexposed “dark” frames and 50 “flood” frames acquired with no object in the field of view.

Imaging dose

The radiation dose was characterized as a function of kVp (80, 90, and 110 kVp) and tube output (varied 0.1–0.5 mAs per exposure) for a fixed added beam filtration of 4 mm Al + 0.3 mm Cu. Measurements were performed using a RadCal Accu-Pro 9096 multipurpose radiation meter (Radcal, Monrovia, CA) with a high dose-rate, 0.6 cc active volume ionization chamber at the center of a 16 cm CTDI phantom (Radcal model 20CT6). The imaging bench was set to emulate the geometry and the CTDI phantom was placed at isocenter. The general setup (i.e., a long cylindrical phantom and Farmer chamber) is generally consistent with the methods suggested in AAPM Task Group 111 (Ref. ³⁶) for volume CT dosimetry. For each combination of kVp and mAs, 30–40 exposures were acquired, and the measured doses were averaged to yield the dose per projection at the isocenter (D_proj, mGy). The total dose at the isocenter was given by the number of exposures (nominally N_proj = 480) times the dose per projection: D_center = N_proj · D_proj. Note that a direct comparison of the total point dose at isocenter (D_center) with CT imaging dose reported in terms of CTDI_vol (as in Biswas et al.¹³) is problematic due to differences between the methodology used here (typical for volumetric beam dosimetry in CBCT) and the standard setup employed for measuring CTDI_vol. Peripheral dose is not accounted for in D_center, as opposed to CTDI_vol. A simple experiment, in which the peripheral dose measured in the CTDI phantom for two projection angles (0° and 45°) were interpolated to simulate a 240° acquisition, demonstrated however that the central dose D_center gives only a ∼10% underestimate of the dose computed with inclusion of peripheral measurements in a manner analogous to CTDI_w ($D_w=1∕3·D_{\mathrm{center}}+2∕3\stackrel{-}{D_{\mathrm{periph}}}$, where $\stackrel{-}{D_{\mathrm{periph}}}$ is the mean of the doses measured in the 4 cardinal peripheral locations). This result was confirmed with direct measurements on the prototype scanner. The point dose at isocenter can therefore serve as a reasonable approximation of the average dose in the central imaging plane for the short scan orbit on the proposed system. In this sense, an indirect correspondence exists between D_center and CTDI_vol, which can similarly be interpreted as a predictor of the axial plane average dose at the center of the scan length. CTDI_vol therefore serves as a reasonable benchmark (“yardstick”) against dose measurements presented in this paper, recognizing the limitations of such a comparison caused by differences in the overall radiation distribution between the cone-beam system proposed here and conventional CT. The effective dose at isocenter was derived from the absolute dose (D_center) times the scan length (nominally 20 cm) and organ-specific weighting factor for distal extremities (F_extremity = 0.0005 mSv/mGy · cm).^{37, 38}

SDNR measurements and assessment of antiscatter grid

A custom antiscatter grid (Jungwon Precision Industrial, Korea) was developed for the proposed scanner. The grid is 33 × 34 cm² in size and incorporates a linear set of Pb strips interspersed with Al at 200 lines per in. The grid ratio is 10:1, and the focal distance (56 cm nominal focus with 40–70 cm specified focal length range) is consistent with the compact geometry of the scanner. The effect of the grid on image uniformity and image quality was assessed on the imaging bench using a 16 cm diameter SolidWater^™ cylinder with six tissue-mimicking inserts: 2 × “adipose”, 2 × “solid water”, 1 × “breast”, 1 × “inner bone” (Gammex, Madison WI). The phantom was scanned under three scenarios: (i) with a grid and narrow “fan” collimation (∼2 cm beam width at isocenter); (ii) with a grid and full-field (20 cm) collimation; and (iii) no grid and full-field collimation. The signal-difference-to-noise ratio (SDNR) in tissue inserts was measured as a function of dose for each scenario:

$$\mathrm{SDNR}=\frac{2|{\stackrel{-}{\mu }}_{\mathrm{insert}}-{\stackrel{-}{\mu }}_{\mathrm{background}}|}{({\sigma }_{\mathrm{insert}}+{\sigma }_{\mathrm{background}})},$$

where μ_insert is the mean voxel value in a (18 × 18 × 1) voxel region of interest (ROI) within an insert, μ_background is the mean voxel value in ROI of the same size in the immediate neighborhood of the insert at the same radius, and σ_insert and σ_background are the standard deviation of pixel values in the two ROIs. The SDNR was computed for 21 reconstruction slices centered on the central slice. System performance was characterized in terms of the mean and standard deviation of this ensemble of slice SDNRs.

Cadaver study

As an initial qualitative comparison of potential image quality anticipated with the prototype scanner in comparison to conventional CT, a fresh cadaveric knee and hand were scanned on both the benchtop and a clinical CT scanner (Siemens Somatom Definition, Siemens, Germany). Each specimen was imaged using the nominal CBCT bench protocols specified above, with and without the antiscatter grid. The CT images were acquired using clinical protocols standard for extremities at our institution – viz., for the knee: 120 kVp, 229 total mAs, (0.422 × 0.422 × 0.75) mm voxels; and for the hand: 120 kVp, 182 total mAs, (0.275 × 0.275 × 0.75) mm voxels. Basic qualitative assessment of spatial resolution, soft-tissue visualization, and potential diagnostic utility were conducted in collaboration with two expert musculoskeletal radiologists.

RESULTS

MTF

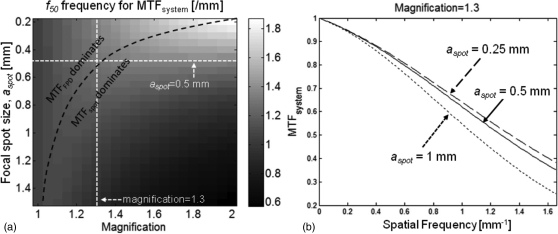
Figure 3a presents f₅₀ of the system MTF as a function of system magnification (horizontal axis) and focal spot size. The interplay between the detector MTF and focal spot MTF leads to an optimal ridge of elevated f₅₀, denoted by black dashed line. In the area below this boundary, the system resolution is dominated by MTF_spot, with f₅₀ decreasing with increased magnification. The x-ray source intended for the use in the proposed scanner provides a 0.5 mm focal spot. For this focal spot size, system magnification of 1.3 corresponds to the optimum at which MTF_system transitions from the region dominated by the detector to the region dominated by the focal spot. This is further illustrated in Fig. 3b, where the system MTF is depicted for a fixed magnification of 1.3 and variable focal spot size. There is diminishing return in decreasing the focal spot size below 0.5 mm, indicating that the system resolution becomes determined mainly by the detector pixel aperture. The system presampling MTF for a_spot = 0.5 mm declines to 50% at ∼1.3 mm⁻¹ and to 10% at ∼2.7 mm⁻¹, consistent with sub-millimeter spatial resolution. Based on this analysis, magnification of 1.3 was chosen for the proposed system in order to achieve optimal trade-off between source and detector blur.

Figure 3.

MTF analyzed as a function of system geometry and focal spot size. (a) Frequency at which MTF_system = 0.5 (f₅₀) is shown as a function of focal spot size and system magnification. The dashed black line indicates the boundary between the region dominated by detector MTF and the region dominated by focal spot MTF. (b) System MTF plotted for three values of focal spot size at a fixed magnification of 1.3. Reducing the focal spot size below 0.5 mm yields only marginal improvements in MTF_system, where this combination of magnification factor and focal spot size (marked with white dashed lines in (a)) corresponds to the optimum between regions dominated by MTF_FPD and MTF_spot.

DQE

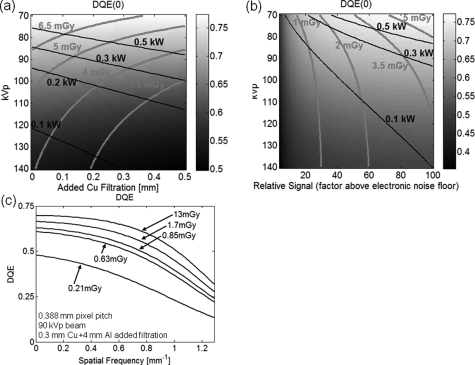
Figure 4a shows zero-frequency DQE as a function of tube voltage (vertical axis) and added Cu filtration. The detector signal level behind the knee model in this calculation was fixed to 100 × the electronic noise floor σ_add. The dose required for achieving this signal level for a given combination of kVp and added Cu filtration is represented by the black isodose lines; similarly, pink iso-power lines signify the required source power. The DQE increases with decreasing kVp due to increased absorption in the detector, at a cost however of increased patient dose because of larger attenuation in the tissues. Similarly, the source power required to achieve a given signal level increases for softer beams. For a fixed tube current, using more aggressive filtration has small effect on DQE and tends to reduce the imaging dose, at the cost however of increasing the source power output needed to achieve a given detector signal. The fixed anode x-ray tube intended for the extremities CBCT system can deliver powers of up to 0.875 kW, but for frequent, repeated scanning, maintaining the output at approx. 0.5 kW provides a desirable safety margin with respect to heating considerations. This, combined with the desire to maintain the dose below ∼5 mGy per scan (approx. 1/3 of the mean CTDI_vol value reported to be 18.39 mGy for conventional knee CT exams¹³) suggest using x-ray tube voltage of approximately 90 kVp and added filtration of approx. 0.3 mm Cu for optimal DQE. Figure 4b shows the dependency of zero-frequency DQE on tube voltage and the detector signal level for a fixed filtration of 0.3 mm. After an initial steep increase, DQE(0) becomes a relatively slowly increasing function of detector signal, and thus also of imaging dose. Across all the kVp values investigated here, DQE(0) is largely independent of dose for doses above approx. 2 mGy. This indicates diminishing effect of electronic noise and quantum-limited operation of the system. Figure 4c further validates this point by analyzing the spatial-frequency-dependent DQE as a function of dose. For all the frequencies up to the Nyquist frequency of the detector, the gain in DQE for imaging doses larger than ∼1.5 mGy is small, suggesting quantum-limited operation of the system. Overall, the calculations suggest that employing an x-ray technique of 90 kVp + 0.3 mm added Cu filtration will provide quantum-limited operation and relatively high DQE, while maintaining patient dose below 5 mGy and with source power requirements below 0.5 kW per pulse.

Figure 4.

DQE analyzed as a function of kVp, filtration, and dose. (a) Zero-frequency DQE as a function of x-ray spectrum (kVp) and added Cu filtration for a fixed detector signal level of 100 × electronic noise floor. The dose and source power required to achieve detector signal of 100 × electronic noise are indicated by the pink isodose contours and black iso-power contours. Operating at 90 kVp and 0.2–0.4 mm Cu gives relatively high DQE (∼0.7) while maintaining the dose below 5 mGy and the source power below 0.5 kW. (b) Zero-frequency DQE as a function of kVp and the detector signal level for a fixed filtration of 0.3 mm Cu. The system appears to be quantum limited for doses above ∼2 mGy. This is further corroborated in (c) where DQE(f) is plotted for various dose levels and a fixed beam of 90 kVp + 0.3 mm Cu. The frequency axis covers the range up to the Nyquist frequency of the detector. There is little improvement in DQE above ∼1.5 mGy, indicating quantum-limited operation of the system.

Imaging dose

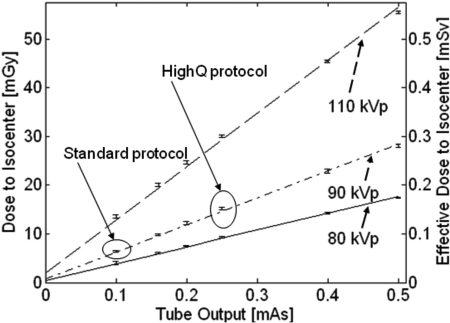
Measurements of dose on the test-bench in the proposed scanner geometry are summarized in Fig. 5. Linear fits to the measured data are superimposed over the experimental results. The error bars represent plus/minus one standard deviation of the repeated measurements of dose. For tube output of 0.1 mAs per projection and a 90 kVp + 0.3 mm Cu beam (corresponding to the “Standard” protocol defined in Sec. 2D), the measured dose is approx. 6.4 mGy (0.064 mSv) for a scan of 480 projections; for tube output of 0.25 mAs/projection (the “HighQ” protocol), the dose is approx. 15 mGy (0.15 mSv). The results obtained in the experimental study of cadaveric extremities indicate that the detector signal behind a knee for a single exposure at 0.1 mAs is approx. 100 times the electronic noise (estimated as standard deviation in an ensemble of 50 offset frames), closely resembling the conditions simulated in the cascaded systems model of DQE. Whereas the cascaded systems model calculations estimated the dose for this signal level to be 4–5 mGy, the measured value was 6.4 mGy, with discrepancies most likely due to inaccuracies in modeling of the x-ray spectrum and x-ray scatter.

Figure 5.

Dose to the center of a 16 cm CTDI phantom placed at the iso-center of the proposed extremities CBCT system as a function of tube output (mAs) for a scan of 480 projections. Solid line: 80 kVp beam, dash-dotted line: 90 kVp beam, dashed line: 110 kVp beam. The two imaging protocols used throughout this study are marked on the graph: the bone protocol at 0.1 mAs/projection and the soft-tissue protocol at 0.25 mAs.

SDNR and the efficacy of the antiscatter grid

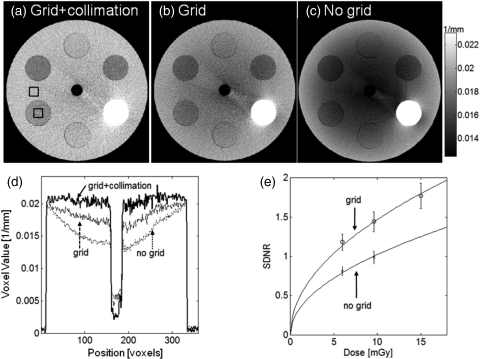
The short object-detector distance of the proposed extremities scanner leads to a relatively large contribution of scatter to the detected signal. Figure 6a shows a reconstruction of a 16 cm diameter cylindrical phantom obtained in a setup where the scatter fraction was minimized by using a narrowly collimated beam and an antiscatter grid. Even in the presence of the grid, a cupping artifact emerges when the collimation is widened to cover the full field of view [Fig. 6b]. The artifact becomes significantly more severe if no grid is employed [Fig. 6c]. Comparison of image profiles [Fig. 6d] indicates that the antiscatter grid yields almost 50% decrease in the magnitude of the cupping artifact compared to a grid-less acquisition. The influence of a grid on the contrast-to-noise ratio in the reconstruction is a trade-off between the reduction in noise and increase in image uniformity caused by the rejection of scattered photons and the decrease in the primary x-ray flux due to attenuation in the grid. Figure 6e compares the SDNR of one of the soft-tissue inserts of the phantom for acquisitions with and without the grid. The error bars represent the standard deviation of the SDNR measurement across 21 reconstruction slices. The use of a grid improves the SDNR compared to grid-less acquisition for all the investigated imaging doses. The tradeoff between improved contrast and potentially increased noise therefore favors the use of a grid for the compact scanner geometry. The significant decrease in the magnitude of cupping and lack of apparent deterioration of SDNR confirm the usefulness of the grid in the proposed CBCT system.

Figure 6.

Comparison of reconstructions of a cylindrical phantom acquired under the following conditions: (a) collimated beam and an antiscatter grid (low scatter conditions), (b) grid with full FOV collimation, (c) no grid and full FOV collimation (high scatter conditions). (d) Image profiles along central the horizontal row of the reconstructions shown in (a), (b), and (c). (e) Signal-difference-to-noise ratio as a function of dose for imaging with and without the grid. The SDNR is measured using the two ROIs marked with black squares in (a). The use of the grid improves SDNR without increase in dose.

Image quality in cadaveric specimens

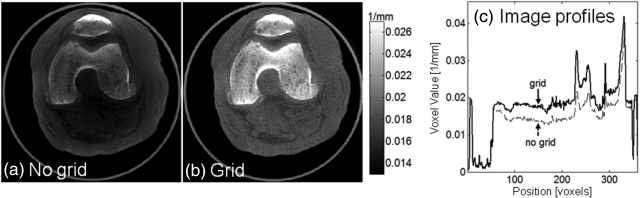
The effect of the antiscatter grid in a realistic imaging scenario is investigated in Fig. 7, comparing a reconstruction of a cadaveric knee obtained with and without the grid. Reduction in cupping and improvement in the visualization of soft tissues is apparent, further supporting the use of an antiscatter grid in the proposed system. Of course, scatter correction algorithms are the subject of ongoing work, and the eventual clinical solution likely involves both an antiscatter grid and a scatter correction algorithm.

Figure 7.

A cadaveric knee imaged (a) without and (b) with an antiscatter grid. Comparison of central vertical image profiles through (a) and (b). The grid improves image uniformity and soft-tissue contrast resolution.

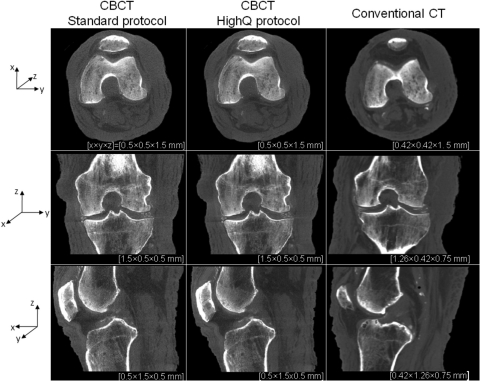
Figure 8 compares the reconstructions of a cadaveric knee obtained on the test-bench emulating the proposed CBCT system and on a conventional CT scanner employing the protocol typically used at our institution for extremities imaging. The CBCT reconstructions, originally obtained on an isotropic grid of 0.5 mm voxels, were averaged in the direction perpendicular to the displayed slice in order to reduce noise. The conventional CT reconstructions are at matching voxel size. The level of soft tissue visibility in the CBCT images is comparable to that of conventional CT, although there remains significant improvement to be gained through further optimization of reconstruction techniques and artifact correction. There is an appreciable decrease in image noise when the higher-dose “HighQ” protocol is used, but the overall level of soft-tissue discrimination is similar in both CBCT images, in agreement with the results of the CSA studies of detectability. The spatial resolution of the FPD-based system is slightly higher than that of a conventional CT, which is apparent in the visualization of bony details and of calcifications in the joint space.

Figure 8.

Reconstructions of a cadaveric knee obtained on the CBCT test-bench emulating the proposed extremities scanner and on a conventional CT system. CBCT images are shown for protocols corresponding to high-contrast bone visualization (0.1 mAs per projection and 2 × 2 detector binning) and soft-tissue visualization (0.25 mAs per projection and 2 × 2 detector binning). Axial, coronal, and sagittal slices through the reconstructions are presented (top to bottom row); in each case several slices perpendicular to the display direction were averaged to reduce noise. Voxel dimensions are listed beneath each image, with x, y, and z directions indicated by the axes at left.

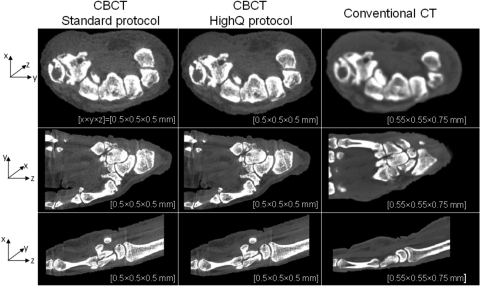
In Fig. 9, reconstructions of a cadaveric hand obtained with the benchtop simulating the proposed scanner geometry are compared to conventional CT in a manner similar to the knee images in Fig. 8. The images demonstrate that the proposed CBCT system should be capable of providing similar soft-tissue discrimination and slightly higher spatial resolution than conventional CT.

Figure 9.

Comparison of reconstructions of a cadaveric hand obtained on the CBCT test-bench emulating the proposed extremities scanner and conventional CT system. Similar to Fig. 8 CBCT images obtained with the “Standard” and “HighQ” protocols are shown. Voxel sizes are roughly matched between the CBCT and conventional CT for sake of comparison. The CBCT images exhibit similar contrast resolution and slightly improved spatial resolution in comparison to conventional CT.

DISCUSSION AND CONCLUSIONS

A novel cone-beam CT system for imaging of musculoskeletal extremities has been developed in a process that utilized cascaded systems analysis to guide scanner design within the constraints imposed by clinical requirements and basic mechanical considerations. The system is unique in that it allows imaging of weight-bearing extremities in natural stance and permits side entry into the bore, thus greatly simplifying patient setup. The system naturally combines capability for 2D projection imaging, fluoroscopy, and 3D tomography in a single compact device that has a footprint similar to a typical radiographic unit. The small size of the scanner posed various design challenges, including high scatter fraction resulting from a very short air gap. To address this issue, a custom focused antiscatter grid was manufactured. Its initial evaluation demonstrated significant reduction in cupping artifact and improvement in SDNR over a gridless acquisition, with no increase in patient dose.

Clinical requirements for the scanner included sub-millimeter spatial resolution and adequate soft-tissue visibility at imaging dose no larger than conventional extremities CT. Cascaded systems analysis of the proposed design indicated that this clinical requirement could be attained within the power and focal spot size limitations of the x-ray source for x-ray technique of 90 kVp (+0.3 mm Cu) and system magnification of 1.3. This theoretical finding was corroborated by test-bench cadaver studies. The resulting hand and knee images demonstrate soft-tissue visibility comparable to and spatial resolution likely exceeding that of conventional CT at radiation dose of approximately 6.4 mGy per scan. Note that the imaging protocols considered in this work were obtained through CSA analysis based exclusively on a knee model (worst-case scenario in terms of object attenuation); significant reduction in the dose required for hand imaging is expected after further optimization considering such a smaller object. The experimental results provided validation for the basic assumptions behind the CSA scanner model, demonstrating acceptable agreement between the simulation results and the measured dose values and detector signal level.

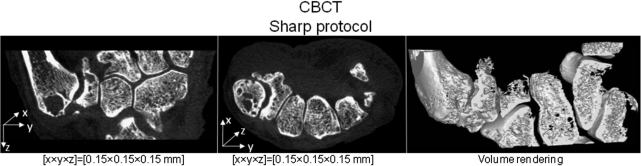
The flexibility of FPD technology and the open and task-specific design of the proposed system present an opportunity to develop and rapidly deploy dedicated image acquisition and reconstruction techniques. This in turn may enable novel diagnostic capabilities that reach beyond current clinical practice. As an example, Fig. 10 shows a reconstruction obtained using “Sharp” protocol, which combines full resolution read-out with the same x-ray technique as in the “HighQ” protocol. Exquisite visualization of bone and joint morphology has been achieved. Such high-resolution, volumetric in-vivo imaging may prove valuable in the diagnosis of degenerative diseases of the MSK system, e.g. arthritis and osteoporosis. Current work on novel applications for the scanner includes dual-energy imaging, functional 3D/4D motion studies, and advanced reconstruction methods, including statistical, iterative, and model based approaches.

Figure 10.

Coronal and axial slice through the reconstruction of a cadaveric hand obtained from a test-bench scan using the ”Sharp” protocol, as defined in the paper (1 × 1 detector binning, voxel size of 0.15 mm and 0.25 mAs per projection). Volume rendering of this data (performed along a curved surface) is shown in the rightmost column, demonstrating the fine level of structural detail provided by the CBCT system.

A number of limitations of the proposed system are recognized. The scan time is expected to be ∼30 s, which may necessitate immobilization of the extremity under examination to avoid motion artifacts. Analogous MR imaging systems with even longer scan times (e.g., the ONI extremities scanner³), accomplish immobilization primarily through simple insertion of cushions about the extremity within the bore. Initial testing of somewhat more sophisticated solutions (e.g. an inflatable bladder within the gantry) show promise and will be deployed based on initial experience gained from a patient imaging pilot study. Imaging in the presence of metallic implants is a notoriously difficult problem in CT and a frequent challenge in MSK radiology. A variety of artifact correction methods are under development, and promising results have been obtained with a model-based approach in which exact knowledge of a prosthetic shape is combined with an iterative, statistical reconstruction algorithm that simultaneously computes the image reconstruction and the position of the implant.³⁹ This approach has been evaluated for surgical spine hardware, and its adaptation to the context of joint implants is ongoing. Other pertinent corrections under development include implementation of scatter and beam-hardening corrections. Reduction of scatter artifacts beyond that achieved with the antiscatter scatter grid is being investigated with both simple measurement-based techniques⁴⁰ and a more sophisticated reconstruction-based approach employing GPU-accelerated Monte Carlo simulation of the scatter fluence.⁴¹

The proposed system addresses a breadth of clinical needs in MSK radiology by overcoming major limitations of digital radiography (superposition of anatomical structures) at a fraction of the cost and complexity of conventional CT and MRI and at a low imaging dose. The value of high-resolution volumetric imaging in the diagnosis of MSK extremities has been indicated by several studies, e.g., for arthritis² and occult fractures.¹ It is therefore expected that the proposed system will have significant impact on the standard of care by making volumetric imaging more accessible and combining it with digital radiography and dynamic real-time fluoroscopy within the same platform. Furthermore, the capability to image weight-bearing extremities offers improved capabilities in imaging tissue impingement syndromes, thus opening avenues for novel diagnostic approaches. A prototype scanner has been constructed¹² based on the studies detailed above and will be deployed in pilot studies targeting orthopedic imaging of the knee (including weight-bearing exams and total knee replacement) and the hand (including monitoring of fracture healing and arthritis therapy response).