Comparisons of four approximation algorithms for large-scale linkage map construction

Abstract

Efficient construction of large-scale linkage maps is highly desired in current gene mapping projects. To evaluate the performance of available approaches in the literature, four published methods, the insertion (IN), seriation (SER), neighbor mapping (NM), and unidirectional growth (UG) were compared on the basis of simulated F₂ data with various population sizes, interferences, missing genotype rates, and mis-genotyping rates. Simulation results showed that the IN method outperformed, or at least was comparable to, the other three methods. These algorithms were also applied to a real data set and results showed that the linkage order obtained by the IN algorithm was superior to the other methods. Thus, this study suggests that the IN method should be used when constructing large-scale linkage maps.

Introduction

The development of molecular markers is necessary for genetic mapping and gathering genetic information that can increase the accuracy of genetic predictions for traits of economic importance in crop and animal species. Linkage mapping, as one of the most important steps in genetic mapping, plays a crucial role in identifying genes and/or quantitative trait loci. With the advance of technology and increasing demand for high-quality linkage maps, the number of loci examined in different chromosome regions is continuously growing, resulting in a quickly increasing computational burden. Thus, a linkage method combining both the speed and the accuracy for ordering a large number of loci is greatly needed.

Marker ordering was once considered as a special case of the travelling salesman problem (Liu 1998), a classical, non-deterministic polynomial time complete problem (Wilson 1988; Olson and Boehnke 1990; Falk 1992). There are two types of approaches for tackling this problem. The first approach is to find the global optimal solution by performing exhaustive searches. However, this approach requires computing all the possible orders of the genetic loci. Given n loci on a chromosome, n!/2 distinct orders would need to be evaluated. Even for just 10 loci on one chromosome, there are 1,814,400 possible orders. In actual situations, n might vary from dozens to several hundred loci. An exhaustive search is clearly computationally intractable when the number of loci is greater than 30 (Mester et al. 2003a, b; Van Os et al. 2005). Therefore, algorithms to obtain near-optimal solutions are more desirable for large-scale linkage mapping (Liu 1998; Wu et al. 2003).

To date, several approximate algorithms for determination of linkage order have been proposed, including seriation (SER) (Buetow and Chakravarti 1987), simulated annealing (SA) (Thompson 1984; Weeks and Lange 1987), branch and bound (BB) (Lathrop et al. 1985), stepwise likelihood (Lathrop et al. 1984), neighboring mapping (NM) (Ellis 1997), evolutionary strategy (ES) algorithm (Mester et al. 2003b), nearest-neighboring-end algorithm (Crane and Crane 2005), recombination counting and ordering (RECORD) (Van Os et al. 2005), the unidirectional growth (UG) approach (Tan and Fu 2006), and minimum spanning tree (MST) approach (Wu et al. 2008). The insertion (IN) algorithm, which is one element of the RECORD algorithm, is a pseudo BB algorithm with the advantage of reaching a better solution (Van Os et al. 2005). Many of these algorithms have been implemented in software packages such as LINKAGE (Lathrop et al. 1984), MAPMAKER (Lander et al. 1987), LINKAGEMAP (Eppig and Eicher 1983), JoinMap (Stam 1993; Stam and Van Ooijen 1995), LINKAGE-1 (Suiter et al. 1983), GMendel (Echt et al. 1992), PGRI (Lu and Liu 1995), MSTMap (Wu et al. 2008), and CarthaGene (de Givry et al. 2005).

Olson and Boehnke (1990) compared eight different methods for marker ordering. In addition to multilocus likelihood, they also considered simpler criteria for preliminary, large-scale multipoint marker ordering problems based on two-point linkage data (by minimizing the sum of adjacent recombination frequencies, SARF or the sum of adjacent distances, SAD) (Falk 1992). In addition to SARF and SAD, other proposed criteria for searching for an optimal solution order based on two-point linkage data of a given set of loci included Lalouel’s least squares method (Jensen and Jorgensen 1975; Weeks and Lange 1987), product of adjacent recombination fraction (PARF) (Wilson 1988), sum of adjacent LOD scores (SALOD) (Weeks and Lange 1987), SALOD divided by the equivalent number of informative meioses (SALEQ) (Edwards 1971), and COUNT (Van Os et al. 2005). Olson and Boehnke (1990) concluded that the SARF and SALEQ were the best overall criteria for linkage mapping. These two criteria were derived with the biologically reasonable assumption that the true order of a set of linked loci has a minimum SARF or a maximum SALOD.

In this study, simulated F₂ data were used to evaluate the performance of four commonly used approaches for linkage mapping: IN, SER, NM, and UG. An actual set of data was also used to compare the performance of these four methods. Thus, the purpose of this study is to test which of these algorithms is most useful for constructing large-scale linkage maps with a combination of both speed and accuracy.

Linkage algorithms and simulation scenarios

There are many approximation algorithms available currently; however, without losing our focus, only four representative linkage algorithms that were the most popularly used in the literature were chosen for our numerical comparisons. The four selected methods were SER (Buetow and Chakravarti 1987), NM (Ellis 1997), UG (Tan and Fu 2006), and IN (Van Os et al. 2005). The rationale of the first three algorithms is to start with two loci (with the shortest distance or smallest recombination frequency, for example) and then to expand the linkage group by adding one of the remaining loci to either end of the linkage map. The key difference of the IN algorithm compared to the three algorithms is to start any two linked loci and expand the linkage group by putting one of the remaining loci into any position of the initial linkage group. Thus, the IN algorithm can be repeated many times by randomly selecting one of unmapped loci at each step to achieve a more desirable linkage map. Without loss of generality, recombination frequency was used in the four compared methods as a criterion for both simulation and actual data analysis. Readers interested in these algorithms may refer to the papers by Buetow and Chakravarti (1987), Ellis (1997), Tan and Fu (2006), and Van Os et al. (2005) for detailed information. In addition, as detailed in the discussion of this paper, we chose JoinMap (Stam 1993) and MSTMap (Wu et al. 2008) to compare with the IN method for the two single simulated data sets with known linked orders.

Since in reality, few real data sets are available with known marker orders, we used computer simulation to generate the data so that the performance of these algorithms could be evaluated. Although there are several widely used experimental populations for linkage mapping, in this study we chose to simulate an F₂ cross derived from two different inbred lines. Probability distributions for distance between adjacent markers are as follows: P (1 < d (cm)<5) = 0.7, P (5 < d (cm) <10) = 0.15, P (10 < d (cm) <30) = 0.10, and P (30 < d (cm) <40) = 0.05, with even distribution within each of four ranges. Two missing genotype rates (0 and 10%) were used across each simulated data set. We also considered both the presence and the absence of recombination interference. In the case of the presence of recombination interference, the recombination interference coefficient was selected with equal probability from the four possible values: 1.0 (no interference), 0.0 (complete positive interference), 0.5 (partial positive interference), and 2.0 (negative interference). The recombination frequency between any two markers was calculated by the EM algorithm (Liu 1998). Since the percentage of correct order (PCO) (Liu 1998) for each locus has been widely used to evaluate the linkage mapping power, the mean PCO values over different loci for different configurations were used to compare the different mapping methods. All simulations were repeated 200 times for each of these configurations. The simulations were conducted by a computer program written by the authors in C++. Though we conducted simulations for linked loci numbers ranged from 10 to 1,000, we only present some representative results for three numbers of co-dominant loci (10, 20, and 50), with population sizes of 50, 100, 150, 200, 250, 300, 350, and 400.

Simulation results

The impact of replications on PCO for the insertion method

Since the linkage order obtained by the insertion algorithm may depend on which pair of loci are used for an initial order, repeating this method is necessary to achieve a desirable solution if a distance matrix is not monotonic, that is, an increase in map distance does not necessarily translate into a larger physical distance, which could result in more than one locally optimal solutions (Liu 1998). Therefore, it is helpful to find how many repetitions are sufficient to achieve a high PCO. The results over four population sizes (50, 100, 150, and 200) and two missing genotype proportions (0 and 10%) for two linked loci numbers (20 and 50) per chromosome and the two statuses of crossover inferences are presented in Fig. 1. Although there are n!/2 possible orders with n loci on the same chromosome, as shown in Fig. 1, the PCO values stabilized after repeating the insertion process more than five times for various configurations. Therefore, we selected 50 repetitions to provide conservative estimates for PCO in the insertion method for each simulated data set.

Fig. 1.

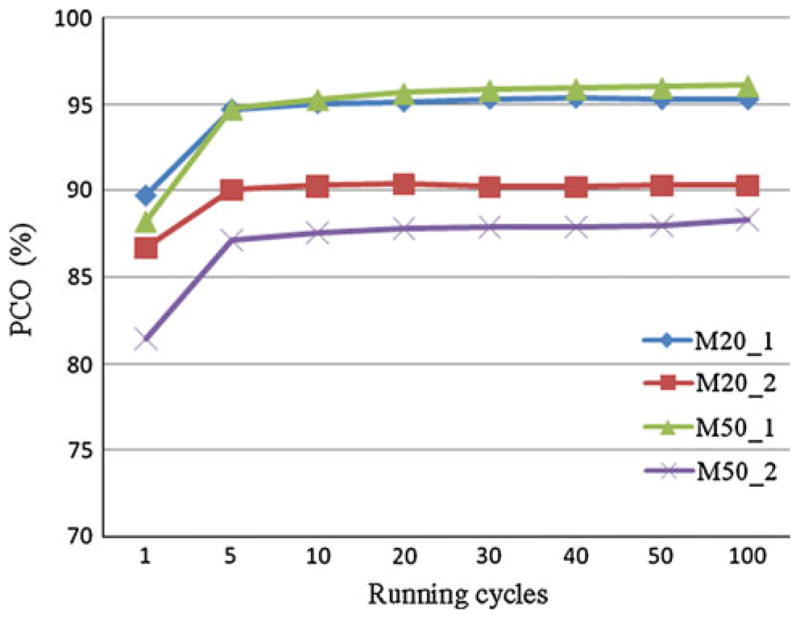
The impact of replications by the insertion method on percentage of correct order (PCO). The first number following capital letter M is the number of markers on a chromosome and the second number is an indication of absence and presence of interference (1 means absence and 2 means presence). For example, M20_1 means 20 markers on one chromosome with no interference

Comparisons of PCO values among four mapping algorithms

The empirical PCO values for eight population sizes, two missing genotype rates, and absence or presence of crossover inference are summarized in Tables 1, 2, and 3. The results showed that the IN algorithm was consistently equal to or greater than the other algorithms in terms of the PCO values for all parameters simulated (Tables 1, 2, 3), suggesting this method is superior among these four algorithms. The major reason is that the locally optimal solution can be avoided by repeatedly using the IN procedure. On average, the NM algorithm was the poorest among the four methods and was the most sensitive to different parameters simulated in this study. The other two algorithms (SER and UG) performed almost equally well in our simulation study.

Table 1.

The percentage of correct orders (PCO, %) obtained by four algorithms for eight different population sizes (PS), absence and presence of crossover interference, and two different missing genotype rates (MS, %) for 10 markers on one chromosome

Independence
PS	MS	SERa	UG	NM	IN (50)
50	0	63.50	68.55	42.80	72.00
	10	59.00	59.85	37.90	66.10
100	0	91.65	92.40	70.75	96.00
	10	87.75	90.40	62.35	94.15
150	0	99.20	99.10	87.50	99.60
	10	96.45	96.30	77.95	98.70
200	0	99.30	99.40	90.90	100.00
	10	98.70	97.80	84.50	99.00
250	0	99.90	99.70	91.70	100.00
	10	99.65	100.00	87.95	100.00
300	0	100.00	99.50	94.00	100.00
	10	99.80	99.70	89.15	99.70
350	0	100.00	100.00	94.40	100.00
	10	100.00	100.00	90.85	100.00
400	0	100.00	100.00	95.20	100.00
	10	100.00	100.00	92.00	100.00
Interference
50	0	82.90	85.00	71.75	90.35
	10	80.45	80.75	64.15	84.65
100	0	93.45	94.90	79.75	96.05
	10	88.65	90.25	73.75	90.95
150	0	92.85	93.65	84.35	94.80
	10	91.85	93.25	78.40	93.60
200	0	96.80	96.30	88.55	97.35
	10	96.40	96.05	83.25	96.85
250	0	96.75	96.30	91.60	97.20
	10	95.90	96.10	84.30	96.50
300	0	94.60	95.10	90.50	95.25
	10	95.45	94.30	87.15	96.00
350	0	95.60	94.95	91.85	96.00
	10	95.35	94.45	87.75	95.45
400	0	97.65	97.65	93.65	97.85
	10	96.20	95.75	86.40	96.50

^aSER seriation, UG unidirectional growth, NM neighbor mapping, IN (50) insertion with 50 repetitions

Table 2.

The percentage of correct orders (PCO, %) obtained by four algorithms for eight different population sizes (PS), absence and presence of crossover interferences, and two different missing genotype rates (MS, %) for 20 markers on one chromosome

Independence
PS	MS	SERa	UG	NM	IN (50)
50	0	81.58	87.63	71.73	91.42
	10	68.63	75.28	54.00	82.80
100	0	97.40	98.17	89.22	99.25
	10	94.83	92.30	82.90	98.32
150	0	99.58	99.05	93.97	100.00
	10	97.67	96.10	85.17	99.30
200	0	99.85	99.80	97.78	100.00
	10	99.15	98.60	90.48	99.70
250	0	99.90	98.45	97.80	99.95
	10	99.22	99.20	92.92	99.75
300	0	100.00	100.00	98.13	100.00
	10	99.70	99.67	92.30	99.85
350	0	100.00	99.95	98.60	100.00
	10	99.95	99.85	95.08	100.00
400	0	100.00	99.50	99.17	100.00
	10	100.00	99.90	95.90	100.00
Interference
50	0	80.63	78.13	72.13	89.72
	10	71.23	72.42	52.90	80.67
100	0	91.50	89.18	85.88	94.85
	10	85.08	81.25	67.17	89.80
150	0	93.10	88.20	89.22	94.13
	10	92.13	89.60	77.83	94.10
200	0	94.00	89.03	88.75	94.90
	10	92.25	89.35	82.97	94.58
250	0	96.30	90.63	94.50	96.85
	10	95.45	93.15	86.30	96.23
300	0	95.38	93.05	92.55	96.63
	10	92.53	90.83	84.65	93.73
350	0	94.47	91.15	92.22	96.10
	10	94.85	92.90	88.35	95.15
400	0	95.35	92.17	94.15	95.60
	10	96.17	91.63	90.10	96.75

^aSER seriation, UG unidirectional growth, NM neighbor mapping, IN (50) insertion with 50 repetitions

Table 3.

The percentage of correct orders (PCO, %) obtained by four algorithms for eight different population sizes (PS), absence and presence of crossover interferences, and two different missing genotype rates (MS, %) for 50 markers on one chromosome

Independence
PS	MS	SERa	UG	NM	IN(50)
50	0	86.75	85.62	77.46	94.80
	10	70.23	71.68	52.62	87.66
100	0	97.64	95.78	94.44	99.69
	10	91.50	87.50	74.27	97.24
150	0	99.66	97.60	98.30	99.98
	10	97.53	90.67	85.51	99.29
200	0	99.90	99.32	98.67	100.00
	10	98.97	96.35	91.77	99.80
250	0	99.98	98.90	99.38	100.00
	10	99.56	97.07	90.95	99.90
300	0	99.96	98.92	99.44	100.00
	10	99.45	97.09	92.81	99.92
350	0	100.00	99.36	99.73	100.00
	10	99.79	97.36	94.80	99.96
400	0	100.00	99.50	99.87	100.00
	10	99.94	99.38	97.18	100.00
Interference
50	0	76.83	77.30	70.25	89.34
	10	62.97	64.27	45.59	79.38
100	0	88.99	88.30	86.51	93.82
	10	80.24	78.58	63.76	87.99
150	0	92.18	90.42	90.36	95.19
	10	90.66	85.95	77.11	96.50
200	0	92.48	90.06	91.60	95.59
	10	93.30	90.93	84.26	96.02
250	0	95.04	93.68	93.82	97.59
	10	91.23	87.58	83.12	94.78
300	0	88.96	85.52	88.47	90.69
	10	93.07	90.16	87.21	95.95
350	0	94.80	92.52	94.44	97.07
	10	91.18	89.01	86.20	92.90
400	0	96.21	92.33	95.97	97.04
	10	95.08	91.32	90.02	96.35

^aSER seriation, UG unidirectional growth, NM neighbor mapping, IN (50) insertion with 50 repetitions

As expected, the mapping power increases as the population size increases or the missing genotype rates decrease. The presence of crossover interference was associated with reduced PCO values. In case of no missing data and absence of interference, a desirable mapping power (≥95%) could be achieved by SER, UG, and IN when population size is 100 or greater. With a missing genotype rate of 10% and absence of interference, a desirable mapping power (≥95%) could be achieved for the SER, UG, and IN methods when populations size is 200 or greater. We also observed that the UG method performed better than the SER and NM for most cases when population size is small (~50). The results were in good agreement with a previous report by Tan and Fu (2006).

With the increase of linked loci (100–1,000) (data not shown), the conclusions remained the same for the small numbers of linked loci. Additional simulations for mis-genotyping rates (10 and 15%) showed that the IN algorithm was the best among these four algorithms. For example, the PCO values for the IN algorithm can keep a desirable level (95%) for 500 linked loci when the population size was 100 and above with mis-genotyping rates of 10 and 15%, on the contrast, the PCO values were less than 15% for the other three algorithms. The results suggested that the IN algorithm was tolerant to high mis-genotyping rates.

A numerical example

To evaluate the performance of these algorithms, we also applied them to a real data set of 26 loci on barley chromosome I from the North American Barley Genome Mapping project (see Liu 1998, p. 288). The linkage orders obtained by the other three methods include the combination of SA and BB algorithms (Liu 1998), UG algorithm (Tan and Fu 2006), and the SER algorithm (Buetow and Chakravarti 1987). Linkage order results for these three methods plus the IN algorithm with 50 repetitions are summarized in Table 4. The linkage orders obtained by the SER and IN algorithms were based on the two-point recombination frequencies. The genetic distances for all four linkage orders were calculated based on Haldane’s mapping function (Haldane 1919), so the total distances listed in Table 4 for the two published linkage orders could be slightly different from the published distances (Liu 1998; Tan and Fu 2006). Even though the different mapping functions may result in different genetic distances, the patterns from different mapping functions should remain the same. Results showed that the total distances obtained by the UG algorithm and the combination of SA and BB algorithms were very similar (150.38 cm vs. 150.11 cm, respectively) (Table 4). The SER algorithm was the poorest in this case, which generated the largest genetic distance (225.52 cm). The IN algorithm with 50 repetitions generated the shortest genetic distance (148.08 cm) and thus it was the best among these four methods.

Table 4.

Marker orders and their genetic distances (cm) obtained from different mapping algorithms for the numerical example

SA and BB		UG		SER		IN (50)
Order	Dist	Order	Dist	Order	Dist	Order	Dist
1a	0.00	1	0.00	1	0.00	1	0.00
2	12.65	2	12.65	2	12.65	2	12.65
3	4.80	3	4.80	3	4.80	3	4.80
4	15.52	4	15.52	5	16.47	5	16.47
5	3.94	5	3.94	4	3.94	4	3.94
6	11.55	7	13.03	7	11.61	7	11.61
7	0.76	6	0.76	6	0.76	6	0.76
8	8.68	9	5.05	8	7.67	9	5.05
9	0.77	8	0.77	9	0.77	8	0.77
10	1.52	10	2.11	10	1.52	10	2.11
11	2.93	11	2.93	11	2.93	11	2.93
12	2.25	12	2.25	12	2.25	12	2.25
13	5.22	14	2.27	14	2.27	13	5.22
14	4.51	13	4.51	15	3.10	14	4.51
15	3.10	15	7.89	16	8.42	15	3.10
16	8.42	16	8.42	17	13.29	16	8.42
17	13.29	17	13.29	18	6.99	17	13.29
18	6.99	18	6.99	19	21.89	18	6.99
19	21.89	19	21.89	20	3.54	19	21.89
20	3.54	20	3.54	21	2.21	20	3.54
21	2.21	21	2.21	22	0.00	21	2.21
22	0.00	22	0.00	24	0.73	22	0.00
23	2.17	23	2.17	23	1.48	23	2.17
24	1.48	24	1.48	25	8.34	24	1.48
25	3.70	25	3.70	26	8.21	25	3.70
26	8.21	26	8.21	13	79.68	26	8.21
	150.11b		150.38		225.52		148.08

^aMarker codes for 1–26 are described on page 288 (Liu, 1998)

^bThe genetic distance obtained by Haldane’s function (Haldane 1919)

SA&BB simulated annealing and branch bound algorithms, UG unidirectional growth, SER seriation, and IN(50) insertion with 50 repetitions

The IN method can generate different locally optimal solutions each time the search procedure is repeated. Based on the results of 500 repetitions by using the IN method, 90 different linkage orders were obtained. With few exceptions, the total genetic distances based on these linkage orders were around 150 cm, which was very close to distances based on two published linkage orders (Liu 1998; Tan and Fu 2006). In addition, we observed that there were 19 times with genetic distance 148.08 cm (the shortest distance), 35 times with the linkage order obtained by Liu (1998), and two times with the linkage order obtained by Tan and Fu (2006). Though the total genetic distance obtained by the SER method was much larger than the other three genetic distances, we found that their linkage orders were similar except marker 13, which was put at the end of the linkage group by the SER method. Suppose that marker 13 is the last marker to be added to the linkage group by using the SER method, this marker can be placed between markers 12 and 14 by employing the IN method, thus, the total linkage distance can be greatly reduced. The above results suggest that the insertion method provides a great opportunity to detect different locally optimal linkage orders by repeatedly running this method. Thus, it also provides an opportunity to achieve the globally optimal linkage order.

Discussion

As mentioned in the “Introduction”, an exhaustive search algorithm is the only feasible for finding the globally optimal solution when the number of marker loci on a chromosome is small. The ES algorithm (Mester et al. 2003b) has the potential to find a desirable linkage order, yet it is computationally intensive and the final solution is dependent on many factors including the cross operator, the mutation operator, and the population size. On the other hand, many approximation algorithms like NM, SER, and UG have the advantage of speed yet they may have a reduced mapping power for some cases because each method is sequential and only one locally optimal linkage order can be found. If a two-point data set for linkage mapping is monotonic, all these approximation algorithms should reach the globally optimal linkage order. However, for the two-point data set, the recombination frequency matrix is calculated from a genetic data set, which could be influenced by the factors such as population size, genetic distance between markers, presence of crossover interference, missing genotype rates, and mis-genotyping rates (Mester et al. 2003a, b). Thus, a recombination frequency or distance matrix sometimes may not be monotonic, which could cause many locally optimal solutions for marker ordering, suggesting that the approximation algorithms are not satisfactory either.

Our simulations showed that the IN method is the best among the four methods evaluated to recover the true linkage orders. The application to an experimental data set (Liu 1998) also showed that the IN method could find the linkage order with the shortest linkage distance. The IN method also has the advantage of speed. Given n loci on a chromosome, a total of (n² + n − 4)/2 steps are needed to reach a locally optimal solution for running one time. Thus, this method is comparable to the SER, near-neighbor, and UG methods regarding speed. The computational load is much smaller compared to the exhaustive search (n!/2) even if this process is repeated for a number of times. Given 1,000 loci per chromosome, it took less than 1 h using a P4 personal computer with a 3.4 GHz CPU and 2.0 GB Ram using the insertion process with 50 repetitions.

A genetic map is a statistical order because it depends on many factors like population type, mapping size, and order algorithm. With the rapid development in DNA sequencing technologies, many DNA markers can be physically positioned on specific chromosomes. Thus, mapping powers for different ordering algorithms can be validated by comparing genetic linkage orders with physical maps in sequenced species. On the other hand, many other species have not been sequenced yet and the IN algorithm can be employed to construct a dense linkage map for the large-scale unmapped loci.

The distance between the adjacent markers has been shown to affect the linkage mapping power. Distances between markers of <5 or >30 cm can reduce mapping power because these distances often have large genetic sampling variations, especially in the presence of crossover interference for small sample sizes (≤100). All four methods can achieve similarly high PCO values with the adjacent distances between markers of 10–20 cm without crossover interference (additional simulated results not shown). In our simulation study, 70% of adjacent marker distances ranged from 1 to 5 cm and 15% of adjacent distances ranged from 5 to 10 cm. For these genetic distances, the IN approach can provide consistently higher mapping power than the other three methods, even for a small population size of 50 individuals (Tables 1, 2, 3). Missing genotype rates and mis-genotyping rates may also be associated with mapping power. Our simulation results showed that the IN algorithm was the best among these four algorithms. It appeared that the IN was robust in obtaining a high PCO value for various missing genotype rates or mis-genotyping rates whereas the SER, UG, and NM algorithms were sensitive to mis-genotyping rates.

Four linkage algorithms were included for our simulation studies. We realized several linkage methods are currently available but were not included in our numerical comparisons. Though some algorithms have been incorporated into some software packages (i.e., MultiQTL, JoinMap, and MSTMap), it is difficult to employ these algorithms for our repeated simulations because these tools can only run one data set at a time and require different data formats. Without losing our focus, we chose JoinMap 4.0 and MSTMap to compare with the insertion method for the two single simulated data sets with known linked orders (F₂ data with 200 linked, sample size 100, and 10% misgenotyping rate, DH data set with 100 linked loci and 100 lines). The F₂ data set was generated by us while the DH data set with an unknown mis-genotyping rate was downloaded from the website http://alumni.cs.ucr.edu/~yonghui/mstmap.html). The F₂ data set was used to compare the insertion method and JoinMap because the MSTMap could not analyze the F₂ data set. The result showed that IN was better than JoinMap. While the DH data set was used to compare JoinMap, MSTMap, and the IN algorithm. The results showed that the MSTMap and the IN algorithm performed equally well (rank correlation was 0.999 for both) but were better than the JoinMap. Thus, we concluded that the IN method was one of robust and desirable linkage algorithms.

Many mapping populations were experimental, each developed from two homozygous parental lines in an acceptable time frame (Liu 1998). Such populations are generally not available for forest trees due to time and/or other practical constraints (i.e. Pekkinen et al. 2005). An alternative way is to use several small families (i.e. Hu et al. 2004; Pekkinen et al. 2005) to construct a reliable linkage map. The calculation of joint recombination frequency may be complicated dependent on data structures. Once the joint recombination frequencies are obtained, these target loci can be grouped and ordered accordingly.