New Methods to Evaluate Craniofacial Deformity and to Plan Surgical Correction

Abstract

The success of cranio-maxillofacial (CMF) surgery depends not only on surgical techniques, but also upon an accurate surgical plan. Unfortunately, traditional planning methods are often inadequate for planning complex cranio-maxillofacial deformities. To this end, we developed 3D computer-aided surgical simulation (CASS) technique. Using our CASS method, we are able to treat patients with significant asymmetries in a single operation which in the past was usually completed in two stages. The purpose of this article is to introduce our CASS method in evaluating craniofacial deformities and planning surgical correction. In addition, we discuss the problems associated with the traditional surgical planning methods. Finally, we discuss the strength and pitfalls of using three-dimensional measurements to evaluate craniofacial deformity.

Each year in the United States, a significant number of patients require CranioMaxillofacial Surgery (CMF) for the correction of congenital and acquired conditions of the head and face. The surgical correction of these deformities is among the most challenging. The success of these surgeries depends not only on the technical aspects of the operation, but to a larger extent, on the formulation of a precise surgical plan.^1–10 Over the last 50 years, there have been significant improvements in the technical aspects of surgery (e.g., rigid fixation, resorbable materials, distraction osteogenesis, minimally invasive approaches, etc). However, the planning methods have remained mostly unchanged^{3, 4, 6, 10}. Unfortunately, many of the unwanted surgical outcomes are the result of deficient planning.

Critical review of traditional methods used to plan CMF surgery

Surgical planning in CMF surgery involves a series of logical steps. These steps include 1) data gathering, 2) diagnosis and quantification of the condition, 3) establishment of a preliminary surgical plan, 3) surgical simulation, 4) establishment of the final surgical plan, and 5) transfer of the plan to the patient.

Data is gathered from a multitude of difference sources. They include the physical examination, medical photographs, plain x-rays (e.g., cephalogram, orthopantomogram), computed tomography (CT) and mounted plaster dental models.^{1, 2} Each of these sources provides a portion of the whole data set that is needed for successful planning. In practice, an orthodontist or a surgeon evaluates in a sequential manner each one of these studies and creates a complete 3D mental picture.

The next step in the planning process is the diagnosis and quantification of deformity. In orthognathic surgery an important part of this process is cephalometric analysis^{1, 11}. After the doctor has formulated the diagnosis, a preliminary plan is developed and in many instances alternative plans.

To test the feasibility of the preliminary plan(s), a surgeon or an orthodontist simulates the planned surgery. In orthognathic surgery, this is done by completing prediction tracings and dental model surgery.^{1, 2} Prediction tracings are done by tracing the silhouette of the facial bones from a two-dimensional cephalogram onto a piece of acetate paper. These tracings are then cut and moved to evaluate possible outcomes. The same prediction tracing can also be done in the computer. Dental model surgery is done on plaster dental models which have been mounted on an articulator. It is done by physically cutting the models and moving them to the desired position. In other types of surgery (e.g., trauma, pathology and reconstruction), the extent of surgical simulation is even more limited. In clinical practice, most of these surgeries are not simulated. Occasionally, surgeons obtain CT-based rapid prototyping physical models (e.g., stereolithography) to simulate skeletal surgery.

After the simulation has been completed, in the 4^th step, the surgeon formulates the final surgical plan. The final step in the planning process is to transfer the surgical plan to the patient at the time of surgery. In orthognathic surgery, this is done by using surgical splints and selected measurements. The splints are fabricated on the same plaster dental models on which the surgery was simulated. In CMF surgeries that do not involve the dentition, surgeons currently do not have a method of transferring the surgical plan to the patient. Although certain measurements taken during the planning process can be used to guide surgery, most of the time the process is more of an art than a science. There have been reports on the use of surgical navigation of this purpose,^12–15 but this technique has not been universally adopted.

There are a number of problems with the traditional planning system. These include:

1. The various data sources utilize different coordinate systems. The physical examination and the medical photographs are taken with the patient’s head oriented to the Natural Head position (NHP). The cephalogram is oriented to the Frankfurt Horizontal (FH) plane and the articulated dental models are oriented to the axis-orbital plane.¹⁶ On an average, these planes differ from each other by about 8°.¹⁶ Currently, most surgeons are unaware of this problem and fail to account for these differences. This discrepancy alone can be responsible for a 15% difference in maxillary projection between planned and actual outcomes.¹⁶

2. Using the traditional method, surgeons are never able to visualize the whole data set in 3 dimensions^{3–5, 10, 17, 18}. As stated above, the surgeons have to create this picture in their minds. This creates a problem communicating with the other members of the treatment team. As it expected, it is impossible to assure that all involved have the same picture.

3. The cephalometric analysis is 2-dimensional. Therefore, it only measures structures in a single plane. It may be appropriate for patients with symmetrical deformities, but is grossly inadequate for patients with asymmetric conditions.^{3, 8} It has been reported that 34% of patients with dentofacial deformities have asymmetric conditions.¹⁹

4. The orientation of dental models mounted on an articulator is often inaccurate. The occlusal plane inclination of models mounted on a semi-adjustable articulator is on average 8° too steep.^{16, 20} In addition, there are design flaws in the current devices used to orient the dental models on an articulator (i.e., the facebow). A patient can easily tilt the facebow during the registration process creating an inaccurate recording of the occlusal cant (roll of the upper jaw). An inaccurate initial model position will always create an inaccurate plan.²⁰

5. The plaster dental models do not depict the surrounding bones. Dental model surgery is done for 2 purposes. The first one is to establish the occlusion and the second is to reorient the models to assure that the bones are placed in the ideal position at surgery. Because plaster dental models do not depict the surrounding bones, the surgeon is unable to visualize the effects of model position on the facial skeleton.^{5, 6, 21} Therefore, the ability to obtain the ideal bone position becomes a random event.^{4, 6, 7}

6. Prediction tracing and model surgery are two separate processes, which are often inaccurate and time consuming.^{3, 22, 23} Currently, an experienced surgeon spends 3–5 hours completing these steps.²⁴

7. As stated above, some surgeons utilized CT-based rapid prototyping models to plan complex surgeries.¹⁷ The drawbacks to these rapid prototyping models include expense (a single model costs about $2500) and inability to simulate different iterations of a given plan on a single model. Once the model is cut, the cut cannot be undone. Finally, they also fail to render the teeth with the precision necessary for surgical planning.^{3, 4, 10}

8. The fabrication of splints is time consuming. A busy surgeon performs several of these operations per week and many patients require 2 splints. The fabrication of each splint may take an additional hour.^{2, 24}

9. For surgeries that do not involve the dentition, surgeons do not have a way of transferring the surgical plan to the patient.^{3, 6, 8, 13}

CASS System for CMF Surgery

Our group has developed a 3D computer-aided surgical simulation (CASS) system in order to improve the traditional surgical planning methods. We have used this system in maxillofacial surgery^{9, 25–27}, craniofacial surgery²⁸, trauma and distraction osteogenesis^28–30. Surgeons can perform “virtual surgery” with this system and create a 3D prediction of the patient’s surgical outcomes as if they are performing surgery in the operating room. We have documented the clinical feasibility^{4, 10}, the accuracy³¹ and cost-effectiveness²⁴ of the system.

Our CASS system has incorporated three distinctive features and innovations: 1) multiple imaging modalities are incorporated to create an accurate model of the craniofacial skeleton; 2) special techniques are used to orient the computerized model in the natural head position; and 3) Computer Aided Design/Computer-Aided Manufacturing (CAD/CAM) techniques are used to fabricate accurate surgical splints and templates to transfer the surgical plan to the operating room.

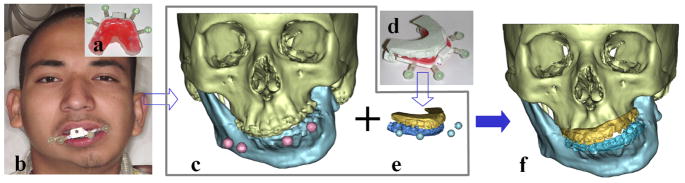
The first step in the computerized planning process is to create a composite skull model. A bite jig with a set of fiducial markers is created (Fig. 1a). A CT scan of the patient’s craniofacial skeleton is obtained with the patient biting on the bite-jig (Fig. 1b). This generates 3 separate but correlated computer models: a midface model, a mandibular model and a fiducial-marker model (Fig. 1c). The plaster dental models with the bite-jig in place are scanned in a micro-CT scanner creating digital dental models (Fig. 1d). This generates 3 additional separate but correlated computer models: an upper digital dental model, a lower digital dental model, and a fiducial-marker model (Fig. 1e). By aligning the fiducial markers, the digital dental models are incorporated into the CT skull model. This results in a computerized composite skull model, which accurately displays both the bony structures and the teeth (Fig. 1f).

Fig 1. The creation of the computerized composite skull model.

a. Bite-jig is created with CT/MRI compatible fiducial markers

b. The patient is biting on the bite-jig with fiducial markers during CT scan.

c. Three separate but correlated computer models are reconstructed: a midface model, a mandibular model and a four-fiducial-marker model.

d. The bite-jig with fiducial markers is placed between the upper and lower plaster dental models during the scanning process.

e. Three separate but correlated computer models are also reconstructed: an upper digital dental model, a lower digital dental model, and a four-fiducial-marker model.

f. The computerized composite skull model simultaneously displays an accurate rendition of both the bony structures and the teeth. (Color version of figure is available online.)

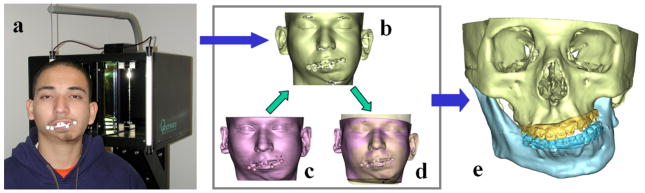
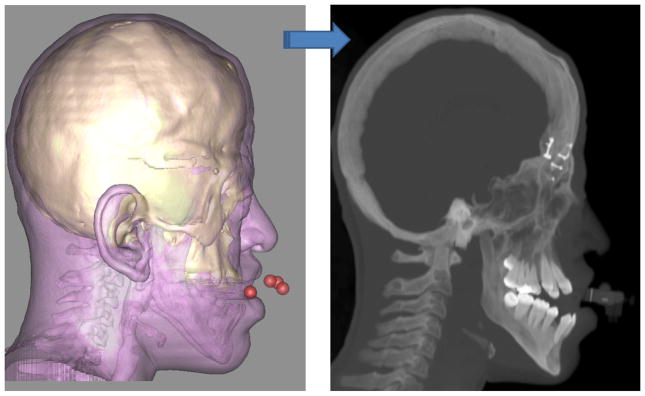
The second step in the process is to orient the composite skull model in the Natural Head Position (NHP). Because many of our patients have significant asymmetries of the upper face and skull base, normal landmarks and planes cannot be used to orient the composite model in the NHP. We have developed 2 techniques to orient the composite model to the NHP. One uses a 3D laser surface scanner (Cyberware Inc., Monterey, CA) (Fig 2) and the other uses a digital gyroscope. With the first technique the surface geometry of the facial soft tissues is captured by a laser surface scanner while the patient is in the HNP. This creates a correctly oriented 3-dimensional image of the face. The soft tissues of the composite model are then rendered and the model is aligned to the NHP by matching its soft-tissues to the scanned image.^{32, 33} With the digital gyroscope the pitch, roll and yaw of the face are recorded, and this information is used to reorient the composite skull model. The advantage of the gyroscope technique is cost. A laser surface scanner costs 100 times more than a gyroscope.

Fig 2. Orientation of the composite skull model to the NHP.

a. The patient is sitting in the center of a calibrated laser scanner with the bite-jig in place.

b. A 3D facial surface model in NHP is generated by the laser scanner.

c. A soft tissue facial model is rendered from the CT scan in addition to the bone models.

d. The soft tissue facial model and its underlying bone models are registered to the laser scanned NHP model.

e. After the CT models are reoriented to the NHP, the soft tissue model is marked hidden. (Color version of figure is available online.)

The third step in the process is to quantify the deformity. A unique 3D coordinate system is created for the composite skull model in NHP. The origin of the coordinate system is soft tissue Nasion. Cephalometric analyses and virtual anthropometric measurements are performed with linear, angular, area and volumetric measurements. This will be discussed in detail in the next section.

The fourth step in the process is to simulate the surgery in the computer. With this system, an operator can simulate any type of osteotomy e.g., Le Fort I, sagittal split, genioplasty, etc. After the bones are cut, the user is able to move them to the desired position. In patients requiring bimaxillary surgery, the maxilla is usually repositioned first. After the upper jaw is moved, the user then proceeds to reposition the lower jaw. This is done by moving it until maximum intercuspation is attained against the upper jaw. Unfortunately, the establishment of this position in the computer is quiet difficult. While the establishment of maximum intercuspation on a set of plaster dental models is quick and accurate, the same is not true in the virtual world. The dental arches are represented by two 3D images which lack collision constraints. The computer system does not stop the images from moving through each other once the model surfaces have made contact. In addition, the operator has no tactile feedback when articulating the models. To solve this problem, our laboratory is developing novel algorithms to automate this function. Once the simulation is completed, the simulated outcomes and surgical movements are recorded. With this system, an operator is able to simulate different surgical alternatives and select the most appropriate plan.

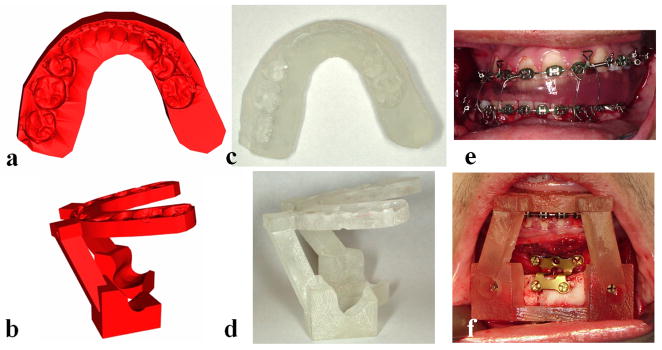
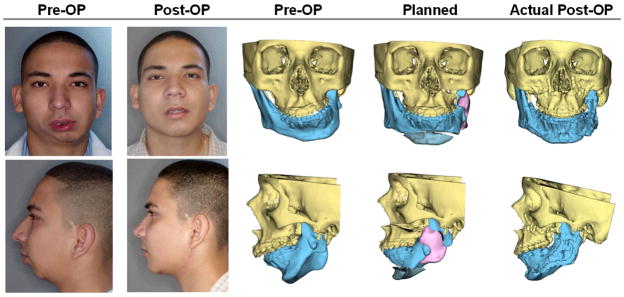
The final step in the planning process is the transfer of the computerized surgical plan to the patient. Surgical dental splints and templates are created for this purpose. They are created by inserting a digital wafer between the maxillary and mandibular dental arches. A Boolean operation is then performed, resulting in a digital surgical splint (Fig. 3a). In surgeries that do not involve the teeth, the system can also generate digital templates (Fig. 3b). These templates record the 3D surface geometry of the area of interest so that the templates fit on the bone in a unique position. Finally, the system exports the digital splints and templates in .stl format to fabricate physical splints and templates using a rapid prototyping machine (Fig. 3c & 3d). They are used at time of surgery (Fig. 3e & 3f). A comparison of a patient’s pre-operative, planned and post-op outcomes is shown in Figure 4.

Fig 3. Surgical dental splints and templates are created using our computer-aided designing/computer-aided manufacturing technique.

a. Digital surgical splint.

b. Digital chin template.

c. Physical surgical splint.

d. Physical chin template.

e. The use of physical surgical splint at the time of the surgery.

f. The use of physical chin template at the time of the surgery. (Color version of figure is available online.)

Fig 4.

Comparisons of a patient’s pre-operative, planned and post-op outcomes. (Color version of figure is available online.)

Evaluation of Craniofacial Deformity

As stated above, one of the basic steps during the planning process is analysis and quantification of the deformity. Traditionally, this has been done by direct anthropometry, cephalometry or by visually inspecting a 3D CT model. Before the relatively recent advent of 3D imaging, craniofacial analysis had to be done in 2 dimensions. Therefore, most anthropometric tables and cephalometric norms in existence today are 2-dimensional. Fortunately, with advances in computer technology, we are now able to perform these analyses in 3-dimensions. In traditional cephalometry all structures are projected onto a single plane and bilateral landmarks are averaged. In 3D cephalometry, these landmarks exist in 3-dimensions which allows for true 3D measurements. However, these measurements are often difficult to interpret. A simple example is the gonial angle (Ar-Go-Me). In 2 dimensions, changes in this angle are easy to interpret. If the angle is outside the normal range, it can be said that the “bend” of the mandible is abnormal. The same is not necessarily true in three-dimensions. Anatomically, the mandibular condyle (Ar) and the gonial angle (Go) are on the lateral side of the face and are significantly separated from the sagittal plane where Menton (Me) is located. Three-dimensionally, the gonial angle is described by a line that goes from Ar (top) to Go (bottom) and another that goes from Go anteromedially to Me. The size of this 3D angle differs from the size of its 2D projection on the sagittal plane (Fig 5).

Fig 5.

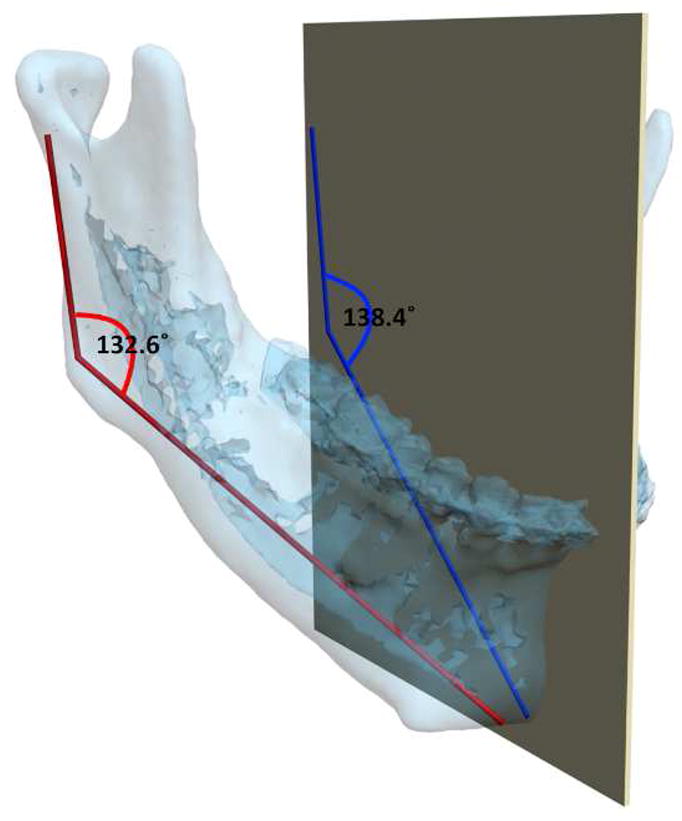
The mandibular condyles (Ar) and the gonial angles (Go) are on the lateral side of the face which are significantly separated from the midsagittal plane where the Menton (Me) is located. In this patient, the gonial angle (Ar-Go-Me) is measured as 132.6° 3-dimensionally (in red in the online version), while the projection of the gonial angle on the midsagittal plane is measured as 138.4° (in blue in the online version). (Color version of figure is available online.)

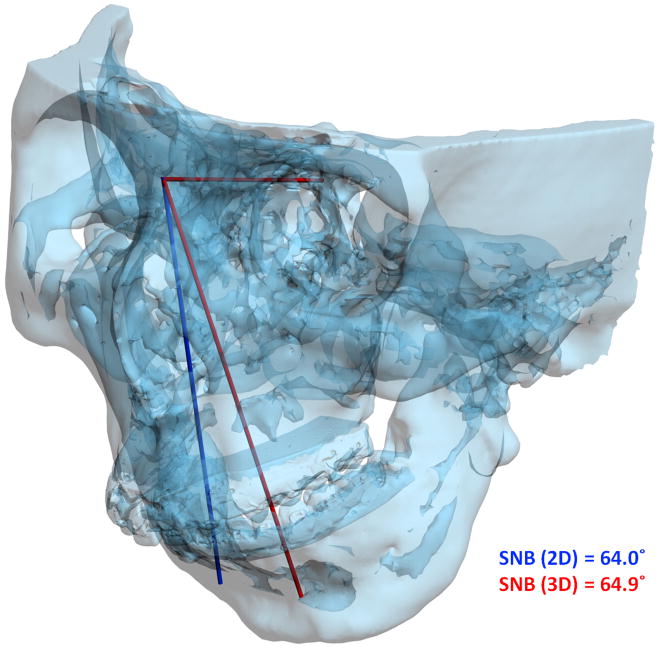
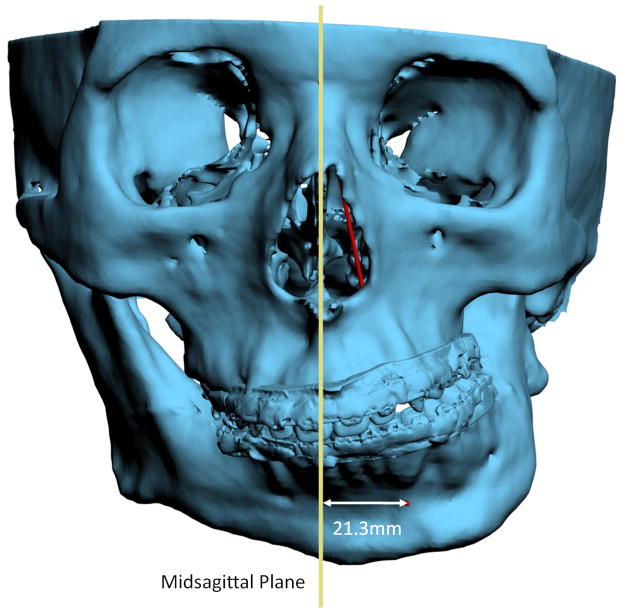
For angles that theoretically exist in the sagittal plane (e.g. SNA), differences between 3D measurements and 2D measurements are relatively minor and clinically insignificant. An example of this is a patient with significant laterognathia (lateral chin deviation). In this patient point B is displaced laterally and the 3D SNB angle on this patient only differs slightly from its 2D counterpart (Fig 6).

Fig 6. For angles that theoretically exist in the sagittal plane (e.g. SNB), differences between 3D measurements and 2D measurements are relatively minor and clinically insignificant.

a. SNB was measured as 64.9° 3-dimensionally (in red in the online version), while the projection of SNB on the midsagittal plane is measured as 64° (in blue in the online version).

b. Point B is deviated to the left by 21.3 mm. (Color version of figure is available online.)

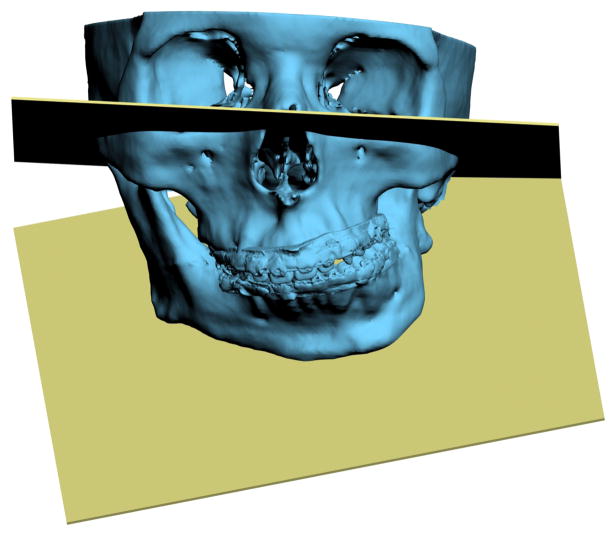
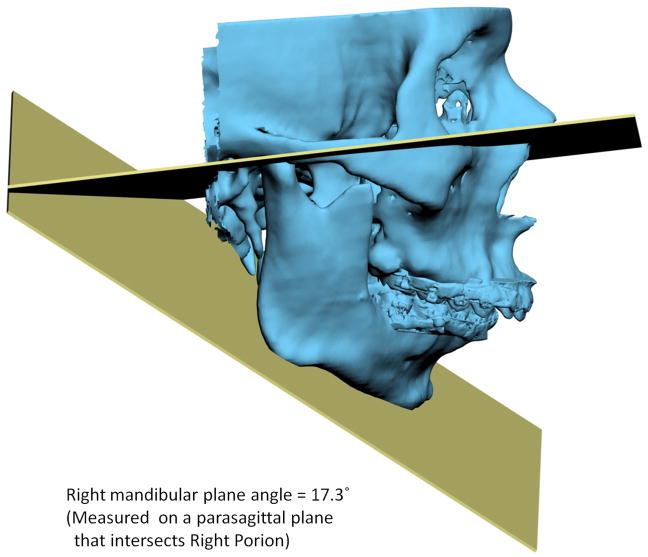
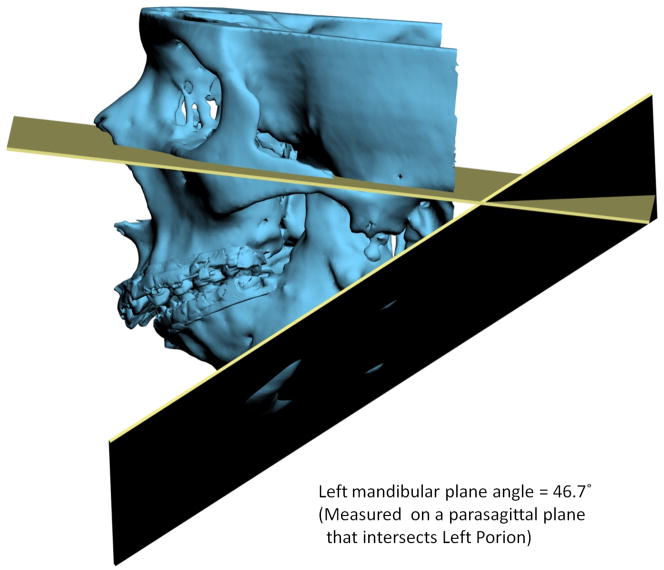
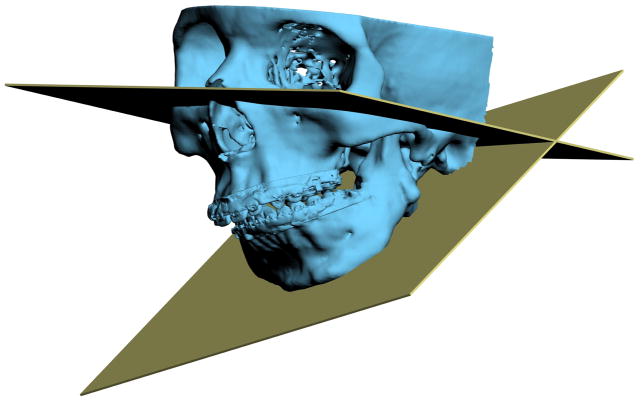
Another problem in 3D cephalometry is that of angles made by planes. To illustrate this problem we can look at the mandibular plane angle. This angle is made by the intersection of the mandibular plane and the Frankfurt Horizontal (FH) plane. Geometrically, a plane is constructed by 3 points. For the mandibular plane, these points are Right Gonion, Left Gonion and Menton. For the FH plane, the situation is more complicated. Theoretically, this plane is made up of 4 points: the right and left Orbitale and the right and left Porion. Unfortunately, most of the time, these points are not in the same plane. This situation brings to question: how should the plane be defined? Should one of the points be ignored? Should we average 2 points, 3 points or all 4? An even bigger problem exists when the patient has an asymmetric deformity. In this scenario, the right and left landmarks are not symmetrical. Therefore, the two planes diverge from each other in all planes of space. In this situation the size of the angle between the planes would vary depending on where it is measured (Fig 7).

Fig 7. Angles made by planes are problematic in 3D cephalometry. For example, the mandibular plane angle is made by the intersection of the mandibular plane and the Frankfurt Horizontal (FH) plane. In this illustration, the mandibular plane is simply created by 3 points: Right Gonion, Left Gonion and Menton. The FH plane is more complicated. It is created by the least-square averaged 4 points: the right and left Porion and right and left Orbitale. Since the right and left landmarks are not symmetrical, the 2 planes diverge from each other in all planes of space. The size of the angle between the planes varies depending on where it is measured.

a. Frontal view.

b. Right view. The right mandibular plane angle is 17.3° measured on a parasagittal plane that intersects Right Porion.

c. Left view. The left mandibular plane angle is 46.7° measured on a parasagittal plane that intersects Light Porion.

d. Three quarter view. (Color version of figure is available online.)

In our clinical practice, we plan most surgeries in 3-dimensions using our CASS system. Because of the difficulties interpreting 3D data, we often revert to conventional 2D analyses. Our system is programmed to use volume rendering to project the CT voxels into the sagittal plane creating a virtual cephalogram (Fig 8). Although all the cephalometric landmarks are digitized in 3-dimensions, the virtual lateral cephalogram allow us to visualize a 2D analysis as conventionally done. In this mode, we make decisions regarding the anteroposterior projection, the vertical dimension, and the inclinations of the occlusal plane and the mandibular plane (pitch).

Fig 8.

A cephalogram is emulated using volume rendering to project the CT voxels onto the sagittal plane. (Color version of figure is available online.)

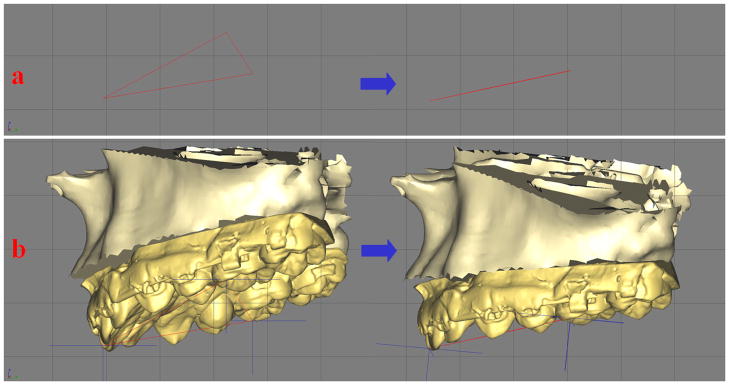
Three-dimensional analysis is used to examine the structures for symmetry. Initially we examine the symmetry of the maxilla. For this purpose, we have developed a method based on the work of Grayson.^34–36 This method creates a triangular spline on the maxillary dentition by digitizing 3 landmarks: 1) the dental midline, 2) the mesiobuccal cusp of the maxillary right first molar and 3) the mesiobuccal cusp of the maxillary left first molar. This triangle is linked to the maxilla so that any movement of the triangle is automatically transferred to the upper jaw. The computer then reads the x, y and z coordinates of the triangle vertices and moves them into symmetry (Fig 9). This method works well when the dental arch is itself symmetrical. It automatically corrects any roll or yaw deformities.

Fig 9. In triangle method, a triangular spline is created on the maxillary dentition by digitizing 3 landmarks: 1) the dental midline, 2) the mesiobuccal cusp of the maxillary right first molar and 3) the mesiobuccal cusp of the maxillary left first molar. This triangle is linked to the maxilla.

a. The computer reads the x, y and z coordinates of the triangle vertices and moves them to symmetry.

b. The movement of the triangle is automatically transferred to the maxilla. (Color version of figure is available online.)

After the maxilla has been made symmetrical and placed in its final position, the distal mandible is moved to maximal intercuspation. The proximal segments of the mandible are then aligned and the genioplasty is completed. Although the osteotomies are completed and all the segments are repositioned, it is still possible to have an asymmetry. In most patients with facial asymmetries, the bones are not only asymmetrically displaced but also differ in size and shape from one side to the other. Therefore, even after simulation of jaw movements, it is still necessary to check for asymmetries. The CASS system has a tool called the “mirror-image” that is very useful for this purpose. In the mirror-image routine one half on the face is selected, copied, flipped (mirror-imaged) and superimposed on the contralateral side. The software then uses Boolean operations to calculate differences between the sides. The surgeon may decide to add volume (grafting), remove volume (ostectomy), or adjust the position of the segments (camouflage). The software is capable of making volumetric measurements which is impossible in 2D cephalometry. These measurements are proven to be very useful in the quantification of airway and orbital volumes (Fig 10).

Fig 10. Volumetric measurements are used to measure the size of the airway.

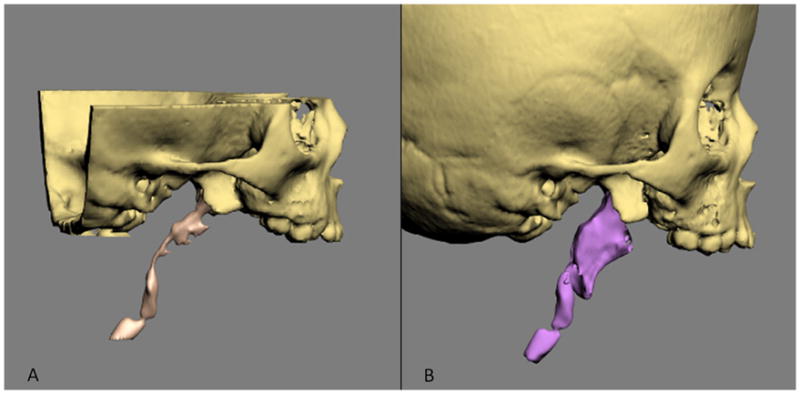
a. Airway preoperatively.

b. Airway postoperatively. (Color version of figure is available online.)

Providers involved in CMF surgery understand that the best outcomes are obtained when there is an excellent communication between the treating surgeon and the orthodontist. In complex cases such as those with syndromic conditions, having a craniofacial orthodontist familiar with these types of conditions is advantageous. This new technology, if adopted by surgeons as well as by orthodontists, will provide the common data platform and visualization tools needed for optimal patient care.