Abstract
The vibrational spectroscopy of hydration water in dilauroylphosphatidylcholine lipid multi-bilayers is investigated using molecular dynamics simulations and a mixed quantum∕classical model for the OD stretch spectroscopy of dilute HDO in H2O. FTIR absorption spectra, and isotropic and anisotropic pump-probe decay curves have been measured experimentally as a function of the hydration level of the lipid multi-bilayer, and our goal is to make connection with these experiments. To this end, we use third-order response functions, which allow us to include non-Gaussian frequency fluctuations, non-Condon effects, molecular rotations, and a fluctuating vibrational lifetime, all of which we believe are important for this system. We calculate the response functions using existing transition frequency and dipole maps. From the experiments it appears that there are two distinct vibrational lifetimes corresponding to HDO molecules in different molecular environments. In order to obtain these lifetimes, we consider a simple two-population model for hydration water hydrogen bonds. Assuming a different lifetime for each population, we then calculate the isotropic pump-probe decay, fitting to experiment to obtain the two lifetimes for each hydration level. With these lifetimes in hand, we then calculate FTIR spectra and pump-probe anisotropy decay as a function of hydration. This approach, therefore, permits a consistent calculation of all observables within a unified computational scheme. Our theoretical results are all in qualitative agreement with experiment. The vibrational lifetime of lipid-associated OD groups is found to be systematically shorter than that of the water-associated population, and the lifetimes of each population increase with decreasing hydration, in agreement with previous analysis. Our theoretical FTIR absorption spectra successfully reproduce the experimentally observed red-shift with decreasing lipid hydration, and we confirm a previous interpretation that this shift results from the hydrogen bonding of water to the lipid phosphate group. From the pump-probe anisotropy decay, we confirm that the reorientational motions of water molecules slow significantly as hydration decreases, with water bound in the lipid carbonyl region undergoing the slowest rotations.
INTRODUCTION
Lipid bilayer membranes surrounding cells and organelles are ubiquitous in biology. Such bilayers are typically viewed as a complex two-dimensional sea of lipids interspersed with membrane-associated proteins. Membranes serve to regulate the flow of molecules (such as water) and ions into and out of cells and organelles, as well as engage in cellular signal transduction and molecular recognition. Membrane fission and fusion processes are also necessary for cellular division and intracellular membrane trafficking.1 The hydration of lipid molecules by water strongly influences a bilayer's properties, such as its stability, fluidity, phase, and membrane fusion processes. For example, in the biologically relevant fluid Lα lamellar phase, a lipid molecule such as dipalmitoylphosphatidylcholine (DPPC) is hydrated by roughly 30 water molecules, whereas in the gel Lβ′ phase, each lipid is hydrated only by around 13 water molecules.2, 3, 4, 5 The structure and dynamics of water associated with other biological molecules, such as proteins and DNA have been extensively studied, and the properties of such water molecules are distinct from bulk water.6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 An atomistic picture of lipid bilayer hydration is thus vital for a better understanding of both membrane and water properties in biological systems.
Lipid bilayer hydration has been studied through a variety of techniques, such as x-ray and neutron scattering,3, 4, 17, 18 NMR,19, 20, 21, 22 dielectric relaxation,23, 24, 25 time-resolved fluorescence,26, 27, 28 and infrared (IR) spectroscopy.29, 30, 31, 32, 33 In addition, molecular dynamics simulations have become an important tool for understanding water structure and dynamics in lipid bilayers.34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50 From these various techniques, a picture emerges where water molecules are strongly hydrogen-bonded to the lipid phosphate oxygen atoms. Water also binds to the carbonyl oxygens of the glycerol backbone, and thus it penetrates deeply into the bilayer headgroup region.18, 40 However, very little water is present in the hydrophobic tail region.22, 51 In phosphatidylcholine (PC) lipids, molecular dynamics simulations have also suggested that water forms a clathrate-like cage around the choline group,34, 35, 36 and recent neutron scattering studies further note a possible weak hydrogen bond between the choline methylene group and water.18 Other phospholipids such as phosphatidylethanolamine do not show clathrate-like hydration, but instead allow hydrogen bonds between water and the amine hydrogens.35, 36 Related vibrational sum frequency generation spectroscopy experiments have been used to study the orientation of water molecules at lipid∕water interfaces.52, 53, 54, 55 Water in the headgroup region of the lipids is preferentially aligned according to the lipid charge. In the case of zwitterionic PC, the negatively charged phosphate group dominates, and water is weakly aligned with its oxygen atom pointing away from the lipid bilayer surface. The diffusion and reorientation dynamics of water around biological molecules, such as proteins and DNA,6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 as well as inside reverse micelles,56, 57, 58, 59, 60, 61are typically slower than that in bulk water. A similar trend has been observed in simulations of lipid bilayers, with water molecules deep in a bilayer exhibiting significantly longer reorientation times and slower translational motion.39, 42, 50, 62 The time scale for water molecules to exchange between the lipid headgroup region and the bulk has been examined by both simulations and NMR studies, and is on the order of 100 ps.22, 34, 40, 62
IR spectroscopy of the OD stretch of dilute HDO in H2O is a useful probe of local structure and hydrogen bonding in, for example, bulk water and ice,63, 64, 65, 66, 67, 68 aqueous salt solutions,69, 70, 71 and reverse micelles,57, 58, 59, 60 because the OD stretching frequency depends sensitively on hydrogen bonding to the deuterium atom, the direction of the transition dipole is tied to the molecular frame, and the isotopic mixture suppresses the effects of intra- and inter-molecular vibrational energy transfer found in bulk water.67 Zhao et al. have recently used IR spectroscopy of dilute HDO in H2O as a probe of the hydration of dilauroylphosphatidylcholine (DLPC) lipid aligned multi-bilayers.33 They observed a red-shift in the absorption spectrum as the hydration level is decreased. This is in contrast to an observed blue-shift in the analogous spectrum in reverse micelles as the size of the micelle, and thus the water content, is decreased.57, 61 The red-shift is interpreted as arising from water bound to phosphate oxygens.33 The spectra are quantitatively reproduced with a model assuming two water components, with phosphate-associated lipid water, and choline-associated bulk-like water. Zhao et al. also performed, as a function of hydration, isotropic and anisotropic pump-probe experiments, which are related to vibrational population and rotational relaxation, respectively. The isotropic pump-probe decay was bi-exponential, which they interpreted as arising from water molecules in these two different environments. The vibrational lifetime of the lipid water was faster than that for bulk-like water, for all hydration levels, and both lifetimes increased as the amount of water in the multi-bilayer was decreased. The anisotropic pump-probe decay showed a dramatic slow-down as hydration decreased, indicating slower rotational dynamics.
Zhang and Berkowitz50 recently performed molecular dynamics simulations on this DLPC lipid multi-bilayer system, in part to help understand the experiments of Zhao et al.33 They did not focus on the vibrational aspects of the problem, but, rather, focused on the water dynamics. They calculated the second-rank rotational time-correlation function, and compared their results with the experimental anisotropic pump-probe decay measurements, for different hydration levels. Agreement with experiment out to 5 ps was quite good, although the calculations were scaled to agree with experiment at 200 fs. Zhang and Berkowitz decomposed their rotational time-correlation functions for water molecules in different environments, considered stretched exponential fits at much longer times, and analyzed the rotational dynamics in terms of a molecular jump model.72, 73, 74, 75
In this paper, we essentially repeat the molecular dynamics simulations of Zhang and Berkowitz,50 but now complement them with direct calculations, using methods developed by our group, of the experimental observables measured by Zhao et al.:33 the FTIR absorption spectrum, and isotropic and anisotropic pump-probe decay. Our motivation for this work is three-fold. First, we hope to support and illuminate the spectroscopic aspects of the experimental results. Second, we would like to assess the robustness of our theoretical methods. We have developed ab initio-based spectroscopic maps for liquid water,68, 76, 77 for use with classical molecular dynamics simulations, which allow us to calculate spectroscopic observables (IR and Raman spectra, pump-probe, peak shift, 2DIR, etc).76, 77, 78, 79, 80 We then applied our methods to study the water liquid∕vapor interface81, 82, 83, 84, 85, 86 and ice.68, 87 Perhaps surprisingly, our methods describe these two situations quite well, even though the configurations that the water molecules sample therein are somewhat different from those in the bulk liquid (for which the maps were parameterized). We next considered salt solutions, specifically NaBr.88 We wanted to describe some subtle line shape (and more dramatic dynamics) changes as a function of concentration. For this problem we found it necessary to extend our maps, by considering separately the electric fields from the cations and anions. Our hope is that these maps are robust enough to use for all ionic solutions (and that it is therefore not necessary to develop new maps for each new cation or anion). We have not performed a systematic evaluation of this. However, we did study water in reverse micelles,61 whose AOT surfactant molecules have anionic sulfonate headgroups and Na+ counterions. Again, one goal was to see if the maps we had developed for NaBr were adequate to describe the spectroscopy in this more complex system. Our conclusion was that, again, they worked quite well.61 For the present multi-bilayer problem, the lipids have charged phosphate and choline groups, and in addition, water molecules can hydrogen bond to carbonyls. Can the same spectroscopic maps work well for this even more complex system? For example, can the same maps that gave the correct blue-shift (from bulk water) for reverse micelles, produce a red-shift in the case of hydrated lipid bilayers?
Our third motivation is to provide a unified theoretical treatment of all spectroscopic observables. The framework of linear and nonlinear response functions89 allows one to include, as needed, non-Gaussian frequency fluctuations, non-Condon effects (where the magnitude of the transition dipole depends on the molecular environment), and molecular rotations, in the calculation of any spectroscopic observable. There are many levels of approximation one can make to simplify this situation considerably, and this is often done. For water, we do not believe that most of these simplifying approximations are justified.76, 77, 79, 90, 91 For water in more complex heterogeneous situations, such as salt solutions, inside reverse micelles, or in hydrated lipid bilayers, the situation is even more complicated, because the vibrational lifetime is distributed (in the simplest model, with just two possible values, depending on molecular environment). A correct description of the lifetimes is important for all the spectroscopic observables. Traditionally, these lifetimes have been determined by direct fitting to the isotropic pump-probe decay.33, 57, 69 An alternative approach is to calculate the isotropic pump-probe decay from the third-order response functions, and then fit these results to experiment to obtain the lifetimes. Such a calculation is model dependent, in that one needs to make assumptions about how many distinct water “populations” are there, and how to define them. But one needs to do this anyway, since the same model is used for calculations of the other observables. It is only through this alternative approach that one can obtain a completely consistent and unified description of all experimental observables. This is the approach we take herein, and we are particularly interested in assessing the necessity of this extra step.
In Sec. 2 of this paper, we briefly summarize the methodologies developed in our group for the calculation of the spectroscopic observables. We also detail the computational procedures used for the lipid multi-bilayer simulations. In Sec. 3, we first present our two-population model for multi-bilayer hydration and then use this model to determine vibrational lifetimes for each water population. Our calculated absorption spectra and anisotropic pump-probe decays for various hydration levels are then compared to the experimental results, and we further analyze both observables in terms of contributions from different water populations. Finally, we summarize our findings in Sec. 4.
COMPUTATIONAL PROCEDURES
Molecular dynamics
Methods for the simulation of lipid bilayer systems have undergone a great deal of development in recent years. Molecular dynamics has been used to study the dynamics, structure, and phase behavior of single-component37, 41, 43, 44, 47, 48 and multi-component45, 46, 49 bilayer systems. Several early studies focused on lipid hydration and water structure around lipid headgroups,34, 35, 36, 40 and various coarse-grained methods have been used to investigate bilayer properties on longer length and time scales.48, 92 Force fields based on the GROMOS,93, 94, 95CHARMM,96, 97 and AMBER98, 99, 100 potentials all yield reasonable bilayer properties, and the effects of an applied surface tension and various temperature and pressure coupling schemes have also been investigated.37, 101, 102
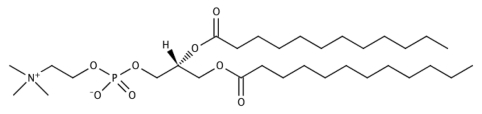
We have simulated DLPC lipid multi-bilayers in the NpT ensemble with various hydration levels using GROMACS 3.3.1.103 Figure 1 depicts the chemical structure of DLPC. The hydration level, X, is defined as the number of water molecules per lipid molecule, and simulations were performed for X = 2, 4, 6, 8, and 16. The highest hydration level, X = 16, corresponds to nearly full hydration, as similar PC lipids have been shown to interact with 20–30 water molecules per lipid.2, 3, 4, 5 In our simulations, multi-bilayers were prepared by stacking lipid bilayers in the z direction using periodic boundary conditions. The united atom force field and partial charges of Berger et al.93, 104 were used for the lipid parameters, and water was modeled with the SPC∕E force field.105 We used a time step of 2 fs and Lennard-Jones and Coulomb potential cutoffs of 1.0 nm, and long-range electrostatics were treated using the particle-mesh Ewald method.106 The temperature was maintained at 310 K using a Nosé-Hoover thermostat107 with a time constant of 0.5 ps, and the pressure was held at 1 bar using semi-isotropic, Parrinello-Rahman pressure coupling108 with a time constant of 2 ps and a compressibility of 4.5 × 10−5 bar−1. All bonds were constrained with the LINCS algorithm.109
Figure 1.
The chemical structure of dilauroylphosphatidylcholine (DLPC).
An initial lipid multi-bilayer structure was derived from an equilibrated DPPC bilayer with 128 lipid molecules and 3655 water molecules.37, 43 The DPPC carbon chains were transformed into DLPC by the removal of four carbons from the palmitic acid chains, and the resulting structure was re-equilibrated for 100 ns. Water molecules were then slowly and randomly removed to form the desired hydration cases, X = 16 (where 2048 waters remain), 8, 6, 4, and 2. Each different hydration level was then further equilibrated for at least 100 ns, and up to 300 ns for X = 2. The bilayer thickness and area per lipid were monitored, and our results for the equilibrated multi-bilayer were similar to those from previous studies.3, 37, 47 Spectra were calculated from multiple 500 ps production runs with data collected every 10 fs. Figure 2 depicts representative snapshots from equilibrated multi-bilayers with X = 2 and 16, with water molecules shown in blue, phosphate oxygen atoms in red, the choline nitrogen in pink, phosphorous in orange, carbonyl oxygens in green, and all (united) carbon atoms in gray.
Figure 2.
Snapshots of equilibrated lipid multi-bilayers with X = 2 (top) and X = 16 (bottom). Water molecules are depicted in blue, phosphate oxygen atoms are shown in red, carbonyl oxygens are shown in green, nitrogen and phosphorous atoms are shown in pink and orange, respectively, and (united) carbon atoms are shown in gray.
Response theory and spectroscopy
For the calculation of spectroscopic observables for dilute HDO in H2O, we adopt a mixed quantum∕classical model wherein the OD stretch is treated quantum mechanically, other stretching modes and the water bend are ignored, and all other motions are treated classically. (In the actual simulation, all water molecules are H2O, but when calculating spectroscopic observables we consider each H atom to be the putative D atom.) In order to compute spectroscopic observables for this isolated chromophore case, we require electrostatic maps relating the OD stretching frequencies ωij (for the transition between vibrational states i and j) and transition dipole matrix elements to the component of the electric field along the OD bond at the location of the deuterium atom.76, 88 The dipole matrix elements are taken to lie along the OD bond vector, and the magnitude of the dipole is given by
| (2.1) |
where xij is the i-j matrix element of the OD stretch coordinate operator and μ′ is the dipole derivative. These electrostatic maps are given in Table 1 and were determined from electronic structure calculations on water and salt water clusters.76, 88 As previously described, the effective electric field, Eeff, was calculated from the simulation point charges on each water and lipid atom within 7.831 Å of the water oxygen atom. Lipid partial charges were scaled by 0.8137 for positively charged atoms and 0.92017 for negatively charged atoms, as described in previous calculations of NaBr aqueous solutions.88
Table 1.
Electrostatic maps for the effective electric field Eeff, OD transition frequencies ω10 and ω21, the dipole derivative μ′ (normalized by the gas-phase value ), and the 1-0 and 2-1 matrix elements of the OD stretching coordinate x. EH2O, E+, and E− are the electric fields at the D atom due to neighboring water molecules, cations, and anions, respectively. All electric fields are given in atomic units, while frequencies are in units of cm−1, and the coordinate matrix elements are in units of Å.
| Eeff=EH2O+0.81379E++0.92017E− |
| x10 = 0.0880 − 1.105 × 10−5ω10 |
| x21 = 0.1229 − 1.525 × 10−5ω21 |
Within linear response theory,89 the IR absorption spectrum is given by the real part of the half-Fourier transform of the time-domain linear response function. For our mixed quantum∕classical model for the OD stretch, the spectrum I(ω) is simply
| (2.2) |
| (2.3) |
In Eq. 2.3, is the 1-0 matrix element of the transition dipole operator, ω10(τ) is the frequency of the OD stretch fundamental at time τ, T1(τ) is the vibrational lifetime, and the brackets indicate an ensemble average over classical degrees of freedom. The polarization of the incident electric field is denoted by , and as the laser beams in the experimental setup33 are directed along the lipid multi-bilayer normal (the direction), we shall only consider . Note that we allow the magnitude of the transition dipole element to depend on its environment, and hence on time (since the environment is time-dependent). This “non-Condon” effect has been shown to be important in the vibrational spectroscopy of bulk water.90, 110 The vibrational lifetime for the OD vibration is primarily determined by the density of available accepting modes, and as such it depends on the local environment and the solvent structure,31, 52, 111, 112, 113, 114 and consequently it also fluctuates in time.
In the inhomogeneously broadened limit, we ignore the effect of dynamics in Eq. 2.3; if we also ignore lifetime broadening altogether, we can replace I(ω) with the spectral density ISD(ω):
| (2.4) |
We shall use this spectral density in our analysis of the OD absorption spectrum.
In a polarization-resolved pump-probe experiment, a linearly polarized pump beam interacts with the sample, followed by a time-delayed probe beam that is linearly polarized either parallel or perpendicular to the pump beam. The anisotropy decay, r(t; ω), is then determined from79
| (2.5) |
where S∥ and S⊥ are the absorption changes when the probe beam polarization is parallel or perpendicular to the pump, respectively. The time delay between the pump and probe beams is labelled t, and the signal is frequency resolved at ω. The terms S∥ and S⊥ in Eq. 2.5 can be calculated from the third-order response function,
| (2.6) |
where the superscripts i and k indicate the or components of the transition dipole (as in Eq. 2.3). For the parallel component, i = k, and for the perpendicular component, . The response function Riikk is defined in Eq. A4 of Appendix A.
Frequently, the anisotropy decay is approximated by57, 67, 71
| (2.7) |
where P2 denotes the second Legendre polynomial, is a unit vector along the OD bond, and the brackets indicate an ensemble average. Lin et al.79 have shown that in order to derive Eq. 2.7 from Eq. 2.5, one must make the Condon approximation to the transition dipole matrix elements, assume a single vibrational lifetime, and use frequency-integrated detection. The anisotropy decays calculated from Eqs. 2.5, 2.7 will differ, implying that the experimental r(t) should not generally be interpreted solely in terms of rotational motions.
The isotropic pump-probe decay, P(t), is similarly calculated from the parallel and perpendicular components of the third-order response function,
| (2.8) |
If the system is characterized by a single, constant vibrational lifetime T1, and if we make the Condon approximation to the transition dipole, then57
| (2.9) |
For systems with several distinct populations with different vibrational lifetimes, the experimental isotropic pump-probe decay is often fit by a multi-exponential decay, with the resulting time constants interpreted as the vibrational lifetimes. If the Condon approximation is not valid, the populations exchange sufficiently quickly, or the vibrational lifetime is correlated to the time dependence of the transition dipoles, then this interpretation of the experimental data may not be accurate.
RESULTS AND DISCUSSION
Two-population water model
Water molecules in the headgroup region of a DLPC lipid multi-bilayer inhabit a highly inhomogeneous environment. Water may hydrogen-bond to the lipid phosphate group or to other water molecules as a part of a clathrate structure around the choline.33 Deeper into the bilayer, water molecules may hydrogen-bond to the glycerol carbonyl oxygens, and a small subset of water hydrogens may even point into the hydrophobic tail region. Each of these hydrogen-bonding environments results in a different spectral response as well as different rotational and diffusive dynamics. In order to simplify this situation, we introduce a two-population model in which a water molecule hydrogen (or deuterium) atom is either defined to be “lipid-associated” or “water-associated.” We only consider two populations because the experimental lifetime measurements33 only provide evidence for two vibrational lifetimes and we do not want to introduce additional parameters. If the hydrogen atom in question is closer to any lipid oxygen atom than it is to a water oxygen atom (on a different molecule), then it is defined to be lipid-associated. The majority of such water hydrogens are hydrogen-bonded to either a phosphate or carbonyl oxygen. If the water hydrogen is closer to the oxygen atom of another water molecule, then it is defined to be water-associated. It should be emphasized that water-associated hydrogens are not bulk water,33 as they may still be within the lipid headgroup region. Also, water hydrogen atoms that are not hydrogen bonded will be classified as either lipid- or water-associated, even though these hydrogens inhabit quite different environments and likely have distinct vibrational lifetimes. We have found that the number of non-hydrogen bonded water hydrogens is relatively small and makes little contribution to the calculated spectra. The lipid- and water-associated populations are defined mathematically as
| (3.1) |
⟨n⟩ is therefore the average lipid-associated fraction.
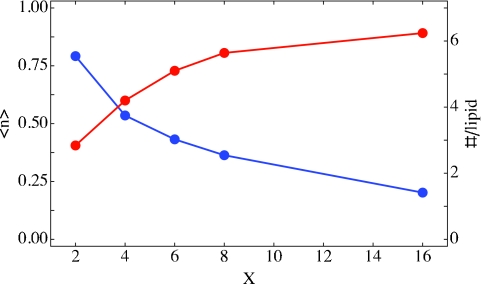
In Fig. 3 we depict both the average fraction ⟨n⟩ (blue) of lipid-associated hydrogens, as well as the average number of lipid-associated hydrogens per lipid molecule (red), as a function of the hydration level X. As the hydration increases, the relative fraction of lipid-associated waters declines; however, the total number of lipid-associated water hydrogens actually increases. In Table 2, rows 1–3, we list the average fraction ⟨n⟩, along with the number of water hydrogen atoms (per lipid) closest to lipid phosphate oxygens (row 2) and lipid carbonyl oxygens (row 3). The sum of phosphate- and carbonyl-associated waters is the total number of lipid-associated water hydrogens (per lipid). Note that while water molecules may, in principle, also be associated with the lipid alkoxy oxygens, we find that only a small fraction of water hydrogens are in this situation, in agreement with recent simulations on DLPC membranes47 and small phosphatidylcholine lipids in solution.18 From Fig. 3 and Table 2, we see that the fraction of lipid-associated water hydrogens ranges from 72% in the low hydration, X = 2, case down to only 20% for X = 16. From the table we deduce that the fraction associated with phosphate oxygen ranges from 48% at X = 2 to 12% at X = 16. These numbers are in qualitative agreement with those determined by Zhao et al.33 At the highest hydration level, the number of water hydrogens per phosphate group is about 4, also in agreement with Zhao et al.33 Note that at this highest hydration level, there is just over one water hydrogen associated with each carbonyl oxygen.
Figure 3.
The fraction of lipid-associated hydrogens, ⟨n⟩ (blue), and the number of lipid-associated (both phosphate and carbonyl) hydrogens per lipid (red), as a function of hydration level X. Even though the fraction of lipid-associated hydrogens declines with increasing hydration level, the absolute number of these hydrogens increases through X = 16.
Table 2.
The fraction of water hydrogens associated with either lipid phosphate or carbonyl groups, ⟨n⟩, along with the number of water hydrogens per lipid associated with each lipid component. The vibrational lifetimes for both water- and lipid-associated molecules, as discussed in relation to Fig. 5, are given in units of picoseconds. The peak maxima ωpeak and full widths at half-max (FWHM) for both the theoretical and experimental linear absorption spectra, shown in Fig. 7, are presented in units of cm−1.
| X | 2 | 4 | 6 | 8 | 16 | Bulk |
|---|---|---|---|---|---|---|
| ⟨n⟩ | 0.72 | 0.54 | 0.43 | 0.36 | 0.20 | ... |
| #∕phosphate | 1.9 | 2.6 | 3.1 | 3.5 | 3.8 | ... |
| #∕carbonyl | 0.95 | 1.6 | 1.9 | 2.2 | 2.5 | ... |
| Twater | 6.7 | 3.3 | 2.8 | 2.7 | 2.4 | 1.8 |
| Tlipid | 3.1 | 1.7 | 1.5 | 1.5 | 1.5 | ... |
| ωpeak, theory | 2474 | 2474 | 2480 | 2485 | 2498 | 2515 |
| ωpeak, expt. | 2489 | 2497 | 2501 | 2505 | 2508 | 2514 |
| FWHM, theory | 203 | 219 | 214 | 215 | 211 | 178 |
| FWHM, expt. | 160 | 173 | 177 | 177 | 177 | 167 |
The exchange of water hydrogens between lipid- and water-associated populations can be examined by calculating the population fluctuation time-correlation function Cn(t):
| (3.2) |
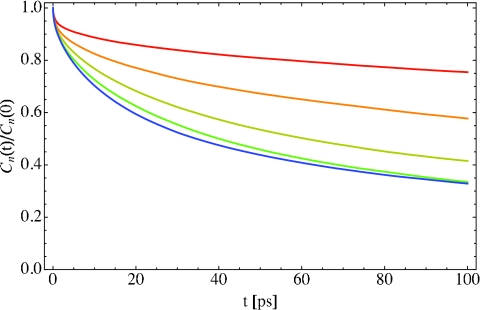
where the brackets indicate an ensemble average and δn(t) ≡ n(t) − ⟨n⟩. This correlation function, normalized to unity at t = 0, is plotted in Fig. 4, where the red, orange, yellow, green, and blue lines correspond to X = 2, 4, 6, 8, and 16, respectively. As the hydration level decreases, the typical exchange time increases, but for all hydration levels studied, the exchange time scale is still on the order of 100 or more ps. Note, however, that for all hydration levels, some exchange takes place at shorter times, say within 10 ps. Also note that the X = 8 curve is quite similar to the X = 16 case, indicating a saturation of the exchange process. Thus, for larger hydration levels, we do not expect a significant decrease in the rate of population exchange. An exchange time scale of 100 ps is also consistent with previous experimental and theoretical findings on other lipid bilayer systems.22, 34, 40, 62
Figure 4.
Population fluctuation time-correlation function Cn(t), Eq. 3.2, for hydration levels X = 2 (red), 4 (orange), 6 (yellow), 8 (green), and 16 (blue). The population n is defined in Eq. 3.1, and the correlation function has been normalized to unity at t = 0.
Isotropic pump-probe decay
Zhao et al.33 measured the isotropic pump-probe decay as a function of hydration level, in each case fitting the decay to a bi-exponential. They assumed that the decay rate constants represented the vibrational lifetimes of OD in two different environments. They assigned the slower component to choline-associated bulk-like water, and the faster component to phosphate-associated water. The relative amplitudes change with the hydration level (higher amplitude of the bulk-like component at higher hydration levels), and the lifetimes themselves decrease with increasing hydration level, going from 2.1 to 0.62 ps for the phosphate-associated water as X increases from 2 to 16, and from 4.5 to 2.1 ps for the bulk-like component.
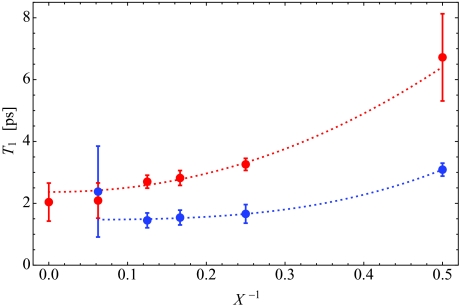
As an alternative approach to determining the vibrational lifetimes, using our microscopic definition of two OD populations, we can calculate the isotropic pump-probe decay from Eq. 2.8, using the lifetimes of each population as fit parameters. That is, in the response functions in Appendix A, we set T1 = Tlipid when n = 1, and T1 = Twater when n = 0. P(t) is then calculated from Eq. 2.8 with the lipid- and water-associated vibrational lifetimes treated as free parameters. P(t) is frequency-resolved at the peak frequency of the IR absorption spectrum, ωpeak, for each hydration level, as in experiment.33 As we need to adjust the absolute intensity to match experiment, and the experimental results do not capture the rapid decrease in P(t) for very short times, the theoretical and experimental curves have both been normalized to unity at t = 200 fs. The vibrational lifetimes that yield the best fit to the experimental data, as determined by least-squares, are shown in Fig. 5, where the red data points indicate the lifetime for water-associated OD stretches, and the blue points indicate the lipid-associated lifetime. The error bars are three standard deviations, and the dotted lines are the result of a power law fit and are meant to guide the eye. Due to the large uncertainty for Tlipid for X = 16, a better value is the one that is in agreement with the trend extrapolated from lower hydration levels (as in the figure). We take Twater = 1.8 ps for bulk water, as this is the traditional value,115 and it is subsumed by our error bar. Our final best-fit lifetimes (in ps) are shown in Table 2. These results are in qualitative, but not quantitative, agreement with those of Zhao et al.33 Our “water” lifetime is the longer of the two, and both lifetimes decrease with increasing hydration, as found by Zhao et al.,33 but in all cases our lifetimes are longer than those of Zhao et al.,33 sometimes by over a factor of 2.
Figure 5.
Best-fit vibrational lifetimes Twater (red) and Tlipid (blue) versus the inverse hydration level X−1 along with 3σ error bars.
The vibrational lifetime of the OD stretch is determined by the possible pathways for energy relaxation. Typically, one quantum of the OD stretch vibration in dilute HDO in H2O (at 2500 cm−1) relaxes to the water bend fundamental (at about 1400 cm−1), or directly to the ground state, exciting H2O bends and liberations.115, 116 For low hydration levels, the density of such modes is smaller than that in bulk water, and the vibrational lifetime will thus be larger.114, 117 This increase in the vibrational lifetime is also consistent with population relaxation decay measurements on water confined in reverse micelles and Nafion membranes.57, 118, 119 For lipid-associated water stretches, other possible pathways involve relaxation to the lipid phosphate vibrations (around 1200 cm−1) or other lipid modes. This may account for the shorter vibrational lifetime for lipid- vs. water-associated OD stretches.
In Fig. 6a, our theoretical results for the isotropic pump-probe decay, P(t), are compared to the experimental bi-exponential fits,33 where each color corresponds to a different hydration level, as in Fig. 4. One sees excellent agreement between theory and experiment. Note, that due to non-Condon effects, the frequency resolution of P(t), exchange between populations, and correlations between the transition dipole matrix elements and the vibrational lifetime, the theoretical P(t) is not simply a bi-exponential with two decay constants Tlipid and Twater. The quantitative agreement between theory and experiment in Fig. 6a indicates that our population model is consistent with the experimental pump-probe data. This analysis suggests that care must be taken in the interpretation of experimental isotropic pump-probe decays, as multiple definitions of populations and lifetimes may be consistent with the data. We will now use our fits to the vibrational lifetimes for each water population to calculate the IR absorption spectra and pump-probe anisotropy decays as a function of lipid hydration.
Figure 6.
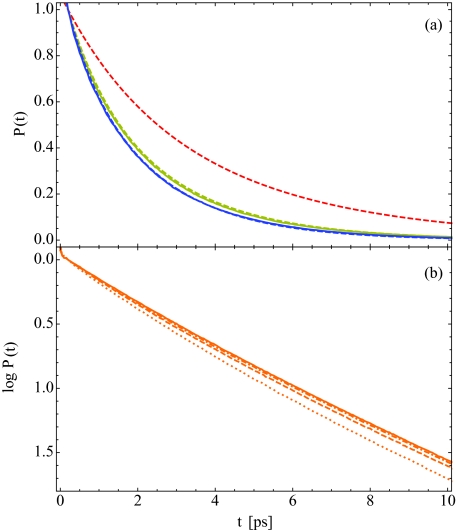
(a) Theoretical (solid) and experimental (dashed) isotropic pump-probe decay curves, P(t), for hydration levels X = 2 (red), 6 (yellow), and 16 (blue). (b) The isotropic pump-probe decay on a logarithmic scale for hydration level X = 4 as a function of the detection frequency, ω = 2458 (dotted), 2488 (dashed), 2516 (dotted-dashed), and 2546 cm−1 (solid).
Before we do this, however, we briefly consider the frequency dependence of the isotropic pump-probe decay. In Fig. 6b, we plot P(t) for the X = 4 hydration level for several detection frequencies ω. The dotted, dashed, dotted-dashed, and solid lines, respectively, correspond to ω = 2458, 2488, 2516, and 2546 cm−1. These frequencies were chosen to correspond to the detection frequencies used in Fig. 6B of Ref. 33, though they are shifted by 23 cm−1 to account for the difference in the peak absorption frequency between our calculations and the experimental results.33 In Fig. 6b, we observe qualitative, though not quantitative, agreement with experiment, with P(t) detected at lower frequencies decaying more quickly than P(t) detected at higher frequencies due to a relatively larger contribution from lipid-associated water stretches.
Absorption spectra and the origin of the observed red-shift
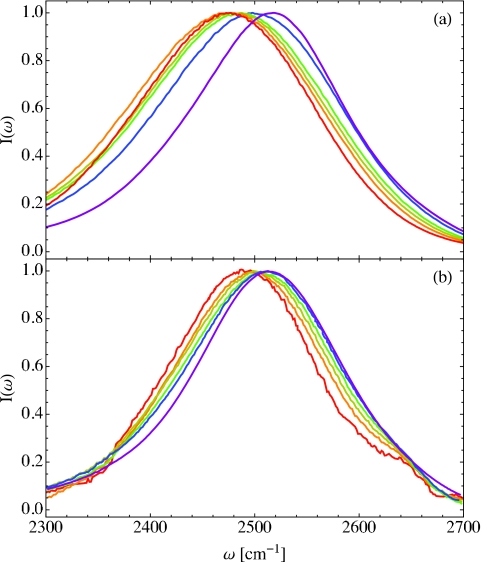
As the hydration level for the DLPC lipid multi-bilayer decreases, the experimental FTIR absorption spectrum exhibits a characteristic red-shift,33 in contrast to an observed blue-shift in the spectrum in reverse micelles as the micelle size decreases.57, 61 In order to investigate this red-shift, we now calculate the theoretical absorption spectrum for the OD stretch in dilute HDO in H2O. Unlike in neat water,77, 80, 120 the OD stretch acts as an isolated chromophore and thus provides a local probe into its electrostatic and hydrogen-bonding environment. The absorption spectra for the lipid multi-bilayer systems are calculated using Eqs. 2.2, 2.3 and the electrostatic frequency maps in Table 1. The vibrational lifetimes are taken from the values in Table 2, as discussed above, and only the and components of the transition dipole matrix elements are utilized in Eq. 2.3. The resulting theoretical absorption spectra are shown in Fig. 7a, where the colors indicate the hydration levels, X, as in Fig. 4, and the purple curve indicates the bulk water result. For comparison, the experimental results from Fig. 2 of Ref. 33 are shown in Fig. 7b. The theoretical and experimental peak frequencies (ωpeak) and full widths at half-max (FWHM) are summarized in Table 2 in units of cm−1.
Figure 7.
Theoretical (a) and experimental (b) linear absorption spectra for dilute HDO in H2O for membrane hydration levels X = 2 (red), 4 (orange), 6 (yellow), 8 (green), 16 (blue), and bulk water (purple). The theoretical spectra were calculated from Eq. 2.2 with vibrational lifetimes given in Table 2, and the experimental spectra were adapted from Fig. 2 of Ref. 33.
As can be seen in Fig. 7, we qualitatively reproduce the observed red-shift in the absorption spectrum as hydration decreases. The FWHM also changes with hydration, first becoming broader from bulk water to X = 16, and then narrowing for low hydration levels. This trend is again in qualitative agreement with experiment. In all cases, however, the red-shift we predict is systematically too large, as are the peak widths. This quantitative inaccuracy may result from the electrostatic maps for the OD stretch frequency or transition dipole elements, which were parameterized in water clusters (with salt ions), not in lipid multi-bilayer environments. Also note that the experimental spectra have a shoulder at high frequency that is attributed to OD stretches in HDO molecules where the D atom is not hydrogen-bonded. In lipid multi-bilayers, this may result from waters deep in the bilayer that point towards the hydrophobic tail region. In our calculations, we observe a similar shoulder in the frequency distribution (not shown); however, the intensity of this shoulder in the spectrum is greatly decreased by the frequency dependence of the transition dipole elements (non-Condon effects).
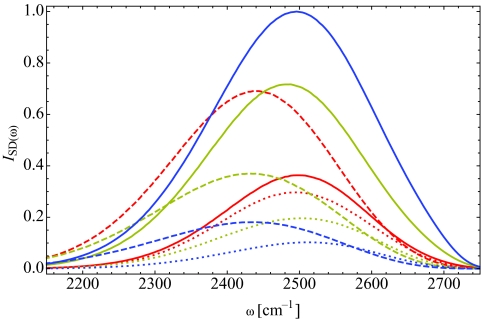
In order to understand better the origin of the observed red-shift, we have calculated the spectral density, Eq. 2.4, as a function of hydration for three different water populations. Figure 8 shows these spectral densities for X = 2 (red), 6 (yellow), and 16 (blue). The solid line indicates the spectral density due to water-associated molecules, as defined previously in Eq. 3.1. The dashed lines correspond to phosphate-associated water molecules, and the dotted lines indicate carbonyl-associated molecules. The sum of the phosphate- and carbonyl-associated spectral densities is equal to the response from all lipid-associated waters. From Fig. 8, we immediately note that phosphate-associated waters are significantly red-shifted from both water- and carbonyl-associated molecules. This is a direct result of the strong hydrogen bond between the water hydrogen and phosphate oxygen atoms, as suggested by Zhao et al.33 In our electrostatic frequency maps, the red-shift in frequency stems from a large effective electric field due to both the relatively short phosphate oxygen∕water hydrogen bond (∼1.67 Å) and the overall negative charge on the lipid phosphate group. The hydrogen bonds between waters and between a water hydrogen and a lipid carbonyl oxygen are weaker, and thus result in a smaller electric field and higher OD stretching frequencies. As the hydration level decreases, the fraction of phosphate-associated waters increases, and thus the overall absorption spectrum shifts to lower frequencies. A close examination of the spectral densities of any one population in Fig. 8, as a function of hydration, does show small shifts in the peak frequency due to other changes that take place in the lipid headgroup region as water molecules are removed. However, the dominant contribution to the shift in the frequency of the OD stretch is the hydrogen-bonding environment of the D atom,70 and therefore the spectral red-shift is governed primarily by the fraction of water molecules bound to the lipid phosphate group.
Figure 8.
Spectral density, from Eq. 2.4, for dilute HDO in H2O for X = 2 (red), 6 (yellow), and 16 (blue). The dashed lines indicate contributions from phosphate-associated water molecules, while the dotted lines show contributions from carbonyl-associated waters. The solid line gives the spectral density for water-associated molecules. For all hydration levels, the spectral density due to phosphate-associated waters is red-shifted relative to the water-associated and carbonyl-associated components.
Anisotropic pump-probe decay
The anisotropic pump-probe decay, r(t), is typically interpreted in terms of molecular reorientations. The short-time decay of r(t) results from water librational motions that maintain the existing hydrogen-bonding network, while the decay on longer time scales results from hydrogen-bond restructuring.67 In bulk water, changes in the hydrogen-bonding network typically result from large, very fast angular jumps—a molecular jump mechanism.72, 73, 74, 75 Zhao et al.33 measured the pump-probe anisotropy decay for water in DLPC multi-bilayers as a function of hydration, and found that the anisotropy decay slows significantly as hydration decreases. Molecular dynamics simulations on this system by Zhang and Berkowitz50 confirm this finding (though they also observe hydrogen-bond switching events that do not include a rapid molecular jump). This slowing of the anisotropy decay was explained by a decrease in the density of available hydrogen-bond acceptors in lipid multi-bilayers at reduced hydration. As there are few water molecules available, a water in the lipid headgroup region simply has no choice other than to remain in its hydrogen-bonding environment.121
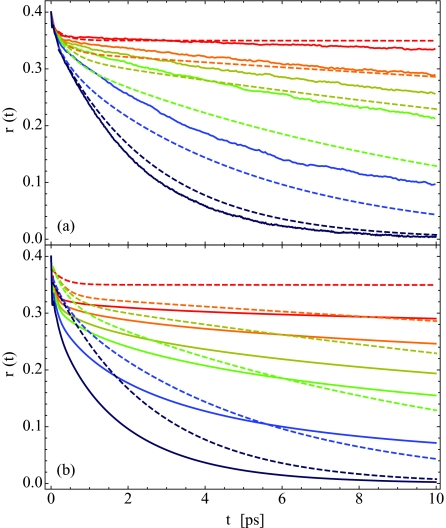
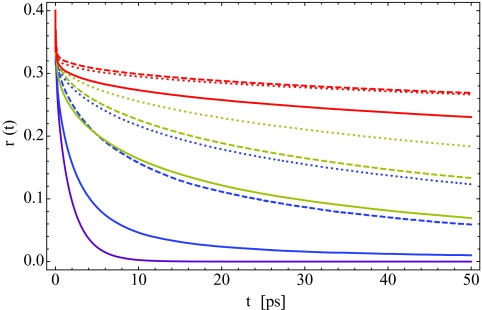
To explore further these rotational dynamics, we now calculate the pump-probe anisotropy decay using Eqs. 2.5, 2.6 and the mixed quantum∕classical model presented in Sec. 2A. Rather than invoking the P2 approximation to the anisotropy, Eq. 2.7, as was done by Zhang and Berkowitz,50 we include non-Condon and population-dependent vibrational lifetime effects in our treatment. The pump-probe anisotropy decay curves are presented in Fig. 9a, where the solid curves are our theoretical results and the dashed lines are bi-exponential fits to the experimental data.33 The colors indicate the lipid hydration level, as in Fig. 7. The theoretical results are frequency resolved at the peak frequency of the FTIR absorption spectrum, as in experiment. Note that these curves have not been normalized in any way—both theory and experiment begin at 0.4 at t = 0, as they should.
Figure 9.
(a) Theoretical (solid) and experimental (dashed) pump-probe anisotropy decay, r(t), for the same hydration levels as in Fig. 7. The theoretical results are calculated using Eq. 2.5, and are frequency resolved at ωpeak, as given in Table 2. The experimental curves are bi-exponential fits to the anisotropy decay data, as discussed in Table IV and Fig. 8 of Ref. 33. (b) Same, except theory is calculated within the P2 approximation.
For all hydration levels, we achieve qualitative agreement with experiment. As hydration decreases, the anisotropy decays over a longer time scale, and for the low hydration X = 2 case, r(t) barely decays at all after an initial sub-picosecond drop. This is consistent with the idea that waters in lipid multi-bilayers at low hydration have greatly arrested rotations due to a paucity of available hydrogen-bonding partners. While our results for X = 2, 4, and 6 are quite good, the quantitative agreement between theory and experiment is rather poor for X = 8 and 16. As with the absorption spectra, this may be due to issues with our molecular dynamics simulations or problems with the frequency maps presented in Table 1. This slow-down with decreasing hydration is in agreement with the anisotropy results calculated by Zhang and Berkowitz50 within the P2 approximation.
However, we note two things about the comparison of the P2 results of Zhang and Berkowitz50 with the experimental results of Zhao et al.33 First, the theoretical results were shifted to agree with experiment at 200 fs, and second, the comparison goes out only to 5 ps. Except to be able to visualize the correspondence between theoretical and experimental time scales, there is no theoretical justification for shifting the theoretical curve. Therefore, to make a heads-up comparison of the P2 approximation with experiment, in Fig. 9b, we show our calculated P2 results (which are essentially identical to those of Zhang and Berkowitz50). One sees that within this approximation the agreement with experiment is substantially worse.
As noted in Refs. 33 and 50, the anisotropies presented in Fig. 9 decay on multiple time scales. Zhang and Berkowitz fit their calculated anisotropies to multi-exponential decays or stretched exponentials, but they discovered that the fitting parameters depended rather strongly on the time range over which fitting took place. However, Zhang and Berkowitz did calculate the anisotropy in the X = 16 case separately for water molecules inside the lipid headgroup region and for bulk-like waters. They determined that r(t) for bulk-like waters decays on a more rapid time scale than waters within the lipid headgroup. We shall similarly decompose the anisotropy in terms of water populations. In Fig. 10, we present r(t), calculated within the P2 approximation of Eq. 2.7, for X = 2 (red), 6 (yellow), 16 (blue), and bulk water (purple). The solid lines indicate water-associated OD stretches, while the dashed and dotted lines indicate phosphate- and carbonyl-associated waters, respectively. These water populations were previously discussed in connection to Fig. 8. For each hydration level, we observe that water molecules deeper within the lipid multi-bilayer (carbonyl-associated) reorient on a slower time scale than waters near the multi-bilayer surface. The anisotropy for each population also decays on multiple time-scales. For each hydration level, water-associated molecules rotate on the fastest time scale, but in no case do they rotate as quickly as in the bulk. Note that phosphate-associated molecules have a more rapid anisotropy decay than carbonyl-associated waters, despite the stronger phosphate oxygen∕water hydrogen-bond. This is consistent with the picture from the molecular jump mechanism, where the time scale for water reorientations is driven by the availability of other hydrogen-bonding networks, rather than the time scale for breaking one individual hydrogen bond.73
Figure 10.
P2 approximation to the anisotropy decay r(t), from Eq. 2.7, for the same hydration levels as in Fig. 8. The dashed and dotted lines represent contributions from phosphate- and carbonyl-associated waters, respectively, while the solid lines give the water-associated orientational relaxation. The anisotropy decay for HDO in bulk H2O within the P2 approximation is shown as the purple line for reference. For each hydration level, the water-associated molecules have faster orientational relaxation than lipid-associated molecules.
CONCLUSIONS
We have investigated the structure, dynamics, and vibrational spectroscopy of hydration water in DLPC multi-bilayers using molecular dynamics simulations and a mixed quantum∕classical model. We have pursued a simple two-population model for the hydration water OD stretches and used this model, and the experimental isotropic pump-probe decay, to obtain fits to the vibrational lifetimes for both lipid- and water-associated OD stretches. We then calculated the FTIR absorption spectra and pump-probe anisotropy decays as a function of the lipid hydration, and in each case found qualitative agreement with recent experiments.33 The observed red-shift in the absorption spectrum with decreasing hydration was analyzed in terms of three OD populations (lipid-associated OD stretches have been further subdivided into phosphate- and carbonyl-associated groups) and attributed to a relatively large proportion of water molecules strongly hydrogen-bonded to lipid phosphate groups at low hydration, as previously suggested by Zhao et al.33 As hydration decreases, we find, as have others,50 that water rotations slow dramatically. In fact, the slowest molecules are those bound to lipid carbonyls; these molecules have few hydrogen-bond accepting groups.50, 72
When analyzing vibrational spectroscopy experiments in complex systems, there are several levels of theory that one can invoke. At the simplest level, one assumes that the frequency fluctuations are Gaussian (and hence one makes the cumulant approximation), makes the Condon approximation for the magnitude of the transition dipole, neglects rotational dynamics in the spectrum and isotropic pump-probe decay, and assumes that all chromophores share the same lifetime. In this case, analysis of experiment is straightforward. The isotropic pump-probe decay gives the experimental lifetime. Linear (FTIR) and nonlinear (peak shift, two-dimensional IR) experiments can be described by a single line-shape function g(t) or frequency time-correlation function, and pump-probe anisotropy experiments are analyzed in terms of the P2 rotational time-correlation function. This kind of analysis is physically illuminating, and often qualitatively correct. For more complicated systems, one can imagine two (or more) independent and non-exchanging ensembles of chromophores, each with their own lifetime, line-shape function, and P2 correlation function. In this situation, analysis is still relatively straightforward.
At the other extreme are very complex systems, without well-defined distinct, independent, and non-exchanging ensembles, where the frequency fluctuations are non-Gausssian (and hence the cumulant approximation should not be made), non-Condon effects are important, there is a heteregeneous distribution of vibrational lifetimes, and rotational dynamics is strongly correlated with transition frequencies and lifetimes. In these circumstances, unfortunately, it is difficult to perform an analysis of experiment without microscopic dynamical calculations. However, using the full infrastructure of response functions,89 together with models for the instantaneous chromophore transition frequencies, direction and magnitude of transition dipoles, and vibrational lifetimes, one can calculate all experimental observables from a classical molecular dynamics simulation. This is the approach taken herein. We use an existing force field to generate the molecular trajectories, and model the frequency and transition dipoles with existing maps. While one could, in principle, use microscopic theory to calculate the vibrational lifetime in different environments, here we adopt a phenomenological approach. Motivated by the discussion and experimental results of Zhao et al.,33 we assume that the vibrational lifetime can have two values, and propose a microscopic model for assigning these lifetimes. This allows us to calculate the isotropic and anisotropic pump-probe decays, and line shapes, within a single unified microscopic framework. Our experimentally determined lifetimes are quantitatively different from those determined more simply by Zhao et al.33 (although our calculated isotropic pump-probe decay is still in excellent agreement with experiment), and our calculation of the pump-probe anisotropy decay is in significantly better agreement with experiment than if one makes the simple P2 approximation.
Though we obtain qualitative agreement with experiment for the vibrational absorption spectra and pump-probe anisotropy decay as a function of hydration, our results are not quantitative. There are a variety of potential sources for error, including our simulation methods and the calculation of the spectroscopic observables. The electrostatic maps used to determine the environmental dependence of the transition frequencies and dipoles were parameterized from quantum calculations on water clusters in salt solution—not for water in lipid environments. As bulk water is blue-shifted relative to lipid-bound water, it is possible that the maps presented in Table 1 are not as accurate for low frequencies (high effective electric fields). Moreover, for determining the electric fields in our maps, for example, from the phosphate and carbonyl groups, we use charges assigned to these atoms in the force field. This means that a different force field would lead to different results for the spectroscopic observables. In addition, our two-population model for assigning vibrational lifetimes may not be sophisticated enough. The calculation of vibrational spectra also depends sensitively on the structure and sub-picosecond dynamics of water molecules in the simulations. As force fields are not typically parameterized to reproduce dynamics, it is not immediately clear if the molecular dynamics simulations are sufficiently accurate for quantitative agreement. Finally, dynamics in lipid bilayers are greatly slowed at low hydration levels. Even though we have allowed our lipid multi-bilayer simulations to equilibrate for over 100 ns, it is not certain that the simulated membranes properly sample the experimentally relevant region of phase space. One could, and perhaps should, spend time improving all of these aspects (check several different force fields, improve force fields, reparameterize spectroscopic maps, etc.). However, in the meantime, we are confident that our level of modeling is adequate for a qualitative understanding of the structure, dynamics, and spectroscopy in this important and complicated system, and furthermore, that our methods are transferable enough to allow for a similar qualitative understanding of other relevant biological systems.
In this article, we have demonstrated that our theoretical models can both predict and be used to analyze the results of both linear and third-order vibrational spectroscopy on lipid multi-bilayers as a function of hydration. In part II of this work, we will extend our calculations to observables not yet examined experimentally—peak shift and two-dimensional IR spectroscopy. We will also more closely assess the effects of various theoretical approximations for the calculation of such spectra.
ACKNOWLEDGMENTS
The development of the theoretical spectroscopic methods is supported by the National Science Foundation through Grant No. CHE-1058752, the calculation of the spectroscopic observables is supported by the Department of Energy through Grant No. DE-FG02-09ER16110, and the development and implementation of the lipid bilayer simulations is supported by the National Institute of Health through Grant No. R01-DK088184. The authors wish to thank both Dr. P. Pieniazek and Professor M. Fayer for helpful conversations.
APPENDIX A: NONLINEAR RESPONSE FUNCTIONS
In this appendix we present the three (rephasing) third-order response functions necessary for the calculation of the pump-probe anisotropy decay r(t; ω), Eq. 2.5, and the isotropic decay, P(t), in Eq. 2.8:
| (A1) |
| (A2) |
| (A3) |
The full (rephasing) response function Riikk is the sum of Eqs. A1, A2, A3:
| (A4) |
In Eqs. A1, A2, A3, we have included vibrational lifetime effects only during the t2 population period. The indices i and k indicate the , , and components of the dipole matrix elements, though in all calculations presented here, we have considered only the and components; as in the experimental setup, the incident laser beams are directed perpendicular to the multi-bilayer.33 Note that since the system is macroscopically aligned, we do not have to average over all possible orientations of the molecular frame,122 as was done in, for example, previous calculations on ice.68
References
- van Meer G., Voelker D. R., and Feigenson G. W., Mol. Cell. Biol. 9, 112 (2008). 10.1038/nrm2330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koynova R. and Caffrey M., Biochim. Biophys. Acta 1376, 91 (1998). 10.1016/S0304-4157(98)00006-9 [DOI] [PubMed] [Google Scholar]
- Nagle J. F. and Tristram-Nagle S., Biochim. Biophys. Acta 1469, 159 (2000). 10.1016/S0304-4157(00)00016-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tristram-Nagle S. and Nagle J. F., Chem. Phys. Lipids 127, 3 (2004). 10.1016/j.chemphyslip.2003.09.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milhaud J., Biochim. Biophys. Acta 1663, 19 (2004). 10.1016/j.bbamem.2004.02.003 [DOI] [PubMed] [Google Scholar]
- Ball P., Chem. Rev. 108, 74 (2008). 10.1021/cr068037a [DOI] [PubMed] [Google Scholar]
- Zhong D., Pal S. K., and Zewail A. H., Chem. Phys. Lett. 1, 1 (2010). 10.1021/jz9001899 [DOI] [Google Scholar]
- Giovambattista N., Lopez C. F., Rossky P. J., and Debenedetti P. G., Proc. Natl. Acad. Sci. U.S.A. 105, 2274 (2008). 10.1073/pnas.0708088105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- England J. L., Lucent D., and Pande V. S., J. Am. Chem. Soc. 130, 11838 (2008). 10.1021/ja802248m [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeFlores L. P. and Tokmakoff A., J. Am. Chem. Soc. 128, 16520 (2006). 10.1021/ja067723o [DOI] [PubMed] [Google Scholar]
- Smolin N. and Daggett V., J. Phys. Chem. B 112, 6193 (2008). 10.1021/jp710546e [DOI] [PubMed] [Google Scholar]
- Tarek M. and Tobias D. J., Phys. Rev. Lett. 88, 138101 (2002). 10.1103/PhysRevLett.88.138101 [DOI] [PubMed] [Google Scholar]
- Russo D., Murarka R. K., Copley J. R.D., and Head-Gordon T., J. Phys. Chem. B 109, 12966 (2005). 10.1021/jp051137k [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu H. and Berne B. J., J. Phys. Chem. B 105, 11929 (2001). 10.1021/jp012749h [DOI] [Google Scholar]
- Ebbinghaus S., Kim S. J., Heyden M., Yu X., Heugen U., Gruebele M., Leitner D. M., and Havenith M., Proc. Natl. Acad. Sci. U.S.A. 104, 20749 (2007). 10.1073/pnas.0709207104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furse K. E. and Corcelli S. A., J. Am. Chem. Soc. 130, 13103 (2008). 10.1021/ja803728g [DOI] [PubMed] [Google Scholar]
- Fitter J., Lechner R. E., and Dencher N. A., J. Phys. Chem. B 103, 8036 (1999). 10.1021/jp9912410 [DOI] [Google Scholar]
- Foglia F., Lawrence M. J., Lorenz C. D., and McLain S. E., J. Chem. Phys. 133, 145103 (2010). 10.1063/1.3488998 [DOI] [PubMed] [Google Scholar]
- Hsieh C.-H. and Wu W.-G., Biophys. J. 71, 3278 (1996). 10.1016/S0006-3495(96)79520-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Z., Sayer B. G., Hughes D. W., Stark R. E., and Epand R. M., Biophys. J. 76, 387 (1999). 10.1016/S0006-3495(99)77205-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurze V., Steinbauer B., Huber T., and Beyer K., Biophys. J. 78, 2441 (2000). 10.1016/S0006-3495(00)76788-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gawrisch K., Gaede H. C., Mihailescu M., and White S. H., Eur. Biophys. J. 36, 281 (2007). 10.1007/s00249-007-0142-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klosgen B., Reichle C., Kohlsmann S., and Kramer K. D., Biophys. J. 71, 3251 (1996). 10.1016/S0006-3495(96)79518-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tielrooij K. J., Paparo D., Piatkowski L., Bakker H. J., and Bonn M., Biophys. J. 97, 2484 (2009). 10.1016/j.bpj.2009.08.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berntsen P., Svanberg C., and Swanson J., J. Phys. Chem. B 115, 1825 (2011). 10.1021/jp110899j [DOI] [PubMed] [Google Scholar]
- Pal S. K., Sukul D., Mandal D., and Bhattacharyya K., J. Phys. Chem. B 104, 4529 (2000). 10.1021/jp993348t [DOI] [Google Scholar]
- Sykora J., Kapusta P., Fidler V., and Hof M., Langmuir 18, 571 (2002). 10.1021/la011337x [DOI] [Google Scholar]
- Sykora J., Jurkiewicz P., Epand R. M., Kraayenhof R., Langner M., and Hof M., Chem. Phys. Lipids 135, 213 (2005). 10.1016/j.chemphyslip.2005.03.003 [DOI] [PubMed] [Google Scholar]
- Grdadolnik J., Kidrič J., and Hadži D., Chem. Phys. Lipids 59, 57 (1991). 10.1016/0009-3084(91)90063-H [DOI] [Google Scholar]
- Hübner W. and Blume A., Chem. Phys. Lipids 96, 99 (1998). 10.1016/S0009-3084(98)00083-8 [DOI] [Google Scholar]
- Volkov V. V., Palmer D. J., and Righini R., J. Phys. Chem. B 111, 1377 (2007). 10.1021/jp065886t [DOI] [PubMed] [Google Scholar]
- Volkov V. V., Palmer D. J., and Righini R., Phys. Rev. Lett. 99, 078302 (2007). 10.1103/PhysRevLett.99.078302 [DOI] [PubMed] [Google Scholar]
- Zhao W., Moilanen D. E., Fenn E. E., and Fayer M. D., J. Am. Chem. Soc. 130, 13927 (2008). 10.1021/ja803252y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alper H. E., Bassolino-Kilmas D., and Stouch T. R., J. Chem. Phys. 99, 5547 (1993). 10.1063/1.465947 [DOI] [Google Scholar]
- Damodaran K. V. and Merz K. M., Langmuir 9, 1179 (1993). 10.1021/la00029a005 [DOI] [Google Scholar]
- Damodaran K. V. and Merz K. M., Biophys. J. 66, 1076 (1994). 10.1016/S0006-3495(94)80889-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tieleman D. P. and Berendsen H. J.C., J. Chem. Phys. 105, 4871 (1996). 10.1063/1.472323 [DOI] [Google Scholar]
- Scott H. L., Curr. Opin. Struct. Biol. 12, 495 (2002). 10.1016/S0959-440X(02)00353-6 [DOI] [PubMed] [Google Scholar]
- Rog T., Murzyn K., and Pasenkiewicz-Gierula M., Chem. Phys. Lett. 352, 323 (2002). 10.1016/S0009-2614(02)00002-7 [DOI] [Google Scholar]
- Lopez C. F., Nielsen S. O., and Klein M. L., J. Phys. Chem. B 108, 6603 (2004). 10.1021/jp037618q [DOI] [Google Scholar]
- de Vries A. H., Yefimov S., Mark A. E., and Marrink S. J., Proc. Natl. Acad. Sci. U.S.A. 102, 5392 (2005). 10.1073/pnas.0408249102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murzyn K., Zhao W., Karttunen M., Kurdziel M., and Rog T., Biointerphases 1, 98 (2006). 10.1116/1.2354573 [DOI] [PubMed] [Google Scholar]
- Sapay N., Bennett W. F.D., and Tieleman D. P., Soft Matter 5, 3295 (2009). 10.1039/b902376c [DOI] [Google Scholar]
- Vacha R., Siu S. W.I., Petrov M., Bockmann R. A., Barucha-Kraszewska J., Jurkiewicz P., Hof M., Berkowitz M. L., and Jungwirth P., J. Phys. Chem. A 113, 7235 (2009). 10.1021/jp809974e [DOI] [PubMed] [Google Scholar]
- Berkowitz M. L., Biochim. Biophys. Acta 1788, 86 (2009). 10.1016/j.bbamem.2008.09.009 [DOI] [PubMed] [Google Scholar]
- Vacha R., Berkowitz M. L., and Jungwirth P., Biophys. J. 96, 4493 (2009). 10.1016/j.bpj.2009.03.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stepniewski M., Bunker A., Pasenkiewicz-Gierula M., Karttunen M., and Rog T., J. Phys. Chem. B 114, 11784 (2010). 10.1021/jp104739a [DOI] [PubMed] [Google Scholar]
- de Meyer F. J.-M., Benjamini A., Rodgers J. M., Misteli Y., and Smit B., J. Phys. Chem. B 114, 10451 (2010). 10.1021/jp103903s [DOI] [PubMed] [Google Scholar]
- Broemstrup T. and Reuter N., Biophys. J. 99, 825 (2010). 10.1016/j.bpj.2010.04.064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z. and Berkowitz M. L., J. Phys. Chem. B 113, 7676 (2009). 10.1021/jp900873d [DOI] [PubMed] [Google Scholar]
- Khandelia H. and Kaznessis Y. N., Biochim. Biophys. Acta 1768, 509 (2007). 10.1016/j.bbamem.2006.11.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonn M., Bakker H. J., Ghosh A., Yamamoto S., Sovago M., and Campen R. K., J. Am. Chem. Soc. 132, 14971 (2010). 10.1021/ja106194u [DOI] [PubMed] [Google Scholar]
- Nagata Y. and Mukamel S., J. Am. Chem. Soc. 132, 6434 (2010). 10.1021/ja100508n [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X., Hua W., Huang Z., and Allen H. C., J. Am. Chem. Soc. 132, 11336 (2010). 10.1021/ja1048237 [DOI] [PubMed] [Google Scholar]
- Mondal J. A., Nihonyanagi S., Yamaguchi S., and Tahara T., J. Am. Chem. Soc. 132, 10656 (2010). 10.1021/ja104327t [DOI] [PubMed] [Google Scholar]
- Faeder J. and Ladanyi B. M., J. Phys. Chem. B 104, 1033 (2000). 10.1021/jp993076u [DOI] [Google Scholar]
- Piletic I. R., Moilanen D. E., Spry D. B., Levinger N. E., and Fayer M. D., J. Phys. Chem. A 110, 4985 (2006). 10.1021/jp061065c [DOI] [PubMed] [Google Scholar]
- Dokter A. M., Woutersen S., and Bakker H. J., Proc. Natl. Acad. Sci. U.S.A. 103, 15355 (2006). 10.1073/pnas.0603239103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moilanen D. E., Fenn E. E., Wong D., and Fayer M. D., J. Phys. Chem. B 113, 8560 (2009). 10.1021/jp902004r [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moilanen D. E., Fenn E. E., Wong D., and Fayer M. D., J. Chem. Phys. 131, 014704 (2009). 10.1063/1.3159779 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pieniazek P. A., Lin Y.-S., Chowdhary J., Ladanyi B. M., and Skinner J. L., J. Phys. Chem. B 113, 15017 (2009). 10.1021/jp906784t [DOI] [PubMed] [Google Scholar]
- Bhide S. Y. and Berkowitz M. L., J. Chem. Phys. 123, 224702 (2005). 10.1063/1.2132277 [DOI] [PubMed] [Google Scholar]
- Asbury J. B., Steinel T., Stromberg C., Corcelli S. A., Lawrence C. P., Skinner J. L., and Fayer M. D., J. Phys. Chem. A 108, 1107 (2004). 10.1021/jp036266k [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loparo J. J., Roberts S. T., and Tokmakoff A., J. Chem. Phys. 125, 194521 (2006). 10.1063/1.2382895 [DOI] [PubMed] [Google Scholar]
- Loparo J. J., Roberts S. T., and Tokmakoff A., J. Chem. Phys. 125, 194522 (2006). 10.1063/1.2382896 [DOI] [PubMed] [Google Scholar]
- Moilanen D. E., Fenn E. E., Lin Y.-S., Skinner J. L., Bagchi B., and Fayer M. D., Proc. Natl. Acad. Sci. U.S.A. 105, 5295 (2008). 10.1073/pnas.0801554105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakker H. and Skinner J. L., Chem. Rev. 110, 1498 (2010). 10.1021/cr9001879 [DOI] [PubMed] [Google Scholar]
- Li F. and Skinner J. L., J. Chem. Phys. 132, 204505 (2010). 10.1063/1.3430518 [DOI] [PubMed] [Google Scholar]
- Park S. and Fayer M. D., Proc. Natl. Acad. Sci. U.S.A. 104, 16731 (2007). 10.1073/pnas.0707824104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith J. D., Saykally R. J., and Geissler P. L., J. Am. Chem. Soc. 129, 13847 (2007). 10.1021/ja071933z [DOI] [PubMed] [Google Scholar]
- Bakker H. J., Rezus Y. L.A., and Timmer R. L.A., J. Phys. Chem. A 112, 11523 (2008). 10.1021/jp8012943 [DOI] [PubMed] [Google Scholar]
- Laage D. and Hynes J. T., Science 311, 832 (2006). 10.1126/science.1122154 [DOI] [PubMed] [Google Scholar]
- Laage D. and Hynes J. T., Chem. Phys. Lett. 433, 80 (2006). 10.1016/j.cplett.2006.11.035 [DOI] [Google Scholar]
- Laage D. and Hynes J. T., Proc. Natl. Acad. Sci. U.S.A. 104, 11167 (2007). 10.1073/pnas.0701699104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji M., Odelius M., and Gaffney K. J., Science 328, 1003 (2010). 10.1126/science.1187707 [DOI] [PubMed] [Google Scholar]
- Auer B. M., Kumar R., Schmidt J. R., and Skinner J. L., Proc. Natl. Acad. Sci. U.S.A. 104, 14215 (2007). 10.1073/pnas.0701482104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auer B. M. and Skinner J. L., J. Chem. Phys. 128, 224511 (2008). 10.1063/1.2925258 [DOI] [PubMed] [Google Scholar]
- Yang M. and Skinner J. L., Phys. Chem. Chem. Phys. 12, 982 (2010). 10.1039/b918314k [DOI] [PubMed] [Google Scholar]
- Lin Y.-S., Pieniazek P. A., Yang M., and Skinner J. L., J. Chem. Phys. 132, 174505 (2010). 10.1063/1.3409561 [DOI] [PubMed] [Google Scholar]
- Jansen T. L.C., Auer B. M., Yang M., and Skinner J. L., J. Chem. Phys. 132, 224503 (2010). 10.1063/1.3454733 [DOI] [PubMed] [Google Scholar]
- Auer B. M. and Skinner J. L., J. Chem. Phys. 129, 214705 (2008). 10.1063/1.3012568 [DOI] [PubMed] [Google Scholar]
- Auer B. M. and Skinner J. L., Chem. Phys. Lett. 470, 13 (2009). 10.1016/j.cplett.2009.01.010 [DOI] [Google Scholar]
- Auer B. M. and Skinner J. L., J. Phys. Chem. B 113, 4125 (2009). 10.1021/jp806644x [DOI] [PubMed] [Google Scholar]
- Stiopkin I. V., Weeraman C., Pieniazek P. A., Shalhout F. Y., Skinner J. L., and Benderskii A. V., Nature (London) 474, 192 (2011). 10.1038/nature10173 [DOI] [PubMed] [Google Scholar]
- Pieniazek P. A., Tainter C. J., and Skinner J. L., J. Am. Chem. Soc. 133, 10360 (2011). 10.1021/ja2026695 [DOI] [PubMed] [Google Scholar]
- Pieniazek P. A., Tainter C. J., and Skinner J. L., J. Chem. Phys. 135, 044701 (2011). 10.1063/1.3613623 [DOI] [PubMed] [Google Scholar]
- Li F. and Skinner J. L., J. Chem. Phys. 133, 244504 (2010). 10.1063/1.3516460 [DOI] [PubMed] [Google Scholar]
- Lin Y.-S., Auer B. M., and Skinner J. L., J. Chem. Phys. 131, 144511 (2009). 10.1063/1.3242083 [DOI] [PubMed] [Google Scholar]
- Mukamel S., Principles of Nonlinear Optical Spectroscopy (Oxford, New York, 1995). [Google Scholar]
- Schmidt J. R., Corcelli S. A., and Skinner J. L., J. Chem. Phys. 123, 044513 (2005). 10.1063/1.1961472 [DOI] [PubMed] [Google Scholar]
- Schmidt J. R., Roberts S. T., Loparo J. J., Tokmakoff A., Fayer M. D., and Skinner J. L., Chem. Phys. 341, 143 (2007). 10.1016/j.chemphys.2007.06.043 [DOI] [Google Scholar]
- Venturoli M., Sperotto M. M., Kranenburg M., and Smit B., Phys. Rep. 437, 1 (2006). 10.1016/j.physrep.2006.07.006 [DOI] [Google Scholar]
- Berger O., Edholm O., and Jahnig F., Biophys. J. 72, 2002 (1997). 10.1016/S0006-3495(97)78845-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandrasekhar I., Kastenholz M., Lins R. D., Oostenbrink C., Schuler L. D., Tieleman D. P., and van Gunsteren W. F., Eur. Biophys. J. 32, 67 (2003). 10.1007/s00249-002-0269-4 [DOI] [PubMed] [Google Scholar]
- Podger D., van Gunsteren W. F., and Mark A. E., J. Comput. Chem. 31, 1117 (2010). 10.1002/jcc.21396 [DOI] [PubMed] [Google Scholar]
- Sonne J., Jensen M. O., Hansen F. Y., Hemmingsen L., and Peters G. H., Biophys. J. 92, 4157 (2007). 10.1529/biophysj.106.087130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor J., Whiteford N. E., Bradley G., and Watson G. W., Biochim. Biophys. Acta 1788, 638 (2009). 10.1016/j.bbamem.2008.10.013 [DOI] [PubMed] [Google Scholar]
- Wang J., Wolf R. M., Caldwell J. W., Kollman P. A., and Case D. A., J. Comput. Chem. 25, 1157 (2004). 10.1002/jcc.20035 [DOI] [PubMed] [Google Scholar]
- Jojart B. and Martinek T. A., J. Comput. Chem. 28, 2051 (2007). 10.1002/jcc.20748 [DOI] [PubMed] [Google Scholar]
- Rosso L. and Gould I. R., J. Comput. Chem. 29, 24 (2008). 10.1002/jcc.20675 [DOI] [PubMed] [Google Scholar]
- Anezo C., de Vries A. H., Holtje H. D., Tieleman D. P., and Marrink S. J., J. Phys. Chem. B 107, 9424 (2003). 10.1021/jp0348981 [DOI] [Google Scholar]
- Siu S. W. I., Vacha R., Jungwirth P., and Bockmann R. A., J. Chem. Phys. 128, 125103 (2008). 10.1063/1.2897760 [DOI] [PubMed] [Google Scholar]
- Lindahl E., Hess B., and van der Spoel D., J. Mol. Model. 7, 306 (2001). [Google Scholar]
- Chiu S.-W., Clark M., Balaji V., Subramaniam S., Scott H. L., and Jakobsson E., Biophys. J. 69, 1230 (1995). 10.1016/S0006-3495(95)80005-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendsen H. J. C., Grigera J. R., and Straatsma T. P., J. Phys. Chem. 91, 6269 (1987). 10.1021/j100308a038 [DOI] [Google Scholar]
- Essmann U., Perera L., Berkowitz M. L., Darden T., Lee H., and Pedersen L. G., J. Chem. Phys. 103, 8577 (1995). 10.1063/1.470117 [DOI] [Google Scholar]
- Hoover W. G., Phys. Rev. A 31, 1695 (1985). 10.1103/PhysRevA.31.1695 [DOI] [PubMed] [Google Scholar]
- Parrinello M. and Rahman A., J. Chem. Phys. 76, 2662 (1982). 10.1063/1.443248 [DOI] [Google Scholar]
- Hess B., Bekker H., Berendsen H. J.C., and Fraaije J. G. E. M., J. Comput. Chem. 18, 1463 (1997). [DOI] [Google Scholar]
- Skinner J. L., Auer B. M., and Lin Y.-S., Adv. Chem. Phys. 142, 59 (2009). 10.1002/SERIES2007 [DOI] [Google Scholar]
- Lawrence C. P. and Skinner J. L., J. Chem. Phys. 117, 5827 (2002). 10.1063/1.1502248 [DOI] [Google Scholar]
- Chieffo L., Shattuck J., Amsden J. J., Erramilli S., and Ziegler L. D., Chem. Phys. 341, 71 (2007). 10.1016/j.chemphys.2007.06.024 [DOI] [Google Scholar]
- Chieffo L. R., Shattuck J. T., Pinnick E., Amsden J. J., Hong M. K., Wang F., Erramilli S., and Ziegler L. D., J. Phys. Chem. B 112, 12776 (2008). 10.1021/jp8012283 [DOI] [PubMed] [Google Scholar]
- Skinner J. L., Theor. Chem. Acc. 128, 147 (2011). 10.1007/s00214-010-0834-3 [DOI] [Google Scholar]
- Schäfer T., Lindner J., Vöhringer P., and Schwarzer D., J. Chem. Phys. 130, 224502 (2009). 10.1063/1.3151673 [DOI] [PubMed] [Google Scholar]
- Tian G., Chem. Phys. 328, 216 (2006). 10.1016/j.chemphys.2006.06.029 [DOI] [Google Scholar]
- Lawrence C. P. and Skinner J. L., J. Chem. Phys. 119, 3840 (2003). 10.1063/1.1591178 [DOI] [Google Scholar]
- Moilanen D. E., Piletic I. R., and Fayer M. D., J. Phys. Chem. A 110, 9084 (2006). 10.1021/jp0623084 [DOI] [PubMed] [Google Scholar]
- Moilanen D. E., Piletic I. R., and Fayer M. D., J. Phys. Chem. C 111, 8884 (2007). 10.1021/jp067460k [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auer B. M. and Skinner J. L., J. Chem. Phys. 127, 104105 (2007). 10.1063/1.2766943 [DOI] [PubMed] [Google Scholar]
- Laage D., Stirnemann G., Sterpone F., Rey R., and Hynes J. T., Annu. Rev. Phys. Chem. 62, 395 (2011). 10.1146/annurev.physchem.012809.103503 [DOI] [PubMed] [Google Scholar]
- Hochstrasser R. M., Chem. Phys. 266, 273 (2001). 10.1016/S0301-0104(01)00232-4 [DOI] [Google Scholar]