Direct Quantification of the Attempt Frequency Determining the Mechanical Unfolding of Ubiquitin Protein

Abstract

Understanding protein dynamics requires a comprehensive knowledge of the underlying potential energy surface that governs the motion of each individual protein molecule. Single molecule mechanical studies have provided the unprecedented opportunity to study the individual unfolding pathways along a well defined coordinate, the end-to-end length of the protein. In these experiments, unfolding requires surmounting an energy barrier that separates the native from the extended state. The calculation of the absolute value of the barrier height has traditionally relied on the assumption of an attempt frequency, υ^‡. Here we used single molecule force-clamp spectroscopy to directly determine the value of υ^‡ for mechanical unfolding by measuring the unfolding rate of the small protein ubiquitin at varying temperatures. Our experiments demonstrate a significant effect of the temperature on the mechanical rate of unfolding. By extrapolating the unfolding rate in the absence of force for different temperatures, varying within the range spanning from 5 to 45 °C, we measured a value for the activation barrier of ΔG^‡ = 71 ± 5 kJ/mol and an exponential prefactor υ^‡ ∼4 × 10⁹ s⁻¹. Although the measured prefactor value is 3 orders of magnitude smaller than the value predicted by the transition state theory (∼6 × 10¹² s⁻¹), it is 400-fold higher than that encountered in analogous experiments studying the effect of temperature on the reactivity of a protein-embedded disulfide bond (∼10⁷ m⁻¹ s⁻¹). This approach will allow quantitative characterization of the complete energy landscape of a folding polypeptide from highly extended states, of capital importance for proteins with elastic function.

Introduction

A deep understanding of protein dynamics relies on the accurate determination of the free energy surface that governs the (un)folding reaction. In the case of small proteins, the (un)folding process is generally described by a two-state scenario, whereby the native and unfolded states are separated by a prominent energy barrier (1). The conversion between these two states has been traditionally given the treatment of a first-order chemical reaction, where the concentration of the reactant species, the native state of the protein, decreases exponentially with time (2). Such a simplified kinetic analysis provides the framework to study the (un)folding reaction in terms of the Eyring transition state theory (TST),³ which allows quantification of the rate constant for a given chemical reaction as a function of temperature (3, 4)

where υ^‡ is the prefactor, k_B is the Boltzmann constant, T is the absolute temperature, and ΔG^‡ is the activation energy. In this simplified equation,

where C° is the standard state concentration, h is the Planck's constant, and n is the order of the reaction. The factor (k_BT/h) is a frequency factor, equal to 6 ps⁻¹ at 300 K, for the crossing of the transition state. The generalized transmission coefficient, γ(T), relates the actual rate of the reaction to that obtained from the simple transition state theory, in which γ(T) = 1. Over the last two decades, a great number of studies have reported the effect of temperature on the (un)folding kinetics of a plethora of distinct proteins using different biochemistry bulk techniques. With a few exceptions (5), the apparent consensus (6) is that although protein unfolding usually follows simple Arrhenius kinetics, the folding kinetics exhibit more complex dependences with temperature, resulting in curvature in the ln k_f versus 1/T plots (7–12). The origin of such non-Arrhenius behavior during the folding reaction can be generically explained either in terms of the rate of escape from different minima along a rough energy landscape, thus yielding super-Arrhenius kinetics, or most likely, based on the hydrophobic effect, involving a large change in heat capacity during the folding process (13–15), with the heat capacity of the transition state placed somewhere in between the folded and unfolded states (16).

Single molecule force spectroscopy has provided a new vista on the molecular mechanisms underlying protein (un)folding at the subnanometer scale (17). In stark contrast with protein unfolding experiments conducted using traditional bulk experiments, where the radius of gyration of the protein increases by only ∼10 Å upon unfolding (18), in mechanical experiments, proteins are extended tens of nanometers, to almost their contour length (19). Hence, when using force as a denaturing agent, proteins visit regions of the energy landscape that have not been explored before (20). By now, more than 200 different proteins have been studied using single molecule force spectroscopy (21, 22). These studies have provided valuable information regarding their nanomechanical properties, which are intimately related to the structural topology. Previous single molecule mechanical studies have investigated the effect of temperature on the nanomechanical properties of proteins (23–28). Qualitatively, these works reported an expected decrease in the mechanical stability of the protein as the temperature was increased. However, it remained elusive whether the effect of temperature was uniquely to lower the height of the energy barrier, ΔG^‡, or whether the distance to the transition state, Δx, which determines the width of the barrier, was also altered by the change in temperature. Most importantly, in all these studies, the absolute value of the height of the energy barrier limiting the unfolding process has been calculated assuming an attempt frequency, υ^‡, which has been given a value that varied over a wide range, spanning from 10⁶ s⁻¹ up to 10¹³ s⁻¹ (29–31). In this vein, Schlierf and Rief (25) reported that for the protein filamin, temperature induced a significant increase in the distance to the transition state while keeping the height of the energy barrier unaltered. Nonetheless, these experiments were conducted under constant velocity conditions, where the length of the protein, the force, and the loading rate are dynamically changing during the force-extension cycle over wide ranges in a short timescale, thus necessitating the use of Monte Carlo models to interpret the results (32).

Force-clamp spectroscopy excels at directly extracting the kinetic parameters defining the free energy landscape of a single molecule placed under a constant stretching force. This approach has revealed a wealth of new information regarding the kinetics involved in protein unfolding, protein folding, and chemical reactions under force (17, 30, 33, 34). Here we study the mechanical unfolding of the small protein ubiquitin at varying temperatures to experimentally obtain, for the first time in single molecule mechanical experiments, the attempt frequency prefactor for protein unfolding, υ^‡, together with the height and width of the energy barrier separating the native from the extended states of the protein. This study complements the extensive work conducted with the protein ubiquitin, the mechanical behavior of which has been vastly characterized in different regions of the folding energy landscape (17, 31, 35–37). Furthermore, the remarkable thermal stability of ubiquitin (above 100 °C) makes it an ideal candidate for the thermal studies under force (10). Our experiments demonstrate a significant effect of the temperature on the mechanical rate of unfolding. We analyzed our data within the framework of simple TST theory (Equation 1) under the assumption, as a first approximation, that the value of the transmission coefficient γ(T) = 1. By extrapolating the unfolding rate in the absence of force for different temperatures, varying within the range 5–45 °C, we measure a value for the activation barrier of ΔG^‡ = 71 ± 5 kJ/mol and an exponential prefactor υ^‡ ∼4 × 10⁹ s⁻¹. Contrary to the results reported for filamin (25), and similar to the case of the I27 protein (26), the major effect of temperature is to significantly lower the height of the energy barrier, whereas the distance to the transition state increases only slightly within the range of temperatures probed in our experiments. The measured value for the exponential prefactor for mechanical unfolding, υ^‡, on the nanosecond timescale, places an upper limit to the diffusive mean first passage time for unfolding. This value will be used to unambiguously determine the absolute height of the energy barrier for mechanical unfolding, which will be of paramount importance to fully reconstruct the energy landscape of elastic proteins with mechanical function, of common occurrence in nature.

EXPERIMENTAL PROCEDURES

Protein Engineering

Wild-type (WT) ubiquitin polyprotein was subcloned using the BamHI and BglII restriction sites (29, 38). The nine-domain ubiquitin was cloned into the pQE80L (Qiagen) expression vector and transformed into the BLRDE3 Escherichia coli expression strain(29). The construct was purified by histidine metal-affinity chromatography with Talon resin (Clontech) and by gel filtration using a Superdex 200 HR column (GE Biosciences).

Force Spectroscopy

Force-clamp atomic force microscopy experiments were conducted at varying temperatures using a home-made setup under force-clamp conditions, as described elsewhere (17). The sample was prepared by depositing 1–10 μl of protein in PBS solution (at a concentration of 1–10 mg ml⁻¹) onto a freshly evaporated gold cover slide. Each cantilever (Si₃N₄ Veeco MLCT-AUHW) was individually calibrated using the equipartition theorem, which gave a typical spring constant of 15 pN nm⁻¹. Single proteins were picked up from the surface by pushing the cantilever onto the surface with a contact force of 500–1,000 pN to promote the nonspecific adhesion of the proteins on the cantilever surface. The piezoelectric actuator was then retracted to produce a set deflection (force), which was kept constant throughout the experiment using an external, active feedback mechanism while the extension was recorded. The force feedback was based on a proportional, integral, and differential amplifier, the output of which was fed to the piezoelectric positioner. The feedback response was limited to ∼2–5 ms. The high resolution piezoelectric actuator allowed our measurements of protein length a peak-to-peak resolution of ∼0.5 nm. Data from the force traces were filtered using a pole Bessel filter at 1 kHz. The range of pulling forces was chosen such that the unfolding trajectories would not be compromised by the feedback bandwidth or cantilever drift occurring over much longer timescales. Temperature was controlled by a thermoelectric device (Custom Thermoelectric) that was glued to the gold-coated cover slides by heat-conductive paste. The device can convert the input electric voltage to temperature difference between the two sides of it (Peltier effect). The side opposite to the gold cover slide sample was connected to a heat sink, which was placed on top of the piezoelectric actuator and could exchange heat with air or a flux of chilling water. The switch between heating and cooling could be conveniently achieved by changing the polarity of the input voltage. The temperature in the fluid cell was monitored during the whole experiment by a thin-wire thermocouple (Physitemp Intruments Inc.). The temperature set point was achieved within ±0.1 K accuracy and controlled by a custom software written in Igor Pro 6.0 (WaveMetrics).

Data Analysis

All data were recorded and analyzed using custom software written in Igor Pro 6.0 (WaveMetrics). The fingerprint of a single polyprotein in our unfolding experiments was considered to be at least six well resolved steps of 20 nm exhibiting long detachment times in order not to bias the unfolding probability. We summed and normalized numerous individual unfolding trajectories (n = 5–25) for each particular pulling force and temperature. To obtain the rate of unfolding under each particular condition of force and temperature, we fitted these averaged traces with a single exponential function. To estimate the error on our experimentally obtained rate constants, we conducted a non-parametric bootstrap method. At a given value of force and temperature, n staircases were randomly drawn with replacement from our original dataset. These were summed and fitted to a single exponential function to obtain a rate constant. This procedure was repeated 500 times for each dataset, resulting in a distribution that provided the standard error of the mean corresponding to the unfolding of the native state of the ubiquitin polyprotein under each particular condition of force and temperature.

RESULTS

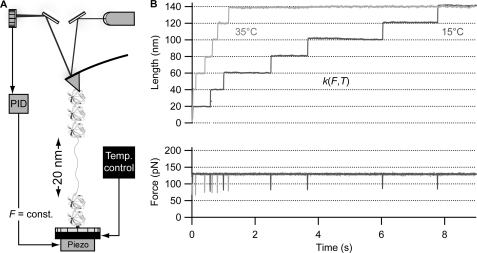
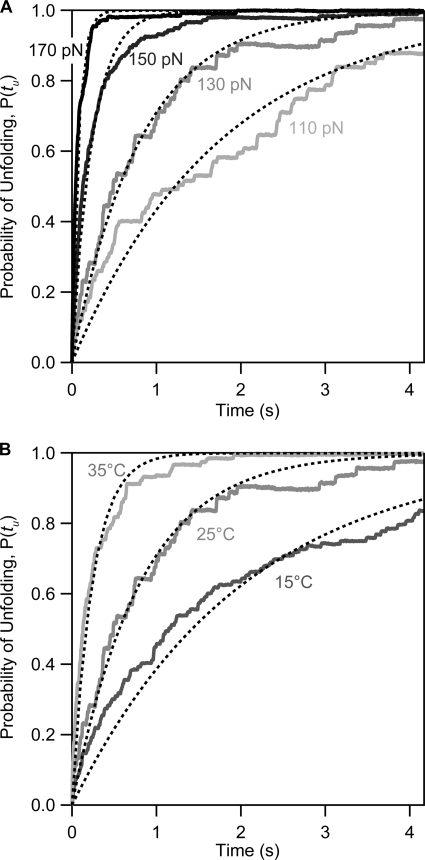
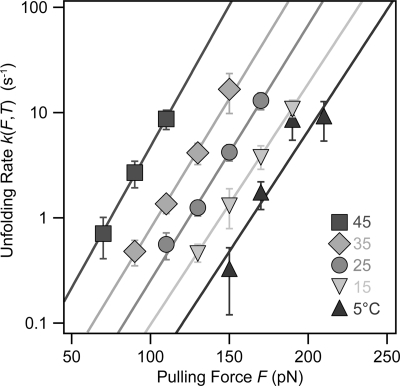
In our experimental force spectroscopy assay, we stretched individual ubiquitin polyproteins of nine identical domains under constant force conditions (Fig. 1A). The resulting unfolding trajectories resembled a staircase, where each ∼20-nm step corresponded to the unfolding of an individual ubiquitin monomer in the polyprotein chain. For a given constant force, we observed that the rate of unfolding was significantly increased upon raising the temperature. This was qualitatively shown by the two unfolding trajectories measured under a constant force of 130 pN (Fig. 1B), in which the complete unfolding of ubiquitin at 35 °C occured much faster than the unfolding process at 15 °C. By averaging and normalizing several unfolding trajectories such as those shown in Fig. 1B at a given value of force and temperature, we obtained the cumulative probability of unfolding as a function of time for each particular experimental condition. Fig. 2A shows the cumulative probability for ubiquitin unfolding, P(t_u), at different stretching forces spanning from 110 to 170 pN, whereas the temperature was set constant at 25 °C. At each force, P(t_u) was fitted with a single exponential curve (dashed lines) according to the two-state model for protein unfolding. Although force-clamp experiments on an extensive pool of unfolding data have revealed deviations from two-state kinetics in ubiquitin (35, 37), the single exponential fit gives rise to a reasonable first approximation of the rate of unfolding at each particular force (39). The significant effect of temperature on the mechanical stability of ubiquitin is demonstrated in Fig. 2B, which shows the cumulative probability of unfolding at a constant pulling force of 110 pN for different temperatures ranging from 15 to 35 °C. As before, the cumulative unfolding probability at each probed temperature was fitted with a single exponential, yielding the rate of unfolding for each particular force-temperature pair. The dependence of the unfolding rate obtained from Fig. 2 as a function of the pulling force is shown in Fig. 3. This plot highlights the significant softening of the native state of ubiquitin induced by a temperature increase. The force dependence of the rate of unfolding was fitted to a simple Arrhenius/Bell term (40) (Fig. 3, solid lines).

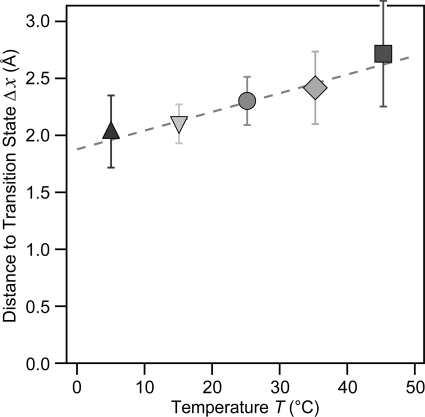
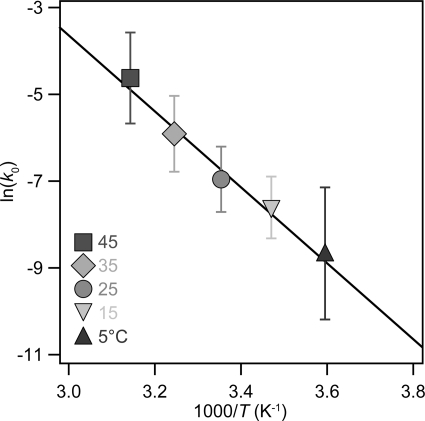
where k(F, T) is the unfolding rate at each constant pulling force and k₀(T) stands for the extrapolated unfolding rate in the absence of force. From the fit, we obtained the value of k₀ for each particular temperature as well as the value of the distance to the transition state, Δx. As it can be directly observed from the rate versus force graph (Fig. 3), upon increasing the temperature, the rate of unfolding significantly increased for a given force. Notably, for all given temperatures, the Arrhenius/Bell equation fits rather well the experimental data within the entire range of forces sampled in our experiments, spanning from 5 to 45 °C. In a recent study using a statistically significant pool of data gathered at room temperature, we showed that the time distribution for ubiquitin unfolding at a constant pulling force deviated from single exponential kinetics (37). We explained such a non-exponential behavior using a generalized Arrhenius equation that includes static disorder of conformational degrees of freedom (37). Briefly, this model explains the non-exponential kinetics of ubiquitin unfolding by assuming a normal distribution of disorder with respect to the average value both in the height of the energy barrier, ΔG^‡, and also in the distance to the transition state, Δx. Our experiments demonstrated that the measured variance shows both force-dependent and force-independent components, where the force-dependent component scales with F². It is noteworthy that in the experiments presented here, where we measured the effect of temperature on the kinetics of ubiquitin unfolding for a wide range of forces and with a smaller set of data, the exponential trend between the unfolding rate and the pulling force was still retained, reproducing the average unfolding rate obtained at room temperature for a much extended dataset containing a few thousands of individual unfolding events (37). This observation indicated that in our measurements as a function of temperature, we already captured the peak of the distribution of unfolding times as a function of the stretching force. Although far from the scope of the present work, studying the effect of temperature on the degree of static disorder underlying ubiquitin unfolding at different forces certainly invites experimental investigation for future research. According to the Bell expression (Equation 3), the value of Δx for each particular temperature can be obtained from the slope of semilogarithmic plot (Fig. 3). The obtained values for Δx as a function of the temperature are plotted in Fig. 4. The obtained value of Δx exhibited a slight monotonic increase with temperature, varying from 2.0 ± 0.3 Å at 5 °C to 2.7 ± 0.4 Å at a temperature value as high as 45 °C. Notably, the value of 2.3 ± 0.4 Å measured at 25 °C was in good agreement with previous experiments conducted at room temperature (37). From the extrapolation of the values corresponding to the unfolding rate in the absence of force (Fig. 3), we obtained the values of k₀ for each temperature probed in our experiments. Fig. 5 shows the plot of the ln k₀ as a function of 1/T. Fitting Equation 1 to the experimental data (black line, r² = 0.98) directly yields the value for the height of the activation energy barrier ΔG^‡ = 71 ± 5 kJ/mol and for the prefactor υ^‡ = 4 × 10⁹ s⁻¹. This treatment assumes that the activation energy is temperature-independent. The goodness of the fit over the whole range of temperatures probed in our experiments suggested that, as a first approximation, the unfolding reaction follows a simple Arrhenius-like model (Equation 1) with a well defined activation energy barrier as the rate-limiting step. Hence, from the fit of the linearized Arrhenius equation to the experimental data, we can extract the main features defining the microscopic origins of the force-induced unfolding reaction.

FIGURE 1.

Unfolding the ubiquitin polyprotein in a force-clamp at varying temperatures. A, schematics of the experimental force-clamp setup, provided with a Peltier element that lies just below the gold cover slide onto which single proteins are deposited. const., constant; Temp. control, temperature control. B, unfolding the ubiquitin polyprotein under a constant force of 130 pN results in a staircase-like elongation, where the unfolding of each monomer in the chain occurs stochastically at a time Δt after the application of force, eliciting steps of ∼20 nm in length. The time course of unfolding is accelerated with the temperature at which the experiments are conducted. PID, (proportional integral differential) force feedback.

FIGURE 2.

The combined effect of force and temperature on the kinetics of the mechanical unfolding of ubiquitin. A, four averaged and normalized polyubiquitin unfolding time courses obtained at a constant temperature of 25 °C at different constant stretching forces: 110, 130, 150, and 170 pN. Discontinuous black lines correspond to single exponential fits with associated rate constants presented as circles in Fig. 3. B, average time course of unfolding at a constant force of 130 pN at varying temperatures: 15, 25, and 35 °C. Discontinuous black lines correspond to single exponential fits, yielding the values for the associated unfolding rate constants presented in Fig. 3.

FIGURE 3.

The effect of temperature on the force dependence of polyubiquitin unfolding. Semilogarithmic plot of the rate of unfolding of ubiquitin, k(F, T), as a function of the pulling force at: 5 °C (triangles), 15 °C (inverted triangles), 25 °C (circles), 35 °C (diamonds), and 45 °C (squares). The solid colored lines in each case represent fits to the Arrhenius/Bell term (Equation 3 under “Results”) to the experimental data. From these fits, we obtained the associated Δx and k₀ value for each probed temperature. The range of forces probed for each particular temperature is chosen such that they do not compromise the measurement due to limited feedback response at fast unfolding rates and cantilever drift for slow unfolding kinetics.

FIGURE 4.

The value of the Δx is slightly increased upon raising the temperature in the range of 5–45 °C. The increase in Δx, although small, is significant (Student's t test for a 95% confidence). From the Arrhenius/Bell fit to the data (Fig. 3 and Equation 3 under “Results”), we obtained the Δx value for each given temperature. The obtained value ranges from 2.0 ± 0.3 Å at 5 °C to 2.7 ± 0.4 Å at 45 °C. Linear fit to the data (dashed line) yields a slope of (1.6 ± 0.5) × 10⁻³ nm/°C.

FIGURE 5.

The dependence of k₀ with 1/T allows calculation of the unfolding energy barrier and the collision frequency factor. From the Arrhenius/Bell fit shown in Fig. 3, we obtained the value of the unfolding rate in the absence of force k₀ for each temperature probed: 5 °C (triangle), 15 °C (inverted triangle), 25 °C (circle), 35 °C (diamond), and 45 °C (square). The solid black line represents the fit of Equation 1 to the data, giving rise to values for the activation barrier of ΔG^‡ = 71 ± 5 kJ/mol and for exponential prefactor, υ^‡ = ∼10^{9.6 ± 0.99} (±S.D.), corresponding to a mean value of υ^‡ = 4 × 10⁹ s⁻¹.

DISCUSSION

Here, we investigated the combined effect of a constant mechanical force and temperature on the rate of unfolding of the small protein ubiquitin. Unlike classical unfolding experiments using chemicals or large temperature jumps, the mechanical unfolding of proteins is a highly localized process mainly involving the rupture of a few key hydrogen bonds within the structure of the protein native state, which constitutes the crucial structural motif that provides the protein with mechanical stability (41). In the case of the ubiquitin protein, the mechanical clamp is placed between the β1–β5 sheets (42). After the rupture of this mechanical clamp, which constitutes the major energy barrier for unfolding, the protein extends up to almost its contour length without any extra enthalpic energy cost. Therefore, the molecular mechanisms that underlie mechanical protein (un)folding are likely to be different from those involved in protein unfolding when using chemicals or temperature as denaturing agents. Hence, the features of the energy landscape governing the mechanical unfolding process, namely the height and width of the energy, as well as the frequency attempt, will surely differ from those probed using traditional biochemistry tools, occurring over completely different reaction coordinates. Indeed, the value for the pre-exponential factor obtained for ubiquitin unfolding using bulk techniques using nanosecond laser temperature jumps, where the disruption of interhydrogen bonds between β-strands III–V was probed with non-linear infrared spectroscopy as a function of temperature (53–67 °C), was measured to be ∼1.2 × 10¹⁵ s⁻¹(43). In similar experiments combining rapid mixing T-jump and laser T-jump with fluorescence detection, the fluorescence changes of Tyr-59 located on the 3₁₀-helix of ubiquitin were measured as a function of the temperature, varying within the range 45–65 °C (10). These experiments yielded a pre-exponential factor of 8.3 × 10³³ s⁻¹. Hence, these studies conducted in bulk reported values for the pre-exponential factor for the ubiquitin unfolding reaction that are markedly different from the ones that we measured at the single molecule level using force as a denaturant. The discrepancies between both results may arise from the different temperature range and pH conditions probed in each study but especially from the distinct unfolding mechanism probed in bulk and single molecule mechanical experiments, sampling a totally different set of reaction coordinates.

In our single molecule force-clamp approach, we experimentally measured a value of the pre-exponential factor υ^‡ = 4 × 10⁹ s⁻¹. This value is roughly 3 orders of magnitude smaller than that predicted by the transition state theory (∼6 × 10¹² s⁻¹ at room temperature) (3, 44, 45). The attempt frequency of chemical reactions occurring with small reagents and in the gas phase is often close to that predicted by the transition state theory and close to the vibration frequency of single bonds (3, 46, 47). By contrast, when reactions occur in solution and involve bigger reactive systems as proteins, the pre-exponential factor decreases significantly (4). For example, in the case of enzymatic catalysis, the transmission coefficient γ(T) (Equation 2) can be significantly high (4, 48, 49). Hence, although chemical reactions involving the rupture and formation of covalent bonds between small molecules can effectively occur in the picosecond timescale, proteins are simply too large to (un)fold on such ephemeral timescales (4). Indeed, biochemical assays conducted in bulk for distinct proteins have established a consensus threshold for the “folding limit” to be at ∼2 μs (50, 51), as reported by fast-folding proteins such as the five-helix bundle protein λ_6–85 (50), the cold-shock CspTm protein (52), cytochrome c (53), or the recently measured transcription factor homeodomain Pit1 (54). According to this accepted kinetic scenario for protein folding, the rate of interchain diffusion and contact formation (55), which occurs on the nanosecond timescale, provides an upper limit to protein collapse. After collapsing to an unstructured globule, local motions drive the protein to search for the native structure (56). Such a final stage occurs on a much expanded timescale, spanning from microseconds up to several seconds. In general, based on diffusion theory and scaling laws from polymer physics considerations, the pre-exponential factor, which marks the upper limit for protein folding and unfolding, can be approximated to N/100 μs, where N is the number of residues in the polypeptide chain (51, 57). Therefore, a value of ∼10⁶ s⁻¹ serves as a practical general estimate for the prefactor (57). This value contrasts with the much higher value υ^‡ = 4 × 10⁹ s⁻¹ that we obtained in the mechanical experiments. The lower values obtained in classical biochemistry assays have often been explained in terms of Kramers' theory (58–60), which relates the rate at which the protein diffuses to the transition state (52, 61–63) under high friction conditions. Both the TST and the Kramers' formalisms share the Arrhenius exponential term. However, the pre-exponential term in the case of Kramers' theory sets the mean first passage time for transition from the native state to the reaction transition state (62). Hence, the prefactor in Equation 2 can be rewritten as

where ω_A is the characteristic frequency of the harmonic well of the native state of the protein, ω^‡ is the frequency around the saddle point of the reaction, and γ is the friction coefficient (61). The inverse relation between the pre-exponential factor and the friction coefficient γ is the hallmark of the Kramers' framework. Unlike the TST theory, where barrier recrossing is not possible, the diffusive mechanism of Kramers' theory allows for multiple, random recrossings of the barrier (60). These recrossings reduce the rate considerably. Therefore, the TST formalism invariably sets a higher limit to the reaction rate.

In our experiments on mechanical protein unfolding, the pre-exponential factor based on the TST formalism was higher than that predicted by simulations based on chain length, in the order of ∼10⁶ s⁻¹ (57). Such a discrepancy can stem from the different reaction coordinate probed in the force spectroscopy experiments, where the end-to-end length of the protein is recorded over time, and also from the different molecular mechanisms underlying the mechanical unfolding process. The accumulated evidence through both experiments and molecular dynamics simulations demonstrates that water insertion within the structural mechanical clamp is a key and necessary step to trigger mechanical unfolding (30, 37, 41, 64, 65). Indeed, recent experiments have shown that the value of Δx measured for protein unfolding under force is determined by the bridging length of solvent molecules at the transition state structure of the reaction (30). Thus, it is plausible that a “discrete diffusion” scenario, where a defined number of solvent molecules bridging the β1–β5 sheets catalyzes the rupture of the key backbone hydrogen bonds, may explain the unfolding process under force. Such a solvent insertion picture does not preclude that water molecules in the hydration shell contributing to the solvent motion also play a fundamental role in the (un)folding reaction (66). Within this framework, it is tempting to speculate that the value for the pre-exponential factor that we measured reflects the fast rate of diffusion and insertion of the solvent molecules into the mechanical clamp of the protein under force. In our experiments, we observed an increase in the distance to the transition state upon increasing the temperature (Fig. 4). Therefore, it is plausible that this observation affected the diffusion time and consequently the prefactor in a non-trivial manner. Because water insertion does not impose steric constraints nor marked directionality to the reaction, it is conceivable that many “attempts” will be successful, thus leading to the cooperative rupture of the force-bearing hydrogen bonds. Such a fast diffusive process on a highly localized region of the protein is likely to account for the high value for the pre-exponential factor measured in our mechanical experiments, which contrasts with the much lower value ∼10⁶ s⁻¹ estimated in bulk experiments, in which temperature has a more global effect on the probed protein.

The high pre-exponential factor that we measured for protein unfolding (∼4 × 10⁹ s⁻¹) contrasts with the lower prefactor (∼10⁷ m⁻¹ s⁻¹) encountered in analogous experiments where we studied the effect of temperature on the reactivity of a protein-embedded disulfide bond (67). In these experiments, the force-activated cleavage of an individual disulfide bond by a nucleophile occurs via a S_N2 mechanism (68–70). Such a concerted chemical mechanism requires a back-side attack to satisfy the 180° angle at the transition state between the nucleophile, the electron-deficient center, and the leaving group, resulting in the Walden inversion. The combination of steric constrains within the bulky protein groups together with the geometrical requirements imposed by the S_N2 reaction made the attempt frequency of this chemical reaction occurring within the core of a protein 2 orders of magnitude lower than the unfolding process studied here. The discrepancy in the prefactor values measured for both distinct reactions occurring at the single molecule level (i.e. protein unfolding and chemical reactions under force) thus reflected the different molecular mechanisms underlying both reactions.

The calculations of the prefactor that we measured in this work are based upon the extrapolation of the unfolding rate in the absence of force, k₀, as shown in Fig. 3. The linearity of the semilogarithmic plot of the unfolding rate as a function of force in the low force regime has been recently disputed by theoretical and single molecule works conducted in force-extension mode (71–73). However, our experimental observations under constant force conditions on protein L over an expanded force regime showed a linear behavior in the semilogarithmic plot down to forces as low as 13 pN (74). These experiments excluded any experimental evidence for the presence of curvature at low pulling forces. Interestingly, from the Arrhenius/Bell fit (Fig. 3), we obtained a value for the distance to the transition state that slightly increases with the temperature (Fig. 4). The increase in the Δx value that we observed upon increasing the temperature (2.0 ± 0.3 Å at 5 °C to 2.7 ± 0.4 Å at 45 °C) was similar to the increase reported for the I27 protein in the temperature range of 2–30 °C, increasing from 1.9 to 2.7 Å (26). According to our experimental evidence that demonstrates that solvent molecules are intricately part of the transition state structure of the unfolding reaction, this finding suggests that temperature is likely to induce a conformational expansion of the mechanical patch, such that water molecules can accommodate with slightly different conformations. Despite the measured slight increase in Δx, the mechanical softening that we observed was mainly due to the temperature-induced lowering of the energy barrier. From the fit of Equation 1 to the experimental k₀ versus 1/T data, we obtained a value of the ΔG^‡ = 71 ± 5 kJ/mol and a prefactor υ^‡ = 4 × 10⁹ s⁻¹.

The obtained value for the height of the energy barrier for ubiquitin unfolding (∼28.6 k_BT) is likely to be different for each studied protein under force because different topologies of the mechanical clamp will directly determine the height of the probed energy barrier in each case. Regarding the value for the measured prefactor, future experiments will help elucidate whether the large variability in the structural design of the mechanical transition state of proteins also correlates with a change in the measured value of the attempt frequency. The value that we measured here will be used as a reference value for proteins exhibiting β-sheet structure, the transition state structure of which is determined by the water insertion mechanism. The challenge is now to study the effect of temperature on all the distinct energy barriers present in the folding energy landscape of a folding polypeptide from highly extended states. These include the barrier separating the unfolded from the ensemble of collapsed states (31) or the generic entropic barrier that appears as a common feature of proteins under the application of force (75). It is plausible that the folding process will exhibit a more complex temperature dependence than the simple Arrhenius behavior that we have measured here for the forced unfolding of the native state of ubiquitin. Moreover, future experiments using a combination of force and temperature to induce mechanical unfolding with an expanded set of data will lay the groundwork to study the effect of temperature on the static disorder of both the height and the width of the energy barrier governing the force-activated unfolding reaction (37). In general, conducting these experiments at different temperatures will allow us to get valuable insights into the ruggedness the properties of the energy landscape (62). These experiments will permit, for the first time, full quantitative characterization of the energy landscape of a folding polypeptide from highly extended states, of capital importance for proteins with elastic function.