The Mechanism of Superoxide Production by the Antimycin-inhibited Mitochondrial Q-cycle

Abstract

Superoxide production from antimycin-inhibited complex III in isolated mitochondria first increased to a maximum then decreased as substrate supply was modulated in three different ways. In each case, superoxide production had a similar bell-shaped relationship to the reduction state of cytochrome b₅₆₆, suggesting that superoxide production peaks at intermediate Q-reduction state because it comes from a semiquinone in the outer quinone-binding site in complex III (Q_o). Imposition of a membrane potential changed the relationships between superoxide production and b₅₆₆ reduction and between b₅₆₂ and b₅₆₆ redox states, suggesting that b₅₆₂ reduction also affects semiquinone concentration and superoxide production. To assess whether this behavior was consistent with the Q-cycle mechanism of complex III, we generated a kinetic model of the antimycin-inhibited Q_o site. Using published rate constants (determined without antimycin), with unknown rate constants allowed to vary, the model failed to fit the data. However, when we allowed the rate constant for quinol oxidation to decrease 1000-fold and the rate constant for semiquinone oxidation by b₅₆₆ to depend on the b₅₆₂ redox state, the model fit the energized and de-energized data well. In such fits, quinol oxidation was much slower than literature values and slowed further when b₅₆₆ was reduced, and reduction of b₅₆₂ stabilized the semiquinone when b₅₆₆ was oxidized. Thus, superoxide production at Q_o depends on the reduction states of b₅₆₆ and b₅₆₂ and fits the Q-cycle only if particular rate constants are altered when b oxidation is prevented by antimycin. These mechanisms limit superoxide production and short circuiting of the Q-cycle when electron transfer slows.

Introduction

Mitochondria generate superoxide during oxidative metabolism. Damage caused by this and other reactive oxygen species (ROS)² has been implicated in the pathology of many diseases and the general phenomenon of aging (1–4). Isolated mitochondria generate superoxide from a number of sites, including the electron transport chain complexes I and III, glycerol 3-phosphate, 2-oxoglutarate, and pyruvate dehydrogenases and perhaps complex II and electron transfer flavoprotein-quinone oxidoreductase (5–7). The quinone (Q)-binding sites of NADH:Q oxidoreductase (complex I) and the cytochrome bc₁ complex (complex III) have the highest maximum rates of superoxide production (7, 8). Superoxide from complex III is thought to arise from the reaction of oxygen with a semiquinone produced in the Q_o site (the quinone binding site on the outer or cytosolic face of the protein) (9, 10).

Complex III operates by a Q-cycle mechanism (11–13). Quinol is oxidized in the Q_o site by a bifurcated electron transfer reaction that directs the two electrons down divergent paths. The first electron is passed down the high potential chain from the Rieske Fe-S center through cytochrome c₁ to cytochrome c and complex IV. The second electron is passed down the low potential chain from cytochrome b₅₆₆ through cytochrome b₅₆₂ to half-reduce a quinone in the Q_i site of complex III (located on the inner or matrix face of the protein). In this way, two turns of the Q cycle result in the oxidation of two quinols in the Q_o site and the reduction of one quinone in the Q_i site. Energy conservation by formation of a protonmotive force is achieved by the net movement of two electrons down the electron transport chain from one quinol to cytochrome c driving the loss of two protons from the matrix and the appearance of four protons in the intermembrane space (setting up a pH gradient), and the transport of two negative charges from the intermembrane space to the matrix (setting up a membrane potential).

Complex III produces superoxide at high rates in the presence of the Q-cycle inhibitor, antimycin A (9). This is because antimycin A binds in the Q_i site and blocks the oxidation of the cytochrome b hemes in the low potential chain (14). The backup of electrons on the cytochrome b hemes limits the oxidation of semiquinone in the Q_o site and allows it sufficient time to interact with and reduce molecular oxygen to generate superoxide (10).

Conditions that favor formation of semiquinone in the Q_o site should yield the highest rates of superoxide production. Following this logic, one might predict that a fully reduced Q pool in the presence of antimycin should give maximal formation of semiquinone in the Q_o site and therefore would result in the highest rates of superoxide production. Remarkably, however, conditions of substrate limitation, which presumably allow partial oxidation of the Q pool, result in significantly higher rates of superoxide production from the antimycin-inhibited bc₁ complex (15, 16). Using submitochondrial particles, Dröse and Brandt (16) observed that ROS production from complex III was highest when oxidation of the substrate succinate was restricted by the presence of the competitive inhibitor malonate. They suggested that the mechanism for increased ROS production must be related to the lower reduction state of the Q pool when succinate oxidation was restricted, and they proposed that electron flow from cytochrome b₅₆₆ to reduce Q may be the mechanism by which semiquinone and superoxide are increased. Recently, Sarewicz et al. (17) further examined this hypothesis in Rhodobacter capsulatus experimentally and using a kinetic model. They found evidence to support an important role of this pathway.

In this study, we investigate, model, and describe the mechanism underlying this phenomenon in isolated mitochondria. We show that it is consistent with a conventional Q-cycle mechanism for complex III, but only if the rate constant for QH₂ oxidation is assumed to be very small when antimycin is present (and even smaller when cytochrome b₅₆₆ is reduced), and the semiquinone is assumed to be stabilized when cytochrome b₅₆₂ is reduced.

EXPERIMENTAL PROCEDURES

Mitochondria

Mitochondria were isolated from hind limb skeletal muscle of female Wistar rats aged 5–8 weeks by differential centrifugation (18, 19).

Superoxide Production by Isolated Mitochondria

Superoxide production was measured indirectly as H₂O₂ production after dismutation by endogenous and exogenous superoxide dismutases. H₂O₂ production rates were determined by measurement of Amplex UltraRed fluorescence (Invitrogen) in a Shimadzu RF5301-PC spectrofluorometer (Kyoto, Japan) at the wavelength couple excitation = 530 nm and emission = 580 nm. Horseradish peroxidase was added to catalyze the reaction of extramitochondrial H₂O₂ with Amplex UltraRed to form the fluorescent product resorufin. Mitochondria (0.25 mg/ml) were incubated at 37 °C in standard assay medium containing 120 mm KCl, 5 mm HEPES, 1 mm EGTA (pH 7.2 at 20 °C), and 0.3% (w/v) bovine serum albumin. All assays contained 50 μm Amplex UltraRed, 5 units of horseradish peroxidase/ml, and 12 units of superoxide dismutase/ml. Exogenous superoxide dismutase was added to maximize conversion to H₂O₂ of extramitochondrial superoxide produced by complex III (20). Fluorescence emission data were collected and translated to H₂O₂ amounts using H₂O₂ standard curves obtained under identical conditions (20). Linear rates of change were measured for 30–60 s for each substrate condition. Superoxide production from the Q_o site was defined by sensitivity to the Q_o site inhibitor, stigmatellin; all data in this study refer to rates that were inhibitable by stigmatellin, with all stigmatellin-insensitive H₂O₂ production subtracted before further calculations. All data were corrected for H₂O₂ consumption by matrix glutathione peroxidase as described previously (21). The best current estimate of the topology of superoxide production by complex III is that 63% is directed to the matrix (21), based on the empirical observation of 50% matrix-directed superoxide production (22) and correcting for matrix glutathione peroxidase activity. We therefore corrected the empirical rates of stigmatellin-sensitive H₂O₂ production using equation 1 (21),

All chemicals were purchased from Sigma unless otherwise noted.

ATP-generated Protonmotive Force

Mitochondrial membrane potential in the presence of respiratory chain inhibitors, nigericin, and ATP is equal to the protonmotive force and was determined using an electrode sensitive to methyltriphenylphosphonium as described previously (23). Skeletal muscle mitochondria were incubated under the same conditions as for H₂O₂ production measurements at 37 °C in standard buffer with nigericin. ATP hydrolysis routinely generated a protonmotive force of 130–150 mV, similar to values described previously (24).

Reduction States of Cytochromes b₅₆₆ and b₅₆₂

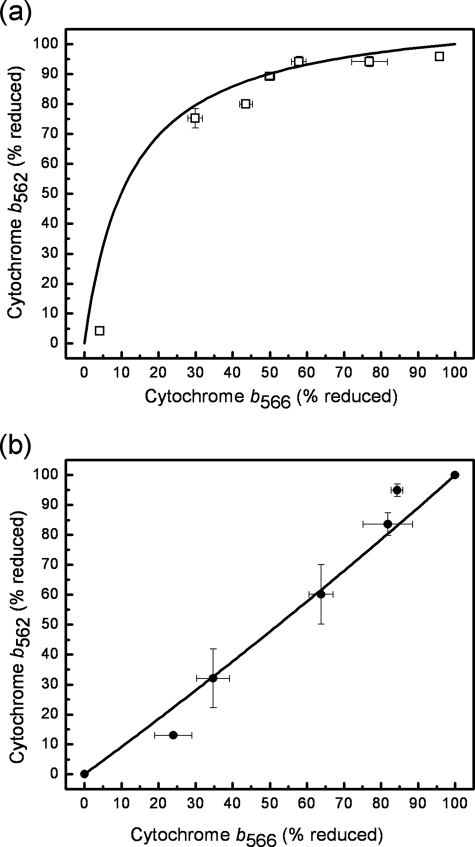
Experiments were performed in parallel with measurements of H₂O₂. Mitochondria were suspended at 1 mg/ml in standard assay medium, and absorbance change was measured in an Olis DW-2 dual wavelength spectrophotometer (Bogart, GA). The b₅₆₆ signal was followed at the wavelength pair 566–575 nm at 37 °C with stirring (25, 26). Reduction of b₅₆₆ was assumed to be 0% with no added substrate and 100% with saturating substrates plus antimycin A. The contribution of cytochrome b₅₆₂ to the b₅₆₆ signal was corrected by subtracting 50% of the signal at 561–569 nm (26). Where experimental data were normalized to moles of superoxide produced per mol of bc₁ complex, calculations used the cytochrome b₅₆₆ extinction coefficient ϵ = 25 liters·mmol⁻¹·cm⁻¹ (27). The cytochrome b₅₆₂ signal was followed at 561–569 nm (26). For the modeling (see below) the redox state of b₅₆₂ (b₅₆₂^%red) was calculated as a function of b₅₆₆ redox state (b₅₆₆^%red in %) by assuming thermodynamic equilibrium between the two b hemes (Equation 2).

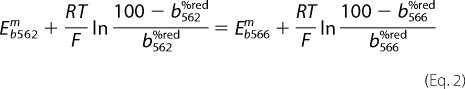A function was generated by solution of Equation 2 for the reduction state of b₅₆₂ shown in Equation 3,

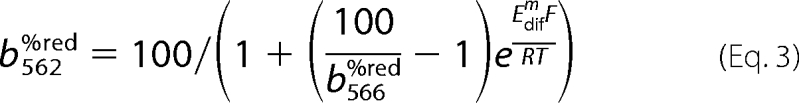where E_dif^m = E_b566^m − E_b562^m; R is the molar gas constant (8.314 J·K⁻¹·mol⁻¹); T is the temperature (310 K), and F is the Faraday constant (96485 C·mol⁻¹).

Nonlinear regression on the b heme reduction data (see Fig. 4) was performed using Equation 3, taking E_dif^m as a regression parameter E_dif^m was −60 ± 3 mV in de-energized mitochondria and 2.4 ± 5 mV in the presence of ATP. A similar redistribution of electrons between the b hemes in the presence of ATP was observed previously (28).

FIGURE 4.

Relationships between the steady-state reduction of cytochromes b₅₆₂ and b₅₆₆ in the absence and presence of ATP. Cytochrome b₅₆₆ was measured at 566–575 nm with correction for cytochrome b₅₆₂ by subtracting 50% of the signal at 561–569 nm. Cytochrome b₅₆₂ was measured at 561–569 nm. a, ATP absent, conditions as Fig. 1e. b, 2 mm ATP present, conditions as Fig. 3. Solid curves indicate the best fits of Equation 3, plotted with the relevant values of E_dif^m, see “Experimental Procedures.”

Modeling of Q_o Site Kinetics and Superoxide Production

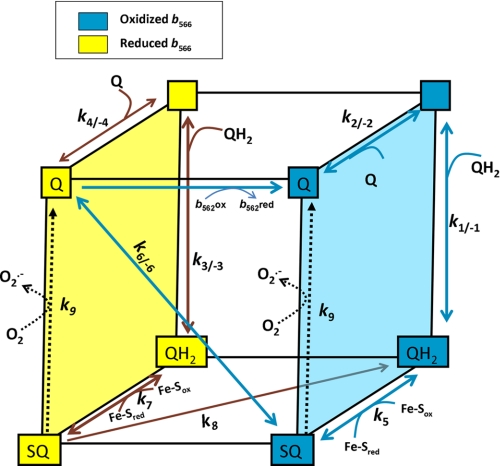
A kinetic model of the Q_o site (Fig. 5) was built in CellDesigner^TM 4.01 (29), then translated into the Systems Biology Markup Language, and exported to Mathematica 5.2 (Wolfram Research, Champaign, IL). It was solved by numerical differential equation using the SBMLNDSolve function in MathSBML 2.9.0 for a set of 15 QH₂/Q ratios. Superoxide production rates and % reduction of cytochrome b₅₆₆ were calculated in steady state (at t = 10 s). A total Q pool concentration of 7 mm in the lipid phase was assumed (30, 31).

FIGURE 5.

Kinetic model of the Q_o site of complex III. The cubic model of the Q_o site describes the eight possible states of the Q_o site (quinone-binding site empty or occupied by Q, QH₂, or SQ; cytochrome b₅₆₆ oxidized (right or blue face of cube) or reduced (left or yellow face of cube)) and the reactions that connect them and contribute to superoxide formation in the presence of antimycin A. Rate equations (reactions 1–9 in Table 1) were written for each step of the model. For normal Q-cycle activity with cytochrome b₅₆₆ mostly oxidized (blue arrows), pool QH₂ binds to an open site (top right) in reaction 1 in Table 1, and one electron is donated to the high potential electron transport chain in reaction 5 to form a semiquinone (bottom right). If semiquinone accumulates, it can react with oxygen to form superoxide by reaction 9 in Table 1 (or it leaves the Q_o site then reacts with oxygen to form superoxide, not shown). The second electron is donated to cytochrome b₅₆₆ in reaction 6 in Table 1, forming Q (top left). In the absence of antimycin, cytochrome b₅₆₆ is reoxidized by cytochrome b₅₆₂; Q is released by reaction 2, and the Q-cycle proceeds. In the presence of antimycin, cytochrome b₅₆₆ cannot be reoxidized through the low potential chain once cytochrome b₅₆₂ is reduced, so Q is released by reaction 4 in Table 1. The next QH₂ to enter binds to the reduced complex (reaction 3 in Table 1) and generates a semiquinone by reaction 7. This semiquinone can be reduced to QH₂ by cytochrome b₅₆₆ in reaction 8 (Table 1), or it can be reoxidized by forming superoxide in reaction 9. However, if Q enters instead of QH₂ (reaction 4 in Table 1), it can reoxidize cytochrome b₅₆₆ in reaction 6, forming semiquinone.

To fit the model to the experimental data, the values of rate constants were optimized within defined boundaries. Ranges of rate constants for complex III from Rhodobacter sphaeroides were taken from Ref. 32, with wider ranges of values allowed based on values for bovine submitochondrial particles (35) described in Table 1. The fitting algorithm was based on the iterative solution of the model using SBMLNDSolve with varying parameters. A weighted, multiterm least squares error function (Equation 4) that estimated the goodness of fit and penalized deviations from empirical thermodynamic relationships was calculated for each solution and minimized using the “NMinimize” numerical optimization function of Mathematica. The optimization was performed using the “DifferentialEvolution” method with default parameters. To calculate the error function, modeled rates were interpolated, yielding superoxide production rate as a function of b₅₆₆^%red.

TABLE 1.

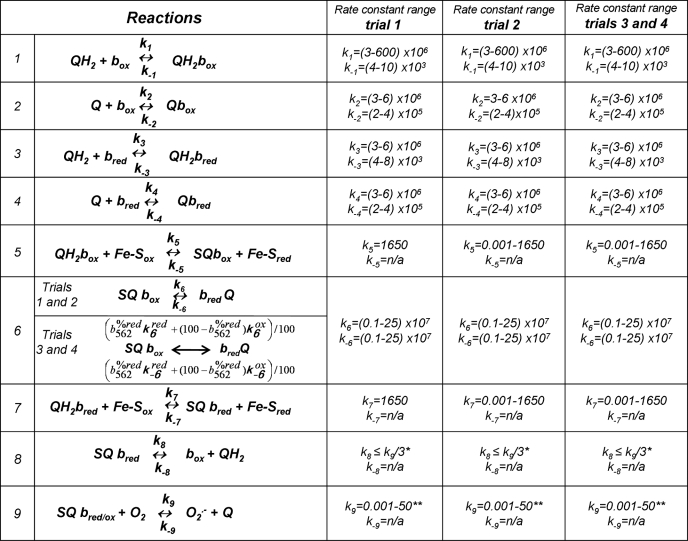
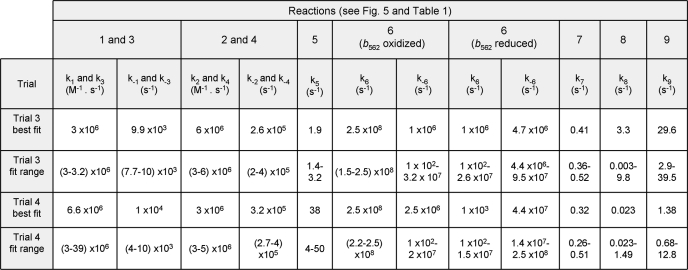
Q_o site reactions and ranges of their rate constants allowed in different modeling trials

Numbering of reactions corresponds to Fig. 5. Ranges of published rate constants for bacterial complex III were taken from Ref. 32 and expanded to include mammalian values (35). In trial 1, values were constrained to the indicated ranges and k₅ = k₇ = 1650 s⁻¹. In trial 2, k₅ and k₇ were allowed to vary independently over the range indicated. Trial 3 and trial 4 allowed k₅ and k₇ to vary and also assumed that the rate constants of reaction 6 were defined by a function of the reduction state of cytochrome b₅₆₂: k₆ = (b₅₆₂^%redk₆^red + (100 − b₅₆₂^%red)k₆^ox)/100 and k₋₆ similarly. n/a, not applicable because the Riesk Fe-S center in reactions 5 and 7 was assumed to reoxidize instantly, and reaction 9 was considered to be essentially irreversible.

* See under “Experimental Procedures.”

** Value not known therefore arbitrarily constrained as indicated.

The first term of the error function estimated the goodness of fit of the interpolated modeled rates (y_i) to the experimental data (x_i) at corresponding cytochrome b₅₆₆ redox states (i) (Equation 4).

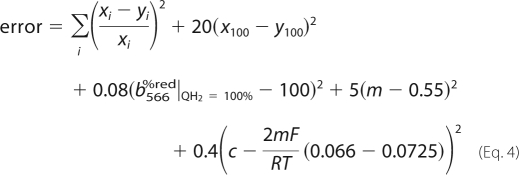To further constrain the optimization, additional terms were included in the error function. First, the superoxide production rate at fully reduced b₅₆₆ (x₁₀₀) was given additional weight, because it was well determined in the experimental data. This term was multiplied by the number of experimental observations (20 data points) to give it equivalent weight to the sum of squares. Second, at 100% Q-reduction, the model was expected to provide close to 100% reduced b₅₆₆. Third, although the model is kinetic, the results were expected to obey the known thermodynamics in steady state; therefore the known empirical relationship between Q/QH₂ and b_total^ox redox pairs (25) was assessed. To accommodate this, the average b heme redox state was calculated using the modeled b₅₆₂^%red from Equation 3. Linear regression was performed by taking ln(Q/QH₂) as an independent variable and ln(b_total^ox/b_total^red) as dependent. The slope (m) of the fit is the reciprocal of the number electrons passed between QH₂ and b₅₆₆, and its deviations from the observed value of 0.55 (25) were weighted into the error sum. The ordinate intercept (c) is F/RT times the difference of midpoint potentials of QH₂ (E_QH2^m = 66 mV at pH 7) and the average b (E_b^m = 72.5 mV at pH 7) (25). Squared errors between the expected and modeled c values were added to the error function. Weights were empirically set to obtain a robust fitting. Alternative weightings were also tested, resulting in similar fits (data not shown). The Differential Evolution optimization algorithm initializes optimization with a randomly seeded population of rate constant sets. The “convergent evolution” of this population through a random process to the global minimum of the error function provides the best fit. Therefore, optimization was repeated many times with different seeds to ensure that a global optimum was found.

Between seven and nine rate constants were optimized within specified ranges (see Fig. 5 and reactions and ranges in Table 1). We assumed that the redox state of b₅₆₆ did not affect the binding of Q and QH₂ (k₁ = k₃, k₋₁ = k₋₃, k₂ = k₄, k₋₂ = k₋₄). For simplicity, k₈ was set at k₉/3 (10). Reactions given no backward rate constant were considered to be physiologically irreversible because of negligible product accumulation: reactions 5 and 7 in Table 1 where no reduced Fe-S protein accumulates, and reaction 9 where superoxide is irreversibly removed by the assay system. The backward rate of reaction 8 in Table 1 was considered to be negligible.

Using the same model (Fig. 5), the fitting algorithm was built to increasing complexity in four trials by increasing the number of fit parameters and including dependence of the rate of reaction 6 on the redox state of cytochrome b₅₆₂ (Table 1). In trial 1, a set of 13 optimization runs on different seeds of the random generator were performed with seven parameters varied as follows: k₁, k₋₁, k₂, k₋₂, k₆, k₋₆, and k₈, with fixed k₅ = k₇ = 1650 s⁻¹. In trial 2, k₅ and k₇ were allowed to take a wider range of values (Table 1), and the optimization was performed 11 times and typically resulted in convergence within 200 iterations in a 20-h run time on a standard PC at 2.2 GHz (Intel(R) Core^TM2 Duo processor). Trial 3 was the same as trial 2, but in addition, k₆ and k₋₆ were assumed to be dependent on the redox state of b₅₆₂. k₆ and k₋₆ were calculated as an average of rate constants in the presence of reduced and oxidized b₅₆₂, weighted by the b₅₆₂ reduction state (calculated by Equation 3 from b₅₆₆^%red). Trial 4 used the same constraints on rate constants as trial 3, but the model was solved for both energized and de-energized mitochondria. The same rate constants, but a different b₅₆₂ to b₅₆₆ redox state function (Equation 3), were used, and the error function was calculated as the sum of Equation 4 calculated for the two conditions. Because this added extra constraints, the last two terms in Equation 4 were omitted for trial 4, resulting in a wider range of fitted values. Each run for trials 3 and 4 typically converged within 400 iterations in 22 and 82 h, respectively. The presence or absence of inflections and peaks in the superoxide production rate curves was determined by numerical differentiation and root search to ensure objectivity.

RESULTS

Substrate Limitation Increases Superoxide Production from Complex III in Isolated Mitochondria

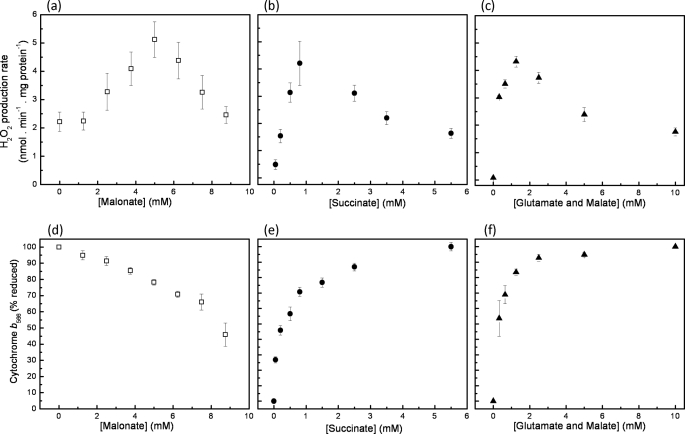
Previous work (15, 16) showed that addition of malonate, a competitive inhibitor of succinate dehydrogenase, causes a substantial increase in ROS production from antimycin-inhibited isolated complex III and submitochondrial particles in the presence of a high concentration of succinate. Fig. 1a recapitulates this result in isolated skeletal muscle mitochondria (where malonate inhibits both succinate dehydrogenase and succinate transport). At saturating succinate concentration (5 mm), in the absence of malonate and the presence of rotenone to inhibit complex I and antimycin A to inhibit electron flow through the Q_i site of complex III, the stigmatellin-sensitive H₂O₂ production rate was about 2 nmol·min⁻¹·mg protein⁻¹. The sensitivity to stigmatellin defined superoxide generated in the Q_o site of complex III, with the reasonable assumption that no other superoxide-generating site changed redox state when stigmatellin was added under these conditions. As malonate was progressively added, the rate of H₂O₂ production more than doubled, with a peak rate of 5 nmol·min⁻¹·mg protein⁻¹, before decreasing again at higher malonate concentrations as the supply of electrons from succinate was attenuated.

FIGURE 1.

Effect of substrate supply on superoxide production and steady-state reduction of cytochrome b₅₆₆ in the Q_o site of complex III. Stigmatellin-sensitive superoxide production (measured as hydrogen peroxide production) of isolated skeletal muscle mitochondria in the presence of 2 μm antimycin A is shown. a, 4 μm rotenone plus 5 mm succinate with subsequent additions of malonate as shown. b, 4 μm rotenone plus succinate at the concentrations shown. c, equimolar glutamate plus malate each at the concentration shown. All data were corrected for the rates remaining after addition of 1 μm stigmatellin and for matrix H₂O₂ losses through glutathione-dependent peroxidases (see under “Experimental Procedures”) and are means ± S.E. (n = 4–5). b₅₆₆ measurements were conducted in parallel to those above. Conditions are as follows: 2 μm antimycin A and 4 μm rotenone plus 5 mm succinate with subsequent additions of malonate as shown (d), 4 μm rotenone plus succinate at the concentrations shown (e), or equimolar glutamate plus malate each at the concentration shown (f). All data were corrected for the contribution from cytochrome b₅₆₂ to the 566–575 nm wavelength pair (see “Experimental Procedures”) and are means ± S.E. (n = 4).

To examine previous suggestions that this effect was caused by oxidation of the Q pool, and was not specific to malonate or complex II, we tested whether it could be reproduced in other ways. Fig. 1b shows that the result could be replicated by progressive titration with succinate; H₂O₂ production increased with succinate concentration, reached a peak at about 1 mm succinate, and then decreased at higher succinate concentrations. Fig. 1c shows that the same was true when complex II was bypassed, and electrons entered the Q pool from complex I instead, during titration with glutamate plus malate in the absence of rotenone.

These results show that saturating substrate concentrations do not lead to maximal superoxide production from the Q_o site of complex III; instead, the results are consistent with superoxide generation being maximal at an intermediate Q reduction state.

Superoxide Production Rate Is a Function of Cytochrome b₅₆₆ Redox State

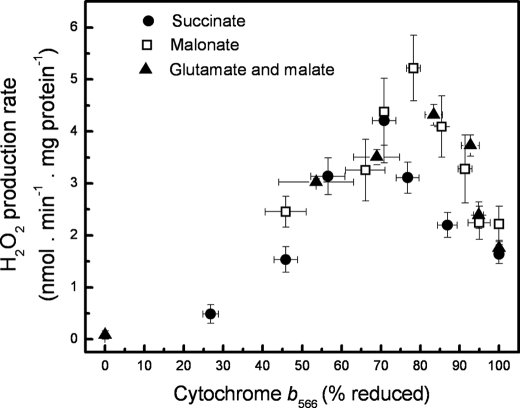
Cytochrome b₅₆₆ receives the second electron during quinol oxidation at the Q_o site. In the presence of antimycin, excess substrate, and oxygen to keep cytochrome c₁ oxidized, b₅₆₆ will become maximally reduced because the normal egress of electrons from the system through site Q_i is inhibited. Fig. 1 (d–f) shows the redox behavior of cytochrome b₅₆₆ during the substrate titrations in Fig. 1 (a–c). In each case, as the available substrate increased, b₅₆₆ became more reduced. When the rates of H₂O₂ production were plotted against the reduction state of cytochrome b₅₆₆ (Fig. 2), each substrate combination gave a bell-shaped curve. The three curves were very similar, suggesting that there was a single relationship between H₂O₂ production and the reduction state of cytochrome b₅₆₆ under these conditions; in each case maximal H₂O₂ production occurred at ∼70–80% reduction of b₅₆₆.

FIGURE 2.

Relationship between superoxide production rate from the Q_o site of complex III and the reduction state of cytochrome b₅₆₆. Hydrogen peroxide production rates with each substrate from Fig. 1, a–c, are plotted against the appropriate percent reduction of cytochrome b₅₆₆ from Fig. 1, d–f. Data are means ± S.E. (n = 4–5).

The Dependence of Superoxide Production on Cytochrome b₅₆₆ Reduction Is Altered by Protonmotive Force

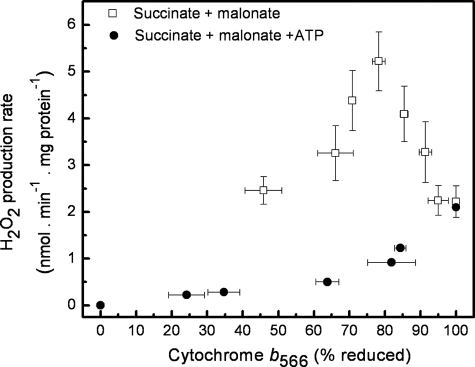
In the presence of antimycin, oxidation of succinate (or of glutamate plus malate) is inhibited, and protons are not pumped across the mitochondrial inner membrane. Under these conditions, hydrolysis of added ATP by the F₁F₀-ATPase can be used to generate a protonmotive force (measured to be 130–150 mV under our conditions). Fig. 3 shows that addition of 2 mm ATP caused a dramatic change in the relationship between superoxide production and cytochrome b₅₆₆ reduction; the maximum rate of superoxide production was strongly decreased, and the peak at intermediate reduction of b₅₆₆ was no longer apparent. The suppression of superoxide production at intermediate substrate supply required ATP hydrolysis, because it was prevented by addition of oligomycin to inhibit the F₁F₀-ATPase (data not shown).

FIGURE 3.

Relationship between superoxide production rate from the Q_o site of complex III and the reduction state of cytochrome b₅₆₆ in the presence of ATP. Filled symbols, superoxide production rate and cytochrome b₅₆₆ reduction were measured as in Fig. 1, a and d, respectively, except that 2 mm ATP was present, and the total concentration of succinate plus malonate was kept constant at 5 mm while altering their ratio. Data are means ± S.E. (n = 4). Open symbols, data for malonate titration of succinate as substrate, taken from Fig. 2, for comparison.

The Distribution of Electrons between Cytochrome b₅₆₆ and Cytochrome b₅₆₂ Is Altered by ATP Hydrolysis

ATP hydrolysis generates an electrical potential across the mitochondrial inner membrane, which is expected to alter the distribution of electrons between cytochrome b₅₆₆ (on the cytosolic side of the mitochondrial inner membrane) and cytochrome b₅₆₂ (on the matrix side) (34). Because of its more positive midpoint potential, b₅₆₂ is the preferred electron acceptor when there is no membrane potential (28). However, in the presence of membrane potential, the apparent midpoint potentials become similar, leading to a more equal distribution of electrons. These predictions were checked under the conditions of Figs. 2 and 3. Fig. 4a shows that in the presence of rotenone and antimycin, but the absence of a membrane potential, cytochrome b₅₆₂ initially remained almost fully reduced, but cytochrome b₅₆₆ became oxidized as malonate concentration was increased, consistent with the more positive midpoint potential of b₅₆₂. However, Fig. 4b shows that in the presence of rotenone, antimycin, and ATP, the electron distribution between b₅₆₆ and b₅₆₂ was more equal, and both became oxidized as malonate increased, indicating that in the presence of a membrane potential b₅₆₂ was no longer preferentially reduced.

Thus, the imposition of a membrane potential markedly changed the relationship between superoxide production and b₅₆₆ reduction (Figs. 2 and 3). It also markedly changed the relationship between the redox states of cytochromes b₅₆₂ and b₅₆₆ (Fig. 4). These results suggest that the imposition of a membrane potential affects superoxide production rate from the Q_o site of complex III by changing the redox state of cytochrome b₅₆₂. This suggestion is examined more fully below.

Is the Observed Maximum in Superoxide Production Rate Predicted by the Q-cycle?

To test whether maximum superoxide production at submaximum substrate supply and submaximum cytochrome b₅₆₆ reduction (Fig. 2) can be quantitatively explained by the Q-cycle mechanism of complex III, we generated a kinetic model of the Q_o site of the antimycin-inhibited Q-cycle (Fig. 5).

The Q_o site contains a Q-binding site and cytochrome b₅₆₆ (and the Rieske Fe-S center, which was assumed for simplicity to be rapidly reoxidized by cytochrome c₁ whenever it became reduced). Because there are four states of the Q-binding site (empty, QH₂-bound, Q-bound, and semiquinone (SQ)-bound) and two states of cytochrome b₅₆₆ (reduced, shown in yellow on the left, and oxidized, shown in blue on the right in Fig. 5), there are eight possible states. These states are shown in Fig. 5 as the vertices of a cube, connected by the reactions that interconvert them. These reactions are detailed in Table 1, where reactions 1–4 describe quinone binding, reactions 5–8 describe internal electron movements, and reaction 9 describes the reaction of semiquinone with O₂ to form superoxide. The semiquinone can be formed by the single electron oxidation of the quinol, in Q-cycle fashion (reactions 5 and 7 in Table 1), or it can be formed by reverse electron flow from reduced cytochrome b₅₆₆ to an oxidized Q (reaction 6 in reverse). Normal Q-cycle reactions would be as follows: binding of QH₂ (reaction 1 in Table 1); quinol oxidation by the Rieske FeS center to form the semiquinone (reaction 5); electron transfer to b₅₆₆ to form Q (reaction 6); passage of the electron from b₅₆₆ through b₅₆₂ to Q in the Q_i site (prevented in this scheme by the presence of antimycin), and release of Q from the Q_o site (reaction 2).

To test whether the observed data could be modeled with the reaction scheme shown in Fig. 5, the model was numerically solved to predict superoxide production rates as a function of cytochrome b₅₆₆ redox state. Rate constants were optimized within specified ranges to provide the best fit to the experimental data and known relationships of cytochrome b and Q redox states (see “Experimental Procedures”). The numerical optimization algorithm was built to increasing complexity in four trials. In each trial the optimization procedure was repeated several times because the algorithm used random seeding of initial parameters.

Trial 1

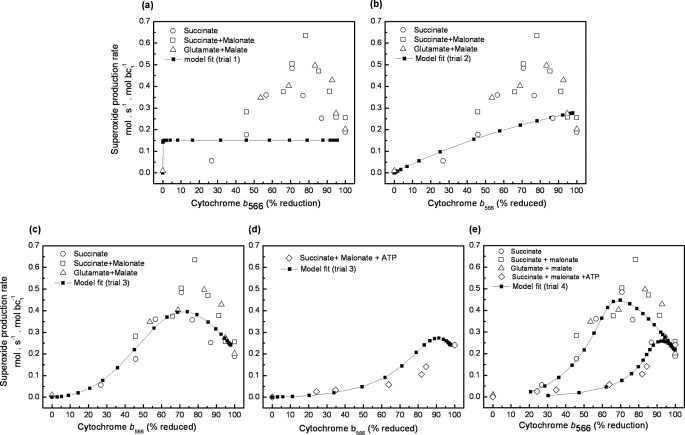
In trial 1, we attempted to fit the observed data in Fig. 2 (absence of ATP) using plausible ranges of rate constants from the literature (Table 1). We used the constants from R. sphaeroides (32), because they are well determined, but relaxed the allowed ranges to include those found using bovine heart submitochondrial particles (35), because these may be more relevant for the mammalian (rat) mitochondria used here. The values of k₅ and k₇ were fixed at 1650 s⁻¹, which is the approximate rate constant for this step (32), and k₋₆ was allowed to vary widely because its value is unknown. To model different conditions of substrate supply, we fixed QH₂/Q at a range of different values and calculated the superoxide production rate and the reduction state of cytochrome b₅₆₆ from the steady-state solution of the model. In this trial, as we varied QH₂/Q we found no acceptable fits to the observed bell-shaped curve depicting H₂O₂ as a function of b₅₆₆ reduction. Specifically, fits lacked the peak at 70–80% reduction of b₅₆₆ and the concave inflection at lower b₅₆₆ reduction and had poor least squares values (Table 2). The best of these poor fits (lowest value of the error function given by Equation 4) is shown in Fig. 6a. Thus, a straightforward model of the Q-cycle, with strict adherence to published Q-cycle rate constants, failed to fit the observed superoxide production data.

TABLE 2.

Criteria used to determine the best fits in each trial

The experimental data in Fig. 2 showed both an inflection point (below 50% reduction of cytochrome b₅₆₆) and a peak (between 70 and 80% reduction of b₅₆₆). Therefore, the best model fits were selected based on four criteria as follows: 1) presence of an inflection point; 2) presence of a peak; 3) best least squares fit of the line to the raw data in Fig. 2 with no extra weighting, calculated using only the first term in Equation 4; 4) best least squares fit of the line to the raw data in Fig. 2 with extra weighting as described under “Experimental Procedures,” calculated using Equation 4. The presence or absence of inflections and peaks in the superoxide production rate curves was determined by numerical differentiation and root search to ensure objectivity.

Trial	Criterion
	Inflection	Peak	Unweighted least squares error (truncated Equation 4)	Weighted least squares error (full Equation 4)
1	No	No	8.9	9.2
2	No	No	8.9	9.2
3	Yes	Yes	0.95	1.7
3+ATP	Yes	Yes	2.9	3.4
4	Yes	Yes	0.93	3.4

FIGURE 6.

Model-generated fits to the data in Fig. 2. The experimental data (open symbols) were converted to moles of superoxide per s per mol of bc₁ complex. The antimycin-inhibited Q-cycle model (Fig. 5) was solved in steady state by numerical optimization of the rate constants within the ranges specified in Table 1, in four separate trials with different constraints, to give the best fit to the data and the known thermodynamic relationships between Q and the b hemes. The black squares show the best fit for each trial; superoxide production rates were reevaluated with finer steps of QH₂/Q ratios using the best fit rate constants. The criteria for goodness of fit are shown in Table 2. a, Trial 1. Rate constants were held to strict Q-cycle ranges. b, Trial 2. As trial 1, but rate constants for semiquinone formation (k₅ and k₇) were allowed to vary within a wide range. c, Trial 3. As trial 2 but rate constants for reaction 6 were allowed to depend on the reduction state of cytochrome b₅₆₂ (see Table 1). d, rate constants from trial 3 used to fit the data in Fig. 3 with ATP present. In this case, the model used the b₅₆₂ reduction profile shown in Fig. 4b instead of that in Fig. 4a to calculate reaction 6 rate constants. e, Trial 4. As trial 3, but the model simultaneously fit the data sets from Figs. 2 and 3 using the relevant b reduction profiles from Fig. 4, a and b, to generate a single set of rate constants that defined both data sets.

Trial 2

In trial 2, we relaxed the constraints on the rate constants for semiquinone formation by reactions 5 and 7 in Table 1, because in the presence of antimycin A, the rates of Q cycle reactions have been observed to slow considerably (36–38). In particular, the rate of quinol oxidation (reactions 5 and 7 in Table) was suggested to slow as much as 500-fold in the presence of antimycin A (13). We allowed k₅ and k₇ to vary independently of each other between 0.001 and 1650 s⁻¹. With this change, the best fits in trial 2 produced a curve, but, as shown in Table 2 and Fig. 6b, failed to recapitulate the inflection point and peak found in the experimental data in Fig. 2 and did not produce an acceptable fit. Thus, a straightforward model of the Q-cycle, with the constraints on the rate constants of quinol oxidation relaxed to accommodate particular experimental observations from the literature, still failed to fit the observed data. This was the case even though the mechanism proposed by Dröse and Brandt (16), reduction of Q in the Q_o site by cytochrome b₅₆₆, was a fully functioning part of the model.

Trial 3

The inflection point in the observed superoxide production rate suggests a pseudo second order process. Therefore, in trial 3, we took into account the possibility that a variable related to the reduction state of b₅₆₆ also affected certain rate constants and therefore the rate of superoxide production in this system. As noted above, the redox state of cytochrome b₅₆₂ is a candidate for this related variable. The presence of antimycin A in the Q_i site does not slow entry of the first pair of electrons from QH₂ into the Q_o site but only subsequent pairs once cytochromes c₁ and b₅₆₂ are reduced (13). This important observation suggests that the reduction state of cytochrome b₅₆₂ (and not simply the presence of antimycin) may influence rate constants in the Q_o site. Therefore, trial 3 not only allowed the rate constants k₅ and k₇ to vary independently of each other as in trial 2, but also allowed the rate constants of reaction 6 in Table 1 to vary as a function of the reduction state of cytochrome b₅₆₂. To do this, one set of reaction 6 rate constants was used when b₅₆₂ was reduced, and a different set when b₅₆₂ was oxidized (Table 1). Reaction 6 in Table 1 was chosen partly because it is the most obvious way to allow the redox state of cytochrome b₅₆₂ to affect semiquinone concentration and superoxide production, and partly because there is some experimental evidence suggesting that it is crucial in superoxide formation (17). Notably, similar trials implementing an effect of b₅₆₂ redox state on k₅ and k₇ did not produce acceptable fits (data not shown).

Every run that converged in trial 3 (25 of 34 attempts) produced acceptable fits to the data in Fig. 2 (Table 2), with only small ranges for most of the rate constants (Table 3). The fit from Table 3 with the smallest error is shown in Fig. 6c. All fits shared two significant characteristics as follows: slowed rate constants for quinol oxidation, particularly when b₅₆₆ was reduced, and stabilization of the Q_o site semiquinone when b₅₆₂ was reduced.

TABLE 3.

Values of rate constants generated in trials 3 and 4

Trial 3 generated 34 fits (25 of which converged successfully), and trial 4 generated 12 fits (7 of which converged). The reactions are outlined in Table 1. The values generated in the best fit are shown, followed by the range of the values from all successful fits.

In every run, the rate constant for quinol oxidation to form the semiquinone when b₅₆₆ was oxidized (k₅) was between 1.4 and 3.2 s⁻¹, 500–1200 times slower than the rate constant of 1650 s⁻¹ during Q-cycle operation. When b₅₆₆ was reduced, values of k₇ were between 0.36 and 0.52 s⁻¹, 4.2 times slower (range was 3–6) than when b₅₆₆ was oxidized. Thus, successful fits required the rate constant for quinol oxidation to be about 1000 times slower in our experiments (with antimycin present and cytochrome b₅₆₂ mostly reduced) than when the Q-cycle runs (with antimycin absent and b₅₆₂ mostly oxidized), and about 4000 times slower when cytochrome b₅₆₆ was also reduced.

Because we allowed the rate constants for the transfer of an electron between b₅₆₆ and the semiquinone in the Q_o site (k₆ and k₋₆) to vary independently, trial 3 was able to test whether the redox state of b₅₆₂ affected the equilibrium constant of this reaction (K_eq6 = (Q.b_{566, red})/(SQ.b_{566, ox}) = k₆/k₋₆), i.e. the preference of the electron for SQ compared with reduced b₅₆₆ in the Q_o site. Without exception, all trial 3 fits changed the equilibrium constant of semiquinone formation when b₅₆₂ was reduced. Values of the equilibrium constant were always greater than 1 when b₅₆₂ was oxidized (median value = 245) and always less than 1 when b₅₆₂ was reduced (median value = 0.023), strongly suggesting that reduction of b₅₆₂ stabilizes the semiquinone bound to oxidized b₅₆₆ compared with quinone bound to reduced b₅₆₆.

Thus, the Q-cycle explains the observed data well, but only when the redox states of the cytochrome b hemes in the enzyme are allowed to exert considerable control over the rate constants of semiquinone formation and oxidation in the Q_o site.

The model also predicted other unknown rate constants, such as that for superoxide production. For simplicity, this rate constant (k₉) was assumed to be the same regardless of the reduction state of the enzyme but was otherwise allowed to vary widely, yet all fits gave values between 2.9 and 39.5 s⁻¹ (Table 3). Other rate constants, such as those for QH₂ and Q binding (reactions 1–4 in Table 1), were within the delineated range, but are not particularly illuminating as they are well described in the literature.

A powerful test of the robustness of the model was to ask if the rate constants fitted to Fig. 2 in trial 3 could predict the quite different relationship between superoxide production and the redox state of b₅₆₆ observed in the presence of a membrane potential, shown in Fig. 3. In this case, instead of defining the rate constants in reaction 6 (Table 1) with the b₅₆₂ reduction state described in Fig. 4a, we used the relationship between b₅₆₂ and b₅₆₆ determined in the presence of ATP (Fig. 4b). All 25 sets of rate constants generated from the data in the absence of ATP predicted a relationship approximating the experimental data shown in Fig. 3 in the presence of ATP (Table 2; trial 3 plus ATP). Fig. 6d shows the fit using the rate constants of Fig. 6c overlaid on the data from Fig. 3. Bearing in mind that the parameters were generated using a completely different dataset, the fit is remarkably good. However, each set of rate constants from Table 3 predicted a small peak between the last two experimental data points that was not resolved by our experimental data.

Trial 4

In trial 3 above, the rate constants were optimized to fit the data measured under de-energized conditions (Fig. 2) and subsequently applied to the data measured under energized conditions (Fig. 3), giving a reasonable prediction of the energized results (Fig. 6d). In contrast, in trial 4 we optimized a single set of rate constants to provide the best fit to both sets of data simultaneously. Trial 4 gave seven runs that converged (out of 12 attempts). It gave similar results to trial 3, fitting both data sets well, and (as expected) giving an even better fit to the energized data (Table 2 and Fig. 6e), but there was greater variability between runs. The values of the rate constants for the best fit and their ranges for the different fits are given in Table 3, and give similar conclusions to trial 3.

Thus, the Q-cycle can explain the experimental data in both de-energized (Fig. 2) and energized conditions (Fig. 3), whether the model is fitted to one data set or to both, as long as the model uses one set of rate constants of semiquinone formation and oxidation in the Q_o site when cytochrome b₅₆₂ is reduced and another when b₅₆₂ is oxidized.

DISCUSSION

We examined the kinetic mechanism of superoxide production by complex III. In mitochondria given succinate and antimycin, superoxide production increased when malonate was added and then decreased as malonate concentration was increased further (Fig. 1a). This effect was not specific to malonate or to succinate dehydrogenase, as it was recapitulated by low concentrations of succinate (Fig. 1b) or glutamate plus malate (Fig. 1c). Thus, limitation of substrate in three different ways maximized superoxide production from complex III, presumably by allowing partial oxidization of the Q pool, the first intermediate that is common to all three conditions. These observations suggest that the Q-pool redox state affects superoxide production from complex III (through its effects on reduction of cytochromes b₅₆₆ and b₅₆₂).

The observation that malonate addition caused oxidation of cytochrome b₅₆₆ (Fig. 1d), even though the thermodynamic driving force for Q reduction was unaltered, implies that this system was kinetically limited, with inflow of electrons maintaining a steady-state reduction of intermediates against a background rate of electron flow out of the Q_o site (to O₂ to form superoxide, and by any other reactions that bypass inhibition by antimycin A). The substrate-limiting conditions applied in these experiments should then allow a quasi-equilibrium to be achieved among the intermediates between electron entry and exit, i.e. between the redox states of bound Q and cytochrome b₅₆₆. Therefore, the redox status of cytochrome b₅₆₆ acts as a reporter of the concentration of semiquinone in site Q_o (as long as cytochrome b₅₆₂ redox state is constant). Because superoxide production rate should be a function of semiquinone concentration in the Q_o site, cytochrome b₅₆₆ reduction state is also a reporter of superoxide production rate from this site. With the same constraint, cytochrome b₅₆₆ reduction state also reports the redox status of the bulk Q pool. Indeed, in redox titrations, the b_total^ox/b_total^red couple has been shown to be a function of the redox status of the QH₂/Q couple (25).

In the absence of membrane potential, superoxide production was a function of the reduction state of the b₅₆₆ heme in the superoxide-generating Q_o site (Fig. 2), with the highest rates at 70–80% reduction of b₅₆₆, independently of the substrates used. However, the relationship was different in the presence of a membrane potential (Fig. 3). In the absence of a membrane potential, b₅₆₂ was preferentially reduced (Fig. 4a), but in the presence of a membrane potential electrons were distributed more equally between the two b hemes (Fig. 4b). We propose that the altered relationship between superoxide production and b₅₆₆ results from changes to the stability constant of the semiquinone, which is controlled directly by b₅₆₂ redox state and indirectly by membrane potential. Indeed, membrane potential was shown to play a defining role in superoxide production by the reconstituted bc₁ complex (39).

Decrease in the Rate Constant for Quinol Oxidation Caused by Antimycin and b₅₆₆ Reduction

The fits in trials 3 and 4 indicate that the rate constants for quinol oxidation decrease considerably in the presence of antimycin. When b₅₆₆ is oxidized, the rate constant (k₅) is ∼1000 times smaller than during normal Q-cycle operation. When b₅₆₆ is reduced, k₇ is ∼4000 times smaller than normal, and ∼4-fold slower than when b₅₆₆ is oxidized (Table 3). There is considerable precedent for this behavior. Q_o site catalysis is strongly decreased by the presence of antimycin A in the Q_i site (40–42), and it has been proposed that this functions to decrease bypass reactions that short circuit the Q-cycle (13). However, antimycin does not slow the entry of the first pair of electrons from QH₂ into the complex it only slows subsequent pairs once cytochromes c₁ and b₅₆₂ are reduced (13). Therefore, we propose that the changes in rate constants for quinol oxidation and semiquinone oxidation are not (entirely) due to the presence of antimycin in site Q_i, which would be physiologically irrelevant, but could also be caused indirectly by the reduction of the b cytochromes.

The electron transfer capacity of the Rieske Fe-S protein is mediated by macro movements of its soluble head domain, which swings on a “hinge” between the b position (near cytochrome b) and the c₁ position (near cytochrome c₁) during each electron transfer event (43, 44). The macro movements and equilibrium position of the mobile head domain are modified by the presence of inhibitors in either the Q_i or Q_o site (43). Mutations to cytochrome b residues result in dramatic alterations in rates of electron transfer through the Fe-S protein (45). This suggests that the properties of cytochromes b₅₆₂ and b₅₆₆ are communicated to the Fe-S protein. This communication could be achieved through large scale protein conformation changes, or it is conceivable that the reduction of b₅₆₆ affects its interaction with nearby amino acid residues, particularly the glutamate within the conserved PEWY region of the protein, and thereby alters the rate constants of the Q_o site-Fe-S protein interaction (13).

Stability of the Q_o Site Semiquinone

Trials 3 and 4 allowed semiquinone oxidation (reaction 6 in Table 1) to use two sets (k₆^red, k₋₆^red, and k₆^ox, k₋₆^ox) of rate constants depending the redox state of cytochrome b₅₆₂. The model predicts that k₆ alters relative to k₋₆ when b₅₆₂ becomes reduced, and so alters the equilibrium constant (K_eq6 = (Q.b_{566, red})/(SQ.b_{566, ox}) = k₆/k₋₆) of reaction 6 in Table 1 and the stability of “semiquinone.b_{566, ox}” relative to “quinone.b_{566, red}.” To maintain the thermodynamics of the QH₂/Q couple, this implies that k₅/k₋₅ also changed, but this was not apparent in the model because we assumed that reaction 5 in Table 1 was irreversible under our conditions. K_eq6 was large when b₅₆₂ was oxidized (semiquinone destabilized) and small when b₅₆₂ was reduced (semiquinone stabilized).

There are many models of Q_o site catalysis and little consensus on the stability of the semiquinone. Some models suggest it is stabilized (46, 47) and others that it is destabilized to limit its concentration and reaction with oxygen (48, 49). Our model predicts that the fully reduced low potential chain will maximally stabilize the semiquinone. Therefore, under the more physiologically relevant conditions of an ATP-generated membrane potential (Fig. 3), where cytochrome b₅₆₂ is less reduced at intermediate substrate levels, we observe the highest rate of superoxide production near to the maximal reduction of the complex, as semiquinone is less stabilized at intermediate substrate levels. Conversely, the data in Fig. 2 can also be described by semiquinone stabilization. The peak rate of superoxide production observed when b₅₆₂ becomes fully reduced but b₅₆₆ is only 60–80% reduced (Figs. 2 and 4) is explained by the increased semiquinone stability coupled to increased rate of semiquinone formation (reaction 5 in Table 1) under these conditions.

The Q_o site semiquinone is notoriously difficult to observe by electron paramagnetic resonance even under conditions that should favor its presence; this has led to proposals that it is spin-coupled and EPR silent or that the site is primarily occupied by QH₂ with oxidized Rieske Fe-S (50). However, under anaerobic conditions utilizing freeze-quench, the semiquinone was detectable (48). Our model agrees with these findings as follows: when b₅₆₆ is reduced, the rate constant for semiquinone formation (k₇) is 0.3–0.4 s⁻¹ (Table 3), considerably slower than the rate constant for its reaction with O₂ to form superoxide (k₉), at 5–17 s⁻¹, so as soon as semiquinone is formed, it readily reacts with O₂ and is removed, and the semiquinone concentration in the steady state is very low. At zero O₂, reaction 9 (Table 1) stops, and the semiquinone becomes detectable by EPR (48). We predict that with subsaturating substrate, detection of semiquinone by EPR may be possible even in the presence of O₂.

Explanation of the Peak in Superoxide Production at Intermediate Substrate Availability

The bell shapes of the curves in Figs. 1 (a–c) and 2 are explained by the effect of bulk QH₂/Q on the rate of production and stability of semiquinone, mediated by b₅₆₆ and b₅₆₂ redox states. Reduction of Q by cytochrome b₅₆₆ (reaction −6) produces semiquinone, as proposed by Ref. 16, but this alone is not sufficient to give a bell-shaped response to substrate availability (trials 1 and 2; Fig. 6, a and b). However, this reaction also tends to generate the state in which b₅₆₂ is reduced but b₅₆₆ is oxidized, and this state sets rate constants that are necessary for the highest semiquinone concentrations and the highest peaks of superoxide production from complex III (trials 3 and 4; Fig. 6c). When ATP is present, b₅₆₂ never reaches much higher reduction level than b₅₆₆, and the peak is suppressed (Fig. 6d).

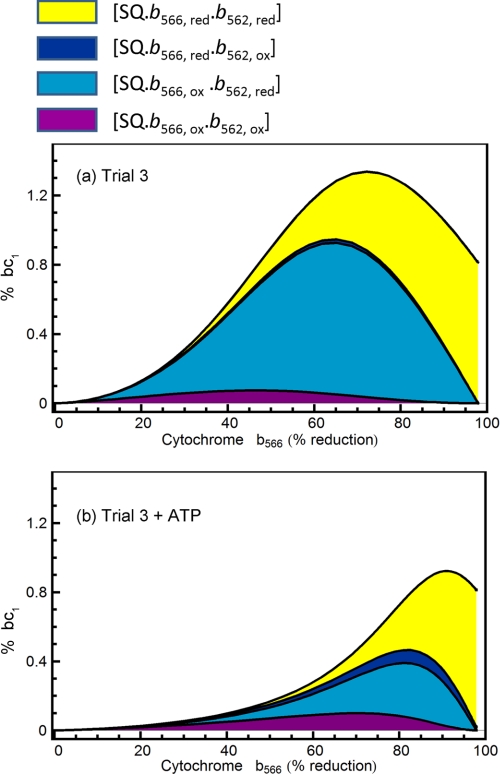
Fig. 7 summarizes these effects, showing the modeled percent of complex III occupied by a superoxide-generating semiquinone in different environments as a function of b₅₆₆ reduction. In the absence of membrane potential (Fig. 7a), at intermediate b₅₆₆ reduction states when b₅₆₂ is reduced, semiquinone concentration peaks then falls, accounting for the observations in Figs. 1 and 2. It is clear that the model predicts that it is the concentration of semiquinone on complex III in which cytochrome b₅₆₆ is oxidized but b₅₆₂ is reduced that is responsible for the bell-shaped curve in Fig. 2. In the presence of membrane potential, b₅₆₂ reduction tracks b₅₆₆ reduction, and the peak is diminished and pushed to the right (Fig. 7b).

FIGURE 7.

Model-generated prediction of the percentage of bc₁ complexes occupied by semiquinone under different conditions. Rate constants from the best fit in trial 3 applied without (a) and with (b) ATP added were used to calculate the steady-state concentrations of different forms of complex III at different imposed QH₂/Q ratios. Colors correspond to Fig. 5 as follows: yellow represents semiquinone bound to the complex with cytochromes b₅₆₆ and b₅₆₂ reduced; dark blue represents semiquinone bound to the complex with b₅₆₆ reduced and b₅₆₂ oxidized; light blue represents semiquinone bound to the complex with b₅₆₆ oxidized and b₅₆₂ reduced, and purple represents semiquinone bound to the complex with b₅₆₆ and b₅₆₂ oxidized. The top contour corresponds to the total concentration of semiquinone, which is proportional to superoxide production. The thickness of each band within the peak describes the proportion of each semiquinone species contributing to the total.

Physiological and Biochemical Implications of the Model

Slowing QH₂ oxidation by reduction of cytochrome b₅₆₂ (and further slowing by reduction of b₅₆₆) could be a critically important physiological mechanism in two ways. First, to limit short-circuiting of the Q-cycle, in which the second electron follows the first down the high potential chain, and proton pumping and energy conservation by the Q-cycle is lost. As electrons accumulate on the b hemes, which would tend to promote the short circuit, the entry of electrons is slowed to oppose this trend. The second mechanism that could be of physiological importance is to limit superoxide production by complex III when substrate is abundant but energy demand is low. Under these “state 4” conditions, protonmotive force is high, electrons back up into complex III, and there is a risk that the semiquinone in site Q_o will build up and cause very high superoxide production. Despite the potential for a stabilized semiquinone under these conditions, the reaction is limited by semiquinone formation rates. Although the small K_eq6 makes the reduction of Q to generate semiquinone a possibility, this is not observed unless there is enough Q present in the Q_o site to facilitate this reaction. Note that state 4 conditions would ensure a relatively reduced Q-pool and limit the possibility of electron backflow from b₅₆₆ to Q to generate semiquinone. In this light, the slowing of the rate constants for semiquinone formation in site Q_o would ensure that the site is largely occupied by QH₂ and would act as a safety mechanism to prevent excessive superoxide production by complex III.

Our conclusion that reduction of cytochrome b₅₆₂ lowers the rate constant for semiquinone production and that reduction of cytochrome b₅₆₆ lowers it further could explain two confusing observations in the literature. First, it explains why the rate of superoxide production at site Q_o when cytochrome b is reduced is essentially independent of [O₂] above about 10 μm concentration (51) and not second-order and proportional to [O₂] as might be expected; most of the rate limitation is in semiquinone formation and not superoxide formation (Table 3). Only when [O₂] is very low does control shift away from quinol oxidation and allow sensitivity to [O₂] to appear. Second, it may explain why superoxide production from complex III in the presence of antimycin increases under hyperoxia (10, 52) even though the reaction is already saturated with O₂ under normoxia (51). This could occur if oxygen at very high concentrations can mimic Q in the Q_o site and oxidize cytochrome b₅₆₆, increasing the rate constant for quinol oxidation, causing increased superoxide production by the mechanism discussed above.

The results of our study imply that cytochrome b₅₆₆ and b₅₆₂ redox states can reliably predict the rate of superoxide generation by the Q_o site of complex III in the presence of antimycin A. They strongly suggest that reduction of cytochromes b₅₆₂ and b₅₆₆ slows electron input into complex III from quinol oxidation at site Q_o and modulates the stability of semiquinone. This could be a physiologically relevant mechanism that prevents short circuiting of the Q-cycle, strongly limits superoxide production from complex III, and makes this superoxide production independent of [O₂] except when [O₂] is very low or very high.