Abstract
Basilar membrane (BM) motion and auditory nerve fiber (ANF) tuning are generally very similar, but the ANF had appeared to be unresponsive to a plateau mode of BM motion that occurs at frequencies above an ANF’s characteristic frequency (CF). We recorded ANF responses from the gerbil, concentrating on this supra-CF region. We observed a supra-CF plateau in ANF responses at high stimulus level, indicating that the plateau mode of BM motion can be excitatory.
Keywords: cochlea, tuning curve, frequency threshold curve, characteristic frequency, hair cell
Introduction
To the first order of approximation, the mechanical response of the basilar membrane (BM) is well matched to the auditory nerve fiber (ANF) response (Narayan et al. 1998; Ruggero et al. 2000; Temchin et al. 2008). Hence, a second filter (Evans and Wilson 1975; Zwislocki and Kletsky 1979) is not necessary in the mammalian cochlea. However, to a higher order, the ANF response is not a simple linear transformation of the macromechanics of the BM. For example, high-pass filtering in the BM displacement is needed in order to match the sub-characteristic frequency (CF) responses of the ANF (Ruggero et al. 2000). (The CF is the frequency at which the sound level needed to attain the threshold is a minimum.) This has been explained in part by the fact that inner hair cell (HC) stereocilia are not attached to the tectorial membrane (Lim 1980), so they are stimulated by fluid flow rather than by the relative displacement of the tectorial membrane and reticular lamina directly (Dallos et al. 1972). As another example, recent results of Guinan and colleagues suggest that HCs can be excited by modes of organ of Corti motion that are not always evident in BM motion (Lin and Guinan 2000; Guinan et al. 2005). Longitudinal coupling of the outer HCs (Geisler and Sang 1995; Yoon et al. 2011), tectorial membrane resonance (Gummer et al. 1996), fluid flow in the tunnel of Corti (Karavitaki and Mountain 2007), or waves along the tectorial membrane (Ghaffari et al. 2007; Ghaffari et al. 2010) are examples of possible mechanisms for producing differences between BM and ANF tuning.
The BM’s traveling wave motion drops off dramatically beyond its peak at the CF and plateaus at a nearly constant level apically beyond its peak, corresponding to a piston-like mode of BM motion, without a traveling wave pattern (Robles and Ruggero 2001). This supra-CF plateau in the BM motion, where the BM moves up and down together (with the same phase) has been observed in the apex and the base (Cooper and Rhode 1996; Narayan et al. 1998; Ruggero et al. 2000; Ren and Nuttall 2001; Dong and Cooper 2006; Rhode 2007). The physical basis for the BM plateau—this piston-like mode of BM motion—is not well understood, but it is likely related to a compressive pressure that dominates the traveling wave pressure in the supra-CF region. Such a pressure was theoretically predicted (Peterson and Bogert 1950) and has been observed in measurements of intracochlear pressure (Olson 2001). In some cochlear models, non-traveling wave modes exist and might explain the observed supra-CF motion plateau (Taber and Steele 1981; Watts 2000).
In the plateau region, in contrast to the traveling wave region, the usual correspondence between BM and ANF tuning seems to have completely broken down. In the literature, it appears that BM motion of amplitude that is excitatory to ANF in the traveling wave region was not excitatory at all in this supra-CF plateau region because ANF supra-CF plateaus were reported missing (van der Heijden and Joris 2003), even to the highest SPLs probed (Narayan et al. 1998; Ruggero et al. 2000). The reported absence of ANF plateaus suggests that the wave pattern of BM motion that occurs at frequencies lower than those of the plateau produces a very different effect from the piston-like motion at frequencies within the plateau; the differential longitudinal motion might be critical to HC excitation, leading to ANF response.
The internal organ of Corti motions that give rise to excitation are not well understood. By studying the plateau region, we can investigate whether the curvature of the BM plays a role in HC excitation and, in turn, further our knowledge of the relationship between macromechanical BM motion and micromechanics at the level of the organ of Corti. As a first step, this study will probe the notion that the piston-like motion in the plateau is not excitatory at the same amplitude that could have been excitatory otherwise in other regions. Thus, we asked the question: Can the plateau region of BM motion produce ANF excitation?
Methods
Animal preparation
Thirteen adult female Mongolian gerbils, 50–60 g in mass, were used in this study. The care and use of animals were approved by the Institutional Animal Care and Use Committee of Columbia University. The animal was first sedated with ketamine (40 mg/kg) and then anesthetized with sodium pentobarbital (initial dose, 60 mg/kg; maintenance, 10 mg/kg/h) Buprenorphine was used as an analgesic (0.2 mg/kg). A tracheotomy was performed to maintain a patent airway. Glycopyrrolate (initial dose, 0.02 mg/kg; maintenance, 0.0067 mg/kg/h) was administered to suppress production of mucus in the trachea. The animal lay on a heated blanket to keep its body temperature at 37°C. Sokolich’s approach was used to gain access to the ANF (Sokolich and Smith 1973; Chamberlain 1977). The ventral–lateral surface of the left auditory bulla was surgically removed to expose the cochlea. The gerbil round window membrane is recessed inside the round window antrum. A hole was made inside the antrum to allow insertion of a glass microelectrode for ANF recording. Following the experiment, the animal was euthanized with pentobarbital.
Acoustic stimulus
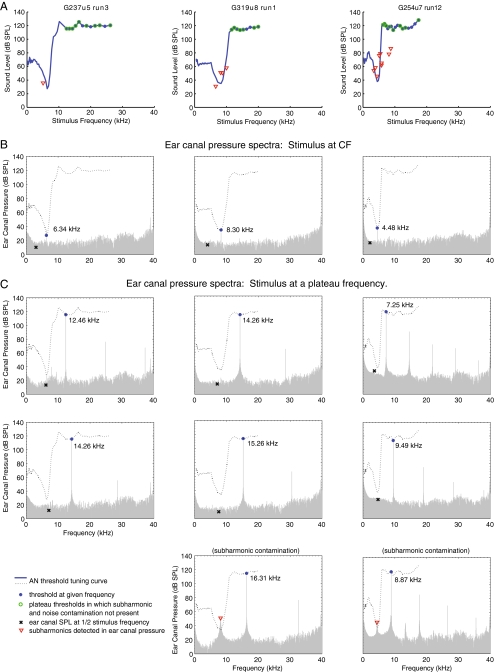
Stimulus tones were delivered to the ear canal (EC) of the animal in a closed-field configuration, in which the speaker (Radio Shack Super Tweeter) was coupled to the external EC via a short tube that was terminated with a T-tube. The sound pressure inside the EC was monitored by a ½″ Brüel and Kjær microphone (type 4134, with a post-amplifier type 2804) coupled to a probe tube that was inserted into another arm of the T-tube. The microphone signal was band-pass-filtered (PARC EG&G amplifier) between 10 Hz and 300 kHz. The probe tube with the microphone had been calibrated off-line in a cavity against a ¼″ Brüel and Kjær microphone (type 4938). TDT System III microprocessors (RX6 and RV8) and custom-designed software, modified from that of Laurel Carney (Carney and Yin 1988) generated the stimuli and recorded the signals corresponding to the sound pressure in the EC and spike timing of the spike trains. Stimuli were single tones that were 50 ms in duration, and each tone included a 2.5 ms on-ramp and off-ramp. The tones were calibrated in situ inside each animal’s EC at a location 2 ∼ 3 mm in front of the eardrum. The sampling frequency for stimulus generation and EC pressure recording was 200 kHz. Sound pressure in the EC was measured during the entire 100 ms stimulus-on and stimulus-off periods. Custom-designed Matlab programs computed 4096-point FFTs of the EC pressure to obtain the spectral plots shown in Figure 7. Spectral plots of the EC pressure were generated using 20.5 ms in the middle of the stimulus-on period. We chose this duration in order to sample the steady-state response, primarily to address a concern about persistent middle-ear generated subharmonics. (Concerns about onset–offset artifacts were addressed separately, by evaluating the spike patterns in rate-level functions.) Each spectral plot is from a single presentation, without any time averaging. In the absence of time averaging, microphone noise at ∼20–30 dB SPL usually set a limit on our ability to determine the actual acoustic noise level. However, for SPLs ≥120 dB SPL, the noise level sometimes increased, and subharmonics were sometimes apparent. Both elevated noise and subharmonics might stimulate the ANF and lead to erroneous threshold detection. We monitor both of these potentially confounding effects with the EC pressure measurements and discuss them when presenting the results.
FIG. 7.
EC stimuli at plateau threshold levels. A FTCs for three ANFs (G237u5-3, G319u8-1, and G254u7-12, also shown in Figures 3, 4, 5, and 6). B–C Representative examples of EC pressure spectra while a stimulus tone was presented during acquisition of the corresponding FTCs. B EC pressure spectra with stimulus tone at CF. C Cases of EC pressure spectra with stimulus at a plateau frequency without subharmonic contamination (first two rows) and with subharmonic contamination (bottom row). The blue filled circle symbol denotes the stimulus tone that was produced by the speaker at a threshold level. To distinguish the plateau region from the rest of the FTC, only the plateau thresholds were labeled with blue filled circles. For each plateau threshold, subharmonic components were inspected. The red triangle symbol denotes the ear drum produced subharmonic if it was detected inside the EC. If no subharmonic above the noise floor could be detected, the level of the noise floor was noted instead and denoted by the black X symbol. To determine if any pressure other than the stimulus fundamental inside the EC could potentially be excitatory to this particular ANF, the FTC of the same ANF was also plotted in the pressure spectrum as a black dotted curve. A plateau threshold is labeled with a green open circle in the FTCs in A, if no excitatory pressure other than the stimulus fundamental existed inside the EC. Note: the actual acoustic noise floor might be lower than what was shown in the spectra.
Compound action potential
The ANF’s compound action potential (CAP) response to tones was used to gauge cochlear condition (Johnstone et al. 1979). Tone bursts 3 ms in duration, with rise and fall time of 0.5 ms, and ranging in frequency from 0.5 to 40 kHz were used to elicit CAP. Sixty responses were averaged. Cochlear microphonic (CM) is an AC electrical potential generated by the HCs in response to acoustic stimulation and is picked up by the CAP electrode. The effects of the CM were reduced in the averaged response by alternating the polarity of the tone bursts. The CAP was defined to have reached a threshold when a 5 to 10 μV peak-to-peak response can be distinguished visually. CAP was measured at least twice during an experiment. The initial CAP measurement was made after the hole was made inside the round window antrum and before the electrode was inserted. In a healthy gerbil ear, CAP thresholds are below 35 dB SPL over a wide frequency range (Muller 1996; Dong and Olson 2006). Experiments were terminated if CAP thresholds were elevated to greater than 60 dB SPL.
Single unit recordings
Glass electrodes pulled with a Sutter P97 electrode puller were filled with 3 M NaCl and had impedance of 30–70 MOhms. The electrode was positioned inside the round window antrum under visual guidance and advanced remotely with a Kopf hydraulic manipulator (model 640). Broad-band noise was used as a search stimulus.
Extracellular action potentials were recorded from single unit fibers. To ensure that single units were isolated: (1) electrical waveforms of action potentials were visually monitored on an oscilloscope. Once a good contact with a fiber was made, it was very rare to detect significant presence of action potentials (of a different shape and amplitude) from a neighboring fiber. (2) Only those units whose action potentials had a high signal-to-noise ratio (large peak amplitudes relative to the noise floor) and shape uniformity were selected for processing. (3) Interspike interval (ISI) histograms were plotted post-experimentally to confirm that ISIs were not shorter than 0.7 ms (Ruggero 1992). ISIs that were shorter than 0.7 ms would indicate that more than one fiber, or that contamination such as CM or electrical noise or pick-up, was contributing to the response. The presence and timing of individual spikes were identified with a peak-detection circuit. The experimenter monitored the electrode voltage and adjusted the circuit’s cut-off voltage once a nerve fiber had been isolated. The peak-detection circuit then determined the peak location of each spike above the cut-off voltage by finding a local maximum. It generated a rectangular voltage pulse to represent the timing of the peak of each spike. An event timer, TDT RV8, recorded the timing of the rectangular pulses for accurate spike timing. The RV8 event timer was programmed to sample in 10 μs windows; it can count one spike every 10 μs with time accuracy of 40 ns within each window.
ANF threshold frequency tuning curves (FTCs) were obtained by a computer-controlled automated tracking algorithm. This algorithm was designed by Kiang and Moxon (Kiang and Moxon 1974) and subsequently adapted by others (Carney and Yin 1988; Schmiedt 1989; van der Heijden and Joris 2003; Louage et al. 2006). Briefly, the algorithm works by varying the sound pressure level of the stimulus tone up and down in order to determine the threshold, one frequency at a time. A threshold is defined as the sound pressure level required in order for a fiber to fire more than its spontaneous firing rate by a threshold criterion. If the stimulus level was above the fiber’s threshold, the subsequent stimulus level was lowered until the threshold was crossed (until the stimulus-on and stimulus-off rates were equal). At this point the stimulus level was adjusted in the opposite direction (down-up and then up-down) so that the threshold was crossed at least two more times to confirm the detected threshold. The same searching procedure was repeated for subsequent frequencies until the entire FTC was traced out. Each stimulus sweep is 100 ms in duration; the stimulus tone is turned off during the first 50 ms and turned on during the last 50 ms. The threshold criterion was one additional spike during the on period compared with the off period (spontaneous rate), a rate increase of 1 spike/50 ms. Each subsequent frequency was 1.07 times the preceding frequency, thus the frequency resolution was∼0.1 octave.
Our reported spontaneous rate was determined by calculating the average spike rate during all the 50 ms tone-off periods that preceded the tone-on periods, for the entire duration when a FTC was obtained. Rate-level functions were obtained with the stimulus tone turned on in the first and off in the second 50 ms window. Stimulus frequencies and levels advanced from low to high. Rate-level functions were used in part to evaluate whether onset–offset artifacts were influencing (producing or suppressing) threshold detections. Vector strength (Goldberg and Brown 1969) was used to quantify phase locking. Rayleigh test (phase lock criterion, L > 13.8; significance level, p = 0.001) was used to determine statistical significance of vector strength. (Buunen and Rhode 1978; Narins and Wagner 1989; Furman et al. 2006; Versteegh et al. 2011)
Results
Data used in this study were collected from 43 ANF in 13 gerbils. The CFs ranged from 525 Hz to 35.6 kHz. Multiple ANF FTCs were obtained for many fibers, and a total of 78 FTCs contributed to the results.
ANF FTCs exhibit supra-CF plateau responses
We recorded ANF responses through frequencies well above the CF, where the BM motion is expected to be in the plateau, a region where others had failed to detect ANF responses. The primary result of this study was the observation of ANF responses in the supra-CF region. 61 FTCs from 38 ANFs showed a supra-CF plateau. Seventeen FTCs from ten ANFs did not show a plateau. Five ANFs showed a plateau in some but not all FTCs. The plateau typically appeared at SPLs close to the maximum that our sound system could produce, and it is very possible that the FTCs in which the plateau was not detected would have demonstrated a plateau at a higher SPL.
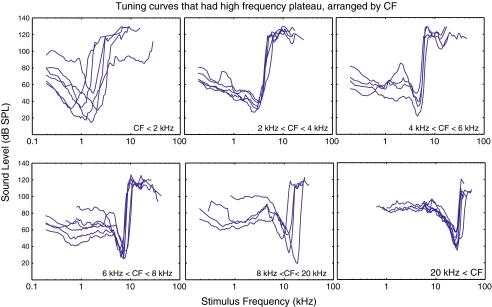
Figure 1 shows our basic result. Thirty FTCs that contained a supra-CF plateau are shown in six panels of different CF range, representing much of the gerbil’s frequency range. Our speaker system could deliver 120 dB SPL below 20 kHz, and the maximum deliverable level dropped at higher frequencies. This set a ceiling on the threshold level we could detect. Above 30 kHz, the maximum varied with frequency. Related to this, supra-CF plateau responses could sometimes be detected at some frequencies but not others, and, when presenting these data, we simply connected the adjacent points in which thresholds were detected. The supra-CF plateaus, for most ANFs, extended to 20–30 kHz, regardless of their CF.
FIG. 1.
ANF FTCs that contain a supra-CF plateau FTCs were organized and plotted into one of the six panels according to their CFs. The collective frequency range of the six panels roughly covers that of the gerbil hearing. These FTCs are representative of our data.
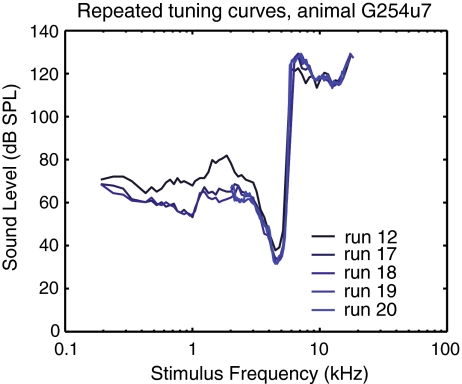
When possible, multiple FTCs were collected to test the robustness of the observation and to explore whether the use of high SPL stimuli changed the sensitivity or selectivity of the unit (Lin and Guinan 2000). Figure 2 shows an ANF from which five FTCs were collected. Overall, the sensitivity and the selectivity of the tip changed little during repeated runs. The tip threshold of the first run (run 12) was actually 4 dB higher than the later four runs (run 17 to run 20). Between runs 12 and 17, a rate-level series was performed, as in Figure 3. The variation in the tip thresholds for the later four runs was within 2 dB. The plateau thresholds also showed a high degree of repeatability. This degree of robustness and repeatability was observed in four other ANFs for which at least three repeated FTCs were measured.
FIG. 2.
Repeats of ANF FTCs from a single ANF (animal G254; ANF unit 7). The run numbers are denoted in the legend. CF = 4.48 kHz. This set of FTCs demonstrated the robustness of obtaining supra-CF plateaus.
FIG. 3.
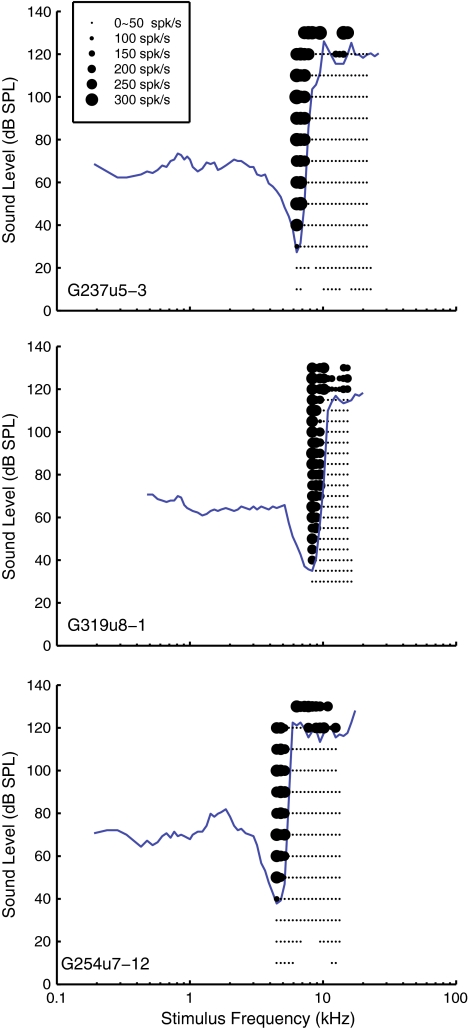
ANF FTCs obtained by a tracking algorithm along with the ANFs’ average firing rates obtained subsequently during rate-level function acquisition. The firing rates are represented by the size of the black dots and are shown here as a second method of verifying the thresholds detected by the tracking algorithm. ANF G237u5: CF = 6.34 kHz; spontaneous rate = 5.9 spikes/s, rate-level function step size = 10 dB SPL. ANF G319u8: CF = 8.30 kHz, spontaneous rate = 1.8 spikes/s, rate-level function step size = 5 dB SPL. ANF G254u7, CF = 4.48 kHz, spontaneous rate = 0.5 spikes/s, rate-level function step size = 10 dB SPL.
The new finding of this study was illustrated in the FTCs of Figure 1. Figures 3, 4, 5, 6, and 7 validate the result by examining firing patterns in the plateau region, using examples from three ANFs: G237u5, G319u8, and G254u7. These three are shown because we had full data sets of rate-level functions for them. Figure 8 uses all the FTCs in our data set to show familiar ANF firing metrics.
FIG. 4.
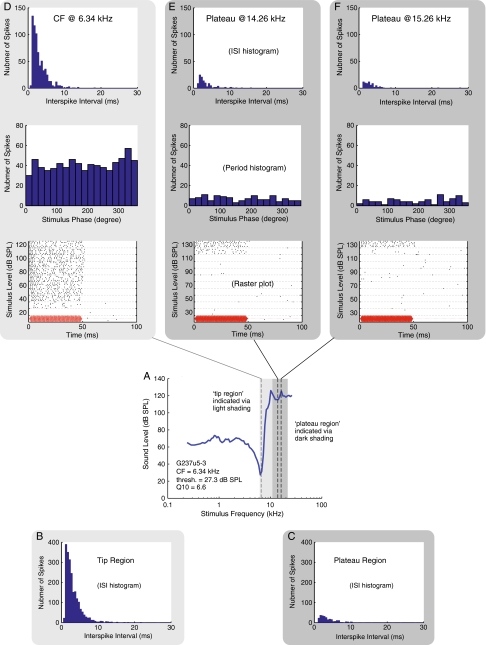
The firing patterns of ANF G237u5-3 (also shown in Figure 3). A Threshold FTC. B Interspike interval (ISI) histogram of the neural responses aggregated within the tip region, from the CF of 6.34 kHz to 10.16 kHz. C ISI histogram of the neural responses aggregated within the plateau region, from 10.87 kHz to 21.36 kHz. D–F ISI histogram, period histogram and raster plot at the CF and two plateau frequencies. In the raster plots, the stimulus waveform (arbitrary magnitude) and duration are depicted in red on the bottom of the raster plots to provide a visual reference to when the stimulus tone was turned on and off. There were five repetitions at every stimulus level.
FIG. 5.
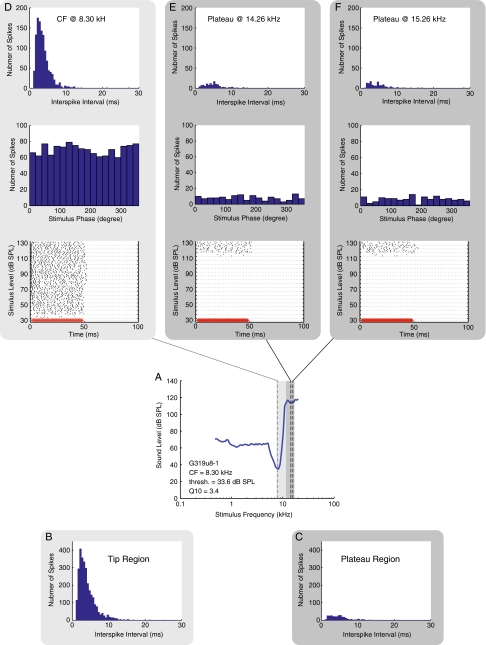
Similar to the previous figure, except data are shown for ANF G319u8-1 (also shown in Figure 3). The tip region in B included frequencies aggregated from the CF of 8.30 to 10.87 kHz. The plateau region in C included frequencies aggregated from 11.64 to 15.26 kHz.
FIG. 6.
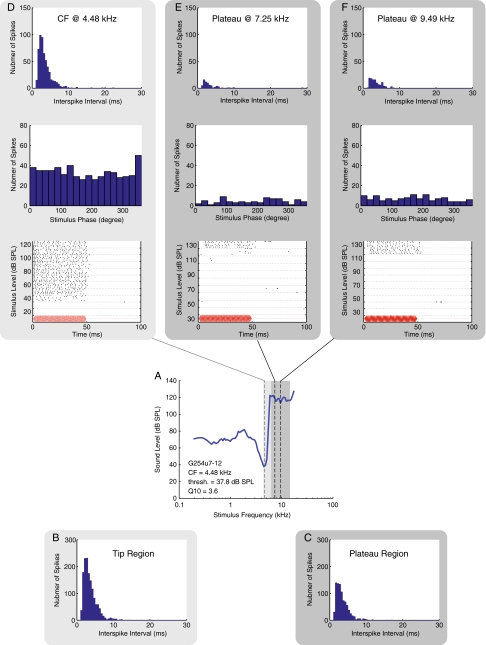
Similar to the previous figure, except data are shown for ANF G254u7-12 (also shown in Figure 3.) The tip region in B included frequencies aggregated from the CF of 4.48 kHz to 5.89 kHz. The plateau region in C included frequencies aggregated from 6.31 to 12.45 kHz.
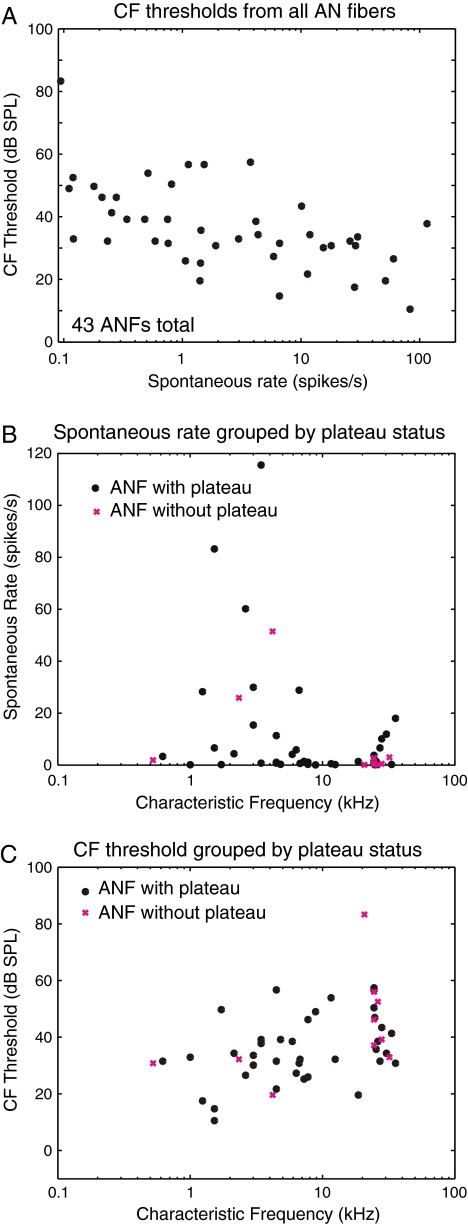
FIG. 8.
Basic parameters related to the ANF FTC. A CF threshold versus spontaneous rate. B Spontaneous rate versus CF. C CF threshold versus CF.
Figure 3 shows FTCs obtained by the tracking method and the firing rates obtained via rate-level functions recorded after the FTC had been obtained and serves to confirm that the threshold-tracking algorithm found the correct threshold level in both the plateau and tip regions. Neural activity is plotted as black dots, with the size of the dot representing the firing rate. Each dot is the mean firing rate of five stimulus sweep repetitions. The dots of the smallest size below the FTC represent the spontaneous firing rate of the fiber. Near the sound level of the tracking-algorithm-determined threshold, there was a dramatic increase in firing rate. The dynamic ranges of the rate-level functions were similar in the tip and plateau region. For G237u5 and G254u7, the dynamic range was between 20 and 40 dB, estimated from stimulus level steps of 10 dB. For G319u8, the dynamic range was between 15 and 20 dB, estimated from stimulus level steps of 5 dB. The dynamic ranges were in agreement with those of the cat dynamic range ≤35 dB at CF (Palmer and Evans 1980; Schalk and Sachs 1980; May and Sachs 1992). In the literature, in some units, the dynamic range at CF was wider than off-CF, especially for high CF units in very healthy preparations (Cooper and Yates 1994). This observation was attributed to cochlear mechanical nonlinearity. We did not sample SPL finely enough or measure rate-level functions in enough units to explore this further; in our set of results, rate-level functions appeared similar in the CF and plateau regions.
ANF supra-CF plateau responses similar to CF responses
In Figures 4, 5, and 6 we show details on the firing patterns of these three units, with each figure displaying results from one ANF. In each figure, an FTC is shown in the fourth row in panel A. Because rate-level functions were obtained for these units, we had sufficient spike data to generate ISI histograms. In the row below the FTC, in panel B, we show an ISI histogram from stimulus frequencies within the tip region. In panel C, we show an ISI histogram from stimulus frequencies within the plateau region. The light and dark gray frames color-code the peak and plateau frequency regions in all the panels in the figure. The ISI histograms appeared to have an overall exponential distribution beyond the refractory period. This distribution is expected for responses collected at non-phase-locking frequencies, as was the case in our results (Kiang 1965). ISI distributions were similar for plateau-response spikes and tip-response spikes, other than the fact that the total number of spikes in the plateau region was lower. The lower number was expected because in the plateau region the increase in firing occurs at high stimulus levels.
In the rows above the FTC, we show data from three stimulus frequencies. Panel D shows data at the CF, and panel E and F are two plateau frequencies. In the bottom row of panels D to F, raster plots are shown to illustrate the spike timing. In a raster plot, each dot represents a detected spike, and the resulting spike train shows the time pattern of the neural response in each stimulus presentation. The sound stimulus is depicted in red on the bottom of the raster plots to provide a visual reference of when the stimulus tone was turned on and off. (The red curve is the driving voltage with arbitrary amplitude, and a 0.4 ms acoustic delay and a 1.25 ms of neural and synaptic delay (Liberman 1978; Ruggero and Rich 1987) have been accounted for in the plots.) The raster plots illustrate an overall increase in firing throughout the stimulus tone-on period for levels above the threshold. The patterns of increased firing were similar in the tip region and in the plateau. In G254u7, a delay in the initial onset of firing was ∼6 ms near the threshold of firing in the data presented from the plateau region. The delay was comparable to the delay of ∼4 ms at the CF near threshold.
Above the raster plots, period histograms are shown, and above the period histograms ISI histograms are shown for the three frequencies of stimulation. These three ANFs all had CFs >4.4 kHz, and the rate-level functions were found for frequencies at CF and greater. No periodicity or significant phase locking (significance level, p = 0.001) was found at these stimulus frequencies, a result consistent with Versteegh’s observation of the phase locking limit in the gerbil (Versteegh et al. 2011). The highest phase locking frequency in our ANF data (data not shown) was 3.43 kHz. The ISI histograms, period histograms, and raster plots in Figures 4, 5, and 6 and rate-level functions in Figure 3 all demonstrate that ANF plateau responses were similar to tip responses and were tonic, which was to be expected at the stimulus frequencies.
Possible confounding effects at high SPLs
The results in Figures 4, 5, and 6 address concerns about possible artifacts. First, we address possible onset–offset artifacts. The raster plots in Figures 4, 5, and 6 show that the firing rate was elevated throughout the stimulus presentation, both at the CF and at the supra-CF frequencies corresponding to the plateau region of the FTC. The observation that the firing rate was elevated throughout the stimulus-on period alleviates concerns that stimulus onsets or offsets were producing false threshold detection with the threshold-tracking algorithm. Second, we address possible contamination of the neural recording by other electrical activity. Because CM potential grows ∼linearly with SPL over a wide range (Tasaki et al. 1952) and the recording electrode was close to the round window where CM potential can be observed, we had to consider the possibility that, at high sound pressure levels, the CM might become large enough to contaminate the spike train in the recording electrode. Electrical pick-up from the speaker is another potential source of contamination. Responses that contained an ISI shorter than 0.7 ms were excluded from the study. Hence, FTCs contaminated with CM potential >1.4 kHz were automatically discarded. There were only three ANFs that had CFs <1.4 kHz, and the lowest plateau frequency in our data set was 1.86 kHz. Thus, there is no possibility for CM contamination in any of the plateau results. To further ensure that CM response did not disturb the spike trains in the plateau region, spike trains obtained through a second method (rate-level functions) were inspected for anomalies in two ways. First, the ISI histograms were inspected. Examples are shown in Figures 4, 5, and 6, panels B, C and first row of D to F. They appeared exponential beyond the refractory period, as was expected. Second, period histograms were plotted and vector strength computed. For the data sets that were available, no significant phase locking (significance level, p = 0.001) was found for stimulus frequencies >4 kHz, as in the examples in Figures 4, 5, and 6, panels D to F. (One preparation showed contamination from CM and one from electrical pick-up, and all the data from these preparations were excluded from the results.)
In addition to onset–offset and CM-pick-up artifacts, two other potentially confounding effects need to be considered—elevated noise levels and the presence of stimulus subharmonics—and we illustrate and discuss these two issues next. At high stimulus levels, it is possible that the noise level in the stimulus would become elevated, either due to driving the speaker too hard or due to nonlinear interactions with ambient noise. Harmonic distortion was present at high stimulus levels, but harmonic frequencies generated when stimulating within the supra-CF plateau stimulus region were far away from the sensitive frequencies of a given ANF and did not pose a problem. On the other hand, subharmonic distortion could pose a problem because their frequencies might be close to the CF, where only a low stimulus level is needed for excitation. We did observe subharmonics in the EC pressure in many of the experiments. Most of them were even-order subharmonics whose frequencies were half of that of the stimulus fundamentals. Subharmonics were not produced by our acoustic and recording system, which had been tested in a cavity at a very high sound pressure level. In fact, even-order subharmonics had been reported to be generated by the eardrum at stimulus levels starting at ∼120 dB SPL (Dallos 1966; Dallos and Linnell 1966a, b, c). They are generated within the middle ear and emerge into the EC and cochlea, and in order to gauge the effect of the subharmonics on our study, we needed to understand the relationship between EC and intracochlear subharmonics. Thus, in a separate study, we measured subharmonics in the EC and in intracochlear pressure. (Huang, S., Dong, W., and Olson, E.S., Subharmonics and Auditory Nerve Tuning Curves in Gerbil. Assoc. Res. Otolaryngol. Abs.:726, ARO 2010 and manuscript in preparation). Here, we simply state the result of that is needed for the study at hand: When they emerge, EC subharmonics will likely be excitatory if they are as large or larger than an excitatory EC stimulus tone delivered by the speaker at the same frequency. Based on this, we can infer whether subharmonics would be excitatory by observing their levels in the EC.
In Figure 7, we show FTCs from our three example units, along with EC stimulus pressure spectra. The figure shows that, while the confounding effects of noise and subharmonics are problematic for our study, they do not invalidate our detection of supra-CF plateau responses. In the upper panels of Figure 7, section A, threshold FTCs from the three example ANFs are shown, plotted here with the frequency axis on a linear scale. Examples of the EC pressure spectra at several frequencies are presented beneath each FTC (sections B–C), along with the FTC in the dotted line. The fundamental stimulus frequency is evident in the large spectral component highlighted by the blue filled circle. The spectral component at half the fundamental frequency is indicated by a red triangle or black X when a subharmonic was or was not detected, respectively. When components of the EC spectra fall within the dotted FTC (either due to noise or due to subharmonics), they would be expected to be excitatory. (Note that at moderate sound levels the noise level is set by voltage noise in the microphone at ∼20–30 dB SPL, and this sets the limit at which these EC spectra are able to inform us about the noise—we can detect acoustic noise only when it is elevated above this limit. We observed such elevations in some but not all cases when our sound level was >120 dB SPL.) In section B and the upper two rows of C cases are shown in which noise and subharmonics were not excitatory. In the bottom row of section C, cases in which subharmonics were excitatory are shown for G319u8 and G254u7.
Within the FTC in panel A, at each plateau threshold where ANF responses could not be attributed to either an excitatory noise floor or subharmonic, the plateau threshold was marked with a green open circle. Thus, at these green-open-circle-marked thresholds, the ANF responses represent clean supra-CF plateau detections. The red triangles indicate subharmonic detection. When these are outside the FTC, they are not expected to be excitatory. However, when they are within the FTC, they are expected to be excitatory, and the corresponding threshold detection for such a point would not have a green open circle. The absence of a green open circle also can result from elevated noise. For G237u5, of 12 plateau thresholds detected, nine were clean (with green circles). For the other three, the noise floor recorded by the microphone was high enough to have crossed the threshold FTC, thus could have contributed to the plateau response. G319u8 had seven clean plateau thresholds out of nine. G254u7 had nine clean plateau thresholds out of 16. Reporting from our total data set of the 38 ANFs that contained plateau threshold detection, in seven subharmonics or noise could have been responsible for the entire plateau. Nine plateau-containing FTCs (eight ANFs) were fully free from subharmonic distortion.
Comparison to normative population data
In Figure 8, we describe the spontaneous rates and CF thresholds of the ANF firing patterns in our study. We compare these properties in units that did and did not contain plateaus and also compare to data in the literature. The relationship between CF thresholds and spontaneous rates for the 43 ANFs in our study are in Figure 8A. Over half of the ANFs had spontaneous rate less than 10 spikes/second, and a third had spontaneous rate less than one. This distribution of spontaneous rate is consistent with previous findings in the gerbil (Schmiedt 1989; Ohlemiller and Echteler 1990; Muller 1996), who also showed a large grouping of very low spontaneous rate fibers. High spontaneous rate fibers had lower CF thresholds, also consistent with previous findings in the gerbil (Schmiedt 1989; Ohlemiller and Echteler 1990)
Our lowest thresholds were 10 dB higher than those of Ohlemiller and Echteler, and our distribution of CF thresholds lay between 10 and 60 dB SPL, ∼20 dB higher than the range of CF thresholds reported by Muller (1996) and Schmiedt (1989). However, Ohlemiller and Siegel (1994) observed that two of 65 FTCs had thresholds of 50 dB SPL, closer to our 60 dB maximum. Muller (1996) and Schmiedt (1989) both also had several FTCs with thresholds near 60 dB SPL. The threshold elevation in our results compared with others might suggest that our preparations were either not as healthy or that the animal’s head was not kept as warm, since cool temperature is known to give rise to threshold elevations (Ohlemiller and Siegel 1992; Ohlemiller and Siegel 1994). It is notable that the gerbil CAP thresholds in our lab are typically at least 20 dB SPL (from 5 to 25 kHz) and often ∼30 dB SPL, as opposed to the ∼10 dB SPL CAP threshold reported in the study of Ohlemiller and Siegel (1992). Thus, there might be systematic differences in such things as the way sound level was measured or the strain of gerbil, which are contributing to the CF threshold differences.
Figures 8B and 8C differentiate data depending on whether a supra-CF plateau was observed. The relationship between the spontaneous rate and CF is shown in Figure 8B, and the relationship between CF threshold and CF is in Figure 8C. The data from ANFs with/without a plateau are denoted with black dots and magenta Xs, respectively. (As noted above, five ANFs had FTCs that showed a plateau in some runs but not in others. Those ANFs have one data point (black dot) representing a FTC with a plateau and one data point (magenta Xs) representing a FTC without a plateau in the same figure.) The two groups overlap both in spontaneous rate and CF threshold. Except for the presence/absence of plateau detection, the ANFs are similar in the two groups. This similarity, and the fact that the plateau was detected at SPLs close to the maximum our sound system could deliver, leads us to believe that the ANFs that did not show a plateau threshold would likely have shown one if the SPL could have been raised just slightly.
Our population data are sparser than in the studies of Muller (1996), Schmiedt (1989), and Ohlemiller and Echteler (1990). Ohlemiller and Echteler (1990) pooled their data from 361 ANFs from 50 animals; Schmiedt (1989) pooled from 245 ANFs and Muller (1996) pooled from 523 ANFs. Because our objective was to determine whether the supra-CF plateau of BM motion was coded in the ANF, we gathered adequate data to establish that result. Except for the CF threshold elevation, which can be attributed to reasonable causes as noted above, our results are consistent with their precedents.
Supra-CF plateau in ANF
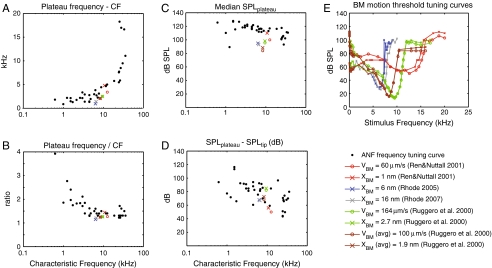
ANF plateau-specific metrics are presented in Figure 9. We show: A the frequency distance between the lowest plateau frequency and the CF, B the ratio of the lowest plateau frequency to the CF, C the median SPL of the detected plateau thresholds, and D the dB difference between the plateau and the CF tip. Results from our data are in the black dots; the meaning of the colored symbols will be explained shortly. Panels A and B illustrate the frequency separation between CF and the beginning of the plateau, A as a difference (in kilohertz) and B as a ratio. From B, the ratio is generally less than 2 for ANFs with CF > 2 or 3 kHz. For ANFs of CF ∼ 1–2 kHz, the ratio is usually between 2 and 3. Panel A presents the same information in B and where the ratio is quite flat in B (CFs > ∼2.5 kHz), the difference plotted in A increases linearly with frequency, thus increases steeply when plotted on a logarithmic frequency scale. The variation in ratio with CF illustrated in B can be attributed to the relative steepness of the high-frequency side of the tuning curve of mid and high-CF ANFs compared with that of low-CF ANFs. It is analogous and comparable to chinchilla ANFs’ upper limb bandwidth (Temchin et al. 2008). Panel C shows the threshold SPL of the plateau and D the difference between this SPL and the SPL of the FTC tip. From C, the threshold SPL of the plateau was usually 110–130 dB SPL, except for the highest CF ANFs (∼20 kHz and greater) for which the plateau threshold typically occurred at ∼100 dB SPL. There is one low-CF plateau threshold at 90 dB SPL. This FTC is easy to identify in Figure 1 panel A and except for the low plateau threshold, it is similar to the other low-CF FTCs. The difference between the plateau and tip threshold shown in panel D is more variable than the plateau threshold in C simply because the tip threshold has substantial variability. Thus the panel C results appear to be a more informative metric than D for representing the plateau threshold.
FIG. 9.
Parameters related to the supra-CF plateau of ANF and BM. A (lowest plateau frequency—CF) versus CF, B (lowest plateau frequency/CF) versus CF, C ANF plateau thresholds versus CF, D (ANF Plateau SPL–tip SPL) versus CF, E BM motion FTCs compiled from literature. VBM = basilar membrane velocity; XBM = basilar membrane displacement. Ren and Nuttals’ (2001) BM tuning data was obtained in a gerbil. All the others were obtained in chinchillas. BM FTCs, CF = 13 kHz, Threshold = 50 dB SPL(Ren and Nuttall, 2001); CF = 6.3 kHz, Threshold = 27 dB SPL(Rhode, 2005); CF = 6.7 kHz, Threshold = 26 dB SPL (Rhode 2007); CF = 9.5 kHz, Threshold = 13.3 dB SPL(Ruggero et al. 2000); Averaged data, CF = 8.4 kHz, Threshold = 15.8 dB SPL(Ruggero et al. 2000).
Discussion
Comparison of ANF plateaus to BM plateaus
This study’s objective was to determine whether the plateau in BM motion responses was coded in the ANF responses. For the purposes of comparison, Figure 9E shows BM “isodisplacement” and “isovelocity” FTCs from the literature. We show them on a linear frequency scale so that the plateau region is emphasized. The BM FTCs were extracted from BM input–output functions in the publications referenced in the legend. The color-coding in Figure 9E identifies particular data sets. The symbol coding identifies whether the FTC was constructed based on BM displacement or BM velocity. We found BM FTCs from BM response curves using the method described by Ruggero et al. (2000). Briefly, in a set of BM responses at different levels, we chose a “response threshold”, for example, a 1-nm displacement. Then, the SPL required to elicit the 1 nm displacement at each frequency was estimated. Plotting SPLs versus frequency resulted in a BM equal-displacement response curve or equivalently a BM FTC. The “response threshold” (1 nm in this example) is somewhat arbitrary, but a reasonable value would be based on the CF threshold SPL of a known ANF FTC whose CF was the same as that of the BM measurement. In the curves presented in Figure 9E, in Narayan et al.’s (1998) chinchilla data, BM FTCs were obtained by matching the BM’s CFs to chinchilla ANFs from the same animal, as in their original study. In our representation of the gerbil data of Ren and Nuttall (2001) and of the chinchilla data of Rhode (2005; 2007), the BM threshold was chosen by matching the BM responses to a gerbil ANF FTC in our data set. (Ren and Nuttall’s BM data were the only gerbil data available for making a BM FTC that extended into the plateau region.) Because ANF thresholds vary over a range of ∼50 dB SPL, a substantial range of BM FTCs can result from a single set of BM responses. The BM response is nonlinear, so these BM FTCs will not be simply vertically offset from each other. However, the plateau region of BM motion is linear, and choosing a threshold value of 10 nm rather than 1 nm will result in a 20 dB increase in the plateau region SPL in the resulting BM FTC. In the example curves of Figure 9E, to achieve the matching between BM responses and an ANF FTC required BM motion thresholds of 1, 2.7, 6, and 16 nm. The BM data all come from the base and are within the 6 to 12 kHz CF region.
The metrics identified in Figure 9A–D can also be found from BM FTCs, and these are included, using the color and symbol coding from Figure 9E. The relationship between plateau frequency and CF in panels A and B are the same for BM and ANF FTCs—the colored and black dot symbols overlie each other. The plateau values in Figure 9C give the most important comparison for the purposes of this study. Using the gerbil data from Ren and Nuttal, the BM plateau (red symbols) was found to be ∼110 dB SPL when the threshold we used was 1 nm BM displacement and ∼100 dB SPL when the threshold we used was 60 mm/s BM velocity. In this one case, the BM plateau was only slightly lower than our ANF plateau. In the chinchilla data, the BM motion plateaus range from ∼85 to 100 dB SPL. This is in general lower than the ∼120 dB SPL value we found was needed for exciting the ANF near the 10 kHz frequency range (in gerbil). Discounting the species difference, this aspect of our results—that the BM motion plateau is lower than the ANF plateau—is in agreement with the observations of Ruggero et al (2000), in which they noted that the ANF did not contain a plateau at SPLs where one would be expected based on the BM data. This comparison confirms the notion that BM motions that are excitatory to the ANF in the peak region are not excitatory in the plateau region.
To conclude, in this study supra-CF ANF plateaus were detected, typically at ∼110 to 120 dB SPL. In the chinchilla ANF measurements, the probing SPL might not have been high enough to detect a plateau response, but in a recent model such a plateau has been assumed: Temchin et al. (2011) constructed synthetic transfer functions of the chinchilla cochlea from ANF FTCs and signal front delays measured from click responses. In order for their synthetic transfer functions to predict the features of cochlear mechanical vibrations, a supra-CF plateau was artificially created in their chinchilla ANF FTCs, even though the ANF plateau had not been observed. The artificial ANF plateaus were 90 dB larger than their CF thresholds. This constraint of their model is approximately in line with our empirically determined plateau levels in gerbil. Approximately half of the ANFs in Figure 9D had a plateau level that was 80 to 100 dB greater than that of their CF. However, the other half of the ANFs had a plateau to tip difference less than 80 dB. It is possible that the plateau levels we recorded were biased because the acoustic ceiling prevented a complete survey in sound pressure levels above 120 dB SPL. Also, our CF thresholds were ∼20 dB higher than what had been found by others in gerbil, and with more data, we might extend our CF thresholds to lower SPLs. This would likely also lead to generally larger plateau to tip differences.
As noted previously, investigations have stated that the ANF plateau was absent (Narayan et al. 1998; Ruggero et al. 2000; van der Heijden and Joris 2003; Temchin et al. 2008). Temchin and colleagues noted that neural plateaus were not detected at levels where they would be expected based on the size of the BM response, and in fact were never found, even at sound levels sometimes as high as 90 dB above the CF threshold. However, that study was not designed to look for the plateau response and they did not pursue the question; in particular, the maximum SPL delivered was always less than 100 dB SPL. Based on our results and their own more recent analysis, with a slightly higher SPL the plateau would likely have been detected. In the literature, there are hints of supra-CF plateaus; we are not the first to observe it. Muller (1996) presented a handful of gerbil ANF FTCs that appeared to contain supra-CF plateaus, usually at SPLs between 90 and 100 dB SPL. Several ANF FTCs of the cat and the mouse appeared to have a short plateau (Liberman 1978; Taberner and Liberman 2005). A clear plateau was observed and noted in CM responses in gerbil (Schmiedt and Zwislocki 1977). These previous observations lend further credence to our observation of supra-CF plateau responses.
Implications to mechanics
Previous results from joint BM-ANF measurements in chinchilla showed that the BM plateau motion needed for ANF excitation, if the plateau region was ever excitatory, must be larger in the plateau region than in the traveling wave region, but those results could not pinpoint how much bigger. The results we present here clearly show that at high enough SPL, the supra-CF region does excite the ANF. Based on the comparison data in Figure 9C, we can roughly estimate that the BM motion that is excitatory in the supra-CF region is approximately a factor of ten larger than the motion that is excitatory in the peak. Because longitudinal differential motions are not present in the BM plateau, complete absence of an ANF plateau would suggest that longitudinal differential motions are necessary to ANF excitation. On the other hand, presence of an ANF plateau, at a level corresponding to an existing BM plateau, would suggest differential motions are not necessary. Our detection of an ANF plateau, at a level higher than a corresponding BM plateau, suggests that longitudinal differential motions help in increasing the sensitivity. Between BM motion and ANF responses lies HC excitation. Several theoretical studies have explored the relationship between BM and hair bundle motion, and this relationship is far from well understood (Neely and Kim 1986; Steele and Lim 1999; Cai and Chadwick 2003; Cai et al. 2004; Steele and Puria 2005; Reichenbach and Hudspeth 2010). These models and in vitro experimental results (Nowotny and Gummer 2006) indicate that BM motion is not a direct predictor of hair bundle motion. For example, the model developed by Chadwick and colleagues shows a frequency-dependent sheer gain that quantifies the amount of hair bundle bending due to BM deflection (Cai and Chadwick 2003; Cai et al. 2004). Such a model could be employed to explore whether the sheer gain is different in the plateau versus the traveling wave frequency region, and the results presented here inform and constrain such efforts. It was a mystery as to why the supra-CF region was not excitatory, and the results here, that it was excitatory, turn the mystery into a tractable and quantitative question. Thus, the results here advance our understanding of the micromechanical interface between BM motion and HC excitation, which is a fascinating and incompletely understood stage of auditory transduction.
Acknowledgments
We thank L.H. Carney, Y. Gai, J.C. Saunders, M. van der Heijden, and S.W.F. Meenderink for sharing their knowledge of ANF recording, and also M.A. Ruggero, A.N. Temchin, T. Ren and their colleagues for sharing their data presented in Figure 9E. C. Bergevin, W. Dong, O. de La Rochefoucauld and S.M. Khanna helped tremendously in many ways. Two anonymous reviewers also provided many invaluable comments. This work was supported by a grant from the National Institute on Deafness and other Communication Disorders (NIDCD).
Conflicts of interest The authors declare that there is no conflict of interest.
Contributor Information
Stanley Huang, Phone: +1-212-305-3993, Email: sh2365@columbia.edu.
Elizabeth S. Olson, Phone: +1-212-305-3993, Email: eao2004@columbia.edu
References
- Buunen TJF, Rhode WS. Response of fibers in the cat's auditory nerve to the cubic difference tone. J Acoust Soc Am. 1978;64:772–781. doi: 10.1121/1.382042. [DOI] [PubMed] [Google Scholar]
- Cai H, Chadwick R. Radial structure of traveling waves in the inner ear. SIAM J Appl Math. 2003;63:1105–1120. doi: 10.1137/S0036139901388957. [DOI] [Google Scholar]
- Cai H, Shoelson B, Chadwick RS. Evidence of tectorial membrane radial motion in a propagating mode of a complex cochlear model. Proc Natl Acad Sci USA. 2004;101:6243–6248. doi: 10.1073/pnas.0401395101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carney LH, Yin TC. Temporal coding of resonances by low-frequency auditory nerve fibers: single-fiber responses and a population model. J Neurophysiol. 1988;60:1653–1677. doi: 10.1152/jn.1988.60.5.1653. [DOI] [PubMed] [Google Scholar]
- Chamberlain SC. Neuroanatomical aspects of the gerbil inner ear: light microscope observations. J Comp Neurol. 1977;171:193–204. doi: 10.1002/cne.901710205. [DOI] [PubMed] [Google Scholar]
- Cooper NP, Yates GK. Nonlinear input-output functions derived from the responses of guinea-pig cochlear nerve fibres: Variations with characteristic frequency. Hear Res. 1994;78:221–234. doi: 10.1016/0378-5955(94)90028-0. [DOI] [PubMed] [Google Scholar]
- Cooper NP, Rhode WS. Fast travelling waves, slow travelling waves and their interactions in experimental studies of apical cochlear mechanics. Audit Neurosci. 1996;2:207–217. [Google Scholar]
- Dallos PJ. On the generation of odd-fractional subharmonics. J Acoust Soc Am. 1966;40:1381–1391. doi: 10.1121/1.1910237. [DOI] [Google Scholar]
- Dallos PJ, Linnell CO. Subharmonic components in cochlear–microphonic potentials. J Acoust Soc Am. 1966;40:4–11. doi: 10.1121/1.1910063. [DOI] [PubMed] [Google Scholar]
- Dallos PJ, Linnell CO. Even-order subharmonics in the peripheral auditory system. J Acoust Soc Am. 1966;40:561–564. doi: 10.1121/1.1910119. [DOI] [PubMed] [Google Scholar]
- Dallos PJ, Linnell CO. Origin of subharmonics in the peripheral auditory system. J Acoust Soc Am. 1966;39:1252. doi: 10.1121/1.1942862. [DOI] [PubMed] [Google Scholar]
- Dallos P, Billone MC, Durrant JD, Wang C, Raynor S. Cochlear inner and outer hair cells: functional differences. Science. 1972;177:356–358. doi: 10.1126/science.177.4046.356. [DOI] [PubMed] [Google Scholar]
- Dong W, Cooper NP. An experimental study into the acousto-mechanical effects of invading the cochlea. J The R Soc Interface. 2006;3:561–571. doi: 10.1098/rsif.2006.0117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong W, Olson ES. Middle ear forward and reverse transmission in gerbil. J Neurophysiol. 2006;95:2951–2961. doi: 10.1152/jn.01214.2005. [DOI] [PubMed] [Google Scholar]
- Evans E, Wilson J. Cochlear tuning properties: concurrent basilar membrane and single nerve fiber measurements. Science. 1975;190:1218–1221. doi: 10.1126/science.1198110. [DOI] [PubMed] [Google Scholar]
- Furman AC, Avissar M, Saunders JC. The effects of intense sound exposure on phase locking in the chick (<i > Gallus domesticus</i>) cochlear nerve. Eur J Neurosci. 2006;24:2003–2010. doi: 10.1111/j.1460-9568.2006.05068.x. [DOI] [PubMed] [Google Scholar]
- Geisler CD, Sang C. A cochlear model using feed-forward outer-hair-cell forces. Hear Res. 1995;86:132–146. doi: 10.1016/0378-5955(95)00064-B. [DOI] [PubMed] [Google Scholar]
- Ghaffari R, Aranyosi AJ, Freeman DM. Longitudinally propagating traveling waves of the mammalian tectorial membrane. Proc Natl Acad Sci. 2007;104:16510–16515. doi: 10.1073/pnas.0703665104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghaffari R, Aranyosi AJ, Richardson GP, Freeman DM. Tectorial membrane travelling waves underlie abnormal hearing in Tectb mutant mice. Nat Commun. 2010;1:96. doi: 10.1038/ncomms1094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol. 1969;32:613–636. doi: 10.1152/jn.1969.32.4.613. [DOI] [PubMed] [Google Scholar]
- Guinan JJJ, Lin T, Cheng H. Medial-olivocochlear-efferent inhibition of the first peak of auditory-nerve responses: Evidence for a new motion within the cochlea. J Acoust Soc Am. 2005;118:2421–2433. doi: 10.1121/1.2017899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gummer AW, Hemmert W, Zenner HP. Resonant tectorial membrane motion in the inner ear: its crucial role in frequency tuning. Proc Natl Acad Sci USA. 1996;93:8727–8732. doi: 10.1073/pnas.93.16.8727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnstone JR, Alder VA, Johnstone BM, Robertson D, Yates GK. Cochlear action potential threshold and single unit thresholds. J Acoust Soc Am. 1979;65:254–257. doi: 10.1121/1.382244. [DOI] [PubMed] [Google Scholar]
- Karavitaki KD, Mountain DC. Imaging Electrically Evoked Micromechanical Motion within the Organ of Corti of the Excised Gerbil Cochlea. Biophys J. 2007;92:3294–3316. doi: 10.1529/biophysj.106.083634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiang NY-s (1965) Discharge patterns of single fibers in the cat's auditory nerve. Cambridge, Mass., M.I.T. Press
- Kiang NYS, Moxon EC. Tails of tuning curves of auditory-nerve fibers. J Acoust Soc Am. 1974;55:620–630. doi: 10.1121/1.1914572. [DOI] [PubMed] [Google Scholar]
- Liberman MC. Auditory-nerve response from cats raised in a low-noise chamber. J Acoust Soc Am. 1978;63:442–455. doi: 10.1121/1.381736. [DOI] [PubMed] [Google Scholar]
- Lim DJ. Cochlear anatomy related to cochlear micromechanics. A review. J Acoust Soc Am. 1980;67:1686–1695. doi: 10.1121/1.384295. [DOI] [PubMed] [Google Scholar]
- Lin T, Guinan JJJ. Auditory-nerve-fiber responses to high-level clicks: Interference patterns indicate that excitation is due to the combination of multiple drives. J Acoust Soc Am. 2000;107:2615–2630. doi: 10.1121/1.428648. [DOI] [PubMed] [Google Scholar]
- Louage DHG, Joris PX, Heijden M. Decorrelation Sensitivity of Auditory Nerve and Anteroventral Cochlear Nucleus Fibers to Broadband and Narrowband Noise. J Neurosci. 2006;26:96–108. doi: 10.1523/JNEUROSCI.2339-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May BJ, Sachs MB. Dynamic range of neural rate responses in the ventral cochlear nucleus of awake cats. J Neurophysiol. 1992;68:1589–1602. doi: 10.1152/jn.1992.68.5.1589. [DOI] [PubMed] [Google Scholar]
- Muller M. The cochlear place-frequency map of the adult and developing Mongolian gerbil. Hear Res. 1996;94:148–156. doi: 10.1016/0378-5955(95)00230-8. [DOI] [PubMed] [Google Scholar]
- Narayan SS, Temchin AN, Recio A, Ruggero MA. Frequency Tuning of Basilar Membrane and Auditory Nerve Fibers in the Same Cochleae. Science. 1998;282:1882–1884. doi: 10.1126/science.282.5395.1882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narins PM, Wagner I. Noise Susceptibility and Immunity of Phase Locking in Amphibian Auditory-Nerve Fibers. J Acoust Soc Am. 1989;85:1255–1265. doi: 10.1121/1.397456. [DOI] [PubMed] [Google Scholar]
- Neely ST, Kim DO. A model for active elements in cochlear biomechanics. J Acoust Soc Am. 1986;79:1472–1480. doi: 10.1121/1.393674. [DOI] [PubMed] [Google Scholar]
- Nowotny M, Gummer AW. Nanomechanics of the subtectorial space caused by electromechanics of cochlear outer hair cells. Proc Natl Acad Sci USA. 2006;103:2120–2125. doi: 10.1073/pnas.0511125103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohlemiller KK, Echteler SM. Functional correlates of characteristic frequency in single cochlear nerve fibers of the Mongolian gerbil. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1990;167:329–338. doi: 10.1007/BF00192568. [DOI] [PubMed] [Google Scholar]
- Ohlemiller KK, Siegel JH. The effects of moderate cooling on gross cochlear potentials in the gerbil: Basal and apical differences. Hear Res. 1992;63:79–89. doi: 10.1016/0378-5955(92)90076-Y. [DOI] [PubMed] [Google Scholar]
- Ohlemiller KK, Siegel JH. Cochlear basal and apical differences reflected in the effects of cooling on responses of single auditory nerve fibers. Hear Res. 1994;80:174–190. doi: 10.1016/0378-5955(94)90109-0. [DOI] [PubMed] [Google Scholar]
- Olson ES. Intracochlear pressure measurements related to cochlear tuning. J Acoust Soc Am. 2001;110:349–367. doi: 10.1121/1.1369098. [DOI] [PubMed] [Google Scholar]
- Palmer AR, Evans EF. Cochlear fibre rate-intensity functions: no evidence for basilar membrane nonlinearities. Hear Res. 1980;2:319–326. doi: 10.1016/0378-5955(80)90065-9. [DOI] [PubMed] [Google Scholar]
- Peterson LC, Bogert BP. A dynamical theory of the cochlea. J Acoust Soc Am. 1950;22:84–84. doi: 10.1121/1.1917149. [DOI] [Google Scholar]
- Reichenbach T, Hudspeth AJ. A ratchet mechanism for amplification in low-frequency mammalian hearing. Proc Natl Acad Sci. 2010;107:4973–4978. doi: 10.1073/pnas.0914345107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren T, Nuttall AL. Basilar membrane vibration in the basal turn of the sensitive gerbil cochlea. Hear Res. 2001;151:48–60. doi: 10.1016/S0378-5955(00)00211-2. [DOI] [PubMed] [Google Scholar]
- Rhode WS. Auditory mechanisms: Processes and Models Proceedings of the Ninth International Symposium. In: Ren T, Gillespie P, Grosh K, Boer E, editors. (Nuttall AL. Portland, Oregon: World Scientific Publishing Co; 2005. pp. 63–69. [Google Scholar]
- Rhode WS. Basilar membrane mechanics in the 6–9 kHz region of sensitive chinchilla cochleae. J Acoust Soc Am. 2007;121:2792–2804. doi: 10.1121/1.2718397. [DOI] [PubMed] [Google Scholar]
- Robles L, Ruggero MA. Mechanics of the Mammalian Cochlea. Physiol Rev. 2001;81:1305–1352. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggero M (1992) Physiology and Coding of sound in the auditory nerve. In: Popper AN, Fay RR (eds) The Mammalian auditory pathway: neurophysiology. New York, Springer-Verlag, p 38
- Ruggero MA, Rich NC. Timing of spike initiation in cochlear afferents—dependence on site of innervation. J Neurophysiol. 1987;58:379–403. doi: 10.1152/jn.1987.58.2.379. [DOI] [PubMed] [Google Scholar]
- Ruggero MA, Narayan SS, Temchin AN, Recio A. Mechanical bases of frequency tuning and neural excitation at the base of the cochlea: comparison of basilar-membrane vibrations and auditory-nerve-fiber responses in chinchilla. Proc Natl Acad Sci U S A. 2000;97:11744–11750. doi: 10.1073/pnas.97.22.11744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schalk TB, Sachs MB. Nonlinearities in auditory-nerve fiber responses to bandlimited noise. J Acoust Soc Am. 1980;67:903–913. doi: 10.1121/1.383970. [DOI] [PubMed] [Google Scholar]
- Schmiedt RA. Spontaneous rates, thresholds and tuning of auditory-nerve fibers in the gerbil: comparisons to cat data. Hear Res. 1989;42:23–35. doi: 10.1016/0378-5955(89)90115-9. [DOI] [PubMed] [Google Scholar]
- Schmiedt RA, Zwislocki JJ. Comparison of sound-transmission and cochlear-microphonic characteristics in Mongolian gerbil and guinea pig. J Acoust Soc Am. 1977;61:133–149. doi: 10.1121/1.381283. [DOI] [PubMed] [Google Scholar]
- Sokolich WG, Smith RL. Easy access to the auditory nerve in the Mongolian gerbil. J Acoust Soc Am. 1973;54:283. doi: 10.1121/1.1978024. [DOI] [Google Scholar]
- Steele CR, Lim KM. Cochlear model with three-dimensional fluid, inner sulcus and feed-forward mechanism. Audiol Neurootol. 1999;4:197–203. doi: 10.1159/000013841. [DOI] [PubMed] [Google Scholar]
- Steele CR, Puria S. Force on inner hair cell cilia. IJSS. 2005;42:5887–5904. [Google Scholar]
- Taber LA, Steele CR. Cochlear model including three-dimensional fluid and four modes of partition flexibility. J Acoust Soc Am. 1981;70:426–436. doi: 10.1121/1.386785. [DOI] [PubMed] [Google Scholar]
- Taberner AM, Liberman MC. Response properties of single auditory nerve fibers in the mouse. J Neurophysiol. 2005;93:557–569. doi: 10.1152/jn.00574.2004. [DOI] [PubMed] [Google Scholar]
- Tasaki I, Davis H, Legouix JP. The space–time pattern of the cochlear microphonics (guinea pig), as recorded by differential electrodes. J Acoust Soc Am. 1952;24:502–519. doi: 10.1121/1.1906928. [DOI] [Google Scholar]
- Temchin AN, Rich NC, Ruggero MA. Threshold tuning curves of chinchilla auditory-nerve fibers I. Dependence on characteristic frequency and relation to the magnitudes of cochlear vibrations. J Neurophysiol. 2008;100:2889–2898. doi: 10.1152/jn.90637.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temchin AN, Recio-Spinoso A, Ruggero MA. Timing of cochlear responses inferred from frequency-threshold tuning curves of auditory-nerve fibers. Hear Res. 2011;272:178–186. doi: 10.1016/j.heares.2010.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heijden M, Joris PX. Cochlear phase and amplitude retrieved from the auditory nerve at arbitrary frequencies. J Neurosci. 2003;23:9194–9198. doi: 10.1523/JNEUROSCI.23-27-09194.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Versteegh C, Meenderink S, van der Heijden M (2011) Response Characteristics in the Apex of the Gerbil Cochlea Studied Through Auditory Nerve Recordings. JARO: Journal of the Association for Research in Otolaryngology 1–16 [DOI] [PMC free article] [PubMed]
- Watts L. The mode-coupling Liouville–Green approximation for a two-dimensional cochlear model. J Acoust Soc Am. 2000;108:2266–2271. doi: 10.1121/1.1310194. [DOI] [PubMed] [Google Scholar]
- Yoon Y-J, Steele CR, Puria S. Feed-forward and feed-backward amplification model from cochlear cytoarchitecture: an interspecies comparison. Biophys J. 2011;100:1–10. doi: 10.1016/j.bpj.2010.11.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwislocki J, Kletsky E. Tectorial membrane: a possible effect on frequency analysis in the cochlea. Science. 1979;204:639–641. doi: 10.1126/science.432671. [DOI] [PubMed] [Google Scholar]