A faster pedigree-based generalized multifactor dimensionality reduction method for detecting gene-gene interactions

Abstract

We proposed a faster pedigree-based generalized multifactor dimensionality reduction algorithm, called PedG-MDR II (PII), to detect gene-gene interactions underlying complex traits. Inherited from our previous framework of PedGMDR (PI), PII can handle both dichotomous and continuous traits in pedigree-based designs and allows for covariate adjustment. Compared with PI, this faster version can theoretically halve the computing burden and memory requirement. To evaluate the performance of PII, we performed comprehensive simulations across a wide variety of experimental scenarios, in which we considered two study designs, discordant sib pairs and mixed families of varying size, and, for each study design, we considered five common factors that may potentially affect statistical power: minor allele frequency, missing rate of parental genotypes, covariate effect, gene-gene interaction, and scheme to adjust phenotypic outcomes. Simulations showed that PII gave well controlled type I error rates against population admixture. Under a total of 4,096 scenarios simulated, PII, in general, had a higher average power than PI for both dichotomous and continuous traits, and the advantage was more pronounced for continuous traits. PII also appeared to be less sensitive than PI to changes in the other four factors than the magnitude of genetic effects considered in this study. Applied to the Mid-South Tobacco Family study, PII detected a significant interaction with a p value of 5.4 × 10⁻⁵ between two taster receptor genes, TAS2R16 and TAS2R38, responsible for nicotine dependence. In conclusion, PII is a faster supplementary version of our previous PI for detecting multifactor interactions.

1. INTRODUCTION

Although their exact inheritance pattern remains unknown, complex traits are influenced by a combination of relevant genes and environmental factors, and often lack a one-to-one genotype to phenotype correspondence (Phillips 2008). This poses a great challenge in dissecting the genetic architecture underlying them. The traditional single factor-based statistical strategies assuming that a gene causes a detectable perturbation in a phenotypic outcome, although having achieved a limited success in hunting determinants for complex traits, are underpowered for most risk factors given the widespread existence of gene-gene (G × G) and gene-environment (G × E) interactions. A preferable strategy is to tackle interacting factors simultaneously as much as possible.

Many approaches have been proposed to detect G × G interactions for various genetic designs. Logistic regression methods are well adapted to estimate the effects of interactions (Bastone et al. 2004; Cook et al. 2004; Kooperberg et al. 2001; Tahri-Daizadeh et al. 2003; Zhu and Hastie 2004) but confront a dramatic explosion of parameters in terms of multifactor dimension searching of interacting terms. Recently, a novel category of methods that can project multi-dimension searching of interaction down to one-dimension space have been proposed, alleviating the restrictions associated with the logistic regression methods. Depending on the category of a phenotypic outcome, multifactor dimensionality reduction (MDR) method (Ritchie et al. 2001) and its modifications offer solutions for detecting interactions for dichotomous traits (Hahn and Moore 2004; Hahn et al. 2003; Lee et al. 2007; Moore et al. 2006), while the combinatorial partition method (Nelson et al. 2001) and its variants (Culverhouse et al. 2004) are dedicated to quantitative traits. By implanting the generalized linear model into the MDR framework, Lou et al. (2007) proposed a generalized multifactor dimensionality reduction (GMDR) approach, which provides a unified framework for handling both continuous and discrete traits and further permits adjustment of phenotypes for covariates. These methods aforementioned, however, are largely applicable to population-based design (MDR can analyze discordant sib pairs, viewed as a special case of case-control samples), a genetic design that is well appreciated but requires control and case samples of a homogeneous genetic origin, and, if possible, being well matched on other related factors. A population-based design is subject to spurious association in the presence of population admixture and thus a technical adjustment is usually performed prior to association analysis, to rule out effects of population admixture (Price et al. 2006).

Pedigree-based design, another popular alternative in genetic studies, is inherently robust against the effect of population admixture in population-based design. In sexual reproduction, a pair of genetic complementary haploids is produced from diploid germline cells in a form of cell division called meiosis; a human genome is composed of two, from each of one’s parents respectively, haploid genomes. Instead of recruiting a control that can potentially come from a heterogeneous population, we can use the untransmitted genetic counterpart of an offspring, which is inferable given sufficient pedigree information, as an internal control, so pedigree-based design largely reduces spurious association even in the existence of population admixture, balancing a sound statistical power and a controlled type I error rate. Martin et al. (2006) proposed a pedigree-based MDR to detect G × G interactions. To utilize the genetic information in pedigrees more thoroughly and handle both dichotomous and continuous traits, we developed PedGMDR (abbreviated as PI thereafter), which built a minimal sufficient statistic approach (Rabinowitz and Laird 2000) into the GMDR framework (Lou et al. 2008).

In the present study, we propose a new pedigree-based framework, called PedGMDR II (PII), that can handle both dichotomous and continuous traits and permits adjustment of covariates with arbitrary missing marker information. PII is more computationally efficient and also, as demonstrated in simulation, outperforms, or is comparable to, PI especially for quantitative traits.

2. METHODS

2.1 Test statistics for PII

Consider a set of biallelic loci and there are up to three genotypes at each locus, e.g., aa, Aa, and AA for locus A, and bb, Bb, and BB for locus B, and so on. Let g(x_ij ) denote an indicator vector of x_ij, a set of genotypes at loci of interest for individual j in family i, whose length is determined by the number of loci for a G × G interaction being tested. Let y_ij denote the phenotypic value of offspring j in family i, and t(y_ij ) is its phenotypic function, which can take the form of score statistics in the exponential family class of distributions by choosing appropriate link functions (Lunetta et al. 2000). Let μ = E(y_ij ) and l(·) be an appropriate link function depending on the distributions of phenotypic outcomes, and a generalized linear model can be expressed as follows,

$$l({\mu }_{ij})={\beta }_0+{\beta }_{1}g(x_{ij})+{\beta }_2{z}_{ij}$$ (1)

where β₀ is the intercept, β₁ is a vector of the effects of the loci being tested, g(x_ij ) indicates a vector coding for genotype x_ij, β₂ represents the effects of the covariate(s), and z_ij is the covariate value(s). The above model is easy to extend by adding other covariates or interaction terms if there are any. When y_ij follows a normal distribution, the natural link function is the identity; or it can be,

$$\text{logit}({\mu }_{ij})=\text{logit}\left[\frac{{\mu }_{ij}}{1-{\mu }_{ij}}\right]={\beta }_0+{\beta }_{1}g(x_{ij})+{\beta }_2{z}_{ij}$$

if y_ij is a dichotomous trait. We can further define a general score statistic,

$$s_{ij}=t(y_{ij})g(x_{ij})$$ (2)

as an analogue to the statistic in the FBAT (Laird et al. 2000). However, here x_ij refers to a combination of loci, whereas x_ij codes a single locus only in the FBAT statistic, viewed as a special case of our statistics. We suggest here to use the score of Eq. (1) under the null hypothesis: β₁ = 0, in the place of t(y_ij ), and different schemes for covariate adjustment can be considered in generating the score statistics — for example, we can either adjust the phenotypes with covariates or not, and either include the founders or not in adjustment.

Different from PI in which an informative nonfounder generates a pair of statistics for transmitted and pseudo nontransmitted individuals, respectively, we only use here the transmitted to construct the statistic, but the non-transmitted individuals contribute to construct the genotypic distribution under the null hypothesis of G × G interaction associated with a trait being tested. Thus, in contrast to PI, the sample size entering into multifactor reduction will be halved, as is the computing burden and memory requirement, thus providing a faster implementation.

2.2 Multifactor-reduction algorithm

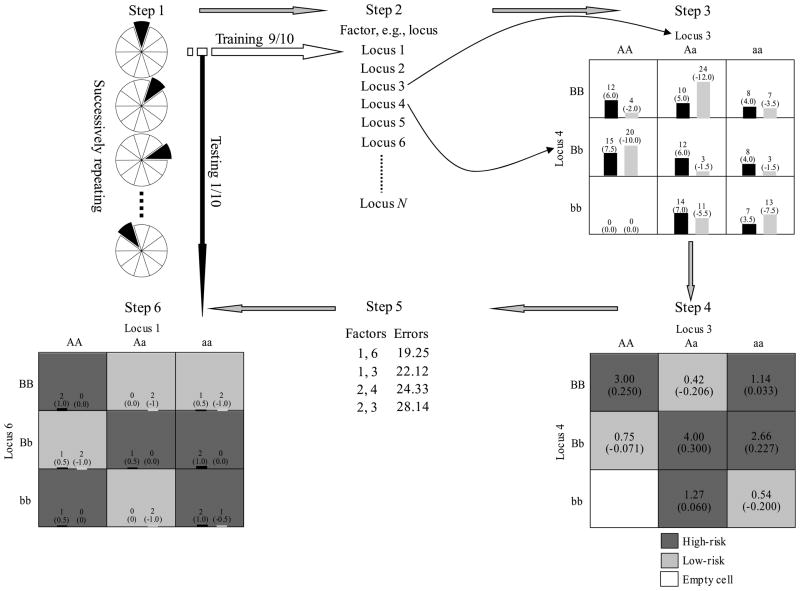
The new method is devised by integrating the family statistic defined in Eq. (2) into the GMDR framework, whose implementation of k-fold cross-validation is summarized as follows. The six steps involved in PII are illustrated in Figure 1.

Figure 1.

Illustration of the multifactor reduction algorithm of PII. Summary of the steps involved in implementing the data reduction algorithm (adapted from the work of Lou et al. (2007)) in PII, under the context of discordant sib pair design and without adjustment of phenotypic outcomes with the covariate(s). For a detailed description of the steps, please see the “Multifactor-reduction algorithm” subsection. In step 3, bars represent hypothetical distributions of affected individuals (left, dark shading) and unaffected individuals (right, light shading); numbers not in parentheses above bars are the numbers of affected and unaffected individuals, and those in parentheses are the sums of the scores. In steps 4 and 6, numbers not in parentheses are the ratios of the number of cases to the number of controls, and those in parentheses are the average scores. “High-risk” cells are indicated by dark shading, “low-risk” cells by light shading, and “empty” cells by no shading.

• In step one, randomly partition the nonfounder individuals, regardless of their family origins, into k even or nearly even subdivisions. We use k = 10, which can be other integers, throughout the paper. Motsinger and Ritchie (2006) showed that reducing the number of CV intervals from ten to five caused no loss of power and accuracy.

• In step two, a subset of γ discrete factors of either genetic and/or environmental origin are selected from all ω factors of interest. We have a total of $\left(\begin{array}{c}\omega \\ \gamma \end{array}\right)$ combinations.

• In step three, this set of factors stretches into γ-dimensional space, and each genotyped subject in the training set is allocated to a cell accordingly. The values of statistic, defined in equation 2, are averaged over each cell respectively. Each nonempty cell is labeled either high-risk if its average statistic value is not less than some threshold T ( $T=\frac{\sum s_{ij}}{n}$, where n is the number of individuals employed in the multifactor-reduction algorithm, the overall mean that is a natural extension of T = 0 to unbalanced case-control studies, is used throughout the paragraphs below), or low-risk otherwise.

• In step four, an interaction model is formed by pooling high- and low-risk cells into two distinct groups, i.e., high-risk and low-risk groups. The classification accuracy can be assessed by the averages of the statistic values in the high-risk and the low-risk groups: a higher accuracy indicates a better classification for the two groups.

• In step five, all other possible γ factor combinations in the training set are iterated, and the best γ-factor model is selected based on the classification accuracy.

• In step six, the independent testing set is used to evaluate the best model from step five.

As there are k different pairs of training-testing sets, the above procedure repeats k rounds on the k training sets.

2.3 Distribution of the test statistic for interaction

The PII allows different statistics to evaluate an interaction, and we employed testing accuracy (TA) as a testing statistic

$$\text{TA}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}}$$ (3)

where TP is True Positive defined as having a high-risk value in the high-risk group, TN is True Negative defined as having a low-risk value in the low-risk group, FP is False Positive defined as having a low-risk value in the high-risk group, and FN is False Negative defined as having a high-risk value in the low-risk group. Although the theoretical distribution of TA remains unknown, when the sample size is sufficiently large, as the result of the central limit theorem, an approximate Z score statistic can be constructed $Z=\frac{\text{TA}-E(\text{TA})}{\sqrt{\mathit{Var}(\text{TA})}}$, where E(TA) and Var (TA) are the mathematical expectation and the variance of TA under the null hypothesis.

The test procedure takes the genetic dependence among the relatives into account. Given a mating type (parental genotypes) or its minimal sufficient statistic, we have the genotypic distribution of offspring under the null hypothesis, denoted by G_M; different mating types have their respective genotypic distributions of offspring. Each of these genotypic distributions follows Mendel’s law only, and thus is independent of any phenotype and can serve as the reference distribution. Nevertheless, the genotypic distribution of offspring may differ conditional on the mating type and a trait of interest in the presence of genotype-phenotype association, denoted by G_M,T. The difference between G_M and G_M,T is the basis for detecting gene-gene interactions under-lying the trait. Noticeably, the numerator of Testing Accuracy consists of two parts which are respectively calculated from the observed family data, following G_M,T, and evaluated from the null hypothesis, following G_M. As the genetic dependency affects both parts in parallel, the discrepancy between them will ascribe to the association of the combination of loci with the trait only, thus eventually eliminating the impact from genetic dependency through comparison between G_M,T and its reference distribution G_M.

Evaluating the p value of the Z score test above needs to calculate the three terms involved, where the first term, TA, can be calculated directly conditioning on the traits and the marker scores, yet its mathematical expectation and variance under the null hypothesis, the second and the third terms accordingly, closely depend on the distributions of genotypes and the traits observed, the ascertainment condition, and other factors which might be unavailable. However, these two terms can be investigated empirically conditioning on the traits observed and the offspring’s genotypes under the null hypothesis of no association of interacting factors with the phenotype. Following Mendel’s law, each parent transmits either allele to each offspring independently with a probability of 0.5, and the genotypic distribution under the null hypothesis is easily constructed when all parent genotypes are available. It is plausible that the genotypes of founders are incomplete for late onset diseases, e.g., Parkinson’s disease and Alzheimer’s disease. Rabinowitz and Laird gave a unified algorithm (Rabinowitz and Laird 2000) on constructing the genotype distribution of offspring under the null hypothesis for various scenarios of incomplete parental genotypes. In general, conditioning on the traits and the null distribution of offspring genotypes, E(TA) and Var (TA) under the null distribution can be evaluated by Monte Carlo simulations.

3. MONTE CARLO SIMULATIONS

To evaluate the performance of the proposed method and compare with PI, we carried out a comprehensive simulation study. Without loss of generality, we considered a total of 10 independent diallelic markers in Hardy-Weinberg equilibrium, none of and two of which are functional loci, respectively, for assessment of the Type I error rate and the power. In the latter case, loci 1 and 3 were chosen as interacting loci, and two digenic interaction models of low marginal effects were adopted to demonstrate the ability of identifying interacting loci: checkerboard models (aaBb, Aabb, AaBB, and AABb are labeled to a high-value genetic group and the rest to low) and diagonal models (aabb, AaBb, and AABB are labeled to a high-value genotypic group and the rest to low) (Culverhouse et al. 2004). Eq. (1) was used to simulate phenotypic outcomes, and corresponding to the type of phenotypes, we chose an appropriate link function, i.e., logit for dichotomous traits or identity for continuous traits. We set β₀ = −5.3 for dichotomous traits and 0 for continuous ones, x_ij = 1 for high risk genotype and 0 otherwise, and z_ij ~ N (0, 1). We set four levels of the interaction: β₁=0.25, 0.50, 0.75, and 1.00, respectively, for dichotomous traits, and β₁ = 0.125, 0.250, 0.375, and 0.500, respectively, for continuous traits. β₂ was assigned the values of 0.25, 0.50, 0.75, and 1.00, respectively. Thus, there are up to 16 combinations of the two factors, genotype relative risk of high- to low-risk genotypes ranging from 1.25 to 2.60 for dichotomous traits, and for continuous traits heritability ranged from about 0.0018 to 0.0500 given equi-frequent biallelic loci; such ranges are reasonably well established in the literature (Flint and Mackay 2009; Iles 2008). In addition, three other factors that potentially affect statistical power were examined in simulations: minor allele frequency (MAF) (three levels: 0.10, 0.25, 0.50), average genotype missing rate for each parent (five levels: 0.00, 0.25, 0.50, 0.75, 1.00), and the schemes for generating score statistics (four schemes: scheme 1, using the phenotype of both parents and offspring with covariate adjustment; scheme 2, using the phenotype of offspring with covariate adjustment; scheme 3, using the phenotype of both parents and offspring without adjustment; scheme 4, using the phenotype of offspring without adjustment). These five factors took up to 960 scenarios, a comprehensive coverage that was expected to provide a broad reference for the method investigated.

The samples were simulated based on two genetic designs in this study. The first one was a discordant sib pair (DSP) design consisting of 300 families. If a sibling was affected for a dichotomous trait, or a continuous phenotypic value of interest located in the upper 10% of the distribution of a phenotype simulated, this individual was identified as a proband. When a full sib of the proband did not reach the criterion for proband status, these two sibs as well as their parents were recruited to the study. The second one comprised a mixture of three categories of families (MF) consisting of two, three, and four sibs, respectively, and each category had 100 families, of which at least two sibs had proband phenotypes. In the MF design, the MAF of each locus was randomly assigned either 0.10, 0.25, or 0.50, and parental genotype was set to a missing rate of 0.25.

Type I error rates of PII were examined with a DSP design consisting of a total of 300 families for both dichotomous and continuous outcomes to verify the robustness to population admixture. To generate an admixed population, we portioned the 300 families into 3 even groups; families in each group were randomly assigned an MAF of either 0.10, 0.25, or 0.50 to each locus, and simulated samples according to the ascertainment criteria described above. Furthermore, we adopted β₂ = 1 to check whether the existence of covariates would inflate type I error rates under different schemes of calculating score statistics. Simulations were replicated for 500 times and the empirical Type I error rate was calculated. The simulated data were analyzed with PI and PII. In an exhaustive searching strategy for all possible digenic models, the one that had the greatest CVC (the one with the greatest TA was preferred if there was a tie in CVC) after 10 cross-validations was selected. After the mathematical expectation and variance of TA were computed, the p value of the Z score could be calculated, and we counted the interaction was significant at alpha level 0.05 if its p value was less than 0.05. Statistical power was calculated as the proportion of the simulations yielding a significant p value at 0.05 significance level and the correct model in all 200 simulations. For PI, 1,000 replications of shuffling the transmitted set and the nontransmitted set, with each family as a permuting unit of phenotypic score, were used to evaluate the empirical cutoff point of nominal 0.05 significance level (Lou et al. 2008).

The simulation results showed that, under the given scenarios, the empirical type I error rates were well controlled as indicated in Table 1, regardless of population admixture and schemes of generating score statistics, verifying the validity of the proposed test procedure.

Table 1.

Type I error rate of PII at 0.05 significance level

Including Founders	Dichotomous Traits		Continuous Traits
	Adjustment	Without Adjustment	Adjustment	Without Adjustment
True	0.044	0.044	0.050	0.048
False	0.060	0.045	0.050	0.036

We simulated 300, of three subpopulations consisting of 100 families in each, discordant sib pairs. For families in each category, the MAF of each locus was randomly assigned either 0.1, 0.25, or 0.5 independently.

To provide an overall picture of comparison between PI and PII, the average powers were listed in Table 2. Each number derived from the DSP design listed in Table 2 was the mean of 960 scenarios, whereas for the MF design that was the mean of 64 scenarios because different levels of MAF and parental genotype missing rates had already been randomly assigned in the MF design. In general, PII outperformed PI in average power for all cases except for one; the average improvement in power for PII ranged from 0 to 0.14. The only outlier was under the MF design for dichotomous traits simulated under the diagonal models: PI was advanced by 0.02 in power. For both genetic designs, the power difference of the two methods was < 0.10 for dichotomous traits but > 0.10 for continuous traits. In three respects, PII appeared to perform better for continuous traits. First, there was a higher averaged power compared with that for dichotomous traits. Second, the advantage of averaged power of PII over PI was bigger for the continuous traits. Third, for two genetic designs used, the greatest average powers were observed for continuous traits; those of the DSP design and the MF design were 0.46 and 0.54, respectively, under the checkerboard interaction model.

Table 2.

Average power of PII and PI under various scenarios

Design	Model	Dichotomous Traits		Continuous Traits
		PII	PI	PII	PI
DSPa	Checkerboard	0.40	0.35	0.46	0.35
	Diagonal	0.32	0.32	0.41	0.29
MFb	Checkerboard	0.46	0.38	0.54	0.40
	Diagonal	0.34	0.36	0.45	0.34

^aFor the DSP design, the power was averaged over 960 scenarios from different combinations of 5 factors, MAF, genotype missing rate of parents, magnitude of a covariate, magnitude of a interaction, and the scheme of adjusting phenotypes.

^bFor the MF design, the power was averaged over 64 scenarios from different combinations of 3 factors, excluding the MAF and genotype missing rate of parents, which were built into the MF design. Average powers in bold were compared and illustrated in Figures 2 and 3.

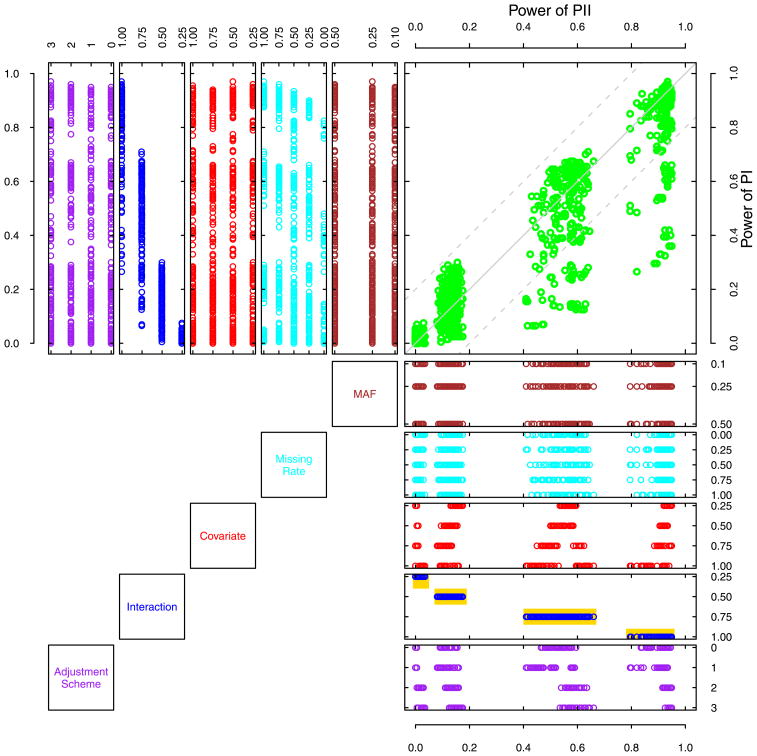
To better demonstrate and compare the performance of two PedGMDR versions, we detailed two sets, highlighted in bold in Table 2, of statistical power, in which one was of the DSP design for dichotomous traits simulated under the checkerboard model and the other was of the MF design for continuous traits simulated under the diagonal model, by drawing Probability-Probability (PP) plots in which points should go along the diagonal if the two methods were of equivalent performance in power. For the case of the DSP design for dichotomous traits, simulated under the checkerboard model where the average powers were of 0.40 for PII and of 0.35 for PI, respectively, the scattered points seemed to largely fall in four groups as shown in the PP plot (Figure 2). Although a small proportion of points was located off the diagonal due to a dropping of power of PI when interaction was either of 0.75 or of 1, most points fell on or near the diagonal area, in which, given a scenario, the power difference of PII and PI was not greater than 0.20. To further investigate the robustness of both methods in regard to power given different factors, we projected each point into two sets of secondary panels, vertically oriented and horizontally oriented, generating the distribution of 960 power scores along a simulation parameter in each panel. In PII (Figure 2), the power of 960 scenarios (points) was distributed in four clearly cut blocks defined by the size of epistatic interaction effects (highlighted in yellow) while in PI, the power blocks appeared to overlap with their neighboring one(s), suggesting that the interaction effect size is a key determinant of power and that PII has a better discriminability. There was no recognized difference in power distribution across different levels of covariate effects, implying that the impact of covariates can be controlled in both PI and PII. Although, compared with that of PI, the power distribution of PII seemed more unevenly distributed at different levels of MAF, the effect of MAF was not essential for PII (neither for PI). Neither parental genotype missing rates nor schemes of adjusting phenotypes were major players in determining power distributions. The powers of both methods were largely determined by the size of epistatic effects and remained robust to the other factors. A similar trend was also found in the comparison of power for all dichotomous traits studied (data not shown).

Figure 2.

A Probability-Probability plot of the power of PI and PII across 960 scenarios for dichotomous traits simulated under the checkerboard model in the discordant sib pair design. In the main panel, the top-right one, the horizontal and the vertical axes are statistical powers of PII and PI, respectively, and the horizontal and the vertical coordinates of each point are determined by the statistical power of PII and PI of a given scenario. The distributions of the simulation parameters are represented graphically in the vertically tiled panels and the horizontally tiled panels for PI and PII, respectively. The horizontal axes of the vertically tiled panels are the power of PII; the vertical axes of the horizontally tiled panels are the power of PI.

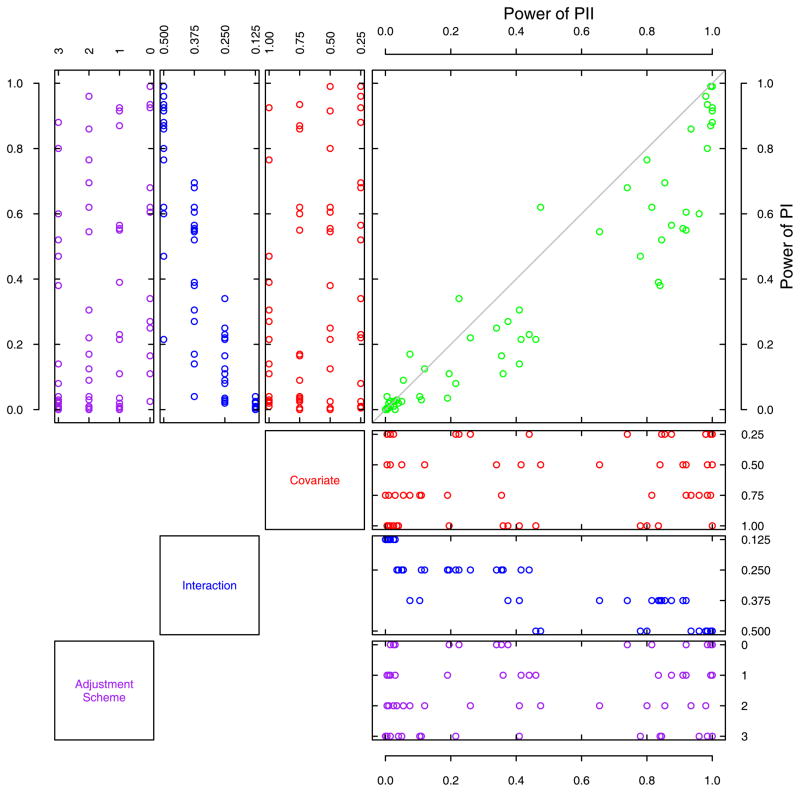
For continuous traits simulated under the diagonal model in the MF design, we plotted a PP distribution for the power values of PII and PI (Figure 3), where there was a difference of 0.11 in the average power as listed in Table 2. As the MAF and a genotype missing rate of 0.25 had already been used for generating the MF design, only three factors remained, yielding a total of 64 scenarios (points). As shown in Figure 3, the power points were largely located in the lower triangles, indicating a dominant performance of PII, which carried out an average power of 0.45 compared with that of 0.34 for PI. When the effect of interaction was small, where the powers of both PI and PII were close to zero, PII did not have a distinguishably better power than that of PI. But PII had increased power when the interaction effect parameter was greater than 0.25. As with the dichotomous traits, the magnitude of interaction effects was the major factor affecting statistical power. The magnitude of covariate effects and the schemes on adjusting phenotypes did not appear to influence the power very much. For the other three average power comparisons between PII and PI for continuous traits, the PP plots had a similar pattern (data not shown). In general, PII appeared to have a better power than PI in detecting interaction underlying continuous traits.

Figure 3.

A Probability-Probability plot of the power of PI and PII across 64 scenarios for continuous traits simulated under the diagonal model in the mixed families design. In the main panel, the horizontal and the vertical axes are statistical powers of PII and PI, respectively, and the horizontal and the vertical coordinates of each point are determined by the statistical power of PII and PI of a given scenario. The distributions of the simulation parameters are represented graphically in the vertical panels and the horizontal panels for PI and PII, respectively (in the mixed families design, minor allele frequency and parental missing genotype rates were built-in parameters in generating populations). The distributions of the simulation parameters are represented graphically in the vertical panels and the horizontal panels for PI and PII, respectively. The meanings of the vertical and horizontal axes are the same as in their corresponding panels in Figure 2.

4. WORKED EXAMPLE

We applied PII to detect susceptibility genes to nicotine dependence (ND) in the U.S. Mid-South Tobacco Family. The data come from our previous reports (Lou et al. 2008; Mangold et al. 2008). Briefly, all the participants involved in this study were recruited primarily from Tennessee, Mississippi, and Arkansas in the U.S. during 1999–2004, and are of either African-American (AA) or European-American (EA) origin. A proband smoker was required to have smoked for at least the last 5 years, to smoke an average of 20 or more cigarettes per day for the last 12 months, and to be at least 21 years of age. Once a smoker proband was identified, all siblings and biological parents of the proband of interest were recruited whenever possible, regardless of their smoking status. In this sample, there were a total of 2,037 individuals, 1,366 individuals from 402 AA families, and 671 individuals from 200 EA families. For more detailed demographic and clinical characteristics of this study, please refer to previous reports (Li et al. 2005; Li et al. 2006). All participants provided informed consent. Institutional review boards approved all protocols, forms, and procedures used in this study.

We focused on a pair of taste receptor genes TAS2R16 and TAS2R38 both on chromosome 7, and each of them had three SNPs genotyped. The detailed genetic information of the six SNPs is shown in Table 3. To demonstrate the use of the proposed PII method and investigate whether there was an epistatic interaction between these two genes, we used the Fagerström Test for ND score (FTND) (Heatherton et al. 1991), a well appreciated measure for ND, as phenotype. The phenotype was adjusted for covariates age, sex, and ethnicity. The PII results are summarized in Table 4. As shown in Table 4, a trilocus model of rs846664 from TAS2R16, and rs1726866 and rs10246939 from TAS2R38, gave a significant interaction with a p value of 5.4 × 10⁻⁵.

Table 3.

Information on the SNPs scored in the two genes in this study

Gene	Chromosome	dbSNP ID	Positiona	Allele
TAS2R38	7	rs713598	141319814	C/G
		rs1726866	141319174	G/A
		rs10246939	141319073	T/C
TAS2R16	7	rs2233989	122422465	A/G
		rs846664	122422409	A/C
		rs1204014	122422079	C/T

^aThe information was provided at NCBI dbSNP Build 131 for Human.

Table 4.

Interaction of TAS2R16 and TAS2R38 detected by PII

No. of Loci	Model	Testing Accuracy	Z score	p value
1	rs846664	0.745	1.29	0.099
2	rs1204014, rs846664	0.745	−0.27	0.606
3	rs846664, rs1726866, rs10246939	0.816	3.87	5.4 × 10−5
4	rs846664, rs713598, rs1726866, rs10246939	0.818	3.19	0.00071
5	rs1204014, rs846664, rs713598, rs1726866, rs10246939	0.823	3.24	0.00060

The SNP IDs in italic font are located in TAS2R38.

Human taste receptors, including type 2 taste receptor (TAS2Rs) are rich in taste buds of gustatory papillae on the tongue surface and palate epithelia. Bitter sensitivity varies among individuals, and previous genetic studies pointed to association between genetic variants with TAS2R and diverse bitterness sensitivity (Kim et al. 2003). Psychologically, stimulation at the receptors of bitterness in human tongues feedbacks a rejection of a substance to avoid a potential toxic. As tobacco smoking basically exerts on human tongues a pharmacological signal equivalent to bitterness, interaction among genes seems possible to associate with ND. However, the role of TAS2R in the plasticity of smoking behavior is complex; to profile their metabolic details, further investigation is required.

5. DISCUSSION

To detect G × G interactions poses a great challenge to statistical genetics in both the aspects of statistical methodologies and computation feasibility. GMDR was recognized as an efficient method to detect interactions, and in this study we proposed a new pedigree-based approach to detecting G × G interactions underlying complex traits. As a pedigree-based approach, it was robust to population admixture. Compared with a previously proposed pedigree-based GMDR approach (Lou et al. 2008), the proposed method showed an increased statistical power in a comprehensive set of simulation scenarios. As only transmitted genotypes are used, PII halves the computing sample size compared with PI, which uses both transmitted and nontransmitted genotypes. PII is consequently faster and more economical in utilizing computer memory, representing a progress that may be nontrivial in the exercise of genome-wide association studies for detecting G × G interactions.

Both PII and PI combine GMDR and sufficient statistics together, but they are different in using the transmitted and nontransmitted genotypes. PI infers the nontransmitted genotypes of an individual to construct a control for each offspring, doubling the sample size. Then statistics, such as TA and CVC, are calculated. Permutation is employed to evaluate the significance of a selected interaction in PI. However, PII calculates the statistics on the observed sample directly, and evaluates their p values by constructing the empirical reference distributions on the basis of the sufficient statistic on a null distribution. An analytical solution, in the context of discordant sib pair design, profiles the mechanical difference of PII and PI in details (Chen 2009). Compared with other similar methods, PII is advanced in tackling both dichotomous and continuous traits and allows phenotypic outcomes to be adjusted with covariates.

As simulation studies remain a rule of thumb in evaluating the performance of methods, we carried out an intensive simulation study of 4,096 scenarios, covering a set of consensus factors probably perturbing the power of statistical methods in genetic epidemiological studies. Given the present study, it was demonstrated that PII rivaled PI for dichotomous traits and was more advantageous to detect interactions for continuous traits. However, the real world involves more complicated circumstances which cannot be thoroughly scrutinized but may distort statistical power of PII and PI. As the simulation study had largely focused on digenic epistasis, whether the conclusion can straightforwardly be applied to detect G × G interaction over two loci still needs to be determined by simulations.

PII is model free, but prior information on genetic models can be taken into account because g() promises flexibility to code additional information. For example, if there is evidence supporting biological equivalence of a pair of genotypes, say, AA and Aa, we can tune g() to code AA and Aa the same indicator. Currently, high throughput genotyping platforms generate high density SNP data, promising a productive future for genome-wide association studies of G × G interactions. To enhance the selection of tagging SNPs, it may be important to select biologically relevant SNPs to control the burden of computation.

In general, as the generalized linear model is embedded to handle both continuous and dichotomous traits, it is feasible to accommodate various kinds of data in genetic epidemiology. The frameworks of PII, as well as PI, are flexible in that after some straightforward modification, they can evolve to handle other kinds of issues in genetic epidemiological studies. If we change the coding schema of t(), replacing it with a output score given survival analysis, it can be applied to survival analysis in terms of the fundamental roles of G × G interaction. It should also be noted that, in genetic epidemiological studies, a set of related phenotypes, such as longitudinal data, are measured, and PII can be easily extended to accommodate phenotypes of interest, and a test statistic can be constructed as [TA−E(TA)]^T V ⁻[TA−E(TA)] ~ χ², where V is the variance-covariance matrix of TA (a vector), has an asymptotically central χ² distribution with its degrees equal to the rank of V. However, heterogeneity of interactions, probably common in ethnicity-specific diseases, can be a concern to the current approach, which only chooses the best model but discards other competitive ones that potentially reveal diseases of different etiologies. The appropriate methods to entertain such heterogeneities are needed.