Multivariate relationships between international normalized ratio and vitamin K-dependent coagulation-derived parameters in normal healthy donors and oral anticoagulant therapy patients

Abstract

Background and objectives

International Normalized Ratio (INR) is a world-wide routinely used factor in the monitoring of oral anticoagulation treatment (OAT). However, it was reported that other factors, e. g. factor II, may even better reflect therapeutic efficacy of OAT and, therefore, may be potentialy useful for OAT monitoring. The primary purpose of this study was to characterize the associations of INR with other vitamin K-dependent plasma proteins in a heterogenous group of individuals, including healthy donors, patients on OAT and patients not receiving OAT. The study aimed also at establishing the influence of co-morbid conditions (incl. accompanying diseases) and co-medications (incl. different intensity of OAT) on INR.

Design and Methods

Two hundred and three subjects were involved in the study. Of these, 35 were normal healthy donors (group I), 73 were patients on medication different than OAT (group II) and 95 were patients on stable oral anticoagulant (acenocoumarol) therapy lasting for at least half a year prior to the study. The values of INR and activated partial thromboplastin time (APTT) ratio, as well as activities of FII, FVII, FX, protein C, and concentration of prothrombin F1+2 fragments and fibrinogen were obtained for all subjects. In statistical evaluation, the uni- and multivariate analyses were employed and the regression equations describing the obtained associations were estimated.

Results

Of the studied parameters, three (factors II, VII and X) appeared as very strong modulators of INR, protein C and prothrombin fragments F1+2 had moderate influence, whereas both APTT ratio and fibrinogen had no significant impact on INR variability. Due to collinearity and low tolerance of independent variables included in the multiple regression models, we routinely employed a ridge multiple regression model which compromises the minimal number of independent variables with the maximal overall determination coefficient. The best-fitted two-component model included FII and FVII activities and explained 90% of INR variability (compared to 93% in the 5-component model including all vitamin K-dependent proteins). Neither the presence of accompanying diseases nor the use of OAT nor any other medication (acetylsalicylic acid, statins, steroids, thyroxin) biased significantly these associations.

Conclusion

Among various vitamin K-dependent plasma proteins, the coagulation factors II, VII and X showed the most significant associations with INR. Of these variables, the two-component model, including factors II and VII, deserves special attention, as it largely explains the overall variability observed in INR estimates. The statistical power of this model is validated on virtue of the estimation that the revealed associations are rather universal and remain essentially unbiased by other compounding variables, including clinical status and medical treatment. Further, much broader population studies are needed to verify clinical usefulness of methods alternate or compounding to INR monitoring of OAT.

Introduction

Oral anticoagulation (OAC) is a vital therapy for many patients, e.g. suffering from tromboembolic events, atrial fibrillation and after heart valves replacement [1,2]. It has been well established that the incidence of complications due to haemorrhage or thromboembolism in these patients depends on the ability to maintain the level of anticoagulation within therapeutic ranges. Due to individual response to OAC, dose adjustment according to regular monitoring, is necessary. Amongst a huge variety of coagulation-related parameters, the prothrombin time (PT) is of special interest since it directly reflects the rate of thrombin generation [3]. Numerous in vitro studies have shown that the rate of thrombin generation is linearly related to the concentration of factor II (FII) in the assay system, thus suggesting a key role of prothrombin levels in the expression of antithrombotic activity of oral anticoagulant treatment (OAT). It was reported recently that FII levels may reflect the true in vivo degree of anticoagulation better then International Normalized Ratio (INR) values in both stable and early phase of anticoagulation [4]. The problem of the possible usefulness of other parameters of blood coagulation has also been occasionally raised, however the evidence accumulated hitherto seems conflicting [5-9]. Therefore, although INR is still widely used in routine OAT monitoring, there is a continuous search for other reliable markers of individual coagulation/anticoagulation status under different clinical conditions.

In this study we employed the calculus of multivariate methods to characterize the associations of INR with other vitamin K-dependent plasma clotting factors in a heterogenous group of individuals, including healthy donors, patients on OAT and patients not receiving OAT. Despite this primary objective, our secondary aim was also to determine whether the associations between INR and other coagulation variables may be biased by the influence of co-morbid conditions (including accompanying diseases) and co-medications (including different intensity of OAT).

Materials and method

Study subjects

After obtaining an informed consent, 203 subjects were involved in the study. Of these, 35 were normal healthy donors (group I) and 73 were suffering from different medical conditions and therefore were on single or compounding medication but were not the users of OAT (group II). Group III consisted of 95 subjects on stable and permanent oral anticoagulant therapy lasting for at least half a year. A basic demographic information and medical history was obtained by means of a short questionnaire. The study protocol was approved by the Ethical Committee of Medical University of Lodz.

Clinical Laboratory Methods

Peripheral venous blood samples (4.5 ml) were collected using a 21 gauge needle and Vacutainer System (Becton Dickinson) tubes containing 0.105 M sodium citrate. Once drawn, the samples were immediately tested in those devices requiring whole blood according to the manufacturer's instructions. The remaining portions of blood were separated into blood cells and platelet poor plasma (1500 × g, 15 min), and the latter was kept frozen at -80°C until assayed as described below.

Coagulant activities of factor II, VII and X, as well as prothrombin time (INR), activated partial thromboplastin time (APTT) ratio; protein C activity and fibrinogen were measured in processed plasma in one-stage assays on the ACL 7000 analyzer (Instrumentation Laboratory, USA) using commercially available reagents and immunodepleted plasmas (IL Test™ APTT-SP (liquid), IL Test™ PT-Fibrinogen Recombinant, IL Test™ Factor Deficient Plasma II, VII, X and IL Test™ Test Protein C, respectively, Instrumentation Laboratory, Italy). For the measurements of INR and the vitamin K-dependent coagulation factors we used the same thromboplastin (Test PT-Fib.Recombinant™, Instrumentation Laboratory, USA, ISI = 0.99). Calibration curves were obtained and given by manufacturer and confirmed by ourselves using dilutions of normal pooled plasma collected from 40–60 apparently healthy subjects. The concentration of prothrombin F1+2 fragments was measured by a commercially available ELISA kit: Enzygnost^® F 1+2 micro (Dade Behring, Germany), using an ELISA reader (BioRad Benchmark 550 Microplate Reader).

Statistical analysis

Due to departures of distributions of raw measurements from normality (according to the Shapiro-Wilk test), data are given as median and 25–75 percentile range (Me, 25–75%QR). The sets of data that showed asymmetric distributions were transformed and analyzed with the relevant parametric tests, as described in the 'Results' section.

The differences between groups of thus transformed data were evaluated by one-way analysis of variance and Tukey's test for multiple comparisons.

The associations between variables presented as raw data were analyzed with Spearman rank correlation (R); for those between transformed data we employed either Pearson's linear correlation or multiple regression analysis and partial correlation. In the multivariate analysis of all data we used finally the ridge regression model of multiple regression (standard and stepwise approaches of multiple regression analysis).

The outlying observations were censored using residual regression analysis and the typical tests for outliers (Dixon's Q test, Grubbs' test) [10-12]. Data allocation to dispersion ellipses was performed using a forward stepwise discriminant analysis.

Clinical (accompanying diseases) and pharmacological parameters (treatment) were ranked dichotomically based on the presence or absence of a given character/treatment.

To calculate the optimal cut-off point (≤ x or x ≥) between the subjects on OAT treatment and the remaining donors and patients with the sensitivity/specificity weighting ratio possibly closest to 1.0, we employed the ROC analysis. To assess the agreement between the two methods we used the statistical procedure reported by Bland and Altman [13,14]. In this method the association between the differences from the paired outcomes of the two compared methods and the averaged outcomes for all the concordant and discordant pairs of data were regarded as the measure of compatibility of the data collected with the use of either direct monitoring of INR (INR_experimental) or statistical evaluation of INR on virtue of the collected values of other plasma coagulation parameters (INR_predicted).

The calculations were performed using the statistical software: Statistica^®PL for Windows version 5.5 (StatSoft, Inc. 2000) and StatsDirect^® (StatsDirect Ltd. 2000).

Results

Demographic and clinical characteristics of the studied subjects, as well as the use of the drugs of known influence on the coagulation status (acetylsalicylic acid, statins, steroids, thyroxin), are presented in Table 1. All patients in group III received acenocoumarol (synthetic derivate of 3-(α-acetonylbenzyl)-4-hydroxycoumarin, vitamin K antagonist that impairs the synthesis of active plasma coagulation factors: II, VII, IX, X; Acenocoumarol^®,Polfa-Warszawa, Poland) as a standard medication (Me = 18 mg/6 days, 25–75%QR = 12–24 mg/6 days). Indications for OAT in patients representing group III are listed in Table 2.

Table 1.

Demographic and clinical characteristics of the studied subjects

		group I (n = 35)	group II (n = 73)	group III (n = 95)
gender	males	11	25	19
	females	24	48	76
age (years)	mean	47.4	59.4	59.5
	range	22–74	32–78	24–74
compounding medication (n)	acetylsalicylic acid	7	33	4
	statins	0	11	7
	steroids	0	16	3
	thyroxin	0	5	13

Table 2.

Indications for OAT in patients representing group III (with more than one indication for a patient possible)

Indication for therapy	% of patients
atrial fibrillation	14
venous thromboembolism	5
postmyocardial infarction	14
cerebrovascular disease	5
prosthetic heart valve	79
miscellaneous	2

In this study we expectedly found differences in all studied parameters between representatives of the group III (patients on OAT) and the remaining donors and patients. No significant differences were revealed between normal healthy donors (group I) and patients of the group II, except for prothrombin F1+2 which was significantly higher in group II compared to healthy donors.

Further, for all the analyzed parameters but fibrinogen and APTT ratio the cut-off points discriminating between users and non-users of OAT lie far beyond the 25–75 percentile ranges estimated for group III by ROC curve analysis (Table 3).

Table 3.

Laboratory parameters values

	group I (n = 35)	group II (n = 73)	group III (n = 95)	cut-off point
PT [sec]	11.3 (10.8–12.3)	10.8 (10.4–11.6)	24.0 a (20.4–29.4)	13.21 (0.979, 0.990)
INR	1.02 (0.98–1.11)	0.98 (0.92–1.04)	2.16 a (1.84–2.60)	1.20 (0.979, 0.990)
APTT ratio	1.01 (0.96–1.10)	0.98 (0.92–1.10)	1.17 a (1.08–1.33)	1.03 (0.870, 0.645)
Fibrinogen [g/l]	3.36 (2.85–3.83)	3.60 (3.19–4.09)	4.17 b (3.59–4.63)	4.13 (0.537, 0.815)
FII [%]	132 (117–142)	133 (122–145)	25 a (19–35)	83.0 (0.989, 0.971)
FVII [%]	125 (108–133)	135 (125–142)	47 a (32–64)	91.1 (0.946, 0.963)
FX [%]	108 (92–120)	104 (96–113)	15 a (11–20)	68.1 (1.0, 0.942)
protein C [%]	118 (103–138)	125 (110–137)	54 a (46–64)	91.0 (0.968, 0.935)
prothrombin F1+2 [ng/ml]	0.87 (0.57–1.26)	1.26 c (0.98–1.71)	0.27 a (0.19–0.40)	0.528 (0.840, 0.934)

Data represent median and 25–75 percentile range. Cut-off points between users (group III) and non-users of OAT (groups I and II) estimated by ROC curve analysis with an a priori weighing of sensitivity:specificity ratio equal 1.0; the post hoc sensitivity and specificity estimates given in parentheses. Significance of differences between groups estimated for normalized data by one-way ANOVA (p « 0.0001 for all variables) and Tukey's test for multiple comparisons: ^a p « 0.0001; ^b p < 0.0002; ^c p < 0.05.

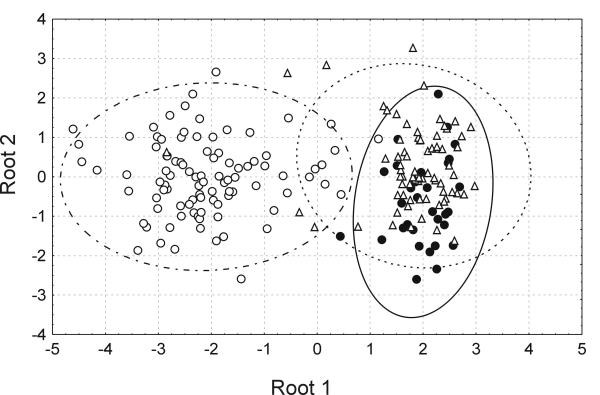
Secondly, using a multiparametric discriminant function analysis we showed all the groups were significantly separated apart (Fig. 1) and the variables which mostly contributed to a significant discrimination of the groups, with a maintenance of a minimum tolerance of 0.5, were factor X (partial Wilk's lambda = 0.812, p « 0.0001), protein C (partial Wilk's lambda = 0.907, p < 0.0002), fibrinogen (partial Wilk's lambda = 0.922, p < 0.001) and prothrombin F1+2 (partial Wilk's lambda = 0.939, p < 0.003). The most precise a posteriori allocation of cases to the a priori assigned groups was found for the OAT patients (93%), whereas the least precise characterized the control healthy donors (41%).

Figure 1.

Classification of donors and patients according to the multivariate discriminant function analysis including studied coagulation parameters. Dispersion ellipses (95%CI) are drawn based on the coordinates of two orthogonal discriminant functions (roots) estimated in the course of a stepwise forward discriminant function analysis (overall Wilk's lambda = 0.191, p « 0.0001), including five variables (factor X, protein C, prothrombin F1+2, fibrinogen and APTT ratio), each with a tolerance of at least 0.5. Analysis performed on log-transformed data in three groups: healthy donors (group I) (●), patients who were non-users of OAT (group II) (△) and OAT users (group III) (○).

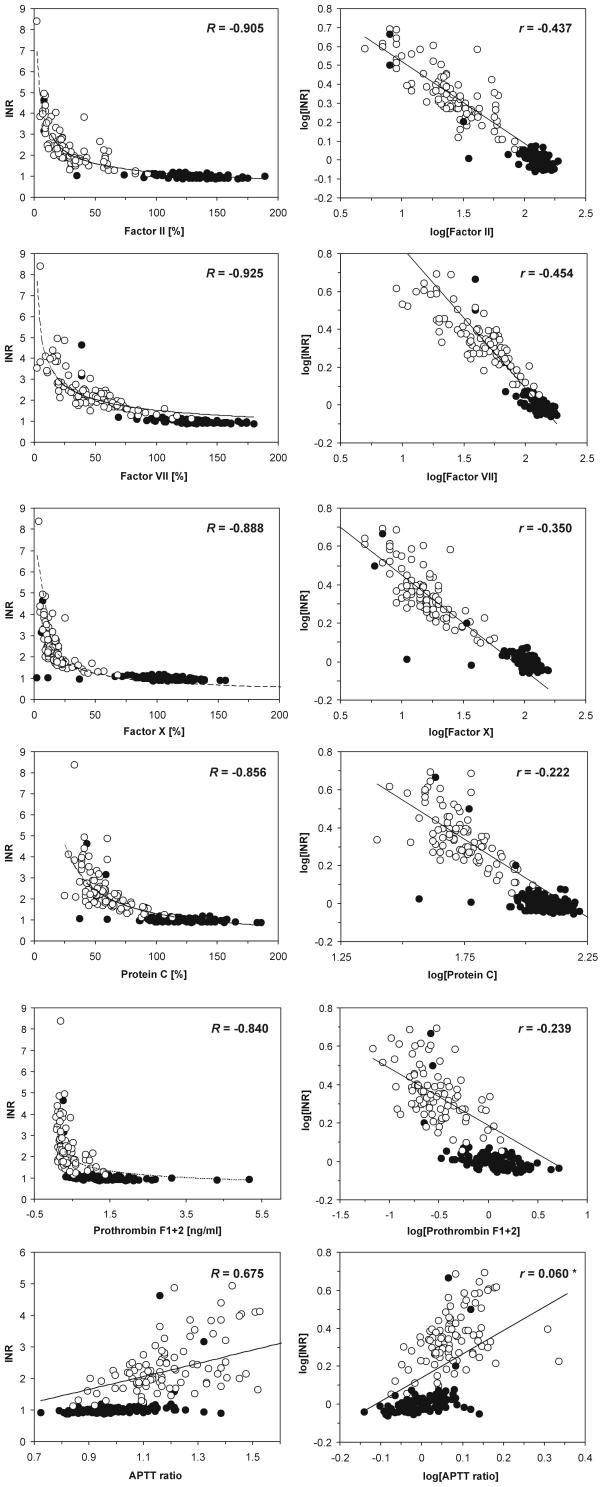
Third, the associations between raw data of INR and each of the remaining tested variables were apparently hyperbolic and characterized by very significant Spearman's rank correlation coefficients (Fig. 2 inserts and legend). To cope with the requirements of data linearity for multivariate parametric analyses, we verified various mathematical transformations of raw data (logarithmic, semilogarithmic, reciprocal, square root). Based on the estimates of individual linear correlation coefficients and homogeneity of raw data distributions we chose the logarithmic transformation of raw data (X' = log(X) and Y' = log(Y)). Fig. 2 (right panels) shows the linear partial associations between INR and other variables. Contrary to rank correlation, we observed significant linear associations of INR with all variables but the APTT ratio and fibrinogen (the latter not shown). Simple linear (Pearson's) correlation coefficients between all the analyzed variables are given in Table 4.

Figure 2.

Relationships between INR and plasma clotting factors, protein C and F1+2 prothrombin fragments in normal donors and patients on OAT. Cases representing patients on OAT are marked as open circles (○), those representing healthy donors or patients not receiving OAT are marked by closed circles (●). For non-linear associations of raw data (left panel) correlation coefficients represent Spearman's non-linear correlation; for log transformed data correlation coefficients represent partial correlation (for the model including all variables); insignificant coefficients marked with an asterisk, for the remaining p « 0.0001; coefficients estimated for whole set of experimental data (n = 203). In both methods the lines were computer-fitted to the data using the quasi-Newton algorithm.

Table 4.

Simple linear correlation coefficients between investigated coagulation parameters

	INR	Fibrinogen	APTT ratio	Factor II	Factor VII	Factor X	Protein C	Prothrombin F1+2
Fibrinogen	0.320		0.203	-0.353	-0.298	-0.345	-0.275	-0.298
APTT ratio	0.627	0.203		-0.603	-0.630	-0.600	-0.606	-0.582
Factor II	-0.955	-0.353	-0.603		0.891	0.939	0.878	0.835
Factor VII	-0.941	-0.298	-0.630	0.891		0.874	0.862	0.771
Factor X	-0.940	-0.345	-0.600	0.939	0.874		0.882	0.810
Protein C	-0.883	-0.275	-0.606	0.878	0.862	0.882		0.751
F1+2	-0.828	-0.298	-0.582	0.835	0.771	0.810	0.751

The coefficients were estimated for log-transformed data in the cohort including all 203 cases enrolled to the study (donors and patients). All coefficients were significant with at least p < 0.05.

In general, to reason on which of independent variables contributes mostly to the variability of INR, we employed the analysis of multiple regression. The residual analysis (including testing for normality, homoscedasticity, autocorrelation, linearity and outlying observations) was always employed as a routine prior to the appropriate multiple regression analysis performed on log-transformed data. In the standard classical model of multiple regression we included one dependent variable (INR) and all 7 independent variables: fibrinogen, APTT ratio, FII, FVII, FX, protein C and prothrombin F1+2. The significant regression coefficients were found only for five of these variables, whereas neither fibrinogen nor APTT ratio contributed significantly to the explaining of INR variability. Due to the low tolerance values for all of thus included significant variables (0.1–0.3), pointing to a considerable collinearity of all independent variables in such a model, we further employed the ridge model of a forward stepwise multiple regression with a lambda = 0.1. By the extension of such criteria we finally built up the regression function including five significant independent variables: FII, FVII, FX, protein C, prothrombin F1+2, altogether explaining over 92% of INR variability and each having a tolerance of at least 0.22 (Table 5). Then, we gradually eradicated from the model the independent variables with the lowest significance and F_remove values to finally approach a two-component model including only FII and FVII (overall R² = 0.903, tolerance = 0.378 for each, partial correlation coefficients: r_FII = -0.711, r_FVII = -0.659, p « 0.0001 for each).

Table 5.

Summary of a ridge multiple regression model for clotting parameters explaining the variability of INR as a dependent variable

independent variable	R2	βs	p	βoverall	p
Fibrinogen	0.095	0.315 ± 0.068	5.91*10-6	-0.002 ± 0.019	0.921
APTT ratio	0.396	0.631 ± 0.055	1.98*10-23	0.024 ± 0.023	0.301
Factor II	0.893	-0.944 ± 0.024	0	-0.277 ± 0.042	3.07*10-10
Factor VII	0.884	-0.919 ± 0.028	0	-0.310 ± 0.036	1.68*10-15
Factor X	0.874	-0.935 ± 0.025	0	-0.229 ± 0.040	3.98*10-8
Protein C	0.783	-0.886 ± 0.033	0	-0.083 ± 0.035	0.019
Prothrombin F1+2	0.671	-0.820 ± 0.041	0	-0.088 ± 0.030	0.004

Model estimated for log-transformed data in all variables with the accepted value of λ = 0.1. The values in the columns 2 and 4 of the table refer to the standardized regression coefficients (b_i) in the individual regression models (β_s ± SE [β_s]) including the individual independent variables, or to the overall ridge multiple regression model (β_overall ± SE [β_overall]) comprising all examined independent variables. The values of the determination coefficients (R²) denote the individual contributions of any given variable (estimated in single variable regression models) in explaining the overall INR variability; for the overall multiple regression model the corrected overall R² = 0.9289; both individual and overall R² were significant with p at least 0.0001. For the model of a ridge multiple regression with INR as a dependent variable and comprising all the independent variables the partial correlation coefficients r_p are given in fig. 2.

Using the above algorithm we accomplished the following regression equations – for the complete five-component model:

[INR] = -0.136 * [FII] -0.211 * [FVII] -0.104 * [FX] -0.088 * [protein C] -0.048 * [prothrombin F1+2] + 1.133

and the other for the "eradicated" two-component model:

[INR] = -0.251 * [FII] -0.296 * [FVII] + 1.168,

where [INR] = log(INR), [FII] = log(FII activity), [FVII] = log(FVII activity), [FX] = log(FX activity), [protein C] = log(protein C activity), [prothrombin F1+2] = log(concentration of prothrombin fragment F1+2).

In summary, (i) three of the assayed clotting parameters (factors II, VII and X) appeared as very strong modulators of prothrombin time (INR), (ii) protein C and prothrombin fragments F1+2 had moderate influence, (iii) whereas both APTT ratio and fibrinogen had no significant impact on INR variability.

It should be emphasized that regardless of the complexity of the overall multiple regression model, comprising from 2 to 7 independent variables, the variability of INR was largely explained by the variabilities of the included independent variables (from 90.3% for the 2-component model up to 92.9% for the models including 5–7 variables). Further, the dominance of the complex multiple regression model (with 5 independent variables of significant contribution) over single variable models in explaining the total variability of INR was from 3.6% for FII and 5% for either FVII or FX to over 25% for F1+2. This clearly demonstrates that each of these most significant contributors (clotting factors II, VII or X) remained apparently sufficient in explaining the vast portion of an overall INR variability. Moreover, due to collinearity and low tolerance of independent variables included in the multiple regression model, one should rather consider such a ridge multiple regression model which compromises the minimal number of independent variables with the maximal overall determination coefficient. If so, there is no need to monitor a large variety of clotting-related parameters and rather to choose a few most discriminating variables. Our estimates show that such conditions are generally substantiated in the multiple regression model comprising FII and FVII that altogether explained over 90% of overall INR variability.

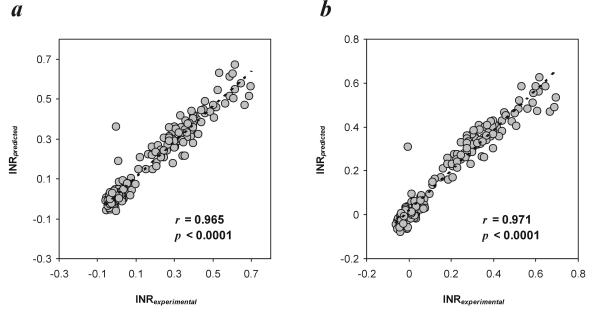
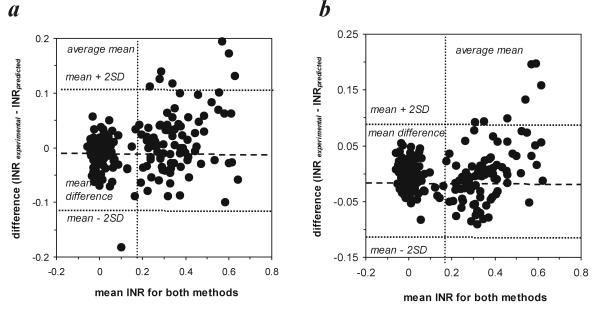
To verify such an assumption we made a comparison between a standard method (monitoring of INR) and other (alternate) methods (prediction of INR based on the monitoring of selected clotting factors and/or coagulation-related variables). We used the above mentioned regression equations (for the 2-component model or for the 5-component model) to calculate the predicted INR values and compared the latter with the experimental INR evaluated using a standard laboratory procedure [13]. Despite a very significant linear correlation between INR_experimental and INR_predicted (Fig. 3), we were further interested whether these two approaches may be interchangeably applied in diagnostic practice, i.e. whether these methods produce comparable data. The differences between INR_experimental and INR_predicted within the pairs of data exceeded the range of doubled SD_difference only in 4.5% and 3% of cases for the 2-component model and the 5-component model, respectively, which points to a very good compatibility between both methods used to monitor INR (Fig. 4). The mean difference between the methods enables to extrapolate the results obtained with a regression method (INR_predicted) to those predicted to be read with the other one (INR_experimental), provided the dispersion of differences lies in a narrow confidence limit around the mean difference in the sample (Fig. 4). Considering the dispersion of the differences recorded within the pairs of data (since the standard errors of lower or upper limit are respectively 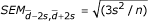= 0.00666 for the 2-component model and 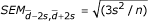= 0.00594 for the 5-component regression model, and assuming the normal distributions of the differences for the 2-component model 95% 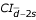= -0.1112 ± 0.1081 (-0.1248; -0.0976) and 95% 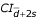= 0.1051 ± 0.1081 (0.0915; 0.1187) and for the 5-component model 95% 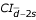= -0.0987 ± 0.0965(-0.1105;-0.0863) and 95% 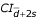= 0.0947 ± 0.0965 (0.0826; 0.1068)), we may conclude that the outcomes of the 'experimental' method of the monitoring of INR are likely to be by up to 10^0.1112 = 1.29 lower or by up to 10^0.1187 = 1.31 higher compared to the results obtained with the use of the regression method including 2 independent variables, and by up to 10^0.0987 = 1.26 lower or by up to 10^0.0947 = 1.24 higher compared to the results obtained with the use of the regression method including 5 independent variables. Overall, we conclude that it is fully justified to state that both methods of the estimation of INR as the hallmark of the overall plasma coagulation capacity (INR_experimental and INR_predicted) may be used interchangeably.

Figure 3.

Linear regression as a measure of association between the values of INR_experimental and INR_predicted for (a) two-component model and (b) five-component model of multiple regression.

Figure 4.

Scatter plot of the differences between pairs of data collected with the use of either 'experimental' or 'statistical' method as a measure of agreement between the compared methods for (a) the two-component model and (b) the five-component model of multiple regression The plot presents the dependence between the measurement error (the difference between the outcomes of two compared methods) and the estimated true INR (the mean of means for both methods, the best μ of the selected sample population). The mean differences for the 2-component regression model and the 5-component regression model were respectively -0.00304 ± 0.0541 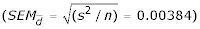and -0.00185 ± 0.0483 .

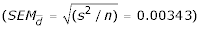Finally, we employed the above mentioned multiple regression models to verify whether and how far the assigned relationships may be affected by (1) medication or co-medication and (2) co-morbid conditions. The first group of variables included (a) the use of OAT and its dosing, (b) the use of acetylsalicylic acid and dosing, (c) use of other drugs grouped into four classes: statins, steroids, thyroxin, (d) OAT as the excluded grouping variable. The second group of variables concerned the presence of other accompanying diseases and disorders, including venous thromboembolism, ischaemic heart disease, myocardial infarction, stroke, diabetes, hypertension, liver and intestinal tract diseases including ulceration, thyroid diseases, cancer, osteoporosis, uraemia and kidney diseases, mastopathy, gynaecological disorders, allergy, and rheumatoid diseases.

Neither the use of OAT, nor acetylsalicylic acid nor any other medications affected significantly the variability of the observed experimental INR. Also, we did not observe the statistically significant impact of any accompanying disorders and diseases on INR_experimental.

Discussion

Several recent studies have focused on evaluating markers of activation of the haemostatic system in terms of thrombin generation, such as prothrombin fragment F1+2, thrombin-antithrombin (TAT) complexes, or clotting factors [4,9,15]. Normally, small amounts of these proteins are found in bloodstream, and are considered hallmarks of the ongoing thrombin generation occurring at sites with exposed tissue factor [16]. Obviously, in situations with increased thrombin generation (e. g., thromboembolism, surgery) these parameters may be elevated, while they become markedly suppressed during anticoagulant therapy [8,17-19]. On the other hand, the prothrombin time (PT) may be subject to various modulators, like oral anticoagulants [20]. To avoid biases from both system-derived (variations among coagulation analyzers) and reagent-derived sources (different batches of thromboplastins), the prothrombin time is more often expressed in terms of the International Normalized Ratio (INR) [3]. In the clinical settings, the monitoring of INR as an aid tool for OAT is only sporadically accompanied by the routine laboratory assessment of other coagulation-related haemostatic parameters. The accomplished evidence remains inconsistent in linking various coagulation factors' activities to the INR values. In this study we intended to characterize the associations of INR with the activities of some vitamin K-dependent plasma proteins and thus to evaluate how far the monitoring of INR might be extended by or 'enriched' with the monitoring of other coagulation-derived variables.

To perform this study, and for the purpose of the analysis, we have chosen selected clotting factors directly participating in subsequent steps of a coagulation pathway dependent on tissue factor and factor VII, previously referred to as extrinsic coagulation pathway. In addition, we picked up two other factors either directly or indirectly related to thrombin generation: protein C and prothrombin fragment F1+2 [17]. Whereas the former is crucial in haemostatic feedback mechanisms governing de novo thrombin generation [21], the latter is claimed to be less affected by various compounding variables than for example TAT, and therefore it appears to reflect coagulability more accurately [22]. To ensure that the estimated associations are representative as much as possible, we have deliberately enrolled into the study a large cohort of people representing not only healthy donors, but also those in whom co-morbid conditions and/or co-medication might be observed.

All the parameters selected to this study have already been proven to be affected by OAT [23]. The vitamin K-dependent coagulation factors VII and X, as well as inhibitor protein C have been reported to show a highly significant correlation with treatment intensity [4,17,24]. Therefore, by the inclusion of a heterogenous study population comprising both patients on OAT and healthy donors, as well as varying group of patients without OAT (of whom 20% were on aspirin), we deliberately broadened up the naturally existing variability of the studied parameters.

Overall, the prothrombin time (INR) was affected mostly by three of the assayed clotting factors: FII, FVII and FX. Protein C and prothrombin fragments F1+2 had moderate influence, whereas no significant impact on INR variability has been revealed for either APTT ratio or fibrinogen. As deduced from R² values, each of assayed parameters explained a very significant part of INR variability (from 10% in the case of fibrinogen up to nearly 90% in the case of factor II), when analyzed in the single variable regression models. Based on the values of partial correlation coefficients, only 5 parameters (mainly factors VII, II and X which explained up to 92–93% of INR variability) showed significant partial contributions to INR, whereas the effects of both fibrinogen or APTT ratio remained negligible. It clearly points that each of these insignificant parameters bears a large portion of a 'hidden' variability resulting probably from their associations with other plasma coagulation-derived variables and not necessarily with INR. It goes along with the results of Jerkeman et al., who found the strongest associations with PT in the case of factor X, protein C, factor VII, IX and protein S. Unfortunately, factor II was not covered by the scope of that study [17]. These results correspond also with those obtained recently by D'Angelo et al., who found FII monitoring to be a good alternative for INR monitoring, as the parameter reflecting more closely in vivo antithrombotic potential [4]. Similar type of agreement analysis has been reported by Kumar et al., however, the authors claimed only 50–77% proportion of variability of the INR explained by the activities of clotting factors II, VII, IX and X [23]. Our estimates only partly correspond to those reported by Weinstock et al., who investigated the group composed of 80 OAT patients on initial- and long-term warfarin therapy and 40 healthy volunteers, and, using a univariate analysis, they concluded that factor VII, and not prothrombin, may be the predominant factor monitored by INR [9]. On the other hand, Lind et al. pointed that plasma levels of the vitamin K-dependent coagulation factors are not equal in long-term OAT patients. Using a multivariate analysis they showed factor II levels to be the least significant of the three clotting factors (II, VII, X) measured in the determining of the international normalized ratio in plasma or whole blood [8], which opposes our present findings. Considering such a moderately consistent array of data, the question may be raised why not all studies in this area reached the same estimates concerning the contributions of factors II and VII to INR. We suggest that the conflicting results with other authors' findings may be due to different PT reagents for INR, since different PT reagents have different sensitivities to individual coagulation factors and inhibitors.

Another problem which needs to be addressed here is why FVII and FII activities, which were significantly lower in patients on OAT, did not contribute significantly to the discrimination of the three groups of subjects. To reasonably interpret such an inconsistence we have to remember that the inclusion of any variables into the model of discriminant function analysis is based on the compromise between the largest contribution of a given variable to the improvement of the model (given by the partial Wilk's lambda) and non-collinearity of included variables (given by tolerance). In our analysis, both FII and FVII were highly redundant parameters, collinear with other parameters and characterized by low tolerance values (below 0.240). On the other hand, both FII and FVII showed merely moderate contributions (partial lambda Wilks' values close to 1), compared to other analyzed variables. Therefore, despite their significant differences between groups, these two parameters were not included in the model as the best discriminating parameters.

It is worth emphasizing that the associations obtained by us were still valid in both healthy subjects and patients suffering from different diseases. Neither the use nor the intensity of OAT, nor the use of acetylsalicylic acid nor of any other medications biased significantly these associations. This finding appears especially worth mentioning, since it implies that the revealed association is a more generalized phenomenon, not merely attributed to either OAT patients on one hand, or to healthy individuals with undisturbed haemostasis on the other. In our opinion such a universality of the estimated relationship is challenging in looking forward to novel strategies of the monitoring of an overall haemostatic capacity in health or disease. On the other hand, however, we need to admit that our estimates apply predominantly to acenocoumarol since other anticoagulants have not been studied in our present approach.

To date the INR was considered a solely used universal measure of an overall coagulation blood capacity and numerous studies have proved its excellent usefulness for the monitoring of OAT. The evidence that such a usefulness exists for other haemostatic parameters is no so profound. Our present study points to other parameters characterizing the overall haemostatic capacity that might be potentially employed either alternatively or in a conjunction with INR for the monitoring of OAT. This observation is of particular value as there is a continuous search for a reliable OAT monitoring in point-of-care setting. Despite the observed lack of the impact of numerous pharmacological (oral anticoagulant dose, compounding medication) and clinical parameters (accompanying disorders and diseases), which seems very intriguing, it needs to be emphasized that our opinion presented in this study is merely a statistical point of view. Moreover, given that various thromboplastins may differ in their sensitivities to reduced activities of different vitamin K-dependent clotting factors, it is important to note that outcomes obtained with different reagents may not be statistically equal. Therefore, further, much broader population studies are certainly needed to verify the observed associations and to validate the potential usefulness of the coagulation parameters as compounding or alternate to INR measures of coagulation capacity in both healthy donors and OAT treated patients.