Grid cells and theta as oscillatory interference: Electrophysiological data from freely-moving rats

Abstract

The oscillatory interference model (Burgess, Barry, & O’Keefe, 2007) explains the generation of spatially stable, regular firing patterns by medial entorhinal cortical (mEC) grid cells in terms of the interference between velocity-controlled oscillators (VCOs) with different preferred directions. This model predicts specific relationships between the intrinsic firing frequency and spatial scale of grid cell firing, the EEG theta frequency, and running speed (Burgess, 2008). Here we use spectral analyses of EEG and of spike autocorrelograms to estimate the intrinsic firing frequency of grid cells, and the concurrent theta frequency, in mEC layer II in freely-moving rats. The intrinsic firing frequency of grid cells increased with running speed, and decreased with grid scale, according to the quantitative prediction of the model. Similarly, theta frequency increased with running speed, which was also predicted by the model. An alternative Moiré interference model (Blair, Welday, & Zhang, 2007) predicts a direction-dependent variation in intrinsic firing frequency which was not found. Our results suggest that interference between VCOs generates the spatial firing patterns of entorhinal grid cells according to the oscillatory interference model. They also provide specific constraints on this model of grid cell firing, and have more general implications for viewing neuronal processing in terms of interfering oscillatory processes.

Introduction

The amazingly regular spatial distribution of firing shown by grid cells recorded in layer II of the medial entorhinal cortex (mEC) of freely moving rats (Hafting, Fyhn, Moser, & Moser, 2005; Moser & Moser, 2008) has prompted a search for the underlying physiological mechanism. Current models either emphasize oscillatory properties of the hippocampal formation (Blair et al., 2007; O’Keefe & Burgess, 2005; Burgess et al., 2007) or recurrent connectivity (Fuhs & Touretzky, 2006; McNaughton, Battaglia, Jensen, Moser, & Moser, 2006). The theoretical issues surrounding the oscillatory interference model of grid cell firing (Burgess et al., 2007), and the experimentally testable predictions it makes, are made clear in (Burgess, 2008). Here we examine the predictions of that model for extra-cellular recording in freely moving rats.

The EEG of freely-moving rats is dominated by the movement-related theta rhythm, a strong oscillation in the range 7-11Hz in adult rats, see (Buzsaki, 2002; O’Keefe, 2006) for reviews. The oscillatory interference model predicted that the firing of layer II grid cells should be modulated in the theta band, but at a slightly higher frequency than the on-going theta rhythm (O’Keefe & Burgess, 2005; Burgess et al., 2007), so that it would show ‘theta phase precession’ similar to that found in place cells (O’Keefe & Recce, 1993). More specifically (Burgess, 2008), the model predicts that the frequency of firing rate modulation (the ‘intrinsic firing frequency’, f_i(t)) of the grid cell will depend upon the frequency of the theta rhythm while stationary, f₀ (see below), the running speed of the rat, s(t), and the spatial scale of the firing pattern, G, according to:

$${<f_i>}_{\varphi \left(t\right)}=f_0+\frac{2(\pi +1)}{\sqrt{3}\pi G}s\left(t\right),$$ (1)

where <> _φ(t) denotes the average over all directions of movement, φ(t), during the rat’s exploration, and f₀ is the theta frequency extrapolated to zero running speed. The intrinsic firing frequency f_i(t) is estimated from the power spectrum of the spike train autocorrelogram. The model also predicts a linear relationship between theta frequency and running speed:

$$f_{\theta }\left(\mathrm{s}\right(t\left)\right)=f_0+<\beta >s\left(t\right),$$ (2)

thus, f₀ can be estimated as the intercept of the plot of theta frequency versus running speed. The meaning of the constant <β> is explained below.

These predictions are tested in Figures 2 and 4, while Figure 5 tests the predictions of an alternative, spatial, interference model (Blair et al., 2007). In the remainder of the introduction we briefly describe the oscillatory interference model and its predictions, see (Burgess, 2008) for details.

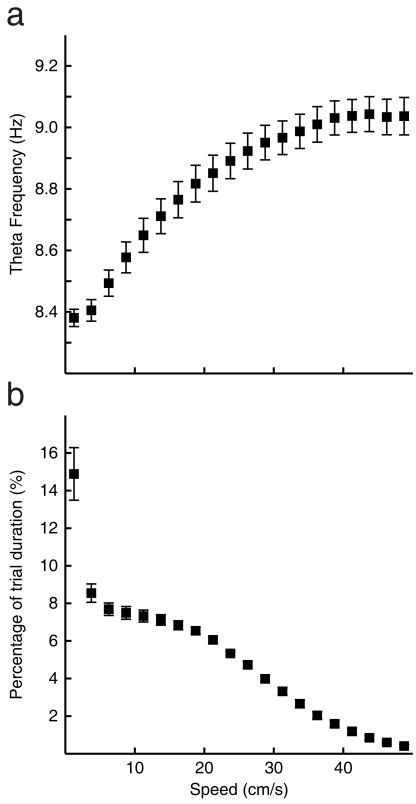
Figure2.

The dependence of theta frequency on running speed. a) Theta frequency as a function of running speed, the mean frequency and standard error is shown for the 24 trials in 13 rats which entered the analyses. Linear regression of this curve between 5 and 30 cm/s gives the y-intercept as 8.28 Hz and the slope as 0.02 cm/s². b) The distribution of running speeds during these trials.

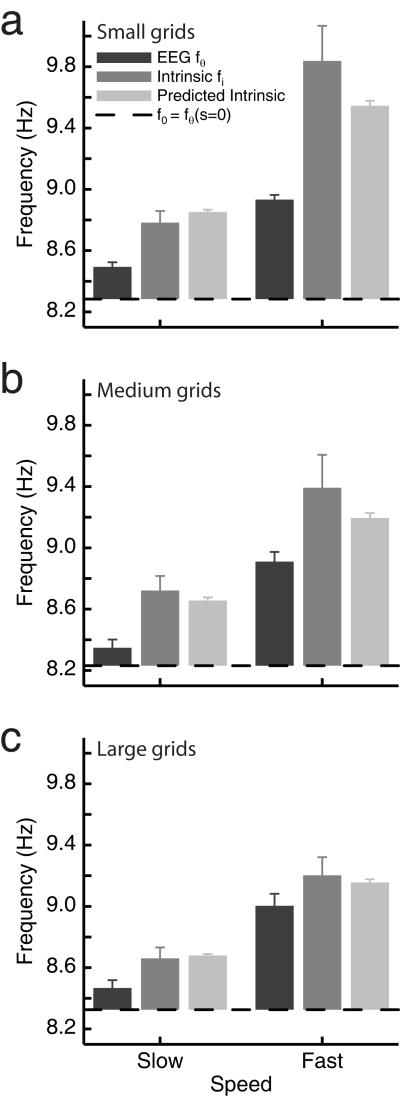
Figure 4.

Grid cells’ intrinsic firing frequency (f_i) depends on grid scale and running speed as predicted by the oscillatory interference model (equation 6). The mean intrinsic firing frequency is shown for slow runs (left) and fast runs (right) for grid cells with small (a), medium (b) and large (c) grids. Values are combined across trials by subtracting the value of f₀ for each trial (i.e. values shown are relative to the horizontal black line which indicates f₀ and is shown at the mean f₀ across the trials used). The corresponding values for theta frequency and predicted intrinsic frequency are also shown with each plot. The mean of the median speed in slow and fast runs is 12.4 and 28.2 cm/s respectively. The mean scale of grids in the small, medium and large divisions is 33.6 cm, 44.1 cm and 53.4 (16 cells per division).

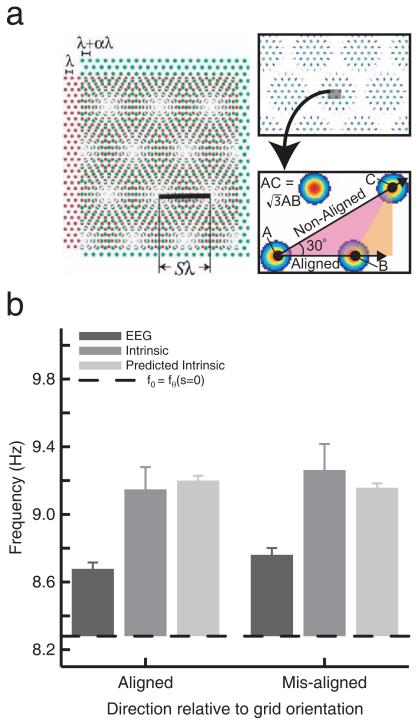
Figure 5.

Effect of running direction on grid cells’ intrinsic firing frequency (aligned or mis-aligned to the grid). a) Predicted increase in intrinsic firing frequency by a factor √3 for aligned versus misaligned runs, according to the Moiré interference model. b) Data. Intrinsic firing frequency was calculated separately for runs aligned or mis-aligned with the grid. Values are combined across trials by subtracting the value of f₀ for each trial (the horizontal black line, which is shown at the mean value of f₀ across trials for conversion into average absolute frequencies). There is no sign of a prediction of the Moiré interference model. The corresponding values for theta frequency and the oscillatory interference model’s predicted intrinsic frequency are also shown with each plot.

The oscillatory interference model

The oscillatory interference model generalizes the 1-D interference model originally proposed to explain the theta-phase precession effect seen in hippocampal place cells (O’Keefe & Recce, 1993; Lengyel, Szatmary, & Erdi, 2003) and recently also documented in entorhinal layer II stellate cells (Hafting, Fyhn, Bonnevie, Moser, & Moser, 2008). The effect consists of action potentials being fired at systematically earlier phases of theta as the animal moves through the cell’s firing field (or fields) so that firing phase reflects the distance travelled through the field (O’Keefe & Recce, 1993; Burgess, Recce, & O’Keefe, 1994; Skaggs, McNaughton, Wilson, & Barnes, 1996; Jensen & Lisman, 2000). The 1-D model assumes the cell’s membrane potential to be the sum of two components: an oscillatory input at a baseline frequency, f_b(t), related to the EEG theta rhythm, and an active membrane potential oscillation (MPO) whose frequency, f_a(t), increases above the baseline frequency as the synaptic input to the cell increases. The synaptic input to the place cell is assumed to be proportional to running speed so that the frequency difference is proportional to running speed, i.e. f_a(t)−f_b(t)= βs(t), where s is speed and β is a constant. In this way, the phase of the MPO relative to the baseline oscillation will be proportional to distance travelled, since phase is the time integral of frequency (see Figure 1a). Evidence consistent with this model includes voltage-dependent intrinsic oscillations in hippocampal pyramidal cells (Kamondi, Acsady, Wang, & Buzsaki, 1998) and place cells whose intrinsic firing frequencies vary with running speed (Geisler, Robbe, Zugaro, Sirota, & Buzsaki, 2007) and with the size of the firing field (Maurer, Vanrhoads, Sutherland, Lipa, & McNaughton, 2005). See (O’Keefe & Burgess, 2005; Burgess et al., 2007; Burgess, 2008) for further discussion.

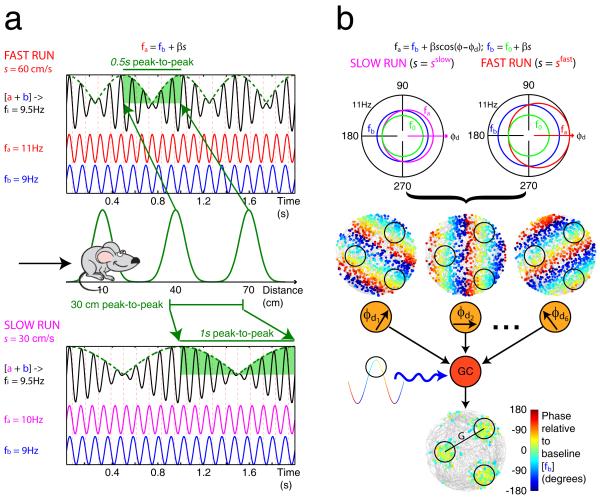
Figure 1.

The oscillatory interference model. a) 1-D model. Two oscillations a (red for fast runs and magenta for slow runs) and b (blue) differ in frequency by an amount proportional to running speed, s(t), so that f_a(t)=f_b(t)+βs(t), where β is a constant. Thus the phase of oscillation a relative to oscillation b varies with distance travelled. When combined, their interference pattern varies in amplitude as they go in and out of phase with each other. The distance between peaks in the interference pattern (where both are in phase) remains constant whether the rat runs fast (above) or slow (below), producing spatially constant firing when the rat runs along a linear track (middle). b) 2-D model. The frequency of a ‘velocity-controlled oscillator’ (f_a(t), red for fast runs and magenta for slow runs) increases above a baseline frequency f_b(t) (blue) by an amount proportional to the component of running velocity in a ‘preferred’ direction, φ_d, so that f_a(t)=f_b(t)+βs(t)cos(φ(t)−φ_d), where φ(t) is the current heading direction (top; NB in this model f_b also increases with running speed: f_b(t)=f₀+βs(t), where f₀ (green) is a common minimum frequency for all oscillations). Thus, the phase of the velocity-controlled oscillator (VCO) relative to the baseline oscillation varies with the distance travelled along its preferred direction, irrespective of the trajectory taken by the rat. The locations of the peaks of a VCO, (dots representing spikes, superimposed on grey line representing the rat’s trajectory) coloured by their phase relative to baseline, as a simulated rat forages in a cylindrical arena (middle). Grid cell firing is generated by combining the inputs from six VCOs (orange circles) with preferred directions (φ_d1 to φ_d6) differing by multiples of 60°. The grid cell (red circle) membrane potential performs leaky integration of its inputs, thus acting as a coincidence detector, and is also modulated by the baseline oscillation (blue wavy line). Spikes are fired at locations where the VCO inputs are sufficiently similar in phase, during the positive phases of the baseline input (black circles; below). The firing of VCO inputs to a layer II grid cell (shown) are assumed to be directionally modulated. See main text and Burgess (2008) for details. Adapted from Burgess (2008).

The 2-D model (Burgess et al., 2007; Burgess, 2008) assumes that grid cells are driven by multiple “velocity controlled oscillators” (VCOs). Each VCO has an MPO frequency, f_a(t), which increases above the baseline frequency, f_b(t), due to depolarization by a synaptic input proportional to the component of movement velocity in a preferred direction φ_d, i.e.:

$$f_a\left(t\right)=f_b\left(t\right)+\beta s\left(t\right)\cos \left(\varphi \right(t)-{\varphi }_d),$$ (3)

where φ(t) and s(t) are the direction and speed of motion and β is a constant. Each VCO corresponds to a different dendritic subunit or afferent cell, see also (Hasselmo, 2008). The phase of a VCO relative to baseline signals distance travelled in the preferred direction. This is because the phase difference between the active and baseline oscillations is the time integral of their frequency difference which is proportional to running speed in the preferred direction, see equation 3.

To ensure that VCOs only increases their frequency in response to excitatory synaptic input indicating speed and direction:

$$f_a\left(s\right(t),\varphi (t),\beta ,{\varphi }_d)=f_0+\beta s\left(t\right)(1+\cos \{\varphi \left(t\right)-{\varphi }_d\left\}\right),$$ (4)

where f₀ is a common minimum frequency for all VCOs when receiving no input (i.e., when speed is zero). The baseline oscillation corresponds to the average frequency of all local VCOs (i.e., the average over all preferred directions <f_a>_φd):

$$f_b\left(s\right(t),\beta )={<f_a>}_{{\varphi }_d}=f_0+\beta s\left(t\right)$$ (5)

A layer II grid cell is assumed to receive inputs from six VCOs with different preferred directions, φ_d, differing by multiples of 60°, and to be driven by those VCOs whose preferred directions are within 90° of the current direction of motion. See Figure 1b and Burgess (2008) for further explanation.

The model predicts that the distance between adjacent grid nodes, G, is proportional to running speed divided by the difference in active and baseline frequencies, and that this will be a fixed value set by β:

$$G=2∕\sqrt{3}\beta .$$ (6)

This follows from the fact that the difference in frequencies is itself proportional to running speed (i.e., G = s(t)/(f_a(t)−f_b(t)) and, from equation 3, f_a(t)−f_b(t) = βs(t)√3/2 when running between adjacent grid nodes, which are 30° offset from the preferred direction of the linear interference patterns, see Figure 1b).

Equation 1 comes from equation 4, substituting for β using equation 6, averaging over the frequencies (f_a) of the local VCO inputs driving grid cell firing (i.e. those with preferred directions within 90° of the current direction of movement) and taking account of their interaction with the baseline frequency input, see (Burgess, 2008). The global average frequency of all VCOs in mEC is identified with the movement-related theta, f_θ(t). This gives equation 2, averaging equation 5 over all values of β which is assumed to decrease dorso-ventrally to produce the observed dorso-ventral increase in grid scale (Hafting et al., 2005; Brun et al., 2008), see equation 6. Thus, <β> is the mean β found throughout the dorso-ventral extent of the mEC.

The appropriate set of directional inputs (i.e., with directions separated by multiples of 60°) is assumed to result from a large-scale self-organising developmental process, since concurrently recorded cells all have grids with the same orientation (Barry, Hayman, Burgess, & Jeffery, 2007). The presence of a velocity-dependent synaptic input is consistent with speed-modulated ‘head-direction’ responses recorded in mEC (Sargolini et al., 2006). Evidence for the model from intra-cellular recording includes the voltage-dependent intrinsic oscillations in medial entorhinal stellate cells (Alonso & Klink, 1993). The frequency of the intrinsic MPO of these cells increases with depolarization, and the slope of this relationship (β, above) decreases with the dorso-ventral location of the slice so as to match the increase in grid scale G, following equation 6, see (Giocomo, Zilli, Fransen, & Hasselmo, 2007; Giocomo & Hasselmo, 2008).

Methods

Animals & surgery

Data from seven male Long Evans rats (animals 1 – 7) and six male Lister Hooded rats (animals 6 – 13; 250-470g at implantation) are reported in this study. Recordings from animals (1-7) have previously been reported in (Fyhn, Hafting, Treves, Moser, & Moser, 2007), and these data were kindly provided by those authors for analysis here. A further three animals were reported in (Barry et al., 2007); complete details of surgery and animal housing can be found therein. Three additional animals (11-13) received mEC microdrives according to the same protocol (Barry et al., 2007). Briefly, in this protocol, each animal received a single microdrive loaded with four tetrodes (Recce & O’Keefe, 1989) of twisted 17-25μm HM-L coated platinum-iridium wire (90% - 10%) (California Fine Wire, USA). Electrodes were implanted above the right dorso-lateral medial entorhinal cortex (mEC), 4.5mm lateral to the midline, 0.2 – 0.5mm anterior to the sinus, angled forwards in the sagittal plane at 8 - 10°, and to a depth of 1.0 – 2.5mm. The most anterior screw on the right side was used as a ground electrode. All experiments were performed in accordance with relevant ethics committee approval and national legislation (e.g., the UK Animal (Scientific Procedures) Act 1986).

Recording and behavioural training

Training and screening was performed post-surgically. Axona recording systems (Axona Ltd., St. Albans, UK) were used to acquire the single unit, EEG, and positional data from all rats. The local field potentials recorded from each of the 16 channels were passed through a RC-coupled, unity-gain operational amplifier mounted on the animal’s head and fed to the recording system using lightweight wires. For single units, each channel was amplified 10,000 to 40,000 times, bandpass filtered (500 Hz – 7 kHz) and recorded differentially against a channel on a separate tetrode. Spikes exceeding a trigger threshold were sampled at 48 kHz (50 samples from each of four channels) and time stamped with a 96 kHz clock signal. A single channel was used to record EEG, the signal was amplified 8,000-20,000 times, band-pass filtered at 0.34 - 125 Hz and sampled at 250 Hz. The position of the rat was captured using an overhead video camera to record the position of the one or two LEDs on the animal’s head-stage amplifier. The image was digitized and sampled at a rate of 50 Hz, to identify the rat’s trajectory, which was smoothed with a 400ms window. Running speed and direction were inferred from the change in position between adjacent time points. Prior to recording, tetrodes were advanced in 50 – 100 μm steps until multiple large-amplitude units were obtained. This process took place in the experimental room while animals remained in an elevated holding area. Animals were returned to their home cage for at least four hours between screening sessions.

Entorhinal activity was recorded while animals foraged in a 100cm × 100cm square enclosure placed centrally on the floor of the experimental room. For animals 1-7 the enclosure was constructed from aluminium while animals 8-13 experienced a Perspex environment, in all cases the walls were 50cm high. Directional information was provided by a clearly visible white cue displayed in a constant location. Before data collection, rats were familiarised with the enclosure over several days. The majority of recording sessions consisted of multiple 20 minute trials, some with the enclosure in different configurations. Rats 1-7, however, experienced 10 minute trials. For the purposes of the present paper, only the data from the first trial of the day, which was always run with the enclosure in a familiar configuration (see Barry et al., 2007), were used. The tetrode movement protocol, spike waveforms and the locations of peak firing were used to ensure that each cell was submitted for analysis once only.

Data analysis

Relationship between EEG theta frequency and running speed

In order to characterise the dynamic relationship between theta frequency and running speed a cycle-by-cycle approach was used to estimate momentary EEG frequencies. The recorded EEG signal was filtered using a 6-12Hz, 251-tap, Blackman windowed, band-pass sinc (sine cardinal) filter. Windowing the filter achieves good stop-band attenuation and small pass-band ripple. An analytic signal was then constructed using the Hilbert transform and takes the form S_a(t_k)= S(t_k)+ iH[S(t_k)], where H specifies the Hilbert transform, S(t_k) is the filtered EEG signal, t_k = kΔ, where k = 1,…,K indexes the time-step and Δ is the inverse of the sampling rate. The phase of the analytic signal φ(t_k) gives the phase of the EEG at t_k and the difference in phase between each time point defines the frequency. Since the EEG sampling rate was five times that of position, instantaneous frequency was averaged over every five consecutive values corresponding to each position sample. Thus, concurrent measurements of speed and EEG theta frequency were produced every 20 ms. Figure 2 shows the mean frequency-speed relationship over all trials.

To quantify the linear relationship between theta frequency and speed in each trial, a regression line was fitted to the data from that trial corresponding to running speeds between 5 cm/s and 30 cm/s. This avoids non-theta behaviours at low speeds, such as rearing chewing and grooming, and very high speeds for which the linearity of the relationship appears to break down, see Figure 2. In this way f₀ (equations 1 and 2) was defined for each trial as the intercept of the regression line, i.e., EEG theta frequency extrapolated to 0cm/s.

Spike sorting & binning

Spike sorting was performed offline using a data analysis suite (Tint, Axona Ltd., St. Albans, UK). Action potentials were assigned to putative cells based on amplitude, waveform and temporal autocorrelation criteria applied elsewhere to entorhinal grid cells and hippocampal place cells (Barry et al., 2007). The animal’s recorded positions and concomitant spikes were binned into a 64 × 64 bin array covering the camera’s field of view; each bin being the equivalent of 8 × 8 pixels, roughly 2 × 2 cm. Unsmoothed rate maps were calculated by dividing the number of spikes assigned to a bin by the cumulative occupancy of the bin. Smoothed rate maps were constructed as follows, the firing rate for bin i was the number of spikes in a 5 × 5 kernel centred on i, divided by the cumulative occupancy of the same bins. A similar approach was used to construct 64 bin directional ratemaps which were then smoothed with a 5 bin kernel.

Gridness, grid scale and grid orientation

Spatial autocorrelograms of unsmoothed rate maps were used to assess the periodicity, regularity and orientation of cells with multiple firing fields, see (Hafting et al., 2005; Sargolini et al., 2006). Specifically the spatial autocorrelogram was defined as:

$$r({\tau }_x,{\tau }_y)=\frac{n\sum \lambda (x,y)\lambda (x-{\tau }_x,y-{\tau }_y)-\sum \lambda (x,y)\sum \lambda (x-{\tau }_x,y-{\tau }_y)}{\sqrt{n\sum \lambda {(x,y)}^2-{\left(\sum \lambda (x,y)\right)}^2}\sqrt{n\sum \lambda {(x-{\tau }_x,y-{\tau }_y)}^2-{\left(\sum \lambda (x-{\tau }_x,y-{\tau }_y)\right)}^2}}$$ (7)

Where r(τ_x, τ_y) is the autocorrelation between bins with spatial offset of τ_x and τ_y. λ(x,y) is the firing rate in bin at (x,y) and n is the number of bins over which the estimate was made. The autocorrelogram was then smoothed with a two dimensional Gaussian kernel of width 2.5 bins. The six peaks surrounding the central peak on the autocorrelogram were considered to be the local maxima closest to, but excluding, the central peak. The extent of each peak was defined as the contiguous set of bins around the peak with a value greater than half the value of the peak bin. The spatial autocorrelograms, constructed from unsmoothed rate maps, were used to estimate the orientation, gridness, and grid scale of each cell, following (Hafting et al., 2005; Sargolini et al., 2006). The orientation of the grid was the angle between a nominal horizontal reference line and an axis defined by the centre of the spatial autocorrelogram and the peak closest to the reference line in an anti-clockwise direction. Grid scale, was the median distance from the central peak to the six surrounding peaks. Gridness, a measure of spatial periodicity, was calculated by first defining a mask of the spatial autocorrelation centred on but excluding the central peak and bounded by a circle passing around the outside edge of the outermost of the six central peaks. Next, this area was rotated in 30° increments up to 150°, and for each rotation the Pearson product moment correlation coefficient was calculated against the un-rotated mask. Gridness was then expressed as the lowest correlation obtained for rotations of 60° and 120° minus the highest correlation obtained at 30°, 90° or 150°. Cells with gridness of 0 or greater were classified as grid cells.

Directionality

The Rayleigh test for non-uniformity of a circular distribution was used to assess the extent to which each cell’s firing was modulated by head direction. Specifically, the test statistic was calculated for each cell’s directional ratemap. A cell was considered to be directional if the test showed a significant departure from circularity at the p=0.05 level; a value that provided good accordance with the experimenter’s judgement.

Spectral analyses

Estimates of the intrinsic firing frequency (f_i) were obtained from the spike-train of each cell during continuous ‘runs’ of at least 0.5s, in which the animal’s speed consistently exceeded 5cm/s. This minimum speed was chosen to exclude non-theta behaviours such as rearing, grooming and chewing.

For analyses of the effect of running speed, fast and slow runs were defined as continuous periods of at least 0.5s, running at a speed between s_min and s_max. For slow runs s_min = 5 cm/s and s_max = s_M; for fast runs s_min = s_M and s_max = ∞, where s_M is the mean of the speeds at which spikes were fired when running at above 5cm/s.

A cell’s intrinsic firing frequency (f_i) was estimated from the power spectrum of its spike train autocorrelogram. The spike-train for each run was used to construct a temporal autocorrelogram (bin width 2 ms), using ‘unbiased’ normalization by the number of bins at each lag. The average autocorrelogram was calculated from the autocorrelograms from each run, weighted by the duration of the run. The average autocorrelogram was truncated to the first 0.5s, zero-padded to 2¹⁶ elements, its power spectrum found, and f_i defined as the frequency of the peak power spectrum between 7 and 11 Hz. See Figure 3.

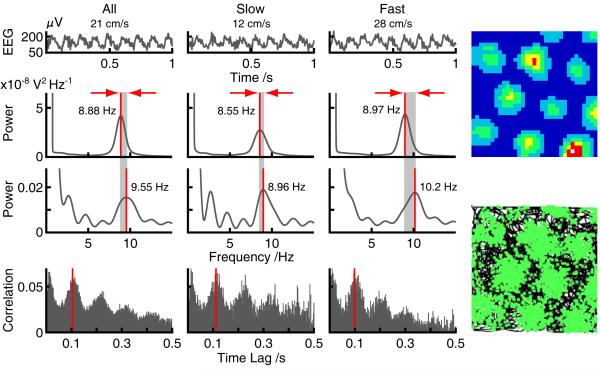
Figure 3.

The temporal characteristics of grid cell firing. Examples of raw EEG (top), EEG power spectra (upper middle), autocorrelogram power spectra (lower middle) and spike-train autocorrelograms (bottom) for all runs above 5cm/s (1st column) and for slow (2nd column) and fast runs (3rd column) for one trial. Right: smoothed grid cell firing rate map (100×100cm environment) (top) and raw traces showing the rat’s path in black and spike locations in green (bottom). Note that, as predicted by the oscillatory interference model, the intrinsic firing frequency exceeds the theta frequency and by a greater amount during fast than slow runs (red arrows and grey shading).

The power spectrum of each cell’s spike-train autocorrelogram was also used to assess the extent to which the cell’s spiking was modulated by theta. Theta modulated cells were defined as those with mean power within 1 Hz of the peak in the 7-11Hz band that was at least 50% greater than the mean spectral power.

The average theta frequency for the runs used in the estimation of intrinsic firing frequency, f_i, was also calculated for comparison. EEG segments corresponding to the runs were concatenated and zero padded to 2¹⁹ elements. Power spectra were constructed by performing a fast Fourier transform (FFT) on the resulting sequence, where the square-modulus of each Fourier frequency coefficient represents the signal power at that frequency. Power spectra were smoothed using a Gaussian kernel with standard deviation 0.2Hz (results were robust to variations in kernel size and shape), and f_θ defined as the frequency of the peak in the power spectrum between 7 and 11 Hz.

Histology

At the end of the experiment all rats received either an overdose of Equithesin (rats 1-7) or Euthatal (rats 8-13) and were transcardially perfused first with phosphate buffered saline and then with 4% paraformaldehyde (PFA) solution. The brains were removed and stored in 4% PFA for at least one week prior to sectioning. 30-40 μm frozen sagittal sections were cut, mounted on gelatine-coated glass slides and stained with crestyl violet. High resolution images were acquired using either an Olympus microscope and Xli digital camera (XL Imaging Ltd.) or Zeiss Axioimager-Z1 microscope and were imported into Photoshop CS2 for PC (Adobe Systems). The depth and layer at which cells were acquired was extrapolated by reference to the record of tetrode movements after taking account of brain shrinkage.

Results

112 grid cells were recorded from 13 rats over 54 trials. All recordings were made while rats foraged in a familiar 1m × 1m square and included robust, concurrent EEG. Histology confirmed that all cells were located in superficial layers (II/III) of dorso-lateral mEC, although it was not always possible to unequivocally distinguish which of those two layers, e.g., when the electrode track closely followed or cut across the layer II/III boundary. Here we focus on the non-directional, theta-modulated grids typical of layer II mEC (Sargolini et al., 2006; Hafting et al., 2008) which the oscillatory interference model was initially proposed to explain. We excluded from our analyses cells that exhibited poor theta modulation (n=42) or showed directional firing (n=20; see Methods for criteria). Finally one trial exhibited an unusually high frequency theta rhythm (>11Hz), which we attribute to non-theta “flutter” generated outside the entorhinal cortex (Nerad & Bilkey, 2005), preventing estimation of f₀. The cells recorded on this trial were also rejected (n=2). In total, 48 putative layer II grid cells from 24 trials were submitted to further analysis.

Our analysis of theta frequency versus running speed revealed a clear monotonic relationship, linear for low speeds and saturating at 30-40cm/s. See Figure 2. Regression on the data in each trial, corresponding to speeds between 5 and 30 cm/s, revealed a mean intercept <f₀> = 8.275Hz and a mean slope <β> = 0.02cm⁻¹, see equation 2. The mean slope calculated in this manner estimates the mean β over all grid cells in the mEC. This mean slope would correspond to a grid scale of 56.5cm, according to equation 6.

Our analysis used power spectra to estimate the mean intrinsic firing frequency of the grids (f_i) over runs conforming to specific behavioural criteria, the mean frequency of the theta oscillations in the EEG for these runs was also calculated for comparison (f_θ). Only runs with duration >=0.5s in which the animals’ velocity did not fall below 5cms/s were considered. Inspection of the data for individual trials reveals that the EEG power spectra consistently show a strong peak in the theta range (7-11Hz; for example see Figure 3), identified as the mean theta frequency (f_θ) for those runs. A similar peak is present in the power spectrum of the spike train autocorrelogram, identified as the intrinsic firing frequency (f_i) for that grid cell during those runs. The intrinsic firing frequency was generally slightly higher than the concurrent theta frequency, and higher in fast runs than for slow runs (see Figure 3).

The mean intrinsic firing frequency of grid cells with small, medium and large grids over fast and slow runs is shown in Figure 4. The predicted value of intrinsic firing frequency was also calculated for each cell, using equation 1, given f₀ from the plot of theta versus speed for each trial, β from the grid scale G via equation 6, and the mean running speed for the runs used. These are also shown in Figure 4, along with the mean theta frequency for the same runs for comparison. To combine data across trials and rats all values are shown relative to the value of f₀ for that trial (the horizontal black line is shown at the mean value of f₀ across trials for conversion into average absolute frequencies), as the absolute value of theta frequency varied somewhat across rats and trials.

The intrinsic firing frequencies, with f₀ subtracted, were entered into a 3×2 ANOVA over grid scale (small, medium, large) and running speed (slow, fast). Intrinsic firing frequency was found to consistently increase with running speed (main effect of running speed: F_1,2=47.72; P=2×10⁻⁸) and to decrease with grid size (main effect of grid size: F_2,45=3.42, P=0.04), with an interaction in the direction of larger speed-related increases for smaller grids which did not reach significance (F_2,45=1.95; P=0.15). The corresponding theta frequencies were entered into a similar analysis and showed a significant effect of running speed (F_1,45=245.26; P=7×10⁻²⁰). Finally, the predicted and actual intrinsic firing frequencies were entered into a 3×2×2 ANOVA over grid scale, speed, and status (predicted, actual). There was no significant main effect of status, reflecting the good overall fit between the model and the data, and a non-significant interaction between status and speed reflecting the better fit for lower speeds (F_1,45=2.89, P=0.096).

Together, these results are consistent with the oscillatory interference model of grid cell firing: intrinsic firing frequency increasing with running speed and decreasing with grid size according to the quantitative prediction of equation 1. They are also consistent with the interpretation that theta frequency reflects the mean frequency of all of the velocity controlled oscillators (VCOs). Thus, theta frequency increases with running speed, but not as fast as the frequencies of the VCOs driving the grid cell firing, see Figure 4, Burgess (2008) and equations 3-5.

Analysis of the Moiré interference model

A related model (Blair et al., 2007) posits the existence of spatial grids of firing on a micro-scale (with firing fields separated by the distance travelled per theta cycle). Superposition of micro-grids with slightly different scale or orientation would produce a spatial (Moiré) interference pattern corresponding to the observed (large-scale) grid firing pattern. Under this model, a grid cell’s intrinsic firing frequency would reflect the rat moving across the spatial micro-structure of the interference pattern. Thus, the Moiré interference model predicts significantly higher intrinsic firing frequencies for runs aligned with the principal axes of the grid than for misaligned runs (by a factor √3 ≈ 1.73), see Figure 5. In contrast, the oscillatory interference model predicts little difference between intrinsic frequency for aligned and mis-aligned runs (see (Burgess, 2008) for further details), other than that caused by any differences in running speed in those directions.

Figure 5 shows grid cells’ intrinsic firing frequency during runs either aligned or mis-aligned with the axes of their grid-like firing pattern. Theta frequency during these runs is also shown for comparison. There was no significant difference in intrinsic firing frequency between aligned versus misaligned runs (t₄₇=0.016, P=0.45). These results are consistent with the oscillatory interference model (predicted frequencies also shown in Figure 5), but not with the Moiré interference model.

Discussion

Grid cell firing and EEG were recorded from the superficial layers of medial entorhinal cortex in freely moving rats. The intrinsic firing frequency for each grid cell during fast and slow runs was estimated, and results combined across trials and rats by subtracting f₀ for each trial (the theta frequency extrapolated to zero speed). The results support the pattern predicted by the oscillatory interference model of grid cell firing (Burgess et al., 2007; Burgess, 2008). Specifically, spectral analyses showed that the intrinsic firing frequency of putative layer II mEC grid cells increases with running speed and decreases with grid scale according to equation 1. In addition, theta frequency increased with running speed at a slower rate than intrinsic frequency, consistent with the interpretation that it reflects the combined frequency of all velocity-controlled oscillators (VCOs) in mEC, while grid cell firing is driven by the local VCOs, whose preferred directions match the current running direction. Dorso-ventral variation in the slope of the local VCO response to depolarisation (β) causes the dorso-ventral variation in grid scale (Hafting et al., 2005; Brun et al., 2008), according to equation 6.

Our results specifically support the ‘directional’ or ‘rectified’ implementation of the model in which only VCOs with frequencies above baseline (i.e. with preferred directions consistent with the current running direction) drive the firing of the grid cell, see equations 3-5 and (Burgess et al., 2007; Burgess, 2008). This implementation is also consistent with the recently observed phase precession in layer II grid cells as the rat runs on a linear track (Hafting et al., 2008), i.e., firing always shifting from later to earlier phases. Thus, for layer II at least, we can reject the implementation in which the VCO inputs driving a grid cell oscillate both above and below the baseline frequency according to the match between the current running direction and the preferred direction, which is also consistent with equation 3, see (Burgess, 2008) for further discussion.

These results also support the interpretation that theta frequency is not an independent variable, but reflects the mean frequency of all of the velocity controlled oscillators. Thus theta frequency increases with running speed, but not as fast as the frequencies of those VCOs driving the grid cell, i.e., those with preferred directions close to the current direction of running, see equations 2-5 and Burgess (2008). This interpretation is consistent with the observation that the movement-related component of theta, but not the atropine-sensistive component, is impaired by lesions of entorhinal cortex (Kramis, Vanderwolf, & Bland, 1975). Of course, the frequency of movement-related theta reflects an interaction between EC, hippocampus and, critically, the medial septum, see (Burgess, 2008; O’Keefe, 2006; Buzsaki, 2002) for further discussion. According to the model, the slope of the relationship between theta frequency and running speed indicates the mean value of β within the mEC, and we observed a value of <β> = 0.0204cm⁻¹ over the range 5 to 30 cm/s, see Figure 2. This corresponds to a median grid scale of 56.5cm, which is close to the small end of the range of observed grid scales (30cm to at least 4m, Brun et al., 2008). If the model of theta as the mean baseline frequency of all grid cells is correct (equations 2 and 5), then the observed value of <β> indicates that there must be proportionately more grid cells with small grids than with large ones, see Burgess (2008). This would be consistent with efficient coding strategies (see e.g., Fiete, Burak, & Brookings, 2008), and with indications that grid scales increases in exponential steps (each grid 1.7 times larger than the last, Barry et al., 2007), but see also (Brun et al., 2008).

Our results are consistent with similar findings in place cells, namely a dependence of intrinsic firing frequency on place field size (Maurer et al., 2005) and running speed (Geisler et al., 2007). They are also consistent with previous findings of a dependence of theta frequency on running speed (Rivas, Gaztelu, & Garcia-Austt, 1996; Slawinska & Kasicki, 1998). Thus our results, and indeed the model’s predictions, are consistent with phase precession in layer II mEC grid cells being a 2D phenomenon. This suggests that Hafting et al.’s (2008) recent characterisation of phase precession in these cells, based on experiments run on a linear track, can likely be extended to 2D; in a similar way as phase precession in place cells was extended from 1D (O’Keefe & Recce, 1993) to 2D (Burgess et al., 1994; Skaggs et al., 1996; Huxter, Senior, Allen, & Csicsvari, 2008).

Our results also raise some questions. i) Does the non-linear relationship between theta frequency and running speed at speeds above 30cm/s (see Figure 2) reflect actual fast movements during the pellet-chasing task rather than resulting from e.g. head-shaking? If so, can equation 3 remain true so that spatially stable grid cell firing would be maintained during these movements, and does such stability exist in the data? The only differences we could find in the data from the London and Trondheim groups, was that theta frequency increased linearly with running speed over a wider range of speeds in the Trondheim data (up to 50cm/s, cf. saturating at around 30cm/s in the London data), and correspondingly slightly higher intrinsic firing rates for ‘fast’ runs. These may reflect differences in behavior or tracking, or of physiology between the Hooded Lister and Long-Evans strains used in London and Tronheim. ii) Do our two components of theta frequency, f₀ and <β>s(t), see equation 2, correspond to the well-known atropine-sensitive, arousal-related, and atropine-resistant, movement-related components (Buzsaki, 2002; O’Keefe, 2006), as suggested by Burgess (2008)? If so, how can other contributions to theta be accommodated, since behavioural variables other than speed contribute to movement-related theta, such as acceleration and preparation for acceleration (Whishaw & Vanderwolf, 1973; Lenck-Santini, Fenton, & Muller, 2008).

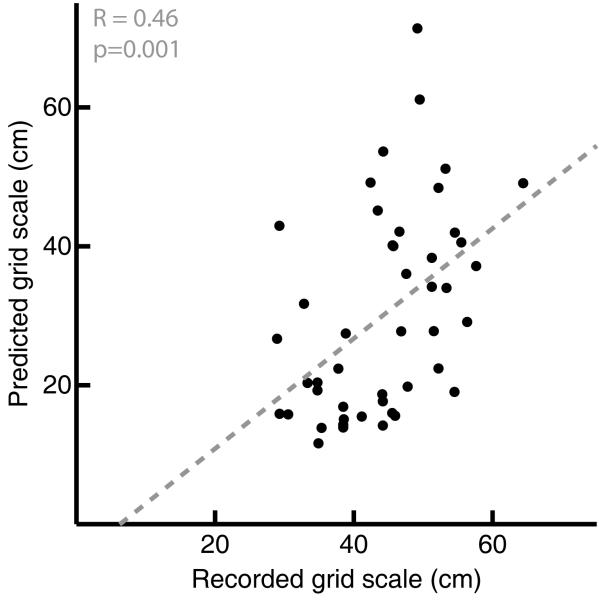
One limitation of our analysis is that we have to categorise behavior rather crudely to produce enough runs of at least 0.5s of behavior continuously within each category to be able to form a robust autocorrelogram for each category. Thus we are restricted to dividing runs into ‘slow’ or ‘fast’, rather than performing more fine-grained analyses. However, we could attempt to predict each grid’s spatial scale from the frequency data in Figure 4 by estimating β as the rate of change in intrinsic frequency with speed and thence estimate grid scale G via equation 6. One problem is that differences between noisy estimates of frequency are even noisier, and inverting them (equation 6) can produce infinite or even negative values for G. We used the three measures of frequency for each cell (f_i for slow and for fast runs, and f₀ which should correspond to f_i at zero speed) to produce three estimates of β (one for each pair of values) for each of the 48 grid cells. We discarded estimated values β corresponding to grid scales more than twice the size of the environment (200cm; of the 3×48=144 estimates of β, 17 below 2/(200√3) were discarded, including 11 below zero). Figure 6 shows the spatial scale predicted from the mean of the 2 or 3 remaining estimates of β for each grid cell (two cells with one or no remaining estimates were discarded, leaving n=46).

Figure 6.

Predicting a grid cell’s spatial scale from the frequency data in Figure 4. For each cell (n=46), β is calculated from rates of change of intrinsic firing frequency with speed, using f₀ and f_i for slow and fast runs (see Discussion), translated into grid scale using equation 6 and plotted on the y-axis against measured grid scale (see Methods). The grey dashed line shows the line of best fit through the data, with a gradient of 0.8 and intercept of −5 (r=0.46, p=0.001).

The measures of intrinsic frequency are clearly highly variable, but, outlying values excluded, it is possible to make a reasonable prediction of grid scale from these frequencies (r=0.46, p=0.001). It is not clear to what extent this variability reflects measurement error, ‘real’ neuronal noise, the problems of averaging over relatively crude categories of behavior, or departures of grid cell firing from the model. See Hasselmo (2008) for discussion of noisy membrane potential oscillation frequencies in vitro, an alternative mechanisms for regular spiking. There are also undoubtedly influences on grid scale other than the oscillatory interference path integration mechanism proposed for mEC. Sensory environmental information must provide a spatial reset to any path integration mechanism to avoid the accumulation of error. We have proposed that, in familiar environments, this takes the form of a phase-resetting input from place cells via synaptic connections that form between place cells and grid cells with overlapping firing fields (O’Keefe & Burgess, 2005; Burgess et al., 2007). See Burgess et al (2007) for simulation of correction of path integration by phase-resetting within the oscillatory interference model. In support of this proposal, deformation of the boundary of a familiar environment deforms the spatial firing pattern of grid cells (Barry et al., 2007) in a manner consistent with the deformation of the spatial firing pattern of place cells under this manipulation (O’Keefe & Burgess, 1996).

Future progress will require the development of more sophisticated analyses, of experimental paradigms capable of manipulating the frequencies of the relevant oscillators, and of the model itself. One limitation of the current model, is that it is a single-cell model. While this is a good place to start, and has advantages of simplicity, we do not doubt the presence of network properties, e.g., in generating theta, or in the clustering of grid orientations and scales (Barry et al., 2006). The role of interconnectivity between grid cells is the focus of the alternative, attractor, models of grid cell firing (McNaughton et al., 2006; Fuhs & Touretzky, 2006). The oscillatory interference model may be complementary to these models, in that it might provide the initial firing pattern required to allow the formation of appropriate recurrent connectivity to stabilise grids relative to other grids (McNaughton et al., 2006; Fuhs & Touretzky, 2006) or relative to the environment (via connectivity with place cells: Burgess et al., 2007). A related limitation of the model of theta is that it does not include critical systems-level interactions with the medial septum or hippocampus. See Burgess (2008) and (Blair, Kishan, & Zhang, 2008) for further discussion.

We cannot say whether or not our results uniquely support the oscillatory interference model, as other models do not offer testable predictions for the variables we have measured to either verify or falsify. However, we can say that the oscillatory interference model has been uniquely useful in driving forward the experimental program reported here, as it did that reported by (Giocomo et al., 2007).

In conclusion, the oscillatory interference model correctly predicts the intrinsic firing frequency of grid cells across relatively coarse categorizations of running speed and grid scale. More generally, our findings support a novel model of neuronal processing, and theta, based on interfering oscillatory processes, extending results in hippocampus (O’Keefe & Recce, 1993; Lengyel et al., 2003; Maurer et al., 2005; Geisler et al., 2007) to entorhinal neocortex.