Eddies in a Bottleneck: An Arbitrary Debye Length Theory for Capillary Electroosmosis

Abstract

Using an applied electrical field to drive fluid flows becomes desirable as channels become smaller. Although most discussions of electroosmosis treat the case of thin Debye layers, here electroosmotic flow (EOF) through a constricted cylinder is presented for arbitrary Debye lengths (κ⁻¹) using a long wavelength perturbation of the cylinder radius. The analysis uses the approximation of small potentials. The varying diameter of the cylinder produces radially and axially varying effective electric fields, as well as an induced pressure gradient. We predict the existence of eddies for certain constricted geometries and propose the possibility of electrokinetic trapping in these regions. We also present a leading-order criterion which predicts central eddies in very narrow constrictions at the scale of the Debye length. Eddies can be found both in the center of the channel and along the perimeter, and the presence of the eddies is a consequence of the induced pressure gradient that accompanies electrically driven flow into a narrow constriction.

Many techniques for particle characterization involve passing a particle through a constriction or aperture using various driving forces and detection methods. In the first practical and successful modern instrument for counting and analyzing cells, the Coulter Counter, a single aperture separates two reservoirs of ionic solution where the cells from one reservoir are driven into a second reservoir by hydrostatic pressure or an electrical field; the resulting change in the aperture’s electrical conductivity is used to count and analyze the cells [1]. With fabrication technologies used in Micro-Electro-Mechanical-Systems, miniaturization of such instruments into microfluidic devices is possible. Unlike traditional fluidics in which volumes of fluids are usually driven through channels using pressure gradients, in microfluidic (and increasingly nanofluidic) systems a new set of engineering challenges arise for the integration and quantitative understanding of essential components such as mixers, pumps, sensors, or reactors. To address some of these challenges, many have pointed to microfluidic flows driven by electrokinetics, e.g., electroosmosis.

Electroosmotic flow (EOF), or the flow of solvent with respect to a charged surface in the presence of an applied electric field, offers many advantages for microfluidic environments and has been the subject of many investigations (e.g., see [2, 3]). In addition to the classical discussions and applications in colloid and interface science [4], EOF has recently been investigated for use as a microchannel mixer [5, 6], in binding enhancement between a biological pore and a biological molecule [7], as an artificial synaptic transmitter [8], and as an electrokinetic battery [9]. The revival of the study of EOF, a classic electrokinetic phenomenon, is directly related to the increasing importance of microfluidic devices through which laminar low-Reynolds-number flows dominate [10].

The best known aspect of EOF is a uniform velocity distribution outside of the thin charged layer adjacent to the channel boundary. While a uniform flow velocity profile throughout most of the channel width is often advantageous, non-uniform velocity distributions are needed for integrated fluidic devices and many have gone to great lengths to achieve unusual EOF velocity profiles. It is known, for example, that surface charge variations can give rise to recirculating flows [6, 11, 12, 13, 14, 15, 16, 17]. Non-uniform charge distributions can be imposed by patterned adsorption of differently charged molecules [17], or induced on polarizable (often metal) electrode surfaces by applying uniform or non-uniform applied electric fields [18, 19, 20, 21]. It is also known theoretically that transverse electroosmotic flows in slab geometries are possible [22] where an induced pressure gradient along the direction normal to the applied electrical field leads to a transverse recirculation of the fluid. In addition, recent studies have shown that recirculating flows can be produced with AC fields near the surfaces of externally controlled electrode arrays ([23, 24]). Obviously, the controlled generation of eddies has been studied in many contexts. Unlike these known cases of eddy formation that result from surface heterogeneities, we show that an ordinary constriction in a homogeneous surface can, surprisingly, give rise to eddies in EOF. Hence, a simply fabricated geometric variation can produce recirculating eddies in a system that is characterized elsewhere by the uniform laminar flow usually seen in EOF. Our work thus complements two other recent demonstrations of eddies in channel-like configurations: Thamida and Chang [25] describe an “electrokinetic jet” in the neighborhood of a sharp corner and Bazant and Squires [18] illustrate eddies due to induced-charge electro-osmosis about a conducting cylinder in a confined channel. We also address the increasingly important study of EOF in nanoscale fluidic devices, such as a nanopore [26], with an EOF theory that can be applied to arbitrary Debye lengths. We provide an explicit calculation that predicts eddies in the center and perimeter of a channel based on variations of the wavelength and amplitude of channel radius and Debye length.

In most theoretical approaches to EOF, the Debye screening length κ⁻¹ is assumed to be much smaller than the mean tube radius a₀, and there is an effective slip velocity, μ_EE along the surface, where μ_E is the electroosmotic mobility, which is proportional to the surface charge density σ or the zeta (ζ) potential, and E is the applied external electric field. If there is no applied pressure, and the solution and surface properties are uniform and constant (e.g., μ_E = constant), then it can be shown that the fluid velocity at any position x is everywhere proportional to the electric field, i.e., u(x) = μ_EE(x). The pressure distribution then remains constant and unaffected by E since both fields (u and E) are incompressible. Nevertheless, there are situations in which this collinearity of u and E no longer holds. For example, when the electroosmotic mobility μ_E is no longer constant, as is the case when the surface charge density varies, then we expect that the pressure distribution is affected by the applied field [11]. Also, the influence of finite permittivity of the channel boundaries, which gives rise to a small normal component of the electric field at the wall, has been argued to produce pressure gradients in EOF that lead to eddies [20].

It might be expected then that perturbations such as a radial shape variation or a finite, non-negligible Debye layer thickness may disrupt the perfect alignment of u and E. Here, we analyze EOF in an axisymmetric, constricted geometry, e.g., a bottleneck or hourglass shape for arbitrary Debye lengths. We assume that there is a constant surface charge density along the channel. Even in the absence of an applied pressure difference, there is an induced pressure gradient that arises in this constricted geometry when an external electric field E is applied. This induced pressure gradient is a combination of resistive and osmotic pressure effects. The resistive pressure gradient is due to the physical constriction opposing the fluid flow. The osmotic component arises because both the equilibrium surface electrostatic potential, and an “excess” electric potential due to EOF, maintain an ion concentration gradient normal to the surface. As a consequence of this induced pressure gradient, we find eddies in certain constricted geometries without any variation of surface charge densities. We utilize a perturbation expansion method in the field strength and go beyond the usual lubrication approximation to more fully represent the effects of the geometric variations.

Theory

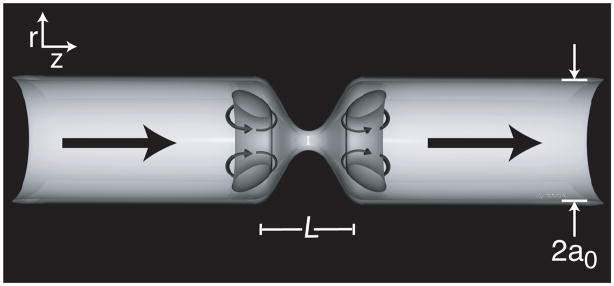
We consider cylindrical geometries and so utilize a cylindrical (r, z) coordinate system as defined in Fig. 1. We assume a constant surface charge density σ along the channel and a constant applied potential difference V across a distance L representative of the constriction (see Fig. 1). The radius of the channel which varies along the z-axis, is denoted a(z), and the invariant radius or the channel, away from the constricted region, is a₀. The usual discussion of electroosmosis assumes that the equilibrium ion distribution is unperturbed by the applied electric field E and, conversely, that the applied electric field is unperturbed by the ion distribution. For infinitely thin double layers, the slip velocity is then proportional to the electric field. But for arbitrary double layer thickness in a cylinder with radial shape variations, however, the changes in the applied field can significantly perturb the charge distribution, as we calculate below. At steady state, we can write the mass conservation equation for the ith ion species as [27]

Figure 1.

Schematic of an axisymmetric cylinder with radial shape variation viewed as a cross-section along the Z-axis. The “perimeter” eddy paths – discussed in the Results and Discussion section – are mapped out in grey with the direction of the eddies indicated by the curved arrows. The larger arrows indicate the overall direction of EOF. The perturbation wavelength is L and the invariant radius of the channel away from the constriction region is a₀.

$$\nabla ·[n^i\mathbf{v}-{\omega }^i(k_{B}T\nabla n^i+{ez}_i{n}^i\nabla \phi )]=0,$$ (1)

where ωⁱ denotes the ion mobility, ez_i is the charge on an ion, nⁱ the number density of the ith ionic species ( ${\rho }_e={\sum }_{i=1}^m{ez}_i{n}^i$), and φ is the total electric potential. The first term on the left-hand side is due to the ion convection with the fluid velocity v, and the second and third terms are relative motion of the ions due to thermal diffusion and electric forces, respectively.

Because we allow for the coupling between the electric field E and the ion distribution, the ensuing governing equations become prohibitively complicated. To tackle this complication, we will follow the formalism of Saville [27] and Sherwood and Stone [28] and write a perturbation expansion — of the fluid velocity v, electric potential φ, the number density of the ith ion species nⁱ, and therefore the charge density ρ_e — in the dimensionless field strength β = eV/k_BT. It is most common to study the low-field limit, i.e., β < 1, i.e., we assume

$$\{\mathbf{v},\phi ,n^i,{\rho }_e\}=\{\mathbf{0},{\phi }_0,n_0^i,{\rho }_0\}+\beta \{\mathbf{u},{\phi }_1,n_1^i,{\rho }_1\}+\cdots$$ (2)

where we have used the set notation and each variable can be written out independently, e.g., φ = φ₀ + βφ₁ + ···. The subscript 0 refers to an equilibrium quantity in the absence of the applied field, and the subscript 1 refers to a perturbation due to the applied field from that quantity. We recognize at the outset that the applied electric field, though often small in uniform sections, can be large in constrictions, and so the approximation of β < 1 cannot be quantitatively accurate in all cases, but we believe that it captures the most essential qualitative features, as shown below.

Using the continuity equation for the fluid motion (∇ · v = 0), and assuming small equilibrium electric potentials and small Péclet numbers (i.e., ion convection negligible compared to thermal motion, Pe = u_ca₀/(ωⁱk_BT) ≪ 1 where u_c is a characteristic speed of the motion), Eq. 1 can be written

$$0=\nabla ·\left(k_{B}T\nabla n_0^i+{ez}_i{n}_0^i\nabla {\phi }_0\right).$$ (3)

This equilibrium result provides a Boltzmann distribution of ions, $n_0^i=n_{\infty }^{i}exp(-{ez}_i{\phi }_0/k_{B}T)$, and via Gauss’s law (∇ · E = ρ_e/ε, where ε is the dielectric constant of the solution) leads to the usual Poisson-Boltzmann equation, or the Debye-Hückel equation with the approximation of small equilibrium electrostatic potentials [4], i.e., |ez_iφ₀/k_BT| ≪ 1 so that ∇²φ₀ = κ²φ₀, where ${\kappa }^2={\sum }_{i=1}^m{e}^2{z}_i^2{n}_{\infty }^i/(\epsilon k_{B}T)$. As usual, κ⁻¹ represents the Debye screening length and ρ₀ = −εκ²φ₀. With an applied electric field, i.e., taking terms of order of the dimensionless field strength ( 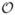(β)), the ion-transport equation (Eq. 1) in the small Péclet number limit becomes

$$0={ez}_i{n}_0^i{\nabla }^2{\phi }_1+{ez}_i{n}_1^i{\nabla }^2{\phi }_0+k_{B}T{\nabla }^2{n}_1^i.$$ (4)

We note that the Péclet number is proportional to the transverse dimension of the channel and so the small Péclet number approximation becomes even better as the channel dimensions are reduced (as is common in lubrication calculations, a refined analysis would introduce a further aspect ratio, a₀/L, where a₀ is the tube radius and L is a typical axial dimension, in an improved definition of the Péclet number). Consistent with the small equilibrium potential approximation, the second term on the right-hand side of Eq. 4 can be neglected relative to the third term. So we multiply Eq. 4 by ez_i/k_BT and sum over i to obtain

$${\nabla }^2{\phi }_1+{\nabla }^2\frac{{\rho }_1}{{\kappa }^2\epsilon }=0$$ (5)

or ∇²χ = 0, where χ = φ₁ + ρ₁/(κ²ε) now plays the role of the effective applied electric potential.

Using the above results, the total electrical body force on the fluid ρ_eE = −ρ_e∇φ can be expanded to give

$${\rho }_e\nabla \phi \approx -\nabla \left(\frac{1}{2}\epsilon {\kappa }^2{\phi }_0^2-\beta {\rho }_1{\phi }_0\right)+{\rho }_0\beta \nabla \left({\phi }_1+\frac{{\rho }_1}{\epsilon {\kappa }^2}\right)+\cdots$$ (6)

This result can be substituted into the Navier-Stokes equation (−∇p + η∇²v+ ρ_eE = 0, where η is the fluid viscosity) which describes the momentum transport in the fluid. Writing only the terms of order β, i.e., only the terms that arise due to EOF, we obtain

$$\mathbf{0}=-\nabla \mathrm{\Pi }+\eta {\nabla }^2\mathbf{u}+\epsilon {\kappa }^2{\phi }_0\nabla \chi$$ (7)

where the total pressure p = p₀ + βΠ + … and $p_0=-\epsilon {\kappa }^2{\phi }_0^2$ is the equilibrium osmotic pressure that results in the absence of hydrostatic pressure.

The above equation can be made dimensionless and we specifically consider the case with radius a(z) and the radius at the invariant portion of channel a₀. Thus we define the dimensionless radius A(Z) = a(z)/a₀, radial coordinate R = r/a₀, axial coordinate Z = z/L, induced pressure Π̂ = Π/(κσV), electrostatic potential φ̂₀ = εκφ₀/σ, effective applied electric potential χ̂ = χ/V, and axial velocity $U_Z=u_z\eta L/(\kappa \sigma V{a}_0^2)$. The volume flux $Q=2\pi {\int }_0^{a(z)}{u}_z\mathit{rdr}$ is made dimensionless according to $\widehat{Q}=Q\eta L/(\kappa a_0^4\sigma V)$. We next wish to treat explicitly geometric variations in shape and so introduce the aspect ratio δ ≡ a₀/L, which represents the magnitude of the assumed slow variations, |da/dz| ≪ 1. The applied electric potential has boundary condition, χ̂ → 0 at Z → 0 and χ̂ → 1 at Z → 1, the pressure boundary condition, Π̂ → 0 at Z → 0, 1, and the radial velocity U_R → 0 at Z → 0, 1. With Eq. 7, the fluid continuity equation ∇ · u = 0, and the above boundary conditions, Π̂, U_R, and U_Z can be determined using the lubrication (or the long wavelength, i.e., δ ≪ 1) approximation, e.g., [14, 22], though here we retain more of the geometric complexity by working beyond the leading-order terms.

We can expand the variables, defined above, perturbatively in δ,

$$\{U_Z,U_R,\widehat{\mathrm{\Pi }},\widehat{\chi },{\widehat{\phi }}_0,\widehat{Q}\}=\{U_{Z,0},U_{R,0},{\widehat{\mathrm{\Pi }}}_0,{\widehat{\chi }}_0,{\widehat{\phi }}_0^{(0)},{\widehat{Q}}_0\}+{\delta }^2\{U_{Z,2},U_{R,2},{\widehat{\mathrm{\Pi }}}_2,{\widehat{\chi }}_2,{\widehat{\phi }}_0^{(2)},{\widehat{Q}}_2\}+\cdots$$ (8)

where we have again used the set notation. Note that odd-powered terms in δ disappear and only the even-powered terms remain.

We first find the electrical components, φ̂₀ and χ̂, which can be determined from the Debye-Hückel equation and boundary conditions, and then solve for the dimensionless velocity field U. The Debye-Hückel equation for φ̂₀(R, Z; δ),

$$\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial {\widehat{\phi }}_0}{\partial R}\right)+{\delta }^2\frac{{\partial }^2{\widehat{\phi }}_0}{\partial Z^2}=k^2{\widehat{\phi }}_0,$$ (9)

where k ≡ κa₀, can also be written as an expansion in δ². The constant surface charge density boundary condition states that ${\frac{\partial {\widehat{\phi }}_0^{(0)}}{\partial R}|}_{R=A(Z)}=k$ and ${\mathbf{n}·\nabla {\widehat{\phi }}_0^{(j>0)}|}_{R=A(Z)}=0$, where n is the unit outward normal to the surface, for which the solution to (δ²) is

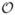$${\widehat{\phi }}_0(R,Z;\delta )=\frac{I_0(kR)}{I_1(kA)}+{\delta }^2[B_1{I}_0(kR)+B_2{RI}_1(kR)]+\mathcal{O}({\delta }^4)+\cdots$$ (10)

where, through Eq. 9 and the boundary conditions, B₁ and B₂ are found to be

$$B_1=\frac{{AI}_0(kA)}{2{kI}_1(kA)}\frac{d^2}{{dZ}^2}\left[\frac{1}{I_1(kA)}\right]+\frac{A^{\prime }{I}_0(kA)}{{kI}_1(kA)}\frac{d}{dZ}\left[\frac{1}{I_1(kA)}\right]+\frac{{A^{\prime }}^2}{2I_1(kA)}$$ (11a)

$$B_2=-\frac{1}{2k}\frac{d^2}{{dZ}^2}\left[\frac{1}{I_1(kA)}\right].$$ (11b)

From Eq. 5, i.e., ∇²χ̂ = 0, and the condition that the surface is impermeable to the ions, i.e., n · χ̂ = 0, the effective electric field in the Z-direction is then

$$\frac{\partial \widehat{\chi }}{\partial Z}=\frac{b_0}{A^2}\left\{1+{\delta }^2\left[\frac{(3{A^{\prime }}^2-A^{″}A)(A^2-2R^2)}{4A^2}\right]+\dots \right\}$$ (12)

where A′ = dA/dZ, A″ = d²A/dZ², and b₀ is a constant.

In order to complete the solution, we find it convenient to work in terms of average quantities. For example, the average potential difference is,

$${\int }_0^1\langle \frac{\partial \widehat{\chi }}{\partial Z}\rangle dZ\equiv {\int }_0^1\left[\frac{2}{A^2}{\int }_0^A\frac{\partial \widehat{\chi }}{\partial Z}\mathit{RdR}\right]dZ=1,$$ (13)

which, using Eq. 12, defines the integration constant $b_0={[{\int }_0^{1}dZ/A^2]}^{-1}$, which involves the entire shape variations.

We can substitute Eqs. 10 and 12 into the Navier-Stokes equation (Eq. 7) and separate the R-and Z-components:

$$-\frac{\partial \widehat{\mathrm{\Pi }}}{\partial R}+{\delta }^2\frac{\partial }{\partial R}\left[\frac{1}{R}\frac{\partial }{\partial R}({RU}_R)\right]+{\delta }^4\frac{{\partial }^2{U}_R}{\partial Z^2}+{\widehat{\phi }}_0\frac{\partial \widehat{\chi }}{\partial R}+\cdots =0$$ (14)

$$-\frac{\partial \widehat{\mathrm{\Pi }}}{\partial Z}+\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial U_Z}{\partial R}\right)+{\delta }^2\frac{{\partial }^2{U}_Z}{\partial Z^2}+{\widehat{\phi }}_0\frac{\partial \widehat{\chi }}{\partial Z}+\cdots =0$$ (15)

which can be further separated into terms of the same order in δ².

The leading-order term in Eq. 14 implies an R-independent Π̂₀, and therefore the leading-order term in Eq. 15 can be integrated with respect to R (and the integration constant is determined by imposing the no-slip condition) to yield

$$U_{Z,0}(R,Z)=\frac{1}{4}\frac{\partial {\widehat{\mathrm{\Pi }}}_0}{\partial Z}(R^2-A^2)-\frac{b_0}{k^2{A}^2}\left[\frac{I_0(kR)-I_0(kA)}{I_1(kA)}\right]$$ (16)

where A(Z) brings in the shape variation and k ≡ κa₀. Eq. 16 is the solution to the usual pressure- and electrically-driven flow in a locally cylindrically geometry [2], though here it is applicable at leading order in A(Z).

With the pressure boundary condition imposed in the form ${\int }_0^1\langle \frac{\partial \widehat{\mathrm{\Pi }}}{\partial Z}\rangle dZ=0$, where $\langle \partial \widehat{\mathrm{\Pi }}/dZ\rangle =(2/A^2){\int }_0^A(\partial \widehat{\mathrm{\Pi }}/dZ)\mathit{RdR}$, the volume flux, and the induced pressure gradient can be calculated

$${\widehat{Q}}_0=\frac{2\pi b_0}{k^2{\int }_0^{1}dZ/A^4}{\int }_0^1\left[\frac{I_0(kA)}{2A^4{I}_1(kA)}-\frac{1}{{kA}^5}\right]dZ$$ (17)

$$\frac{d{\widehat{\mathrm{\Pi }}}_0}{dZ}=-\frac{8{\widehat{Q}}_0}{\pi A^4}+\frac{16b_0}{k^2{A}^4}\left[\frac{I_0(kA)}{2I_1(kA)}-\frac{1}{kA}\right].$$ (18)

The above equations are substituted into Eq. 16 to obtain the axial velocity distribution, which for R = 0, reduces to

$$U_{Z,0}(0,Z)=\frac{2{\widehat{Q}}_0}{\pi A^2}-\frac{4b_0}{k^2{A}^2}\left[\frac{I_0(kA)}{2I_1(kA)}-\frac{1}{kA}\right]+\frac{b_0}{k^2{A}^2}\left[\frac{(I_0(kA)-1)}{I_1(kA)}\right].$$ (19)

In the next section we will show that the leading-order velocity field (Eq. 16) can change sign and that reversal in sign of the velocity at R = 0, U_Z,0(0, Z), is indicative of eddies in the center of the channel.

To proceed to higher order in the shape variations, the 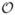(δ²) term in Eq. 14 can be integrated using the continuity equation ([∂(RU_R,0)/∂R] = −R(∂U_Z,0/∂Z)). The Z-derivative of the result can be substituted into Eq. 15 along with the boundary condition U_Z,2(R = A) = 0, and the pressure boundary condition is then used to obtain U_Z,2. The details are straightforward but laborious and are not reported here, but are used in the calculations below. We expect the perturbation expansion, which is in powers of δ², to be a good representation of the physical situation since retaining just two terms has errors of 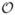(δ⁴).

Results and Discussion

To illustrate the basic effect of a geometric constriction in EOF, we take a cylinder that has a sinusoidal perturbation in channel radius (see Fig. 1), i.e.,

$$A(Z)=\alpha cos(2\pi Z)+(1-\alpha ),$$ (20)

where α is the amplitude (0 ≤ α < 1/2) and 0 ≤ Z ≤ 1. The geometry is thus characterized by a dimensionless wavenumber (or aspect ratio) δ and amplitude α. The axial velocity U_Z, the induced pressure gradient (∂Π̂/∂Z), and the electrical body force, which in dimensionless terms is φ̂₀(∂χ̂/∂Z), can be calculated analytically. We expect that as the amplitude α and the wavenumber δ change, both the induced pressure gradient and the effective electrical body force, as well as the velocity distribution, will be affected. The magnitudes of each will depend on the dimensionless Debye parameter k ≡ κa₀. Note that below we consider values of δ as large as 0.4–0.5, which may be considered large for the lubrication approximation, but the expansion is developed in powers of δ² with an error 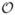(δ⁴) which is then expected to be 2.5–6.3%. In this long wavelength approximation, the amplitude α of the constriction can have any value.

There are two effects that arise from the presence of the constriction in the channel. One is that there is an induced pressure gradient due to the geometric resistance to flow at the constriction. This resistance decreases the flow rate and alters the uniform EOF profile to that similar to pressure- and electrically-driven flows in a straight uniform channels, where an applied pressure flow can oppose the electrically-driven flow. This effect can be seen in the leading-order velocity expression (Eq. 16). The second effect is from the redistribution of ions from the static equilibrium ion distribution due to flow through the constricted geometry, and arises at 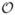(δ²) through the χ̂ term.

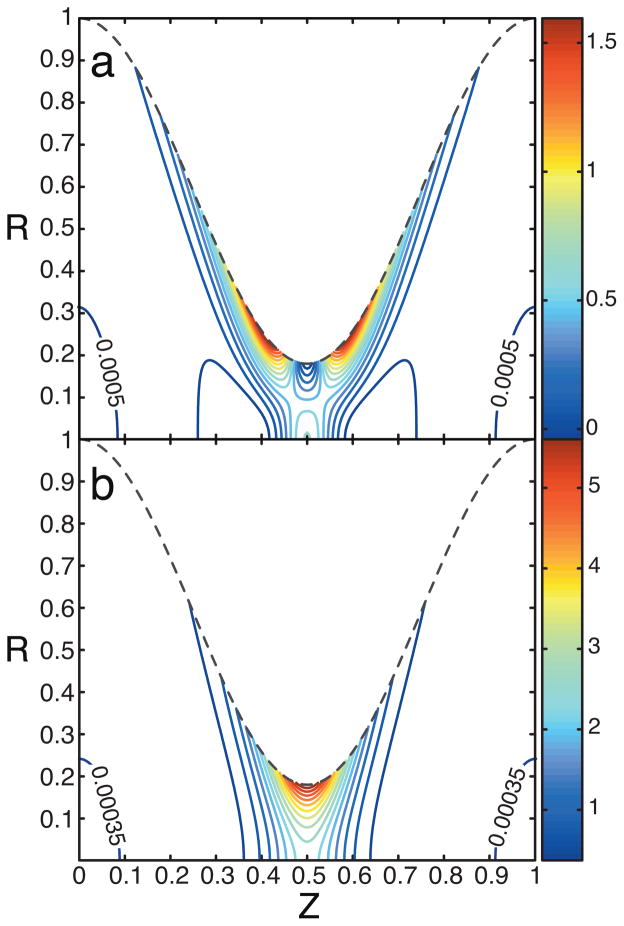
These effects can be illustrated with plots of the dimensionless induced pressure gradient ∂Π̂/∂Z and the dimensionless electrical body force φ̂₀∂χ̂/∂Z. In Fig. 2 we report these quantities for δ = 0.4, α = 0.41, and κa₀ ≡ k = 10. Here δ and α are large, and k is small enough (i.e., the Debye length is large enough), so that the dimensionless induced pressure gradient is comparable to the electrical body force.

Figure 2.

(a): the dimensionless induced pressure gradient (∂Π̂/∂Z) and (b): the electrical body force φ̂₀(∂χ̂/∂Z) for δ = 0.4, α = 0.41, and k ≡·κa₀ = 10. Dashed lines show the outline of the constricted channel where R is the dimensionless radius and Z the dimensionless axial distance. Note that R = 0 corresponds to the center of the channel. The color bars next to the contour plots show the magnitudes of these force densities. Extra contours with the corresponding numerical values are plotted near Z = 0.1 and 0.9 for both a and b to show the central region in which the pressure gradient is larger than the electrical body force.

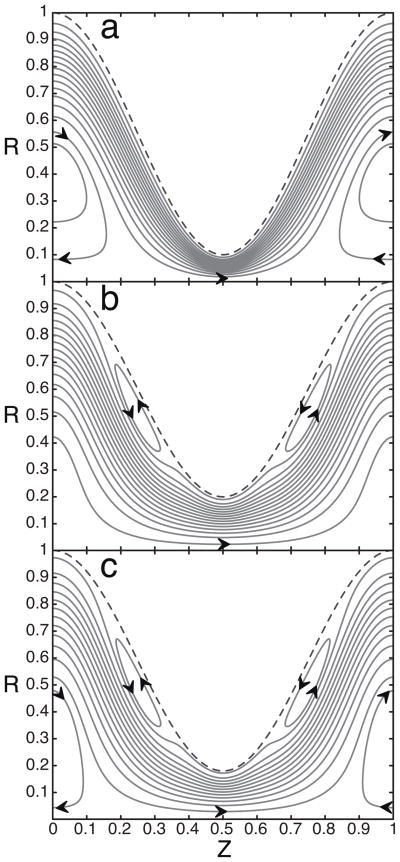
The result of the competition between these two force densities is illustrated in Fig. 3 where streamlines are plotted for various α and δ values for k = 10, each of which shows eddies either at the center and/or near the boundary of the channel. If the induced pressure gradient is larger than the electrical body force near the center of the channel, then a reversal of flow is expected in this region, similar to combined pressure- and electrically-driven flows in straight channels [2]. For example, for Z ≤ 0.1 and Z ≥ 0.9, the pressure gradient dΠ̂/dZ is larger in magnitude than the electrical body force φ̂₀(∂χ̂/∂Z) at R = 0 (Fig. 2). There exists then a recirculating “central” eddy in this region (Fig. 3a). The direction of the resulting recirculation should be counter to the net flow direction near the center and aligned with the net flow direction near the surfaces. Because the induced pressure gradient must disappear in the unperturbed portion of the channel, the size of this central recirculating eddy must roughly correspond to the size of the perturbation wavelength.

Figure 3.

Streamlines for k = 10, and (a): δ = 0.2, α = 0.45 showing “central” eddies; (b): δ = 0.4, α = 0.4 showing “perimeter” eddies; and (c): δ = 0.4, α = 0.41 showing “central” and “perimeter” eddies. Dashed line shows the outline of the constricted channel and the arrows indicate the flow direction. A scan in the thin region along the surface of the channel in a showed absence of “perimeter” eddies and a scan in the empty region towards the center in b revealed an absence of “central” eddies.

On the other hand, as shown in Fig. 2, near the surface R ≈ A, and for 0.25 ≤ Z ≤ 0.4 and 0.6 ≤ Z ≤ 0.75, the pressure gradient is also comparable or larger in magnitude than the electrical body force. Then, the local flow will oppose the net flow direction and there exists a recirculating “perimeter” eddy in this region as can be seen in Fig. 3b. The size of such a perimeter eddy should correspond to the size of the region with the largest induced osmotic pressure distribution. Further, if the pressure gradient is large enough in both regions, then we should see both types of eddies as in Fig. 3c.

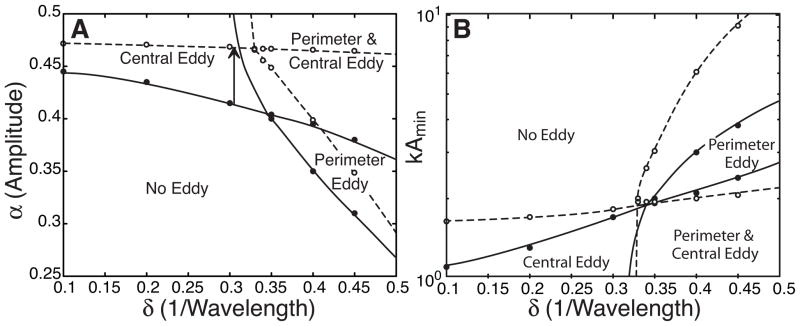
A phase diagram summarizing the existence of both central and perimeter eddies as a function of the amplitude (α) and the wavenumber (δ) parameters is plotted in Fig. 4 for k = 10 and 30. As the arrow in Fig. 4 indicates, the parameter regimes containing eddies decrease in size as k increases (i.e., as the Debye layer becomes thinner).

Figure 4.

Eddy “phase” diagram (A) for various amplitudes α and aspect ratios (inverse perturbation wavelength) δ for k = 10 solid lines and k = 30 dashed lines. (B) shows the same diagram in terms of kA_min and δ. The circles are the calculated boundary points and the lines (solid for k = 10 and dashed for k = 30) represent approximate boundary lines. The diagram shows four regions: with perimeter eddies, with central eddies, both eddy types, and no eddies (unidirectional flow). The arrow indicates the shift in α and δ values needed to observe eddies for the larger k value.

Since the central eddies are predominantly due to the leading-order induced pressure term, we can evaluate the leading-order force densities and obtain a criterion for one aspect of eddy formation. Using Eqs. 17 and 18, the volume flux can be estimated for kA ≥ 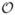(1) as Q̂₀ ≈ (πb₀/k²)[1 − 2/(kA_min)], where A_min = (1 − 2α) is the minimum channel radius for the specific shape given by Eq. 20, which leads to dΠ̂₀/dZ ≈ (16b₀/k³A⁴)(1/A_min − 1/A). This force density should be larger than the maximum electrical body force (i.e., b₀/A²) to obtain an estimate for a “central eddy criterion”:

$$\frac{16}{k^3{A}^3}\left[\frac{A}{A_{min}}-1\right]>1$$ (21)

The left-hand term has a maximum for A = (3/2)A_min. The typical minimum constriction radius $A_{min}^{\ast }$ that meets the central eddy criterion is then

$$k(1-2\alpha )\equiv {kA}_{min}^{\ast }<\frac{4}{3},$$ (22)

which states that as the Debye length decreases, i.e., as k increases, the constriction radius must decrease to obtain a central eddy. Since this is a leading-order estimate, it only involves the constriction amplitude, and not the perturbation wavelength. Hence, only the central eddies are present in Fig. 4 for small values of δ. We note that the prediction Eq. 22 is in good agreement with the results in Fig. 3, e.g., for k = 10, we predict central eddies when α > 0.43 and for k = 30, when α > 0.48. The basic conclusion is that when the Debye length is comparable to the minimum channel radius, central eddies are formed.

As the wavenumber increases, the second-order effect due to the 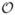(δ²) induced pressure term becomes more important and perimeter eddies appear. We attribute this pressure effect to the redistribution of ions during EOF; increasing k, or decreasing the Debye length, confines this redistribution effect to a thinner layer around the cylinder surface. Indeed, the phase region containing perimeter eddies in Fig. 4 is smaller for k = 30 than for k = 10 and the amplitude α and wavenumber δ values required for the perimeter eddies increase with k.

In general, given the qualitative shifts observed theoretically, we predict that eddies should be only observable for large amplitude perturbations as the Debye length becomes small. Further, we predict that only the central eddies should be observable in the small Debye length limit and the eddies should disappear in the limit of infinitely thin Debye lengths.

Although it is common to consider electroosmotic flow to be uni-directional, we have theoretically demonstrated that a sinusoidal perturbation of the channel radius of sufficient amplitude can have significant influences on the local velocity profiles. We have also shown that controlling the amplitude and wavenumber of the shape perturbation can lead to eddies in the center and/or the perimeter regions of the channel (Fig. 3). The various parameter values that give rise to eddies (Fig. 4A) further show that as k decreases, eddies become more observable for a larger array of δ and α values.

As mentioned in the introduction there are other microfabrication methods that lead to eddies in electrically driven flows, and the choice of any particular method must depend on the parameters and desired outcome. Flows driven by induced-charge electro-osmosis, for example, vary as the square of the field, unlike the results here which vary linearly in the electric field. Smaller magnitudes in field are required for similar eddy formation, and may be, therefore, more advantageous for certain applications. However, there are some attractive experimental controls for the DC electrokinetic effects. Similar to eddy formation in AC fields, which can be controlled through the changes in frequency, eddy formation in DC fields with geometric constrictions can also be controlled in situ through proper material choices. For example, Unger et al. [29] have shown that “soft” valves can be fabricated using multilayer soft lithography. Additionally, field-effect transistor (FET)-type control of flow, as discussed in Schasfoort et al. [30], are possible for bottlenecks made from glass (or other insulating) capillaries. As various applications are developed, each of the different approaches may find uses in integrated devices.

The Debye length in current microfluidic systems is always considered much smaller than the channel width, i.e., k ≡ κa₀ range typically from 10⁵ to 10⁶. As fabrication techniques allow for even smaller channels, the values of k will decrease. For example, in experiments performed with ion-beam sculpted nanopores at 1M KCl [26], k ≈ 100 and A_min ≈ 0.05. We expect that given such a marked radial variation and moderate value of k, eddies exist in the nanopore system.

As is well known in inertial flows, eddies can be used as fluid mixers. Furthermore, particles passing through a small-scale device, such as a nanopore [26], will be influenced by the fluid motion near such a device, particularly in the presence of eddies where the velocity field is non-uniform. With non-uniformity in the velocity field, we may be able to stretch, stall, or locally concentrate molecules in a very small fluid volume for use as sensors or reactors. For such applications, it will be important to better understand the parameters that must be controlled, explore a more extensive phase space, and determine whether finite wall permittivity [20] also contributes to eddy formation.

A Appendix

In this appendix we report the details necessary for the determination of the function χ̂ to O(δ²), which was given in Eq. (12) in the main body of the paper. Since ∇²χ̂ = 0, and as we use a perturbation expansion χ̂ = χ̂₀ + δ²χ̂₂ + ···, then we have

$$\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial {\widehat{\chi }}_0}{\partial R}\right)+{\delta }^2\left(\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial {\widehat{\chi }}_2}{\partial R}\right)+\frac{{\partial }^2{\widehat{\chi }}_0}{\partial Z^2}\right)+\cdots =0.$$ (23)

At leading order, we have $\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial {\widehat{\chi }}_0}{\partial R}\right)=0$ and so conclude that χ̂₀ is only a function of Z, i.e. χ̂₀(Z). At O(δ²) we have

$$\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial {\widehat{\chi }}_2}{\partial R}\right)+\frac{d^2{\widehat{\chi }}_0}{{dZ}^2}=0$$ (24)

which may be integrated twice to obtain (the boundedness of the solution has been invoked)

$${\widehat{\chi }}_2(R,Z)=-\frac{R^2}{4}\frac{d^2{\widehat{\chi }}_0}{{dZ}^2}+c_1(Z),$$ (25)

where c₁(Z) is a function to be determined. With the condition that the surface r = a(z) or R = A(Z) is impermeable to ions, n · ∇χ̂ = 0 (here n is the unit outward normal to the surface), we find

$$0=\frac{\partial {\widehat{\chi }}_0}{\partial R}+{\delta }^2\left(\frac{\partial {\widehat{\chi }}_2}{\partial R}-A^{\prime }\frac{\partial {\widehat{\chi }}_0}{\partial Z}-\frac{A^{\prime }}{2}\frac{\partial {\widehat{\chi }}_0}{\partial R}\right)+O\left({\delta }^4\right)\text{at}R=A(Z).$$ (26)

Since χ̂₀(Z) guarantees that $\frac{\partial {\widehat{\chi }}_0}{\partial R}=0$, then the condition $\frac{\partial {\widehat{\chi }}_2}{\partial R}-A^{\prime }\frac{\partial {\widehat{\chi }}_0}{\partial Z}=0$ from (26) and the use of Eq. (25) yields, after some simplification,

$$\frac{d}{dZ}\left(A^2\frac{d{\widehat{\chi }}_0}{dZ}\right)=0.$$ (27)

Thus, dχ̂₀/dZ = b₀/A², where b₀ is a constant to be determined.

To complete the solution for χ̂ to O(δ²) we need the O(δ⁴) term in the expansion in Eq. (23): $\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial {\stackrel{\sim }{\chi }}_4}{\partial R}\right)+\frac{{\partial }^2{\stackrel{\sim }{\chi }}^2}{\partial Z^2}=0$. Using Eq. (25) we have

$$\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial {\widehat{\chi }}_4}{\partial R}\right)=\frac{R^2}{4}\frac{d^4{\widehat{\chi }}_0}{{dZ}^4}-\frac{d^2{c}_1}{{dZ}^2},$$ (28)

which, with an integration and the need for boundedness, leads to

$$\frac{\partial {\widehat{\chi }}_4}{\partial R}=\frac{R^3}{16}\frac{d^4{\widehat{\chi }}_0}{{dZ}^4}-\frac{R}{2}\frac{d^2{c}_1}{{dZ}^2}.$$ (29)

Evaluating this equation at R = A(Z) and using the boundary condition at R = A(Z) from Eq. (26) that $\frac{\partial {\widehat{\chi }}_4}{\partial R}-A^{\prime }\frac{\partial {\widehat{\chi }}_2}{\partial Z}=0$ (this result follows naturally since $\frac{\partial {\widehat{\chi }}_0}{\partial R}=0$ and we also utilize the O(δ² condition) we find

$$\frac{1}{8}\frac{d}{dZ}\left(A^4\frac{d^3{\widehat{\chi }}_0}{{dZ}^3}\right)=\frac{d}{dZ}\left(A^2\frac{{dc}_1}{dZ}\right).$$ (30)

Upon integration we obtain an equation for c₁(Z),

$$\frac{{dc}_1}{dZ}=\frac{A^2}{8}\frac{d^3{\widehat{\chi }}_0}{{dZ}^3}-\frac{c_2}{A^2},$$ (31)

where c₂ is a constant. This result is sufficient to obtain $\frac{\partial \widehat{\chi }}{\partial Z}$:

$$\frac{\partial \widehat{\chi }}{\partial Z}=\frac{b_0}{A^2}+{\delta }^2\left(-\frac{R^2}{4}\frac{d^3{\widehat{\chi }}_0}{{dZ}^3}+\frac{{dc}_1}{dZ}\right)$$ (32a)

$$=\frac{b_0}{A^2}+{\delta }^2\left(\frac{1}{8}\left(A^2-2R^2\right)\frac{d^3{\widehat{\chi }}_0}{{dZ}^3}-\frac{c_2}{A^2}\right).$$ (32b)

Finally, we impose a condition on the average (based first on an integration over the cross section) potential change along the bottleneck:

$$1={\int }_{-\infty }^{+\infty }\left[\frac{2}{A^2}{\int }_0^{A(Z)}\frac{\partial \widehat{\chi }}{\partial Z}R\text{d}R\right]\text{d}Z.$$ (33)

Substituting with Eq. (32) leads to the conclusion c₂ = 0 and

$$b_0=\frac{1}{{\int }_{-\infty }^{+\infty }\frac{1}{A{(Z)}^2}\text{d}Z}.$$ (34)

These results leads to (12).