Pulsed ENDOR Determination of Relative Orientation of g- and Molecular-Frames of Imidazole-Coordinated Heme Center of iNOS

Abstract

Mammalian nitric oxide synthase (NOS) is a flavo-hemoprotein that catalyzes the oxidation of L-arginine to nitric oxide. Information about the relative alignment of the heme and FMN domains of NOS is important for understanding the electron transfer between the heme and FMN centers, but no crystal structure data for NOS holoenzyme are available. In our previous work [Astashkin, A. V.; Elmore, B. O.; Fan, W.; Guillemette, J. G.; Feng, C. J. Am. Chem. Soc. 2010, 132, 12059–12067], the distance between the imidazole-coordinated low-spin Fe(III) heme and FMN semiquinone in a human inducible NOS (iNOS) oxygenase/FMN construct has been determined by pulsed electron paramagnetic resonance (EPR). The orientation of the Fe – FMN radius-vector, R_Fe-FMN, with respect to the heme g-frame was also determined. In the present study, pulsed electron-nuclear double resonance (ENDOR) investigation of the deuterons at carbons C2 and C5 in the deuterated coordinated imidazole was used to determine the relative orientation of the heme g- and molecular frames, from which R_Fe-FMN can be referenced to the heme molecular frame. Numerical simulations of the ENDOR spectra showed that the g-factor axis corresponding to the low-field EPR turning point is perpendicular to the heme plane, while the axis corresponding to the high-field turning point is in the heme plane and makes an angle of about 80° with the coordinated imidazole plane. The FMN-heme domain docking model obtained in the previous work was found to be in qualitative agreement with the combined experimental results of the two pulsed EPR works.

Introduction

Mammalian NOS, a homodimeric flavo-hemoprotein, is the enzyme responsible for NO biosynthesis.¹ Each subunit contains a C-terminal electron-supplying reductase domain with binding sites for NADPH, FAD and FMN, and an N-terminal catalytic heme-containing oxygenase domain. The oxygenase and reductase domains are connected by a calmodulin (CaM)-binding region, which is irreversibly bound to CaM in iNOS, while reversible CaM binding is observed for nNOS and eNOS (this requires an increase in intracellular [Ca²⁺]).^1,2 CaM binding to eNOS/nNOS acts as a “molecular switch” to enable electron flow from flavin cofactors in the reductase domain to the heme,^3–5 and thus activate NO production. The substrate, L-arginine, and a cofactor, (6R)-5,6,7,8-tetrahydrobiopterin (H₄B), both bind near the heme center in the oxygenase domain.⁶ The oxidation mechanism of the substrate by NOS is novel, and many details of the catalytic mechanism remain to be elucidated.^7–12

The CaM-controlled interdomain (intraprotein) electron transfer (IET) between the heme and FMN centers is essential for the NO synthesis in the catalytic heme domain⁵ and represents a key step in NOS function.^1,2,13,14 It is generally accepted that the CaM binding has little or no effect on the thermodynamics of redox processes in NOS,^15–18 indicating that the regulation of the IET by the CaM binding is accomplished dynamically by controlling conformational changes required for effective IET.^19,20 The crystal structural data of a CaM-bound iNOS FMN domain support a possible mechanism for precise control of the FMN–heme IET by tuning the distance and spatial orientation of the redox centers in the NOS protein.²¹ However, the structural basis for the assembly of the NOS domains and CaM during catalysis remains unknown. Therefore it is important to study the FMN–heme IET mechanism by rapid kinetics^{13,14,22–28} and spectroscopic^29–31 approaches.

Generally, the distance between redox centers is a critical parameter controlling electron transfer processes in proteins.³² Specifically for NOS, the knowledge of the docking geometry of the oxygenase and reductase domains, including the distance between the heme and FMN centers, is desirable for better understanding the FMN–heme IET mechanism. While the required distance information can often be extracted from crystal structures, this approach is not currently applicable to NOS because only crystal structures of separate oxygenase and reductase domains of NOS are available.^6,21,33–37 In the absence of crystallographic data for NOS holoenzyme, it is important to utilize other experimental techniques to determine the Fe···FMN distance in the docked state.

One of such alternative techniques based on pulsed electron paramagnetic resonance (EPR) spectroscopy, relaxation-induced dipolar modulation enhancement (RIDME),³⁸ was recently used by us to determine the distance between the imidazole-coordinated low-spin Fe(III) heme and FMN semiquinone (FMNH^•) in a human iNOS oxygenase/FMN (oxyFMN) construct.³¹ Note that the bi-domain oxyFMN construct is a minimal IET complex designed to favor the interactions between the FMN and heme domains.³⁹ The Fe···FMN distance obtained, R_Fe-FMN ~ 18.8 Å,³¹ is in excellent agreement with the IET rate constant determined by laser flash photolysis.⁴⁰ The orientation of the R_Fe-FMN radius-vector with respect to the heme g-frame was also determined,³¹ but its orientation with respect to the heme molecular frame was not clear because the orientation of the g-frame with respect to the molecular frame was unknown. Depending on the specific d-orbital composition of the single-occupied molecular orbital (SOMO), low-spin ferrihemes may have different orientations of their g-frames with respect to the molecular frame.^41–43 The knowledge of this orientation is important for relating the structural information obtained with respect to the g-frame to the molecular coordinate frame.

The orientation of R_Fe-FMN with respect to the heme molecular frame is important for estimating the distance between the heme and FMN π-systems (“edge-to-edge” distance) and providing additional geometrical constraints for the computational docking models. Therefore, in this work we have used pulsed electron-nuclear double resonance (ENDOR) to determine the relative orientation of the g- and molecular frames in the imidazole-coordinated low-spin Fe(III) heme of a human iNOS oxyFMN construct. Our approach was to determine the orientations of the anisotropic hyperfine interaction (hfi) tensors of the deuterons at deuterated imidazole carbons C2 and C5 with respect to the g-frame, and use this information to deduce the orientation of the g-frame relative to the molecular frame. Conceptually similar approach using electron spin echo envelope modulation (ESEEM) spectroscopy was utilized for the heme proteins and model compounds elsewhere.^44–46

Experimental section

EPR sample preparation

Human iNOS oxyFMN construct, in which only the oxygenase and FMN domains along with the CaM-binding region are expressed, was overexpressed and purified as previously described.⁴⁰ Protein samples were concentrated to around 230 μM; buffer: 100 mM Bis-Tris-Propane, 200 mM NaCl, 42% ethylene glycol, 5 mM imidazole, pH 7.6. Two types of samples were prepared in the H₂O buffer, with imidazole-d₄ (denoted here Im-D, 98% D, obtained from Cambridge Isotope Laboratories Inc.) and with imidazole having the natural abundance of hydrogen isotopes (denoted here Im-H, 0.01% D).

Pulsed EPR experiments and numerical simulations

The experiments have been performed on a homebuilt broadband K_a-band (26–40 GHz) pulsed EPR spectrometer⁴⁷ using ²H Mims ENDOR technique.⁴⁸ The radiofrequency (RF) power (provided by the Amplifier Research AR-250L RF amplifier) used in ENDOR measurements was about 250 W. The measurement temperature was 10 K. The detailed experimental conditions are given in the Figure captions.

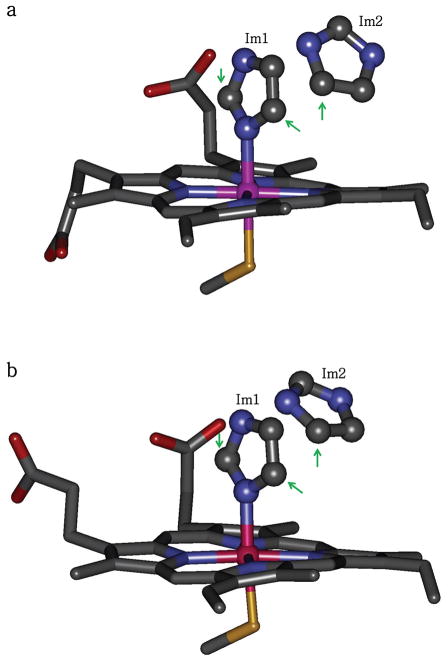
The numerical simulations of the ENDOR spectra were performed using the program SimBud available for download at http://www.cbc.arizona.edu/facilities/epr_facility_software. The simulations were based on a structural model formulated from X-ray crystal structures of iNOS heme domain with coordinated imidazole (Figure 1).⁴⁹

Figure 1.

Heme active sites in murine iNOS heme domain structures (a) 1NOS and (b) 1NOC, which are the only available structures of imidazole-bound iNOS. There are two nearby imidazole molecules in the active site: Im1 (coordinated to the heme iron) and Im2 (H-bonded to Glu371). Note that the positions of Im2 are different in the two structures. The arrows point at the carbon atoms whose bound hydrogens (D2 and D5 of Im1 and D5 of Im2) make the largest contributions to the observed ENDOR spectra in this study.

Results and discussion

1. Experimental results

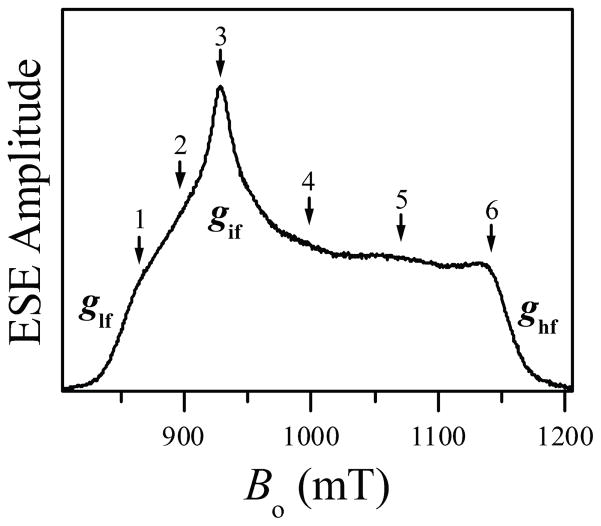
Figure 2 shows the K_a-band field sweep ESE spectrum of the imidazole-coordinated heme center of iNOS oxyFMN. The spectrum is obtained using the three-pulse (stimulated) ESE sequence. The principal g-values determined from this spectrum are (g_hf, g_if, g_lf) = (1.86, 2.30, 2.52), where the subscripts “hf”, “if”, and “lf” stand for “high field”, “intermediate field”, and “low field”, respectively. The arrows with numbers indicate the EPR positions used for pulsed ENDOR experiments. The determined g-values are consistent with those obtained by us earlier³¹ and those determined for low-spin imidazole-bound heme of eNOS.⁵⁰

Figure 2.

Three-pulse ESE field sweep spectrum of human iNOS oxyFMN with heme coordinated by imidazole. Experimental conditions: mw frequency, 29.966 GHz; mw pulses, 311 ns; time interval between the first and second mw pulses, τ= 180 ns; time interval between the second and third mw pulses, T = 4 μs; temperature, 10 K. Principal g-values corresponding to the low-field, intermediate-field and high-field turning points are denoted g_lf, g_if, and g_hf, respectively. The numbered arrows indicate the EPR positions used for pulsed ENDOR measurements; positions 1 through 6 correspond to B_o = 864.8, 897.8, 928.8, 999.8, 1070.3, and 1141.8 mT, respectively. The numbering of the arrows corresponds to that of the traces in the subsequent figures with ENDOR spectra.

As we were primarily interested in ²H ENDOR spectra, the Mims ENDOR technique was employed. The experiments were performed at the time interval between the first and second mw pulses τ = 360 ns. This interval was somewhat shorter than the optimum τ ~ 1 μs (given that the maximum observable deuterium splittings were about 0.7 MHz, see below), but the deep ESEEM from the heme and imidazole ¹⁴N nuclei did not provide much choice (see Figure S1 of Supporting Information). At τ = 360 ns, the first blind spot^48,51 corresponds to the hfi constant A = 1/τ ≈ 2.8 MHz, much larger than the maximum hfi constant expected or observed in ²H ENDOR spectra of this system (see below).

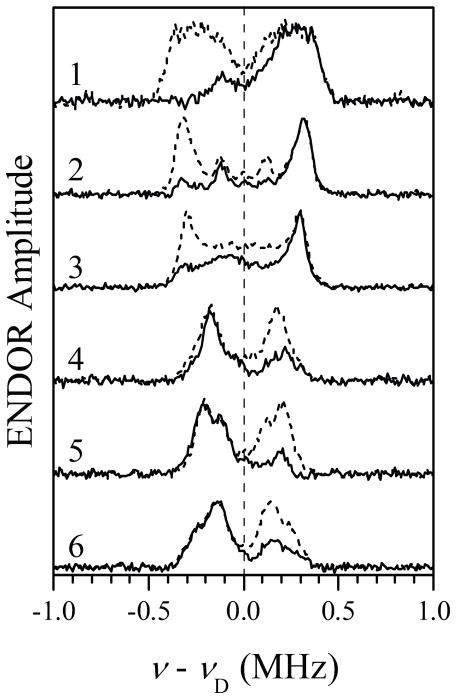
The difference ²H Mims ENDOR spectra were obtained as follows. The spectra were recorded for the samples with Im-D and Im-H, and normalized by the ESE signal amplitude without RF. After this, the spectra obtained for the protonated sample were subtracted from those obtained for the deuterated sample (the examples of both types of spectra are shown in Figure S2 of Supporting Information). The resulting ²H ENDOR spectra are presented in Figure 3 by solid traces. The dramatic lack of symmetry in these spectra with respect to the ²H Zeeman frequency, ν_D, is explained by the so-called implicit TRIPLE effect,⁵² which consists in non-uniform (with respect to the magnetic field orientations or electronic spin manifolds) suppression of the ENDOR effect caused by the extremely deep ¹⁴N ESEEM. In the present case, the effect is mostly that of significant suppression of the ²H ENDOR lines from one of the heme electron spin manifolds. Similar effect was previously observed in ¹H Mims ENDOR spectra of Fe(III) tetraphenyl chlorine.⁴⁶ Symmetrizing the spectra with respect to ν_D diminishes the implicit TRIPLE effects and approximately restores the traditional look of ENDOR spectra (dashed traces in Figure 3).

Figure 3.

²H Mims ENDOR spectra (solid traces) of iNOS oxyFMN with heme coordinated by imidazole. The spectra were obtained as differences between the normalized (by ESE amplitude without RF) spectra obtained in the samples with Im-D and Im-H (see Figure S2 in Supporting Information). Traces 1 through 6 correspond to the six EPR positions indicated in Figure 2 (B_o = 864.8, 897.8, 928.8, 999.8, 1070.3, and 1141.8 mT, respectively). Experimental conditions: mw frequency, 29.966 GHz; mw pulses, 3×11 ns; time interval between the first and second mw pulses, τ= 360 ns; time interval between the second and third mw pulses, T = 60μs; RF pulse, 55μs; temperature, 10 K. Dashed traces are obtained from the solid ones by symmetrization with respect to ν = ν_D.

2. Structural background for numerical simulations

Before considering the numerical simulations of the ENDOR spectra, a structural model was formulated based on the X-ray crystallographic information available in the literature. Only two crystal structures of iNOS heme domain with coordinated imidazole are available: pdb 1NOS and 1NOC, both for murine iNOS.⁴⁹ Although these structures are of monomeric oxygenase domain lacking H₄B and NH₂-terminal residues 77 to 114, it is reasonable to expect that the imidazole positions will be the same in the truncated monomer and the active dimer, as the positions of the amino acid residues surrounding the heme center are the same in both cases. In addition, the high degree of structural conservation at the heme sites in murine and human iNOS makes it very probable that the main structural features related to the imidazole binding will also be conserved between these organisms. Therefore, we used the available X-ray structures of murine iNOS oxygenase domain with coordinated imidazole to facilitate the interpretation of the ENDOR data obtained here for human iNOS.

The analysis of pdb 1NOS and 1NOC shows that there are two imidazole molecules located at the heme site, Im1 and Im2 (Figure 1).⁴⁹ Imidazole Im1 is coordinated to the heme iron, while Im2 is located above the edge of pyrrole ring A of the heme center and is hydrogen bonded to Glu371.⁴⁹ One has to note that the heme pocket is more exposed in these truncated monomeric structures⁴⁹ than in the iNOS dimer. While the position of Im1 is not likely to be affected by this difference, this is less certain for Im2. However, this is not significant because of the minimal effect of Im2 on the ENDOR spectra (see below).

The hydrogens at carbons C2, C4, and C5 (H2, H4, and H5, respectively) are non-exchangeable. Therefore, only these hydrogens (as deuterons) will contribute to the ²H ENDOR spectrum of iNOS prepared with Im-D in the H₂O buffer. The distances from Fe(III) to these hydrogens are summarized in Table 1. Protons H2 and H5 of Im1 are located at the distance from the heme iron of R_FeH = 3.25 ± 0.1 Å. They are the closest to the central Fe(III) ion and are expected to produce the largest splittings in the ENDOR spectra. Interestingly, H5 of Im2 is also located at a comparable distance (as low as 3.46 Å, see Table 1), although its position in the two crystal structures differs by about 0.7 Å. As these two structures correspond to different types of crystals (pdb 1NOS corresponds to the oxygenase domain alone, while pdb 1NOC corresponds to the iNOS oxygenase domain co-crystallized with Escherichia coli type I chloramphenicol acetyltransferase),⁴⁹ this difference may indicate a possible inhomogeneity of the second imidazole position in frozen solutions (in particular, in our EPR samples).

Table 1.

Distances R_FeH from Fe(III) to the protons of imidazole (Im) molecules extracted from pdb 1NOS and 1NOC. The corresponding anisotropic hfi constants T_⊥H are calculated assuming ρ_Fe = 1. The coordinated imidazole is Im1, while the second nearby imidazole is Im2 (for the sake of uniformity, the definitions of H4 and H5 of Im2 in the 1NOC column are swapped compared to those used in the pdb file).

Hydrogen	RFeH from pdb 1NOS	T⊥H (T⊥D), MHz	RFeH from pdb 1NOC	T⊥H (T⊥D), MHz
H2 (Im1)	3.31 Å	−2.18 (−0.33)	3.35 Å	−2.10 (−0.32)
H4 (Im1)	5.13 Å	−0.59 (−0.09)	5.08 Å	−0.60 (−0.09)
H5 (Im1)	3.23 Å	−2.34 (−0.36)	3.16 Å	−2.50 (−0.38)
H2 (Im2)	7.61 Å	−0.18 (−0.027)	7.64 Å	−0.18 (−0.027)
H4 (Im2)	5.25 Å	−0.55 (−0.08)	6.19 Å	−0.33 (−0.05)
H5 (Im2)	3.46 Å	−1.91 (−0.29)	4.13 Å	−1.12 (−0.17)

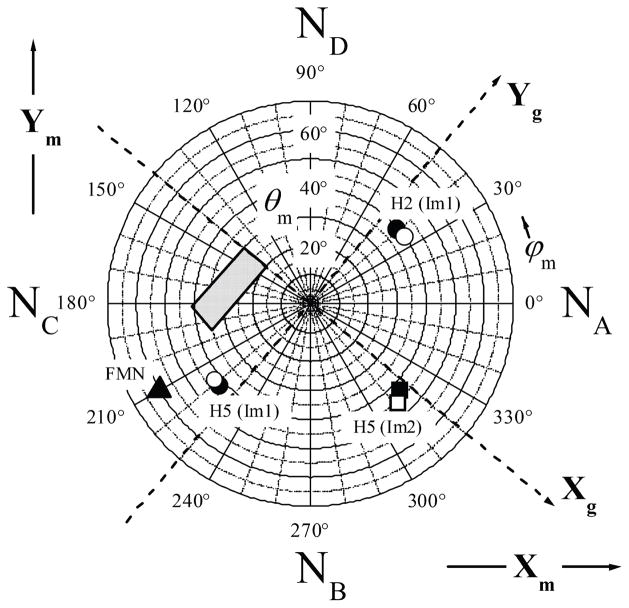
As described in the following section, deuterons D2 and D5 of Im1 and D5 of Im2 make the largest contribution to the amplitude of our ²H ENDOR spectra. The polar plot shown in Figure 4 indicates the angular positions of these three hydrogens with respect to the molecular coordinate frame (X_m, Y_m, Z_m), where axes X_m and Y_m are in the heme plane and aligned with the Fe-N directions, and axis Z_m coincides with the heme plane normal. One can see that all of these hydrogens are located at the polar angles θ_m~ 40°. The azimuthal angles, ϕ_m, for H2 and H5 of Im1 differ by about 180°, as expected from the planar structure of imidazole. For H5 of Im2, the azimuthal angle differs by ~90° from those of the hydrogens of Im1.

Figure 4.

Polar diagram showing the angular positions of H2 and H5 of Im1, H5 of Im2, and N10 of FMN with respect to the molecular coordinated system (X_m, Y_m, Z_m) of the heme center. The directions of X_m and Y_m are indicated, and Z_m is normal to the heme plane. X_g and Y_g are the principal axes of the g-tensor, and their directions shown by dashed lines are determined in this work. The third axis of the g-frame, Z_g, is perpendicular to the heme plane and parallel to Z_m. The positions of hydrogens indicated by the filled symbols are derived from pdb 1NOS, while those indicated by the open symbols are derived from pdb 1NOC. The angular position of N10 of FMN (indicated by filled triangle) was obtained from the docking structure³¹ and reflected with respect to the heme plane (to facilitate comparison with the magnetic resonance data which do not distinguish between θ and 180°-θ). The shaded tetragonal area in the second and third quadrants represents the FMN position as estimated from the combined data obtained in RIDME experiments³¹ and this work. N_A through N_D atoms are the heme pyrrole nitrogens.

In addition to the molecular axes system, Figure 4 introduces the principal axes system of the g-factor (X_g, Y_g, Z_g), with axis Z_g coinciding with the heme plane normal (and thus being parallel with the molecular axis Z_m), and the (X_g, Y_g) plane coinciding with the heme plane. The orientation of X_g and Y_g with respect to X_m and Y_m was not known in advance, and has been determined in this work.

3. Numerical simulations of the ENDOR spectra

In this section we perform numerical simulations of the ²H Mims ENDOR spectra aimed at establishing the orientation of the axis of g_lf with respect to the heme plane. The estimated anisotropic hfi constants T_⊥H (T_⊥D) of various protons (deuterons) belonging to Im1 and Im2 are summarized in Table 1. In these estimates, the spin population of Fe(III) was assumed to be ρ_Fe = 1. The hfi for all of the protons is expected to be predominantly anisotropic, although some minor isotropic contribution can be expected for H2 and H5 of Im1.⁵³ Therefore, the largest splittings in our ENDOR spectra (~ 0.7 MHz) should mostly arise from D2 and D5 of Im1. D5 of Im2 may also contribute to the large splittings. On average, however, the contribution of this deuteron to the ENDOR amplitude should not be more than half of the combined contribution of D2 and D5 of Im1 because under our experimental conditions the multinuclear effects⁵⁴ can be neglected, and the ENDOR amplitude for the non-matrix lines is simply proportional to the number of nuclei. With the possible statistical distribution of R_FeH for D5 of Im2 discussed above, its contribution to the large ENDOR splittings is likely to be even less.

The remaining three deuterons (D4 of Im1 and D2, D4 of Im2) are located at the distances exceeding 5 Å (see Table 1) and are responsible for the inner parts of the ENDOR spectra (splittings < 0.3 MHz). Under our experimental conditions (τ= 360 ns, the first maximum in Mims ENDOR response corresponds to A = 1/(2τ) ≈ 1.39 MHz^48,51), the contribution of each of these remote deuterons to the ENDOR amplitude is significantly smaller than that from the “proximal” deuterons discussed above.

Based on these considerations, the following stepwise strategy was implemented. At the first step, benchmark calculations of ENDOR spectra for various possible orientations of the g-frame with respect to the molecular frame were performed using the structural data for D2 and D5 of Im1. A qualitative comparison of these spectra with the experimental ones was used to select the orientation of the g_lf axis with respect to the heme plane. At the second step, this general assignment was used to fit the external regions of the experimental spectra neglecting all of the deuterons except D2 and D5 of Im1. Finally, at the third step, D5 of Im2 was included into consideration in order to evaluate its effect on the spectra and to make conclusions about the validity of the calculation made in the second step. These three steps are described in detail below.

In the numerical simulations, the axial hfi and nqi tensor were used. The orientation of the hfi tensor axis with respect to the g-frame was described by the polar and azimuthal angles, θ_h and ϕ_h, respectively. Similarly, the orientation of the nqi axis was described by the angles θ_q and ϕ_q. This axis is with good accuracy parallel to the C–D bond. The D2 and D5 deuterons of Im1 were assumed to be spectroscopically equivalent, with θ_h = 40° and θ_q = 105°.

First, we utilized the structural data of Table 1 and Figure 4 to perform model ²H ENDOR calculations that were used as a benchmark for comparison with the experimental spectra. These benchmark calculations were performed for T_⊥D = − 0.35 MHz (corresponds to R_FeH = 3.25 Å and ρ_Fe = 1). The quadrupole coupling constant for imidazole deuterons is e²Qq/h ≈ 0.18 MHz,⁵⁵ but in the benchmark calculations (Figures 5 and 6) e²Qq/h = 0 was used. The reason for neglecting the nqi in these calculations is as follows. According to the Im1 coordination geometry, the difference between the angles θ_h and θ_q of D2(5) is about 65°. Therefore, when the vector of the external magnetic field, B_o, is parallel to R_FeH (which corresponds to the largest hfi splitting), the nqi axis is approximately at the magic angle to B_o, and the nqi splitting is negligible. In the simulations aimed at actually fitting the experimental spectra (Figures 7 and 8 below), however, the nqi is taken into account (see the captions of the figures).

Figure 5.

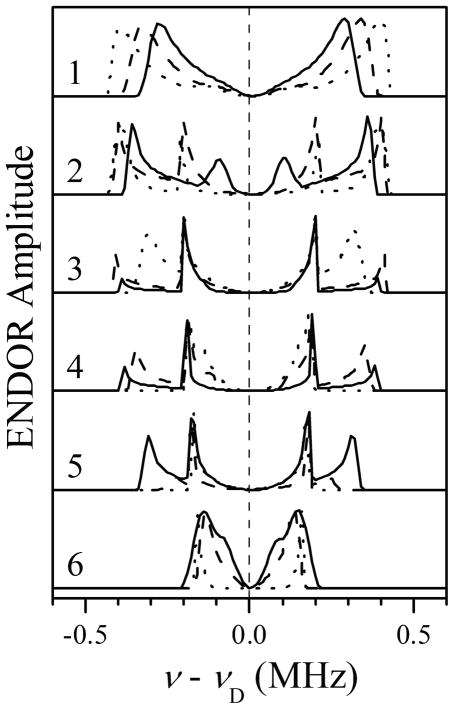
Benchmark simulations of ²H Mims ENDOR spectra for D2 and D5 of Im1, assuming g_lf to correspond to the g-frame axis Z_g (//Z_m). The orientation of the Im1 plane with respect to the g-frame was characterized by azimuthal angles ϕ_h = 0 (solid traces), 45° (long-dashed traces), and 90° (short-dashed traces). Simulation parameters: a_iso = 0 MHz; T_⊥ = −0.35 MHz; e²Qq/h = 0 MHz; mw frequency, 29.966 GHz; τ= 360 ns; B_o = 864.8, 897.8, 928.8, 999.8, 1070.3, and 1141.8 mT for traces 1 through 6, respectively.

Figure 6.

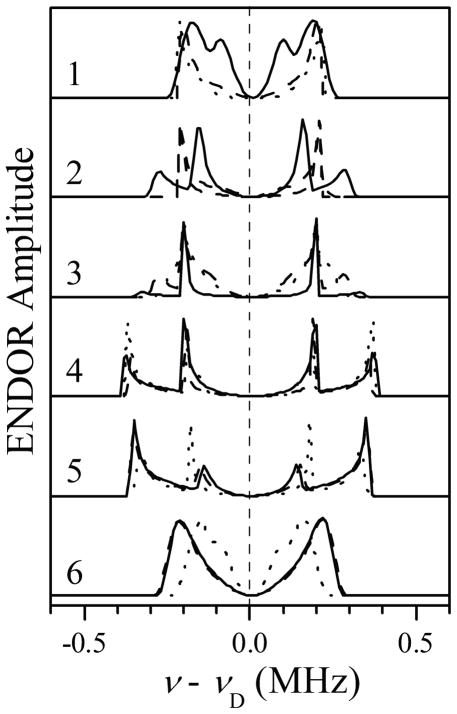
Benchmark simulations of ²H Mims ENDOR spectra for D2 and D5 of Im1, assuming g_hf to correspond to the g-frame axis Z_g (//Z_m). The orientation of the Im1 plane with respect to the g-frame was characterized by azimuthal angles ϕ_h = 0° (solid traces), 45° (long-dashed traces), and 90° (short-dashed traces). Simulation parameters: a_iso = 0 MHz; T_⊥ = −0.35 MHz; e²Qq/h = 0 MHz; mw frequency, 29.966 GHz; τ = 360 ns; B_o = 864.8, 897.8, 928.8, 999.8, 1070.3, and 1141.8 mT for traces 1 through 6, respectively.

Figure 7.

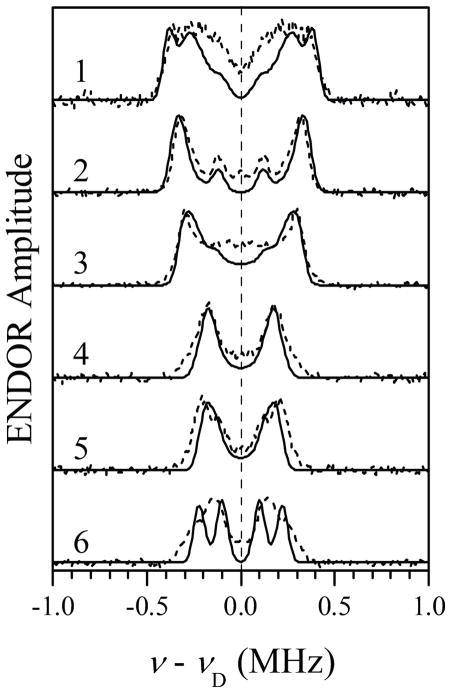
Simulations of ²H Mims ENDOR spectra for D2 and D5 of Im1 (solid traces), assuming g_hf to correspond to the g-frame axis Z_g (//Z_m). The orientation of the Im1 plane with respect to the g-frame was characterized by the azimuthal angle ϕ_h = 80. Simulation parameters: a_iso = −0.04 MHz; T_⊥ = −0.32 MHz; e²Qq/h = 0.18 MHz; η = 0; mw frequency, 29.966 GHz; τ = 360 ns; B_o = 864.8, 897.8, 928.8, 999.8, 1070.3, and 1141.8 mT for traces 1 through 6, respectively. The simulated spectra were convoluted with a Gaussian line with the width of 0.05 MHz between the maximum slope points. Dashed traces, symmetrized experimental spectra reproduced from Figure 3.

Figure 8.

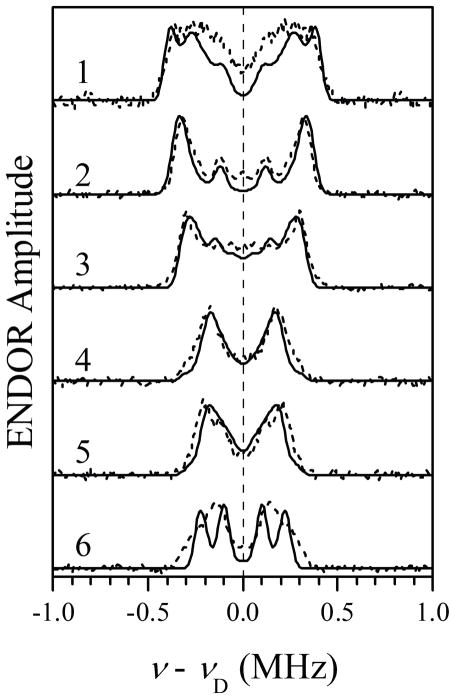
Simulations of ²H Mims ENDOR spectra for D2 and D5 of Im1 and D5 of Im2 (solid traces), assuming g_hf to correspond to the g-frame axis Z_g (//Z_m). The simulation parameters for D2 and D5 of Im1 are the same as those in Figure 7. Simulation parameters for D5 of Im2: a_iso = 0 MHz; T_⊥ = −0.18 MHz; e²Qq/h = 0.18 MHz; η= 0; θ_h = 44°; ϕ_h = −5°; θ_q = 60°; ϕ_q = 20°. Other simulation parameters are the same as in Figure 7. The simulated spectra were convoluted with a Gaussian line with the width of 0.05 MHz between the maximum slope points. Dashed traces, symmetrized experimental spectra reproduced from Figure 3.

Figure 5 shows the ²H ENDOR spectra calculated assuming the axis of g_lf being perpendicular to the heme plane (i.e., coinciding with Z_g//Z_m). The principal axes X_g and Y_g are defined to coincide with the axes of g_hf and g_if, respectively. The orientation of the Im1 plane with respect to axes X_g and Y_g in these calculations was characterized by the azimuthal angle ϕ_h, which is also the azimuthal angle of the hfi tensor axis for H2(5) of Im1. The three sets of calculated spectra shown in Figure 5 by solid, long-dashed, and short-dashed lines correspond to ϕ_h = 0°, 45°, and 90°, respectively. One can see that this arrangement of the principal g-axes results in the largest splittings in the ENDOR spectra being observed for the EPR positions between g_lf and g_if. The alternative situation of the axis of g_hf being perpendicular to the heme plane is presented in Figure 6. In this case, the largest ENDOR splittings are observed for the EPR positions between g_if and g_hf.

In the experimental spectra (Figure 3), the largest ENDOR splitting is attained for trace 2, between g_lf and g_if. According to the calculations presented in Figures 5 and 6, this indicates that the axis of g_lf is perpendicular to the heme plane, while the axis of g_hf is in the plane. This assignment of g_lf to Z_g naturally explains the fact that the scale of the ENDOR splittings observed for D2 and D5 of Im1 in this work, as well as the overall dependence of these splittings on the EPR position, are similar to those observed earlier for bis-imidazole (or histidine) coordinated heme centers.⁵⁶

Our next step was to perform numerical simulations for D2 and D5 of Im1 in order to reproduce the external regions of the experimental ENDOR spectra, and thus to determine ϕ_h and obtain a more accurate estimate of the spectroscopic parameters. As mentioned above, in these simulations D2 and D5 of Im1 were assumed to be spectroscopically equivalent, and the ²H nqi with e²Qq/h = 0.18 MHz and the asymmetry parameter η = 0 (corresponds to the axial nqi tensor) was taken into account. The variable parameters of the simulation were T_⊥D, a_iso, and ϕ_h = ϕ_q. The starting hfi parameters were those used in calculations presented in Figures 5 and 6.

Solid traces in Figure 7 represent the spectra simulated for T_⊥D = −0.32 MHz, a_iso = −0.04 MHz, e²Qq/h = 0.18 MHz, η= 0, ϕ_h = ϕ_q = 80°. To approximate the experimental intrinsic linewidth, the simulated spectra were convoluted with the Gaussian function with the width between the maximum slope points of 0.05 MHz. The short-dashed traces in Figure 7 show the symmetrized experimental spectra. The simulated and experimental spectra are in qualitative agreement. The most dramatic discrepancy is the presence of well-resolved splittings in the simulated spectrum 6, where the experimental spectrum shows only weakly resolved peaks. This difference is caused by the constraints of our simulation model, mostly, the spectroscopic equivalence of D2 and D5 of Im1 and the complete absence of structural disorder. From T_⊥D ≈ −0.32 MHz the spin population of the central Fe(III) ion can be estimated as ρ_Fe ≈ 0.9.

Finally, the effect of D5 of Im2 on the simulated ENDOR spectra was evaluated. In these simulations, the parameters of D2 and D5 of Im1 estimated above were used. Trial simulations have shown that for the EPR positions between g_lf and g_if the effect of the additional deuteron is minimal within the whole range of variation of distances indicated in Table 1. At EPR positions 4 and 5, however, the ENDOR splitting from this deuteron has significantly exceeded the experimental splittings for |T_⊥D| > 0.18 MHz (R_FeH < 3.9 Å, assuming ρ_Fe ~ 0.9). Therefore, for the model with fixed geometry (without a statistical distribution of distances) R_FeH ~ 3.9 Å represents the shortest possible distance from Fe to D5 of Im2. If a distribution R_FeH is assumed, then the minimal distance can be somewhat shorter (just how much shorter will depend on the specific distribution model). As an example, Figure 8 shows the result of simulations with D5 of Im2 having T_⊥D = −0.18 MHz. Note that the spectra of Figure 8 are nearly identical to those of Figure 7, in which D5 of Im2 was not taken into account. This comparison validates the results of numerical simulations for D2 and D5 of Im1 above.

While better agreement between the simulated and experimental spectra could probably be achieved if the structural (strictly equivalent D2 and D5 deuterons) and spectroscopic (axial hfi tensors) constraints were removed, and the implicit TRIPLE effects taken into account, such an improvement would be purely cosmetic, and we did not attempt to achieve it.

The analysis of the experimental g-values of the Im-coordinated heme center of NOS using the expressions derived by Taylor⁵⁷ results in the axis of g_hf being the natural quantization axis for the d-orbitals (so-called proper Z axis), Z_Q. Although this axis is parallel to the heme plane (as established in this work), the unpaired electron predominantly resides in the out-of-plane d-orbitals, and thus the orbital state of Fe(III) can be characterized as d_π. The results of the analysis are summarized in the Supporting Information, Table S1.

It is interesting to compare the combined experimental results obtained here and in our previous work³¹ with the results of the computational docking studies.³¹ The filled triangle in the third quadrant of the polar plot of Figure 4 shows the orientation of the radius-vector R_Fe-FMN joining the heme iron and N10 of FMNH^• (the closest atom with major spin population) with respect to the heme molecular frame, as obtained from the docking model.³¹ The dashed lines show the axes X_g and Y_g that correspond to the angle ϕ_h between X_g and Im1 plane of 80° (actually, there are two possible orientations differing by Δϕ_m ≈ 20°; the shown orientation provides a better agreement between the experimental and calculated orientations of R_Fe-FMN in the g-frame). The shaded tetragonal area extending from the second to the third quadrant represents the range of R_Fe-FMN orientations obtained by combining the results of RIDME measurements³¹ (orientation of R_Fe-FMN with respect to the g-frame) with the results of this work (orientation of the g-frame with respect to the heme molecular frame).

As seen in Figure 4, the smallest differences between the R_Fe-FMN orientations obtained from RIDME and from computational docking in both θ and ϕ are ~20°. Apart from the uncertainty in the determined orientation of X_g and Y_g with respect to the Im1 plane (about ±5°), several other possible factors can contribute to this discrepancy. First, Figure 4 actually combines the spectroscopic data obtained for human iNOS with the X-ray structural data obtained for murine iNOS. Although we expect the structure of the imidazole-bound heme site to be similar in both organisms, some angular differences can be anticipated. The scale of these differences can be estimated as about 10° from comparison of the orientations of the S_γ-C_β bond of the cysteine ligand in human and murine iNOS oxygenase domains (pdb 1NSI and 1NOD, respectively). Second, the docking calculations³¹ used the X-ray structures of the heme and FMN domains without any modifications. The assumption of rigid structures might not entirely correspond to the reality. In fact, our recent MCD studies indicate that the FMN domain docking affects the heme site structure,^29,30 and the same might also be true for the FMN site. The dependence of the Im2 position on the specific crystal packing discussed above also provides evidence of some structural variability within the heme domain caused by external (e.g., interdomain) interactions. Therefore, some relative positional and/or orientational shifts of the heme and FMN cofactors with respect to the calculated docking structure may be expected. The third factor to take into account is that the axis of g_lf is not bound to be exactly parallel to Z_m. In fact, distortions of the heme conformation and axial ligand coordination geometry usually lead to misalignment of the direction of the (average) heme plane normal and that of the out-of plane g-factor axis by a few (up to ~15°) degrees.^58,59 Finally, the limits of possible orientations of R_Fe-FMN with respect to the g-frame in our previous work³¹ were established rather approximately because a 30° grid was used for the azimuthal angle ϕ (as defined in ref. 31; with definitions of this work it mostly translates to θ_m). Additional simulations for the orientations between the grid angles show that a marginal agreement between the experimental and simulated RIDME spectra is possible for the angles up to (θ_m, ϕ_m) ~ (50°, 200°), which would reduce the difference between the experimental and calculated orientations of R_Fe-FMN to about 10°.

Taken separately, each of the above structural factors is unlikely to be responsible for the difference between the experimental results and the predictions of the docking calculations: e.g., the 20° orientational difference at R_Fe-FMN ~ 18.8 Å results in a translational shift of ~ 6.5 Å, which seems somewhat excessive. However a combination of these factors can readily reconcile the experimental and computational results assuming changes in parameters within error limits of their definition or determination (see above). Therefore, from these considerations we conclude that the docking model obtained earlier³¹ is in qualitative agreement with the previous experimental results³¹ and those obtained in this work.

Finally, it is of note that according to the docking model calculated in our previous work,³¹ the angle between the heme and FMN planes is about 10°. It was deduced above that the singly occupied orbital of Fe(III) is essentially d_π, i.e., the orbital strongly interacting with the π-system of the porphyrin ligand. The combination of this orbital configuration, the angle between the heme and FMN molecular planes, and the orientation of R_Fe-FMN at a large angle to the heme plane normal provide the electronic and structural conditions for efficient FMN–heme IET.⁶⁰

Conclusion

The results obtained in this work represent a logical continuation of the structural determination related to the relative spatial arrangement of FMN and heme centers in the docked state of NOS protein, which was started in our previous work.³¹ The aforementioned results³¹ and this work provide structural constraints for validation of computational docking models, and the selected docking model³¹ was found to be in qualitative agreement with the combined experimental results of the two pulsed EPR works.

Abbreviations

NO

nitric oxide

NOS

nitric oxide synthase

iNOS

inducible NOS

CaM

calmodulin

oxyFMN

bi-domain NOS construct in which only oxygenase and FMN domains along with CaM-binding region are present

FMN

flavin mononucleotide

FMNH^•

FMN semiquinone

IET

interdomain electron transfer

EPR

electron paramagnetic resonance

ESE

electron spin echo

ENDOR

electron-nuclear double resonance

ESEEM

electron spin echo envelope modulation

RIDME

relaxation-induced dipolar modulation enhancement

mw

microwave