Large standard deviations and logarithmic-normality

Abstract

While many quantifiable biological phenomena can be described by making use of an assumption of normality in the distribution of individual values, many biological phenomena are not accurately described by the normal distribution. An unquestioned assumption of normality of distribution of possible outcomes can lead to misinterpretation of data, which could have serious consequences. Thus it is extremely important to test the validity of an assumption of normality of possible outcomes. As it turns out, the logarithmic-normal (log-normal) distribution pattern is often far more accurate in describing statistical biological phenomena. Herein I examine large samples of values for circulating blood cell (hemocyte) concentration (CHC) among both wild-type and mutant Drosophila larvae, and demonstrate in both cases that the distribution of individual values does not conform to normality, but does conform to log-normality.

Introduction

“The standard deviation and the standard error of the mean measure two different things and are often confused. Most medical investigators summarize their data with the standard error of the mean because it is always smaller than the standard deviation. It makes their data look better. However, unlike the standard deviation, which quantifies the variability in the population, the standard error quantifies uncertainty in the estimate of the mean. Since readers are generally interested in knowing about the population, data should generally not be summarized with the standard of the mean.”¹

Blood cell (hemocyte) counts can be simply and quickly obtained, and are highly informative indications of an effect of experimental manipulation of Drosophila. Depending on the needs of a given researcher, values can be obtained for total hemocytes per organism or for hemocyte concentration. When experiments include appropriate control classes, such indices can provide immediate clues about the comparative effects of treatments on hemocyte proliferation and differentiation or on the innate cellular immune response.

While the methods used to obtain such counts vary, the read-out of any experiment is the same: a sample of raw count (or concentration) values. Thus the method of statistical analysis of obtained values should be relatively uniform. However, it is not. Most reports on hemocyte count/concentration use of the standard error of the mean,^2–6 while a minority employ the standard deviation.^7–9 Most reports apparently assume a normal distribution when comparing means, while a very few transform raw values prior to analysis.^10–12

There are certainly multiple reasons for this lack of uniformity, but a critically important reason that will be addressed herein is the apparent misperception that large sample standard deviations (i.e., large with respect to the values of the mean) are at best visually unappealing and at worst necessarily erroneous. Consequently, a researcher may decide to present true—but visually unappealing—information in a secondary online supplementary file,¹³ or use the standard error of the mean or even resort to the practice of “dropping outliers”.

The standard error of the mean is not a substitute for the standard deviation. The standard deviation is a measure of the spread of n raw values (from one experiment or from one pooling of multiple experiments). The standard error, however, is the standard deviation not of n raw values, but of n experiments. It is a measure of the spread of n mean values obtained in n experiments, of a “mean of means”. Thus the employment of the standard error, which (when dealing with whole nonnegative integers, such as CHC values) is always going to be less than the standard deviation (standard error = standard deviation divided by the square root of n). The standard error is more visually appealing, and there is a greater likelihood of demonstrating statistically “significant” differences between experimental groups. However, such a practice can lead to a much greater chance of a false conclusion of a significant difference between means.

Yet a second factor contributes to the observed large standard deviations: the erroneous assumption that raw CHC values must necessarily conform to a normal distribution. Yet this is an unreasonable expectation, as multiple factors work against such conformity: (1) CHC values cannot be negative; (2) other than zero, there is no lower limit to wild-type or mutant CHC; (3) there is no practical upper limit to wild-type and mutant CHC values. It ought not to be surprising that this confluence of factors leads to a skewed distribution pattern: higher frequencies between zero and the mean and lower frequencies, but more numerous frequency classes, above the mean. The drive to force CHC values into a normal distribution pattern is not unfounded: many biological indices (e.g., human lean body mass index¹⁴) do indeed conform to normality. But many do not (e.g., height and weight among domestic dogs¹⁵). Thus it is up to the researcher to determine whether the assumption of normality is valid.

In this report, I present evidence that the distribution pattern of a large sample of raw larval CHC values, either wild-type or mutant, violates normality, but is consistent with a logarithmicnormal (log-normal) pattern. An assumption of log-normality allows the calculation of standard deviations that are visually appealing, that accurately summarize raw data, and that do not unduly increase the risk of false negative and false positive interpretations.

Results

In order to determine whether wild-type total CHC values conform to a normal distribution pattern, I performed an analysis of published (n = 50)¹² and as-yet-unpublished (n = 150) individual CHC values (total: n = 200; females: 90; males: 110) obtained for Canton-S larvae. All CHC values were obtained under the same experimental conditions. CHC values were obtained as described¹⁶ from larvae that were 120 ± 4 hr old, and had been raised at 25°C. A summary of statistical data for wildtype raw total CHC values are presented in Table 1.

Table 1.

Statistical data

Parameter	Data treatment
	Raw	Transformed
Minimum	1,010	6.9177
Maximum	29,020	10.2757
Range	28,010	3.3580
Mean ± standard deviation	7,932 ± 4,895	8.8030 ± 0.6898
Coefficient of variance	0.6171	0.0693
Back-transformation	-	6,654 ×/1.8400
Median	6,983	8.8512
No. of bins	10	10
Bin size	2,930	0.3649

Comparison of statistical parameters of raw and transformed Canton-S total CHC data.

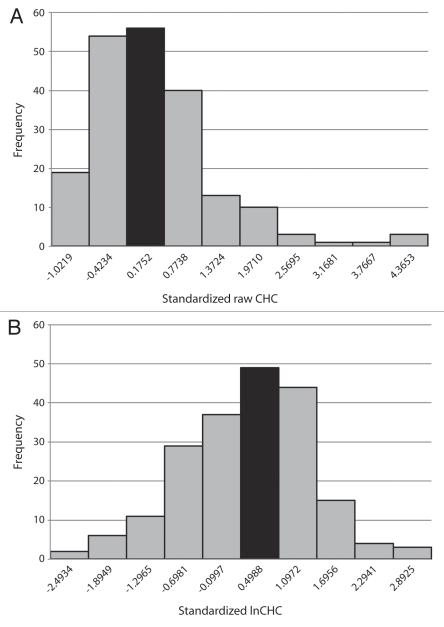
Qualitative examination of the distribution pattern of raw wild-type CHC values (Fig. 1A) reveals a mixture of characteristics, not all of which are consistent with expectations of a normal distribution. For example, consistent with a normal distribution, the mean and median fall into the modal bin. However, further examination reveals contradictory information. Because CHC values cannot be negative, and because there is no symmetrically located upper limit to CHC, the histogram is noticeably skewed to the right. Statistical analysis confirms qualitative impressions. Skewness (√b₁) was determined to be 1.6514, in excess of the critical value of 0.403 at p < 0.01 (Table 2). Furthermore, the kurtosis (b₂) value is 6.9516, which lies outside the upper boundary of the spread of critical values, 3.98 (p < 0.01; Table 2). The observed skewness and kurtosis values indicate a significant difference from those expected for a normal distribution.

Figure 1.

(A) Histogram of raw Canton-S CHC values. Vertical axis: frequency. Horizontal axis: bins for ranges of CHC values. All bins are of equal width: 2,930 cells/microliter. Number under each bin represents the upper CHC boundary value of the bin (in standard units). The lower boundary value of the leftmost bin is zero. Black bar represents the modal bin and also contains the mean and median. (B) Histogram of transformed lnCHC values. Vertical axis: frequency. Horizontal axis: bins for ranges of transformed lnCHC values. All bins are of equal width: 0.3649. Number under each bin represents the upper lnCHC boundary value of the bin (in standard units). The lower boundary value of the leftmost bin is 6.9177 (6.9177 is the minimum observed lnCHC value). Black bar represents the modal bin and also contains the mean and median.

Table 2.

Tests of normality for raw Canton-S CHC data (n = 200)

Parameter	Observed value	Critical value	p at critical value	Reject null hypothesis?
χ2	566.0911	27.88	0.001	reject
√b1	1.6514	0.403	0.01	reject
b2	6.9516	2.37–3.98	0.01	reject

Null hypothesis: there is no difference between the distribution pattern of the observed data and the normal distribution. The distribution of raw CHC values fails three tests for normality: χ² goodness-of-fit test (v = 9 degrees of freedom), skewness (√b₁) test, and kurtosis (b₂) test. Note that all three failures are at very significant levels of probability.

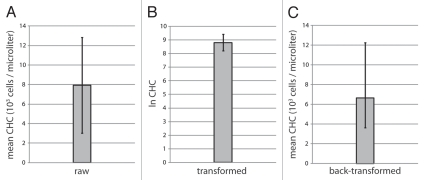
Additional strong support for non-normality is provided by a χ² goodness-of-fit test. The observed value is χ²_0.001 = 566.0911 (degrees of freedom: v = 9), which is much greater than the critical value of 27.88 (p < 0.001; Table 2). Thus, despite the qualitative indication of normality by the mean, median and mode, the distribution pattern in Figure 1A conclusively fails multiple tests for normality. The mean ± standard deviation of raw Canton-S CHC is depicted in Figure 2A. Note that the magnitude of the standard deviation is over 60% that of the mean (Table 1, coefficient of variance; Fig. 2A).

Figure 2.

Bar graph presentations of mean and standard deviations of Canton-S CHC. (A) Raw CHC values. Mean ± standard deviation. Vertical axis: 10³ cells/microliter. (B) Transformed CHC values (lnCHC). Mean ± standard deviation. Vertical axis: lnCHC. (C) Back-transformed CHC values. Mean x/standard deviation. Vertical axis: 10³ cells/microliter.

In striking contrast, the distribution pattern of the natural logarithms of individual CHC values (lnCHC values; Fig. 1B) is obviously different. Again, the mean, median and mode fall into the same bin (Table 1). Yet the histogram appears far more similar to a normal pattern Fig. 1B). Importantly, the results of tests for skewness, kurtosis and goodness-of-fit are all strongly consistent with normality (Table 3). The mean ± standard deviation of logarithmically transformed CHC values is presented in Figure 2B. Note that the magnitude of the standard deviation is less than 7% of that of the mean (Table 1, coefficient of variance; Fig. 2A and B). However, the unit of measurement in this case is an abstraction, lnCHC. In order to express observations in useful real-world units (cells/microliter), a back-transformation is performed,²⁰ in which the exponentials of the mean and standard deviation are calculated (Table 1 and Fig. 2C). Note the difference between the mean raw (7,932 cells/microliter) and mean transformed (6,654 cells/microliter) values.

Table 3.

Tests of normality for transformed Canton-S lnCHC data (n = 200)

Parameter	Observed value	Critical value	p at critical value	Reject null hypothesis?
χ2	7.2230	8.34	0.50	do not reject
√b1	−0.2655	−0.280	0.05	do not reject
b2	3.0774	2.59–3.40	0.10	do not reject

Null hypothesis: there is no difference between the distribution pattern of the transformed data and the normal distribution. The distribution of transformed lnCHC values passes three tests for normality: χ² goodness-of-fit test (v = 9 degrees of freedom), skewness (√b₁) test, and kurtosis (b₂) test. Critical values those for the most significant tabulated p values¹⁹ that were not surpassed by the observed test value.

The data examined thus far represent total CHC in a wildtype genetic background, and no distinction was made among hemocyte classes. The hemocytes that were observed were almost entirely composed of plasmatocytes, with a small percentage (< 5%) of crystal cells. A third hemocyte class, that of the lamellocyte, is occasionally observed in wild-type hemolymph, as lamellocytes only differentiate in large numbers in response to natural parasitic infection or a “tumorous” genetic background.²¹ This raises the question of whether lamellocyte CHC values also conform to a log-normal distribution pattern. Analysis of lamellocyte CHC data from u-shaped (ush) mutant larvae (n = 40; females: 20; males: 20),¹² which exhibit large numbers of lamellocytes in circulation, is presented in Tables 4–6. Once again, three separate tests demonstrate that untransformed data violate the assumption of normality (Tables 4 and 5), while data transformed by the natural logarithm conform to normality (Tables 4 and 6). Analysis of total CHC for these same larvae also demonstrated a violation of normality and a conformation to log-normality (data not shown).

Table 4.

Statistical data

Parameter	Data treatment
	Raw	Transformed
Minimum	565	6.3370
Maximum	36,118	10.4946
Range	35,553	4.1576
Mean ± standard deviation	6,333 ± 8,154	8.2171 ± 1.0093
Coefficient of variance	1.2875	0.1228
Back-transformation	-	3,704 x/ 2.7436
Median	3,544	8.1705
No. of bins	5	5
Bin size	8,345	1.0329

Comparison of statistical parameters of raw and transformed ush CHC data.

Table 6.

Tests of normality for transformed ush lnCHC data (n = 40)

Parameter	Observed value	Critical value	p at critical value	Reject null hypothesis?
χ2	6.9487	7.78	0.10	do not reject
√b1	0.3788	0.450	0.10	do not reject
b2	2.7463	2.19–3.67	0.10	do not reject

Null hypothesis: there is no difference between the distribution pattern of the transformed data and the normal distribution. The distribution of transformed lnCHC values passes three tests for normality: χ² goodness-of-fit test (v = 4 degrees of freedom), skewness (√b₁) test, and kurtosis (b₂) test. Critical values are those for the most significant tabulated p values¹⁹ that were not surpassed by the observed test value.

Table 5.

Tests of normality for raw ush CHC data (n = 40)

Parameter	Observed value	Critical value	p at critical value	Reject null hypothesis?
χ2	226.7998	18.47	0.001	reject
√b1	2.5905	0.870	0.01	reject
b2	9.5806	1.89–5.04	0.01	reject

Null hypothesis: there is no difference between the distribution pattern of the observed data and the normal distribution. The distribution of raw CHC values fails three tests for normality: χ² goodness-of-fit test (v = 4 degrees of freedom), skewness (√b₁) test, and kurtosis (b₂) test. Note that all three failures are at very significant levels of probability.

Discussion

I have demonstrated that the distribution of a large sample (n = 200) of wild-type total CHC values and that of ush mutant lamellocyte CHC values (n = 40), despite initial qualitative tests, do not conform to normality. I further demonstrate that these same ranges of CHC values do not violate the log-normal distribution pattern. Two conclusions can be extracted from these observations: (1) the assumption of normality when comparing mean CHC values is erroneous; and (2) the assumption of log-normality is valid.

Thus I propose that analysis of raw hemocyte counts and concentrations be performed as follows:^{11,12,16,20,22}

1. Assume log-normality: determine the ln of each raw value (n.b.: when comparing not just total CHC, but CHC of hemocyte classes, sometimes a given sample might have a count of, say, zero lamellocytes; in such a case, add 1 to each raw value in all classes; ln 1 = 0).

2. Use the transformed values obtained in Step 1 to obtain the mean and standard deviations.

3. Use tests of significance (e.g., Student's t-test) using the values obtained in Step 2 and draw conclusions.

4. Back-transform the means and standard deviations obtained in Step 2: use the exponential function.

5. Express back-transformed mean and standard deviation as: mean x/standard deviation (the term “x/” is expressed “times or divided by”, just as “±” is expressed “plus or minus”).

Figures depicting comparisons of hemocyte counts/concentrations can still employ bar graphs and error bars (Fig. 2). Presentation of back-transformed values (Fig. 2C)^12,21 are ideal. However, transformed values can also be presented (Fig. 2B)¹¹ if appearance is a concern.

The comparison of CHC values for hemocyte classes such as lamellocytes is also a concern for many researchers. When all larval hemolymph samples in a given larval class produce non-zero lamellocyte CHC values (as they do in tumorous ush larvae) the log-normal transformation is valid (Tables 4–6; importantly, the same can be said of ush total CHC values; data not shown). It is suggested that a researcher nonetheless confirm log-normality as different tumor-inducing genetic backgrounds may produce different distributions of lamellocyte CHC values. When lamellocyte populations are small (<3% of total CHC per larva) and not present in most larvae in a sample, then the distribution of values will include a very large zero bin and multiple small non-zero bins. While it is possible that a model for such a distribution may one day be described, I have not been able to find a probability distribution function that would apply to such a pattern. Furthermore, the distribution of just the non-zero lamellocyte CHC values in Canton-S larvae, both raw and transformed by the natural logarithm, fails the test for normality (data not shown). Fortuitously, genetic backgrounds that produce lamellocyes in a minority of larvae tend to produce very low concentrations of lamellocytes. For instance, 26 of the 200 Canton-S larvae discussed herein exhibited at least one lamellocyte. Only one larva of the 26 exhibited a lamellocyte percentage of greater than 2.02%. Furthermore, I have neither observed nor read of genetic backgrounds that produce infrequent and large populations of lamellocytes; thus whether backgrounds that produce negligible infrequent and small lamellocyte populations actually need a test of significance to demonstrate how low they are is up to the researcher.

Of course, the values of log-normal transformations can be affected by the raw data units that are chosen. For example, transformation of 200 CHC values expressed in terms of cells per liter (as opposed to cells per microliter) produces an lnCHC value of −5.0125 ± 0.6098, which differ considerably from the values reported herein. But as long as a researcher can demonstrate or cite a log-normal distribution, then any tests of significance will be valid.

It must be pointed out that it is possible that there is at least one distribution pattern other than the log-normal that is an even better description of possible CHC values. For instance, regression analysis by way of the trendline function in Microsoft Excel can produce fourth- and fifth-order polynomial functions that fit far more closely (r > 0.99) to the data than does the log-normal assumption. However, such functions, when extended even one or two standard deviations to the right of the boundary of data reported herein, predict huge frequencies in the hundreds and thousands (unpublished observations). Such predictions, in the absence of any supportive information, must be rejected for now.

It is also worth noting that not every published analysis of hemocyte counts/concentrations that has assumed normality is necessarily incorrect in its conclusions. Depending on the observed values, two means may have been separated widely enough that even the assumption of normality would not interfere with the detection of a difference. Importantly, the power of the justified assumption of log-normality lies in the ability to reveal significant differences between groups that would not have been evident otherwise.

In summary, the visually and intellectually unappealing large standard deviations that are obtained when analyzing hemocyte counts/concentrations should not be surprising in the examination of biological systems. Large values for standard deviations of CHC are not necessarily a problem; the real problem is the unfounded and erroneous assumption of a normal distribution of raw values and a refusal to accept the nature and extent of variability in a given phenotypic character, even in an allegedly homogeneous laboratory population. Environment, chance and the as-yet-unexplained will always play roles in phenotype, including in hemocyte counts.

Materials and Methods

Fly stocks.

Canton-S served as a wild-type stock. ush^VX22/ush^r24 larvae were obtained as described.¹²

Egglays.

Flies were maintained using standard cornmealyeast-agar medium. All experiments took place at 25°C. Experimental egglays were allowed to take place in vials containing fly medium for four hours. After four hours had transpired, adults were moved to a new vial and any eggs laid during the egglay period were allowed to develop at 25°C. Hemolymph samples were obtained from individual feeding third-instar (L3) larvae at 120 ± 4 hr after the initiation of the egglay.

Determination of circulating hemocyte concentration (CHC).

CHC was determined as described.¹⁶

Statistical analysis.

n = sample size. Minimum = lowest value in sample. Maximum = greatest value in sample. Range = maximum − minimum. Mean = (sum of all individual CHC values)/(number of CHC values). Standard deviation = [∑(individual CHC value − mean CHC)²]/(n − 1). Median = middle ordinal value or mean of two middle ordinal values, when all CHC values are listed in increasing order. Bin size: h = [3.5 × (standard deviation)]/n^1/3.¹⁷ h was rounded down to the nearest integer. All bins have a width of h. Modal bin = most populous bin. χ² goodness-of-fit test was performed as described.¹⁸ Skewness (√b₁) and kurtosis (b₂) were calculated as described.¹⁹ Backtransformation: the exponentials of the values of the mean and standard deviation of lnCHC values.²⁰

Abbreviations

CHC

circulating hemocyte concentration