Indexing Disease Progression at Study Entry with Individuals At-Risk for Huntington Disease

Abstract

The identification of clinical and biological markers of disease in persons at risk for Huntington Disease (HD) has increased in efforts to better quantify and characterize the epoch of prodrome prior to clinical diagnosis. Such efforts are critical in the design and implementation of clinical trials for HD so that interventions can occur at a time most likely to increase neuronal survival and maximize daily functioning. A prime consideration in the examination of prodromal individuals is their proximity to diagnosis. It is necessary to quantify proximity so that individual differences in key marker variables can be properly interpreted. We take a data-driven approach to develop an index that can be viewed as a proxy for time to HD diagnosis known as the CAG-Age Product Scaled or CAP_S. CAP_S is an observed utility variable computed for all genetically at-risk individuals based on age at study entry and CAG repeat length. Results of a longitudinal receiver operating characteristic (ROC) analysis showed that CAP_S had a relatively strong ability to predict individuals who became diagnosed, especially in the first 2 years. Bootstrap validation provided evidence that CAP_S computed on a new sample from the same population could have similar discriminatory power. Cutoffs for the empirical CAP_S distribution can be used to create a classification for mutation-positive individuals (Low-Med-High) that is useful for comparison with the naturally occurring mutation-negative Control group. The classification is an improvement over the one currently in use as it is based on observed data rather than model-based estimated values.

INTRODUCTION

Huntington disease (HD) is an autosomal dominant illness of the brain caused by the trinucleotide cytosine–adenine–guanine (CAG) expansion in the gene of the protein huntingtin. People affected with HD, known as mutation-positive individuals, have a CAG repeat length between 36 and 250 [Brinkman et al., 1997; Bruland et al., 1999; Kremer et al., 1994; Nance et al., 1999]. There is an inverse relationship between CAG repeat length and age of HD diagnosis with longer lengths being associated with earlier diagnosis. Various statistical models have been developed to account for this phenomenon [Andresen et al., 2007a, 2007b; Andrew et al., 1993; Brinkman et al., 1997; Gutiérrez and MacDonald, 2002, 2004; Langbehn et al., 2004, 2010; Langbehn and Paulsen, 2007; Lucotte et al., 1995; Maat-Kievit et al., 2002; Rubinsztein et al., 1996, 1997; Squitieri et al., 2000; Stine et al., 1993].

The PREDICT-HD study is an ongoing observational study including 32 sites from the United States, Canada, Australia, Germany, Spain and the United Kingdom [Paulsen et al., 2006]. Recruits consist of a large number of participants who have undergone genetic testing for the HD gene mutation, but were not clinically diagnosed with the disease at the time they entered the study. These at-risk participants for HD are described as “prodromal” because they are mutation-positive (CAG repeat length ≥ 36) and show evidence of disease progression based on several key clinical and biological markers [Paulsen, 2010; Paulsen et al., 2008, 2010a]. PREDICT-HD is a prevalent cohort design as it involves cross-sectional sampling criteria for study inclusion. Participants must be adults (≥ 18 years), and those who are mutation-positive for HD must not show manifest signs at study entry as determined by the absence of a diagnosis.

One goal of prodromal research is to better characterize the natural history of HD so that preventive intervention can be initiated at the time best suited to maximize success. Previous research using various clinical and biological markers suggests that the prodromal phase will include an insidious decline followed by a precipitous deterioration about 12 years prior to clinical diagnosis [Campodonico et al., 1996; Paulsen et al., 2006, 2008]. Since the specific epoch of time considered during the relatively long prodrome of HD appears to vary, methods to classify prodromal individuals are essential to understanding the success or failure of interventions.

The prevalent cohort design of PREDICT-HD presents a challenge for statistical analysis as inferences can be biased if certain study characteristics are ignored. Individuals with HD are mutation-positive at birth and this time might be considered the initiating event and the natural time origin for studying disease progression. A problem with using birth as the time origin is that a prevalent cohort design like PREDICT-HD has length bias [Zelen et al., 1969, 2005]. Individuals with a greater time to diagnosis since birth will have a higher probability of being selected for the study, and the selected sample will not be representative of the general population of HD.

Though birth might be considered the natural initiating event, participants are not observed until entry into the study. Study entry is when participants join the cohort, and more importantly, become part of the risk set for determining survival probabilities. For these reasons, the time origin for prevalent cohort designs is commonly defined as the point of entry into the study. The time metric is duration, defined as the current age in years minus the age at study entry. Upon entering the study, individuals are tracked over a number of years. Interest often focuses on changes in a key marker, such as striatal volume, over the study duration.

To minimize length bias and make proper inferences, it is desirable to have a proxy variable of HD progression at the time of study entry. One participant might have a shorter duration to diagnosis than another due to a greater progression, and this must be taken into account in the interpretation of statistical results. Two variables important in characterizing disease progression are CAG repeat length and age (Langbehn et al., [2010]).

A number of proxy variables for baseline HD progression have been suggested, with the work of Langbehn and colleagues being the most pertinent for the present purposes (Langbehn et al., [2004, 2010]). The Langbehn et al. [2010] approach is based on a logistic survival model incorporating age and CAG length. In most applications (see e.g., [Aylward et al., 2010]), an ordered categorical variable is used with groups representing three levels of estimated time to HD diagnosis (TTD). The groups are (i) Far: estimated TTD > 15 years; (ii) Middle (Mid): 9 years < estimated TTD ≤ 15 years; and (iii) Near: estimated TTD ≤ 9 years.

Langbehn et al. had the laudable goal of developing a general model of TTD when no prospective study of prodromal HD existed. PREDICT-HD has conducted comprehensive annual assessments for prodromal HD participants for over 10 years, and there are currently 137 individuals prospectively diagnosed. This wealth of longitudinal data, in concert with the prospectively diagnosed patients evaluated over the course of their transition from presymptomatic to diagnosed, offer a rich resource from which to construct a new classification system.

There are two goals of this paper. The first goal is to develop a “utility variable” for PREDICT-HD participants and other participants in the HD prodrome, which is a summary of two key variables observed at study entrance, age and CAG repeat length. The utility variable can be treated as a proxy variable of TTD for the duration of the study and used as a covariate or control variable to account for variation in disease progression in order to properly interpret the results of statistical analysis.

The second goal is to update the classification of study participants based on the utility variable. Rather than emphasize the distance to HD diagnosis that Far-Mid-Near implies, the classification of Low-Medium-High is suggested to denote the amount of cumulative “disease burden” that participants have at the time they enter the study.

The utility variable is developed from a data-driven approach using a standard parametric survival model, the accelerated failure-time (AFT) model [Klein and Moeschberger, 2003]. It is argued that the adopted model has scientifically useful parameter interpretations and is highly predictive of TTD. We refer to the utility variable as the CAG-Age Product (CAP), as it is computed by multiplying age at entry (Age₀) by a scaling of CAG repeat length, as explained below. A scaled version of CAP, CAP_S, is also discussed that is especially useful for comparing mutation-negative individuals with mutation-positive individuals. Such comparison is a major preoccupation of PREDICT-HD analysis (see, e.g., [Aylward et al., 2010]) and other prodromal HD research, and prepares the way for preventive clinical trials.

METHODS

Overview

Two statistical analyses were performed. The first was concerned with development of CAP and CAP_S, and an evaluation of predictive performance. The second analysis was concerned with development of the Low-Med-High classification and comparison with the Far-Mid-Near groups. The analysis sections provide an overview of the methods and details can be found in the Appendix.

Participants

The first analysis was based on N = 730 prodromal individuals with at least 1 year and up to 7 years of follow-up data. These were participants who tested positive for the HD mutation, but did not have motor features indicating onset of diagnosable HD at the time of enrollment. Participants were seen yearly by clinicians experienced in the evaluation of movement disorders and specifically trained in administration of the Unified Huntington’s Disease Rating Scale (UHDRS) for PREDICT-HD [Huntington Study Group, 1996]. Of the 730 prodromal individuals, 137 received a HD diagnosis over the course of the study.

All aspects of the study were approved by the Institutional Review Board at each participating institution, and all aspects of the study are in compliance with the Declaration of Helsinki.

In accordance with clinical practice, diagnosis was made on the basis of “an otherwise unexplained characteristic movement disorder,” operationally defined as a score of 4 on the HD Diagnostic Rating Scale of the UHDRS. A rating of 4 indicates that the clinician had ≥ 99% certainty that the participant showed “unequivocal presence of an otherwise unexplained extrapyramidal movement disorder.” This method of diagnosis is “standard” in the respect of being approved by authorities such the Huntington Study Group (HSG)[Huntington Study Group, 1996]. Participants were excluded from the analysis if they received a rating of 4 at baseline.

Portions of the second analysis added 233 control participants, for a total sample size of N = 963. The control participants were offspring of at least one HD-diagnosed parent, but tested negative for the HD mutation (CAG repeat length < 36). Additional information about the participants and the PREDICT-HD study can be found in [Duff et al., 2010a; Nopoulos et al., 2011; Paulsen et al., 2010b; Stout et al., 2011].

STATISTICAL ANALYSIS I: MODEL AND UTILITY VARIABLE DEVELOPMENT

The first step in the analysis was a data-driven selection of an appropriate AFT model. The response variable was duration, which was the years since entry to HD diagnosis for individuals who received a diagnosis, and the years since entry to the last observation time for individuals who did not receive a diagnosis. All possible subsets of models with predictors of Age₀, CAG, and their interaction (i.e., Age₀ × CAG) were considered. Reduced models were defined by having one or two of the predictor terms in the structural portion of the AFT. For example, one reduced model had Age₀ as the only predictor, and another had Age₀ and Age₀ × CAG as the predictors, etc.

In applications of the AFT, the exact distribution of the error term is typically unknown and various possibilities are considered. Therefore, the statistical analysis consisted of fitting models defined by combinations of number of predictors and different types of error distributions. There were seven structural models and five error distributions for a total of 35 fitted models. Each model was estimated using maximum likelihood methods assuming right censoring. To assess model fit, Akaike’s information criterion (AIC) was computed for each fitted model. In addition, the prediction error (PE) of the fitted model for the 137 HD diagnosed individuals was also computed (PE =∑|Ŷ − Y|). All models were estimated using the survival package [Therneau and original Splus->R port by Thomas Lumley, 2009] of the R computer program [R Development Core Team, 2010].

The best fitting model according to the AIC had the predictors Age₀ and Age₀ × CAG with a normal error distribution, AIC = 888.1599, PE = 539.9115. The second best fitting model according to the AIC had the same predictors, but a logistic error distribution, AIC = 888.4643, PE = 496.6704. The difference in the AIC values (ΔAIC = 0.3044) indicated the second best fitting model had essentially equal fit as the first, based on the common evaluation criterion of ΔAIC < 2 [Burnham and Anderson, 2002]. The logistic model had a smaller PE value indicating less prediction error for those actually diagnosed. Therefore, the logistic AFT model was selected as the working model for continued development.

Having selected the model with the predictors Age₀ and Age₀ × CAG, certain simplifications were made to yield a scientifically meaningful model with useful parameter interpretations (see the Appendix). The final AFT prediction model was

$$\widehat{Y}=\text{exp}[\alpha +\beta ({\mathit{\text{Age}}}_0)(\mathit{\text{CAG}}+C)].$$ (1)

Parameter estimates obtained via maximum likelihood are shown in Table I. Since C is a ratio of two parameters, the Delta method was used to compute its standard error (see [Casella and Berger, 2002]).

Table I.

Parameter estimates, standard errors (SEs), and 95% confidence intervals (CIs) for the model of Equation (3).

Parameter	Estimatea	SE	95% CI
α	4.4196	0.3364	3.7602, 5.0790
β	−0.0065	0.0007	−0.0079, −0.0051
C	−33.6600	0.7046	−35.0409, −32.2790
log(σ)	−0.8451	0.0710	−0.9843, −0.7060

^ap < 0.0001 for all estimates.

The parameter estimates of Table I provide useful information. The sign of the estimate and the CI limits for C are negative. Assuming the parameter C is negative, CAG + C can be thought of as a type of calibrated or corrected CAG, with C being the correction factor. Thus, we define the corrected CAG repeat length, CAG_C, as

$${\mathit{\text{CAG}}}_C=\mathit{\text{CAG}}+C.$$ (2)

Substantively, CAG_C indexes the toxicity of the mutant huntingtin gene. Individuals with higher values have greater toxicity and those with lower values have less toxicity.

In addition to mutation toxicity, the other important consideration is Age₀. Age₀ is an index of the length of exposure to the mutation toxicity from birth to study entry. It is also the truncation time required to account for length bias [Wolkewitz et al., 2010]. Taking toxicity and length of exposure into account, we define the CAG and Age₀ product (CAP) as,

$$\mathit{\text{CAP}}={\mathit{\text{Age}}}_0\times (\mathit{\text{CAG}}+C)={\mathit{\text{Age}}}_0\times {\mathit{\text{CAG}}}_C.$$ (3)

Based on the data, CAP = Age₀ × (CAG − 33.6600). CAP is interpreted as an index of the cumulative toxicity of mutant huntingtin at study entry and is nearly identical to the measure, sometimes called “genetic burden,” that was introduced by [Penney et al., 1997]. Hence, participants with a larger cumulative genetic toxicity at study entry may likely develop HD sooner. It is emphasized that the CAP score is an observed score computed on an individual’s actual age at study entry and CAG repeat length.

Given the equations above, the CAP model for estimated TTD is written as

$$\widehat{Y}=\text{exp}(\alpha +\beta \times \mathit{\text{CAP}}).$$ (4)

Using the estimates from Table 1, we have Ŷ = exp(4.4196 − 0.0065 × CAP). An important feature of Equation (4) is that estimated TTD is completely determined by CAP based on the fitted model. For this reason, CAP can be regarded as a proxy variable for estimated TTD. The utility is that CAP is computed based on the data, yet it is a substitute for the estimated TTD that is potentially computed from the model.

To enhance the utility of CAP, it can be scaled based on the estimated survival probabilities. Survival probabilities are convenient for studying the process of a disease and are a common means of communicating likelihood of an event, such as HD diagnosis [Kleinbaum and Klein, 2005].

For the survival probability scaling, 5 years is considered a reasonable landmark time, as it allows for a sufficient period of disease progression and is the common duration of clinical trials. Focus is on the key survival probability of 0.5, representing a 50-50 chance of a diagnosis. Given the assumptions mentioned in the Appendix, the scaled CAP, denoted as CAPs, is computed as

$${\mathit{\text{CAP}}}_S=\frac{\mathit{\text{CAP}}}{\left[\frac{\alpha -\text{log}(5)}{-\beta }\right]}.$$ (5)

Based on the data, CAP_S = CAP / 432.3326. CAP_S has a convenient interpretation: CAP_S < 1 indicates a 5-year diagnosis probability of less than 0.5; CAP_S = 1 indicates a 5-year probability equal to 0.5; and CAP_S > 1 indicates a 5-year probability greater than 0.5. CAP_S then, is interpreted as an index of the scaled cumulative mutation toxicity, with the scaling being in reference to a 50-50 chance of diagnosis by 5 years.

An additional practical issue is that mutation-negative individuals (controls) are often considered along with mutation-positive individuals in PREDICT-HD analyses. Controls provide a convenient reference group for evaluating progression of HD in prodromal individuals. The control individuals have at least one parent diagnosed with HD, but their CAG repeat length is less than 36, indicating they will never develop HD. Control individuals have no mutation toxicity, which is represented by setting CAP_S = 0 for these individuals. Suppose the probability of diagnosis after 5 years is D₅. Then the final definition of CAP_S is,

$$\begin{array}{cc}\hfill {\mathit{\text{CAP}}}_s=0\hfill & \hfill \mathit{\text{if mutation−negative}}(D_5=0),\hfill \\ \hfill {\mathit{\text{CAP}}}_s<1\hfill & \hfill \mathit{\text{if}}{D}_5<0.5,\hfill \\ \hfill {\mathit{\text{CAP}}}_s=1\hfill & \hfill \mathit{\text{if}}{D}_5=0.5,\hfill \\ \hfill {\mathit{\text{CAP}}}_s>1\hfill & \hfill \mathit{\text{if}}{D}_5>0.5.\hfill \end{array}$$ (6)

Table II shows CAP_S along with other relevant scores and probabilities for hypothetical individuals aged 50 at study entry and having various CAG repeat length. The CAG repeat lengths are classified as mutation-negative (no penetrance), mutation-positive but reduced penetrance (36–40), and mutation-positive but full penetrance (> 40). These penetrance classifications are based on proportions of individuals in the population expected to display HD symptoms sufficient to warrant diagnosis at some point [Langbehn et al., 2004].

TABLE II.

Scores, probabilities, and estimated TTD for hypothetical individuals aged 50 at study entry with various CAG repeat length.

Age0	CAG	CAGC	CAP	CAPS	D̂5	Ŷ
Mutation-Negative (No Penetrance)
50	≤35	–	–	0.00	0.00	–
Reduced Penetrance
50	36	2.34	117.00	0.27	0.01	38.74
50	37	3.34	167.00	0.39	0.02	27.97
50	38a	4.34	217.00	0.50	0.04	20.19
50	39	5.34	267.00	0.62	0.08	14.57
50	40	6.34	317.00	0.74	0.15	10.52
Full Penetrance
50	41b	7.34	367.00	0.85	0.27	7.59
50	42c	8.34	417.00	0.97	0.45	5.48
50	43	9.34	467.00	1.08	0.63	3.96
50	44d	10.34	517.00	1.20	0.79	2.86
50	45	11.34	567.00	1.32	0.89	2.06
50	46	12.34	617.00	1.43	0.94	1.49
50	47	13.34	667.00	1.55	0.97	1.07
50	48	14.34	717.00	1.66	0.99	0.78
…	…	…	…	…	…	…
50	61e	27.34	1367.00	3.17	> 0.99	0.01

Note.

^aSample minimum;

^blower quartile;

^cmedian;

^dupper quartile;

^emaximum.

The AFT model of Equation (4) can be expressed in terms of CAP_S. Setting β^* = −(α − log(5)), the CAP_S AFT model is,

$$\widehat{Y}=\text{exp}(\alpha +{\beta }^{*}\times {\mathit{\text{CAP}}}_S).$$ (7)

Based on the data, Ŷ = exp(4.4196 − 2.8102 × CAP_s.

The parameters of Equation (7) have the following interpretations. By definition, CAP_S = 0 for mutation-negative individuals (see Equation (6)) meaning that α and β^* are irrelevant for these individuals. For mutation-positive individuals, CAP_S > 0, and α is the intercept and β^* is the slope or acceleration of their scaled cumulative toxicity. As indicated by the CI in the second row of Table I, β is assumed to have a negative sign. Thus, as CAP_S increases, the expected TTD decreases. The acceleration is estimated to be β̂^*=−2.8102, meaning a unit increase in CAP_S is accompanied by a 2.8102 decrease in log duration.

Predictive Performance and Bootstrap Validation

An important issue in the development of the CAP_S utility variable is the extent to which it predicts HD diagnosis. CAP_S is suggested as a proxy for cumulative disease burden, which implies that individuals with higher scores are closer to diagnosis than individuals with lower scores. A popular means of assessing predictive performance is based on the receiver operating characteristic (ROC) curve. In this context, the area under this curve (AUC) is an index of the ability of CAP_S to discriminate between diagnosed and non-diagnosed individuals. AUC varies between 0.5 and 1.0 for reasonable models with higher values being better [Miller et al., 1993].

Since PREDICT-HD is a prospective study, diagnosis accumulates among the cohort over time. This time dependence should be taken into account when constructing the ROC curve. To evaluate the predictive performance of CAP_S, longitudinal AUC was computed based on censored survival times using the methods of [Heagerty and Zheng, 2005]. The R package risksetROC was used for this analysis [Heagerty and packaging by Saha, 2011]. In addition to considering AUC as a function of study duration, an overall index was computed that summarizes the AUC over the time span, known as the integrated AUC (iAUC).

It is well known that predictive performance will decrease when a statistical model developed in one sample is applied to an independent sample. It is desirable to adjust for this “optimism” to provide a more realistic appraisal of predictive performance for out-of-sample data originating from the same population. One method of adjustment is the enhanced bootstrap [Efron, 1986; Efron and Tibshirani, 1993], the details of which are found in the Appendix. The enhanced bootstrap produces adjusted AUC and iAUC. The extent of similarity of the bootstrap-adjusted and unadjusted values is an indication of the interval validity of the AFT and CAP_S [Harrell et al., 1996].. Close agreement suggests that when CAP_S is computed based on a new sample from the same population, it will function similarly as in the original sample.

Bootstrap-adjusted and unadjusted AUC and iAUC were examined using the N = 730 mutation-positive individuals. There were N = 137 participants who received a diagnosis over the course of the study (18.77%), and N = 593 individuals who did not (81.23%).

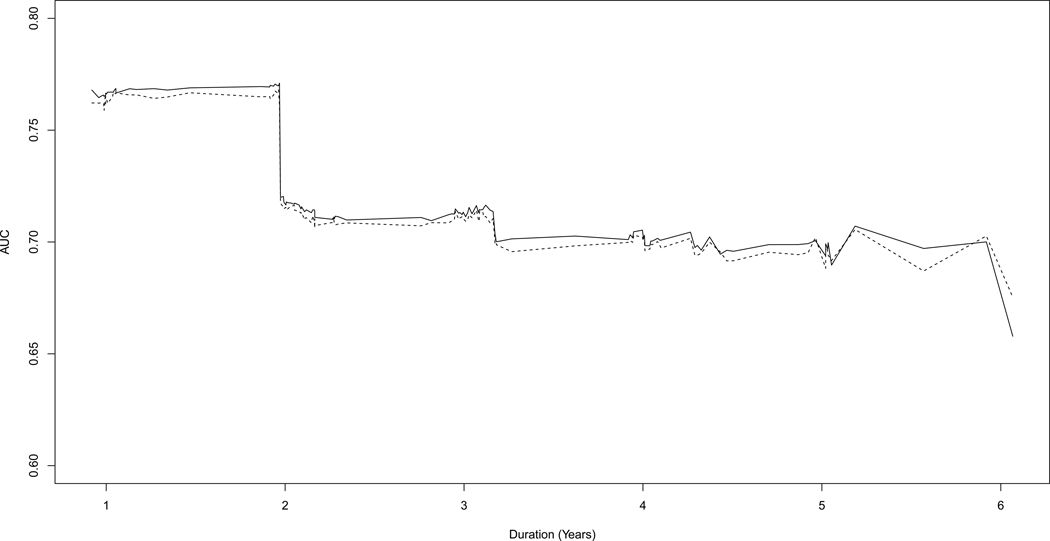
Results of the analysis show the overall unadjusted index was iAUC = 0.7203 and the bootstrap-adjusted value was slightly smaller, 0.7172. Figure 1 shows the AUC as a function of duration. The unadjusted values are depicted by a solid line and the bootstrap-adjusted values with a dashed line. As the figure shows, the AUC (adjusted and unadjusted) was relatively high (AUC > 0.75) for 2 years duration, then dropped to around 0.70 until the last time point. The precipitous drop at 2 years was due to a small group of participants with the highest CAP_S values whose survival probability change from 1 to 0 at this time. The bootstrap-adjusted AUC was only slightly lower that the unadjusted version indicating that CAP_S may have similar discriminatory power for a new sample from the same population.

Figure 1.

AUC as a function of duration using CAP_s as the baseline predictor. Unadjusted AUC is depicted by a solid line, and bootstrap-adjusted AUC is depicted by a dashed line.

STATISTICAL ANALYSIS II: GROUP CLASSIFICATION

CAP_S can be used whenever an index of proximity to diagnosis at study entry is needed. For example, CAP_S might be used in a regression model as a predictor of striatal volume to investigate prodromal indicators of disease progression (see [Aylward et al., 2010]).

There are situations in which researchers might consider using groups based on a categorization of the CAP_S distribution. When mutation-negative individuals (controls) and mutation-positive individuals (cases) are to be analyzed together, grouping has advantages. Mutation-negative individuals constitute a naturally occurring group, and there is no within-group variability of cumulative HD toxicity or proximity to diagnosis. This is reflected by the fact that controls always have CAP_S = 0.

Since the controls constitute a well-defined group, it is perhaps natural for some researchers to form similar mutation-positive groups for comparison. A dichotomous distinction, such as control/case groups, is too coarse a formulation as it ignores the CAP_S variability among mutation-positive individuals (only CAG repeat length is needed for a dichotomous classification). To take advantage of potentially important between-subjects variability in CAP_S, it is desirable to categorize the CAP_S distribution for mutation-positive individuals.

As mentioned in the introduction, there have been previous attempts to formulate groups representing proximity to diagnosis, the Far-Mid-Near of Langbehn et al. being the most relevant. In previous analyses [Aylward et al., 2010; Beglinger et al., 2008; Biglan et al., 2009; Duff et al., 2010a; Klöppel et al., 2009; Nopoulos et al., 2010; Paulsen, 2010; Paulsen et al., 2008, 2010a, 2010b; Rowe et al., 2010; Stout et al., 2011], the formulation of the Far-Mid-Near groups was based on predicted values rather than observed scores with the criteria for categorizing being unclear. To remedy this, we propose using CAP_S and estimated TTD as the basis for grouping. This will help ensure maximal potential group differences of estimated primary outcomes. For continuity with the previous analysis, three groups will be considered. To distinguish the new groups from the old, the descriptors Low, Medium (Med), and High are used.

The cutoffs for group membership among mutation-positive individuals were determined by the algorithm outlined in the Appendix. This resulted in the rounded cutoffs values of CAP_S = 0.67 (lower cutoff), and CAP_S = 0.85 (upper cutoff). Based on Equation (3), these values corresponded to estimated durations of Ŷ = 12.78 and Ŷ = 7.59 years, respectively. Based on the cutoffs, the mutation-positive study participants were classified into the three groups. The fourth Control group consisted of the mutation-negative individuals with CAP_S = 0.

Examination of group differences

There are key variables used by PREDICT-HD researchers to study the progression of HD. These include baseline imaging, motor, cognitive, and psychiatric measures. Descriptive statistics for the key variables and some demographic variables (gender, age, CAG repeat length, education) by classification (Low-Med-High and Far-Mid-Near) were computed. The N = 233 control participants (Control group) were included for a more thorough comparison (total N = 963).

As for the key variables, the imaging measure was striatal volume (as a ratio to total intracranial volume) [Paulsen et al., 2010a], and the motor measure was the UHDRS total motor score. There were two cognitive measures, the Symbol Digit Modalities Test (SDMT), which is a measure of processing speed, and the Hopkins Verbal Learning Test-Revised (HVLT-R), which is a test of immediate recall memory. Three psychiatric measures were included, the Frontal System Behavior Scale (FrSBe) yielding a total score and an executive subscale score, and the Schedule of Compulsions, Obsessions, and Pathologic Impulses (SCOPI) total score. The FrSBe is a self-report symptom inventory that measures behaviors associated with damage to frontal systems of the brain; the executive subscale evaluates problems with working memory, planning, problem solving, and insight [Duff et al., 2010b; Grace and Malloy, 2001]. The SCOPI is a multidimensional self-report measure composed of 47 items with a total score that is the sum of the obsessive checking, obsessive cleanliness, and compulsive rituals subscales [Beglinger et al., 2008; Watson and Wu, 2005].

The difference between the new and old classifications is summarized in the contingency table shown in Table III. As indicated by the values above the diagonal, the new grouping tended to classify study participants into more severe disease groups compared to the Far-Mid-Near classification. For example, the new classification moved 93 of the 275 participants in the Far group (34.55%) to the Med group, and 113 of the 276 in the Mid group (41.30%) to the High group.

Table III.

The relationship between the Low-Med-High classification and the Far-Mid-Near classification.

		Proposed Classification
		Low	Med	High	Total
Current	Far	182	93	0	275 (37.67%)
Classification	Mid	0	163	113	276 (37.81%)
	Near	0	0	179	179 (24.52%)
	Total	182 (24.93%)	256 (35.07%)	292 (40.00%)	730

Descriptive statistics for the key variables by classification are shown in Table IV. Note this is a comparison of Control-Far-Mid-Near and Control-Low-Med-High, with the Control group consisting of the same individuals in both classifications. One of the dramatic differences between the classifications is the sample size of the groups as the percentage of the total (N = 963). Whereas the Near group consists of 18.59% of the total in the old classification, the comparable High group consists of 30.22% in the new classification.

Table IV.

Descriptive statistics of key variables for two classifications.

Old Groups:	Control	Far	Mid	Near	Statistic / p-value	Group Contrasts
New Groups:	Control	Low	Med	High
N (% of total)	233 (24.20%)	275 (28.56%)	276 (28.66%)	179 (18.59%)	-	-
	233 (24.20%)	182 (18.90%)	256 (26.58%)	292 (30.32%)	-
Gender (% F)	63.52	67.64	61.96	58.66	Chi-sq = 4.11, p = 0.25	ns
	63.52	67.03	65.23	59.25	Chi-sq = 3.58, p = 0.31	ns
Age Mean (SD)	43.48 (11.63)	36.54 (8.13)	42.17 (9.74)	44.98 (10.16)	F = 29.36, p < 0.0001	C, N, M > F
	43.48 (11.63)	35.52 (7.49)	41.77 (9.32)	44.33 (9.76)	F = 33.93, p < 0.0001	C, H > M > L
CAG Mean (SD)	20.01 (3.49)	41.00 (1.57)	42.55 (2.14)	44.23 (3.05)	F = 4347.48, p < 0.0001	C < F < M < N
	20.45 (3.49)	40.76 (1.56)	42.00 (1.99)	43.72 (2.77)	F = 4271.10, p < 0.0001	C < L < M < H
Education Mean (SD)	14.65 (2.66)	14.55 (2.50)	14.35 (2.80)	14.16 (2.74)	F = 1.36, p = 0.25	ns
	14.65 (2.66)	14.52 (2.52)	14.43 (2.68)	14.24 (2.76)	F = 1.09, p = 0.35	ns
Striatal Volume Mean (SD)a	15.99 (2.14)	14.92 (2.19)	12.99 (2.33)	10.94 (2.45)	F = 150.93, p < 0.0001	C > F > M > N
	15.99 (2.14)	15.22 (2.15)	13.69 (2.25)	11.59 (2.52)	F = 142.91, p < 0.35	C > L > M > H
UHDRS Motor Score Mean (SD)	2.65 (3.35)	3.37 (3.73)	4.71 (4.76)	7.87 (6.81)	F = 48.69, p < 0.0001	C, F < M < N
	2.65 (3.35)	2.99 (3.33)	4.29 (4.40)	6.82 (6.35)	F = 41.70, p < 0.0001	C, L < M < H
Symbol Digit Mean (SD)	54.03 (8.95)	54.12 (11.30)	49.25 (10.46)	44.06 (11.05)	F = 49.28, p < 0.0001	C, F > M > N
	54.03 (8.95)	56.41 (11.44)	51.20 (10.46)	45.42 (10.93)	F = 50.33, p < 0.0001	C, L > M > H
HVLT Mean (SD)	28.11 (4.43)	27.76 (4.24)	26.18 (5.13)	23.84 (5.42)	F = 33.46, p < 0.0001	C, F > M > N
	28.11 (4.43)	28.03 (4.04)	26.77 (4.95)	24.56 (5.37)	F = 30.58, p < 0.0001	C, L > M > H
FrSBe Total Mean (SD)	55.19 (12.90)	59.79 (19.78)	61.62 (19.87)	57.09 (18.87)	F = 6.00, p = 0.0001	M > C, N; F > C
	55.19 (12.90)	59.42 (20.05)	60.96 (19.76)	59.07 (19.30)	F = 4.27, p = 0.0055	C < M
FrSBe Executive Mean (SD)	24.59 (6.79)	26.53 (10.00)	27.47 (9.65)	25.80 (9.54)	F = 4.40, p = 0.0044	C < M
	24.59 (6.79)	25.23 (9.98)	26.89 (9.53)	26.85 (9.86)	F = 3.36, p = 0.0183	C < M, H
SCOPI Mean (SD)b	73.54 (18.91)	76.66 (21.81)	77.52 (21.30)	71.01 (21.29)	F = 2.02, p = 0.1128	ns
	73.54 (18.91)	75.00 (21.39)	79.30 (22.12)	72.65 (20.88)	F = 2.34, p = 0.0724	ns

Note.

^aStriatal Volume comparison is based on a sample size of N = 798 (Control = 192, Low = 163, Mid = 218, High = 225).

^bSCOPI comparison is based on a sample size of N = 546 (Control = 175, Low = 113, Mid = 130, High = 128).

The descriptive statistics of the other demographic variables were similar for the two classifications. The same can be said for motor score, symbol digit, HVLT, and striatal volume. There were differences between the two classifications for one of the psychiatric variables. For FrSBe Executive, there was a statistically significant difference between the High group and Control in the new classification, but not a similar difference for the two most distant groups in the old classification (i.e., Near and Control). For the remaining psychiatric variables, (FrSBe Total and SCOPI), the Mid group had the largest mean value for the old classification, which was also true for the Med group. However, differences among the FrSBe scores were less pronounced for the new classification.

DISCUSSION

The first aim of this article was to develop a proxy of disease severity or “disease burden” in the form of proximity to diagnosis at study entry based on observed age at entry and CAG repeat length. The result was CAP_S, which is a scaled index of cumulative huntingtin mutation toxicity. The second aim was to develop a new classification of mutation-positive individuals that can be used for comparisons with mutation-negative individuals. The result was a categorization of the observed CAP_S distribution into the groups Control-Low-Med-High.

The predictive performance indexed by the longitudinal AUC values (see Figure 1) suggest that CAP_S is a reasonable index for proximity to diagnosis, especially within the first 2 years. CAP_S is especially convenient for analysis in PREDICT-HD and other prevalent cohort studies because it is an observed score. CAP_S is computed from quantities that are observed with high accuracy at study entrance and CAP_S does not require a statistical model for its estimation. The bootstrap-adjusted AUC in Figure 1 provides evidence that the scaling constants are relatively inconsequential in the sense that when estimated on a new sample from the same population, the predictive performance of CAP_S is essentially the same.

It was demonstrated that the new classification of Low-Med-High based on CAP_S in relation to the old (Far-Mid-Near) represents a migration of individuals from less severe disease categories to more severe categories (see Table III). This migration seems desirable as the PREDICT-HD cohort has aged since the older classification, which has increased the risk of diagnosis in the cohort. As Table IV illustrates, the Low-Med-High classification using CAP_S is clinically meaningful, in that, it is correlated with differences in other widely recognized markers of prodromal HD. Not only does the classification strongly predict TTD, but it also groups prodromal HD participants into potentially more homogeneous cohorts for the study of clinical markers.

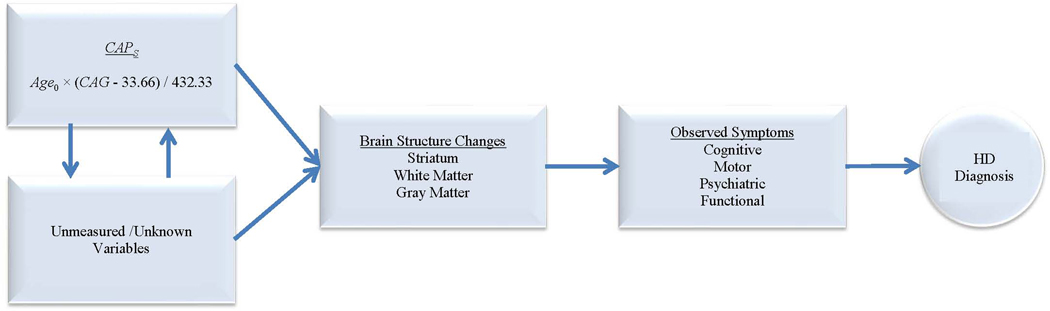
Baseline clinical markers are very important in the study of prodromal HD as they are indicators of disease progression and potentially provide information for understanding the relevant mechanisms involved [Aylward et al., 2010; Beglinger et al., 2008; Biglan et al., 2009; Duff et al., 2010a; Nopoulos et al., 2010; Paulsen, 2010; Paulsen et al., 2008, 2010a, 2010b; Stout et al., 2011]. Figure 2 is a hypothesized illustration of HD disease progression. CAP_S represents a necessary but not sufficient condition for the progression of HD, namely a sufficiently extended CAG repeat length and a sufficiently long exposure period. As opposed to other hypothesized variables, CAP_S is an observed variable that is hypothesized to exert influence at the beginning of the causal change depicted in Figure 2.

FIG. 2.

Hypothesized diagram for HD progression.

Assuming the hypothesized model in Figure 2, the Low-Med-High classification may be important for the design of clinical trials, which is a future goal of PREDICT-HD. The second set of results show that 40% (292 / 730) of prodromal HD participants in the PREDICT-HD study were classified into the High group (see Table IV). For the prodromal HD individuals in this group, the average estimated time to HD diagnosis was 5.47 years with a standard deviation of 1.41, and the average estimated 5-year probability of HD diagnosis was 0.47 with a standard deviation of 0.16. This group may serve as a potential focus group for future clinical trials on therapeutic treatment designed to delay HD progression. For example, suppose a balanced treatment-control clinical trial is designed with the aim of reducing the 5-year HD diagnosis by 40%. If the study participants were enrolled from the High group, the trial would require only 140 participants for each experimental group to demonstrate such treatment efficacy in a two-sided 0.05 level test powered at 0.90. As the PREDICT-HD study has already enrolled 292 individuals that are classified in the High group within 7 years, it is anticipated that the recruitment of study participants for such clinical trials with 5-year follow-up can be achieved in less than 7 years with a multicenter setting.

An important caveat to be highlighted is that CAP_S is intended as a utility variable for analyses in the PREDICT-HD and similar prevalent cohort studies. It is not intended as a true or literal measure of an individual’s distance from HD diagnosis. CAP_S summarizes two of the key variables related to the timing of HD diagnosis: age and CAG repeat length. However, there are undoubtedly numerous other important variables—most unobserved—that influence the TTD, as depicted at the left in Figure 2. PREDICT-HD participants are observed only once a year. Assuming there is a threshold for passing from prodromal to diagnosed, it is impossible to determine the exact TTD based on yearly measures (monthly or daily measures would be required). In addition, there is debate as to the validity of the threshold of CAG ≥ 36 for classifying individuals as mutation-positive. The validity of the threshold is not a concern for the development of CAP_S in this paper because no PREDICT-HD participants had CAG repeated lengths in the range of 35 to 37 inclusive. However, for samples that include numerous individuals with CAG lengths in this range, the estimated AFT and CAP_S will be affected. Therefore, we caution the reader to not over-interpret CAP_S, as it does not represent the true TTD for prodromal HD individuals. The same can be said for the Low-Med-High classifications.

The AFT model developed in the analysis has the desired characteristic of simplicity as compared to related models (see [Langbehn et al., 2010]). The predictive performance of the model, as reflected by the discriminatory ability of CAP_S (see Figure 1), is comparable to that of some other sample-developed models in other areas of medical research (e.g., [Bleeker et al., 2003]). The bootstrap validation suggests that CAP_S might be useful for new samples from the same population; the population consisting of prodromal individuals in prevalent cohort studies. However, the bootstrap adjustment does not address the issue of performance for data from a different population. The utility of CAP_S for individuals with characteristics that differ from those in PREDICT-HD is an open question and probably depends on the similarity of key characteristics [Laupacis et al., 1997].

Conclusion

In conclusion, CAP_S and its associated classification can be used as an index of proximity to HD diagnosis at study entry for individuals in the PREDICT-HD study and in similar prevalent cohort studies. An index of proximity is important for prodromal analyses, so that differences among prodromal HD individuals can be properly interpreted. It is hoped that the use of CAP_S and the Control-Low-Med-High classification will lead to better prediction and greater understanding of the processes of HD.

Appendix

This appendix provides the technical details pertaining to the development of the prediction model and utility variables (CAP and CAPs), the group classifications (Low-Med-High), and the bootstrap adjustment for predictive performance.

Development of the prediction model

Suppose that study entrance is the time origin, so that Y is the time in years to HD diagnosis or the last observation time in the study (i.e., duration). Then the full model AFT is,

$$\text{log}(Y)=\alpha +{\beta }_1{\mathit{\text{Age}}}_0+{\beta }_2\mathit{\text{CAG}}+{\beta }_3({\mathit{\text{Age}}}_0\times \mathit{\text{CAG}})+\sigma \epsilon .$$ (A1)

This is essentially a linear model for Y in the natural logarithm scale with an interaction effect of age at study entrance and CAG repeat length. The model guarantees the positive estimation of TTD [Klein and Moeschberger, 2003]. In Equation (A1), σ is a scaling parameter and ε is a random variable denoting the model error which may be a proxy for many other potentially important predictors not considered. The exact distribution of ε is typically unknown and empirical AFT modeling involves an exploration of various possibilities, usually the Exponential, Weibull, Normal, Logistic, or Generalized Gamma distributions.

Equation (A1) was only one of several potential models with reduced models defined by having one or two of the predictor terms in the structural portion of Equation (A1). As discussed in the text, the selected model had Age₀ and Age₀ × CAG as predictors and a logistic error distribution. The prediction formula for the selected model was

$$\widehat{Y}=\text{exp}[\alpha +{\beta }_1{\mathit{\text{Age}}}_0+{\beta }_3({\mathit{\text{Age}}}_0\times \mathit{\text{CAG}})].$$ (A2)

Certain simplifications were made to yield a scientifically meaningful model with useful parameter interpretations. To simplify Equation (A2), define C = β₁ / β₃, so that β₁ = β₃ × C. Then the selected working model can be written as

$$\widehat{Y}=\text{exp}[\alpha +{\beta }_3({\mathit{\text{Age}}}_0\times C)+{\beta }_3({\mathit{\text{Age}}}_0\times \mathit{\text{CAG}})]=\text{exp}[\alpha +{\beta }_3({\mathit{\text{Age}}}_0)(\mathit{\text{CAG}}+C)].$$

Dropping the subscript for β₃ yields

$$\widehat{Y}=\text{exp}[\alpha +\beta ({\mathit{\text{Age}}}_0)(\mathit{\text{CAG}}+C)].$$ (A3)

Defining CAP = Age₀ × (CAG + C) we have Equation (4) in the text.

CAP_S is a scaling of CAP based on the estimated survival probabilities. Assuming a logistic error, the model of Equation (A3) can be expressed in terms of a survival probability [Klein and Moeschberger, 2003]. The survival probability of being diagnosis-free from study entry to a future time t is given by

$$S_t={\left[1+\text{exp}\left\{\frac{\text{log}(t)-(\alpha +\beta \times \mathit{\text{CAP}})}{\sigma }\right\}\right]}^{-1},$$ (A4)

where all the parameters are as defined above.

Based on the parameter estimates in Table I, the estimated probability of being diagnosis-free at time t is computed as

$${\widehat{S}}_t={\left[1+\text{exp}\left\{\frac{\text{log}(t)-(4.4196-0.0065\times \mathit{\text{CAP}})}{\text{exp}(-0.8451)}\right\}\right]}^{-1}.$$

It follows that the estimated probability of diagnosis at time t is D̂_t = 1 − Ŝ_t.

Focus is on the key survival probability of 0.5, as in this case D̂_t = Ŝ_t and there is a 50-50 chance of a diagnosis. Inspection of Equation (A4) reveals that S_t = D_t = 0.5 = [1 + exp(0)]⁻¹, which occurs when log(t) − (α + β × CAP) = 0. Given t = 5 and estimates of the parameters, CAP can be solved for in this situation. This solution is then used as a basis for scaling CAP.

Suppose we define B = CAP for this special case and solve for B̂ using the sample estimates,

$$\widehat{B}=\frac{\widehat{\alpha }-\text{log}(5)}{-\widehat{\beta }}=\frac{4.4196-1.6094}{0.0065}=432.3326.$$

B̂ is the sample CAP that produces D̂_t = Ŝ_t = 0.5. Then CAP can be divided by B (or its estimate) to compute CAP_S as in Equation (5). Finally, setting β^* = β × B = −(α − log(5)), we obtain the CAP_S AFT model of Equation (6).

Algorithm for determining group membership

Recall that CAP_S can be used as a basis for classifying individuals into groups. Using the sample data, the cutoffs for group membership among mutation-positive individuals were determined by the following steps.

1. For each study participant, CAP_S was computed along with the estimated time to diagnosis, Ŷ, based on Equation (4).

2. To avoid radically different sample sizes among the groups, the potential lower cutoff was constrained to be between the 25^th and 40^th percentiles of the CAP_S sample distribution.

3. The potential upper cutoff was constrained to be between the 60^th and 75^th percentiles of the CAP_S distribution.

4. The grid of all possible pairs of lower and upper percentiles was considered. For each candidate pair of cutoffs (e.g., 26^th and 64^th percentiles), the between-group and within-group variation for the estimated TTD was calculated. The ratio of between-group to within-group variation was used as the selection criterion.

5. The cutoffs for constructing the groups consisted of the pair that yielded the largest value of the ratio.

The optimization algorithm essentially searched for the largest ANOVA F-statistic of the estimated TTD based on the CAP_S percentiles. The selected cutoffs indicated the best separation of the study participants in terms of the estimated TTD.

Bootstrap adjustment of predictive performance

To address the issue of optimistic prediction performance, an enhanced bootstrap procedure was used to adjust the AUC and iAUC (see [Harrell et al., 1996] for additional details). The overly-optimistic apparent performance (AP) was indexed by the AUC and iAUC computed on the original sample. For each bootstrap replication, a bootstrap sample was drawn by sampling from the original data set with replacement using the same sample size (N = 730). For each bootstrap sample, the parameters of Equation (A2) were estimated, CAP_S was computed, and AUC and iAUC were produced. The latter two were indicators of bootstrap performance (BP). Then CAP_S was computed for the original sample based on the estimates for the bootstrap sample, and AUC and iAUC were produced. In this case, AUC and iAUC were indicators of test performance (TP). The bootstrap procedure was replicated 200 times and the adjusted AUC (AUC_adj) was computed as

$${\text{AUC}}_{\text{adj}}={\text{AUC}}_{\text{AP}}-\text{average}({\text{AUC}}_{\text{BP}}-{\text{AUC}}_{\text{TP}}),$$ (A6)

where the average was taken over the 200 replications. A similar adjustment was computed for iAUC. The difference AUC_BP − AUC_TP was an estimate of optimism, and averaging over replications produced a more stable estimate. The average was subtracted from the AUC value computed on the original sample (AUC_AP), which constituted an optimism penalty. A relatively few replications (i.e., 200) were sufficient, as the average was used rather than the empirical quantiles required by other bootstrap methods (e.g., a bootstrap confidence interval).

Appendix. PREDICT-HD Investigators, Coordinators, Motor Raters, Cognitive Raters

Active: September 2009 – August 2010

Thomas Wassink, MD, Stephen Cross, BA, Nicholas Doucette, BA, Mycah Kimble, BA, Patricia Ryan, MSW, LISW, MA, Jessica Wood, MD, PhD, Eric A. Epping, MD, PhD, and Leigh J. Beglinger, PhD (University of Iowa, Iowa City, Iowa, USA);

Edmond Chiu, MD, Olga Yastrubetskaya, PhD, Joy Preston, Anita Goh, D.Psych, Chathushka Fonseka, and Liz Ronsisvalle (St. Vincent’s Hospital, The University of Melbourne, Kew, Victoria, Australia);

Phyllis Chua, MD, and Angela Komiti, BS, MA (The University of Melbourne, Royal Melbourne Hospital, Melbourne, Australia)

Lynn Raymond, MD, PhD, Rachelle Dar Santos, BSc, and Joji Decolongon, MSC, CCRP (University of British Columbia, Vancouver, British Columbia, Canada);

Adam Rosenblatt, MD, Christopher A. Ross, MD, PhD, Barnett Shpritz, BS, MA, OD, and Claire Welsh (Johns Hopkins University, Baltimore, Maryland, USA);

William M. Mallonee, MD, Greg Suter, BA, and Judy Addison (Hereditary Neurological Disease Centre, Wichita, Kansas, USA);

Ali Samii, MD, and Alma Macaraeg, BS (University of Washington and VA Puget Sound Health Care System, Seattle, Washington, USA);

Randi Jones, PhD, Cathy Wood-Siverio, MS, Stewart A. Factor, DO, and Claudia Testa, MD, PhD (Emory University School of Medicine, Atlanta, Georgia, USA);

Roger A. Barker, BA, MBBS, MRCP, Sarah Mason, BSC, Anna Goodman, PhD, Rachel Swain, BA, and Anna DiPietro (Cambridge Centre for Brain Repair, Cambridge, UK);

Elizabeth McCusker, MD, Jane Griffith, RN, Clement Loy, MD, David Gunn, BS, and Linda Stewart, RN (Westmead Hospital, Sydney, Australia);

Bernhard G. Landwehrmeyer, MD, Michael Orth MD, PhD, Sigurd Süβmuth, MD, RN, Katrin Barth, RN, and Sonja Trautmann, RN (University of Ulm, Ulm, Germany);

Kimberly Quaid, PhD, Melissa Wesson, MS, and Joanne Wojcieszek, MD (Indiana University School of Medicine, Indianapolis, IN);

Mark Guttman, MD, Alanna Sheinberg, BA, and Irita Karmalkar, BSc (Centre for Addiction and Mental Health, University of Toronto, Markham, Ontario, Canada);

Susan Perlman, MD and Arik Johnson, PsyD (University of California, Los Angeles Medical Center, Los Angeles, California, USA);

Michael D. Geschwind, MD, PhD, Jon Gooblar, BA, and Gail Kang, MD (University of California San Francisco, California, USA);

Tom Warner, MD, PhD, Maggie Burrows, RN, BA, Marianne Novak, MD, Thomasin Andrews, MD, BSC, MRCP, Elisabeth Rosser, MBBS, FRCP, and Sarah Tabrizi, MD, PhD (National Hospital for Neurology and Neurosurgery, London, UK);

Anne Rosser, MD, PhD, MRCP, Kathy Price, RN, and Sarah Hunt, BSc (Cardiff University, Cardiff, Wales, UK);

Frederick Marshall, MD, Amy Chesire, LCSW-R, MSG, Mary Wodarski, BA, and Charlyne Hickey, RN, MS (University of Rochester, Rochester, New York, USA);

Oksana Suchowersky, MD, FRCPC, Sarah Furtado, MD, PhD, FRCPC, and Mary Lou Klimek, RN, BN, MA (University of Calgary, Calgary, Alberta, Canada);

Peter Panegyres, MB, BS, PhD, Elizabeth Vuletich, BSC, Steve Andrew, and Rachel Zombor, MPSYC (Neurosciences Unit, Graylands, Selby-Lemnos & Special Care Health Services, Perth, Australia);

Joel Perlmutter, MD, Stacey Barton, MSW, LCSW, and Amy Schmidt (Washington University, St. Louis, Missouri, USA);

Zosia Miedzybrodzka, MD, PhD, Sheila A. Simpson, MD, Daniela Rae, RN, and Mariella D’Alessandro, PhD (Clinical Genetics Centre, Aberdeen, Scotland, UK);

David Craufurd, MD, Ruth Fullam, BSC, and Elizabeth Howard, MD (University of Manchester, Manchester, UK);

Pietro Mazzoni, MD, PhD, Karen Marder, MD, MPH, and Paula Wasserman, MA (Columbia University Medical Center, New York, New York, USA);

Rajeev Kumar, MD and Diane Erickson, RN (Colorado Neurological Institute, Englewood, Colorado, USA);

Vicki Wheelock, MD, Terry Tempkin, RNC, MSN, Nicole Mans, BA, MS, and Kathleen Baynes, PhD (University of California Davis, Sacramento, California, USA);

Joseph Jankovic, MD, Christine Hunter, RN, CCRC, and William Ondo, MD (Baylor College of Medicine, Houston, Texas, USA);

Justo Garcia de Yebenes, MD, Monica Bascunana Garde, Marta Fatas, BA, and Asuncion Martinez-Descales (Hospital Ramón y Cajal, Madrid, Spain);

Wayne Martin, MD, Pamela King, BScN, RN, and Satwinder Sran, BSC (University of Alberta, Edmonton, Alberta, Canada);

Anwar Ahmed, PhD, Stephen Rao, PhD, Christine Reece, BS, Janice Zimbelman, PhD, PT, Alexandra Bea, BA, Emily Newman, BA, and Alex Bura, BA (Cleveland Clinic Foundation, Cleveland, Ohio, USA).

Steering Committee

Jane Paulsen, PhD, Principal Investigator, Eric A. Epping, MD, PhD, Hans Johnson, PhD, Megan Smith, PhD, Janet Williams, PhD, RN, FAAN, Leigh Beglinger, PhD, James Mills, MS (University of Iowa Hospitals and Clinics, Iowa City, IA); Elizabeth Aylward, PhD (Seattle Children's Research Institute, WA); Kevin Biglan, MD (University of Rochester, Rochester, NY); Blair Leavitt, MD (University of British Columbia, Vancouver, BC, Canada); Marcy MacDonald, PhD (Massachusetts General Hospital); Martha Nance, MD (Hennepin County Medical Center, Minneapolis, MN); and Cheryl Erwin, JD, PhD (University of Texas Medical School at Houston).

Scientific Sections

Bio Markers: Blair Leavitt, MDCM, FRCPC (Chair) and Michael Hayden, PhD (University of British Columbia); Stefano DiDonato, MD (Neurological Institute “C. Besta,” Italy); Ken Evans, PhD (Ontario Cancer Biomarker Network); Wayne Matson, PhD (VA Medical Center, Bedford, MA); Asa Peterson, MD, PhD (Lund University, Sweden), Sarah Tabrizi, MD, PhD (National Hospital for Neurology and Neurology and Neurosurgery, London); Beth Borowsky, PhD (CHDI); Andrew Juhl, BS, James Mills, MS, Kai Wang, PhD (University of Iowa); and David Weir, BSc (University of British Columbia).

Brain: Jean Paul Vonsattell, PhD (Chair), and Carol Moskowitz, ANP, MS (Columbia University Medical Center); Anne Leserman, MSW, LISW, Lynn Schaul, BA, and Stacie Vik, BA (University of Iowa).

Cognitive: Deborah Harrington, PhD (Chair), Gabriel Castillo, BS, Jessica Morison, BS, and Jason Reed, BS (University of California, San Diego), Michael Diaz, PhD, Ian Dobbins, PhD, Tamara Hershey, PhD, Erin Foster, OTD, and Deborah Moore, BA (Washington University Cognitive Science Battery Development); Holly Westervelt, PhD (Chair, Quality Control and Training, Alpert Medical School of Brown University), Jennifer Davis, PhD, and Geoff Tremont, PhD, MS (Scientific Consultants, Alpert Medical School of Brown University); Megan Smith, PhD (Chair, Administration), David J. Moser, PhD, Leigh J. Beglinger, PhD, Kelly Rowe, and Danielle Theriault, BS (University of Iowa); Carissa Gehl, PhD (VA Medical Center, Iowa City, IA); Kirsty Matheson (University of Aberdeen); Karen Siedlecki, PhD (Fordham University); Marleen Van Walsem (EHDN); Susan Bonner, BA, Greg Elias, BA, and Melanie Faust, BS (Rhode Island Hospital); Beth Borowski, PhD (CHDI); Noelle Carlozzi (University of Michigan); Kevin Duff, PhD (University of Utah); Nellie Georgiou-Karistianis (St. Vincent’s Hospital, The University of Melbourne, Australia); Julie Stout, PhD (Monash University, Melbourne, Australia); Herwig Lange (Air-Rahazentrum); and Kate Papp (University of Connecticut).

Functional: Janet Williams, PhD (Chair), Leigh J. Beglinger, PhD, Anne Leserman, MSW, LISW, Eunyoe Ro, MA, Lee Anna Clark, Nancy Downing, Joan Laing, PhD, Kristine Rees, BA, and Stacie Vik, BA (University of Iowa); Rebecca Ready, PhD (University of Massachusetts); Anthony Vaccarino, PhD (Ontario Cancer Biomarker Network); Sarah Farias, PhD (University of California, Davis); Noelle Carlozzi, PhD (University of Michigan); and Carissa Gehl, PhD (VA Medical Center, Iowa City, IA).

Genetics: Marcy MacDonald, PhD (Co-Chair), Jim Gusella, PhD, and Rick Myers, PhD (Massachusetts General Hospital); Michael Hayden, PhD (University of British Columbia); Tom Wassink, MD (Co-Chair) Eric A. Epping, MD, PhD, Andrew Juhl, BA, James Mills, MS, and Kai Wang, PhD (University of Iowa); Zosia Miedzybrodzka, MD, PhD (University of Aberdeen); and Christopher Ross, MD, PhD (Johns Hopkins University).

Imaging: Administrative: Ron Pierson, PhD (Chair), Kathy Jones, BS, Jacquie Marietta, BS, William McDowell, AA, Greg Harris, BS, Eun Young Kim, MS, Hans Johnson, PhD, and Thomas Wassink, MD (University of Iowa); John Ashburner, PhD (Functional Imaging Lab, London); Steve Potkin, MD (University of California, Irvine); and Arthur Toga, PhD (University of California, Los Angeles). Striatal: Elizabeth Aylward, PhD (Chair, Seattle Children's Research Institute). Surface Analysis: Eric Axelson, BSE (University of Iowa). Shape Analysis: Christopher A. Ross (Chair), MD, PhD, Michael Miller, PhD, and Sarah Reading, MD (Johns Hopkins University); Mirza Faisal Beg, PhD (Simon Fraser University). DTI: Vincent A. Magnotta, PhD (Chair, University of Iowa); Karl Helmer, PhD (Massachusetts General Hospital); Kelvin Lim, MD (University of Ulm, Germany); Mark Lowe, PhD (Cleveland Clinic); Sasumu Mori, PhD (Johns Hopkins University); Allen Song, PhD (Duke University); and Jessica Turner, PhD (University of California, Irvine). fMRI: Steve Rao, PhD (Chair), Erik Beall, PhD, Katherine Koenig, PhD, Michael Phillips, MD, Christine Reece, BS, and Jan Zimbelman, PhD, PT (Cleveland Clinic); and April Bryant (University of Iowa).

Motor: Kevin Biglan, MD (University of Rochester), Karen Marder, MD (Columbia University), and Jody Corey-Bloom, MD, PhD (University of California, San Diego) all Co-Chairs; Michael Geschwind, MD, PhD (University of California, San Francisco); Ralf Reilmann, MD and Zerka Unds (Muenster, Germany); and Andrew Juhl, BS (University of Iowa).

Psychiatric: Eric A. Epping, MD, PhD (Chair), Nancy Downing, RN, MSN, Jess Fiedorowicz, MD, Robert Robinson, MD, Megan Smith, PhD, Leigh Beglinger, PhD, James Mills, MS, Kristine Rees, BA, Adam Ruggle, Stacie Vik, BA, Janet Williams, PhD, Dawei Liu, PhD, David Moser, PhD, and Kelly Rowe (University of Iowa); Karen Anderson, MD (University of Maryland); David Craufurd, MD (University of Manchester); Mark Groves, MD (Columbia University); Anthony Vaccarino, PhD and Ken Evans, PhD (Ontario Cancer Biomarker Network); Hugh Rickards, MD (Queen Elizabeth Psychiatric Hospital); Eric van Duijn, MD (Leiden University Medical Center, Netherlands); Irina Antonijevic, MD, PhD, and Joseph Giuliano (CHDI); Phyllis Chua (The University of Melbourne, Royal Melbourne Hospital); and Kimberly Quaid, PhD (Indiana University School of Medicine).

Core Sections

Statistics: James Mills, MEd, MS, Dawei Liu, PhD, Jeffrey Long, PhD, Wenjing Lu, Kai Wang, PhD, and Ying Zhang, PhD (University of Iowa).

Recruitment/Retention: Martha Nance, MD (Chair, University of Minnesota); Anne Leserman, MSW, LISW, Nicholas Doucette, BA, Mycah Kimble, BA, Patricia Ryan, MSW, LISW, MA, Kelli Thumma, BA, Elijah Waterman, BA, and Jeremy Hinkel, BA (University of Iowa).

Ethics: Cheryl Erwin, JD, PhD, (Chair, McGovern Center for Health, Humanities and the Human Spirit); Eric A. Epping, MD, PhD Janet Williams, PhD, Nicholas Doucette, BA, Anne Leserman, MSW, LISW, James Mills, MS, Lynn Schaul, BA, and Stacie Vik, BA (University of Iowa); Martha Nance, MD (University of Minnesota); and Lisa Hughes, MEd (University of Texas Medical School at Houston).

IT/Management: Hans Johnson, PhD (Chair), R.J. Connell, BS, Karen Pease, BS, Ben Rogers, BA, BSCS, Jim Smith, AS, Shuhua Wu, MCS, Roland Zschiegner, Erin Carney, Bill McKirgan, Mark Scully, and Ryan Wyse (University of Iowa); Jeremy Bockholt (AMBIGroup).

Program Management

Administrative: Chris Werling-Witkoske (Chair), Karla Anderson, BS, Kristine Bjork, BA, Ann Dudler, Jamy Schumacher, Sean Thompson, BA, Leann Davis, Machelle Henneberry, Greg Ennis, MA, and Stacie Vik, BA (University of Iowa).

Financial: Steve Blanchard, MSHA, Kelsey Montross, BA, and Phil Danzer (University of Iowa).