Liquid accumulation in vibrating vocal fold tissue: A simplified model based on a fluid-saturated porous solid theory

Abstract

The human vocal fold is treated as a continuous, transversally isotropic, porous solid saturated with liquid. A set of mathematical equations, based on the theory of fluid-saturated porous solids, is developed to formulate the vibration of the vocal fold tissue. As the fluid-saturated porous tissue model degenerates to the continuous elastic tissue model when the relative movement of liquid in the porous tissue is ignored, it can be considered a more general description of vocal fold tissue than the continuous, elastic model. Using the fluid-saturated porous tissue model, the vibration of a bunch of one-dimensional fibers in the vocal fold is analytically solved based on the small amplitude assumption. It is found that the vibration of the tissue will lead to the accumulation of excess liquid in the midmembranous vocal fold. The degree of liquid accumulation is positively proportional to the vibratory amplitude and frequency. The correspondence between the liquid distribution predicted by the porous tissue theory and the location of vocal nodules observed in clinical practice, provides theoretical evidence for the liquid accumulation hypothesis of vocal nodule formation (Jiang, Ph. D., dissertation, 1991, University of Iowa).

I. Introduction

An appropriate description of vocal fold tissue is the foundation for modeling vocal fold vibration (1), investigating speech production (2-3), and understanding vocal fold pathology (4). The early works considered the vocal folds as mechanical oscillators and simplified the tissue to a few discrete mass blocks connected by a set of springs and dampers. Based on these simple tissue descriptions, a series of vocal fold models, such as the one-mass model (5), the two-mass model (6), and even the multi-mass model (7), were proposed to predict vocal fold vibration and speech synthesis (6, 8). The benefit of these discrete tissue models is that they can provide the simplest mathematical equations, which can be easily solved numerically or even analytically.

The continuous viscoelastic model is a better description of the human vocal fold tissue than the discrete approximation (2-3, 9-10). In this model, the vocal fold tissue is treated as a continuous, transversally isotropic, viscoelastic material capable of propagating compressional shear and surface waves. Using this continuous viscoelastic model, the normal modes in vocal fold tissue were analytically solved (2-3, 10). Furthermore, this tissue model also provided the theoretical foundation for the finite-element vocal fold models (11-12). The finite-element vocal fold models have been widely used to study vocal fold collision (13-15), biphonation (16), vocal fold abduction/adduction (17), and so on. In addition, the viscoelastic biomaterials (fat, hyaluronic acid, and fibronectin) were also designed according to the concepts of the viscoelastic description of tissue (18). Using this viscoelastic physical model, Chan and Titze (2006) simulated the superficial layer of the lamina propria and verified the relationship between the phonation threshold pressure and tissue mechanics (18).

Recently, Tsai et al., (2006) developed another interesting description of vocal fold tissue, namely the intermediate water wave model, where the vocal tissue is treated as a liquid (19). By applying the restoring force provided by the tensioned epithelium instead of that provided by gravity, the equations of a water wave were used to describe the mucosal wave of the vocal fold. With this model, Tsai et al. (2006) predicted elliptic orbits of the vocal tissue particles and found that the behavior of the vocal tissue is analogous to intermediate waters when the depth of the liquids in the lamina propria is 1/2 – 1/20 of the wavelength. This intermediate water wave model was then verified using ultrasound imaging of the vocal fold during modal phonation (19).

The common ground of the aforementioned tissue models is that they reduce the vocal fold tissue to a one phase material (solid for viscoelastic model or liquid for intermediate water wave model). However, vocal fold anatomy and physiology have shown that there is complex composite microstructure in vocal fold tissue, as shown in Fig.1 (4, 20). The mucosal covering consists of a stratified squamous epithelium that wraps over the internal contents of the vocal folds. Inside, the tissue is loosely composed of specialized proteins, carbohydrates, lipids, collagen fibers, and elastin fibers. Liquid fills the spaces among these solid structures. Therefore, it can be said that the vocal tissue is neither a purely continuously viscoelastic solid nor purely liquid. The vocal fold tissue is essentially the composite of an elastic porous solid and the liquid that fills the pores. Therefore, a description combining fluid material and solid material may represent a better approximation of the vocal fold tissue.

Figure 1.

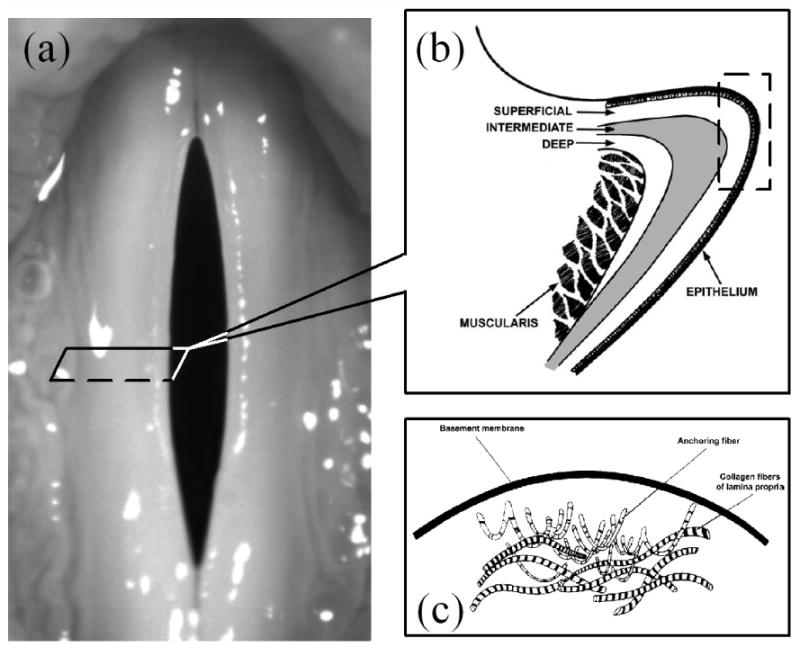
The complex composite microstructure in vocal fold tissue. (a) vocal fold (b) the three layers of the lamina propria of the vocal fold (From reference 44). (c) The basement membrane zone where is full of various fibers. (From reference 43).

In this study, the vocal fold tissue is treated as a fluid-saturated porous material, which is the composite of two phases (solid and fluid) of material. One phase is a transversally isotropic, elastic porous solid, which represents the loose solid structure in the tissue, such as specialized proteins, carbohydrates, lipids, and elastic fibers. Another phase is the fluid occupying the pores in the solid, which represents the liquid component of the tissue. The properties of vocal fold tissue are determined by the porous solid, the fluid, and their interaction. Biot's fluid-saturated porous solid theory (21-24) is employed to quantitatively describe dynamical characteristics of the vocal fold. On this basis, we propose a set of partial differential equations to describe the vibration of the vocal fold in section II. Moreover, we compare this new vocal fold tissue model with the previous model based on continuous viscoelastic theory. In section III, we analytically solve the case of one-dimensional vibration of the vocal fold with a small amplitude assumption and investigate the liquid accumulation in the vocal fold tissue during phonation. In section IV, we discuss the results and their implications for vocal fold physiology and pathology.

II. Vibration of the fluid-saturated porous tissue

In this section, we will develop the equations of motion for the vocal fold. The following basic properties of vocal fold tissue are assumed: 1. the vocal fold tissue can be considered a fluid-saturated solid. 2. the solid component in vocal fold tissue is porous and transversally isotropic. 3. there is no longitudinal dynamic strain. 4. the stress-strain relationship of the porous solid is linear. 5. the fluid contained in the pores is incompressible. The first assumption is according to the anatomy and physiology of the vocal fold (4, 20), as we have discussed in the introduction section. The fact that tissues are generally stiffer in the direction of fibers suggests that the medium is anisotropic. In the following discussion, the direction of the tissue fiber (anterior-posterior direction) is assumed to lie along the y axis, as shown in Fig.2 (a). However, in the plane transverse to the fibers (x-z plane), the elastic properties of the tissue are usually considered to be isotropic (2-3). If the porous distribution is the same at any direction in the transverse plane, the vocal fold tissue can be approximately considered to be isotropic in the transverse cross-section. Therefore, for the sake of simplification, transverse isotropy is assumed for vocal fold tissue in this study. The zero longitudinal strain assumption is based on the observation of the surface dynamics of the vocal fold (25), where it was found that the longitudinal displacement is much smaller than the vertical displacement and the lateral displacement. The linear stress-strain relationship is valid for a small deformation (<15%) (26). Finally, the incompressible fluid assumption comes from the fact that the essential component of the liquid is water, which is practically incompressible.

Figure 2.

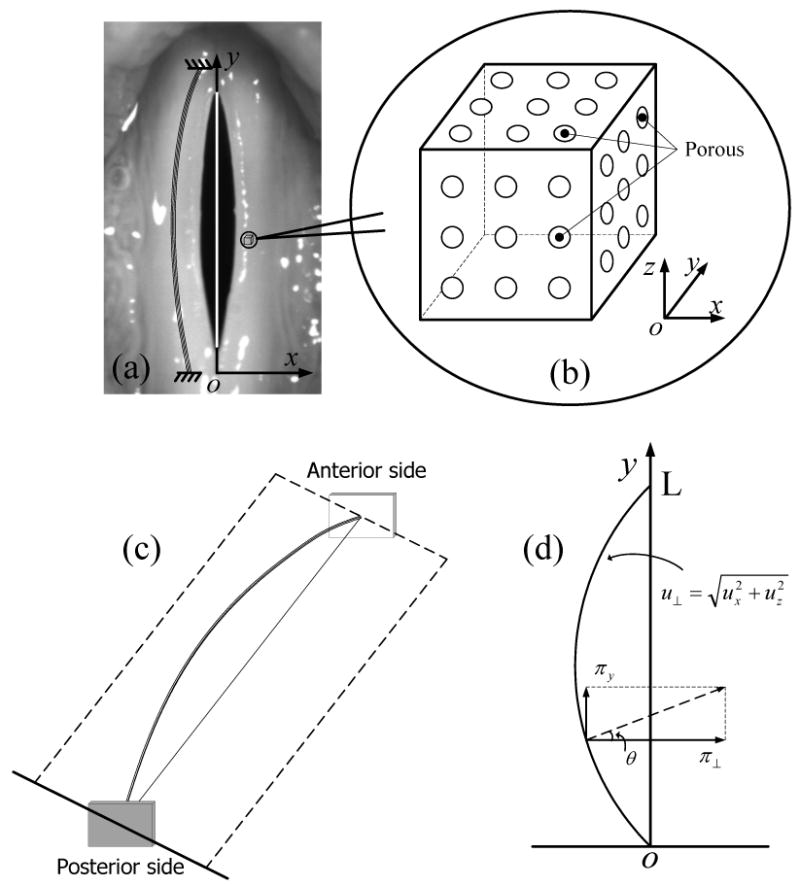
The fluid-saturated porous solid theory of the vocal fold tissue. (a) A bunch of fiber lies along the anterior-posterior direction of the vocal fold. (b) The sketch map of the porous solid. (c)-(d) The vibration of a bunch of fiber in vocal fold.

A. the stress-strain relationship

Consider a small cubic element of the fluid-saturated tissue, as shown in Fig.2 (b), the stress tensor applied on it includes two parts according to Biot's theory (23): One is the stress component applied on the solid parts of each face of the cube:

$$\mathbf{\sigma }=\left\{\begin{array}{rrr}\hfill {\sigma }_{xx}& \hfill {\sigma }_{xy}& \hfill {\sigma }_{xz}\\ \hfill {\sigma }_{yx}& \hfill {\sigma }_{yy}& \hfill {\sigma }_{yz}\\ \hfill {\sigma }_{zx}& \hfill {\sigma }_{zy}& \hfill {\sigma }_{zz}\end{array}\right\}$$ (1)

where σ_ii (i = x, y, z) represents the normal stress in the i-direction and σ_ij (i ≠ j and i,j = x, y, z) represents the shear stress in the i-direction on the j-plane. Another is the force applied on the fluid part of each face of the cube:

$$\mathbf{\text{s}}=\left\{\begin{array}{rrr}\hfill s& \hfill 0& \hfill 0\\ \hfill 0& \hfill s& \hfill 0\\ \hfill 0& \hfill 0& \hfill s\end{array}\right\}.$$ (2)

For a transversely isotropic fluid-saturated porous solid, its stress and strain satisfy the following relationship (22):

$$\left[\begin{array}{r}\hfill {\sigma }_{xx}\hfill \\ \hfill {\sigma }_{yy}\hfill \\ \hfill {\sigma }_{zz}\hfill \\ \hfill {\sigma }_{xy}\hfill \\ \hfill {\sigma }_{yz}\hfill \\ \hfill {\sigma }_{zx}\hfill \\ \hfill s\hfill \end{array}\right]=\left[\begin{array}{ccccccc}C& {\lambda }^{\prime }& \lambda & 0& 0& 0& Q\\ {\lambda }^{\prime }& C^{\prime }& {\lambda }^{\prime }& 0& 0& 0& Q^{\prime }\\ \lambda & {\lambda }^{\prime }& C& 0& 0& 0& Q\\ 0& 0& 0& {\mu }^{\prime }& 0& 0& 0\\ 0& 0& 0& 0& {\mu }^{\prime }& 0& 0\\ 0& 0& 0& 0& 0& \mu & 0\\ Q& Q^{\prime }& Q& 0& 0& 0& R\end{array}\right]\left[\begin{array}{r}\hfill e_{xx}\hfill \\ \hfill e_{yy}\hfill \\ \hfill e_{zz}\hfill \\ \hfill e_{xy}\hfill \\ \hfill e_{yz}\hfill \\ \hfill e_{zx}\hfill \\ \hfill \varepsilon \hfill \end{array}\right]$$ (3)

where C = λ + 2μ and the elastic constant C′ is a measure of the longitudinal stiffness. Here, the Lamé constants λ and μ describe the material's stiffness under compression and shear in the plane transverse to the fiber. The Lamé constants λ′ and μ′ represent the material's stiffness under compression and shear along the longitudinal fiber axis. R is a physical constant, which measure the amount of water being forced into the cube element under a constant pressure. Q and Q′ is a coupling coefficient of the solid volume change and the fluid volume change, respectively, ε is the strain of the fluid:

$$\varepsilon =\nabla \cdot \mathbf{\text{U}},$$ (4)

where U = {U_x, U_y, U_z} is the fluid displacement velocity vector. e_ii (i = x, y, z) are the normal strains of the solid, that is,

$$e_{xx}=\frac{\partial u_x}{\partial x};e_{yy}=\frac{\partial u_y}{\partial y}=0;e_{zz}=\frac{\partial u_z}{\partial z}.$$ (5)

e_ij (i ≠ j and i, j = x, y, z) are the shear strains of solid:

$$e_{xy}=\frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x};e_{yz}=\frac{\partial u_y}{\partial z}+\frac{\partial u_z}{\partial y};e_{zx}=\frac{\partial u_z}{\partial x}+\frac{\partial u_x}{\partial z}.$$ (6)

In Eqs.(5-6), u_i (i = x, y, z) are the components of the displacement vector u of the solid.

B. Equation of motion

According to the theory of elasticity, the solid part in the solid-saturated tissue satisfies the following equation of motion,

$$\nabla \cdot \mathbf{\sigma }+{\mathbf{\pi }}^{S-F}+{\mathbf{\text{g}}}^S=\frac{{\partial }^2{\rho }_s\mathbf{\text{u}}}{\partial t^2},$$ (7)

and the equation of motion of the liquid part has the form,

$$\nabla \cdot \mathbf{\text{s}}+{\mathbf{\pi }}^{F-S}+{\mathbf{\text{g}}}^F=\frac{{\partial }^2{\rho }_F\mathbf{\text{U}}}{\partial t^2}$$ (8)

where σ is the stress component applied on the solid parts [Eq.(1)] and s is the force applied on the fluid part of each face of the cube [Eq.(2)]. π^S-F is the force applied on solid due to solid-fluid interaction and π^F-S is the force applied on fluid part due to solid-fluid interaction, where π^S-F and π^F-S depend on the permeability β of the porous solid, the solid-fluid relative velocity, and so on. Clearly, π^S-F and π^F-S are a pair of acting reacting forces. According to the law of the action and reaction, π^S-F + π^F-S = 0. Because π^S-F and π^F-S are a function of u and U, Eq.(7) and Eq.(8) are coupled together through the interacting forces π^S-F and π^F-S. g^S and g^F are the body force, such as gravity, applied on solid and fluid respectively. ρ_S represents the solid mass in the fluid-solid aggregate per unit volume and ρ_F represents the fluid mass per unit volume of aggregate. It is noticeable that the fluid could move and redistribute in the tissue. Therefore, ρ_F could not be constant in Eq.(8). According the conservation of mass, ρ_F can be related to U by the following equation:

$$\frac{\partial {\rho }_F}{\partial t}=-\nabla \cdot \frac{\partial \mathbf{\text{U}}}{\partial t}$$ (9)

Substituting stress-strain relationship Eq.(3) and the strain-displacement relationship Eqs.(4-6) into Eqs.(7-8), we have

$$\frac{\partial }{\partial x}\left[(\lambda +\mu ){\nabla }_{\perp }\cdot {\mathbf{\text{u}}}_{\perp }+Q\nabla \cdot \mathbf{\text{U}}\right]+{\Delta }_{\perp }{u}_x+{\pi }_x^{S-F}+{\mathit{\text{g}}}_x^S=\frac{{\partial }^2{\rho }_S{u}_x}{\partial t^2},$$ (10)

$$\frac{\partial }{\partial x}\left[Q{\nabla }_{\perp }\cdot {\mathbf{\text{u}}}_{\perp }+R\nabla \cdot \mathbf{\text{U}}\right]+{\pi }_x^{F-S}+{\mathit{\text{g}}}_x^F=\frac{{\partial }^2{\rho }_F{U}_x}{\partial t^2},\text{etc}$$ (11)

where u_⊥ =(u_x, u_z), ${\nabla }_{\perp }=\left(\frac{\partial }{\partial x},\frac{\partial }{\partial z}\right)$ is a transverse differential operator, and ${\Delta }_{\perp }=\mu \frac{{\partial }^2}{\partial x^2}+{\mu }^{\prime }\frac{{\partial }^2}{\partial y^2}+\mu \frac{{\partial }^2}{\partial z^2}$. Identical equations result for u_z, U_y, and U_z if u_x and U_x is expressed in terms of u_z, U_y and U_z in the above procedure. Therefore, six equations have six unknowns {u_x, u_z, U_x, U_y, U_z, ρ_F}. With appropriate initial conditions and boundary conditions, these unknowns can be completely determined from these equations.

C. Relationship to other theories

Eqs.(9-10) provide a general description of the dynamics of the fluid-saturated porous tissue. With appropriate assumptions and simplifications, these general equations of the fluid-saturated porous tissue can be reduced to the previous continuous viscoelastic tissue model. For the comparison of the fluid-saturated solid theory and the continuous elastic theory, in this subsection, we assume that the fluid completely fills the pores in the solid and the fluid in the tissue does not move with respect to the solid, i.e., U = u (we name this the continuous elastic assumption). Then, substituting U = u into Eqs.(10-11), adding Eq.(10) to Eq.(11) and ignoring the gravity, we have:

$$\left(\Lambda +\Gamma \right)\frac{\partial }{\partial x}\left(\frac{\partial u_x}{\partial x}+\frac{\partial u_z}{\partial z}\right)+\Gamma \left(\frac{{\partial }^2{u}_x}{\partial x^2}+\frac{{\partial }^2{u}_x}{\partial z^2}\right)+{\Gamma }^{\prime }\frac{{\partial }^2{u}_x}{\partial y^2}=\rho \frac{{\partial }^2{u}_x}{\partial t^2},\text{etc}.$$ (12)

where Λ = λ + 2Q + R, Γ = μ and Γ′ = μ′. ρ = ρ_F + ρ_S is the density of the vocal fold tissue. Because it is assumed that there is no relative movement between the fluid and porous solid, ρ is a constant in respect to time t and can be taken out from the partial differential operator. It is seen that Eq.(12) has the identical form of the equation of motion for an elastic tissue model [Eq.(16) in reference (3)]. The parameters Λ, Γ and Γ′ in Eq.(12) can be considered the equivalents of the Lamé constants λ, μ and μ′ in the continuous viscoelastic tissue. Moreover, it can be found that with the continuous elastic tissue assumption, the tissue's stiffness under shear only depends on the shear modulus of the porous solid, whereas, the tissue's stiffness under compression, also depends on the liquid parameters Q and R.

In addition, according to the stress-strain relationship of the fluid-saturated porous material (Eq.3), the pressure-strain relationship s = Qe + Rε can be obtained, where e = e_xx + e_yy + e_zz. Then, according to the aforementioned continuums elastic tissue assumption, the above pressure-strain relationship can be simplified by substituting e = ε into it:

$$\text{e}=(\text{Q}+R)\times \varepsilon$$ (13)

Eq.(13) correlates the pressure applied on the vocal fold tissue and the volume change of the tissue. For the porous solid completely filled with incompressible fluid, ε = ▽ · U = 0 can always be satisfied for any pressure value s. Therefore (Q+R) → ∞ and Λ→ ∞ for the continuous elastic tissue model. This conclusion agrees with the properties of the soft tissues composed primarily of fibers and liquid (3, 9). Oestreicher (1951) declared that the Lamé constant λ is many orders of magnitude greater than the Lamé constant μ for a soft tissue (9).

D. Model Simplification

In the subsection A-C, we have proposed a general fluid-saturated poroelastic theory to describe the vocal fold tissue. However, the general Eqs.(9-11) are difficult to solve analytically because of the nonlinear terms and coupling terms; therefore, in order to obtain an analytical solution of this fluid-saturated porous tissue, some assumptions were made to simplify the equations of motion: (i) The body force due to gravity is much smaller than the elastic force. (ii) The relative velocity between the liquid and solid, ‖dU/dt − du/dt‖, is very small compared to the velocity of the solid, ‖du/dt‖. Moreover, this relative velocity in the transverse direction (x, z direction) can be ignored in comparison with that in the longitudinal direction (y direction). This assumption is based on the distribution and orientation of the fibers in the tissue and the existence of the potential space known as Reinke's space. The lamina propria, or intermediate layer in the vocal fold tissue sits between the epithelium and muscle as shown in Fig. 1 (b), and is itself divided into three regions. The vocal fold fibrous proteins, elastin and collagen, mostly occupy the middle and deep lamina propria layers (1). The vast majority of these fibers are aligned longitudinally in these layers (27) and the permeability of fluid parallel to this direction is expected to be significantly higher than in other directions. Happel and Brenner (1973) calculated a factor of 1.4 to 2 times greater permeability for parallel flow over perpendicular flow in a bed of uniform aligned cylinders (28). (iii) the amplitude of oscillation of the vocal fold is much smaller than the vocal fold length.

Furthermore, since the middle and deep layers constitute the vocal ligament, they hold more tension then the superficial layer and consequently, their pores are expected to be more compressed and less permeable. The superficial lamina propria layer has the least amount of fibers and contains mostly proteoglycans, large branching proteins that are highly charged and consequently osmotically active (1, 29). The main function of this layer appears to be in the absorption of vocal fold impact forces (30). A large concentration of liquid helps shield the solid structure from this stress (31). Due to its loose organization, the superficial lamina propria layer can easily be separated from the other layers, creating a potential space termed Reinke's space (1). This space fills with fluid in Reinke's edema, demonstrating the importance of the superficial layer for vocal fold fluid dynamics. All of these factors suggest that most of the fluid flow in the vocal fold tissue will occur in the thin region between the epithelium and vocal ligament in the longitudinal direction. In addition, usually, there is no crack in the epithelium and vocal ligament for a healthy vocal fold. Therefore, to represent this situation, we assume that a perfect fiber tract exists without any fissure.

Based on the above assumption, we investigate the dynamical characteristics of a one-dimensional fiber tract and fluid aggregation in the anterior-posterior direction, which is parallel and close to the vocal fold surface. Based on the second assumption, we can substitute dU_⊥/dt = du_⊥/dt into Eqs.(10)-(11) and add Eq.(10) to Eq.(11), where u_⊥ = (u_x, u_z) and U_⊥ = (U_x, U_z). The motion of the one-dimensional solid part in the vocal tissue can be simplified to the motion of equation of a string:

$$\frac{{\partial }^2(\rho u_x)}{\partial t^2}-{\mu }^{\prime }\frac{{\partial }^2{u}_x}{\partial y^2}=0,$$ (14)

$$\frac{{\partial }^2(\rho u_z)}{\partial t^2}-{\mu }^{\prime }\frac{{\partial }^2{u}_z}{\partial y^2}=0.$$ (15)

And the motion of the fluid part in tissue (Eq. 11) can also be simplified as:

$$\frac{{\partial }^2({\rho }_F{U}_x)}{\partial t^2}-{\pi }_x^{F-S}=0,$$ (16)

$$R\frac{{\partial }^2{U}_y}{\partial y^2}-\frac{{\partial }^2({\rho }_F{U}_y)}{\partial t^2}+{\pi }_y^{F-S}=0,$$ (17)

$$\frac{{\partial }^2({\rho }_F{U}_z)}{\partial t^2}-{\pi }_z^{F-S}=0,$$ (18)

and Eq.(9) can be reduced to

$$\frac{\partial {\rho }_F}{\partial t}+\frac{{\partial }^2{U}_y}{\partial y\partial t}=0,$$ (19a)

Integrating Eq.(19a) by t creates

$${\rho }_F(y,t)={\rho }_0(y)+\Delta {\rho }_F(y,t)\text{with}\Delta {\rho }_F(y,t)=-\frac{\partial U_y(y,t)}{\partial y}.$$ (19b)

The term ρ₀(y) represents the liquid mass before the vocal fold begins vibrating, and the term Δρ_F(y, t) = −∂U_y(y, t)/∂y represents the change of liquid mass after the vocal fold begins vibrating. Assuming the initial liquid distribution is uniform, i.e., ρ₀(y)≡ const. and dρ₀(y)/dy = 0, then substituting Eq.(19b) into Eq.(17) allows Eq.(17) to be rewritten as:

$$R\frac{\partial {\rho }_F}{\partial y}+\frac{{\partial }^2({\rho }_F{U}_y)}{\partial t^2}-{\pi }_y^{F-S}=0$$ (20)

Note that because of the fluid movement in the porous material, the fluid mass (ρ_F) per unit volume of aggregate in Eqs. (14-20), which is a function of the longitudinal displacement y and time t, cannot be constant in this tissue model. Therefore, ρ_F and ρ = ρ_F + ρ_s usually cannot be taken out from the partial derivative operators ∂/∂y and ∂²/∂t². The equation of motion of the fluid part [Eqs.(16-18)] and solid part [Eqs.(14-15)] are coupled together through the variable fluid density.

III. Fluid redistribution in vocal fold tissue

In this section, by analytically solving the simplified model presented in section II-D, we will provide a primary insight into the dynamical characteristics of the vocal fold tissue under the fluid-saturated porous solid assumption.

A. Fluid velocity in a vibrating vocal fold

According to the small amplitude oscillation assumption and the small fluid velocity assumption, the change of ρ_F due to fluid movement in the vocal folds is expected to be much more slight in comparison with ρ_s. Therefore, ρ = ρ_F + ρ_s can be roughly considered to be a constant in Eqs.(14-15). The solution of Eqs.(14-15) can be estimated from the previous experimental data and model simulation (11-12, 15, 19, 32). The general solution of Eqs.(14-15) can be written as:

$$\left\{\begin{array}{c}{u}_x\\ u_z\end{array}\right\}=\left\{\begin{array}{c}{\sum }_n\left[a_{n}sin(n\omega t)sin(\mathit{\text{nky}})\right]\\ {\sum }_n\left[b_{n}cos(n\omega t)sin(\mathit{\text{nky}})\right]\end{array}\right\}$$ (21)

where ω is the fundamental frequency, k = π/L is wavenumber, and L is the vocal fold length. Both the intermediate water vocal fold model (19) and the finite-element vocal folds (12, 15) have predicted that the tissue particles in the vocal fold follow an elliptic orbit. The ultrasound imaging of the vocal fold (19) and the vocal fold surface dynamics measurement (25) confirmed these model simulation results. In addition, applying the eigenfunction analysis of the simulation results from the finite-element model (11) and the measurement from the excised larynx experiment (32), it was found that the first two eigenfunction analyses explain 98% of the variance of the nodal trajectories for regular vocal fold vibration. This suggests that the displacement along the anterior-posterior direction of the vocal fold can be roughly estimated by a sine curve. Based on these model simulation and experimental observation, we can ignore the high-order mode of the above solution [Eq.(21)] and only keep the first-mode, that is,

$$\left\{\begin{array}{c}{u}_x\\ u_z\end{array}\right\}=\left\{\begin{array}{c}asin(\omega t)sin(\mathit{\text{ky}})\\ bcos(\omega t)sin(\mathit{\text{ky}})\end{array}\right\}.$$ (22)

Substituting Eq.(22) into Eqs.16 and 18, the interaction ${\pi }_x^{F-S}$ and ${\pi }_z^{F-S}$ between the fluid and solid can be obtained,

$${\pi }_x^{F-S}=-{\rho }_{F}a{\omega }^{2}sin(\omega t)sin(ky),$$ (23)

$${\pi }_z^{F-S}=-{\rho }_{F}b{\omega }^{2}cos(\omega t)sin(ky),$$ (24)

and then, due to the fluid movement along the fibers, the fluid-solid interaction force component in the y-direction can be obtained according the condition of equilibrium [see Fig. 2 (d)],

$${\pi }_y^{F-S}=\frac{1}{2}{\rho }_{F}k{\omega }^{2}A(\omega t)sin(2ky)+F_y(•)$$ (25)

where A(ωt) = a²sin² (ωt) + b²cos² (ωt). F_y(●) is the viscous resistance due to the movement of the liquid in the porous solid, usually, it is a function of the flow velocity:

$$F_y(•)=-\beta \frac{d{U}_y}{dt}$$ (26)

where the coefficient β describes the permeability of the porous solid. When the vocal fold just begins vibrating, there is not enough time to allow the fluid to redistribute. Therefore, the fluid ρ_F hold its initial distribution, that is, uniform distribution. In this condition, ρ_F is constant, therefore, ignoring the partial of ρ_F respect to y, Eq.(20) can be reduced to

$$\frac{{\partial }^2{U}_y}{\partial t^2}+{\beta }^{\prime }\frac{d{U}_y}{dt}=\frac{1}{2}k{\omega }^2\mathit{\text{A}}(\omega t)sin(2ky),$$ (27)

where β′ = β/ρ_F.

The solution of Eq.(27) with the boundary condition dU_y/dt = 0 at anterior side y = 0 and posterior side y = L and the initial condition dU_y/dt = 0 is

$$V_y=\left[B(0)-B(t)e^{-{\beta }^{\prime }t}\right]sin(2ky)$$ (28a)

with

$$B(t)=\frac{k{\omega }^2}{4{\beta }^{\prime }}\left[\left(a^2+{\text{b}}^2\right)-\frac{\left(a^2-b^2\right)}{\sqrt{1+{(2\omega /{\beta }^{\prime })}^2}}sin(2\omega t+{\phi }_0)\right]$$ (28b)

where φ₀ = tan^-1(β′/2ω) and V_y = dU_y/dt is the fluid velocity. This shows that the fluid velocity follows a sinusoidal distribution in the anterior-posterior direction. Moreover, its wave number is double of the wave number of vocal fold vibration, as shown in Fig. 3 (b). The maximum velocity occurs at the L/4 and 3L/4 positions. In the posterior side of vocal fold, the velocity of liquid is positive, but in the anterior side, the velocity of liquid is negative. In other words, the liquid in both the anterior side and the posterior side will move toward the midmembranous region of the vocal fold during vibration. Moreover, the velocity of the liquid is positively proportional to the vibration frequency and amplitude.

Figure 3.

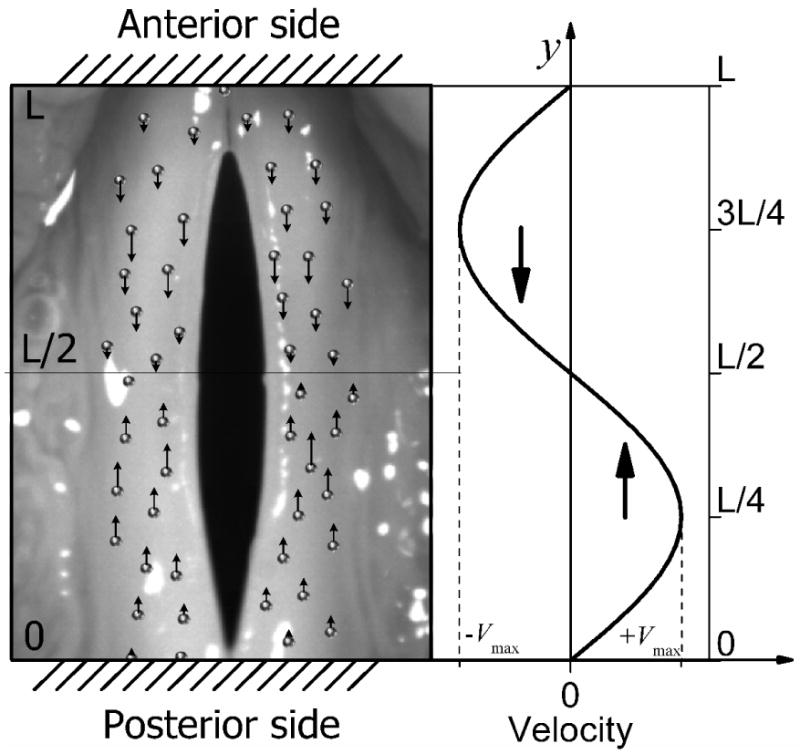
The liquid movement when vocal fold begin vibrating. In spatial, the maximum velocity occurs at the L/4 and 3L/4 positions. In posterior side of vocal fold, the velocity of liquid is always positive, but in the anterior side, the velocity of liquid in vocal fold is always negative. The liquid both in anterior side and in the posterior side will move toward the midmembranous region vocal fold is vibrating. Moreover, the velocity of the liquid is positive proportional to the vibration frequency and amplitude [see Eq.(28)]

B. Fluid redistribution in a vibrating vocal fold

The above fluid velocity information implies that the liquid in the tissue could be redistributed after a long period of phonation. In this subsection, we will investigate the stable liquid distribution in the one-dimensional fiber and fluid aggregation. After a long period of phonation, the liquid in the vocal fold will reach a new equilibrium. In addition, the intermediate water vocal fold model predicts that the maximum vertical displacement of a surface tissue is equal to its maximum lateral displacement (19). The measurement of the medial surface dynamics of the vocal fold also reveals that the maximum vertical displacements are close to the maximum lateral displacements (25). Therefore, based on this fact, we assume a ≈ b to simplify the model. By substituting Eqs.(9, 25-26) into Eq.(20), Eq.(20) can be simplified as:

$$R\frac{d{\rho }_F}{dy}=\frac{1}{2}{\rho }_{F}k{\omega }^2{a}^{2}sin(2ky),$$ (29)

Then, substituting Eq.(19b), ρ_F (y, t) = ρ₀ + Δρ_F (y, t), into Eq.(29), the distribution of liquid in the vocal fold tissue satisfies the following equation:

$$R\frac{d\Delta {\rho }_F}{dy}-\frac{1}{2}k{\omega }^2{a}^{2}sin(2ky)\Delta {\rho }_F=\frac{1}{2}{\rho }_{0}k{\omega }^2{a}^{2}sin(2ky)$$ (30)

Solving Eq.(30), we have:

$$\Delta {\rho }_F=-{\rho }_0+Cexp\left[-\frac{{\omega }^2{a}^2}{4R}cos(2ky)\right],$$ (31)

where the constant C can be determined from the conversation of liquid in tissue ${\int }_0^L\Delta {\rho }_F=0$. In addition, the right term in Eq.(31) can be expanded using Taylor series:

$$\Delta {\rho }_F=-{\rho }_0+C\left\{1-\frac{{\omega }^2{a}^2}{4R}cos(2ky)+\frac{1}{2}{\left[-\frac{{\omega }^2{a}^2}{4R}cos(2ky)\right]}^2+\cdots \right\}$$ (32)

If the frequency and amplitude are small enough to make ω²a²/4R ≪ 1, the high order terms on the right side of Eq.(32) can be ignored. Determining the constant C from ${\int }_0^L\Delta {\rho }_F=0$, it has

$$\frac{\Delta {\rho }_F}{{\rho }_0}\approx -\frac{{\omega }^2{a}^2}{4R}cos(2ky)$$ (33)

Equation (33) shows that the liquid approximately follows a cosine distribution, as shown in Fig.4. For 0 < y < L/4 and 3L/4 < y < L, Δρ_F is negative, which means liquid is lost in these regions. For L/4 < y < 3L/4, Δρ_F is positive and the maximum Δρ_F is located at the midpoint of the vocal fold, which means the liquid accumulates in this region. The loss of liquid implies dehydration and the accumulation of liquid implies edema. Furthermore, the degree of the dehydration and the edema are positively proportional to the vibratory amplitude and frequency.

Figure 4.

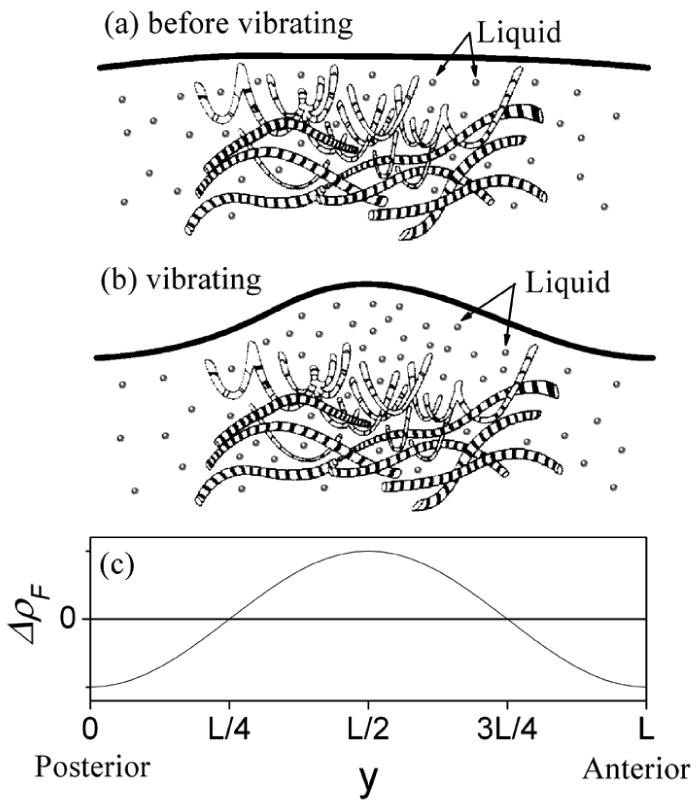
The liquid in vocal fold follow a cosine distribution in the anterior-posterior direction after a stable vibration is sustained. For the region 0 < y < L/4 and 3L/4 < y < L, Δρ_F is negative, which means the liquid are lost in these regions. For the region L/4 < y < 3L/4, Δρ_F is positive and the maximum Δρ_F is located at the midpoint of vocal fold, which means the liquid is accumulated in this region. The figures (a) and (b) are modified from the figures in reference 43.

IV. Discussion and Conclusion

In this study, the vocal fold tissue is treated as a complex material, composed of two types of material with different phases. One is a transversally isotropic, elastic porous solid, which represents the loose solid structure in the tissue. Another is a fluid, which represents the liquid component in the tissue. The solid and the fluid together determine the properties of this vocal fold tissue. Based on the fluid-saturated porous solid theory, a set of system of nonlinear equations, coupled with the equations of motion for the elastic solid and fluid together, is proposed to describe the dynamical behavior of the vocal fold tissue (Eqs. 9-11). Comparing this fluid-saturated porous tissue model with the previous continuous elastic tissue model (3), it was found that by assuming that the fluid in the tissue does not move relative to the solid and completely fills the pores in the solid, the fluid-saturated porous tissue model can be simplified to the continuous elastic tissue model. Therefore, the continuous elastic tissue model is a special case of the fluid-saturated porous tissue model under the condition that the fluid in the tissue does not move relative to the solid. Moreover, the fluid-saturated porous tissue model may represent a more general description of the vocal fold tissue. The fluid-saturated porous tissue model can also be used to explain the properties of vocal fold tissue. It was found that the parameter Λ, which is equivalent to the Lamé constant λ in elastic theory, is many orders of magnitude greater than the Lamé constant μ. This theoretical conclusion agrees with the properties of soft tissue (3, 9).

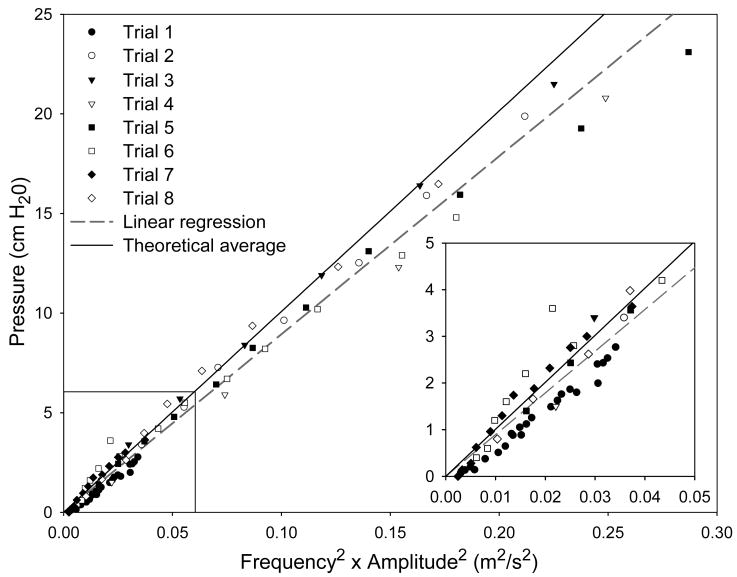
Using this fluid-saturated tissue model, we predicted that when the vocal folds are vibrating, the liquid in the vocal fold tissue will move toward the anterior-posterior midpoint of the vocal fold and finally accumulate in this region [Eq.(33)]. When Eq.(4) and (9) are substituted into Eq.(3), the force s applied on the fluid is determined to be linearly positively proportional to the liquid accumulation, i.e., s ∼ R·Δρ_F. Then, when Eq.(33) is substituted into the above relationship, the pressure of the liquid in the vocal folds is also determined to be proportional to the square of the frequency and amplitude of the oscillating vocal fold. Recently, using a physical blood vessel model, we measured the relationship of intravascular pressure to vibration frequency and amplitude (33). It was found that vocal fold intravascular pressure has a quadratic dependence on both frequency and amplitude, as show in Figure 5. The agreement between the measurement of the physical blood vessel model and the prediction of the proposed tissue model primarily validates the fluid-saturated porous tissue model.

Figure 5.

Pressure plotted with respect to frequency squared and amplitude squared measured from the physical blood vessel. (From reference 33).

The fluid-saturated porous solid model can provide new insight into the etiology of vocal lesions and related vocal disease, such as, polyps and nodules. Vocal nodules are the most common vocal fold disorders. They represent 2-3.9% of the entire ENT case load (34). Usually, the development of vocal nodules is considered to be the consequence of mechanical trauma. According to mechanical pressure hypothesis (35-37), nodules are the result of microtrauma caused by the forces of collision or friction during faulty or excessive vocal use. Titze (1994) analyzed that maximal impact stress occurs in the mid-membranous vocal fold (30). The measurement of the intraglottal pressure in a hemi-excised setup confirmed Titze's analysis (38). Recently, vocal fold model simulations (13-15) found that the maximum stress occurs at the midpoint of membranous fold, which matches the location where nodules are often observed in clinical practice. These results support the mechanical pressure hypothesis.

However, the vocal fold is an organic part of the living body and is much more complex than inorganic materials, such as rubber, plastic, metal, etc. Studies attempting to model phonotary trauma through excessive phonation in canines have only produced mildly similar patterns of injury (39). Therefore, the etiology of vocal fold lesions may be related to multiple factors. The changes in the lamina propria were classified into five stages of maturation (40): edematous (least mature), edematous-angiomatous, angiomatous, angiomatous-hyaline, and hyaline (most mature). Their microscopic examination revealed that the edematous lesions may represent the earliest stage of benign vocal fold lesion pathogenesis. This result opens up the possibility that edema formation may be the inciting factor in, or contribute to, the development of benign vocal fold lesions. It was found that the liquid on a vibrating band tends to accumulate toward the midpoint of the band (41). Moreover, vocal fold nodules and polyps also tend to occur at the midmembranous folds. Based on these factors, Jiang (1991) proposed that the edema due to the accumulation of liquid in a vibrating vocal fold may be another important factor for vocal lesion formation (41). However, there was a lack of direct clinical evidence or theoretical evidence to support Jiang's liquid accumulation hypothesis. In this study employing the fluid-saturated porous tissue model, it was found that when the vocal fold began vibrating, the liquid in the tissue is accelerated toward the midpoint of the vocal fold. After a long period of phonation, the liquid in the vocal fold tissue reached a new equilibrium, with a cosine distribution in the anterior-posterior direction. The liquid in the midmembranous region of a vibrating vocal fold increased, whereas, the liquid in the anterior and the posterior side decreased. The excessive accumulation of liquid in the midmembranous region of the vocal fold indicates localized edema. The location of this edema agrees with the region where nodules and polyps often occur. In addition, the theory of the fluid-saturated porous tissue predicts that the level of accumulation of liquid is positively proportional to the vocal fold vibration amplitude and fundamental frequency, which implies that loud or high pitch phonation is more likely to result in nodules. Clinical observation asserts that the loud voice increase the risk of vocal fold lesions (4). Moreover, vocal nodules are most likely to happen in females and adolescent males, who usually have a high pitch tone (42). The match between the results predicted by the fluid-saturated porous model and the clinical observation suggests that the accumulation of liquid in the vocal fold tissue during phonation could play an important role in the development of vocal fold lesions. Therefore, the fluid-saturated porous tissue model provides the first theoretical evidence to support the liquid accumulation hypothesis of vocal nodules (41). In summary, this study suggested that the fluid-saturated porous solid is a more appropriate description of the vocal fold tissue. The tissue model based on the porous solid should be a useful tool for studying vocal fold physiology and pathology.

Several limitations of the current tissue model need to be resolved in future studies. First, in this study, in order to get an analytical fluid dynamics in a vibrating vocal fold, we have assumed small-amplitude conditions for the oscillation. The resulting accumulation of fluid towards the middle part of the vocal folds, which might be related to clinical findings of locations for vocal fold lesions, polyps and nodules, is also based on this small-amplitude assumption. However, for normal vocal fold oscillation and collision, the small-amplitude condition sometimes cannot be satisfied well. Moreover, most of the damage on the real folds would be made during large oscillations. The current works may not predict the liquid dynamics in a large amplitude situation. This is one important shortcoming of the current study. Second, we assume that a perfect fiber tract exists without any fissure. However, in some specific pathological conditions like vocal scarring, the fissure could exist in the epithelium and the vocal ligament. In these pathological situations, the current assumption could not be validated. In addition, this study mainly focuses on the tissue model of the vocal fold while glottal aerodynamics is ignored. In order to study the liquid accumulation of an oscillating vocal fold, we introduced an oscillating solution [Eq.(22)] according to the previous experimental observation (19, 25, 32). The tissue model itself cannot generate a self-oscillating solution. This is another limitation of the current model. Therefore, development of a self-oscillating vocal fold model based on the fluid-saturated porous tissue model can be expected and will serve as an interesting topic for future studies.

List of Symbols

σ = {σij} (i, j = x, y, z)	Stress tensor of solid	Pa
s = {s}	Stress tensor of liquid	Pa
λ, μ	Transverse Lamé constants	Pa
λ′, μ′	Longitudinal Lamé constants	Pa
C = λ + 2μ	A measure of the transverse stiffness	Pa
C′	A measure of the longitudinal stiffness	Pa
R	A measure of water amount in porous solid under a constant pressure	Pa
Q	Transverse coupling coefficient of the solid and fluid	Pa
Q′	Longitudinal coupling coefficient of the solid and fluid	Pa
ε	Strain of fluid	*
U = {Ux, Uy, Uz}	Fluid displacement vector	m
e = {eij} (i, j = x, y, z)	Strain tensor of solid	*
u = {ux, uy, uz}	Solid displacement vector	m
gS	Body force applied on solid	N/m3
gF	Body force applied on fluid	N/m3
πS-F	Force applied on solid due to solid-fluid interaction	N/m3
πF-S	Force applied on fluid due to solid-fluid interaction	N/m3
ρS	Solid mass per unit volume of aggregate	kg/m3
ρF	Fluid mass per unit volume of aggregate.	kg/m3
ρ = ρF + ρS	Total mass per unit volume of aggregate.	kg/m3
β	Permeability of the porous solid.	kg/s·m3
ω	Fundamental frequency,	Hz
k	Wavenumber	m-1
a, b	Amplitude of vibration in x, z direction.	m
L	Vocal fold length	m

* represent that symbol is dimensionless factor.