On the spontaneous collective motion of active matter

Abstract

Spontaneous directed motion, a hallmark of cell biology, is unusual in classical statistical physics. Here we study, using both numerical and analytical methods, organized motion in models of the cytoskeleton in which constituents are driven by energy-consuming motors. Although systems driven by small-step motors are described by an effective temperature and are thus quiescent, at higher order in step size, both homogeneous and inhomogeneous, flowing and oscillating behavior emerges. Motors that respond with a negative susceptibility to imposed forces lead to an apparent negative-temperature system in which beautiful structures form resembling the asters seen in cell division.

Spontaneous directed motion driven by active processes is crucial to biology. Such motion is only possible because the cell is a far-from-equilibrium many-body system. The cytoskeleton of eukaryotic cells is built, maintained, and adaptively reorganized through active transport and force generation powered by ATP hydrolysis. Oscillations of the mitotic spindle during cell division (1) and cytoplasmic streaming (2) dramatically illustrate that the cell is not at equilibrium. Driven motions of cells are also important at higher levels of organization in living things ranging from mechanosensation (3) to the developmental processes in which the genetic code unfolds to create a multicellar organism (4). Sustained spontaneous collective motion is quite remarkable in many-body physics. Superfluidity and superconductivity are examples of metastable states of motion made possible by quantum statistics. The biological example provided by the cytoskeleton is seemingly quite different, leading not to infinitely long-lived states but to ones that go away when the cell is depleted of fuel and dies. Nevertheless, like the quantum examples, the motion of the cytoskeleton is an emergent many-body phenomenon reflecting broken symmetries.

Here we explore the origin of spontaneous collective motion for systems of many interacting biomacromolecules with motor-driven active processes using a systematic perturbative expansion of the many-body master equation treating nonequilibrium motorized processes. We model the motors as generating a time series of isotropic kicks on the constituents of a many-body assembly. Earlier (5) we showed that quite generally the corresponding master equation, when expanded to the lowest order in the kick step size, yields an effective temperature, T_eff, which explicitly depends on the total motor activity and on the way in which motors respond to imposed forces. A system described by an effective temperature alone (6–8) cannot undergo spontaneous directed motion unless it is quantum mechanical so that spatial and momentum degrees of freedom are coupled by the uncertainty principle. Pursuing the expansion to higher order, however, reveals the possible emergence of spontaneous directed collective motion quite generally from a quiescent homogeneous state, albeit one with rigidity owing to broken translational symmetry, as in a glass. The underlying dynamic instability is induced by a sufficiently strong internal agitation in terms of kick step size. This provides a general mechanism for spontaneous flows in an active assembly of interacting constituents.

Combining a linear stability analysis with a trial solution of the many-body master equation allows us to identify possible dynamic phases that depend on the motor kick step size and susceptibility. We find that for sufficiently large kicks and high activity, susceptible motors (i.e., motors whose kick rate depends on the forces exerted on them) can generate spontaneous flow, whereas adamant motors, indifferent to imposed forces, would merely drive fluidization of an active system. We have also carried out simulations on a minimal cytoskeleton model incorporating motor dynamics to compare with our analytical predictions. The simulations not only verify the predicted phase diagram, but also highlight how the combination of network connectivity with motor susceptibility determines the formation of nonequilibrium structures. The simulations show an oscillatory phase separation at intermediate network connectivity and formation of aster-like patterns/bundle-connected poles when driven by motors with negative susceptibility (i.e., motors that move against the force, energetically uphill). The latter corresponds to a negative-temperature system where interesting structures emerge much like vortex condensation in two-dimensional turbulence (9–11).

We are far from the first to try to understand the physics of spontaneous collective motion in biology. Jülicher and Prost (12) studied a one-dimensional stochastic model that assumed an underlying ratchet potential already breaking translational symmetry. Motor cooperativity then leads to a dynamical phase transition to spontaneous directed motion despite the system’s spatial symmetry. Thinking of the cytoskeleton, an assembly of filamentous polar polymers actively connected by cross-linkers, as an active polar gel has allowed the construction of continuum theories, based on conservation laws and symmetry considerations, which also generate active flows (13–16). Pattern formation in active fluids has also been discussed based on a reaction-diffusion-advection mechanism (17).

Model

Here we model the stochastic nature of the motor kicking via a master equation for the many-body probability distribution function 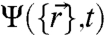(18, 19):

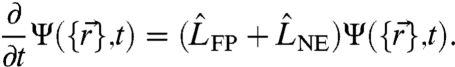[1]

Here 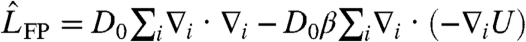is the usual many-body Fokker–Planck operator describing passive Brownian motion with D₀ denoting the ordinary diffusion coefficient at ambient temperature T and β = 1/k_BT. The gradients of the many-body interaction potential 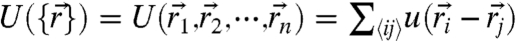give the local forces acting on individual particles, where 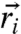is the position of the ith particle and denotes the nearest neighbor pairs. Note that the potential U reflects an average over the solvent degrees of freedom and internal degrees of freedom of the motors and is thus strictly speaking a free energy. The effects due to nonequilibrium motorized processes are summarized by an integral kernel 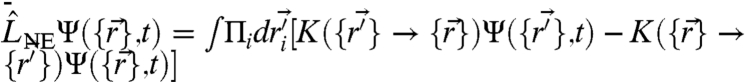, where 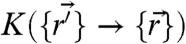encodes the probability of transitions between different particle configurations per unit time. Motor kicking noise is a finite jump process with a rate that depends on whether the free energy is increased or decreased when a step is made:

[2]

Here Θ is the Heaviside step function and 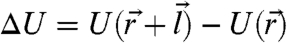is the free energy change due to the kick identified by a vector 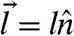. The kick step size l and the basal kicking rate κ define the dimensionless motor activity Δ≔κl²/D₀, an analog of the Peclet number in turbulent diffusion. This model rate couples the chemical reactions leading to the motor activity to the local mechanical forces acting on the motor being parametrized by the susceptibility s, which may take different values for uphill (s_u) moves and for downhill (s_d) moves depending on the biochemical mechanism of the motors. When s → 1, the motors are susceptible, slowing down when they climb up against obstacles and accelerating when they move energetically downhill; in contrast, s → 0 corresponds to completely adamant motors that kick at a rate unperturbed by the free energy landscape.

Systematic Expansion and Stability Analysis

To examine the small kick size limit, we first expand the equation in powers of 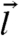up to the quadratic order. The simplest case, isotropic kicking and symmetric susceptibility (i.e., s_u = s_d = s) leads directly to an effective Fokker–Planck equation (5):

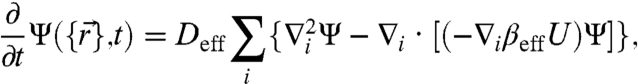[3]

where

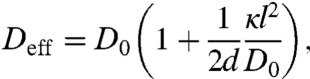[4]

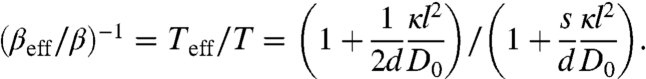[5]

These simple expressions (Eqs. 3–5), valid for general spatial dimensions d, have nontrivial implications. In the small kick limit, the active system, although out of equilibrium, behaves as if it is at an effective canonical equilibrium characterized by an effective temperature T_eff. The effective diffusion constant D_eff (Eq. 4) is enhanced by the active processes regardless of motor adamancy, consistent with recent observations of enhanced cytoplasmic diffusion (20). T_eff (Eq. 5) is fully determined by the motor activity Δ = κl²/D₀ and the motor susceptibility s; susceptible motors with s > 1/2 yield T_eff < T. When motor activity dominates over thermal noise ( i.e., Δ≫1), the effective temperature diverges as T_eff/T ∼ 1/(2s) as s → 0. Thus, intense kicking by adamant motors leads to a very high effective temperature just as observed in experiments (21) and simulation studies (22, 23). A more detailed discussion can be found in a separate work (5).

To probe the dynamic instability that may give rise to the spontaneous motion, we must go beyond the effective equilibrium and expand to quartic order in l obtaining

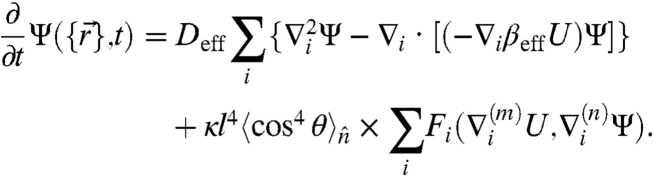[6]

The functional F_i is the divergence of a flux; i.e., 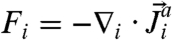, where 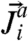is the probability current due to active events on particle i given by

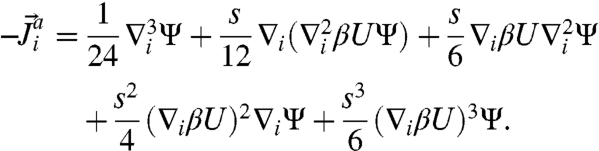[7]

Whereas at quadratic order in l, a motor-driven system exhibits enhanced diffusive dynamics at an effective equilibrium, at quartic order, a net streaming flow becomes possible, as in models of nonequilibrium gene switch (24).

In an earlier study of the stability and dynamics of a motorized assembly, Shen and Wolynes (18) pictured the motors as introducing a modification to the Debye–Waller factors of the localized particles. They found an expression of the deviation of the total localization strength 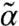from its thermal value α in terms of the motor properties. Thermal self-consistent phonon theory (25) gives α for a central particle that depends on the 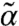of all its neighbors. Combining these two aspects allows a self-consistent determination of mean-field (α, 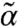) solutions allowing an identification of static stability limits. Assuming s_u = s_d = s, the second moment closure (19) reduces to a simple expression 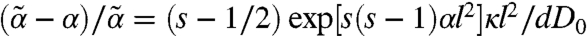. Thus, for s = 1/2 (T_eff = T), chemical noise does not modify the mechanical stability (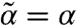); for s < 1/2 (T_eff > T), stability is weakened (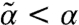); whereas for s > 1/2 (T_eff < T), stability is enhanced ().

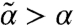For spontaneous collective motion, there must be a nontrivial dynamic first moment that indicates a moving fiducial lattice. The second moment still has its steady-state value describing vibrations about the fiducial configuration. We thus write down a trial function of the master equation as a collection of Gaussians with moving centers and a steady variance:

[8]

where 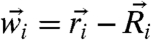denotes the displacement of particle i from its equilibrium position 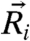, 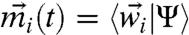defines the dynamic first moment of particle i, and the total localization strength 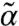of individual particles is inversely related to the second moment.

To account for the neighbor-coupling effects, we adopt the coupled-oscillator expansion of the effective potential, V_e, used earlier by Stoessel and Wolynes (26). Here the gradient of the general many-body free energy becomes 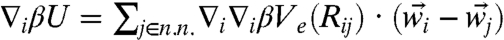, where 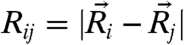denotes the equilibrium separation between the central particle i and its nearest neighbor j. The curvature then follows 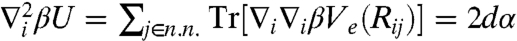. The mechanical localization strength is defined by 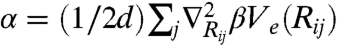. Higher-order gradients of βU vanish at this level of coupling. A nonzero α reflects a (possibly amorphous) state of broken translational invariance, as in a gel. Applying the first moment closure 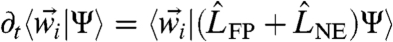to Eq. 6 with the Gaussian ansatz (Eq. 8) as well as the coupled-oscillator expansion of the effective potential leads to coupled equations for the 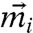s.

To investigate the emergence of directed motion, we carry out a linear stability analysis about the nonmoving state (i.e., 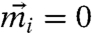). In view of the biological relevance of one-dimensional scenarios, such as the filament sliding in motility assay (27) and flow in the cell cortex (28), we focus here on the 1D case. Consider a spatially varying trial solution of the form

[9]

where 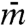denotes the amplitude of the first moment, k the wavenumber of the spatial modulation, and r_k the growth rate. Even if kicks are isotropic and the interaction Hamiltonian preserves rotational symmetry, spontaneous symmetry breaking occurs, giving flow in a specific direction.

In the long-wavelength limit one finds

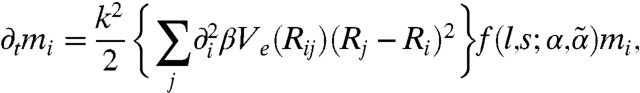[10]

where

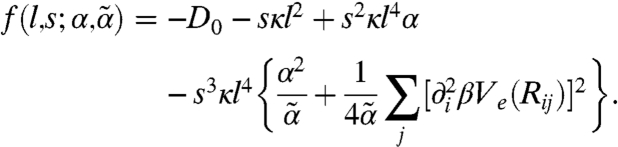[11]

Because ∂_tm_i = r_km_i, the growth rate is proportional to 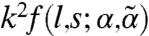up to O(k²). It follows that a strictly uniform state (k = 0) would not undergo small-amplitude dynamic instability regardless of the motor activity and susceptibility, but the nonmoving state is barely stable in the absence of spatial modulation. Moreover, the sign of 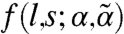determines the stability behavior for small but finite k. When the kick step size l is small, f is negative, indicating diffusive relaxation toward the nonmoving state. As l increases, instabilities grow: f (and thus r_k) becomes positive, signifying a collective flow in a spatially modulated state, when l exceeds a threshold value l_th given by

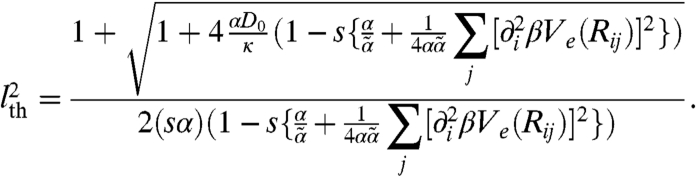[12]

At high motor activity such that 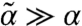and κ≫αD₀, 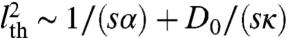. Thus, high susceptibility s and kicking rate κ and large α lead to a low instability threshold (see Fig. S1 for a detailed illustration). Note that assuming a statistically homogeneous structure will remove the i dependence of f and l_th. For the case of asymmetric susceptibility (s_u ≠ s_d), the factor (s_u - s_d) accompanies all the cubic-and-above odd powers in 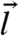in the expansion, leading to a smaller threshold kick size compared to that for the symmetric case where corrections start at quartic order in l.

We carried out the self-consistent calculation described earlier on a minimal model of the cytoskeleton as a cat’s cradle (29, 30) to determine (α, 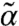) and used this to obtain the growth rate for a model network consisting of nonlinear elastic filaments characterized by relaxed length L_e and stretching stiffness βγ built on a three-dimensional random lattice of cross-links at density ρ. The network connectivity P_c is defined as the fraction of nearest-neighbor pairs of cross-links connected by filaments. The unit of length is the average separation between the neighboring cross-links.

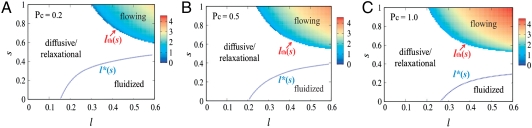
In Fig. 1 we show the phase diagrams for possible dynamic states as a function of kick size l and susceptibility s for several values of the network connectivity. In all the cases, there are two stability boundaries, one for small s (s < 1/2), one for large s (s > 1/2). In the low-s regime, as l reaches a critical value, l^∗(s) (blue dotted line), finite solutions for (α, 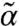) become unstable, i.e., the system becomes fluidized. In the high-s corner, when l exceeds a threshold value l_th (lower boundary of the color-coded region), instability occurs for small but finite k modes indicating the emergence of modulated flowing states. In this region, stable finite (α, 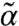) solutions exist with 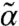being considerably larger than α, reflecting the enhancement of stability by susceptible motor kicking. Note that as motor susceptibility increases, the threshold kick step size decreases. In the rest of the diagram, α and 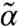are comparable and the negative growth rate indicates diffusive modes. (Close to detailed balance, s = 1/2, diffusive modes persist over the entire relevant range of l.)

Fig. 1.

Phase diagram for possible dynamic states. The parameter plane indicates the motor kick step size l and the motor susceptibility s. The model cytoskeleton used to obtain α and 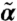is characterized by cross-link density ρ = 0.8, relaxed length of the filaments L_e = 1.2, and stretching stiffness βγ = 5. From A to C, the network connectivity varies with P_c = 0.2, 0.5, and 1, respectively. D₀ = 0.1 and κ = 20. In the flowing regime, there are stable nontrivial (α, ) solutions and positive r_k; in the diffusive/relaxational regime, although there are stable nontrivial (α, 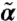) solutions, there is a small negative r_k; in the fluidized regime, finite (α, 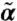) solutions are unstable. As network connectivity rises, the flowing phase region expands, whereas the fluidized state region shrinks. The logarithm of the normalized growth rate r_k/k² for flowing instability is color-coded, showing the increase of instability with l and s.

In the figures, we color-code the logarithm of the normalized growth rate r_k/k² for the flow instability; the growth rate increases with l and s. Comparing the diagrams for different values of connectivity, we see that as P_c increases, the region corresponding to the fluidized state shrinks, because increasing the number of bond constraints stabilizes the system against fluidization. On the other hand, the region corresponding to flow expands toward lower l (and lower s slightly), suggesting that as the mechanical feedback increases (larger α due to higher P_c), a smaller kick is able to trigger the flowing instability when the motors are susceptible.

Simulations

To check these predictions we performed dynamic Monte Carlo (31) simulations on the model cytoskeleton (29, 30). In these simulations we generated initially a three-dimensional random lattice of volumeless nodes (mimicking the cross-linking proteins) and connected the nearest-neighbor nodes (defined by the first shell of the pair distribution function) with nonlinear elastic bonds (30) (mimicking the filamentous proteins) at a given probability P_c. Thermal steps obey Brownian dynamics (32), whereas chemical moves follow the stochastic process defined by the model kicking statistics (Eq. 2). The simulations reveal an interesting interplay of network connectivity with the motor susceptibility dramatically affecting structural development.

At a relatively high network connectivity, P_c ≃ 0.5 (average coordination number z ≃ 6), force transmission through the bonds is efficient and the network structure remains statistically homogeneous in the presence of the motor-driven processes. Nevertheless, varying motor susceptibility drastically changes the dynamics.

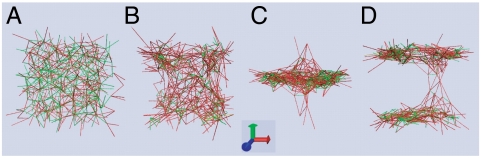
Fluidized state: Under completely adamant kicks (s = 0) with a moderately large step size (l > l^∗), nodes rapidly become fluidized. Elastic stretching of the bonds imposes no constraint on the node motion resulting in vanishing localization strength and zero net flow (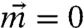). Consequently, as shown in Fig. 2A, almost all the initially floppy bonds (in green) get stretched (in red) and the network becomes very tense.

Fig. 2.

Network structure for various dynamic phases. (A) Fluidized phase with s = 0. An initially relaxed (Left) network rapidly tenses up (Right) under completely adamant motor kicking. Localization strength of the nodes vanishes, and there is no net flow. (B) Diffusive phase with s = 0.2. Spots of concentrated tense/floppy filaments are visible. Nodes exhibit enhanced diffusive motion with a finite localization strength. No spontaneous flow occurs. (C) Flowing phase with s = 1. Network structure remains homogeneous despite the spontaneous flowing motion, reflecting the enhanced rigidity of the structure and coherence of motion by susceptible motor kicking. L_e = 1.2, βγ = 5, P_c = 0.5, and l = 0.25. Red lines stand for tense filaments and green lines for floppy filaments.

Flowing state: At the other extreme, however, under susceptible kicks (s = 1) with above-threshold step size l > l_th, a self-sustained flow develops and the nodes vibrate about a steadily moving fiducial lattice (see Fig. S2 for statistical characteristics of the flowing state) both for regular lattices and for random structures. Apparently disorder in the structure, inherent in the quenched connectivity or dynamically generated through initial random motions, gives rise to local force asymmetry. Sufficiently large kicks then trigger dynamic instability of the quiescent state; the resultant nucleation and propagation of local coordinated motion, mediated by force transmission and orchestrated by susceptible motor kicking, finally leads to a global concerted movement of the whole lattice. High motor susceptibility promotes cooperativity, resulting in “rigidity” of the structure and coherent collective motion. As can be seen in Fig. 2C, the network structure remains homogenous without significant local distortions.

Diffusive state: When the motors are only moderately susceptible (s: 0.2–0.5) but not sufficiently cooperative to drive spontaneous flow, the system exhibits enhanced diffusive relaxation toward the effective equilibrium characterized by T_eff, leading to a homogeneous network structure with modest local density fluctuations. The magnitude of density fluctuations and the tenseness of the network depend on the susceptibility. At relatively low susceptibility (s ≤ 0.3), homogeneously distributed spots of concentrated tense or floppy filaments are visible (Fig. 2B); as the susceptibility rises (s ∼ 0.5), density fluctuations get weaker and the network becomes more homogeneous with a lower degree of stretching, closely resembling the flowing state (Fig. 2C). At relatively high connectivity, the simulations thus verify the possible dynamic phases predicted by the analytical theory.

At intermediate connectivity P_c ≃ 0.3 (z ≃ 3–4) network connectivity is sufficient for tension percolation, yet local force asymmetry becomes significant and widespread over the network. Now under susceptible motor kicks with a considerable step size, dramatic spatial heterogeneity emerges and oscillations of the network in a particular spontaneously chosen spatial direction occur (Fig. 3 and Movie S1). Apparently the overall tenseness of the structure is reduced by collapsing the network into clumps at the cost of a few highly stretched interclump filaments. Fig. 3 C and D display the planar clumps where the floppy filaments (in green) concentrate and which are connected by highly stretched interclump bonds (in red). Our previous analytical mean-field study of an equilibrium nonlinear elastic network (30) already suggests the possibility of phase separation in this system at a finite effective temperature; the pressure exhibits a nonmonotonic dependence on the node concentration, leading to mechanical instability of homogeneous states. [Phase separation induced by contractile instability has also been predicted for active polar gels (13).] When confined by boundaries, such as the cell membrane, these oscillating clumps may become stationary wave patterns with a characteristic length scale of modulation, reminiscent of the mitotic spindles.

Fig. 3.

Temporal development of the phase separation. At intermediate connectivity P_c = 0.3 and under susceptible motor kicking (s = 1) with a considerable step size l = 0.25, the initially homogeneous system (A) phase separates into oscillating clumps and voids (B–D). Notice that the relaxed filaments (green) become concentrated within the planar clumps as well as the presence of highly stretched interclump filaments (red). L_e = 1.2, βγ = 5.

In the presence of susceptible motor kicking (s≥0.6), failure of force percolation at lower values of the network connectivity P_c ≤ 0.2 (z < 3) also yields phase separation, but without any collective motion (Movie S2). Conversely, when there are too many bond constraints at P_c≥0.6 (z > 7), there are significant mechanical barriers that seem to slow down flow initiation and to reduce flow speed.

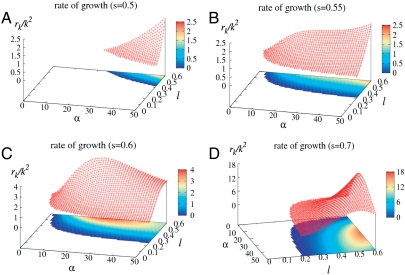
The analytic stability analysis leads to a similar connection between instability growth and the number of bond constraints via the localization strength of individual nodes. In Fig. 4, we display the two-dimensional surface as well as the contour map of the growth rate r_k/k² given by Eq. 10 in the flowing regime (r_k > 0) as a function of localization strength α and kick size l for a series of susceptibilities s. Close to detailed balance (i.e., s = 0.5) (Fig. 4A), flowing instability emerges only at very high α and large l, and the growth rate increases with α. At s = 0.55 (Fig. 4B), a plateau in the growth rate develops at relatively high α. For susceptible motors with s≥0.6 (Fig. 4 C and D), the growth rate has a nonmonotonic dependence on α. As the localization strength of individual constituents increases, the flow instability first speeds up and then slows down with α. There exists an optimal localization strength (or network connectivity) for most efficient flow. This is consistent with simulations (see Movies S3–S7).

Fig. 4.

Dependence of growth rate upon localization strength at different motor susceptibility. The 2D surface and the contour map of the growth rate r_k/k² for flowing instability are displayed over the parameter plane extended by the localization strength α of individual particles and the motor kick step size l. D₀ = 0.1 and κ = 20. (A) s = 0.5; (B) s = 0.55; (C) s = 0.6; (D) s = 0.7. For susceptible motors with s≥0.6, the growth rate develops a nonmonotonic dependence on the localization strength at a sufficiently large kick size, suggesting an optimal strength of mechanical feedback for an efficient flowing motion.

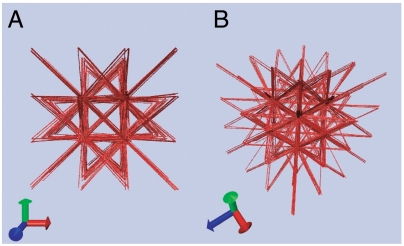
Biological motors can have slip bonds (33, 34) so that an applied force lowers the energy barrier for uphill moves. Slip-bond behavior leads to a negative motor susceptibility, which in turn leads to a negative effective temperature. This implies an intrinsic thermodynamic instability. We investigated this thermodynamically unusual situation. We consider the case for s_u = -1, s_d = 0 where motors are insensitive to energetically downhill slope, whereas they run faster when they go up against obstacles. Starting with a disordered structure at a high connectivity (P_c = 0.5), the motorized network rapidly develops into a highly ordered and tense structure, as shown in Fig. 5.

Fig. 5.

Aster-like patterns/bundle-connected poles formed under kicks of uphill-prone motors with a negative susceptibility. s_u = -1, s_d = 0; L_e = 1.2, βγ = 5, P_c = 0.5, and l = 0.25. A and B are snapshots of the system taken at the same instant from different view angles.

This interesting behavior is not hard to understand: Because of the negative s_u, consistent with the negative effective temperature, the kicks maximize the total energy by separating the bonded nodes as far as possible from each other. The resulting “aster-like” patterns closely resemble those formed by in vitro reconstituted active gels (35), where unidirectional movement of myosin II motors along the polar filament tracks toward the aster core (concentrated “plus” ends of actin filaments) results in considerable stress accumulation at the center, giving rise to the so-called “novas of asters.” Clearly, motor susceptibility dramatically affects development of nonequilibrium structures.

In sum, we have derived an analytical expression for the stability limits of quiescent active gels and proposed a mechanism for spontaneous collective motion within a unified theoretical framework. Simulations of a model cytoskeletal network further highlight that the interplay of network connectivity with motor susceptibility dramatically affects the formation of nonequilibrium structures: Force percolation and mechanochemical coupling conspire to drive and maintain spontaneous flow, whereas adamant motor kicks promote fluidization. Significant force imbalance sensed by susceptible motors induces phase separation into oscillating clumps. Uphill-prone motors with a negative susceptibility give rise to a system at a negative effective temperature. Aster-like patterns form, resembling those seen in reconstituted active gels.