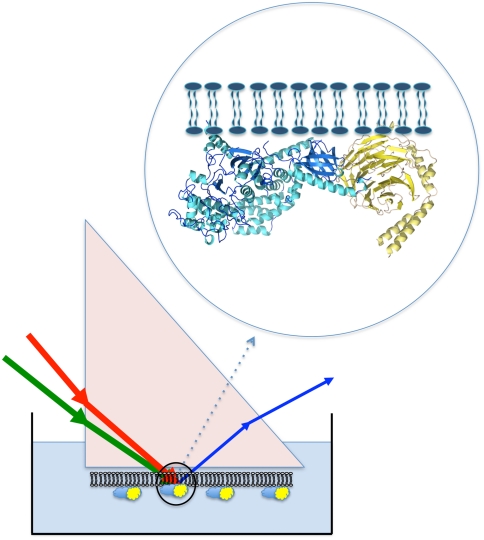
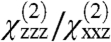Abstract
Few experimental techniques can assess the orientation of peripheral membrane proteins in their native environment. Sum Frequency Generation (SFG) vibrational spectroscopy was applied to study the formation of the complex between G protein-coupled receptor (GPCR) kinase 2 (GRK2) and heterotrimeric G protein β1γ2 subunits (Gβγ) at a lipid bilayer, without any exogenous labels. The most likely membrane orientation of the GRK2-Gβγ complex differs from that predicted from the known protein crystal structure, and positions the predicted receptor docking site of GRK2 such that it would more optimally interact with GPCRs. Gβγ also appears to change its orientation after binding to GRK2. The developed methodology is widely applicable for the study of other membrane proteins in situ.
G protein coupled receptors (GPCRs) are integral membrane proteins that are involved in a wide variety of biological processes in eukaryotic cells (1). In response to extracellular cues such as hormones, odorants, and light, these cell surface receptors activate heterotrimeric GTP-binding proteins found on the inner surface of the cell membrane, which in turn directly interact with membrane associated effectors such as adenylyl cyclase or cGMP phosphodiesterase, which control the level of second messengers (2).
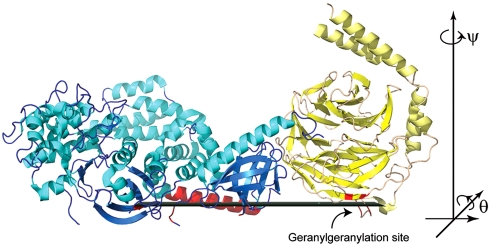
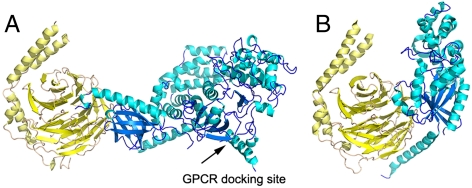
Over the past fifteen years, crystallographic analysis has yielded significant insights into the molecular mechanisms of signal transfer between heterotrimeric G proteins and their effector targets (3, 4). Despite this progress, crystallographic structure determination requires removal of the protein from its native environment, and cannot provide direct information on the orientation of these molecules when they interact with the plasma membrane. Understanding the membrane-bound orientation is critical for understanding how the membrane facilitates higher affinity interactions between signaling molecules, how these molecules are optimally aligned through these interactions for catalysis, and how higher order signaling scaffolds are assembled at the membrane. For example, the interactions of heterotrimeric G proteins, in particular their βγ subunits (Gβγ), with the lipid bilayer facilitate GPCR-catalyzed GTP exchange on the Gα subunit (5). Gβγ subunits are also well known for their interactions with other signaling proteins such as effectors phospholipase Cβ and G protein regulated inwardly rectifying potassium channels, as well as GPCR kinase 2 (GRK2) (6), which is recruited to the membrane by G proteins to phosphorylate activated GPCRs (Fig. 1). Because of its ability to simultaneously interact with activated heterotrimeric G proteins Gαq and Gβγ, GPCRs and the membrane, GRK2 may be involved in the assembly and organization of signaling complexes at GPCRs (7). Although the crystal structure of GRK2 in complex with both Gαq and Gβγ is known, (8) its precise orientation while engaged at the cell membrane is not known because many of the known membrane binding determinants of the complex are disordered or involved in crystal contacts.
Fig. 1.
The GRK2-Gβγ complex in the reference orientation, based on a set of potential membrane interacting residues (shown in red). The fitted plane, which would be parallel to the plane of the lipid bilayer, is shown in dark green. GRK2 is colored blue with cyan helices. Gβγ is colored yellow, with helices shown in pale yellow. The C-terminal residue of the G protein γ subunit is geranylgeranylated, and thus must be in close proximity to the bilayer.
Recently, vibrational spectroscopic techniques such as Sum Frequency Generation (SFG) vibrational spectroscopy have been developed into a powerful, highly surface-specific, and in situ probe of biological molecules at interfaces (9–17). Compared to other techniques such as NMR, SFG experiments can be performed in more biologically relevant systems (single lipid bilayers), using less sample and without the requirement for isotope labeling. Although SFG can not be used to determine a detailed protein structure, the available measurements of protein orientation are relevant to many biological problems. It has previously been shown that α-helical amide I SFG signals can be used to determine the orientation of single peptides, single peptides in a dual orientation distribution, and the Gβ1γ2 (hereafter denoted as Gβγ) subunit of the heterotrimeric G protein in a POPC/POPC lipid bilayer. In the current work, we sought to directly characterize the formation and orientation of the larger GRK2-Gβγ complex in a more biologically relevant lipid bilayer. In particular, we examine (i) whether the orientation of the GRK2-Gβγ complex at the model cell membrane is consistent with predictions made based on an existing crystal structure, and (ii) whether or not Gβγ reorients in order to accommodate binding of GRK2. A method for measuring how subunits reorient upon formation of membrane protein complexes would provide important molecular insights into how multisubunit complexes assemble at biological interfaces, and in particular about how Gβγ is oriented with respect to GPCRs, which are targeted by both Gαβγ heterotrimers and GRK2-Gβγ. The experimental approaches and analysis tools developed in this article are applicable to the study of membrane protein orientation, membrane protein binding, and protein-protein interactions in many other systems in situ and in real time.
Results
In this research, we developed a systematic method to study the formation and orientation of membrane-bound protein-protein complexes without the use of exogenous labels, provided that a crystal structure of the complex is available. Our method includes a software package that facilitates interpretation of SFG spectra collected in multiple polarization combinations, producing a series of heat map-type plots to summarize the most likely protein orientations based on multiple measurements. The formation of the protein-protein complex between Gβγ and GRK2 was observed in real time in situ on a model cell membrane, and the dependence of polarized SFG signals upon protein orientation was calculated using our software program. This information was processed to produce multiple independent measurements for a more complete picture of subunit orientation and reorientation.
SFG Spectra and GRK2-Gβγ Complex Formation.
Proteins were studied by injecting a protein stock solution into the aqueous subphase of a 9∶1 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine/1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoglycerol (POPC/POPG) lipid bilayer and monitoring time-dependent SFG spectra until the protein signal intensity at 1,652 cm-1 was stable (∼1 h). Spectral intensities were the same under continuous collection as when the input laser beams were blocked, and no change was observed over the time scale of these experiments, indicating that the sample did not sustain damage due to laser irradiation. In all cases, Gβγ, GRK2, or the GRK2-Gβγ complex were added to the aqueous buffer for a final concentration of 336 nM. The following samples were examined: (i) GRK2 or (ii) Gβγ alone, (iii) a preformed GRK2-Gβγ complex, (iv) a GRK2-Gβγ complex formed by sequential addition of equimolar Gβγ and GRK2, and (v) Gβγ after the addition of equimolar GRK2-R587Q, a GRK2 mutant deficient in binding Gβγ (18). It has previously been shown that GRK2 binding to the membrane is greatly enhanced by the presence of Gβγ (6), and, therefore, sequential addition experiments in which GRK2 was added first were not performed.
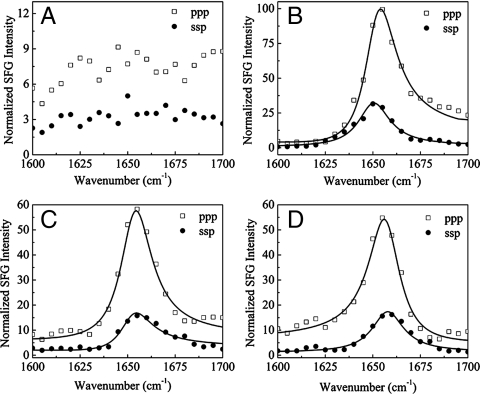
As seen in Fig. 2A, only weak signals were observed in SFG amide I spectra collected from GRK2 alone at the lipid bilayer, presumably due to the relatively weak interactions between the lipid bilayer and GRK2. In contrast, much stronger spectra were observed for the Gβγ subunit alone in the lipid bilayer (Fig. 2B), which is consistent with the fact that Gβγ is geranylgeranylated and thus has a much higher lipid affinity than GRK2 (6). The Gβγ spectra are dominated by a peak at ∼1,652 cm-1, contributed by the α-helical regions of the protein.
Fig. 2.
SFG measurements of GRK2, Gβγ, and their complexes on a POPC/POPG (9∶1 weight ratio) lipid bilayer. (A) Only weak amide I signals were observed from GRK2 injected alone, consistent with the fact that GRK2 itself does not bind to lipids with high affinity. (B) Stronger signals were observed from Gβγ, consistent with the fact that the protein is lipid modified. (C) Signals and ppp/ssp ratios from the preformed complex and (D) from two subunits added sequentially are similar, indicating that the complex can be formed in situ. In both cases, the fitted zzz/xxz ratio is ∼2.20.
To demonstrate the formation of the complex in situ, we collected SFG spectra from the preformed GRK2-Gβγ complex at the membrane interface (Fig. 2C), and compared these to the results from serial addition of GRK2 to Gβγ (Fig. 2D). The spectral intensities (Fig. 2B) and fitted 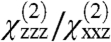 ratios (as calculated in Methods) were similar, but markedly different from those observed for Gβγ alone. As expected, serial addition of the GRK2-R587Q mutant to Gβγ did not alter the Gβγ spectra. These results clearly demonstrate that we are able to form and directly observe the formation of a specific complex in situ using SFG.
ratios (as calculated in Methods) were similar, but markedly different from those observed for Gβγ alone. As expected, serial addition of the GRK2-R587Q mutant to Gβγ did not alter the Gβγ spectra. These results clearly demonstrate that we are able to form and directly observe the formation of a specific complex in situ using SFG.
Fitting of the experimental spectra shown in Fig. 2 yields the following reproducible results: the Gβγ 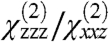 ratio is 2.01, the fitted signal strength in the ssp polarization drops by roughly a factor of 1.39 when GRK2 is added to form the complex, and upon formation of GRK2-Gβγ, the
ratio is 2.01, the fitted signal strength in the ssp polarization drops by roughly a factor of 1.39 when GRK2 is added to form the complex, and upon formation of GRK2-Gβγ, the 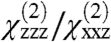 ratio is 2.20.
ratio is 2.20.
Orientation of the GRK2-Gβγ Complex.
A marked drop in signal intensity was observed in the transition from Gβγ alone to the complex with GRK2 (Fig. 2 B and D). As discussed in Methods, SFG signal intensities are a function of molecular orientation, the net molecular hyperpolarizability βprotein, and the number of molecules on the surface (19). Given the expectation that the molar concentration of proteins at the membrane will be driven primarily by the presence of Gβγ (and that geranylgeranylated Gβγ will not dissociate from the lipid bilayer upon addition of GRK2) we can assume that the drop in intensity is due to a change in the net molecular hyperpolarizability upon addition of GRK2, reorientation of the protein segments, or both. Because the observed SFG spectra are dominated almost entirely by single peak centers corresponding to α-helices, we may calculate the net amide I hyperpolarizability for the protein (βprotein) in terms of a “reference” orientation of the known protein structure (Fig. 1).
The crystal structure of Gβγ in complex with GRK2 (PDB entry 1omw) was used as the starting point for all data analysis (20). Although it is possible that proteins can change their conformation upon interacting with membranes, the preponderance of evidence suggests that the GRK2-Gβγ complex does not. First of all, the structure of the GRK2-Gβγ complex has been determined in the presence and absence of detergent micelles (8). Furthermore, GRK2-Gβγ interacts with membranes primarily through regions that are intrinsically poorly ordered (such as the prenylated C terminus of the Gγ subunit and the β1-β2 loop of the GRK2 PH domain). Because these regions are not coupled to the core structure of the complex, it seems unlikely that their interaction with membranes will induce a large conformational change. GRK2 is in fact rigidified by binding Gβγ (21), and the buried surface area in its domain interfaces are very large and therefore unlikely to dissociate. In test calculations, the effect of a small difference in the arrangement of helical segments on our results was minimal. A linear least-squares fitting routine was used to fit a plane through regions of GRK2-Gβγ that were expected to be in close proximity to the lipid bilayer, such as the β1-β2 loop of the PH domain (18) and the C-terminal region of Gγ, which is geranylgeranylated. The full list of residues may be found in SI Text. The resulting fitted plane was used to define a “standard membrane orientation” for further calculations (Fig. 1), which is denoted as the tilt (θ) = 0°, twist (ψ) = 0° position of the complex. The estimated position is consistent with an orientation predicted elsewhere using an implicit solvent model (22). For consistency, this orientation was also used as the reference position for the Gβγ subunit coordinates alone (as extracted from the GRK2-Gβγ complex).
For the purposes of orientation analysis, the SFG macroscopic observables 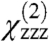 ,
, 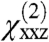 , and
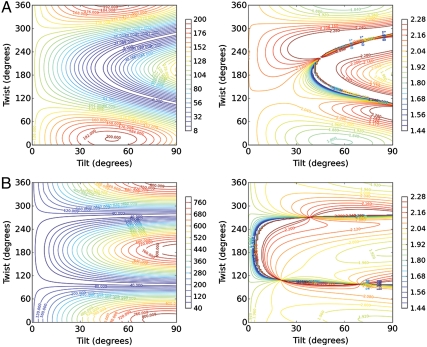
, and  were calculated for all unique combinations of the tilt and twist angles of Gβγ and the GRK2-Gβγ complex (Fig. 3 A and B). Because it is unreasonable to assume that the protein would be upside-down with the geranylgeranyl group far from the bilayer, we have limited the plots to focus on the range of interest (tilt angles 0–90°). It is apparent from the resulting contour plots that many possible combinations of tilt and twist angle can yield computed ratios that are close to the experimentally measured
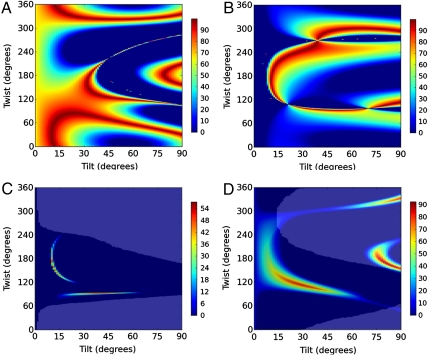
were calculated for all unique combinations of the tilt and twist angles of Gβγ and the GRK2-Gβγ complex (Fig. 3 A and B). Because it is unreasonable to assume that the protein would be upside-down with the geranylgeranyl group far from the bilayer, we have limited the plots to focus on the range of interest (tilt angles 0–90°). It is apparent from the resulting contour plots that many possible combinations of tilt and twist angle can yield computed ratios that are close to the experimentally measured 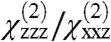 ratio. However, only a subset of these positions are physically reasonable. Many would pull the geranylgeranyl group of Gβγ unreasonably far from the membrane, or force the protein into an orientation that would require a collision with the membrane in order for the geranylgeranyl group at the C terminus of Gγ to insert into the bilayer. The matches between the experimentally measured SFG observables and calculated values (as a function of orientation) are shown in Fig. 4. Interestingly, the results in Fig. 4B show that the experimentally measured
ratio. However, only a subset of these positions are physically reasonable. Many would pull the geranylgeranyl group of Gβγ unreasonably far from the membrane, or force the protein into an orientation that would require a collision with the membrane in order for the geranylgeranyl group at the C terminus of Gγ to insert into the bilayer. The matches between the experimentally measured SFG observables and calculated values (as a function of orientation) are shown in Fig. 4. Interestingly, the results in Fig. 4B show that the experimentally measured 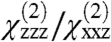 ratio for the GRK2-Gβγ complex does not match the calculated value at the reference position (θ = 0°, ψ = 0°). The nearest high-scoring match is at the position θ = 10°, ψ = 180°. There is, however, a swath of closely related high-scoring orientations with small tilt angles (10–15°) and twists ranging from 120–240°. There is also a narrower stretch of matches in the range from tilt 30–60° and twist of 90°, but in these orientations the PH domain is not positioned such that it can make its expected contacts with the membrane. Our results thus suggest that the most likely orientation of the GRK2-Gβγ complex is such that the bulk of the kinase domain of GRK2 is tilted away from the membrane surface by 10 to 15°. A recent crystal structure of activated G protein-coupled kinase 6 (GRK6) revealed the structure and location of the GPCR receptor docking site of the kinase (23), which is expected to be conserved in GRK2. The residues that constitute this site were disordered in the GRK2-Gβγ structure, and were not considered when defining the reference position. Our SFG results are consistent with a tilt that positions the receptor docking site of GRK2 to interact more efficiently with the cytosolic domain of the GPCR, in a similar orientation to that proposed for activated GRK6.
ratio for the GRK2-Gβγ complex does not match the calculated value at the reference position (θ = 0°, ψ = 0°). The nearest high-scoring match is at the position θ = 10°, ψ = 180°. There is, however, a swath of closely related high-scoring orientations with small tilt angles (10–15°) and twists ranging from 120–240°. There is also a narrower stretch of matches in the range from tilt 30–60° and twist of 90°, but in these orientations the PH domain is not positioned such that it can make its expected contacts with the membrane. Our results thus suggest that the most likely orientation of the GRK2-Gβγ complex is such that the bulk of the kinase domain of GRK2 is tilted away from the membrane surface by 10 to 15°. A recent crystal structure of activated G protein-coupled kinase 6 (GRK6) revealed the structure and location of the GPCR receptor docking site of the kinase (23), which is expected to be conserved in GRK2. The residues that constitute this site were disordered in the GRK2-Gβγ structure, and were not considered when defining the reference position. Our SFG results are consistent with a tilt that positions the receptor docking site of GRK2 to interact more efficiently with the cytosolic domain of the GPCR, in a similar orientation to that proposed for activated GRK6.
Fig. 3.
Contour plots showing the calculated molecular response in the ssp polarization (left), and the predicted ratio of fitted signal strengths χ(∠)zzz/χ(∠)xxz (right) for (A) Gβγ alone, and (B) the GRK2-Gβγ complex.
Fig. 4.
Best matches for (A) the Gβγ zzz/xxz ratio and (B) GRK2-Gβγ complex zzz/xxz ratio (right). Colors indicate the quality of the match (100% = exact). (C) If Gβγ does not reorient, adding a constraint for intensity change yields possible orientations of both Gβγ and the GRK2-Gβγ complex. Using all three available measurements narrows the range of possibilities. (D) Orientation of Gβγ if the orientation of the complex is assumed. Use of two measurements helps to narrow down the best matches. For (C) and (D), matches may be further limited down by adding an additional requirement that the positions of Gβγ be physically as well as mathematically allowed (dark overlay).
Due to the complexity of the molecules studied and the limited number of measurements available, it is not possible to narrow the range of orientations of GRK2-Gβγ to a single unambiguous position. However, the above results demonstrate that in situ measurements can provide more information about protein orientation at a phospholipid bilayer than can be inferred from the crystal structure alone.
Orientation of Gβγ Alone and in the Complex.
Next, we considered whether or not Gβγ must reorient in order to bind GRK2. In the absence of calibrated absolute intensity information, which is challenging to measure accurately, other sources of information are needed to supplement the 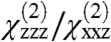 ratio in order to narrow the range of possible orientations. Experimentally, we have observed that signal intensity drops markedly upon formation of the complex (Fig. 2), which is most likely if both Gβγ and the GRK2-Gβγ complex adopt relatively small tilt angles (Fig. 3). This result can be explained in light of the fact that the net SFG response can be thought of as a vector quantity, and signal intensity depends strongly on the relative orientation of the α-helices whose signal dominates the observed spectrum. In the Gβγ subunit, the helical segments are relatively well aligned, and thus SFG signals can be quite strong at low tilt angles. For the GRK2-Gβγ complex, there are more (but less well aligned) helical segments, with a different net orientation that may result in weaker SFG signals for certain orientations. Because the molar amount of membrane associated GRK2-Gβγ should be similar to Gβγ alone, the drop in signal intensity upon formation of the GRK2-Gβγ complex provides an additional constraint that can help to determine the orientation of a single subunit, provided that the orientation of the other subunit can be reasonably assumed.
ratio in order to narrow the range of possible orientations. Experimentally, we have observed that signal intensity drops markedly upon formation of the complex (Fig. 2), which is most likely if both Gβγ and the GRK2-Gβγ complex adopt relatively small tilt angles (Fig. 3). This result can be explained in light of the fact that the net SFG response can be thought of as a vector quantity, and signal intensity depends strongly on the relative orientation of the α-helices whose signal dominates the observed spectrum. In the Gβγ subunit, the helical segments are relatively well aligned, and thus SFG signals can be quite strong at low tilt angles. For the GRK2-Gβγ complex, there are more (but less well aligned) helical segments, with a different net orientation that may result in weaker SFG signals for certain orientations. Because the molar amount of membrane associated GRK2-Gβγ should be similar to Gβγ alone, the drop in signal intensity upon formation of the GRK2-Gβγ complex provides an additional constraint that can help to determine the orientation of a single subunit, provided that the orientation of the other subunit can be reasonably assumed.
We can combine the experimental measurements with the assumption that Gβγ alone has the same orientation as it does in complex with GRK2. Thus, as well as satisfying two  ratios (one each for Gβγ alone and the GRK2-Gβγ complex), the orientation must additionally provide a good match for the signal strength change
ratios (one each for Gβγ alone and the GRK2-Gβγ complex), the orientation must additionally provide a good match for the signal strength change 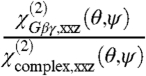 . Alternatively, we can assume that Gβγ alone can adopt an orientation that is distinct from that in the GRK2-Gβγ complex, but that the overall orientation of the entire complex is a fixed, known position (such as the reference orientation shown in Fig. 1). The measured
. Alternatively, we can assume that Gβγ alone can adopt an orientation that is distinct from that in the GRK2-Gβγ complex, but that the overall orientation of the entire complex is a fixed, known position (such as the reference orientation shown in Fig. 1). The measured 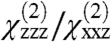 ratio for Gβγ can then be combined with the signal strength change
ratio for Gβγ can then be combined with the signal strength change 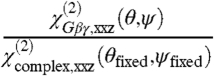 , yielding the possible orientations of the Gβγ subunit in the absence of GRK2.
, yielding the possible orientations of the Gβγ subunit in the absence of GRK2.
If we assume that Gβγ does not reorient upon formation of the complex, two  ratios plus the intensity change can be applied. As shown in Fig. 4C, the range of possible orientations is quite narrow, and even the best match has a score of only ∼60% (for more information on how scores are assigned, refer to Methods). The low scores in this analysis indicate a poor match for all experimental measurements, supporting the hypothesis that Gβγ does not have the same orientation alone as it does when in complex with GRK2. Solutions that are physically plausible (as well as mathematically allowed) are further highlighted using a semitransparent overlay (see SI Text) to indicate the positions where the geranylgeranyl anchoring group of Gβγ is close to the bilayer interface when in complex with GRK2. In this analysis, it appears that the overlay does not eliminate any of the possibilities, but neither does it improve the poor scores of the matches for experimental measurements.
ratios plus the intensity change can be applied. As shown in Fig. 4C, the range of possible orientations is quite narrow, and even the best match has a score of only ∼60% (for more information on how scores are assigned, refer to Methods). The low scores in this analysis indicate a poor match for all experimental measurements, supporting the hypothesis that Gβγ does not have the same orientation alone as it does when in complex with GRK2. Solutions that are physically plausible (as well as mathematically allowed) are further highlighted using a semitransparent overlay (see SI Text) to indicate the positions where the geranylgeranyl anchoring group of Gβγ is close to the bilayer interface when in complex with GRK2. In this analysis, it appears that the overlay does not eliminate any of the possibilities, but neither does it improve the poor scores of the matches for experimental measurements.
If the orientation of the GRK2-Gβγ complex is assumed to be known, our measurements can be used to characterize the orientation of Gβγ. As discussed above, the reference orientation (Fig. 1) was based on a set of presumed membrane-interacting regions, but our measured 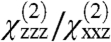 ratio is not consistent with this orientation (Fig. 4B). Based on the likely orientations of GRK2-Gβγ, we revised the assumed position to include a small tilt for the complex (θ = 10°, ψ = 180°), so that the second measurement becomes
ratio is not consistent with this orientation (Fig. 4B). Based on the likely orientations of GRK2-Gβγ, we revised the assumed position to include a small tilt for the complex (θ = 10°, ψ = 180°), so that the second measurement becomes 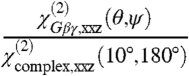 . This new orientation of the complex is reasonable for the purposes of this analysis because other similarly high-scoring orientations that match our experimentally measured
. This new orientation of the complex is reasonable for the purposes of this analysis because other similarly high-scoring orientations that match our experimentally measured 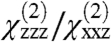 ratio would generally yield similar values of
ratio would generally yield similar values of 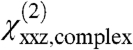 , and therefore would not qualitatively alter the final results (see SI Text for further discussion). The resulting matches produce high scores (> 90%) and physically reasonable positions for Gβγ in terms of the resulting proximity of its geranylgeranyl group with respect to the membrane (Fig. 4D). In this case, considering only physically reasonable positions helps to limit the range of matches. The highest scores are centered around θ = 25°, ψ = 120°), and do not overlap the new assumed position of the GRK2-Gβγ complex. Thus, by either set of assumptions our data indicates that Gβγ will likely alter its orientation upon engaging effectors such as GRK2, which is reasonable because both proteins are expected to form direct interactions with the cell membrane.
, and therefore would not qualitatively alter the final results (see SI Text for further discussion). The resulting matches produce high scores (> 90%) and physically reasonable positions for Gβγ in terms of the resulting proximity of its geranylgeranyl group with respect to the membrane (Fig. 4D). In this case, considering only physically reasonable positions helps to limit the range of matches. The highest scores are centered around θ = 25°, ψ = 120°), and do not overlap the new assumed position of the GRK2-Gβγ complex. Thus, by either set of assumptions our data indicates that Gβγ will likely alter its orientation upon engaging effectors such as GRK2, which is reasonable because both proteins are expected to form direct interactions with the cell membrane.
Conclusions
In this study, we have demonstrated that SFG can be used to study the formation of a multisubunit protein-protein complex in situ. Through the use of multiple constraints and software developed to facilitate SFG data analysis, the orientation of the GRK2-Gβγ complex has been characterized. We find that Gβγ likely reorients by about 15 ° to facilitate binding of GRK2. The GRK2-Gβγ complex orientation differs from the position predicted based on examination of the crystal structure alone, but is consistent with the optimal membrane orientation of the receptor docking site on the GRK2 homolog GRK6. The proposed orientation of Gβγ in the GRK2-Gβγ complex is also compatible with its expected orientation in complex with the heterotrimeric Gα subunit. The Gαβγ heterotrimer (PDB entry 1gp2) can be aligned with Gβγ from the GRK2-Gβγ complex in the specified position (θ = 10°, ψ = 180°) without collisions between the Gα subunit and the expected plane of the membrane (Fig. 5B). As for the docking site of GRK2, this allows the C-terminal helix of Gα, which is typically disordered in crystal structures, to dock productively with the cytoplasmic domain of activated receptors. In principle, SFG can also be used to examine the orientation of βγ in the Gαβγ heterotrimer relative to its position in the GRK2-Gβγ complex.
Fig. 5.
Predicted orientations of Gβγ complexes at phospholipid bilayers. (A) The GRK2-Gβγ complex in a likely membrane orientation, with the expected membrane plane running along the bottom of the box. The receptor docking site of GRK2 was homology modeled based on the structure of GRK6 (PDB entry 3NYN). The small tilt angle suggested by our SFG measurements prevents this newly crystallized region from colliding with the lipid bilayer. (B) The Gαβγ heterotrimer modeled in the same orientation, using Gβγ for alignment. The Gα subunit is shown in blue, and in this orientation it would maintain reasonable contacts with the lipid bilayer.
It is therefore possible to assess protein reorientation upon complex formation using a small set of readily obtainable SFG measurements. Our calculated ratios also show good agreement with both experimental values and physically reasonable positions. In the future, additional measurements can be introduced to yield a clearer and more specific picture of protein orientation for each individual subunit (24). These measurements can include SFG absolute intensities, polarized infrared or higher order spectroscopies, and isotope labeling. The methods presented in this report should be widely applicable to the study of membrane protein binding and orientation in situ.
Methods
SFG Spectroscopy.
Details of the SFG technique and our SFG spectrometer have been described previously (25). In SFG experiments, two laser beams (e.g., a 532 nm visible and a frequency tunable infrared) are overlapped on the sample, generating a signal at the sum frequency (ωvis + ωir = ωsum). Due to the selection rule of this process, signals are only generated in media that lack inversion symmetry, as in the case of surfaces or interfaces. Consequently, SFG provides exceptional submonolayer surface sensitivity and specificity, without the need for background subtraction. Because the SFG process is greatly enhanced by tuning the IR beam over the vibrational resonances of interfacial molecules, the observed peaks correspond to a vibrational spectrum of the interface, and highly surface-specific signals may be produced without the need for exogenous labels. By controlling the polarizations of the input and generated signal beams, information on interfacial molecular orientation can be obtained (15, 16, 26–28). In our experiments, spectra were collected in the ssp and ppp polarization combinations of the sum frequency, visible, and infrared beams, respectively.
SFG Data Analysis.
SFG signal intensity is proportional to the square of the effective second order nonlinear optical susceptibility: 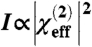 . The effective susceptibility component measured in a given polarization can be obtained by fitting spectra to a Lorentzian lineshape:
. The effective susceptibility component measured in a given polarization can be obtained by fitting spectra to a Lorentzian lineshape:
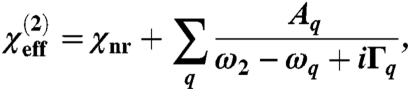 |
[1] |
where ω2 and ωq represent the frequencies of the infrared and qth peak center, respectively, Γq is the damping coefficient, χnr is a constant nonresonant background signal, and Aq is the signal strength. When different polarization combinations of input/signal beams (e.g., ssp or ppp) are used, different components of 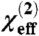 can be determined. The experimentally measured parameters can be related to the actual second order nonlinear optical susceptibility components, which are defined in the lab coordinate system (where z is usually defined as the surface normal and x - y plane is the surface/interface. The x - z plane contains the input and signal beams). Using the near total reflection geometry, we have the relations:
can be determined. The experimentally measured parameters can be related to the actual second order nonlinear optical susceptibility components, which are defined in the lab coordinate system (where z is usually defined as the surface normal and x - y plane is the surface/interface. The x - z plane contains the input and signal beams). Using the near total reflection geometry, we have the relations:
| [2] |
| [3] |
where Lxxz and Lzzz are Fresnel factors that depend on the experimental geometry and indices of refraction of the solution and interface. In this article, we report the fitted 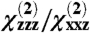 ratio after the correction for Fresnel factors is applied, and error bars are incorporated to consider the effect of uncertainty in Fresnel factors. The fitted
ratio after the correction for Fresnel factors is applied, and error bars are incorporated to consider the effect of uncertainty in Fresnel factors. The fitted 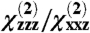 ratio is the principal measurement used for our orientation studies, and it may be measured from the SFG ssp and ppp spectra. The
ratio is the principal measurement used for our orientation studies, and it may be measured from the SFG ssp and ppp spectra. The  ratio is a property of many molecules. To link it to the orientation of an individual molecule, the hyperpolarizability tensor for a single molecule must first be calculated based on knowledge of the functional group or molecule, as described below. Then, the orientation of the molecule may be characterized by relating the response of a single molecule to the response measured in the lab coordinate system. The orientation of a surface functional group or molecule can be characterized by either one tilt angle θ (e.g., in case of a single α-helix) or tilt and twist angles θ and ψ, respectively, (e.g., in the case of a β-sheet or a complicated protein). The rotations corresponding to these angles are shown in Fig. 1. In this study, we focused our data analysis on the α-helical amide I peak observed at ∼1,652 cm-1, which dominates the spectra for Gβγ alone (29) and for the GRK2-Gβγ complex. The signals from β-sheet regions were too weak to be analyzed.
ratio is a property of many molecules. To link it to the orientation of an individual molecule, the hyperpolarizability tensor for a single molecule must first be calculated based on knowledge of the functional group or molecule, as described below. Then, the orientation of the molecule may be characterized by relating the response of a single molecule to the response measured in the lab coordinate system. The orientation of a surface functional group or molecule can be characterized by either one tilt angle θ (e.g., in case of a single α-helix) or tilt and twist angles θ and ψ, respectively, (e.g., in the case of a β-sheet or a complicated protein). The rotations corresponding to these angles are shown in Fig. 1. In this study, we focused our data analysis on the α-helical amide I peak observed at ∼1,652 cm-1, which dominates the spectra for Gβγ alone (29) and for the GRK2-Gβγ complex. The signals from β-sheet regions were too weak to be analyzed.
The GRK2-Gβγ complex contains 31 helical segments (20), and, consequently, analyzing the molecular orientation relies on determining the combined response for all α-helices in the protein (10, 13, 29–31). The net α-helical hyperpolarizability, βprotein, can be determined based on the length and relative orientations of all helical segments in the known crystal structure (PDB entry 1omw), so long as the protein conformation remains unchanged (as in the case of GRK2-Gβγ). The α-helical segments were assigned using the dictionary of secondary structure prediction (DSSP) algorithm as implemented in the UCSF Chimera molecular visualization program (32). For the purposes of this analysis, two angles were used to describe the orientation of the helical segments: the tilt angle (relative to the +z axis) and the azimuthal angle (derived from the rotation matrix for a vector along the helix backbone, 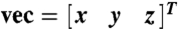 and calculated according to the formula
and calculated according to the formula 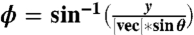 ). The third Euler angle, ψ (representing twist) was ignored due to the cylindrical symmetry of each single α-helix.
). The third Euler angle, ψ (representing twist) was ignored due to the cylindrical symmetry of each single α-helix.
The hyperpolarizability tensor elements for each individual α-helical segment of known residue length were calculated according to the bond additivity model described previously (15). This model incorporates experimentally measured values of the dipole moment and polarizability tensor, and has been shown to produce good agreement with FTIR (33) and NMR (28) studies on simple α-helical peptides. Each of the 27 elements of the combined hyperpolarizability tensor for the entire protein was then calculated as the sum of the response for each individual helix, using a rotation of the axis system to place the z-aligned helical segment into the protein coordinate frame according to the angles calculated above.
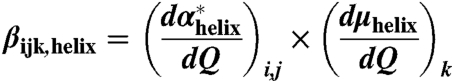 |
[4] |
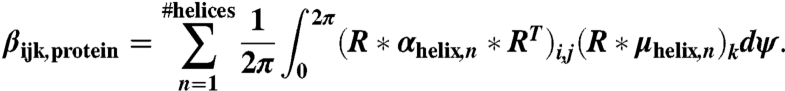 |
[5] |
In the equation above, R represents the Euler rotation matrix in the zyz convention:
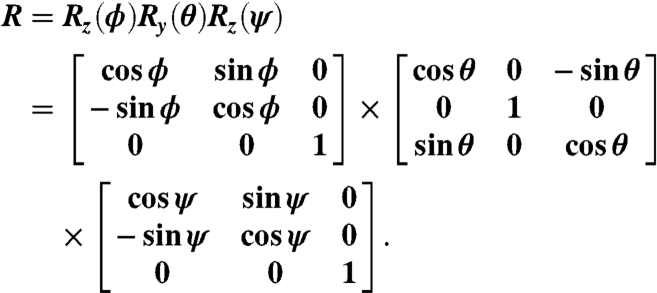 |
[6] |
The tilt angle θ and the twist angle ψ for a protein are defined according to Eq. 6. This method was also used to calculate βprotein for Gβγ, which contains four helical segments.
As discussed above, the SFG surface susceptibility component ratio (e.g., 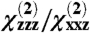 ratio) is related to the hyperpolarizability and orientation of the protein. Quantitatively, the SFG surface susceptibility tensor was calculated by rotating a single molecule into the lab coordinate frame and assuming that all molecules were randomly distributed in the plane of the surface (azimuthal angle ϕ):
ratio) is related to the hyperpolarizability and orientation of the protein. Quantitatively, the SFG surface susceptibility tensor was calculated by rotating a single molecule into the lab coordinate frame and assuming that all molecules were randomly distributed in the plane of the surface (azimuthal angle ϕ):
 |
[7] |
For the amide I vibration, there are two SFG-active vibrational modes to be considered: the A and E1 modes. The peak centers for these two modes are very close and cannot be separated within the resolution of our SFG spectrometer. Consequently the total response from each vibrational mode (as calculated above) must be added together to obtain the experimentally observed value:
| [8] |
Using these relations,  and
and  can be calculated as a function of the protein orientation (tilt and twist angles). The observed signal intensity depends on the number of molecules at the surface, but this dependence cancels when the ratio
can be calculated as a function of the protein orientation (tilt and twist angles). The observed signal intensity depends on the number of molecules at the surface, but this dependence cancels when the ratio 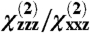 is taken- hence, the ratio is a particularly useful parameter for orientation analysis.
is taken- hence, the ratio is a particularly useful parameter for orientation analysis.
Software for Data Analysis.
The required calculations become prohibitively complex as the size of the protein to be studied increases. Consequently, we have developed a set of Python scripts to perform the required calculations. Our program allows for rapid analysis of any arbitrary protein structure from the Protein Databank (PDB), based on signals from α-helical regions. Unlike a previous study of the Gβγ subunit (29), variations in helix length are explicitly treated in this calculation. As a result, the results of this calculation produce SFG signal strength ratios (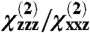 ) for orientation analysis, and also make it possible to compare observed signal intensities across different protein samples or subunits. The latter feature provides the potential for additional constraints that can be used to more uniquely assign molecular orientation (see Results).
) for orientation analysis, and also make it possible to compare observed signal intensities across different protein samples or subunits. The latter feature provides the potential for additional constraints that can be used to more uniquely assign molecular orientation (see Results).
The software performs four tasks. Each script is modular and can be run at any time after the previous step. Repeating the analysis does not require repeating all steps.
First, the protein is oriented into an initial reference position, as described in SI Text. Although this step is not required, it can be helpful for interpreting results. Second: relative to the reference orientation, the length and orientation of each helical segment is determined. The resulting information is saved to a csv file that describes the protein structure.
In the third step, SFG experimental observables are calculated. Good computational performance can be ensured by precalculating the symbolic algebraic forms of Eqs. 5 and 7. By removing the slow numerical integration step, significant performance gains were seen vs. a reference implementation in a commercial mathematical software package. Our program employs the Matplotlib library to produce high quality plots, and the boxes of Fig. 3 were prepared directly from images generated in this step. The raw output was also saved in a text-based format that can be readily imported into other programs for analysis. Fourth and finally, calculated SFG observables were compared to experimental measurements, as described below. We are currently working to extend this software to calculate experimental observables for other vibrational spectroscopies, such as attenuated total reflectance Fourier transform infrared spectroscopy (ATR-FTIR).
Given the complexity of the system studied, and the sensitivity to small experimental errors, multiple solutions must be considered. We have therefore developed a set of heat map style plots to display all orientations for which calculated values fall within ± 10% of the measured Gβγ 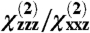 ratio (equivalent to about ± 20% of the measured intensity ratio), and ± 25% of the observed signal strength
ratio (equivalent to about ± 20% of the measured intensity ratio), and ± 25% of the observed signal strength 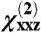 change between the measurements for Gβγ and GRK2-Gβγ. These plots display a score assigned based on how close the calculated value at the nth datapoint was to each experimental (target) value, within the specified % tolerance (“tol”):
change between the measurements for Gβγ and GRK2-Gβγ. These plots display a score assigned based on how close the calculated value at the nth datapoint was to each experimental (target) value, within the specified % tolerance (“tol”):
 |
[9] |
All orientations for which any criterion was not met were assigned a score of 0 by default. Scores were calculated independently for all criteria, and the final quality of the match at that point was determined as the product of i criteria, 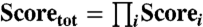 (where a score of 100% indicates that the orientation in question yields an exact match for all target values). This visual approach provides a simple way to incorporate experimental error estimates, while providing an easy-to-peruse summary of the most likely allowed orientations.
(where a score of 100% indicates that the orientation in question yields an exact match for all target values). This visual approach provides a simple way to incorporate experimental error estimates, while providing an easy-to-peruse summary of the most likely allowed orientations.
Supplementary Material
Acknowledgments.
The authors are grateful to Dr. R. J. Lefkowitz (Duke University) for cell pellets containing GRK2 and Gβγ. We would also like to acknowledge B. Bucholz for conducting the flow cytometry protein interaction assays to measure binding between GRK2 (or GRK2-R587Q) and Gβγ. This work was supported by National Institutes of Health (NIH) Grant GM081655 and Office of Naval Research (ONR) Grant N00014-08-1-1211 (to Z.C.), and by NIH grants HL071818 and HL086865 (to J.T.).
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
See Author Summary on page 15019.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1108236108/-/DCSupplemental.
References
- 1.Neves SR, Ram PT, Iyengar R. G protein pathways. Science. 2002;296:1636–1639. doi: 10.1126/science.1071550. [DOI] [PubMed] [Google Scholar]
- 2.Sprang SR, Chen Z, Du X. Structural basis of effector regulation and signal termination in heterotrimeric Gα proteins. Adv Protein Chem. 2007;74:1–65. doi: 10.1016/S0065-3233(07)74001-9. [DOI] [PubMed] [Google Scholar]
- 3.Tesmer JJG, Sunahara RK, Gilman AG, Sprang SR. Crystal structure of the catalytic domains of adenylyl cyclase in a complex with Gsα*GTPγS. Science. 1997;278:1907–1916. doi: 10.1126/science.278.5345.1907. [DOI] [PubMed] [Google Scholar]
- 4.Waldo GL, et al. Kinetic scaffolding mediated by a phospholipase C-β and Gq signaling complex. Science. 2010;330:974–980. doi: 10.1126/science.1193438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Scheerer P, et al. Crystal structure of opsin in its G-protein-interacting conformation. Nature. 2008;455:497–502. doi: 10.1038/nature07330. [DOI] [PubMed] [Google Scholar]
- 6.Pitcher JA, et al. Role of βγ subunits of G proteins in targeting the β-adrenergic receptor kinase to membrane-bound receptors. Science. 1992;257:1264–1267. doi: 10.1126/science.1325672. [DOI] [PubMed] [Google Scholar]
- 7.Dupre DJ, Robitaille M, Rebois RV, Hebert TE. The role of Gβγ subunits in the organization, assembly, and function of GPCR signaling complexes. Annu Rev Pharmacol Toxicol. 2009;49:31–56. doi: 10.1146/annurev-pharmtox-061008-103038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tesmer VM, Kawano T, Shankaranarayanan A, Kozasa T, Tesmer JJG. Snapshot of activated G proteins at the membrane: the Gαq-GRK2-Gβγ complex. Science. 2005;310:1686–1690. doi: 10.1126/science.1118890. [DOI] [PubMed] [Google Scholar]
- 9.Wang J, et al. Detection of amide I signals of interfacial proteins in situ using SFG. J Am Chem Soc. 2003;125:9914–9915. doi: 10.1021/ja036373s. [DOI] [PubMed] [Google Scholar]
- 10.Wang J, Paszti Z, Even MA, Chen Z. Interpretation of sum frequency generation vibrational spectra of interfacial proteins by the thin film model. J Phys Chem B. 2004;108:3625–3632. [Google Scholar]
- 11.Chen X, Wang J, Sniadecki JJ, Even MA, Chen Z. Probing α-helical and β-sheet structures of peptides at solid/liquid interfaces with SFG. Langmuir. 2005;21:2662–2664. doi: 10.1021/la050048w. [DOI] [PubMed] [Google Scholar]
- 12.Weidner T, Apte JS, Gamble LJ, Castner DG. Probing the orientation and conformation of α-helix and β-strand model peptides on self-assembled monolayers using sum frequency generation and NEXAFS spectroscopy. Langmuir. 2010;26:3433–3440. doi: 10.1021/la903267x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen X, Wang J, Boughton AP, Kristalyn CB, Chen Z. Multiple orientation of melittin inside a single lipid bilayer determined by combined vibrational spectroscopic studies. J Am Chem Soc. 2007;129:1420–1427. doi: 10.1021/ja067446l. [DOI] [PubMed] [Google Scholar]
- 14.Chen X, Sagle LB, Cremer PS. Urea orientation at protein surfaces. J Am Chem Soc. 2007;129:15104–15105. doi: 10.1021/ja075034m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nguyen KT, Le Clair SV, Ye S, Chen Z. Orientation determination of protein helical secondary structures using linear and nonlinear vibrational spectroscopy. J Phys Chem B. 2009;113:12169–12180. doi: 10.1021/jp904153z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nguyen KT, King JT, Chen Z. Orientation determination of interfacial β-sheet structures in situ. J Phys Chem B. 2010;114:8291–8300. doi: 10.1021/jp102343h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fu L, Ma G, Yan EC. In situ misfolding of human islet amyloid polypeptide at interfaces probed by vibrational sum frequency generation. J Am Chem Soc. 2010;132:5405–5412. doi: 10.1021/ja909546b. [DOI] [PubMed] [Google Scholar]
- 18.Carman CV, et al. Mutational analysis of Gβγ and phospholipid interaction with G protein-coupled receptor kinase 2. J Biol Chem. 2000;275:10443–10452. doi: 10.1074/jbc.275.14.10443. [DOI] [PubMed] [Google Scholar]
- 19.Chen Z, Shen YR, Somorjai GA. Studies of polymer surfaces by sum frequency generation vibrational spectroscopy. Annu Rev Phys Chem. 2002;53:437–465. doi: 10.1146/annurev.physchem.53.091801.115126. [DOI] [PubMed] [Google Scholar]
- 20.Lodowski DT, Pitcher JA, Capel WD, Lefkowitz RJ, Tesmer JJG. Keeping G proteins at bay: a complex between G protein-coupled receptor kinase 2 and Gβγ. Science. 2003;300:1256–1262. doi: 10.1126/science.1082348. [DOI] [PubMed] [Google Scholar]
- 21.Lodowski DT, et al. The role of Gβγ and domain interfaces in the activation of G protein-coupled receptor kinase 2. Biochemistry. 2005;44:6958–6970. doi: 10.1021/bi050119q. [DOI] [PubMed] [Google Scholar]
- 22.Lomize MA, Lomize AL, Pogozheva ID, Mosberg HI. OPM: orientations of proteins in membranes database. Bioinformatics. 2006;22:623–625. doi: 10.1093/bioinformatics/btk023. [DOI] [PubMed] [Google Scholar]
- 23.Boguth CA, Singh P, Huang CC, Tesmer JJG. Molecular basis for activation of G protein-coupled receptor kinases. EMBO J. 2010;29:3249–3259. doi: 10.1038/emboj.2010.206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang J, Paszti Z, Clarke ML, Chen X, Chen Z. Deduction of structural information of interfacial proteins by combined vibrational spectroscopic methods. J Phys Chem B. 2007;111:6088–6095. doi: 10.1021/jp070383o. [DOI] [PubMed] [Google Scholar]
- 25.Wang J, Chen C, Buck SM, Chen Z. Molecular chemical structure on Poly(methyl methacrylate) (PMMA) surface studied by Sum Frequency Generation (SFG) vibrational spectroscopy. J Phys Chem B. 2001;105:12118–12125. [Google Scholar]
- 26.Lambert AG, Davies PB, Neivandt DJ. Implementing the theory of sum frequency generation vibrational spectroscopy: a tutorial review. Applied Spectroscopy Reviews. 2005;40:103–145. [Google Scholar]
- 27.Shen YR. Surface properties probed by second-harmonic and sum-frequency generation. Nature. 1989;337:519–525. [Google Scholar]
- 28.Nguyen KT, et al. Probing the spontaneous membrane insertion of a tail-anchored membrane protein by sum frequency generation spectroscopy. J Am Chem Soc. 2010;132:15112–15115. doi: 10.1021/ja106508f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chen X, Boughton AP, Tesmer JJG, Chen Z. In situ investigation of heterotrimeric G protein βγ subunit binding and orientation on membrane bilayers. J Am Chem Soc. 2007;129:12658–12659. doi: 10.1021/ja075542w. [DOI] [PubMed] [Google Scholar]
- 30.Perry JM, Moad AJ, Begue NJ, Wampler RD, Simpson GJ. Electronic and vibrational second-order nonlinear optical properties of protein secondary structural motifs. J Phys Chem B. 2005;109:20009–20026. doi: 10.1021/jp0506888. [DOI] [PubMed] [Google Scholar]
- 31.Moad AJ, et al. NLOPredict: visualization and data analysis software for nonlinear optics. J Comput Chem. 2007;28:1996–2002. doi: 10.1002/jcc.20706. [DOI] [PubMed] [Google Scholar]
- 32.Pettersen EF, et al. UCSF Chimera—a visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 33.Nguyen KT, Le Clair SV, Ye S, Chen Z. Molecular interactions between magainin 2 and model membranes in situ. J Phys Chem B. 2009;113:12358–12363. doi: 10.1021/jp904154w. [DOI] [PMC free article] [PubMed] [Google Scholar]