Rapid and Quantitative Imaging of Excitation Polarized Fluorescence Reveals Ordered Septin Dynamics in Live Yeast

Abstract

We report an imaging method for fast, sensitive analysis of the orientation of fluorescent molecules by employing a liquid-crystal based universal polarizer in the optical path of a wide-field light microscope. We developed specific acquisition and processing algorithms for measuring the anisotropy and for correcting artifacts caused by fluorescence bleaching, background light, and differential transmission of optical components. We call this approach the Fluorescence LC-PolScope and we used it to analyze the architectural dynamics of septin-green fluorescent protein (septin-GFP) constructs in the neck region of budding yeast. We describe three different states of highly anisotropic septin arrays in which the prevailing orientation of GFP dipoles was either parallel or perpendicular to the mother-bud axis. The transitions between these ordered states were characterized by transient isotropic states. To analyze the patterns of polarized fluorescence, we modeled the alignment of septin-GFP constructs in different stages of septin ring formation. Based on our model, our experimental data are consistent with the formation of paired rather than single filaments and the axis of the α-helical septin terminus linked to a GFP molecule is likely oriented normal to the cell surface. The Fluorescence LC-PolScope combines the molecular specificity of fluorescence tagging with the structural specificity of polarized light analysis.

Introduction

The anisotropy of fluorescence has its origin in the polarized excitation and emission of single fluorophores. In addition to the chemical specificity due to the specific binding of fluorophores to target molecules, polarized fluorescence provides structural specificity due to the reporting of a preferred orientation of the fluorophores and their targets. As a fluorophore binds to its target molecule, the spatial orientation of the fluorophore and its target become correlated, with the strength of the correlation depending on the rigidity of the molecular linker. In microscopy, the anisotropy of fluorescence (also referred to as fluorescence polarization or polarized fluorescence) has been used to analyze molecular properties and dynamics, such as rotational diffusion (1), molecular binding (2,3), and order-disorder transitions of protein domains (4,5), in in vitro systems and inside living cells. (To avoid confusion with an established method in chemistry, we do not use the term fluorescence anisotropy.)

We describe a method to rapidly and comprehensively record the quasistatic patterns of anisotropy due to the binding of fluorophores to a molecular scaffold that remains static over a timescale of seconds, but might dynamically remodel over minutes and longer. For optimizing the efficiency, we use a wide-field microscope with polarized excitation and recording of all emitted fluorescence, without a polarization filter in the imaging path. Complete polarization analysis is accomplished with a liquid-crystal based universal polarizer that switches the excitation light between four linear polarization states, each rotated by 45°. Subsequently, image arithmetic operations generate maps of anisotropy at a spatial resolution commensurate with the microscope optics used. A map of anisotropy of fluorescence was typically generated in 3 to 5 s, depending on the camera exposure time (typ. 0.6 to 1 s per image). Importantly, this technique can be adapted to a variety of wide-field fluorescence microscopes with only moderate investment.

We have developed and applied the method of measuring the anisotropy of fluorescence for determining the organization of cytoskeletal proteins, called septins, at the cell cortex. The septins are a family of GTP-binding proteins important for many cell processes, including cytokinesis and exocytosis through their ability to act as membrane diffusion barriers and as protein scaffolds (6–8). Septin misregulation is implicated in human neurological disorders such as Alzheimer's and Parkinson's diseases and various cancers (9–12). In vitro, septins can be induced to form linear polymers (13), however it is unclear if and how septin proteins form ordered arrays of filaments within cells. In budding yeast, higher-order septin structure is thought to be tightly linked to filament formation (14), though in other eukaryotes this correlation is not yet clear (6,15). Therefore, modular tools to detect ordered arrays of septins in cells would have wide applications for many researchers and the utility of polarized fluorescence extends to the in vivo analysis of diverse cellular structures.

Structural insights into septin organization in yeast bud necks were recently obtained by analysis of polarized fluorescence of GFP molecules rigidly linked to septin proteins (16,17). In these studies, the method of recording the polarized fluorescence required the step-by-step rotation and image acquisitions of the sample located between fixed, parallel polarizers. Subsequently, the images were registered by hand and analyzed for fluorescence anisotropy. Although this pioneering study gave new insights into the septin alignment in the hourglass and ring structures at the yeast bud neck, the slow nature of the image acquisition and analysis method limited its application to relatively static processes and limited numbers of cells.

For interpreting the spatial and temporal patterns of polarized fluorescence recorded at high resolution, we developed a mathematical model to predict such patterns based on specific properties of the septin filament, its alignment in the hourglass and split ring assemblies, and on excitation and emission properties of the GFP dipole moment. Important results of the modeling effort point to the formation of paired septin filaments for building higher-order septin structures in living yeast, and to the general statement that the symmetry properties of paired filaments always align the anisotropy of fluorescence either parallel or perpendicular to the filament axis, regardless of the exact orientation of the fluorescent dipole that is attached to a septin monomer.

Thus, by combining our experimental and modeling results, we establish firm evidence for paired septin filaments that form higher-order structures in the yeast bud neck made of filaments that run either parallel or perpendicular to the mother-bud axis, including a 90° turn of the filaments during splitting at cytokinesis. Our approach of high-resolution imaging and modeling of polarized fluorescence can be more broadly applied to analyze other macromolecular assemblies where there is some basic structural information available.

Materials and Methods

See the Supporting Material.

Results

Microscope setup

For measuring the anisotropy of fluorescent specimens we used an upright, transilluminating microscope stand (Fig. 1 a, see also Materials and Methods in the Supporting Material). After passing through the interference filter (482/18 nm), the polarization of the excitation light was controlled by a liquid-crystal based universal compensator, which was operated as a variable polarizer. The LC-compensator/polarizer is built from a fixed linear polarizer and two variable retarder plates, made from liquid crystal devices A and B (18). The linear polarization state of light passing through the initial polarizer is subsequently modified by the two liquid crystal devices whose retardance can be independently set to a range of values. This enables the LC-polarizer to transmit any desired polarization, including linear polarizations of different orientations (19). For our measurements, the LC-polarizer was sequentially set to transmit four linear polarization states, each characterized by its angle with respect to the horizontal axis in specimen space. The procedure employed for calibrating the LC-polarizer is described in the Supporting Material.

Figure 1.

Polarized fluorescence measurement scheme. (a) Diagram of transilluminating excitation (blue) and fluorescence emission (green) light path. The universal polarizer is made of a linear polarizer, and liquid crystal elements LC-A and LC-B that are used to rotate the linear polarization. (b) Graph of fluorescence intensity measured in an image point of a GFP crystal (solid circles) versus the angle of linear polarization of the excitation light. The solid line represents the best fit using expression (1), resulting in an anisotropy ratio I_max/I_min = 4.0 and an azimuth = 81°, which coincides with the crystal's long axis orientation. (c) GFP crystal fluorescence I₀, I₄₅, I₉₀, and I₁₃₅ recorded using excitation light of four polarization angles. The fluorescence of the crystals is strongly polarized parallel to the needle axis. Bottom row are ratio and azimuth images computed using image arithmetic based on expressions (2) to (4) in the text. Note that in the bottom left image the ratio is shown to be near 1 (dark) inside the framed region where two crystals cross each other, whereas in the same region, shown enlarged in the right image, the average fluorescence is nearly doubled. In the right image the average fluorescence is overlaid with blue lines indicating the azimuth orientation. The ratio and azimuth values in pixels with near zero average fluorescence (background) are strongly affected by shot noise and are therefore not reliable and blackened using a mask that was generated based on the average image.

Expressions for computing the anisotropy of fluorescence

Our acquisition and analysis routine is based on the observation that the anisotropy of fluorescence is manifested in a sinusoidal variation of the fluorescence intensity as a function of the angle of the transmission axis of a linear polarizer or analyzer (20) (Fig. 1 b). For our analysis of partially oriented septin-GFP constructs, we chose the configuration of polarized excitation and the recording of fluorescence without polarization analyzer. This configuration enables a higher efficiency of fluorescence excitation and detection, compared to a setup that uses unpolarized excitation and polarization analysis of the emitted fluorescence. Although the algorithms for measuring the anisotropy are the same for both configurations, the detection of all emitted fluorescence in the first configuration assures the highest possible efficiency, low bleach rate, and least photo-damage to the sample.

For the same reasons we did not employ a third configuration that uses both, polarized excitation and polarization analysis of the emitted fluorescence. Although this configuration promises higher polarization ratios (20), it suffers from lower efficiency because of the presence of an analyzer in the emission path. Furthermore, the expected functional form of the fluorescence intensity versus polarizer/analyzer angle is a sum of a cosine square and cosine fourth power term (20), making the acquisition and analysis algorithms more complex and further lowering the efficiency. In the Supporting Material, we make a detailed comparison between the relative standard deviations of intensity ratios measured with a setup that uses a single polarizer in the excitation pass versus a setup with two parallel polarizers, one in the excitation and one in the emission path.

When using a polarizer in the excitation and no analyzer in the emission path, the emitted fluorescence intensity I versus polarizer angle ϕ is described by

$$I=\frac{\left(I_{\text{max}}+I_{\text{min}}+(I_{\text{max}}-I_{\text{min}})\text{cos}\left(2\left(\phi -\text{azimuth}\right)\right)\right)}{2}.$$ (1)

The polarization ratio = $I_{\text{max}}/I_{\text{min}}$ is affected by several factors, including the anisotropy of the individual fluorophores, their mutual alignment, and their inclination with respect to the microscope axis. In addition, the ratio is reduced with increasing NA of the excitation and emission optics. The azimuth, on the other hand, represents the axis of net alignment of the fluorophores as projected into the plane perpendicular to the microscope axis. With respect to a laboratory frame of reference, the azimuth can be any angle and will depend on the orientational constraint imposed on the fluorophores by their fusion proteins and the orientation distribution of the septin molecules after incorporation into a larger molecular complex.

We determined the anisotropy of fluorescence based on intensities measured in images recorded at four specified polarizer angles (I₀ through I₁₃₅, Fig. 1 c). Subsequently, image arithmetic is used to calculate the anisotropy for each camera pixel using the following expressions:

$$\mathit{a}=\left({\mathit{I}}_0-{\mathit{I}}_{90}\right),\mathit{b}=\left({\mathit{I}}_{45}-{\mathit{I}}_{135}\right),\mathit{c}=\left({\mathit{I}}_0+{\mathit{I}}_{45}+{\mathit{I}}_{90}+{\mathit{I}}_{135}\right),$$ (2)

$$\text{anisotropy}=\frac{\sqrt{a^2+b^2}}{c},\text{ratio}=\frac{{\mathit{I}}_{\max }}{{\mathit{I}}_{\min }}=\frac{1+2\text{anisotropy}}{1-2\text{anisotropy}},$$ (3)

$$\text{azimuth}=\frac{1}{2}\arctan \left(\frac{b}{a}\right).$$ (4)

When implemented as image arithmetic operations, these expressions generate maps that represent pixel-by-pixel computed anisotropy, ratio, and azimuth values, all at the same spatial resolution as the original intensity images.

The measured anisotropy, ratio, and azimuth values were subject to systematic errors introduced by fluorescence bleaching, superposition of fluorescence from different cell structures or compartments, and differential transmission of optical components in the microscope. To minimize the influence of these systematic errors on our measurements, we have developed calibration and correction procedures described in the Supporting Material.

Polarized fluorescence of GFP crystals

For calibrating the measured orientation of polarized fluorescence, we used the highly anisotropic fluorescence of GFP crystals prepared by dialyzing GFP extracted from Aequorea victoria against deionized water (see the Supporting Material). For these crystals it is well established that the total fluorescence is up to six times higher when the polarization of the excitation light is oriented parallel to the long crystal axis compared to perpendicular to the axis (20). Because of the thin, needle-shaped morphology of the crystals, they represent effective test objects for calibrating the azimuth angle of polarized fluorescence (Fig. 1 c).

Polarized fluorescence of septin-GFP constructs in the yeast bud neck

We applied the Fluorescence LC-PolScope to examine septin organization in Saccharomyces cerevisiae cells where septins were initially discovered and have been most thoroughly analyzed by both conventional fluorescence and polarized fluorescence approaches. Fig. 2 shows differential interference contrast images of four different stages of a budding yeast cell and corresponding fluorescence images of the Cdc12-GFP constructs incorporated into the septin structures at the bud neck. Cdc12 is one of the five septins expressed in vegetative yeast cells and is essential for higher-order assembly. Septins initially form as a patch or ring at the site where a new bud emerges. The patch transitions to form an hourglass shape that remains fixed at the mother-bud neck as the bud emerges. The hourglass persists until splitting at cytokinesis, generating one ring located each in the mother and the bud cell. We analyzed the hourglass and split ring from the top, with the mother-bud axis parallel to the image plane, and in cross section, with the mother-bud axis perpendicular to the image plane.

Figure 2.

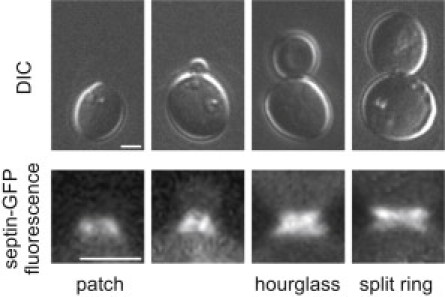
Differential interference contrast and fluorescence images of budding yeast cell (S. cerevisiae), illustrating stages of the budding process and the associated septin structures. The progression from the appearance of first septin patch, transition from patch to hourglass, hourglass and split ring structures are shown. Dim fluorescence filling the cell volume is cytosolic septin-GFP.

Examples of the raw data acquired using polarized excitation of a yeast strain expressing Cdc12 fused to a constrained GFP are shown in Fig. 3 a, and have been packaged for viewing as QuickTime movies (in the Supporting Material) in Movies S1 and S2. In the cross-section view the septin hourglass structure projects as a ring of fluorescence, whereas in the top view it projects as a near-rectangular shape, with fluorescence enhanced near the edges that are parallel to the mother-bud axis (Fig. 3). Both views reveal a preferred orientation of the GFP dipoles perpendicular to the mother-bud axis and tangential to the cell surface, indicative of a highly ordered septin organization. All cells imaged showed these same characteristics, indicating that the septin hourglass consistently assembles in the same highly ordered manner (N > 50 cells).

Figure 3.

Polarized fluorescence of GFP-labeled septin hourglass structure in budding yeast. (a) Polarized fluorescence of GFP attached to septin molecules (Cdc12) lining the bud neck. Viewing direction is either perpendicular (top panels, top view) or parallel to mother-daughter axis (bottom panels, cross-section view). As reported by Vrabioiu (16), in both cases the fluorescence is polarized perpendicular to the mother-daughter axis, as evidenced by the fluorescence intensity modulated by the polarization orientation of the excitation light (double arrows and angles). (b) Polarization ratios (left column) and averaged fluorescence with azimuth lines (right column) indicating the excitation polarization resulting in maximum fluorescence. Gray values in the panels on the left show fluorescence ratio values, while panels on the right represent the fluorescence intensity averaged over the four polarizer angles. The orientation of the short blue lines represents the azimuth value whereas the strength of the anisotropy is expressed by the line length of being proportional to the ratio. Scale bars are 1 μm.

We extended the polarization analysis to the transition periods of septin assemblies going to hourglass and from an hourglass to split ring configurations. Fig. 4 a shows the anisotropy of septins as they initially assemble and the bud emerges. Notably, even the nascent septin patch is anisotropic, indicating the septins are likely polymerized into filaments or at least ordered in some fashion at assembly. The azimuth measured in the patch is parallel to the future mother-bud axis in contrast to the hourglass, which possesses prevailing dipole orientations perpendicular to the axis (Figs. 3 and 4 b). In the transition between the highly anisotropic patch and hourglass states there is a substantial decrease in anisotropy. Similarly, as displayed in Fig. 4 b top, a decrease in anisotropy occurs during the transition from the hourglass to the split ring assembly. In the top view, the split ring is again highly anisotropic but, in contrast to the hourglass, the azimuth is parallel to the mother-daughter axis. Throughout the budding process, including the transition periods, the distribution of total fluorescence remains localized near the bud neck, indicating that septin molecules remain closely associated with this region. Thus, although the hourglass has an azimuth that is perpendicular to the mother-daughter axis, the preceding phase (patch) and subsequent phase (split ring) have azimuths that are parallel to the mother-daughter axis. In cross section the ring is strongly anisotropic with an azimuth parallel to the membrane for Cdc12-conGFP4, which has four amino acids trimmed from the C-terminus of Cdc12 and three amino acids trimmed from the N-terminus of GFP (Figs. 3 b and 4 b, cross section), however in this view the split ring structure does not redevelop significant anisotropy, after it was lost during the transition period.

Figure 4.

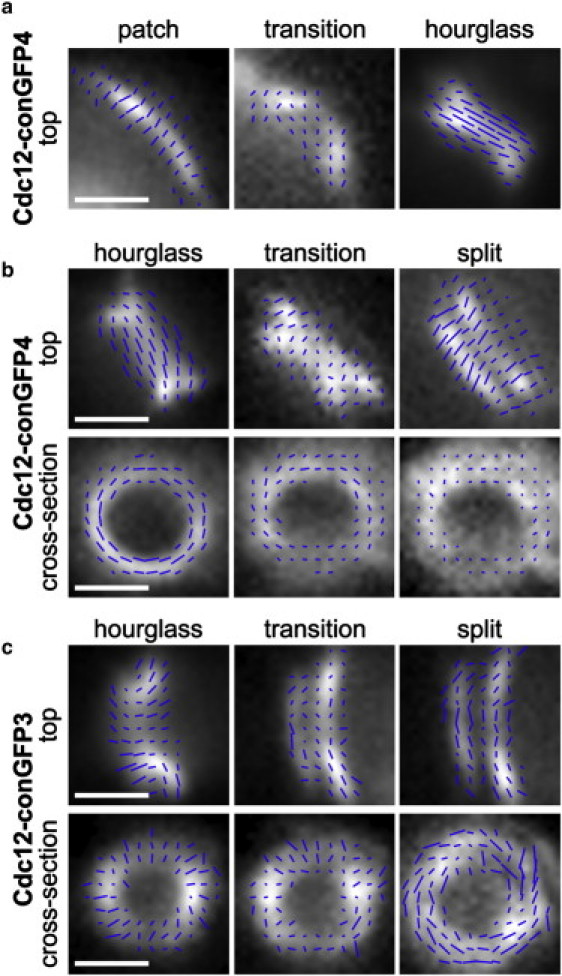
Polarized fluorescence of septin structures formed at different stages of the budding process. (a) Top views from left to right in septin rings incorporating Cdc12-conGFP4: The fluorescence of the initial septin patch is polarized perpendicular to the cell surface and parallel to the developing mother-daughter axis. During the transition from patch to hourglass the fluorescence anisotropy is temporarily lost, but reappears in the hourglass structure, this time with the preferred polarization aligned perpendicular to the mother-daughter axis. (b) During the hourglass to split ring transition the anisotropy for Cdc12-conGFP4 is lost again, only to reemerge a third time in the split rings, with the dominant polarization changed again to align parallel to the mother-daughter axis. Cross-section views of the hourglass incorporating Cdc12-conGFP4: the transition from hourglass to split ring and the split ring structure, with the projected fluorescence appearing ring-shaped for each of the structures. In this viewing direction, the fluorescence of the hourglass is highly anisotropic with the preferred polarization tangential to the ring. However, the anisotropy is lost during the hourglass to split ring transition and does not reappear, even in the late stages of the budding process. (c) In septin rings incorporating Cdc12-conGFP3, the transition of the state of the protein organization mirrors that of the Cdc12-conGFP4 construct, except that the orientations are measured to be perpendicular to what is seen in b. The same moments of isotropy are also observed during the transition states, but in contrast to b, the split ring incorporating Cdc12-conGFP3 reestablishes anisotropy with the polarization aligned parallel to the cell cortex.

We next used a different constrained septin-GFP fusion construct to determine if the specific number of amino acids deleted to constrain the GFP would change the azimuth that we measured. In theory, changing the length of the alpha helix connection between septin and GFP by one amino acid could shift the orientation of the GFP relative to the septin by as much as 100° (17). Strikingly, when these same transitions and ring states are observed using Cdc12-conGFP3 (which differs by the presence of one additional amino acid of the Cdc12 sequence so that there are three amino acids missing from the Cdc12 at the junction between the septin and the GFP), the opposite azimuth patterns are seen. The patch possesses anisotropy perpendicular to the eventual mother-bud axis (data not shown) and the hourglass azimuth is parallel to the axis (Fig. 4 c, top). In the top view, anisotropy is lost as the hourglass transitions to a split ring and the split rings are strongly anisotropic with an azimuth oriented perpendicular to the mother-bud axis (Fig. 4 c). In the cross-section view, Cdc12-conGFP3 rings have an azimuth that is oriented perpendicular to the cell cortex in contrast to the Cdc12-conGFP4, which are parallel to the membrane in cross section (Fig. 4 c). Cdc12-conGFP3 containing septin rings undergo a brief period of transition where anisotropy is lost. However, anisotropy is regained in cross section after ring splitting and the prevailing orientation has switched from being perpendicular to the cell cortex to tangential to it. In summary, for two different constructs, we observed three stages with stable anisotropy (patch, hourglass, and split rings) that are separated by transition periods, during which the anisotropy nearly vanishes (Fig. 4).

Both the Cdc12-conGFP3 and four fusion protein constructs were analyzed for their dipole orientations at the top, middle, and bottom of the septin hourglass from the top view perspective. The fluorescence azimuth and the anisotropy values do not change when the focus is moved from the top to the bottom of the assemblies (Fig. 5). This similarity in orientation at the top and bottom is examined further in the modeling below (Fig. 6). Interestingly, while imaging in the middle of the hourglass (Fig. 5), two different effects were observed. For fusion protein Cdc12-conGFP4 there is a noticeable decrease of anisotropy at the edges of the septin ring as compared to the middle. This is not the case when the same section is imaged in septin rings integrating Cdc12-conGFP3. In those rings, the anisotropy remains high at the edges and clearly follows the curvature of the septin hourglass. The origins of this effect are explored in depth by modeling potential septin filament organizations.

Figure 5.

The orientation of Cdc12-conGFP3 or Cdc12-conGFP4 constructs incorporated into septin rings do not differ appreciably as the same ring is imaged at the top, middle, or bottom of the structure. The central (less curved) region remains perpendicular to the mother-bud axis for the Cdc12-conGFP4 construct while the central region remains consistently parallel to the mother-bud axis for the Cdc12-conGFP3 fusion protein. Notably, the character of the dipole distribution along the edges of the septin does differ between these two constructs. The anisotropy measured at the edge of septin rings incorporating Cdc12-conGFP4 greatly decreases compared to the central region, which does not occur in septin rings incorporating the Cdc12-conGFP3 construct. The increasing blur when focusing from top to bottom is attributed to the increasing thickness of the water layer between coverslip and object plane, as the high NA, oil-immersion objective is focused deeper into the specimen.

Figure 6.

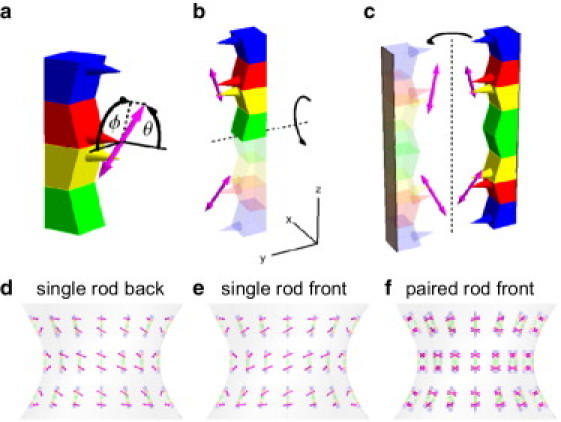
Schematics illustrating the model of septin filaments and their arrangements in the yeast hourglass. (a) Four septin molecules (Cdc3, Cdc10, Cdc11, and Cdc12) form a heterogeneous halfrod, with cones indicating α-helical termini. The terminus of Cdc12 (red) is connected to a GFP molecule with a transition dipole shown in magenta. The dipole orientation is given by angles θ and ϕ in a frame affixed to the septin rod. (b) Two halves form an apolar septin rod in which the two halves are related by a 180° rotation. (c) Two rods related by another 180° rotation form a paired rod. The paired rod is shown with two surfaces (dark rectangles) that have the potential to form associations with a membrane. (d–f) Single and paired rods arranged in an hourglass viewed from the top in an orthographic projection that only shows the front or back surfaces of the hourglass. Note the tilt of the dipoles in the front view of the single rod projection in d. In e the tilt is flipped with respect to the vertical when projecting the back surface. For paired rods the projection of the front and back surface are identical. Note the horizontal orientation of the average dipole moment near the center of the hourglass. However, dipoles near the left and right edge of the hourglass, average out to near zero anisotropy. (The graphical representation and nomenclature of septin rods are similar to those used in (13)).

Except during transitions, the septins appear highly ordered and arranged so that the net alignment of GFP dipoles is either parallel or perpendicular to the mother-bud growth axis and tangential or radially oriented relative to the membrane. The ability of septins to self-assemble into filaments makes it highly likely that order is derived from polymers and potentially restrained by the polymers associating with the membrane. Such filaments could either be in a paired state as seen in vitro for purified septins or unpaired state as individual polymers, potentially bundled together. Paired and unpaired polymers have different numbers of symmetry axes and therefore based on the anisotropy we detect, we should be able to make specific predictions about the state of the polymer. To systematically evaluate the possible outcomes of different septin organizations that can give rise to the consistent anisotropy patterns we measure, we developed a mathematical model to simulate different possible arrangements of septin-GFP dipoles.

Theoretical model

The characteristic patterns of anisotropy observed in the bud neck region at different stages of the budding process led us to develop a mathematical model that allowed us to predict the anisotropy of various fluorophore alignments based on established features of septin assemblies and absorption characteristics of single dipole moments. By comparing the results of the mathematical model with measured patterns of anisotropy, we address the still open question about the building blocks of the hourglass and split ring assemblies in the yeast bud neck: Are the prevailing building blocks single septin filaments or paired ones that have been shown to exist in vitro (13,21).

Septins in budding yeast form heteromeric, apolar filaments composed of septin rods (protofilaments) that can assemble into single and paired filaments (13). As illustrated in Fig. 6, the graphics, which were inspired by illustrations in Bertin et al., half of a septin rod is composed of four different septin molecules (Fig. 6 a), whereas a full septin rod is composed of two halves that are related by 180° rotations (Fig. 6 b). Single filaments form when multiple rods assemble end to end. Paired filaments are composed of two single filaments whose positions are related by another 180° rotation (Fig. 6 c). Current evidence in vitro suggests that filaments pair in register with one another (13).

In our model, the orientation of GFP dipoles was set by two angles θ and ϕ that were measured in a coordinate system affixed to the septin rod. Because of the rotational symmetries between GFP molecules and their predicted environments in a single or paired filament, the orientations of the dipoles are expected to have a fixed relationship and all orientations can be expressed as a function of only θ and ϕ. Hence, we calculated the anisotropy patterns of uniformly aligned septin filaments as a function of the angles θ and ϕ and of the projections of the filament assemblies.

The organization of septin filaments in the living cell is still controversial. However, there is strong evidence from previous measurements of polarized fluorescence (16,17,22) that in the hourglass assembly the average orientation of filaments is parallel to the bud neck axis. In Fig. 6, d–f, we show orthographic projections of single and paired filaments oriented parallel to the bud neck axis and dipoles that are oriented diagonally when projected in the top view. Panel d of Fig. 6 shows single filaments with dipoles that are located on the hourglass surface that is facing the observer. Panel e shows the back surface for the same arrangement, illustrating the flip in diagonal orientation when considering the back versus the front surface. The projections of paired filaments, however, are identical for the back and for the front surface of the hourglass (Fig. 6 f) and their net orientations are aligned either parallel or perpendicular to the mother-bud axis. More generally, because of the symmetry properties of paired filaments, their polarized fluorescence is oriented always parallel or perpendicular to the prevailing filament alignment, regardless of the GFP dipole orientation characterized by angles θ and ϕ. This makes polarized fluorescence a strong predictor for filament alignment, albeit with a 90° ambiguity. Furthermore, as indicated in the caption to Fig. 6 f, the projected dipole moments averaged over small areas near the edge versus the center of the hourglass exhibit characteristic variations that can be used to further elucidate the alignment of filaments and their GFP dipoles.

In addition to three-dimensional, graphical representations of septin molecules and GFP dipoles (see also Fig. S3), we also computed the expected patterns of anisotropy for orthographic projections of hourglass and split ring assemblies in the top and cross-section view. These patterns were calculated and graphically represented using a Mathematica Notebook (Wolfram Research, Champaign, IL) that we developed. Calculations were based on the absorption characteristics of single dipoles and their incoherent superposition to simulate populations of GFP molecules located within an optically resolved area of the specimen. More details on the calculation are available in the Supporting Material.

We computed anisotropy patterns for all septin assembly types and projections that we examined experimentally. As an example, Fig. 7 shows a map of anisotropy patterns for paired filaments in an hourglass assembly in the top view. Additional examples are shown in Fig. S4 and Fig. S5. For all hourglass patterns in Fig. 7, filaments were aligned in the plane of the cell membrane and parallel to the projection of the hourglass axis in the membrane plane. Each orthographic hourglass projection corresponds to a microscope image with a depth of focus extending over the size of the hourglass. When examining the map in Fig. 7, we find that θ values smaller than 45° align dipoles more perpendicular to the cell membrane and computed anisotropies are aligned perpendicular to the cell surface, regardless of ϕ values. However, for θ > 45°, changing ϕ alters the orientation of anisotropies from parallel to perpendicular to the cell surface.

Figure 7.

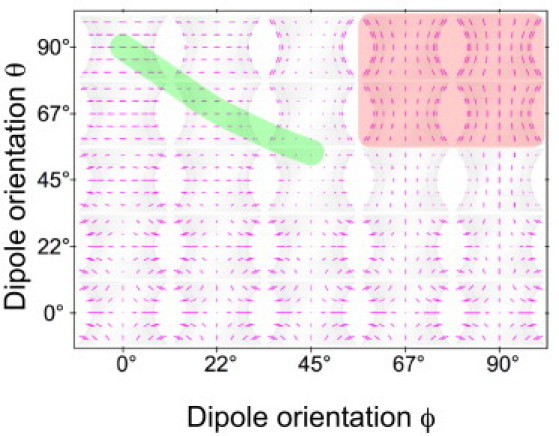
Grid of calculated anisotropy patterns of hourglass septin assemblies in top view as a function of GFP dipole orientations. A single value pair {θ, ϕ} defines the prevailing dipole orientations of septin-GFP constructs in an hourglass. Each hourglass in the grid shows the calculated pattern of anisotropies, which are represented by short magenta lines whose lengths are proportional to the fluorescence ratio and whose orientations are parallel to the polarization that exhibits the strongest fluorescence. The center position of each hourglass in the grid indicates the {θ, ϕ} pair used in the calculation. Patterns for θ or ϕ values larger than 90° would repeat the patterns shown. The red rectangle corresponds to {θ, ϕ} values that lead to anisotropy patterns that are compatible with measured patterns of the Cdc12-conGFP3 construct, whereas CDC12-conGFP4 results are compatible with {θ, ϕ} values associated with the green strip. The latter patterns have two characteristic features: 1), the anisotropy is aligned horizontally throughput the hourglass, and 2), near the left and right edge of the hourglass the anisotropy value goes to zero (ratio = 1). For the calculation, paired filaments were assumed to run parallel to the hourglass axis.

In Fig. 7, {θ, ϕ} values outlined in green result in anisotropy patterns that are compatible with our experimental patterns recorded with Cdc12-conGFP4 constructs (Figs. 3–5). Specifically, both experimental and computed patterns show anisotropy lines that are perpendicular to the hourglass axis throughout the assembly, and the anisotropy vanishes toward the left and right edge of the hourglass. {θ, ϕ} values outlined in red, on the other hand, are compatible with experimental patterns recorded with Cdc12-conGFP3 constructs (Figs. 4 and 5).

We also examined the effect of reorienting the filaments with respect to the hourglass axis. When aligning the filaments perpendicular instead of parallel to the hourglass axis, the anisotropy patterns shown in Fig. 7 are reversed with respect to their association with values of ϕ. A pattern that was associated with ϕ is now associated with 90°-ϕ, or specifically the patterns outlined in green switch their anisotropy lines from perpendicular to the hourglass axis to parallel to the axis. This same switch is observed experimentally when transitioning from hourglass to split ring assembly. Accordingly, the experimental observation is compatible with a reorientation of the paired filaments from parallel to perpendicular to the mother-bud axis.

Finally, we refer to our experimental observation of split ring assemblies incorporating Cdc12-conGFP4 constructs that did not regain measurable anisotropies. Based on our model calculations, this observation favors a dipole orientation characterized by values near 45° for both θ and ϕ, further restricting the range of {θ, ϕ} value pairs compatible with our experiments.

Discussion

Measurement of polarized fluorescence

We report measurements of polarized fluorescence for which we used a liquid-crystal based universal compensator/polarizer in the optical path of the microscope. The universal polarizer is part of a commercial instrument called the LC-PolScope and is manufactured by CRi, now part of Caliper in Hopkinton, MA. When part of the LC-PolScope for measuring birefringence, the universal compensator is used to generate near-circularly polarized light for illuminating the specimen. For measuring polarized fluorescence, we modified the software controlling the liquid crystal device to generate linearly polarized excitation light. For either use, the universal compensator/polarizer is placed in the same position in the illumination path of a wide-field, transmitted light microscope. Other optical components include carefully selected interference filters. For measuring polarized fluorescence, the excitation and emission filters restrict the band paths of the illuminating and imaging light to the wavelength range required by the fluorophore, with an eye on low cross talk and high efficiency (see Materials and Methods in the Supporting Material). Because of its similarity to the LC-PolScope in hardware components and software features, we call the scheme to measure polarized fluorescence introduced here the Fluorescence LC-PolScope.

The algorithms for image acquisition and processing were based on four polarization states of the excitation light and no polarization analysis of the emitted light. Instead of analyzing two orthogonal polarization states, as is often done in fluorescence polarization measurements (23,24), we used four polarization states to unambiguously measure the prevailing orientation of fluorophores assembled into a higher order protein structure.

We report anisotropy measurements based on polarized excitation, although the emitted fluorescence is recorded without a polarization analyzer. It is interesting to note that this approach avoids complications associated with Förster resonance energy transfer between like fluorophores (homo-FRET), which can affect the magnitude and orientation of anisotropy of the emitted fluorescence (25). Homo-FRET only affects the anisotropy of the emission process, and does not significantly alter the total amount of fluorescence, nor does it change the anisotropy of the absorption process. As pointed out by Rosell and Boxer (26), even in the closely packed system of a GFP crystal, the dipole absorption events occur in an oriented ideal gas of transition moments that are minimally influenced by neighboring moments. If, on the other hand, one is interested in the occurrence of homo-FRET in a specimen, it seems possible to make that analysis by comparing the anisotropy measured using polarized excitation, as in our approach, versus measuring the anisotropy of the emitted florescence when using unpolarized excitation.

Statistical errors in our fluorescence images are dominated by shot noise due to photon statistics. To reduce shot noise to an acceptable level, we used exposure times of around 0.3–1 s, long enough to achieve noise levels of a few percent of signal in the raw images. This signal/noise ratio enabled us to measure anisotropy ratios as low as 1.1, where 1 represents isotropy.

Theoretical modeling

Calculated patterns that are compatible with our measurements are associated with high θ values (60° < θ < 90°) that orient the dipole moments more parallel to the hourglass surface (see Fig. 7). Furthermore, the difference in dipole alignment between the two constructs Cdc12-conGFP3 and -conGFP4 is mostly expressed through a change in ϕ by ∼45°, i.e., a rotation around the surface normal.

As suggested by the work of Bertin et al., filament pairs seem to form by overlapping α-helical termini, forming a coiled coil configuration and reducing the protein surface that can interact with the cell membrane. In Fig. 6 c we chose the surface that is apposed to the α-helical termini to associate with the membrane and assumed the orientation of the α-helices to be normal to the cell surface. This choice was guided by the observation that reducing the α-helical linker by one amino acid seemed to have rotated the GFP dipole around an axis that is normal to the cell surface. The approach of systematically reducing the α-helical linker between septin and GFP was taken previously by Vrabioiu and Mitchison to determine symmetry properties of the filaments that represent the building blocks of the higher order septin assemblies (17). With the enhanced measurement system described here and a more detailed model of the filament structure available now, this approach will provide the unique opportunity to determine the preferred orientation of specific α-helices inside a living cell.

Septin organization in the yeast bud neck

The modeling combined with the experimental data support the conclusions that septins are highly ordered at the neck, that the major transitions between different organizations are coincident with isotropic states, and that the order is likely generated from paired filaments rather than single filaments. Ideally, the modeling would also be able to distinguish between paired filaments running either parallel or perpendicular to the mother-bud axis but these data alone do not enable a clear distinction. A parallel study we performed in a filamentous fungus with a different septin assembly than yeast combined with the use of a septin polymerizing drug, however, lead us to favor an arrangement where the majority of paired septin filaments run parallel to the mother-bud axis (22). Importantly, however, the existence of a smaller population of filaments running orthogonally to this majority population cannot be completely discounted as they would not be explicitly detected but rather would simply serve to diminish the strength of the polarization ratios measured. Higher resolution, single molecule imaging of orientational constrained fluorescent proteins should serve to determine if subpopulations of differently oriented filaments exist. Similarly, the basis for the isotropic transition is not clear nor is it possible, with this resolution of imaging, to know if the reestablished anisotropy after the transitions is due to a complete rotation of polymers, a rearrangement of the C-terminal ends of the proteins, or new polymerization of filaments in a different orientation. Future work examining how individual molecules behave during this transition should distinguish between these options.

Conclusion

We report a method for detecting anisotropy that provides rapid, sensitive, and quantitative observation and analysis that can be applied to dynamic structures in living cells. The ability to detect order in the septin cortex using light microscopy is a key step in establishing the mechanisms by which septin filaments assemble into higher-order structures and ultimately function in the diverse cell types in which they are found. The portability, speed, and sensitivity of this technique enable the future examination of septins in different cell types and various mutant or perturbed background strains.